全景图像能够反映摄影位置360°球型范围内的所有景致,避免了一般图像视角单一,不能带来全方位感受的缺憾,已在无人驾驶汽车 (unmanned vehicle)、街景地图 (street view) 和虚拟现实 (VR) 等领域中得到广泛应用[1-5],尤其自2014年Facebook收购Oculus VR以来,VR技术得到极大推广,众多科技公司适时推出自己获取全景图像的VR设备,如2015年谷歌和GoPro联合开发完成的16拼全景相机Google Jump以及2016年Facebook发布的14拼全景相机Surround 360等。目前通过多相机拼接的方式获取全景图像成为主流,多相机图像拼接可将一系列有重叠区域的普通图像或鱼眼图像进行拼接获得全景图,在此过程中,关键的问题是各相机图像间的无缝拼接[6]。目前的拼接方法多通过提取图像重叠区域中特征点或特征线的方式寻找相邻图像间的最佳变换[7-10],如文献[11]用SURF算法提取特征点,实现月表图像的无缝镶嵌;文献[12]用SIFT算法提取细胞图像特征点,实现显微全景图的无缝拼接;文献[13]提出利用彩色空间变换和Contourlet变换结合对比度金字塔分解的图像融合算法,实现了全景图拼接的光学配准;文献[14]使用4个具有高纹理特征的种子点,快速建立更准确的图像对应关系;文献[15]模拟苍蝇复眼的视觉机制,在满足实时性的同时较好地解决了全景拼接错位的问题。
通过求解单应矩阵对图像进行变换获取全景图像会破坏成像中的共线条件,使拼接后的全景图像难以精确进行摄影测量中的三维重建等工作;目前全景图像主要为了满足人眼的视觉要求,但通过对全景图像的量测获取地物的真三维信息等应用也变得越来越重要[16-20]。因此,利用成像时多拼相机的几何关系进行拼接正成为研究的热点,该方式不改变成像中的共线条件,使拼接后全景图像易于进行量测。本文提出一种柱面全景图像拼接方法并对其进行仿真分析,该方法基于摄影测量共线方程,设定拼接相机的数目、成像焦距、成像位置和成像姿态,模拟多拼相机的成图过程,构建从三维点云到二维图像的柱面成像方程,通过成像方程不仅可以实现各图像的全景拼接,而且可对影响全景图像拼接精度的各参数进行定量分析。
1 全景图像拼接本文提出的柱面全景图像拼接方法包括柱面投影成像模型和柱面全景图像拼接两部分。柱面投影成像模型是通过设定拼接相机的个数、成像焦距、成像位置和成像方位,利用三维点云模拟生成柱面投影图像;柱面全景图像拼接是根据相机的个数及姿态计算各影像拼接线位置进行全景图的拼接。成像模型中涉及的参数有:拼接相机个数N,成像位置XS、YS、ZS,成像方位α、β、γ和焦距f(为简化成像模型,各相机摄影中心重合,后文会对不重合的情况进行讨论)。
相机个数 (N):N个相机平均分布于同一平面,各相机的视场角 (FOV) 为2π/N。
成像位置 (XS、YS、ZS):各拼接相机摄影中心重合,XS、YS、ZS为摄影中心的三维坐标。
成像方位 (α、β、γ):α、β、γ为成像时的姿态参数,α为绕X轴旋角,β为绕Y轴旋角,γ为绕Z轴旋角。
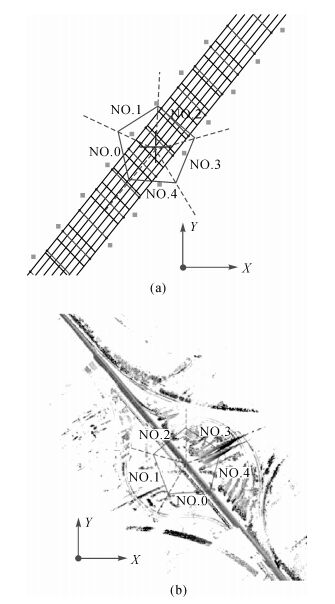
如图 1(a)所示,试验数据Ⅰ为模拟道路点云,模拟道路周边环境,生成路面、路桩、路边护栏、道旁树和顶部护栏等几种地物点云,为易于分析拼接效果,将面状地物采用线型表示,如路面点云表示为格网;在此,顶部护栏点云的作用是分析拼接方法对顶部地物的拼接效果,模拟道路长度为650 m,约有185万点;如图 1(b)所示,试验数据Ⅱ为真实道路点云,车载点云数据位于上海市区沈海高速某段,试验道路长度为1.15 km,约有800万点,点云中包含路面、道旁树、路崖线、广告牌、指示牌等道路附属物。

|
| 图 1 试验数据Ⅰ和试验数据Ⅱ Fig. 1 Test data-set Ⅰ and test data-set Ⅱ |
1.1 柱面投影成像模型
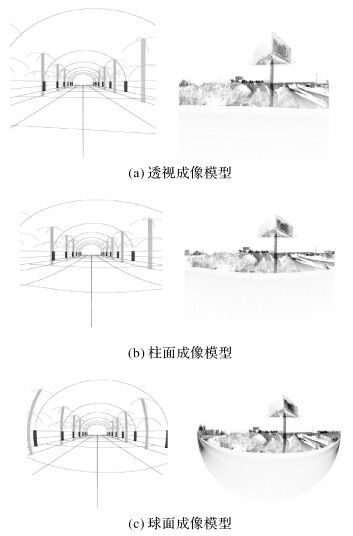
柱面投影图像可以通过对透视图像或鱼眼图像做进一步处理得到。下面分别对透视成像,柱面成像和球面成像的原理进行分析,最后得出3种成像模型之间的转换关系。
(1) 透视成像模型:透视成像模型基于共线方程,但常用共线方程式的投影面为水平面,而全景相机要求投影面为垂直面,因此在透视成像模型中须调整原共线方程旋转矩阵中参数的位置,如式 (1) 所示,在该透视模型中X轴垂直于投影平面
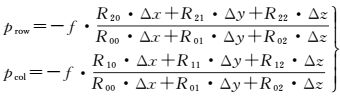 (1)
(1)
式中,R=RX·RY·RZ;Δx=p.x-XS;Δy=p.y-YS;Δz=p.z-ZS,且
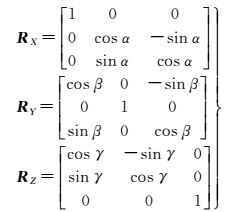
式中,p.x、p.y、p.z为点p的三维坐标;XS、YS、ZS为摄影中心三维坐标;f为摄影焦距;α、β、γ为成像时的姿态参数;prow、pcol为点p在透视投影图像坐标系中的坐标。
(2) 柱面成像模型:柱面成像模型是在透视成像模型基础上对Y(Z) 坐标值进行球面投影,对Z(Y) 坐标值保持不变的一种变换,如式 (2) 所示
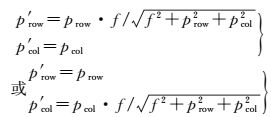 (2)
(2)
式中,p′row、p′col为点p在柱面投影图像坐标系中的坐标,其余参数含义与上文相同。
(3) 球面成像模型:球面成像模型是在透视成像模型的基础上同时对Y和Z坐标值做球面投影,如式 (3) 所示
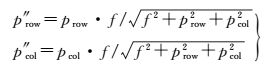 (3)
(3)
式中,p″row、p″col为点p在球面投影图像坐标系中的坐标,其余参数含义与上文相同。
分析上述3种成像模型可知,透视投影相机获取的平面图像和鱼眼相机获取的球面投影图像均可通过计算得到柱面图像;式 (1) 至式 (2) 即为透视图像到柱面图像的变换过程,由球面投影图像到透视投影图像的公式可由式 (3) 推算,如式 (4) 所示
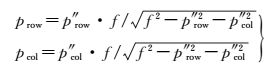 (4)
(4)
分别对数据Ⅰ模拟道路点云和数据Ⅱ真实道路点云采用透视模型,柱面模型和球面模型的方式成像,图 2显示了对上述3种模型的成像结果。
|
| 图 2 3种投影方式在数据Ⅰ和数据Ⅱ中的成像 Fig. 2 Different projection imaging of Test data-set Ⅰ and Test data-set Ⅱ |
1.2 柱面全景图像拼接
柱面全景图像拼接是对各相机获取的柱面投影图像进行拼接,具体拼接步骤为:
(1) 设定拼接相机的数目N,各相机平均分布,因此每个相机的有效视场角为2π/N。将起始相机设为0号相机,其柱面成像方程见式 (1) 和式 (2);1号相机与0号相机相邻,顾及刚体特性,1号相机姿态仅是在0号相机姿态基础上继续绕Z轴旋转2π/N,所以两相机的柱面成像方程中仅旋转矩阵R不同,1号相机的旋转矩阵设为R1
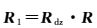 (5)
(5)
式中
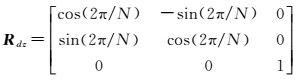
以此类推,可得到第n个相机成像方程中的旋转矩阵Rn
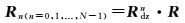 (6)
(6)
(2) 相机成像大小 (row·col),采用对Z值方向做球面投影的柱面成像方式,保持Y值透视投影不变,因此各相机图像与拼接后的全景图像高 (Z方向/row) 均为2倍焦距,可将垂直方向180°内的地物全部投影;图像宽 (Y方向/col) 由焦距f和相机个数N共同决定,以4拼相机为例:
如图 3所示,No.0—No.3分别表示4个均匀分布的拼接相机,各相机焦距为f,视场角均为2π/4,由此可知拼接后全景图的宽度
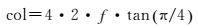 (7)
(7)
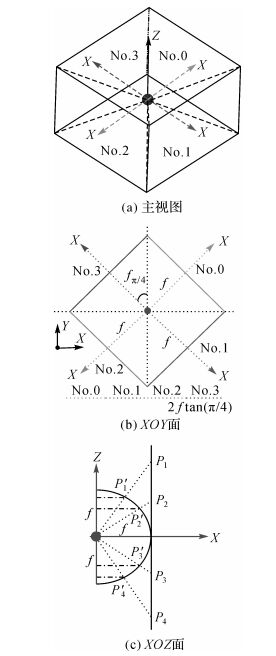
|
| 图 3 4拼相机拼接示意 Fig. 3 Schematic diagram of 4 spell camera |
因此,n拼相机全景图的大小可表示为
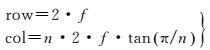 (8)
(8)
(3) 各相机图像拼接,将获取的各透视图像或鱼眼图像按式 (1)—式 (4) 转换为柱面投影图像,然后以像主点为中心点,分别截取Row=2f,Col=2f·tan (π/n) 大小的矩形区域逐次进行拼接。
如图 4所示,按上述全景图像拼接方法,分别使用透视、柱面成像模型获取5拼相机的全景图,其中数据Ⅰ中的焦距f1=600像素,数据Ⅱ中的焦距f2=800像素,α、β为0°,即俯仰角和翻滚角为0°,γ为道路轴线方向,成像位置 (XS, YS, ZS) 在道路中间区域,参考实际成像情况,将摄影高度设为距离地面2 m位置,在所有成像参数已知的情况下即可对获取的各相机图像进行拼接。在此分别对数据Ⅰ和数据Ⅱ进行试验,比较透视图像和柱面图像拼接全景图的差异。
|
| 图 4 5拼相机模拟成像示意 Fig. 4 5 spell camera simulation imaging |
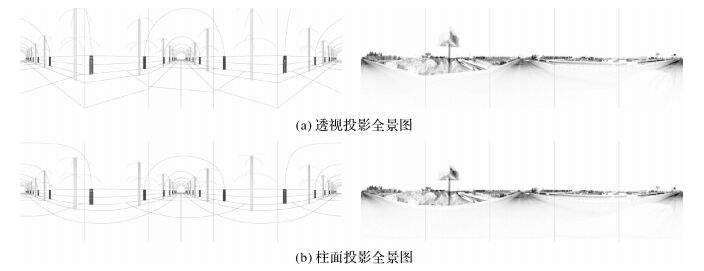
由图 5可知,采用透视投影的方式在相邻相机拼接处会出现地物连续但不平滑的拼接痕迹;采用柱面的投影方法,在高程上 (Z值) 进行球面压缩,不改变水平面内X/Y的中心投影方式,可以在不使用顶部相机的情况下,由单相机获取垂直面内180°的图像,还可达到平滑拼接缝的目的,由此可获得较为完美的全景拼接图;球面投影的图像拼接全景图需对拼接处做较复杂的处理容易破坏全景图的可量测性[21-22],因此柱面成像模型是一种简单可行的全景拼接模型。
|
| 图 5 5拼相机的透视投影和柱面投影全景图 Fig. 5 5 spell camera center/cylindrical panoramic stitching |
2 拼接方法的适用性分析
为检验柱面全景拼接方法的适用性,本节将该方法用于分析全景拼接中的两个问题:一是拼接相机数目对全景拼接的影响;二是倾斜成像对全景拼接的影响。对第一个问题,分别试验不同数目相机的全景拼接效果;对第二个问题,试验在倾斜成像情况下的全景拼接效果;最后,通过对试验结果的讨论验证拼接方法的适用性。
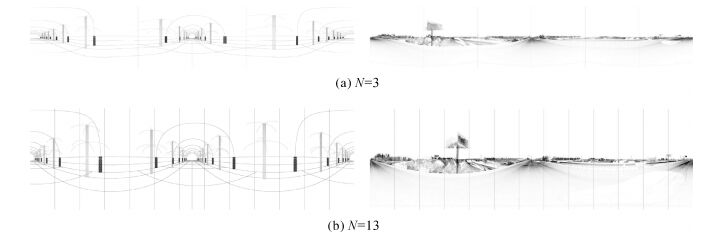
2.1 拼接相机的数目拼接后全景图像的大小由相机数目N和焦距f共同决定,按式 (8) 可计算出数据Ⅰ和数据Ⅱ在不同拼接数目下的成像大小,如表 1所示。使用柱面全景图像拼接方法,选择相机数目为3和13两种情况下的全景图进行分析,其余成像参数与上文相同。
| N | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Col1 | 6234 | 4792 | 4350 | 4152 | 4032 | 3968 | 3924 | 3880 | 3872 | 3840 | 3822 | 3808 | 3810 | 3808 |
| Col2 | 8310 | 6392 | 5810 | 5532 | 5390 | 5296 | 5238 | 5180 | 5148 | 5136 | 5122 | 5096 | 5100 | 5088 |
由图 6可知,不同数目的相机拼接出的全景图像在平滑度上存在较大差异,随着相机数目的增多,全景图像越加平滑,也更加符合人眼视觉的要求。上述试验验证了柱面拼接方法在多拼相机数目选择上的适用性,但均是在多拼相机平均分布于水平面的条件下,下面对多拼相机倾斜成像的情况 (α、β不为0) 进行试验。
|
| 图 6 不同数目相机的全景拼接 Fig. 6 Panorama stitching in different number of cameras |
2.2 倾斜成像全景拼接
全景成像要求多拼相机平面尽量处于水平位置,但不可避免会存在倾斜成像的情况,因此需要试验该拼接方法在倾斜成像下的全景拼接效果。顾及多拼相机整体为不可变的刚体结构,倾斜角对各个相机的影响具有相关性,不失一般性,设0号相机的姿态角α、β分别为10°,γ为道路轴线方向,其余相机的姿态角可由式 (6) 计算得到,以下分别列出数据Ⅰ和数据Ⅱ在5拼相机时的全景图。
由图 7中数据Ⅰ和数据Ⅱ在不同倾斜条件下的拼接结果可知,在存在较大倾角的情况下采用本文提出的柱面投影成像模型和柱面全景拼接方法仍可以获得拼接效果较好的全景图,证明该拼接方法在倾斜成像下的适用性。

|
| 图 7 不同倾斜角下的全景拼接 Fig. 7 Panorama mosaic in inclined condition |
3 拼接方法的容差性分析
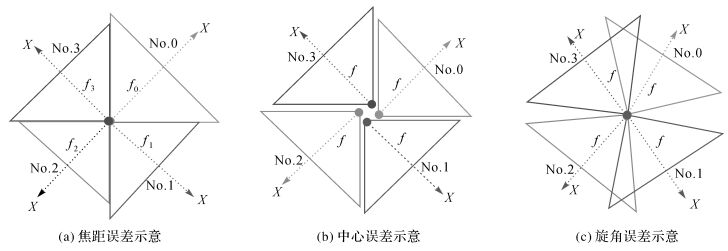
上文提出一种基于柱面成像模型的全景图像拼接方法,并验证了该方法在相机数目选择及倾斜成像下的适用性,但均建立在无误差的基础上;如图 8所示,实际中由于全景相机在生产、组装等过程中,各相机焦距难以保证完全一致,各摄影中心也不会重合,类似的误差均会影响全景图像的拼接效果[23-25],因此,本节讨论各类误差下的全景拼接效果,对柱面全景拼接方法进行容差性分析。以下将利用柱面成像方程,分别从焦距误差、中心误差和旋角误差3方面对拼接效果的影响进行理论推导及试验分析。
|
| 图 8 误差示意 Fig. 8 Diagram of parameter error |
利用柱面投影成像方程,可以推导出各参数误差df、dXS、dYS、dZS、dα、dβ、dγ对像点坐标的影响,推导过程如下:令式 (1) 中
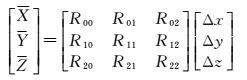 (9)
(9)
则柱面投影成像方程可化简为
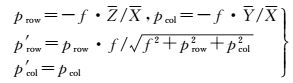 (10)
(10)
对式 (10) 求偏导,获得p′row、p′col关于f、XS、YS、ZS、α、β、γ 7个参数的误差方程式,通过计算可知p′row、p′col关于各参数的误差dp′row、dp′col为
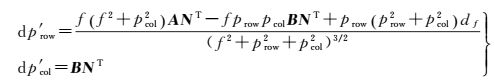 (11)
(11)
式中

式 (11) 为柱面全景图像拼接方法的误差方程,由式 (11) 可知,图像坐标误差dp′row、dp′col不仅与f、XS、YS、ZS、α、β、γ 7个参数及7个参数的误差df、dXS、dYS、dZS、dα、dβ、dγ有关,还与透视成像的点位坐标prow、pcol及地物的三维坐标 (p.x, p.y, p.z) 有关;柱面拼接方法属于几何拼接,仅在拼接缝处存在错位的情况,因此下文讨论的拼接误差即为图像拼接缝处的误差,由于采用垂直方向180°球面投影的方式,所以透视投影中的行坐标prow的取值范围为 (-∞, ∞),列坐标pcol位于拼接缝处,由焦距和拼接相机的数目共同决定 (pcol=f·tan (π/n));地物的三维坐标 (p.x, p.y, p.z) 对拼接误差的影响较为复杂,下文将对其进行分析。
3.1 焦距误差的影响如图 8(a)所示, 焦距不一致导致各柱面图像大小不同, 会影响全景拼接效果, 利用误差方程式 (11) 对焦距误差进行定量分析, 在此仅考虑焦距误差df, 其余参数的误差为0, 可得到仅含焦距误差的误差方程表达式 (12)
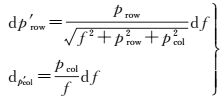 (12)
(12)
由式 (12) 可知,焦距误差对dp′row的影响与焦距f、行坐标prow和列坐标pcol 3个参数有关,对dp′col的影响仅与拼接相机的数目n有关 (pcol/f=tan (π/n)),且dp′row随prow和n增大而增大,随f的增大而减小,但均小于df;dp′col关于n为递减函数,当n>4时,dp′col均小于df。
焦距误差可通过图像重采样的方法校正,通过重采样使各个图像与标准焦距图像大小一致,然后即可完成全景图的拼接,在此对数据Ⅰ试验焦距变化10%时对拼接效果的影响。图 9为数据Ⅰ中7拼相机校正前后拼接生成的全景图,由此可知,只需将各相机图像重采样到同一大小,即可克服焦距误差带来的拼接问题。

|
| 图 9 7拼相机校正前后的全景拼接 Fig. 9 7 spell panorama before and after focal length correction |
3.2 中心误差的影响
如图 8(b)所示, 多拼相机的摄影中心存在不一致的情况, 即为中心误差, 中心误差系偶然误差, 在各相机中的表现无规律性.利用误差方程式 (11) 对中心误差进行定量分析, 在此仅考虑中心误差 (dXS, dYS, dZS), 其余参数误差为0, 可得到仅含中心误差的误差方程表达式 (13)
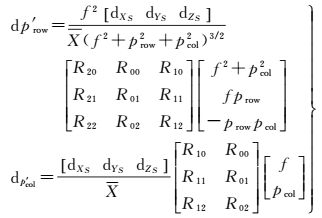 (13)
(13)
由式 (13) 可知,中心误差对dp′row的影响与f、prow、pcol 3个旋角和X等参数有关,对dp′col的影响与f、pcol、3个旋角和X等参数有关;其中,参数X为地物点相对于摄影中心的三维坐标与旋转角的乘积之和,如式 (14) 所示
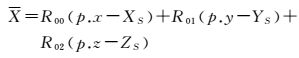 (14)
(14)
式中, dp′row、dp′col均随X的增大而减小.由式 (14) 可知, X表示地物点沿主光轴方向到摄影中心的距离, 即摄影物距 (简称“物距"), 所以dp′row、dp′col跟物距密切相关; 为易于分析各参数对中心误差的影响, 令X=10m, f=800像素, α=β=γ=0°, 然后可将式 (13) 化简为式 (15)
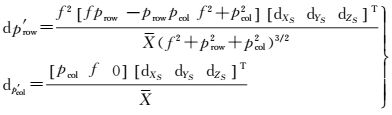 (15)
(15)
并根据式 (15) 分别绘制dp′row、dp′col关于prow、pcol的函数变化图,如图 10所示。(由于pcol=f·tan (π/n), f为固定值,因此对pcol的函数也是对拼接相机数目n的函数,以下试验中n的取值为[3 16])。
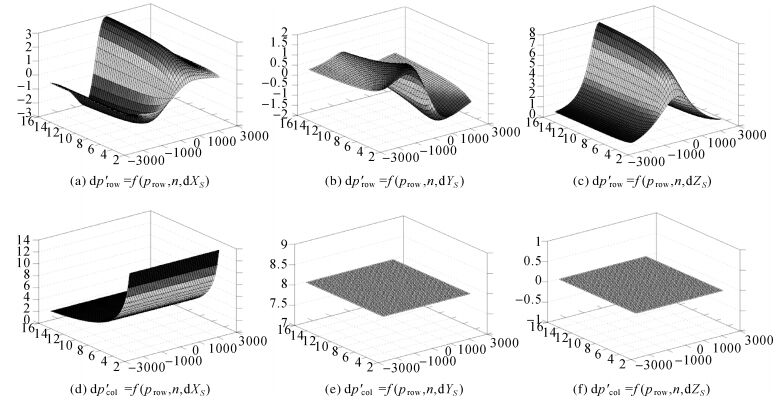
|
| 图 10 中心误差分析 Fig. 10 Analysis of center error |
由式 (15) 和图 10可得到中心误差 (dXS, dYS, dZS) 对dp′row、dp′col的影响,在物距均设为10 m,dXS、dYS、dZS设为0.1 m的情况下,dXS、dYS对dp′row的影响均小于3像素且受拼接相机数目n的影响较小,但dZS对dp′row的影响随prow的增大而减小,当prow=0,n=16时,dp′row的取值最大接近8像素;dXS对dp′col的影响与n相关,且随着n的增大而迅速减小,dYS对dp′col的影响为常数8像素,dZS对dp′col无影响。
利用成像方程模拟含有中心误差的图像拼接,用于分析中心误差对全景拼接的影响。在成像方程中各拼接相机摄影中心的三维坐标上加入中心误差,在此将各相机的摄影中心XS、YS、ZS均随机加入±0.1 m的误差,对数据Ⅰ进行7拼相机的成像试验。图 11为中心误差下7拼相机的整体拼接图,由图 11可知,中心误差在取0.1 m的情况下,柱面拼接方法仍可得到较好的全景拼接图。
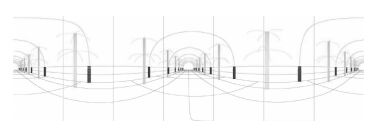
|
| 图 11 中心误差下的7拼全景 Fig. 11 7 spell panorama under central error |
3.3 旋角误差的影响
旋角误差是指各相机主光轴未能完全平均分布于同一平面造成的误差, 可将旋角误差分解到3个旋转轴上, 以dα、dβ、dγ表示, 图 8(c)为dγ不等于0时的4拼相机旋角误差示意图.利用误差方程式 (11) 对旋角误差进行定量分析, 在此仅考虑旋角误差dα、dβ、dγ, 其余参数的误差为0, 可得到仅含旋角误差的误差方程表达式 (16)
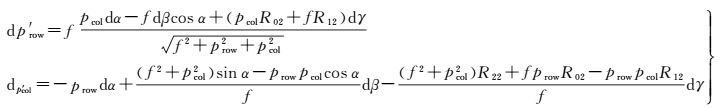 (16)
(16)
由式 (16) 可知, 旋角误差对dp′row、dp′col的影响与f、prow、pcol和3个旋角等参数有关; 为易于分析各参数对中心误差的影响, 令f=800像素, α=β=γ=0°, 然后可将式 (16) 化简为式 (17)
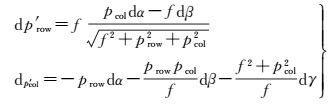 (17)
(17)
根据式 (17) 分别绘制dp′row和dp′col关于prow、pcol的函数变化图,如图 12所示。
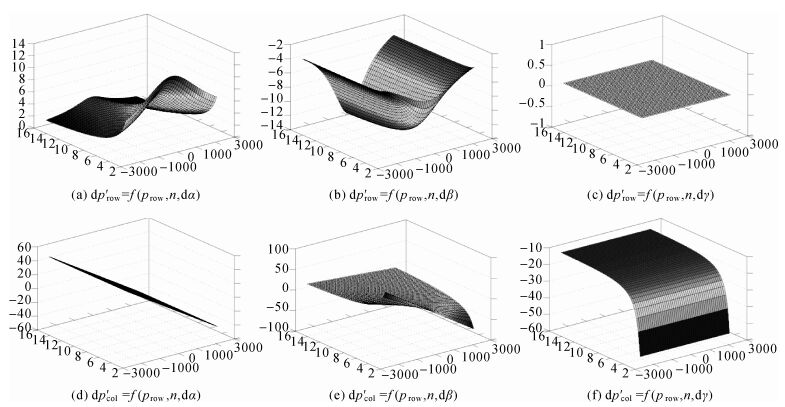
|
| 图 12 旋角误差分析 Fig. 12 Analysis of rotation angle error |
由式 (17) 和图 12可知旋角误差dα、dβ、dγ对dp′row、dp′col的影响,在α=β=γ=0°,dα、dβ、dγ设为1.0°的情况下,dα对dp′row的影响均小于10像素,且随着prow和n的增大而减小;dβ对dp′row的影响均小于14像素,且随着prow的增大而减小,随着n的增大而增大;dγ对dp′row无影响;dα对dp′col的影响仅与prow相关,且与prow成正比;dβ、dγ对dp′col的影响主要与n相关,且随着n的增大迅速减小。
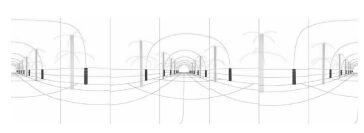
为分析旋角误差对全景拼接的影响,在成像方程中各拼接相机的3轴旋角上分别加入1.0°的旋角误差,试验采用7拼相机,仿真结果如图 13所示。由图 13可知,旋角误差对拼接效果的影响很大,当dα=dβ=dγ=1.0°时,旋角误差对全景图像拼接效果的影响已很明显,由式 (17) 可知,拼接相机的数目的增加有利于减小旋角误差的影响;3轴旋角误差角虽然可以通过相机检校的方法获取,但也难以用于图像拼接的纠正。
|
| 图 13 旋角误差下的全景拼接 (dα=dβ=dγ=1.0°) Fig. 13 Panorama image with rotation angle error (dα=dβ=dγ=1.0°) |
4 结论
本文提出了一种柱面全景图像拼接方法,通过模拟道路点云和真实道路点云分别对不同数目拼接相机和倾斜成像情况下的拼接效果进行试验,验证了拼接方法的适用性;最后利用由成像方程推导的误差方程对引起全景拼接误差的各参数进行具体分析。本文的结论如下:① 建立了三维点云到二维图像的柱面成像方程,适用于模拟任意位置和角度下的全景成像;② 提出的柱面全景拼接方法可用于不同数目相机和倾斜成像下的全景拼接;③ 全景图像拼接的精度受焦距误差,中心误差和旋角误差的影响,其中,焦距误差可通过图像重采样的方法校正,中心误差与物距密切相关,而旋角误差主要受多拼相机数目的影响。上述结论可用于指导全景相机的生产及全景拼接中的误差控制。
| [1] | LAN Jinhui, LI Jian, HU Guangda, et al. Distance Estimation Using a Panoramic Sensor Based on a Novel Spherical Optical Flow Algorithm[J]. Optics & Laser Technology, 2013, 45: 168–176. |
| [2] | TEHRANI M H, GARRATT M A, ANAVATTI S. Horizon-Based Attitude Estimation from a Panoramic Vision Sensor[J]. IFAC Proceedings Volumes, 2012, 45(1): 185–188. DOI:10.3182/20120213-3-IN-4034.00035 |
| [3] | 李德仁. 论地球空间信息的3维可视化:基于图形还是基于影像[J]. 测绘学报, 2010, 39(2): 111–114. LI Deren. 3D Visualization of Geospatial Information: Graphics Based or Imagery Based[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 111–114. |
| [4] | ALMARAZ-CABRAL C C, GONZALEZ-BARBOSA J J, VILLA J, et al. Fringe Projection Profilometry for Panoramic 3D Reconstruction[J]. Optics and Lasers in Engineering, 2016, 78: 106–112. |
| [5] | BRENNAN P F, PONTO K, CASPER G, et al. Virtualizing Living and Working Spaces: Proof of Concept for a Biomedical Space-Replication Methodology[J]. Journal of Biomedical Informatics, 2015(57): 53–61. |
| [6] | 杨化超, 张磊, 姚国标, 等. 局部单应约束的高精度图像自动配准方法[J]. 测绘学报, 2012, 41(3): 401–408. YANG Huachao, ZHANG Lei, YAO Guobiao, et al. An Automated Image Registration Method with High Accuracy Based on Local Homography Constrain[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 401–408. |
| [7] | LOWE D G. Object Recognition from Local Scale-invariant Features[C]//Proceedings of the 7th IEEE International Conference on Computer Vision. Kerkyra: IEEE, 1999(2): 1150-1157. |
| [8] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [9] | SINHA S N, FRAHM J M, POLLEFEYS M, et al. GPU-based Video Feature Tracking and Matching[R]. [S.l.]: UNC Chapel Hill, 2006. |
| [10] | BAY H, ESS A, TUYTELAARS T, et al. Speeded-Up Robust Features (SURF)[J]. Computer Vision and Image Understanding, 2008, 110(3): 346–359. DOI:10.1016/j.cviu.2007.09.014 |
| [11] | 吴凡路, 刘建军, 任鑫, 等. 嫦娥三号全景相机图像全景镶嵌方法的研究[J]. 光学学报, 2014, 34(9): 0915001. WU Fanlu, LIU Jianjun, REN Xin, et al. Research on Panoramic Mosaics Method of Chang'E-3 Pancam Images[J]. Acta Optica Sinica, 2014, 34(9): 0915001. |
| [12] | 霍春宝, 童帅, 赵立辉, 等. SIFT特征匹配的显微全景图拼接[J]. 辽宁工程技术大学学报 (自然科学版), 2015, 34(1): 93–96. HUO Chunbao, TONG Shuai, ZHAO Lihui, et al. Microscopic Panorama Splicing Based on Sift Features Matching[J]. Journal of Liaoning Technical University (Natural Science), 2015, 34(1): 93–96. |
| [13] | 黄立勤, 陈财淦. 全景图拼接中图像融合算法的研究[J]. 电子与信息学报, 2014, 36(6): 1292–1298. HUANG Liqin, CHEN Caigan. Study on Image Fusion Algorithm of Panoramic Image Stitching[J]. Journal of Electronics & Information Technology, 2014, 36(6): 1292–1298. |
| [14] | KIM D H, YOON Y I, CHOI J S. An Efficient Method to Build Panoramic Image Mosaics[J]. Pattern Recognition Letters, 2003, 24(14): 2421–2429. DOI:10.1016/S0167-8655(03)00071-0 |
| [15] | CHEN Haipeng, SHEN Xuanjing, LI Xiaofei, et al. Bionic Mosaic Method of Panoramic Image Based on Compound Eye of Fly[J]. Journal of Bionic Engineering, 2011, 8(4): 440–448. DOI:10.1016/S1672-6529(11)60049-8 |
| [16] | 季顺平, 史云. 车载全景相机的影像匹配和光束法平差[J]. 测绘学报, 2013, 42(1): 94–100. JI Shunping, SHI Yun. Image Matching and Bundle Adjustment Using Vehicle-based Panoramic Camera[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 94–100. |
| [17] | 张正鹏, 江万寿, 张靖. 自适应运动结构特征的车载全景序列影像匹配方法[J]. 测绘学报, 2015, 44(10): 1132–1141. ZHANG Zhengpeng, JIANG Wanshou, ZHANG Jing. An Matching Method for Vehicle-borne Panoramic Image Sequence Based on Adaptive Structure from Motion Feature[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1132–1141. DOI:10.11947/j.AGCS.2015.20140622 |
| [18] | 季顺平, 史云. 多镜头组合型全景相机两种成像模型的定位精度比较[J]. 测绘学报, 2014, 43(12): 1252–1258. JI Shunping, SHI Yun. Comparison of Two Sensor Models for Multi-camera Rig System in Measurements[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1252–1258. DOI:10.13485/j.cnki.11-2089.2014.0169 |
| [19] | 张正鹏, 江万寿, 张靖. 光流特征聚类的车载全景序列影像匹配方法[J]. 测绘学报, 2014, 43(12): 1266–1273. ZHANG Zhengpeng, JIANG Wanshou, ZHANG Jing. An Image Match Method Based on Optical Flow Feature Clustering for Vehicle-borne Panoramic Image Sequence[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1266–1273. DOI:10.13485/j.cnki.11-2089.2014.0172 |
| [20] | 季顺平, 史云. 高噪声环境下基于参考影像的车载序列影像定位方法[J]. 测绘学报, 2014, 43(11): 1174–1181. JI Shunping, SHI Yun. Georegistration of Ground Sequential Imagery with Geo-referenced Aerial Images in High Noise Environments[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1174–1181. DOI:10.13485/j.cnki.11-2089.2014.0181 |
| [21] | URBAN S, LEITLOFF J, HINZ S. Improved Wide-angle, Fisheye and Omnidirectional Camera Calibration[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015(108): 72–79. |
| [22] | HUGHES C, MCFEELY R, DENNY P, et al. Equidistant (fθ) Fish-eye Perspective with Application in Distortion Centre Estimation[J]. Image and Vision Computing, 2010, 28(3): 538–551. DOI:10.1016/j.imavis.2009.09.001 |
| [23] | 隆昌宇, 邾继贵, 郭寅, 等. 基于非参数测量模型的摄影测量方法研究[J]. 光学学报, 2014, 34(12): 1215004. LONG Changyu, ZHU Jigui, GUO Yin, et al. Study on Close-Range Photogrammetry Based on Nonparameteric Measurement Model[J]. Acta Optica Sinica, 2014, 34(12): 1215004. |
| [24] | 赵嘉鑫, 张涛, 张景国, 等. 框幅式航测相机中像移量对直接地理定位精度影响的研究[J]. 红外与激光工程, 2015, 44(2): 632–638. ZHAO Jiaxin, ZHANG Tao, ZHANG Jingguo, et al. Study of the Effects on Frame Aerial Photography Direct-Georeferencing Accuracy Caused by Image Motion[J]. Infrared and Laser Engineering, 2015, 44(2): 632–638. |
| [25] | RUPNIK E, NEX F, TOSCHI I, et al. Aerial Multi-camera Systems: Accuracy and Block Triangulation Issues[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 101: 233–246. DOI:10.1016/j.isprsjprs.2014.12.020 |


