全景相机主要包括折反射全景相机[1]、鱼眼全景相机[2]、线扫描全景相机[3]和组合全景相机[4],其中组合全景相机具有影像获取速度快、影像分辨率高、畸变小、各个方向的分辨率近乎一致等优点[3-5],广泛应用于车载移动测量系统中。
车载组合全景相机所拍摄的场景较为复杂,复杂的场景中存在移动物体以及纹理匮乏且重复的建筑物面,同时大量地物的存在造成影像中地物间存在遮挡,导致阴影的存在[6-8]。这些因素共同造成影像匹配时得到的正确同名点数量稀少或者分布不均,难以利用单个子相机影像作为构像单元并使用常规共线方程构造稳定、完整的空中三角网。对空中三角测量而言,大视场可以提供更稳健的几何结构和更大的重叠区域[9],也可减小影像位置和角度参数之间的不确定性[10]。为了增大构像单元的视场范围和像对间的重叠区域,文献[11-12]将组合全景相机在一个摄站获取的多张影像投影到球面、圆柱面或立方体面上拼接为一张全景影像,来获取单个构像单元水平方向360°的视场角。文献[13-15]基于球面理想构像模型对拼接全景影像进行立体观测和三维重建,该模型以组合全景相机各子相机影像摄影中心的重心作为球面影像的等效摄影中心。由于球坐标系等效摄影中心与像点对应实际摄影中心不重合,导致球面投影像点点位误差的存在;此外,多镜头组合相机影像拼接过程中由于物体景深的不可知性导致拼接区域的融合误差的必然存在[16],最终降低地面点的测量精度。文献[17]提出了组合全景相机拼接全景影像的球严密构像模型,该模型利用全景影像的球坐标系与各子相机影像的像空间坐标系间的相对位姿参数,还原了球面像点对应的实际摄影中心,避免了近似摄影中心引起的球面投影像点误差,但是摄站内拼接区域的融合误差无法消除,造成拼接区域像点的定位精度有所下降。
球模型利用球面像点作为观测值,在模型投影和融合过程中产生了像点误差。常规共线方程以单个子相机影像作为构像单元,其较窄的视场角造成单个构像单元内的同名像点数量少,难以构建稳健完整的空三网。本文将扩展共线方程[18]引入到车载组合相机影像的构网平差中,该方法利用已标定的组合相机各子相机间相对位姿参数,使各子相机影像的摄影光束延伸至基准相机影像的摄影中心,以一个摄站获取的多张影像作为一个构像单元,从而获取构像单元水平方向360°的视场角,同时以组合相机各子相机影像匹配所得同名点作为观测值,不仅扩大单个构像单元的覆盖范围,增加立体模型间连接点的数量和分布的范围,避免以子相机影像为构像单元导致的难以构网问题,而且避免了全景影像模型投影和融合过程中引入的像点误差,从而实现车载组合全景相机序列影像高精度且稳健的构网平差。
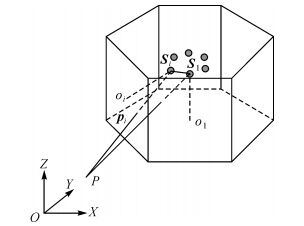
1 组合相机扩展共线方程图 1所示多面体为组合全景相机一个摄站获取的n张子相机影像示意图 (n为组合相机中子相机个数,图 1中n为6),每一个侧面代表一张子相机影像。假设子相机间的相对位姿参数已标定,且在拍摄过程中保持不变。选择1号相机为基准相机,其中S1(XS1, YS1, ZS1) 和Si(XSi, YSi, ZSi) 分别为1号相机影像和i号相机影像的摄影中心在物方坐标系O-XYZ中的位置向量;R1和Ri分别是1号相机影像和i号相机影像的像空间坐标系到坐标系O-XYZ的旋转矩阵 (R由3个旋转角φ、ω、κ按照文献[19]的方法构造)。i号相机相对于1号相机的相对位姿参数可用Ri1和Si1(XSi1, YSi1, ZSi1) 来描述,其中Ri1是i号相机影像的像空间坐标系到1号相机影像的像空间坐标系的旋转矩阵,Si1是i号相机影像的摄影中心在1号相机影像的像空间坐标系中的位置向量。(X, Y, Z) 是地面点P在坐标系O-XYZ中的坐标,pi是地面点P在i号相机影像上的像点,其像空间坐标系坐标为 (xi, yi, -f),oi为i号相机影像的像主点。
|
| 图 1 组合全景相机影像示意图 Fig. 1 The mono camera images of a multi-camera rig |
像点pi满足共线方程
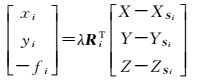 (1)
(1)
如图 1所示,向量间满足Sipi=λ(SiS1+S1P),在i号相机影像的像空间坐标系中可表示为
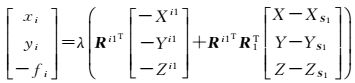 (2)
(2)
式中,λ为比例系数,式 (1) 和式 (2) 右侧相等,可以推导出
 (3)
(3)
 (4)
(4)
将式 (3)、式 (4) 代入式 (1),像点pi所满足的共线方程可表示为
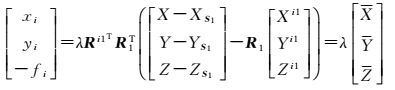 (5)
(5)
式 (1) 为常规共线方程,式 (5) 为扩展共线方程。Ri1和Si1已标定,由式 (5) 可知,以扩展共线方程为函数模型的区域网平差中,一个摄站n张影像的未知参数仅为1号相机影像的外方位元素和地面点的物方坐标。一个摄站内的所有像点通过组合全景相机的相对位姿参数Ri1和Si1与本摄站的1号相机影像建立几何关系,从而将构像单元从一张子相机影像扩展为一个摄站获取的n张影像。式 (5) 改写为共线方程的一般形式如式 (6) 所示
 (6)
(6)
式 (6) 是非线性的,线性化后得到像点观测值的误差方程如式 (7) 所示;将各摄站1号相机影像外方位元素的初始值作为虚拟观测值参与平差,其误差方程如式 (8) 所示
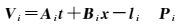 (7)
(7)
 (8)
(8)
式中,t=(dXS1, dYS1, dZS1, dϕ1, dω1, dκ1)T是各摄站1号相机影像的外方位元素改正数;x=(dX, dY, dZ)T是地面点物方坐标的改正数;Ai、Bi是式 (6) 分别对1号相机影像外方位元素、地面点物方坐标计算所得偏导数;li是像点观测值与近似值的差;Pi是像点观测值的权;Et为单位阵;lt是1号相机影像外方位元素初始值与平差值之差;Pt是1号相机影像外方位元素初始值的权。Ai、Bi、li、lt的具体形式为
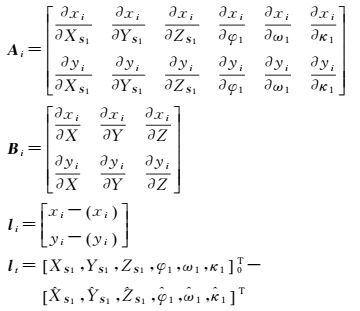 (9)
(9)
式中,xi、yi是像点观测值;(xi)、(yi) 是将平差参数代入式 (6) 所得像点近似值;[XS1, YS1, ZS1, φ1, ω1, κ1]0T是各摄站1号相机影像外方位元素的初始值;
为了验证本文算法定位精度及定位稳定性,采用一组实测数据进行试验分析。试验使用的车载组合全景相机由8个子相机组成,图 2(a)为其实物图,图 2(b)为其内部结构图,其中标注了相机的编号以及车辆前进方向。各子相机的视场角为69.21°,焦距为5 mm,像幅大小为2058×2456像素,像素大小为3.45 μm。

|
| 图 2 组合全景相机实物与内部结构 Fig. 2 The entity and internal structure of the multi-camera rig |
试验所使用的组合全景相机的相对位姿参数标定方法为:先利用车载RIGEL VZ-400三维激光扫描仪静态扫描,获得水平方向360°范围内稠密且精确的地面点云;然后利用点云中的明显点作为控制点,后方交会获得各子相机的外方位元素;最后按照式 (3) 和式 (4) 计算各子相机对于1号相机的相对位姿参数。
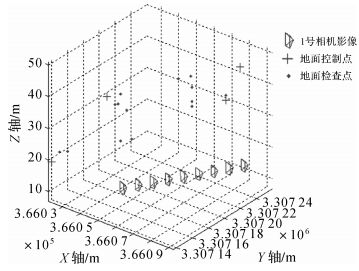
在城市场景的一段平直道路中采集连续的9个摄站共72张影像作为构建空三网的试验数据,相邻摄站间基线长度约为10 m。本文利用SIFT算子提取并匹配同名点,然后利用多种约束条件剔除误匹配后获取空三试验所需同名像点;利用影像外参数初始值及同名像点前方交会得到地面点物方坐标初始值;最终得到地面点606个,对应像点2115个,每一个地面点都是至少3度重叠点。用全站仪量测了18个地面点的物方坐标,其中4个作为控制点,其余14个作为检查点。各摄站及地面点的分布如图 3所示,其中,四面体的顶点是各摄站1号相机影像的摄影中心,四面体底面方向是1号相机的拍摄方向,也是测量车的前进方向。
|
| 图 3 摄站与测量的地面点分布 Fig. 3 The distribution of stations and measured terrain points |
用于空三构网的同名像点在各摄站影像中的分布如图 4所示,一个正八边形代表一个摄站获取的8张子相机影像,中间的数字是摄站序号,边内的数字是子相机影像中的同名点数量,子相机编号见图 2(b)。各摄站影像匹配所得同名点存在下述情况:影像同名点数量极少,如图 5(a)所示;甚至有的影像中同名像点数量为零,如图 5(b)所示;影像同名像点集中在一个小区域内,分布不均匀,如图 5(c)所示;1号与5号相机影像的基线方向近似平行于影像主光轴方向,且像点对应地面点分布在远处的建筑物上,造成地面点的交会角小,交会精度低,如图 5(d)所示。上述影像均得不到充足的几何约束,因此以单个子相机影像为构像单元无法构建稳定且完整的空三网。

|
| 图 4 连续9个摄站影像的同名像点分布 Fig. 4 The distribution of corresponding points in the successive 9 stations |

|
| 图 5 弱几何约束影像 (红点为同名像点) Fig. 5 The images with weak geometric constraints (the red points are corresponding points) |
本文利用上述数据设计了3组试验:对比分析全景影像扩展共线方程空三与球模型空三的定位精度;对比分析球面半径的选择对扩展共线方程与球模型量测精度的影响;分析控制点的数量对扩展共线方程空三定位精度的影响。此外,还利用模拟数据分析了地面点深度对3种构像模型定位精度的影响。球模型像点是利用组合相机子相机影像匹配所得同名点通过球模型投影和摄站内重叠区域取均值所得[16]。
2.2 3种构像模型空三定位精度比较分析利用各影像外参数初始值直接前方交会,以及利用球理想模型、球严密模型、扩展共线方程进行构网平差4种方法对图 3所示序列全景影像进行处理,所得检查点的点位误差如图 6所示。4种方法所得检查点各轴定位中误差μX、μY、μZ,检查点物方点位中误差μP,以及检查点像方点位中误差σp统计如表 1所示。

|
| 图 6 4种方法所得检查点点位误差 Fig. 6 The position errors of check points of the 4 methods |
| 方法 | μX/m | μY/m | μZ/m | μP/m | σp/像素 |
| 直接前方交会 | 0.076 | 0.050 | 0.120 | 0.151 | 5.231 |
| 球理想模型 | 0.046 | 0.039 | 0.028 | 0.066 | 1.796 |
| 球严密模型 | 0.054 | 0.029 | 0.027 | 0.067 | 1.512 |
| 扩展共线方程 | 0.027 | 0.029 | 0.017 | 0.045 | 1.180 |
注:1. μX、μY、μZ是根据检查点物方坐标实测值与平差值之差Δi(i=X, Y, Z) 计算的各轴定位中误差,即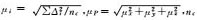 是检查点的数量。 是检查点的数量。2. 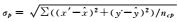 ,其中 (x′, y′) 是检查点物方坐标实测值反投影所得像点坐标, ,其中 (x′, y′) 是检查点物方坐标实测值反投影所得像点坐标,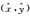 是检查点物方坐标平差值反投影所得像点坐标,ncp是检查点对应像点的数量。 是检查点物方坐标平差值反投影所得像点坐标,ncp是检查点对应像点的数量。 | |||||
观察表 1可知,3种构像模型构网平差都显著地提高了检查点的点位精度,其中,以扩展共线方程为构像模型的空三定位精度最高,原因在于这种构像模型是严密的,误差主要来源于特征像点的定位误差,而球理想模型由于组合相机各子相机摄影中心与球心不重合,在球面投影以及摄站内重叠区域的融合等处理过程中产生了额外的像点误差,降低了地面点定位精度。球面像点额外误差与子相机摄影中心到球心的距离、像点光线与球心和子相机摄影中心连线的夹角、球面半径及物像距离有关[16]。本文各摄站球面半径以地面点到球心的距离均值为准,按照本文硬件设施参数及物像距离,产生的像点误差最大约为2个像素,且大部分球面点的像点误差在1个像素以内[16],所以全景影像球理想模型的空三定位精度较扩展共线方程的空三定位精度降低了约0.02 m。
球严密模型和球理想模型的检查点物方定位精度近乎相同,原因在于本文球模型的半径设置为地面点到球心的距离均值,大部分的地面检查点均分布在投影球面的附近,物像距离小,因此其像点投影差及拼接误差均较小。球严密模型的检查点像方定位精度高于球理想模型的像方定位精度,这是由于除摄站内相邻影像的重叠区域外,球严密模型是几何严密的构像模型,而球理想模型没有消除摄影中心近似处理造成的球面投影误差,致使球严密模型空三平差得到的影像外方位元素精度比球理想模型空三平差得到的影像外方位元素精度高。
2.3 球面半径对3种构像模型定位精度的影响分析当组合相机参数确定后,球面半径和物像距离影响着球面像点的投影误差及重叠区域融合误差,而当进一步确定地面点和摄站位置后,物像距离也成为了球面半径与物距的函数。由于本文所实测地面点均位于建筑物立面上,到各摄站的距离相似,因此球面半径成为了影响球面像点误差的主要因素。本文通过改变球面半径进而改变物像距离来改变球面像点的投影及融合误差,从而分析球面半径对3种构像模型空三定位精度的影响。以10 m为间隔,从10 m到200 m设置球面半径,利用球理想模型、球严密模型和扩展共线方程3种构像模型对图 3所示实测数据进行空三平差的定位精度如图 7所示。

|
| 图 7 不同球面半径下3种构像模型的空三定位精度 Fig. 7 The aerial triangulation positioning accuracy of the 3 imaging models with different spherical radiuses |
在以扩展共线方程为构像模型的空三平差中,以各子相机影像中的同名像点作为观测值,不涉及像点的球模型投影和摄站内相邻影像间重叠区域的融合,因此其空三定位精度与球面半径的选择无关,保持在一个较高的水平。在以球理想模型和球严密模型作为构像模型的空三平差中,以各子相机影像像点的球面投影点作为观测值,检查点的球面投影误差及重叠区域融合误差与球面半径有关。当球面半径等于40 m时,两种球模型均达到了最高空三定位精度,说明检查点大部分集中在距离摄影中心40 m的球面上。地面点的平均物距为40 m,像距为球面半径,在球面的同一侧,随着物像距离的增大,球模型的定位精度下降。当球面半径从40 m增大到200 m时,球模型的空三定位精度下降平缓并趋于平稳,而当球面半径从40 m减小到10 m时,球模型的空三定位精度下降明显,因此为了将所有地面点的量测精度限制在一定的范围内,可将球面半径设置为物距最大值。
球严密模型的定位精度优于球理想模型,且随着物像距离的增大,这种优势更为明显。原因在于,球理想模型所用球面像点受到球面模型投影误差和摄站内重叠区域融合误差的共同影响,两种误差均随着物像距离的增大而增大;而球严密模型恢复了摄站内非重叠区域球面像点的实际摄影中心,消除了模型投影误差。由于球严密模型不能恢复摄站内重叠区域的融合误差,因此其定位精度依然低于扩展共线方程的定位精度。
2.4 控制点数量对扩展共线方程定位精度的影响分析当改变图 3数据的控制点数量时,以扩展共线方程为构像模型的区域网平差定位精度如图 8所示。

|
| 图 8 不同控制点数目下扩展共线方程空三的定位精度 Fig. 8 The aerial triangulation positioning accuracy of the extended collinear equations with different ground control point number |
当控制点的数量从3个增加到5个时,扩展共线方程的空三定位精度有明显的提高,但是随着控制点数量的进一步增加,其定位精度不再有显著变化[20],而是略有起伏。本文共布设了18个实测地面点,均用全站仪量取其物方三维坐标。由于实测地面点数量有限,随着控制点数量的增加,检查点的数量减少,地面点量测误差及像点定位误差使统计所得空三定位精度随着数据的变动而产生起伏,但总体上趋于稳定。
2.5 深度变化对3种构像模型定位精度的影响分析本节利用已知外方位元素的各摄站对不同深度的地面点进行前方交会来分析深度变化对3种构像模型定位精度的影响。试验数据为模拟所得,影像外方位元素和地面点物方坐标无误差。
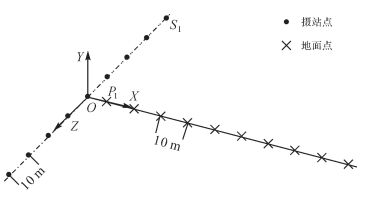
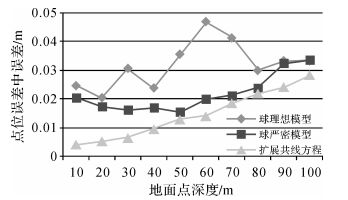
模拟数据中以10 m为间隔布置了9个摄站和10个地面点,如图 9所示,所用组合相机参数与本文实测数据所用组合相机参数相同。10个地面点反投影到9个摄站的影像上共得到118个像点。为了模拟实际数据中的像点误差,在像点坐标中加入均值为0、方差为0.5的随机误差,模拟100次,共生成100组模拟数据。球模型的半径设置为物距最大值100 m。利用球理想模型、球严密模型及扩展共线方程进行前方交会得到各地面点的定位误差如图 10所示。
|
| 图 9 模拟的摄站及地面点分布 Fig. 9 The distribution of simulated stations and terrain points |
|
| 图 10 不同深度地面点前方交会定位精度 Fig. 10 The intersection positioning accuracy of terrain points in different depth |
统计深度30 m处的100个地面点的前方交会点位误差如图 11所示。

|
| 图 11 深度30 m地面点的前方交会定位精度 Fig. 11 The intersection positioning accuracy of terrain points in depth of 30 meters |
观察图 10可知,扩展共线方程的定位精度最高,随着地面点深度的增加,地面点的交会角减小,定位精度随之降低[21]。球理想模型和球严密模型的地面点定位精度受到球面像点误差和交会角的综合影响,由于当像点误差不变时,地面点的交会角随着地面点深度的增大而减小,使地面点的定位精度降低;而球模型半径取所有地面点到摄站距离的最大值,球面像点的投影误差和重叠区域融合误差随着地面点深度的增大而减小,使地面点定位精度升高;在深度较小时,球面像点误差起主要作用,在深度较大时,交会角起主要作用,因此随着地面点深度的增加其定位精度先小幅度提高再降低。球严密模型的观测值影响因素较为单一,只受到摄站内重叠区域融合误差的影响,而球理想模型的观测值受到模型投影误差和重叠区域融合误差的综合影响,因此球严密模型的定位精度高于球理想模型的定位精度,且球严密模型的地面点定位误差随深度的变化较为平缓,而球理想模型的地面点定位精度随着深度的变化较为剧烈。图 11进一步表明扩展共线方程的定位精度最高,同时球严密模型的定位精度高于球理想模型。
3 结束语本文首次将扩展共线方程引入车载组合全景相机影像的空中三角测量中,对比分析了以扩展共线方程、球理想模型和球严密模型为构像模型的空三定位精度,分析了不同的球面半径对3种模型定位精度的影响,分析了地面点深度对3种构像模型定位精度的影响。试验结果表明:扩展共线方程的定位精度高于球严密模型和球理想模型的定位精度。对组合全景相机而言,扩展共线方程与球模型均为水平视场360°的构像模型,均可以克服复杂场景下小视场构像模型构网困难且不稳定的问题,并且扩展共线方程以子相机影像像点作为观测值,避免了球模型方法中球面投影和摄站内重叠区域融合引入的像点误差,避免了球面半径的影响。
| [1] | SUNG C K, LU C H. Single-camera Panoramic Stereo System Model Based on Skew Ray Tracing[J]. Optik-international Journal for Light and Electron Optics, 2012, 123(7): 594–603. DOI:10.1016/j.ijleo.2011.06.001 |
| [2] | LI Shigang. Monitoring Around a Vehicle by a Spherical Image Sensor[J]. IEEE Transactions on Intelligent Transportation Systems, 2006, 7(4): 541–550. DOI:10.1109/TITS.2006.883116 |
| [3] | PARIAN J A, GRUEN A. Sensor Modeling, Self-calibration and Accuracy Testing of Panoramic Cameras and Laser Scanners[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(1): 60–76. DOI:10.1016/j.isprsjprs.2009.08.005 |
| [4] | SATO T, IKEDA S, YOKOYA N. Extrinsic Camera Parameter Recovery from Multiple Image Sequences Captured by an Omni-directional Multi-camera System[M]//PAJDLA T, MATAS J. Computer Vision-ECCV 2004. Berlin: Springer, 2004: 326-340. |
| [5] | GLEDHILL D, TIAN Guiyun, TAYLOR D, et al. Panoramic Imaging—A Review[J]. Computers & Graphics, 2003, 27(3): 435–445. |
| [6] | MICUSIK B, KOSECKA J. Piecewise Planar City 3D Modeling from Street View Panoramic Sequences[C]//Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition. Miami: IEEE, 2009: 2906-2912. |
| [7] | 张正鹏, 江万寿, 张靖. 光流特征聚类的车载全景序列影像匹配方法[J]. 测绘学报, 2014, 43(12): 1266–1273. ZHANG Zhengpeng, JIANG Wanshou, ZHANG Jing. An Image Match Method Based on Optical Flow Feature Clustering for Vehicle-borne Panoramic Image Sequence[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1266–1273. DOI:10.13485/j.cnki.11-2089.2014.0172 |
| [8] | SATO T, PAJDLA T, YOKOYA N. Epipolar Geometry Estimation for Wide-baseline Omnidirectional Street View Images[C]//Proceedings of the 2011 IEEE International Conference on Computer Vision Workshops. Barcelona, Spain: IEEE, 2011: 56-63. |
| [9] | RUPNIK E, NEX F, TOSCHI I, et al. Aerial Multi-camera Systems: Accuracy and Block Triangulation Issues[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 101: 233–246. DOI:10.1016/j.isprsjprs.2014.12.020 |
| [10] | KIM J S, HWANGBO M, KANADE T. Motion Estimation Using Multiple Non-overlapping Cameras for Small Unmanned Aerial Vehicles[C]//Proceedings of the 2008 IEEE International Conference on Robotics and Automation. Pasadena, CA, USA: IEEE, 2008: 3076-3081. |
| [11] | 李松. 基于图像拼接的球面全景图研究[D]. 长春: 长春理工大学, 2012. LI Song. Research of Sphere Panorama Based on Image Mosaic[D]. Changchun: Changchun University of Science and Technology, 2012. |
| [12] | IKEDA S, SAT T, YOKOYA N. High-resolution Panoramic Movie Generation from Video Streams Acquired by an Omnidirectional Multi-camera System[C]//Proceedings of the 2003 IEEE International Multisensor Fusion and Integration for Intelligent Systems. Tokyo, Japan: IEEE, 2003: 155-160. |
| [13] | 季顺平, 史云. 车载全景相机的影像匹配和光束法平差[J]. 测绘学报, 2013, 42(1): 94–100. JI Shunping, SHI Yun. Image Matching and Bundle Adjustment Using Vehicle-based Panoramic Camera[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 94–100. |
| [14] | LI Shigang, FUKUMORI K. Spherical Stereo for the Construction of Immersive VR Environment[C]//Proceedings of the 2005 IEEE Virtual Reality. Bonn, Germany: IEEE, 2005: 217-222. |
| [15] | LI Shigang. Binocular Spherical Stereo[J]. IEEE Transactions on Intelligent Transportation Systems, 2008, 9(4): 589–600. DOI:10.1109/TITS.2008.2006736 |
| [16] | 季顺平, 史云. 多镜头组合型全景相机两种成像模型的定位精度比较[J]. 测绘学报, 2014, 43(12): 1252–1258. JI Shunping, SHI Yun. Comparison of Two Sensor Models for Multi-camera Rig System in Measurements[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1252–1258. DOI:10.13485/j.cnki.11-2089.2014.0169 |
| [17] | SHI Yun, JI Shunping, SHI Zhongchao, et al. GPS-supported Visual SLAM with a Rigorous Sensor Model for a Panoramic Camera in Outdoor Environments[J]. Sensors, 2013, 13(1): 119–136. |
| [18] | EBNER H, KORNUS W, OHLHOF T. A Simulation Study on Point Determination for the MOMS-02/D2 Space Project Using an Extended Functional Model[J]. International Archives of Photogrammetry and Remote Sensing, 1993, 29: 458–464. |
| [19] | 张剑清, 潘励, 王树根. 摄影测量学[M]. 2版. 武汉: 武汉大学出版社, 2009. ZHANG Jianqing, PAN Li, WANG Shugen. Photogrammetry[M]. 2nd ed. Wuhan: Wuhan University Press, 2009. |
| [20] | ZHANG Yongjun, XIONG Xiaodong, SHEN Xiang, et al. Bundle Block Adjustment of Weakly Connected Aerial Imagery[J]. Photogrammetric Engineering & Remote Sensing, 2012, 78(9): 983–989. |
| [21] | 张永军, 张勇. 大重叠度影像的相对定向与前方交会精度分析[J]. 武汉大学学报 (信息科学版), 2005, 30(2): 126–130. ZHANG Yongjun, ZHANG Yong. Analysis of Precision of Relative Orientation and Forward Intersection with High-overlap Images[J]. Geomatics and Information Science of Wuhan University, 2005, 30(2): 126–130. |


