2. 德国地学研究中心, 波茨坦 14473
2. German Research Center for Geosciences, Potsdam 14473, Germany
北斗卫星导航系统 (BeiDou navigation satellite system,BDS) 是我国正在实施的自主发展、独立运行的全球卫星导航系统[1]。截至2016年4月初,5颗新一代北斗导航卫星准确进入预定轨道,标志着北斗卫星导航系统由区域运行向全球拓展的建设目标迈出了坚实的一步。作为全球首个全星座播发三频卫星导航信号的卫星导航系统,多频观测信息极大地改善了北斗卫星导航系统的观测冗余度,提高了导航定位的精度和效率[2-3]。北斗卫星导航系统提供的标准服务定位精度为10 m,测速精度为0.2 m/s,授时精度为20 ns[4]。BDS标准定位服务不能满足用户高精度定位的需求,BDS网络RTK方法是提高BDS定位精度,实现高精度实时动态定位服务的重要手段。
BDS网络RTK的核心问题之一是参考站间载波相位整周模糊度的准确确定,只有正确固定了参考站模糊度才能得到高精度的综合误差或是建立高精度的误差模型[5]。由于网络RTK参考站一般相距几十千米以上,所以参考站间电离层延迟和对流层延迟等误差对双差观测值的影响大于模糊度的半个波长,即使在使用双频观测数据和参考站坐标已知的情况下,整周模糊度也难以与误差分离。
近年来,国内外学者对网络RTK参考站间模糊度进行了大量研究。文献[6]利用卡尔曼滤波算法进行了参考站间整周模糊度的动态解算。文献[7-8]提出了网络RTK参考站间单历元模糊度搜索方法,解决了参考站间模糊度单历元解算问题。文献[9]研究了参考站间双差整周模糊度快速解算的三步法。文献[10]研究了不固定参考站坐标情况下利用GPS双频观测数据仿三频数据的三频模糊度快速算法。文献[11]提出了利用电离层约束模型的网络RTK模糊度解算方法。上述研究工作主要针对GPS网络RTK,BDS能够向亚太地区提供连续无源的导航、定位和授时服务之后,学者们已利用BDS实测数据进行网络RTK参考站模糊度的研究。文献[12]使用综合噪声最小的弱电离层组合构造了一种三频几何模糊度解算策略,由于其使用观测量组合而不是原始观测量,故不可避免地放大了观测噪声影响,影响了参数估计精度。文献[13]研究了基于三频无几何模型的BDS网络RTK方法,主要实现了超宽巷和宽巷模糊度的准确固定,并且具有较高的解算效率,但未对BDS原始频率模糊度进行解算。文献[14]利用B1、B2频率载波相位整周模糊度的线性关系,通过双差电离层延迟误差模型进行B1、B2载波相位整周模糊度单历元固定,但该方法适用于电离层平稳的情况,电离层误差空间相关模型化较难的条件下单历元模糊度解算的可靠性得不到保证。相对于GPS,BDS宽巷组合观测值的噪声较大,模糊度解算的收敛速度慢,固定成功率不高,BDS双频单历元方法由于以单颗卫星为研究对象,没有综合利用所有卫星的观测值信息。
鉴于上述情况,应充分利用BDS提供三频观测信息的优势,进行BDS网络RTK参考站三频整周模糊度解算方法的研究。本文利用BDS三频超宽巷长波长及三频载波相位整周模糊度之间的整数线性关系,提出了BDS网络RTK参考站三频整周模糊度解算方法。该方法利用B2、B3频率的观测值得到超宽巷整周模糊度,将利用多个模糊度固定标准固定的超宽巷整周模糊度与宽巷整周模糊度的线性关系作为约束条件,避免直接利用噪声较大的超宽巷组合观测值对参数估计的影响,然后估计宽巷整周模糊度、相对天顶对流层延迟误差和电离层延迟误差,并搜索确定宽巷整周模糊度。在进行原始频率双差整周模糊度确定过程中也不使用宽巷组合观测值,而是利用固定的宽巷整周模糊度与三频载波相位整周模糊度的整数线性关系,将线性关系加入载波相位整周模糊度参数估计观测模型中,最终可正确有效地确定载波相位整周模糊度。
1 BDS网络RTK参考站三频整周模糊度解算双差组合观测值具有可消除接收机钟差和卫星钟差,大大削弱轨道误差、电离层延迟误差、对流层延迟误差等误差影响的优点,双差载波相位模糊度保持整周特性[15],所以,本文对BDS参考站间的载波相位双差整周模糊度进行解算。通常情况下,BDS网络RTK参考站一般都设在比较开阔的地方,且硬件设备齐全,多采用抗多路径天线,卫星的多路径效应较小,可忽略多路径的影响,则BDS参考站间的B1、B2和B3频率上的双差伪距和载波相位观测方程可表示为
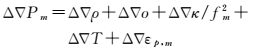 (1)
(1)
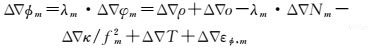 (2)
(2)
式中,Δ▽为双差操作符;P为以距离为单位的伪距观测值;ϕ和φ分别为以距离和周为单位的载波相位观测值;o为卫星轨道误差;κ/fm2为电离层延迟误差一阶项;T为对流层延迟误差;εp和εϕ分别为伪距和载波相位观测值的观测噪声;N为载波相位观测值的模糊度;ρ为卫星到参考站接收机的几何距离;λ=c/f为载波相位的波长, c为真空中的光速,c=2.997 924 58×108m/s, f为频率,北斗卫星导航系统B1、B2和B3的频率分别为1 561.098 MHz、1 207.140 MHz和1 268.520 MHz;下标m为BDS的B1、B2和B3载波相位的频率,其中m=1, 2, 3。
利用BDS 3个频率的载波相位观测值进行组合,可以得到一系列具有较长波长的宽巷和超宽巷组合观测值[16-17],其中B2、B3频率的超宽巷组合观测值对应的波长约为4.884 m,其电离层延迟误差的影响是B1频率电离层延迟误差的1.6倍;B1、B2和B1、B3频率的宽巷组合观测值对应的波长约为0.847 m和1.025 m,二者的电离层延迟误差影响较接近,其载波相位和伪距组合观测值的观测噪声小于B2、B3超宽巷组合观测值的观测噪声。
1.1 参考站间B2、B3超宽巷整周模糊度解算参考站间的双差电离层延迟误差、对流层延迟误差和轨道误差等误差的残差影响随着站间距离的增加逐渐增大,因此,采用不受电离层延迟误差、对流层延迟误差和卫星轨道误差等误差和几何距离影响的M-W组合计算参考站间B2、B3双差超宽巷整周模糊度。如果参考站A、B同步观测卫星p、q,伪距和载波相位观测值的M-W组合观测值如式 (3) 所示,根据式 (4) 可计算B2、B3双差超宽巷整周模糊度
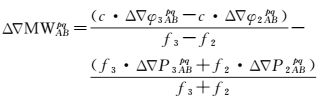 (3)
(3)
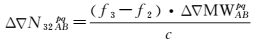 (4)
(4)
式 (3)、式 (4) 中,MW为M-W组合观测值;N32为B2、B3超宽巷整周模糊度;上标表示卫星,下标表示参考站。其他符号与式 (1) 和式 (2) 含义相同。双差M-W组合观测值消除了双差电离层延迟误差一阶项、对流层延迟误差、站星间几何距离 (包含了轨道误差),不受卫星钟差、接收机钟差的影响。从式 (3) 和式 (4) 可以看出,M-W组合模型求解B2、B3超宽巷整周模糊度仅受伪距和载波相位观测值噪声的影响,与参考站间距离无关,适合进行长距离参考站间载波相位整周模糊度的解算。
为了保证式 (3)、式 (4) 的计算为连续弧段的观测数据,利用M-W组合观测值对BDS观测数据进行粗差和周跳探测[18]。由于M-W组合观测值主要受伪距观测值的观测噪声影响,通过取平均值的方法削弱观测值噪声的影响,相应的B2、B3双差超宽巷整周模糊度和方差分别为
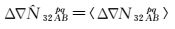 (5)
(5)
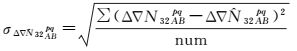 (6)
(6)
式中,〈·〉为多历元求均值;
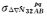
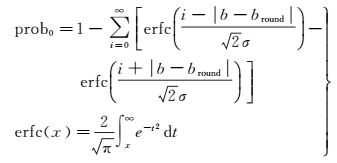 (7)
(7)
式中,prob0为B2、B3双差超宽巷整周模糊度固定为最近整数的概率;b为B2、B3双差超宽巷实数模糊度;bround为B2、B3双差超宽巷实数模糊度的就近整数;σ为B2、B3双差超宽巷整周模糊度的中误差;erfc (·) 为误差函数。
利用严格的模糊度固定标准确定B2、B3双差超宽巷整周模糊度,若双差超宽巷模糊度满足准则条件,则双差超宽巷模糊度为正确值。B2、B3双差超宽巷整周模糊度固定为整数的准则为:
(1) 实数双差超宽巷模糊度与其最近整数之差的绝对值小于0.25周。
(2) 实数双差超宽巷模糊度就近取整成功率大于0.99,保证固定双差超宽巷模糊度的可靠性。
(3) 双差超宽巷模糊度的方差小于等于0.005。
(4) 对于任意两个以上的参考站,双差超宽巷模糊度的代数和在理论上为零。一般BDS网络RTK用于计算区域误差的参考站数量大于3,以参考站A、B和C为例,则
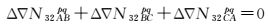 (8)
(8)
参考站间的B1、B2和B1、B3双差宽巷组合载波相位观测方程可表示为
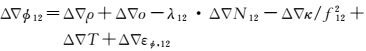 (9)
(9)
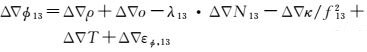 (10)
(10)
当参考站间的B2、B3双差超宽巷整周模糊度Δ▽N32被准确确定之后,则B1、B2双差宽巷整周模糊度Δ▽N12和B1、B3双差宽巷整周模糊度Δ▽N13具有以下唯一的关系
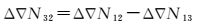 (11)
(11)
由于参考站坐标精确已知,式 (9) 和式 (10) 中包含B1、B2和B1、B3双差宽巷整周模糊度和双差对流层延迟误差及双差电离层延迟误差。影响双差宽巷整周模糊度固定的主要误差源是双差对流层延迟误差和双差电离层延迟误差。将每对双差卫星对应的双差电离层延迟误差作为参数进行估计,双差对流层延迟误差使用Sasstamonion模型改正其干延迟Δ▽Tdry,残余的湿延迟Δ▽Twet采用分段常数进行估计,并使用GMF投影函数将天顶对流层延迟投影到传播路径上[22]。当参考站间的距离在一定范围时,投影函数值较接近,将导致方程病态,因此定义相对天顶对流层延迟 (relative zenith tropospheric delay,RZTD),即
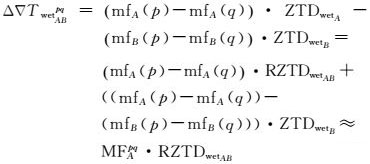 (12)
(12)
式中,mf (·) 为GMF投影函数;MF为星间投影函数之差;Twet为对流层湿延迟误差;ZTDwet为天顶对流层湿延迟误差;RZTDwetAB=ZTDwetA-ZTDwetB为参考站A、B的相对天顶对流层湿延迟误差。式 (12) 右端第2个等式最后一项量级较小,可忽略,因此采用一个相对天顶对流层湿延迟参数估计所有可视卫星的双差对流层湿延迟误差。
由于参考站坐标精确已知,假定历元i,参考站A、B同步观测到s+1颗卫星,联合式 (9)—式 (11) 可得到B1、B2和B1、B3双差宽巷组合载波相位观测值的观测方程
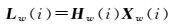 (13)
(13)
式中
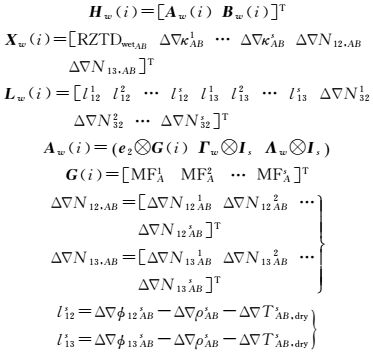
式 (13) 中,⊗、Im和en分别表示克罗内积、m维单位矩阵及各元素均为1的n维列向量;Aw(i) 中子矩阵 (从左到右) 分别是对应于Xw(i) 中相对天顶对流层湿延迟误差、双差电离层延迟误差及双差宽巷整周模糊度的系数矩阵;Bw(i) 为式 (11) 对应的每对双差卫星的超宽巷整周模糊度与宽巷整周模糊度的线性关系的系数矩阵;Γw=[-1/f122-1/f132]T为双差宽巷观测值对应的电离层延迟误差系数;G(i) 为式 (12) 对应的每对双差卫星的星间投影函数之差;Λw=diag (-λ12, -λ13) 为二维对角阵,其对角线元素为双差宽巷整周模糊度对应的波长;上标表示双差卫星,在此省略了基准卫星;Lw(i) 为式 (9)、式 (10)、式 (11) 中双差宽巷载波相位观测方程对应的常数项向量。其他符号的含义与式 (9) 和式 (10) 的含义相同。
式 (13) 在多历元数据处理中将双差电离层延迟误差作为历元参数,相对天顶对流层湿延迟误差作为分段常数,每个历元利用固定的宽巷模糊度计算得到的双差电离层延迟误差仅作为下一历元的初值,采用参数消去法消掉法方程中与双差电离层延迟误差相关的信息,法方程中不进行电离层延迟误差信息的叠加,只进行可被连续跟踪时段内所有卫星的宽巷整周模糊度和相对天顶对流层湿延迟误差的法方程叠加。在参数估计中,采用卫星高度角定权法对双差宽巷组合载波相位观测值进行定权,并将正确固定的超宽巷整周模糊度与宽巷整周模糊度的线性关系作为强约束条件,各双差卫星对应式 (11) 的权给予比卫星高度角最高的宽巷载波相位观测值的权稍大的权值。根据最小二乘计算原理,可估计双差电离层延迟误差、相对天顶对流层湿延迟误差及双差宽巷整周模糊度,之后搜索并确定双差宽巷整周模糊度,并利用类似于式 (8) 的准则进行整周模糊度闭合条件检验。
1.3 参考站间B1、B2和B3整周模糊度解算参考站间的双差宽巷整周模糊度确定之后,其与B1、B2及B3双差整周模糊度具有以下整数线性关系
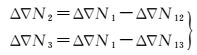 (14)
(14)
将式 (14) 代入式 (2) 中得到B1、B2及B3双差载波相位观测方程
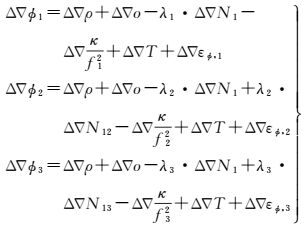 (15)
(15)
假定历元i,参考站A、B同步观测到s+1颗卫星,由式 (15) 可得B1、B2和B3双差载波相位观测方程
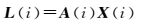 (16)
(16)
其中
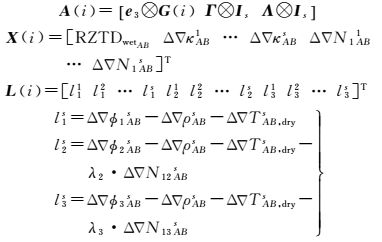
式 (16) 中,Γ=[-1/f12-1/f22-1/f32]T和Λ=[-λ1-λ2-λ3]T分别为B1、B2和B3双差载波相位观测值对应的电离层延迟误差系数和波长;X(i) 中待估的模糊度参数为B1双差整周模糊度;L(i) 为式 (15) 中B1、B2和B3双差载波相位观测方程对应的常数项向量。其他符号的含义与式 (13) 的含义相同。采用卫星高度角定权法对双差载波相位观测值进行定权,并按照式 (13) 中对宽巷整周模糊度和大气延迟误差的处理方法对式 (16) 中的B1双差整周模糊度、电离层延迟误差和相对天顶对流层延迟误差进行参数估计,然后确定B1双差整周模糊度,并利用类似于式 (8) 的准则进行整周模糊度闭合条件检验。利用式 (14) 可进一步得到B2、B3双差整周模糊度,之后即可计算参考站间的误差改正数。
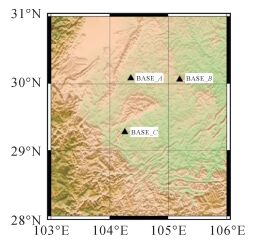
2 算例与分析利用西南地区某省CORS网的BDS实测三频数据进行算法检验,采用1 d的观测数据,采样间隔为1 s,卫星截止高度角为10°。为了验证所提出的BDS参考站三频整周模糊度解算的可行性和有效性,利用精密数据处理软件解算的双差模糊度作为准确值进行验证。该试验数据共有3个参考站,参考站分布如图 1所示,BASE_A到BASE_B距离为70 km,BASE_B到BASE_C距离为113 km,BASE_C到BASE_A距离为78 km。
|
| 图 1 测站分布 Fig. 1 Stations distribution |
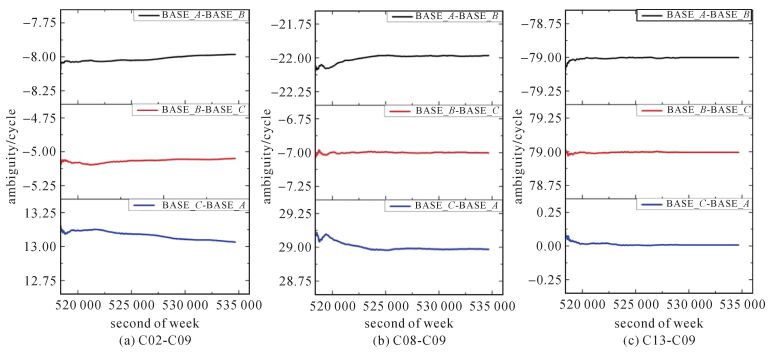
算例验证中分别以卫星C02-C09、C08-C09和C13-C09双差卫星为例,其中C09为观测时段内选择的基准卫星。3组双差卫星的首个连续观测弧段对应的各参考站间B2、B3双差超宽巷整周模糊度计算结果如图 2所示。
|
| 图 2 B2、B3双差超宽巷整周模糊度 Fig. 2 Double differenced extra-wide-lane integer ambiguity of B2、B3 |
从图 2可以看出,卫星C02-C09、C08-C09和C13-C09对应的实数双差超宽巷整周模糊度与其最近整数之差的绝对值远远小于0.25周,3组双差卫星在BASE_A-BASE_B、BASE_B-BASE_C、BASE_C-BASE_A参考站间的双差超宽巷整周模糊度固定解分别为 (-8,-5,13)、(-22,-7,29) 和 (-79,-79,0),双差超宽巷整周模糊度满足闭合条件式 (8),保证了超宽巷整周模糊度的准确性。由于解算超宽巷整周模糊度的数学模型与站间距离无关,3条基线中BASE_B-BASE_C对应的模糊度变化最为平滑,原因可能是其他两条基线中的共同参考站BASE_A的接收机质量和观测环境稍差导致的。利用超宽巷波长较长的优势和双差超宽巷整周模糊度固定为整数的准则可快速确定超宽巷整周模糊度。卫星C02-C09、C08-C09和C13-C09在BASE_A、BASE_B和BASE_C组成的闭合网中模糊度收敛需要的平均历元个数分别为5、8和3。
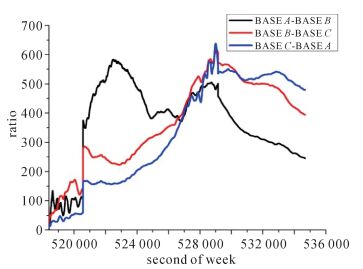
B2、B3双差超宽巷整周模糊度准确固定之后,采用最小二乘方法估计双差宽巷整周模糊度,并搜索确定双差宽巷整周模糊度。图 3给出了各参考站间首个完整观测弧段内利用LAMBDA算法解算双差宽巷整周模糊度的ratio值。由图 3可以看出,由于解算宽巷整周模糊度的数学模型综合利用了所有卫星的观测值进行模糊度解算,加之宽巷整周模糊度之间的线性关系对观测方程的强约束,双差宽巷模糊度解算的可靠性很高,在双差超宽巷整周模糊度准确固定的条件下,双差宽巷整周模糊度可迅速准确固定。
|
| 图 3 双差宽巷整周模糊度的ratio值 Fig. 3 Ratio of double differenced wide-lane integer ambiguity |
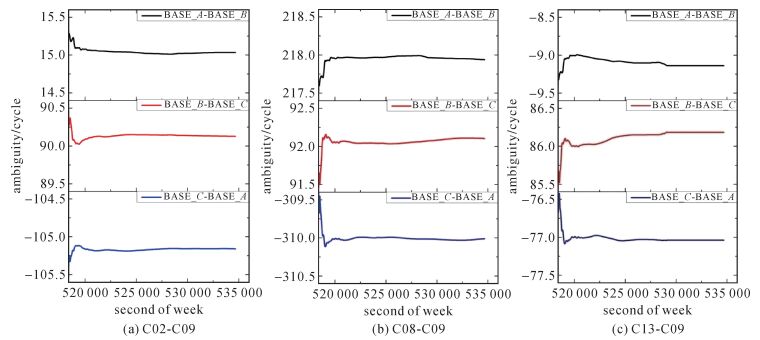
进一步利用固定的宽巷整周模糊度构造三频整周模糊度之间的整数线性关系,将三频整周模糊度之间的整数线性关系加入三频双差载波相位观测方程中,综合利用所有卫星3个频率的观测值进行最小二乘参数估计。各参考站间首个完整观测弧段内卫星C02-C09、C08-C09和C13-C09解算得到的B1双差整周模糊度实数值如图 4所示。精密数据处理软件解算的3组双差卫星在各参考站间的B1双差整周模糊度准确值分别为 (15,90,-105)、(218,92,-310) 和 (-9,86,-77)。由图 4可知,B1双差整周模糊度实数值与模糊度准确值相差最大不超过1周,参数估计得到的模糊度实数值精度较高,利用LAMBDA算法可在两个历元内准确的实现B1双差整周模糊度固定。
|
| 图 4 B1双差整周模糊度 Fig. 4 Double differenced integer ambiguity of B1 |
利用LAMBDA算法搜索并确定B1双差整周模糊度之后,为了进一步验证本文算法所解算的B1双差整周模糊度的正确性和可靠性,可通过B1和B2双差载波相位观测方程线性组合计算得到B1频率的双差电离层延迟误差和双差对流层延迟误差,双差电离层延迟误差和双差对流层延迟误差随时间的变化情况可对所解算的B1双差整周模糊度做出可靠性判断,固定正确的双差整周模糊度对应的双差电离层误差和双差对流层延迟误差会在合理的范围内进行有规律的连续变化,相邻历元间相差较小,不会出现突然增大或减小、不连续及突变的情况,而且满足闭合基线双差电离层延迟误差和双差对流层延迟误差之和等于零。
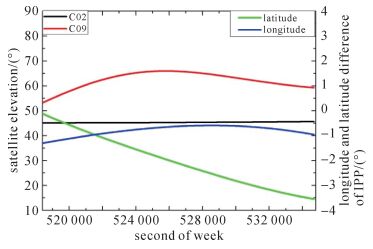
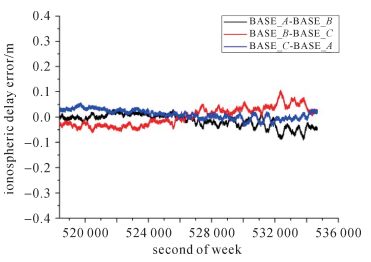
卫星C02-C09高度角和电离层穿刺点的经纬度差值变化如图 5所示,图 5中左侧Y轴表示卫星高度角,右侧Y轴表示电离层穿刺点的经纬度差值。由于GEO和IGSO卫星均为高轨卫星,卫星运行角速度较慢,特别是GEO卫星,其相对参考站的运行角速度几乎为零,因此C02的高度角变化很小,而IGSO卫星的运动周期约为24 h,C09高度角变化较明显。由于GEO卫星电离层穿刺点变化较小,所以C09的穿刺点经纬度变化决定卫星C02-C09电离层穿刺点的经纬度差值的变化。由于IGSO卫星的运行轨道星下点轨迹以子午线为中心,所以C09的电离层穿刺点经度变化较小,纬度变化较大。因此卫星C02-C09电离层穿刺点的经纬度差值中,经度方向的差值变化较慢,纬度方向的差值变化稍大。卫星C02-C09对应的B1频率的双差电离层延迟误差和双差对流层延迟误差如图 6和图 7所示。
|
| 图 5 C02-C09高度角和穿刺点差值 Fig. 5 The elevations and IPP difference of C02-C09 |
|
| 图 6 C02-C09电离层延迟误差 Fig. 6 Ionosphere delay error of C02-C09 |
|
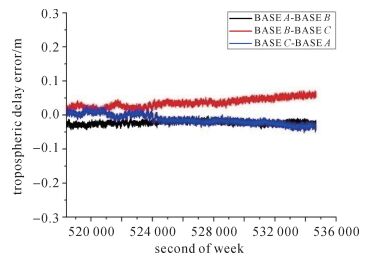
| 图 7 C02-C09对流层延迟误差 Fig. 7 Tropospheric delay error of C02-C09 |
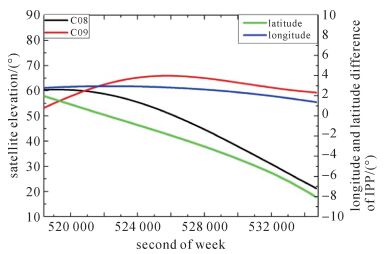
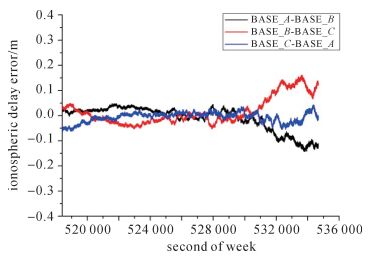
卫星C08-C09高度角和电离层穿刺点的经纬度差值变化如图 8所示。C08和C09均为IGSO卫星,运动周期约为24 h,其高度角变化较大,尤其是C08变化较明显。从图 8可看出,卫星C08-C09电离层穿刺点的经纬度差值变化相对于卫星C02-C09较快。卫星C08-C09电离层穿刺点的经纬度差中,经度方向的差值变化较缓慢,而纬度方向的差值变化较快。卫星C08-C09对应的B1频率的双差电离层延迟误差和双差对流层延迟误差如图 9和图 10所示。
|
| 图 8 C08-C09高度角和穿刺点差值 Fig. 8 The elevations and IPP difference of C08-C09 |
|
| 图 9 C08-C09电离层延迟误差 Fig. 9 Ionosphere delay error of C08-C09 |
|
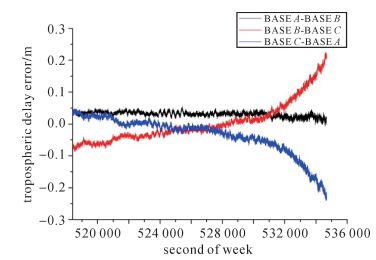
| 图 10 C08-C09对流层延迟误差 Fig. 10 Tropospheric delay error of C08-C09 |
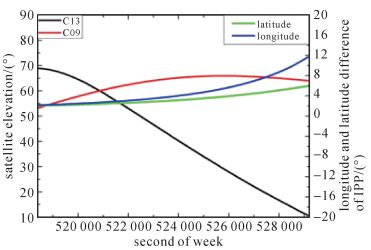
卫星C13-C09高度角和电离层穿刺点的经纬度差值变化如图 11所示。C13为MEO卫星,相比于GEO和IGSO卫星,其卫星运行角速度较快,运动周期约为12 h,其高度角变化较大。卫星C13-C09电离层穿刺点的经纬度差值变化相对于卫星C02-C09和C08-C09较快。卫星C13-C09对应的B1频率的双差电离层延迟误差和双差对流层延迟误差如图 12和图 13所示。
|
| 图 11 C13-C09高度角和穿刺点差值 Fig. 11 The elevations and IPP difference of C13-C09 |
|
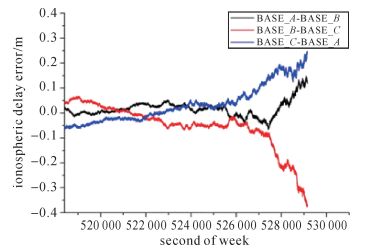
| 图 12 C13-C09电离层延迟误差 Fig. 12 Ionosphere delay error of C13-C09 |
|
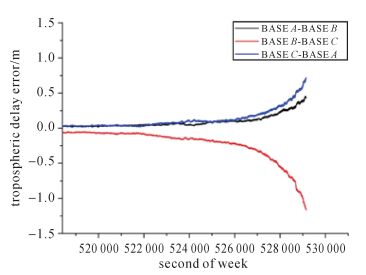
| 图 13 C13-C09对流层延迟误差 Fig. 13 Tropospheric delay error C13-C09 |
从卫星C02-C09、C08-C09和C13-C09的双差电离层延迟误差和双差对流层延迟误差的变化情况可以看出,在观测历元的大部分时段内二者变化比较平缓,双差电离层延迟误差随着双差卫星电离层穿刺点的经纬度方向的差值进行有规律的变化,双差对流层延迟误差随着卫星高度角进行有规律的变化,相邻历元间相差较小,不存在不连续及突变的情况,并且双差大气延迟误差满足闭合基线大气延迟误差之和等于零,即BASE_A-BASE_B、BASE_B-BASE_C和BASE_C-BASE_A上同一对双差卫星的大气延迟误差之和为零。3组双差卫星的双差大气延迟误差在合理范围内进行有规律的连续变化进一步验证了本文算法所解算的B1双差整周模糊度的准确性和可靠性。
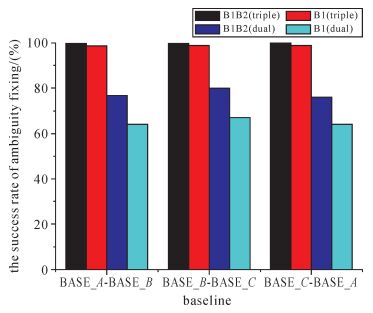
图 14给出了BASE_A-BASE_B、BASE_B-BASE_C和BASE_C-BASE_A参考站间24 h观测数据的B1、B2双差宽巷整周模糊度和B1双差整周模糊度的固定成功率,以精密数据处理软件解算的双差整周模糊度作准确值,使用LAMBDA算法搜索确定整周模糊度 (Ratio>3)。图中B1B2(triple) 和B1(triple) 表示本文方法的B1、B2双差宽巷整周模糊度和B1双差整周模糊度的固定成功率,B1B2(dual) 和B1(dual) 表示在双频观测值条件下利用MW组合和无电离层组合解算的宽巷整周模糊度和B1整周模糊度的固定成功率。
|
| 图 14 模糊度固定成功率 Fig. 14 The success rate of ambiguity fixing |
从图 14中可以看出,由于BDS伪距观测值的噪声较大,消耗了较多的观测历元用于确定宽巷模糊度,导致很多历元模糊度不能固定,在宽巷整周模糊度固定之后,利用无电离层组合模型进行B1整周模糊度解算的成功率也偏低。相比于基于双频观测值的模糊度解算方法,本文方法对应的3条基线的B1、B2双差宽巷整周模糊度具有较高的固定成功率,均为99.99%,在B1、B2双差宽巷整周模糊度固定之后,进一步确定B1双差整周模糊度,其固定成功率分别为98.83%、99.24%和98.81%,B1双差整周模糊度部分不能固定的原因是受大气延迟误差影响较大的低高度角卫星导致的。新方法中B1、B2双差宽巷整周模糊度和B1双差整周模糊度的固定速度较常规的双频模糊度解算方法有明显提高,经统计,新方法中波长较长的超宽巷整周模糊度的平均固定速度为9.8个历元,B1、B2双差宽巷整周模糊度的平均固定速度为2.5个历元,B1双差整周模糊度的平均固定速度为1.5个历元,而常规的基于双频观测值的模糊度解算方法中B1、B2双差宽巷整周模糊度的平均固定速度为303.7个历元,B1双差整周模糊度的平均固定速度为598.4个历元。从B1、B2双差宽巷整周模糊度和B1双差整周模糊度的固定成功率和固定速度可以看出,相比于GPS,BDS的信号质量和接收设备不够完善,常规方法将使BDS网络RTK需要较长的初始化时间,影响BDS网络RTK的实时性,新方法能提高BDS参考站整周模糊度的固定速度,缩短参考站网启动和提供误差改正信息所需的时间,能快速地为流动站用户提供高精度的定位服务。本文方法在进行宽巷整周模糊度和B1整周模糊度确定过程中综合利用了所有卫星的观测值信息,在超宽巷和宽巷整周模糊度固定之后,仅将其构造的模糊度之间的整数线性关系作为约束条件,不直接利用超宽巷和宽巷载波相位观测值,也不进行观测值间的线性组合,避免了放大噪声的不利影响,保证了参数估计的精度,进而可正确有效地固定参考站间三频载波相位整周模糊度,缩短参考站网初始化时间。
3 结论本文研究了一种BDS网络RTK参考站三频整周模糊度解算方法。该方法利用多历元BDS三频观测值,同时考虑大气延迟误差及超宽巷整周模糊度与宽巷整周模糊度的线性约束条件,并将三频载波相位整周模糊度之间的整数线性关系加入原始频率双差载波相位整周模糊度参数估计观测模型中,避免了噪声较大的超宽巷及宽巷组合观测值对参数估计的影响,有助于载波相位整周模糊度的快速、准确固定。通过实测CORS网的BDS三频观测数据进行试验表明,该算法能够实现参考站间整周模糊度的准确固定,且可靠性高。本文方法是针对多历元观测值的BDS网络RTK参考站三频整周模糊度解算,对BDS网络RTK参考站间单历元三频整周模糊度解算方法将作进一步研究。
| [1] | 杨元喜, 李金龙, 徐君毅, 等. 中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(26): 2813–2819. YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Science Bulletin, 2011, 56(26): 2813–2819. |
| [2] | 施闯, 赵齐乐, 李敏, 等. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学:地球科学, 2012, 55(7): 1079–1086. SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of BeiDou Navigation Satellites with Precise Positioning[J]. Science China Earth Sciences, 2012, 55(7): 1079–1086. |
| [3] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [4] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Initial Assessment of the Compass/BeiDou-2 Regional Navigation Satellite System[J]. GPS Solutions, 2013, 17(2): 211–222. DOI:10.1007/s10291-012-0272-x |
| [5] | 高星伟, 陈锐志, 赵春梅. 网络RTK算法研究与实验[J]. 武汉大学学报 (信息科学版), 2009, 34(11): 1350–1353. GAO Xingwei, CHEN Ruizhi, ZHAO Chunmei. A Network RTK Algorithm and Its Test[J]. Geomatics and Information Science of Wuhan University, 2009, 34(11): 1350–1353. |
| [6] | 周乐韬, 黄丁发, 袁林果, 等. 网络RTK参考站间模糊度动态解算的卡尔曼滤波算法研究[J]. 测绘学报, 2007, 36(1): 37–42. ZHOU Letao, HUANG Dingfa, YUAN Linguo, et al. A Kalman Filtering Algorithm for Online Integer Ambiguity Resolution in Reference Station Network[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 37–42. |
| [7] | 高星伟, 刘经南, 葛茂荣. 网络RTK基准站间基线单历元模糊度搜索方法[J]. 测绘学报, 2002, 31(4): 305–309. GAO Xingwei, LIU Jingnan, GE Maorong. An Ambiguity Searching Method for Network RTK Baselines between Base Stations at Single Epoch[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(4): 305–309. |
| [8] | 祝会忠, 刘经南, 唐卫明, 等. 长距离网络RTK基准站间整周模糊度单历元确定方法[J]. 测绘学报, 2012, 41(3): 359–365. ZHU Huizhong, LIU Jingnan, TANG Weiming, et al. The Algorithm of Single-epoch Integer Ambiguity Resolution between Long-range Network RTK Base Stations[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 359–365. |
| [9] | 唐卫明, 刘经南, 施闯, 等. 三步法确定网络RTK基准站双差模糊度[J]. 武汉大学学报 (信息科学报), 2007, 32(4): 305–308. TANG Weiming, LIU Jingnan, SHI Chuang, et al. Three Steps Method to Determine Double Difference Ambiguities Resolution of Network RTK Reference Station[J]. Geomatics and Information Science of Wuhan University, 2007, 32(4): 305–308. |
| [10] | 李博峰, 沈云中, 周泽波. 中长基线三频GNSS模糊度的快速算法[J]. 测绘学报, 2009, 38(4): 296–301. LI Bofeng, SHEN Yunzhong, ZHOU Zebo. A New Method for Medium and Long Range Three Frequency GNSS Rapid Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 296–301. |
| [11] | LI Bofeng, SHEN Yunzhong, FENG Yanming, et al. GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK[J]. Journal of Geodesy, 2014, 88(2): 99–112. DOI:10.1007/s00190-013-0670-z |
| [12] | FENG Yanming. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12): 847–862. DOI:10.1007/s00190-008-0209-x |
| [13] | 高旺, 高成发, 潘树国, 等. 北斗三频宽巷组合网络RTK单历元定位方法[J]. 测绘学报, 2015, 44(6): 641–648. GAO Wang, GAO Chengfa, PAN Shuguo, et al. Single-epoch Positioning Method in Network RTK with BDS Triple-frequency Widelane Combinations[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 641–648. DOI:10.11947/j.AGCS.2015.20140308 |
| [14] | 祝会忠, 徐爱功, 高猛, 等. BDS网络RTK中距离参考站整周模糊度单历元解算方法[J]. 测绘学报, 2016, 45(1): 50–57. ZHU Huizhong, XU Aigong, GAO Meng, et al. The Algorithm of Single-epoch Integer Ambiguity Resolution between Middle-range BDS Network RTK Reference Stations[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 50–57. |
| [15] | 魏子卿, 葛茂荣. GPS相对定位的数学模型[M]. 北京: 测绘出版社, 1998. WEI Ziqing, GE Maorong. Mathematical Model of GPS Relative Positioning[M]. Beijing: Surveying and Mapping Press, 1998. |
| [16] | TANG Weiming, DENG Chenlong, SHI Chuang, et al. Triple-frequency Carrier Ambiguity Resolution for BeiDou Navigation Satellite System[J]. GPS Solutions, 2014, 18(3): 335–344. DOI:10.1007/s10291-013-0333-9 |
| [17] | CHU Fengyu, YANG Ming, WU J. A New Approach to Modernized GPS Phase-only Ambiguity Resolution over Long Baselines[J]. Journal of Geodesy, 2016, 90(3): 241–254. DOI:10.1007/s00190-015-0869-2 |
| [18] | 黄令勇, 翟国君, 欧阳永忠, 等. 削弱电离层影响的三频TurboEdit周跳处理方法[J]. 测绘学报, 2015, 44(8): 840–847. HUANG Lingyong, ZHAI Guojun, OUYANG Yongzhong, et al. Triple-frequency Turboedit Cycle-slip Processing Method Weakening Ionospheric Activity[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 840–847. DOI:10.11947/j.AGCS.2015.20140380 |
| [19] | GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389–399. DOI:10.1007/s00190-007-0187-4 |
| [20] | DONG Danan, BOCK Y. Global of GPS Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J]. Journal of Geophysical Research: Solid Earth, 1989, 94(B4): 3949–3966. DOI:10.1029/JB094iB04p03949 |
| [21] | 潘宗鹏, 柴洪洲, 刘军, 等. 基于部分整周模糊度固定的非差GPS精密单点定位[J]. 测绘学报, 2015, 44(11): 1210–1218. PAN Zongpeng, CHAI Hongzhou, LIU Jun, et al. GPS Partial Ambiguity Resolution Method for Zero-difference Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1210–1218. DOI:10.11947/j.AGCS.2015.20150056 |
| [22] | 葛茂荣, 刘经南. GPS定位中对流层折射估计研究[J]. 测绘学报, 1996, 25(4): 285–291. GE Maorong, LIU Jingnan. The Estimation Methods for Tropospheric Delays in Global Positioning System[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(4): 285–291. |



