2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
绝对重力测量在全球重力基准网建设、监测地壳垂直运动以及国防建设中具有重要意义[1-6]。绝对重力仪的精度在很大程度上直接决定了绝对重力网的观测精度。
FG5绝对重力仪自1992年诞生以来,以其优异的观测精度及稳定性而成为绝对重力仪的行业标准。它采用物体自由落体运动测量原理,让质量块在一个真空的空间里自由下落,通过激光干涉仪产生的光学条纹和激光波长信息记录落体下落的距离,利用铷原子钟记录落体下落所需时间,然后利用自由落体运动公式求解重力加速度。改进的FG5X-246系列绝对重力仪由于采用了稳频氦氖激光器以及高精度的铷原子钟,在理论上保证了重物块移动的位移及下落时间的精度。同时,自由下落物体的轨迹以一个稳定的长周期 (30~60 s)“超级弹簧”系统作为参考并提供隔振作用。以上技术的改进使得FG5X系列绝对重力仪的观测精度可达到1~2 μGal。
绝对重力仪在验收时或使用一段时期后,仪器测量精度是否发生了变化或仪器是否处在最佳工作状态,之前并没有很好的检测手段。目前绝对重力仪的技术指标大多通过同址观测比对的方法来比较和确定绝对重力仪的观测精度。通常采用的方法主要有两种。一种方法是在同一观测点上,通过单台仪器不同时期的观测结果进行自比对[7-11],来检测仪器工作是否正常。通常认为两次或多次观测结果相差很小或比较接近,就认为测量仪器工作正常,这种方法主要用来检测同一台仪器的重复性。当两次观测结果出现差异时,这种差异到底是由仪器本身问题引起的,还是由于观测点处实际真实重力值发生变化而引起的?单纯依靠这种自比对测量方法无法区分出这种差异产生的原因。另一种方法是利用多台绝对重力仪器同址观测比对[12-14],即将多台不同编号的绝对重力仪依次放在同一观测基墩点进行重力观测,然后对不同仪器的观测结果进行相互比较。这种比对方法也会引入因降雨及气压等因素导致的测量误差。当不同仪器间测量结果出现差异时,哪一台仪器的观测结果更可靠或更接近真实值?上述比对方法均无法给出答案。
针对这一比对问题,笔者在实验室中搭建了弱力测试平台力学系统。该弱力测试平台力学系统利用形状规则且质量已知的钨环作为外部扰动质量体,其产生的扰动引力场大小可由扰动质量体的尺寸、质量及其与测量点间的距离参数精确计算得到。将该扰动引力场直接施加在重力观测点上,然后利用绝对重力仪在该观测点进行重力观测。由于扰动引力场的大小可由扰动质量体及平台参数精确计算得到,因而其扰动引力场变化量是精确已知的。通过比较扰动引力场变化量与绝对重力仪捕捉到的引力场变化量之差的绝对值,以此检测绝对重力观测值的准确度。由于扰动引力场的大小可以由平台位置等参数精确计算得到,因此可为绝对重力仪比对提供一种不依赖于第三方的测试方法。
1 测试原理及方案 1.1 弱力测试平台误差分析为保证测试结果的可靠性,首先需要对弱力测试平台所提供的引力场的精度进行误差分析。该平台采用形状为空心圆柱体的钨环作为外部扰动质量,钨环质量为2200 kg,外径为580 mm, 内径为220 mm,厚度为574 mm。圆柱体对其外部轴线方向的引力公式可表示为
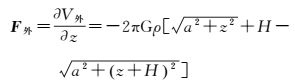 (1)
(1)
式中,a、H、z和ρ分别为钨环的半径、厚度、平台位置距离测量仪器的距离及钨环密度。空心圆柱体对其外部轴线方向的引力可由两个不同半径的同轴圆柱体对其外部轴线方向的引力相减得到。
按照误差传播定理,由式 (1) 可以得到由于钨环半径a、钨环厚度H、平台位置z及钨环密度ρ测量误差引起的扰动引力场的误差影响系数分别为
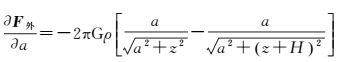 (2)
(2)
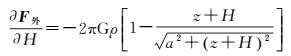 (3)
(3)
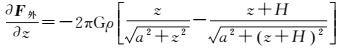 (4)
(4)
 (5)
(5)
则总误差为
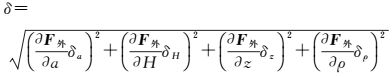 (6)
(6)
在扰动质量钨环的实际验收中,测量钨环内外径使用的游标卡尺精度为0.02 mm,测量厚度使用的千分尺测量精度为0.001 mm,质量测量误差为每100 kg误差不超过2 g,对应密度误差经计算为0.008 84 kg/m3,液压平台举升精度为0.1 mm。误差计算中,假设扰动质量的半径、厚度及液压举升平台的测量误差均为0.1 mm,密度误差为0.008 84 kg/m3。代入式 (2)—式 (6) 分别计算测量误差对扰动引力场的影响结果如表 1所示。
| 误差源 | 误差量 | 引力场误差/μGal |
| 钨环半径 | 0.1 mm | 0.015 9 |
| 钨环厚度 | 0.1 mm | 0.006 3 |
| 钨环密度 | 0.008 84 kg/m3 | 0.029 |
| 平台位置 | 0.1 mm | 0.008 9 |
| 总误差 | 0.035 |
从表 1误差分析结果可以看出,弱力测试平台的理论误差远小于目前绝对重力仪的观测误差,可满足于目前现有绝对重力仪准确度测试。
1.2 测试方案本次试验采用的仪器是目前公认测量精度最高的FG5X型 (编号246) 绝对重力仪。相对于前期产品,FG5X型绝对重力仪采用了更长的落体室及其他改进技术,具有更好的测量精度及稳定性,观测3.75 min即可获得精度为1 μGal的重力观测值。本次试验的思想是利用一定形状的外部扰动质量体产生稳定的扰动引力场,通过改变扰动质量体与测量点之间的距离,来实现重力观测点处扰动引力场大小的变化。由于测量点处叠加了扰动引力场,其绝对重力观测值必然会发生变化,计算绝对重力观测值变化量并与理论扰动引力场变化量进行比较,从而确定绝对重力仪的观测准确度。
在没有扰动引力场的情况下,假设测量点处的绝对重力值为 (背景场)g0。当将扰动质量放置于测量点正上方h1位置时,由于测量点处叠加了扰动引力场Δg1,其绝对重力测量值必然发生变化,记此时测量得到的绝对重力值为g1。然后利用弱力测试平台升降装置上下移动扰动质量体, 依次改变扰动质量体的位置于h2、h3、…、hn高度处,重复上述测量步骤,记各高度处对应的绝对重力观测值分别为g2、g3、…、gn,各高度处对应的扰动引力场分别为Δg2、Δg3、…、Δgn。扰动引力场Δgn的大小可通过扰动质量体的内外半径、厚度、密度以及与测量点之间的距离等参数通过理论公式精确计算出来。如果绝对重力仪的测量值精确,那么在理论上应有下式成立
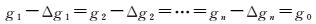 (7)
(7)
其次,当扰动质量体从位置h1移动到位置h2时,其产生的扰动引力场变化量记为Δg12r=Δg1-Δg2,相应的绝对重力观测值变化量记为Δg12c=g1-g2。同理,可得到扰动质量体位置改变引起的扰动引力场变化量Δg13r、Δg23r、…、Δgnmr及相应的绝对重力仪观测值变化量Δg13c、Δg23c、…、Δgnmc(n=1, 2, …, k-1; m=1, 2, …, k)。由于扰动引力场的大小可由扰动质量体及平台参数精确计算得到,因而其扰动引力场变化量Δgnmr是精确已知的。通过比较Δgnmr与Δgnmc差值的绝对值变化,以此检测绝对重力观测值的准确度。本文绝对重力观测值的准确度是指扰动引力场变化量与相应绝对重力仪观测值变化量之差的绝对值|Δgnmr-Δgnmc|。
弱力测试平台准确度测量试验原理剖面图如图 1所示。由于本文的目的是确定绝对重力观测值的准确度,因而在做此类试验时应尽量避免各种未知干扰因素对绝对重力观测值的影响。比如避免在降雨天气以及大气压变化较为剧烈的时期进行此类试验,因为无法获得降雨在空间的精确分布,所以其对绝对重力观测值的影响也无法精确确定;其次,大气压变化对绝对重力观测值的改正也是绝对重力仪观测误差来源的主要因素之一。

|
| 图 1 弱力测试平台准确度测量试验原理剖面图 Fig. 1 The schematic cross-section of accuracy measurement test using the platform |
2 测试结果
在本次绝对重力准确度测量试验中,利用弱力测试平台升降控制系统将扰动质量体分别举升至距离地面1.810 4 m、1.409 9 m和1.010 1 m等3个不同高度位置并进行相应的绝对重力测量。扰动质量体在每一高度处,绝对重力测量均设置了3组绝对重力观测数据,每组绝对重力观测数据包含了100次落体下落,单次落体下落时间设置为10 s,每组测量时间设置为20 min。这样,在每一个高度处测量得到的绝对重力观测值共包含了300次落体下落数据,观测时间为1 h。
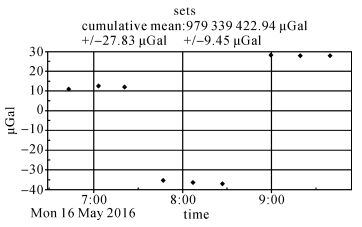
图 2为某一高度处单组100个落体的测量值分布。从图 2可以看出,观测结果的离散度很小,测量值的均方差不超过8 μGal,表明重力观测受周围环境的干扰极小。图 3为外部扰动质量分别在3个不同高度处的重力测量值 (已减去平均值)。从图中可以看出,每一高度处3次观测结果互差变化很小,表明仪器观测状态基本正常。具体测量结果如表 2所示。从表 2可以看到,扰动质量体位于1.810 4 m、1.409 9 m和1.010 1 m等3个位置时,FG5X-246绝对重力测量值分别为434.74 μGal、386.74 μGal和450.94 μGal,固体潮、极移、气压及海潮影响在测量时已经测量软件进行改正,且已隐去绝对重力值相同重复的前6位数字。扰动质量体在不同高度处对应的外部扰动引力场大小分别为-24.68 μGal、-73.49 μGal和-9.24 μGal,负号表示扰动质量体产生的扰动引力方向与地球引力方向相反,使得绝对重力测量值减小。上述3个不同高度处绝对重力测量值经扰动引力因素改正后分别为459.42 μGal、460.23 μGal和460.18 μGal,三者互差小于1 μGal,说明FG5X-246的3次测量结果在1 μGal精度内满足式 (7)。

|
| 图 2 单组100个落体测试结果离散分布 Fig. 2 The distribution of 100 drops measurements of each set |
|
| 图 3 外部扰动质量在3个不同高度处的重力测量值 Fig. 3 The results of gravity measurements when the disturbance mass placed at three different heights |
| μGal | |||||||
| 扰动质量体高度 | 扰动质量体高度变化 | ||||||
| a | b | c | a-b | a-c | b-c | ||
| 外部扰动 引力场 | -24.68 | -73.49 | -9.24 | 48.81 | -15.44 | -64.25 | |
| FG5X-246 测量值 | ~434.74 | ~386.74 | ~450.94 | 48.00 | -16.20 | -64.20 | |
| 改正后绝 对重力值 | ~459.42 | ~460.23 | ~460.18 | — | — | — | |
| 注:“~”表示隐去绝对重力值相同重复的前6位数。 | |||||||
从表 2中还可以看出,当扰动质量体从1.810 4 m高度降到1.409 9 m高度时,外部扰动引力场变化了48.81 μGal,FG5X-246绝对重力仪感应到48.0 μGal的重力变化,FG5X-246绝对重力仪测量值与理论值之差为0.81 μGal。当扰动质量体从1.810 4 m降到1.010 1 m高度时,外部扰动引力场变化了-15.44 μGal,FG5X-246绝对重力仪感应到-16.20 μGal的重力变化,测量值与理论值之差为0.76 μGal。当扰动质量体从1.409 9 m降到1.010 1 m高度时,外部扰动引力场变化了-64.25 μGal,FG5X-246绝对重力仪感应到-64.20 μGal的重力变化,测量值与理论值之差为0.05 μGal。上述测量结果表明,此次FG5X-246绝对重力仪感应到外部引力变化的误差均不超过1 μGal,即其测量值准确度优于1 μGal。
3 结论(1) 排除天气降雨等环境因素干扰,短期内 (1~2 h) 观测点的绝对重力值在观测精度内可认为是恒定不变的,即测量值在观测精度内应近似为一条直线,如扰动质量体位于第3个高度位置时的观测结果。从本次试验结果可以看出,当扰动质量体位于第1个高度位置时,绝对重力测量的第1组观测结果明显比其他2组观测值偏小,这是导致该位置观测值偏小的原因。当扰动质量体位于第2个高度位置时,绝对重力测量的第1组观测结果明显比其他2组观测值偏大,这是导致该位置观测值偏大的主要原因。这两次观测结果偏差的原因可能是由于环境温度变化引起的仪器气泡偏移 (激光光路不垂直) 所致,因为在第1组测量过程中出现了因气泡偏移现象导致的死机。
(2) 本次FG5X-246绝对重力仪重力观测值的准确度优于1 μGal,表明其测量结果在1×10-8m/s2量级上是准确可靠的。
| [1] | 刘冬至, 李辉, 邢乐林, 等. 中国地震重力网绝对重力观测结果分析[J]. 大地测量与地球动力学, 2007, 27(5): 88–93. LIU Dongzhi, LI Hui, XING Lelin, et al. Analysis of Absolute Gravimetry Result of China Earthquake Gravity Network[J]. Journal of Geodesy and Geodynamics, 2007, 27(5): 88–93. |
| [2] | 邢乐林, 孙文科, 李辉, 等. 用拉萨点大地测量资料检测青藏高原地壳的增厚[J]. 测绘学报, 2011, 40(1): 41–44. XING Lelin, SUN Wenke, LI Hui, et al. Present-day Crust Thickness Increasing beneath the Qinghai-Tibetan Plateau by Using Geodetic Data at Lhasa Station[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 41–44. |
| [3] | 邢乐林, 李辉, 李建国, 等. 陆态网络绝对重力基准的建立及应用[J]. 测绘学报, 2016, 45(5): 538–543. XING Lelin, LI Hui, LI Jianguo, et al. Establishment of Absolute Gravity Datum in CMONOC and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 538–543. DOI:10.11947/j.AGCS.2016.20140653 |
| [4] | 王勇, 许厚泽, 张为民, 等. 1996年中国中西部地区高精度绝对重力观测结果[J]. 地球物理学报, 1998, 41(6): 818–825. WANG Yong, XU Houze, ZHANG Weimin, et al. Observational Results of High Precision Absolute Gravity in Central and Western China in 1996[J]. Chinese Journal of Geophysics, 1998, 41(6): 818–825. |
| [5] | 张为民, 王勇, 詹金刚, 等. 1996-2003年中国大陆高精度绝对重力观测[J]. 地球物理学进展, 2005, 20(1): 204–210. ZHANG Weimin, WANG Yong, ZHAN Jingang, et al. High Accuracy Absolute Gravity Observation in Chinese Mainland during 1996-2003[J]. Progress in Geophysics, 2005, 20(1): 204–210. |
| [6] | 王林松, 陈超, 杜劲松, 等. A10-022绝对重力仪在庐山短基线的测量试验与分析[J]. 测绘学报, 2012, 41(3): 347–352. WANG Linsong, CHEN Chao, DU Jinsong, et al. Test Measurements and Analysis of the A10-022 Absolute Gravimeter in the Lushan Short Calibration Line[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 347–352. |
| [7] | 王林松, 陈超, 王同庆, 等. A-10绝对重力仪野外测量精度分析[J]. 大地测量与地球动力学, 2012, 32(1): 60–63. WANG Linsong, CHEN Chao, WANG Tongqing, et al. Analysis of Measuring Accuracy in Field with A-10 Absolute Gravimeter[J]. Journal of Geodesy and Geodynamics, 2012, 32(1): 60–63. |
| [8] | 刘冬至, 邢乐林, 徐如刚, 等. FG5/232绝对重力仪的试验观测结果[J]. 大地测量与地球动力学, 2007, 27(2): 114–118. LIU Dongzhi, XING Lelin, XU Rugang, et al. Experimental Observation Results with FG5/232 Absolute Gravimeter[J]. Journal of Geodesy and Geodynamics, 2007, 27(2): 114–118. |
| [9] | 纪立东, 张宏伟, 肖凡, 等. 永兴岛基准站的重复绝对重力测量研究[J]. 测绘科学, 2014, 39(2): 11–13. JI Lidong, ZHANG Hongwei, XIAO Fan, et al. Repeated Absolute Gravity Surveying at Yongxing Island Base Station[J]. Science of Surveying and Mapping, 2014, 39(2): 11–13. |
| [10] | 邢乐林, 李辉, 何志堂, 等. 成都基准台绝对重力复测结果分析[J]. 大地测量与地球动力学, 2008, 28(6): 38–42. XING Lelin, LI Hui, HE Zhitang, et al. Analysis of Repeat Absolute Gravimetric Results at Chengdu Seismostation[J]. Journal of Geodesy and Geodynamics, 2008, 28(6): 38–42. |
| [11] | 李建国, 李辉, 张松堂, 等. 中国绝对重力仪第二次比对测量[J]. 大地测量与地球动力学, 2014, 34(4): 64–66. LI Jianguo, LI Hui, ZHANG Songtang, et al. Results of the Second Contrast Observation of Absolute Gravimeters (CCAG-2013)[J]. Journal of Geodesy and Geodynamics, 2014, 34(4): 64–66. |
| [12] | 邢乐林, 申重阳, 李辉, 等. 欧洲Walferdange绝对重力仪比对观测[J]. 大地测量与地球动力学, 2009, 29(3): 77–79. XING Lelin, SHEN Chongyang, LI Hui, et al. Comparative Observation of Absolute Gravimeters in Walferdange[J]. Journal of Geodesy and Geodynamics, 2009, 29(3): 77–79. |
| [13] | 何志堂, 韩宇飞, 康胜军, 等. A10/028与FG5绝对重力仪比对测量试验[J]. 大地测量与地球动力学, 2014, 34(3): 142–145. HE Zhitang, HAN Yufei, KANG Shengjun, et al. Contrast Test of A10/028 Absolute Gravimeter with FG5[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 142–145. |
| [14] | 玄松柏, 邢乐林, 何志堂, 等. 国内绝对重力实验观测比对[J]. 大地测量与地球动力学, 2008, 28(4): 72–74. XUAN Songbai, XING Lelin, HE Zhitang, et al. Comparative Experiment of Absolute Gravimeter Surveying in China Mainland[J]. Journal of Geodesy and Geodynamics, 2008, 28(4): 72–74. |



