2. 西安测绘研究所, 陕西 西安 710054
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
1957年,我国确定将青岛大港验潮站作为国家高程基准基本验潮站,将大港验潮站的平均海平面定义为我国高程基准的起算面。我国目前采用的“1985国家高程基准”,是由大港验潮站1952至1979年验潮数据确定的。计算时以19年为周期,滑动步长为1年,得到10组平均海面值,取其平均值242.89 cm作为当地黄海平均海面高,从而求出国家水准原点的高程值为72.260 m[1-3]。
大港验潮站平均海平面的变化直接关系到我国高程基准面的变化。引起验潮站平均海平面发生沉降变化的因素很多,例如温室效应造成的冰川消融、局部地区地下水的开采以及海底地形的变化等[4-5],另外一个不可忽视的变化是地壳的沉降变化。
为了监测我国高程基准面的变化,并研究地壳沉降变化对大港验潮站平均海平面的影响,2005年在距离青岛验潮站约1.5 km处建立了青岛GNSS连续运行观测站,于2005年9月开始试运行。至今,青岛GNSS基准站已经累积观测数据10年左右,对这些数据进行处理,研究其垂向坐标时间序列,分析其趋势项,可以监测我国高程基准面升降变化。基于此,本文首先对青岛GNSS基准站约10年的观测数据进行组网解算,并对准于ITRF2014框架,获得基准站垂向坐标时间序列;然后利用多种方法对垂向坐标时间序列中的粗差、偏差、趋势项和周期分量等分别进行处理和分析,得出青岛GNSS基准站垂向时间序列不存在显著趋势性变化,但受到比较明显的周年和半周年周期变化影响。最后结合青岛大港验潮站数据分析结果得出:青岛大港验潮站平均海平面的绝对上升速率是1.62 mm/a。
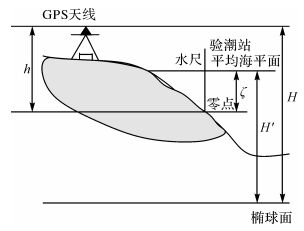
1 大港验潮站平均海平面升降原理图 1为平均海平面绝对变化原理示意图。监测系统由GNSS基准站和近邻的验潮站组成,它们共建在海边的同一处稳定的基岩上,可以认为其地壳运动的影响是相同的。
|
| 图 1 平均海平面绝对变化原理图 Fig. 1 Absolute change of the mean sea level |
通过分析验潮站验潮数据可以获得平均海面相对于水尺零点的高度ζ,通过GNSS基准站可以获得天线处相对于参考椭球面的大地高H,假设GNSS基准站的天线相位中心与验潮站水尺零点高差为h,平均海平面到参考框架椭球面的高度为H′,则
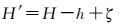 (1)
(1)
将式 (1) 对时间求导即可获得平均海平面相对于参考椭球的变化速度,由于两者共建在很近的同一稳定板块上,GPS观测站的垂直变化与验潮站是一致的,故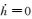
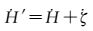 (2)
(2)
式 (2) 描述了平均海面绝对变化。由该式可见,平均海平面的绝对变化包括两方面的影响,即GNSS基准站求得的当地陆地垂直运动和验潮资料求得的海平面相对地壳的变化的共同作用,绝对平均海面变化速度等于验潮站垂直地壳形变与相对海平面变化速度的代数和。
根据参考文献[6],获得青岛大港验潮站平均海平面相对地壳的运动速度是1.62 mm/a。需要求得GNSS基准站地壳垂直运动速度,才能获得青岛验潮站平均海面的绝对变化。
2 青岛GNSS基准站数据预处理在对青岛GNSS基准站垂向坐标时间序列分析之前,首先对原始观测数据进行预处理,主要包括以下两步:
2.1 单日松弛解解算将全球50个稳定、可靠、具有连续观测数据的IGS站与国内包含SDQD在内的43个陆态网络基准站组成一个全球网,采用GAMIT软件对该网2005年第295 d至2015年第365 d的观测数据进行单日松弛解解算,在解算中国际IGS站坐标给予1 m约束,国内基准站坐标给予10 m约束。除去个别天因观测数据异常无法解算或者无观测数据,共计获得3095个单日松弛解。
2.2 单日约束解解算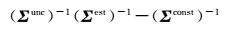 (3)
(3)
式中,Σunc代表去约束之后的协方差阵;Σest代表松弛解获得的协方差阵;Σconst代表GAMIT解算时加入的约束。
然后以50个IGS站的ITRF2014坐标为参考基准,采用如下公式加入最小约束[7-9],将整网坐标对准于ITRF2014
 (4)
(4)
式中,N=(Σunc)-1;ΔX=XC-Xapr,Xapr是坐标近似值 (GAMIT解算时采用的概略坐标),XC是解算获得的站坐标;K是单日松弛解获得的自由项;B=(ATA)-1AT
解算中,2006年第298 d和2007年第86 d因观测数据问题,解算结果异常而剔除,这样共计获得3293 d垂向坐标时间序列,如图 2所示。
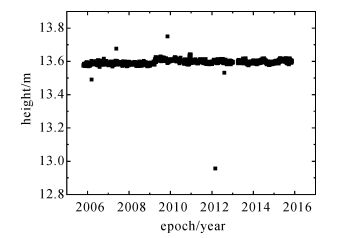
|
| 图 2 青岛GNSS基准站垂向坐标时间序列 Fig. 2 Height time series of Qingdao GNSS station |
3 青岛GNSS基准站垂向坐标时间序列分析
在进行地壳沉降分析之前,需要对GNSS垂向坐标时间序列进行“清理”,获得比较“纯净”的时间序列。GNSS垂向坐标时间序列中包含各种信号和误差影响,主要包括地壳运动引起的长期变化 (地壳沉降)、与地球物理相关的季节性变化、与技术数据处理相关的一些误差以及由于地震、基墩、接收机故障等引起的偏差或者粗差[10]。
3.1 粗差探测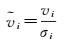 (5)
(5)
式中,vi为残差;σi为均方差因子。
当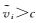
采用STARS算法进行偏差探测,STARS算法最早用于气象数据偏差探测[10, 13-14]。STARS算法的基本原理是基于t分布
 (6)
(6)
式中,diff=|vi-vR|;l是样本长度;vR是i前面l个样本平均值;σl是前面l个样本的均方差。
设定一定的置信度水平,获得临界值t0(事实上,在计算过程中需要根据实际情况,适当放大t0),通过判定t是否大于t0,初步诊断vi是否可能发生偏差跳变。具体确定vi是否真正发生偏差跳变,还需要通过如下指标判断
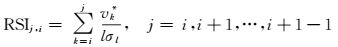 (7)
(7)
式中,如果vi>vR,那么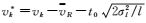
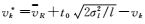
如果RSII+l-1, i>0,就判断vi发生偏差跳变;如果RSIi+1-1, i<0,就判断vi没有发生偏差跳变。
3.3 时间序列频谱分析采用离散傅里叶变换进行时间序列频谱分析
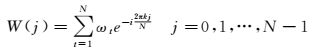 (8)
(8)
式中,W(j) 为频谱值;i为虚数。
3.4 坐标时间序列模型垂向坐标时间序列一般用如下模型描述
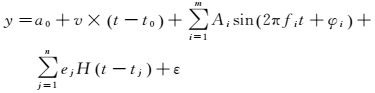 (9)
(9)
式中, y为垂向坐标分量;a0为t0历元的坐标;v是趋势项速度;Ai、φi分别为周期项的振幅和相位;ej为第j个偏差的大小;H(t-tj) 为阶跃函数;ε为残余误差。
通过以上4步不断迭代,探测粗差和偏差,分析周期项。具体步骤如下:
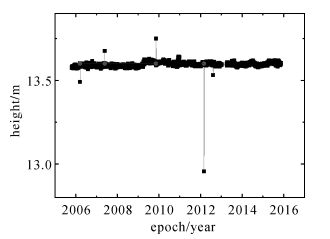
首先假定垂向坐标时间列中存在趋势项,利用式 (9) 去常数项、趋势项、周期项 (假定有周年和半周年周期项,不考虑偏差),对残差进行第1次粗差探测,设定临界值为c=8,探测出4个比较大的粗差,如图 3所示。
|
| 图 3 垂向坐标时间序列及粗差 (第1次探测) Fig. 3 Height time series and outliers (after the first detection) |
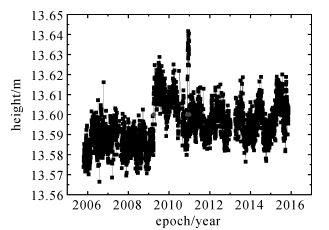
在此基础上,进行第1次偏差探测,设定t0=15(根据实际数据检验获得),共计探测出3个偏差 (发生时刻在2009.249、2010.909、2010.994),如图 4所示。
|
| 图 4 垂向坐标时间序列及偏差 (第1次探测) Fig. 4 Height time series and offsets (after the first detection) |
再次利用式 (9) 去常数项、趋势项、周期项和偏差,对残差进行第2次粗差探测,设定临界值是c=3,探测出30个粗差,如图 5所示。

|
| 图 5 垂向坐标时间序列及粗差 (第2次探测) Fig. 5 Height time series and outliers (after the second detection) |
进行第2次偏差探测,设定t0=10(根据实际数据检验获得),又探测出3个偏差,如图 6所示 (其中有3个是之前探测出的)。
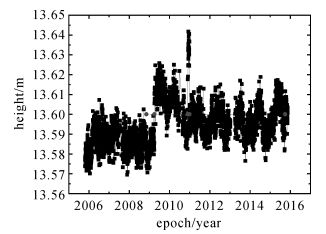
|
| 图 6 垂向坐标时间序列及偏差 (第2次探测) Fig. 6 Height time series and offsets (after the second detection) |
将该时间序列剔除粗差、调整偏差、去常数项和趋势项,对缺失的数据进行修补之后进行频谱分析,如图 7所示。从图中可以看出,垂向坐标时间序列具有较明显的周年 (0.998 2年)、半年周期 (0.477年) 影响,另外还有一个不明原因、周期接近3个月 (0.239年) 的噪声影响。
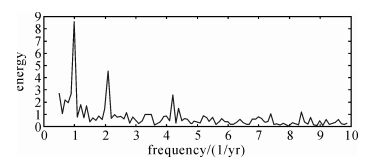
|
| 图 7 垂向坐标时间序列频谱分析 Fig. 7 Spectrum analysis of height time series |
至此,在垂向坐标时间序列中共计探测出粗差30个,偏差6个,并且明确存在周年和半周年周期影响,为下一步地壳沉降分析奠定基础。
4 大港验潮站地壳沉降分析坐标水平分量因板块地壳水平运动一定存在趋势项,但垂向则未必,因此在估计垂向趋势项之前有必要进行趋势项检验。
4.1 趋势项检验采用非参数Mann-Kendall检验[15],提出如下假设
 (10)
(10)
统计量ZS服从正态分布
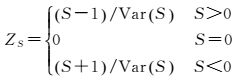 (11)
(11)
在一定的置信水平 (5%) 下,若|ZS|>Z1-α/2、S>0表明时间序列具有上升趋势,若|ZS|>Z1-α/2、S<0表明时间序列具有下降趋势,若|ZS|<Z1-α/2表明时间序列不具有明显趋势项。
Mann-Kendall检验统计量S为
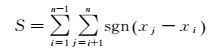 (12)
(12)
式中, n是时间序列长度;xi、xj分别是第i、j个垂向坐标值;sgn是符号函数。
var(S)由下式计算
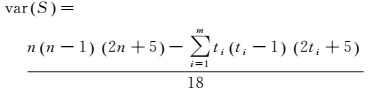 (13)
(13)
式中, m是重复点的集群数;ti是第i个集群的重复点数。
将时间序列剔除粗差、调整偏差、去掉常数项和周期项 (仅考虑周年和半周年项) 后,进行趋势项检验,计算获得S=-24 140,var (S)=3 969 440 389.001,|ZS|=0.383 1<Z1-α/2=1.96,因此认为青岛GNSS垂向坐标时间序列不存在显著性趋势项变化。
4.2 趋势项估计为了进一步验证垂向坐标时间序列中不存在显著性趋势项,采用式 (12),考虑常数项、趋势项、周年和半周年 (接近3个月的周期,因原因不明未考虑)、粗差以及偏差等各项因素,计算获得趋势项速度是-0.1 mm/a,标准差是0.005 mm/a,这进一步验证了垂向坐标时间序列不存在显著性趋势项变化。
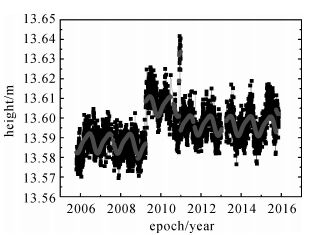
同时估计出周年和半周年周期振幅分别为4.684 mm、1.112 mm。图 8给出垂向坐标时间序列及其拟合曲线图,表 1给出6个偏差的估值及发生时间。
|
| 图 8 青岛GNSS基准站垂向坐标时间序列及其拟合曲线 Fig. 8 Height time series and the fitting curve of Qingdao GNSS station |
| 偏差1 | 偏差2 | 偏差3 | 偏差4 | 偏差5 | 偏差6 | |
| 发生历元/年 | 2008.854 | 2009.249 | 2010.909 | 2010.923 | 2010.994 | 2015.739 |
| 偏差估值/mm | -2.350 | 20.154 | 17.621 | 13.088 | -40.131 | 11.483 |
结合图 8和表 1可以看出,在2009.249、2010.909、2010.923、2010.994发生较大偏差跳变。据了解青岛站在2009年曾经因天线故障更换过接收机天线,但是在天线信息中没有记录,所以会在2009.249发生跳变。2010年陆态网络部分站点进行了整改,但是整改是在2010.495~2010.632历元之间,与2010年发生的3处跳变没有关系,从图 8中也可看出,这3处跳变更像比较短时间内的异常,因此判定是由观测数据异常引起的。另外,2008.249处比较小的跳变可能是由观测数据异常引起的,2015.739处的跳变也许因该站点2015年的拆卸有关,还需更多的数据研究。
5 结论青岛大港验潮站的地壳沉降直接关系到验潮站平均海平面变化的绝对值,研究青岛大港验潮站地壳垂向运动对我国高程基准基准的维持有重要意义。本文将青岛GNSS基准站约10年的观测数据纳入全球网进行综合处理,并进行垂向坐标时间序列分析,得出如下结论:
(1) 青岛GNSS基准站垂直方向受到比较明显的周年和半周年周期项影响,振幅分别为4.684 mm、1.112 mm。另外还受到不明原因的接近3个月的周期因素影响,需要进一步分析其成因。
(2) 青岛GNSS基准站垂直方向发生6次偏差或者跳变,分别在2008.854、2009.249、2010.909、2010.923、2010.994、2015.739历元,偏差估值分别为-2.350 mm、20.154 mm、17.621 mm、13.088 mm、-40.131 mm、11.483 mm,其中,2009.249跳变是由更换天线引起的,2015.739跳变也许与拆卸有关,其余跳变由观测异常引起。
(3) 在现有观测时间序列中,未发现青岛GNSS基准站垂向存在显著趋势性变化,结合文献[6],可以得出青岛大港验潮站平均海平面的绝对上升速率是1.62 mm/a。
| [1] | 郭海荣, 焦文海, 杨元喜, 等. 1985国家高程基准的系统差[J]. 武汉大学学报 (信息科学版), 2004, 29(8): 715–719. GUO Hairong, JIAO Wenhai, YANG Yuanxi, et al. Systematic Error of the 1985 National Height Datum[J]. Geomatics and Information Science of Wuhan University, 2004, 29(8): 715–719. |
| [2] | 陈宗镛. 计算平均海面的方法[J]. 山东海洋学院学报, 1960(1): 65–73. CHEN Zongyong. The Method of Calculating the Mean Sea Level[J]. Journal of Ocean Institute of Shandong, 1960(1): 65–73. |
| [3] | 陈宗镛. 潮汐学[M]. 北京: 科学出版社, 1980. CHEN Zongyong. Tide[M]. Beijing: Science Press, 1980. |
| [4] | 陈俊勇. 对我国建立现代大地坐标系统和高程系统的建议[J]. 测绘通报, 2002(8): 1–5. CHEN Junyong. On the Chinese Modern Geodetic Coordinate System and Height System[J]. Bulletin of Surveying and Mapping, 2002(8): 1–5. |
| [5] | 文援兰, 杨元喜. 我国近海平均海面及其变化的研究[J]. 武汉大学学报 (信息科学版), 2001, 26(2): 127–132. WEN Yuanlan, YANG Yuanxi. Research on Sea Level and Rising Trend of Coastal Waters in China[J]. Geomatics and Information Science of Wuhan University, 2001, 26(2): 127–132. |
| [6] | 吴富梅, 魏子卿, 李迎春. 大港验潮站潮汐分析与国家高程基准面变化[J]. 测绘学报, 2015, 44(7): 709–716. WU Fumei, WEI Ziqing, LI Yingchun. Analysis of Tidal Data for Dagang Tidal Gauge and Study of the Changes for the National Height Datum[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 709–716. DOI:10.11947/j.AGCS.2015.20140110 |
| [7] | ALTAMIMI Z, SILLARD P, BOUCHER C. ITRF2000: A New Release of the International Terrestrial Reference Frame for Earth Science Applications[J]. Journal of Geophysical Research, 2002, 107(B10): 2214. DOI:10.1029/2001JB000561 |
| [8] | ALTAMIMI Z, COLLILIEUX X, LEGRAND J, et al. ITRF2005: A New Release of the International Terrestrial Reference Frame Based on Time Series of Station Positions and Earth Orientation Parameters[J]. Journal of Geophysical Research, 2007, 112(B9): B09401. DOI:10.1029/2007JB004949 |
| [9] | ALTAMIMI Z, COLLILIEUX X, MÉTIVIER L. ITRF2008: An Improved Solution of the International Terrestrial Reference Frame[J]. Journal of Geodesy, 2011, 85(8): 457–473. DOI:10.1007/s00190-011-0444-4 |
| [10] | 明锋, 杨元喜, 曾安敏, 等. 顾及有色噪声的GPS位置时间序列中断探测法[J]. 武汉大学学报 (信息科学版), 2016, 41(6): 745–751. MING Feng, YANG Yuanxi, ZENG Anmin, et al. Offset Detection in GPS Position Time Series with Colored Noise[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 745–751. |
| [11] | KOCH K R, YANG Y. Konfidenzbereiche und Hypothesentests für Robuste Parameterschätzungen[J]. Zeitschrift für Vermessungswesen, 1998, 123(1): 20–26. |
| [12] | KOCH K R. Parameter Estimation and Hypothesis Testing in Linear Models[M]. Berlin: Springer-Verlag, 1988: 271-307. |
| [13] | SERGEI N, RODIONOV. A Sequential Algorithm for Testing Climate Regime Shifts[J]. Geophysical Research Letters, 2004, 31(9): L09204. |
| [14] | MING Feng, YANG Yuanxi, ZENG Anmin, et al. Analysis of Seasonal Signals and Long-term Trends in the Height Time Series of IGS Sites in China[J]. Science China Earth Sciences, 2016, 59(6): 1283–1291. DOI:10.1007/s11430-016-5285-9 |
| [15] | KENDALL M G. Rank Correlation Measures[M]. London: Charles Griffin, 1975: 202. |


