2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 湖北 武汉 430077
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China
空间电离层是影响全球导航卫星系统 (global navigation satellite system, GNSS) 应用最棘手的误差源之一。忽略电离层二阶及高阶项的影响,GNSS双频/多频用户可通过无电离层组合有效消除电离层误差对导航定位的影响[1]。但对占市场多数份额的GNSS单频导航用户而言,各导航系统播发的电离层模型参数仍是电离层误差实时修正的最主要手段[2]。
Klobuchar模型应用时间最长,是单频导航用户较为熟悉的电离层模型之一。由于模型参数并非由实测电离层TEC (total electron content) 信息计算得到,GPS广播的Klobuchar参数仅能在全球中纬度地区实现50%左右的电离层误差改正效果[3]。利用区域/全球GNSS监测站数据实现Klobuchar参数的重新解算,可以改善Klobuchar模型的应用效果[4]。虽然这种方法对Klobuchar模型的精度提升有限,但由于Klobuchar模型结构简单、使用方便,目前北斗区域卫星导航系统、IRNSS及QZSS均采用改进的Klobuchar模型为单频导航用户提供基本的电离层误差修正服务[5]。
Galileo采用NeQuick作为其全球广播电离层模型[6]。NeQuick是一种三维电离层模型,与二维电离层模型在某一给定高度的球面上对天顶电离层TEC (vertical TEC, vTEC) 分布进行模拟不同,NeQuick模型不仅能够计算空间任意给定高度 (包括GNSS卫星高度) 的电子密度,还可通过数值积分给出信号传播路径上的电离层TEC信息。意大利萨拉姆国际理论物理中心 (International Centre for Theoretical Physics, ICTP) 及欧空局 (Europe Space Agency, ESA) 等机构在NeQuick模型的公式改进、数据融合、参数解算及精度评估等方面开展了大量的工作[7-9]。国内有关最新NeQuick2模型的研究较少[10-11];NeQuick模型的数学结构较Klobuchar模型更为复杂,目前在GNSS单频导航用户中的使用也相对较少;2014年之前,Galileo广播星历中并不包含NeQuick电离层参数信息,这进一步限制了对NeQuick模型应用精度的评估。为分析NeQuick电离层模型参数的变化特点及其在全球不同地区的修正效果,本文首先讨论了NeQuick模型播发参数的计算方法,进而利用部分GPS基准站实测数据实现了NeQuick模型参数的解算,最后基于全球电离层格网产品 (global ionosphere map, GIM)、GPS基准站及JASON-2卫星提供的电离层TEC数据,评估不同NeQuick模型参数在全球大陆及海洋地区的实际应用效果,并与GPS广播星历中的Klobuchar模型作对比。
1 NeQuick模型参数的估计方法NeQuick模型采用Chapman函数构造的解析公式描述底层 (地面以上90 km至F2层峰值高度) 及顶层 (F2层峰值高度以上) 电离层的电子密度剖面,该模型包括NeQuick1及NeQuick2两个版本。与NeQuick1相比,NeQuick2中电离层E层、F1层及F2层峰值高度、各层厚度、临界频率等参数的计算公式均有了一系列改进;同时,NeQuick2引入CCIR系数文件代替NeQuick1中的ITU-R系数文件,引入新的地磁纬度文件MODIP代替原有的DIPLATS文件[12]。ESA等机构对NeQuick2的电子密度积分公式进一步优化,形成了适用于Galileo单频电离层误差修正的广播电离层模型-NeQuickG[9]。
NeQuick模型以时间、位置以及太阳活动指数 (如太阳黑子数R12或10.7 cm射电辐射通量F10.7) 为标准输入参数。文献[7]提出利用数据融合的方式来提高NeQuick模型的电离层TEC模拟效果,该方法的核心思路是利用实测电离层信息驱动NeQuick模型计算得到不同位置处的有效电离层水平因子Az,并将Az代替原有的太阳活动指数作为NeQuick模型输入参数。Galileo实际应用中采用类似的处理策略:主控中心基于各监测站前24 h的电离层观测数据,处理得到各监测站对应的Az值;进而在全球范围内采用二次多项式对其进行拟合,计算得到NeQuick电离层模型的3个播发参数a0、a1及a2;注入站将电离层参数信息上注至各卫星,Galileo单频用户利用接收到的3个电离层参数即可驱动NeQuick模型进行电离层延迟误差修正[6]。
a0、a1及a2 3个电离层参数将全球不同地区的Az值描述为随修正磁倾角μ变化的二次多项式
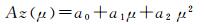 (1)
(1)
式中,修正磁倾角μ由式 (2) 计算得到;φ表示用户位置处的地理纬度;I表示距地面300 km高度处的磁倾角
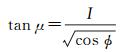 (2)
(2)
各监测站位置处的Az参数由下式计算得到
 (3)
(3)
式中,sTECoi和sTECmi分别表示第i个历元卫星与接收机视线方向的电离层TEC实测值及NeQuick模型计算值;N表示计算时段内的总历元个数。由于难以对式 (3) 进行线性化并给出Az的解析表达式,实际处理中采用搜索法 (如Brent方法) 搜索得到Az的最优解。
Galileo引入有效电离水平因子Az作为NeQuick的输入参数,该参数综合考虑了电离层随太阳及地磁活动的变化。Az参数的引入一方面避免了Galileo对外部太阳活动参数的依赖,使得利用地基GNSS数据实现模型播发参数的计算成为可能;另一方面,基于全球GNSS数据处理得到的模型参数,进一步提升了NeQuick模型的修正精度。需要说明的是,NeQuick模型在使用时需调用MODIP及CCIR文件,这在一定程度上限制了模型的计算效率;此外,MODIP文件每5年左右需要更新一次,以适应地球磁场的不断变化[13]。
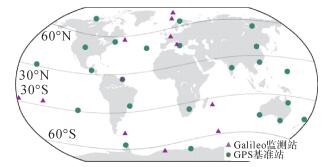
2 NeQuick模型参数的变化特征分析图 1给出了用于NeQuick模型参数计算的全球GPS基准站 (绿色圆点) 及Galileo监测站 (紫色三角) 分布示意图。本文在全球范围内选取23个GPS基准站,各基准站的电离层TEC实测值由GPS双频观测数据基于“相位平滑伪距”计算得到[14];GPS卫星和接收机差分码偏差 (differential code bias, DCB) 参数采用IGGDCB方法处理得到[15-16],GPS卫星P1-C1偏差直接采用欧洲定轨中心 (The Center for Orbit Determination in Europe, CODE) 提供的P1-C1偏差产品进行改正[17];与NeQuickG参数计算类似,NeQuickC参数计算时同样利用前一天的电离层TEC数据,具体的参数解算策略参见文献[18]。需要说明的是,截至2014年底,Galileo在全球共布设12个监测站 (见图 1),且大多分布在欧洲及全球海洋地区;共有4颗在轨卫星,其中E20自2014年6月1日之后仅播发E1单频的信号;Galileo主控中心基于各监测站的Galileo实测电离层信息,处理得到广播星历中播发的NeQuickG电离层参数[9]。
|
| 图 1 NeQuick模型播发参数计算采用的全球监测站分布 Fig. 1 Locations of the global monitoring stations used for NeQuick coefficients estimation |
图 2给出了2014年NeQuick模型参数解算值 (NeQuickC) 与广播星历播发值 (NeQuickG) 的对比情况,其中NeQuickG参数自2014年150 d后才可逐渐获得,且存在部分时段数据缺失的情况。可以看出,NeQuickC对应的a0参数在100~200 sfu之间变化 (1 sfu=1022·m2·Hz-1),远大于a1及a2参数;a2参数最小,该参数在-0.01~0.01 sfu/deg2之间变化。对比时段内,NeQuickC对应的a0参数值明显大于NeQuickG及F10.7指数,a1参数大小基本相同,而NeQuickC对应的a2参数值略小于NeQuickG。

|
| 图 2 2014年NeQuick模型参数解算值及Galileo广播星历播发值对比 Fig. 2 Comparison of the three ionospheric coefficients between the fitted NeQuickC and Galileo broadcast NeQuickG for the year 2014 |
以年积日 (day of year, DOY)180 d、280 d及360 d为例,图 3给出了各GPS监测站的Az计算值及其二次多项式拟合值。图中黑框表示各监测站的Az计算值,紫色实线和绿色虚线分别对应NeQuickC和NeQuickG模型参数对应的拟合值。从图中可以看出,各监测站的Az值与修正磁倾角之间表现出一定的变化规律,采用二次多项式基本可以描述全球不同地区的Az参数随修正磁倾角的变化。具体而言,DOY180 d及DOY360 d NeQuickC与NeQuickG的拟合结果相当,DOY180 d北半球监测站的Az值明显大于南半球,而DOY360 d则恰好相反;DOY280 d NeQuickC与NeQuickG拟合结果差异显著,特别是在磁纬±30°之间。结合图 2可以看出,2014年DOY150—365 d NeQuickC对应的a2参数基本为负值,而NeQuickG对应的a2参数基本为正值;这表明NeQuickC与NeQuickG拟合结果差异较大,特别是在赤道及低纬度地区。

|
| 图 3 各GPS监测站的Az计算值及二次多项式拟合值 Fig. 3 Az parameters estimated at each GPS monitoring station and the corresponding fitted second-order polynomials |
影响NeQuickC及NeQuickG参数拟合结果的因素包括:① 监测站数量与分布-NeQuickC及NeQuickG参数计算时分别在全球选取了23及12个监测站,其中磁纬±30o范围内分别有7个和3个监测站,赤道及低纬地区较少的监测站会影响二次多项式的拟合结果;② 观测数据-NeQuickC及NeQuickG参数计算时分别采用GPS及Galileo实测数据,2014年Galileo仅有4颗在轨卫星,较短的观测弧度及较少的观测数据会影响各监测站的Az计算值;③ 数据处理策略-卫星与接收机DCB参数处理方法、卫星截止高度角等也会对Az参数的计算产生影响,但影响较小[19]。综上所述,较少的Galileo可用卫星及全球监测站数量是NeQuickG与NeQuickC参数之间差异的主要原因。
随着Galileo卫星星座的日益完善,未来Galileo将在全球布设25~30个的监测站。NeQuickC参数计算时以全球23个监测站的GPS实测数据为基础,基本能够反映Galileo系统建成后NeQuickG参数的实际拟合效果。
3 不同NeQuick模型参数的精度分析 3.1 试验方案以IGS (International GNSS Services) 最终GIM产品、GPS基准站 (全球大陆地区选取32个IGS站) 实测电离层TEC以及JASON-2测高卫星电离层TEC为参考,评估不同NeQuick模型参数在全球不同地区的实际应用效果,评估时段为2014年DOY220—365 d。后文中,GPSKlob表示GPS广播星历中播发的Klobuchar模型参数,NeQuickC表示本文基于全球GPS监测站实测数据解算得到的NeQuick模型参数,NeQuickG表示Galileo广播星历中播发的NeQuick模型参数,NeQuick2的模型值由每天的太阳活动参数F10.7驱动计算得到。
需要说明的是,GIM格网、GPS基准站及JASON-2测高卫星提供的电离层TEC精度略有差异。IGS最终GIM产品的精度为2~8 TECu,2012年IGS电离层工作组启动GIM产品再处理后,IGS GIM产品的精度与可靠性均有显著提升[20]。各GNSS基准站基于“相位平滑伪距”计算得到的平滑电离层TEC应用最为广泛;平滑电离层采用逐连续观测弧段取平均的处理方式,在一定程度上易受平滑弧段长度、伪距测量噪声及多路径效应的影响;一般认为,平滑电离层TEC的提取精度在0.5~2.0 TECu左右[21-22]。测高卫星电离层TEC是独立于GNSS之外,全球海洋地区覆盖率最广、连续观测时间最长的电离层数据。测高卫星电离层TEC与GIM之间的偏差约为2~5 TECu[23],该偏差产生的原因之一是测高卫星给出的是卫星轨道高度 (JASON-2的轨道高度为1350 km) 以下至海面的电离层TEC,并没有包含卫星轨道高度以上的电离层信息。为减小这一偏差,本文根据文献[24]将JASON-2电离层TEC归化至GPS卫星轨道高度。综合利用GIM、GPS基准站及JASON-2测高卫星提供的电离层TEC信息,有利于全面反映不同NeQuick参数在全球大陆及海洋地区的电离层误差改正效果。
采用以下3种指标评估不同NeQuick模型参数的电离层误差改正效果
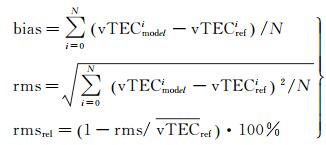 (4)
(4)
式中,bias、rms和rmsrel分别表示不同电离层模型的TEC计算值与TEC参考值之间的平均偏差、均方根及相对改正精度,vTECmodeli表示i历元不同电离层模型的TEC计算值,vTECrefi表示i历元的电离层TEC参考值 (由GIM格网、GPS基准站或JASON-2卫星获得),N表示评估时段内的总历元个数。bias和rms可以作为模型精度评估的绝对精度指标,rmsrel可以作为模型精度评估的相对精度指标。
3.2 与GIM TEC对比分析GIM能够反映不同电离层模型在全球范围内的总体修正情况,图 4给出了试验期间各电离层模型计算值与GIM TEC相比的RMS随时间的变化。不同时段内NeQuick模型的RMS变化较为平稳:NeQuick2及NeQuickG的RMS分别在10.4~11.6及12.5~13.4 TECu之间,NeQuickC与GIM相比的RMS最小,其对应的RMS在6.7~8.4 TECu之间变化。GPSKlob在00:00—12:00时段内误差较大,其RMS在13.8~18.0 TECu之间;12:00以后RMS趋于稳定,基本在12.3~13.1 TECu之间变化。

|
| 图 4 不同电离层模型计算值与GIM相比的RMS随世界时变化 Fig. 4 RMS of the differences between model TEC estimates and GIM TEC at different time bins (UT) |
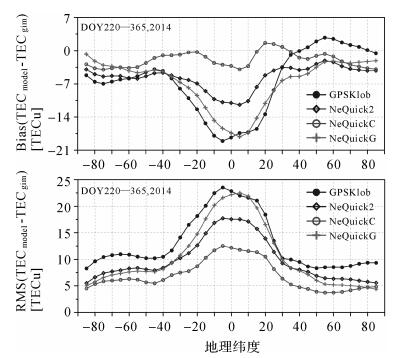
图 5给出了不同电离层模型与GIM相比的偏差及RMS在不同纬度带内的变化,相邻纬度带的间隔为5°。评估时段内,不同电离层模型的TEC计算值与GIM TEC相比均偏小。GPSKlob及NeQuickG在南北纬30°内的偏差值接近,其在赤道附近的偏差最大可达-22.0 TECu;在南北半球中、高纬地区,GPSKlob的偏差在-7.0~3.2 TECu之间,NeQuickG的偏差在-6.8~-0.3 TECu之间。NeQuickC给出的模型值与GIM TEC之间的差异最小,其偏差基本在-4.1~1.3 TECu之间变化。NeQuick2与NeQuickC的偏差变化趋势相同,但NeQuick2在赤道及低纬度地区的偏差明显大于NeQuickC。
|
| 图 5 不同电离层模型计算值与GIM相比的偏差及RMS随地理纬度变化 Fig. 5 Bias and RMS of the differences between model TEC estimates and GIM TEC at different geographic latitude bins |
不同电离层模型与GIM相比的RMS在赤道及低纬地区最大,且随着纬度的增加各电离层模型的RMS逐渐减小。具体而言,GPSKlob的RMS在7.9~23.8 TECu之间变化;NeQuickG在南北纬30°内的RMS大于NeQuick2,在中高纬地区二者的RMS基本相同;NeQuickC在不同纬度带内的RMS均最小,该模型在赤道附近的RMS为12.7 TECu,在中高纬地区的RMS为4.2 TECu。与GIM TEC的对比结果表明,NeQuickC的电离层修正精度明显优于NeQuickG,NeQuick2与NeQuickG修正精度相当,GPS广播星历中播发的Klobuchar模型修正精度最差。
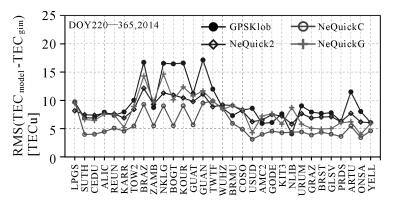
3.3 与GPS TEC对比分析以各GPS检核站获取的电离层TEC评估不同NeQuick参数在全球大陆地区的应用精度,图 6给出了2014年DOY 220—365 d不同电离层模型在各检核站的TEC计算值与GPS实测值相比的RMS。与GPS TEC相比,GPSKlob在赤道及低纬度检核站的误差最大,其RMS在8.7~17.1 TECu之间;NeQuickG在赤道及低纬度检核站的RMS为8.2~14.9 TECu,在中高纬度检核站的RMS为4.7~10.0 TECu;NeQuick2在低纬度检核站的RMS小于NeQuickG,在中高纬度检核站的RMS略大于NeQuickG;NeQuickC在所有GPS检核站的RMS最小,该模型RMS在3.1~10.0 TECu之间变化。
|
| 图 6 不同电离层模型在各检核站的计算值与GPS TEC对比的RMS Fig. 6 RMS of the differences between model TEC estimates and GPS TEC at the individual test station |
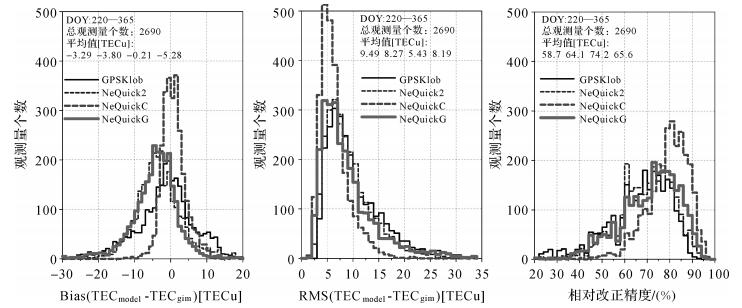
为直观反映不同电离层模型与GPS TEC相比的改正效果,图 7给出了试验期间各电离层模型精度指标的概率分布,从左至右分别对应模型计算值与GPS TEC相比的偏差、RMS及相对改正精度。GPSKlob、NeQuick2、NeQuickC及NeQuickG与GPS TEC之间的偏差分别为-3.29、-3.80、-0.21及-5.28 TECu,NeQuickC的TEC残差分布更为集中且期望接近于0。NeQuickC相对较小的RMS所占比例明显大于其他电离层模型,GPSKlob、NeQuick2、NeQuickC及NeQuickG对应的RMS均值分别为9.49、8.27、5.43及8.19 TECu。NeQuickC的相对改正精度主要分布在70%~90%,NeQuick2及NeQuickG的相对改正精度主要集中在60%~85%。与各GPS检核站电离层TEC相比,GPSKlob、NeQuick2、NeQuickC及NeQuickG在统计时段内的相对改正精度分别可达58.7%、64.1%、74.2%及65.6%。
|
| 图 7 不同电离层模型与GPS TEC相比的精度指标概率分布 Fig. 7 Histograms of the bias, RMS and relative RMS errors of different ionospheric models relative to GPS TEC |
3.4 与JASON-2 TEC对比分析
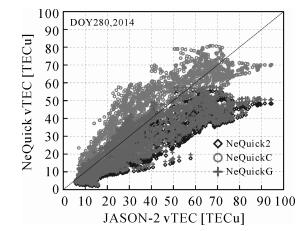
以JASON-2电离层TEC评估不同NeQuick参数在全球海洋地区的应用精度。以2014年280 d为例,图 8给出了该天不同NeQuick模型的TEC计算值与JASON-2实测值的对比情况。图中横坐标表示JASON-2电离层TEC实测值,纵坐标表示不同NeQuick模型给出的计算值。可以看出,NeQuick2及NeQuickG计算得到的TEC在海洋地区明显偏小,NeQuickC给出的TEC计算值与JASON-2实测值之间的一致性较好。
|
| 图 8 2014年280 d不同NeQuick模型的TEC计算值与JASON-2实测值对比 Fig. 8 NeQuick TEC estimates with respect to JASON-2 for DOY 280, 2014 |
图 9进一步给出了试验期间不同电离层模型与JASON-2 TEC相比的RMS随地理纬度的变化。从图中可以看出,不同电离层模型在南半球的RMS大于北半球;同时,各电离层模型沿纬度方向的RMS分布呈现出“双峰”结构,且RMS最大值出现在赤道两侧地区。NeQuickG与NeQuick2、NeQuickC之间的RMS差值在赤道及低纬度地区分别为0.8~2.0 TECu及2.3~7.1 TECu,在其他地区的差异较小。与JASON-2电离层TEC的对比结果表明,本文计算得到的NeQuickC参数与NeQuick2及NeQuickG参数相比在海洋地区同样具有明显优势。

|
| 图 9 不同电离层计算值与JASON TEC相比的RMS随地理纬度变化 Fig. 9 RMS of the differences between model TEC estimates and JASON TEC at different latitudes |
对比图 5、图 6及图 9可以看出,不同NeQuick模型与GIM、GPS及JASON-2 TEC相比的RMS随纬度的变化趋势一致,但NeQuickC的修正精度明显优于NeQuick2及NeQuickG。NeQuick2、NeQuickC及NeQuickG之间最大的区别在于输入参数的不同,可以看出:① 以太阳活动指数F10.7为输入参数的NeQuick2能够反映全球电离层TEC的变化情况,但其误差较大;② NeQuickC以本文拟合的a0、a1及a2为输入参数,该参数的计算利用了全球高、中、低纬度地区的实测电离层TEC信息,其在全球大陆及海洋地区给出的模型值与TEC参考值更为接近;③ NeQuickG以Galileo广播星历中播发的a0、a1及a2为输入参数,该参数在赤道及低纬地区的误差较大,当前较少的Galileo可用卫星数及全球监测站数量是NeQuickG参数在该地区应用效果较差的主要原因。
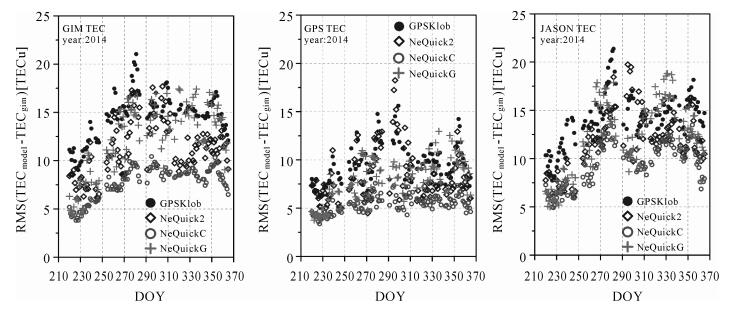
为分析不同电离层模型每天的修正精度情况,图 10给出了2014年DOY220—365 d各电离层模型的TEC计算值与GIM、GPS及JASON-2 TEC相比的RMS时间序列。可以看出,各电离层模型与GPS TEC相比的RMS小于以GIM及JASON-2 TEC为参考的对比结果:与GPS TEC相比,各电离层模型的RMS在3.0~15.0 TECu之间;与GIM及JASON-2 TEC相比,各电离层模型的RMS基本在5.0~20.0 TECu之间变化。与3类电离层TEC参考信息相比,NeQuickC在测试时段内的RMS最小,GPSKlob的RMS最大;NeQuickG与NeQuick2的修正精度相当,略优于GPS广播星历中播发的Klobuchar模型。
|
| 图 10 不同电离层模型计算值与GIM、GPS及JASON-2 TEC相比的RMS时间序列 Fig. 10 Time series of the TEC estimates obtained from different ionospheric models and those from GIM, GPS and JASON-2 satellites |
2014年DOY220—365 d不同电离层模型与GIM、GPS及JASON-2 TEC相比的精度统计见表 1。可以看出,各电离层模型的TEC计算值与以上3类电离层TEC参考信息相比均偏小。以GIM、GPS及JASON TEC为参考,测试时段内NeQuick2的修正精度分别为58.9%、64.1%及65.2%,NeQuickC的修正精度分别为71.9%、74.2%及71.1%,NeQuickG的修正精度分别为54.2%、65.6%及65.8%。基于不同电离层TEC参考信息得到的统计结果略有差异,总体而言,GPSKlob在全球范围内的修正精度最低,NeQuickC的修正精度最高;NeQuick2与NeQuickG修正精度相当,略优于GPSKlob。
| 电离层模型 | GIM TEC | GPS TEC | JASON TEC | ||||||||||
| bias | rms | rmsrel/(%) | bias | rms | rmsrel/(%) | bias | rms | rmsrel/(%) | |||||
| GPSKlob | -6.76 | 14.56 | 45.2 | -3.29 | 9.49 | 58.7 | -6.56 | 9.81 | 57.8 | ||||
| NeQuick2 | -5.76 | 11.17 | 58.9 | -3.80 | 8.27 | 64.1 | -4.53 | 8.67 | 65.2 | ||||
| NeQuickC | -1.85 | 7.71 | 71.9 | -0.21 | 5.43 | 74.2 | 0.99 | 5.73 | 71.1 | ||||
| NeQuickG | -7.12 | 12.58 | 54.2 | -5.28 | 8.19 | 65.6 | -6.64 | 8.40 | 65.8 | ||||
| bias与rms的单位为TECu。 | |||||||||||||
4 结论
本文基于全球23个均匀分布的GPS监测站数据实现了Galileo电离层模型参数NeQuickC的解算,以GIM、GPS基准站及JASON-2测高卫星电离层TEC为参考,全面分析了不同NeQuick模型参数在全球大陆及海洋地区的应用精度,包括以每天的太阳活动指数F10.7为输入参数的NeQuick2,以本文计算的a0、a1及a2为输入参数的NeQuickC,以及以Galileo广播星历中播发的a0、a1及a2为输入参数的NeQuickG,并与GPS广播的Klobuchar模型进行对比。
分析结果表明,NeQuickG与GIM、GPS及JASON-2 TEC相比的修正精度分别可达54.2%、65.6%及65.8%;NeQuick2与NeQuickG修正精度相当,优于GPSKlob约7%~9%;NeQuickC的修正精度最高,优于NeQuickG约5%~17%。NeQuick2及NeQuickG与GPSKlob相比具有一定优势,而NeQuickC与NeQuick2及NeQuickG相比,其电离层修正精度又有了显著的提升。NeQuickG在赤道及低纬地区修正精度较低,这与当前较少的Galileo可用卫星及全球监测站数量有关;随着Galileo卫星星座及地面监测站的日益完善,NeQuickG的拟合精度将进一步提升。后续将利用更多的NeQuickG参数数据,分析其在更长时段内的电离层误差修正效果。
| [1] | 张双成, 涂锐, 张勤, 等. 电离层二阶项模型的构建及其变化规律分析研究[J]. 测绘学报, 2011, 40(S): 105–110. ZHANG Shuangcheng, TU Rui, ZHANG Qin, et al. The Establishment of Ionospheric Second-order Model and the Analysis of Ionospheric Variation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S): 105–110. |
| [2] | YUAN Yunbin, HUO Xingliang, OU Jikun, et al. Refining the Klobuchar Ionospheric Coefficients Based on GPS Observations[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(4): 1498–1510. DOI:10.1109/TAES.2008.4667725 |
| [3] | KLOBUCHAR J A. Ionospheric Time-delay Algorithm for Single-frequency GPS Users[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, AES-23(3): 325–331. DOI:10.1109/TAES.1987.310829 |
| [4] | WANG Ningbo, YUAN Yunbin, LI Zishen, et al. Improvement of Klobuchar Model for GNSS Single-frequency Ionospheric Delay Corrections[J]. Advances in Space Research, 2016, 57(7): 1555–1569. DOI:10.1016/j.asr.2016.01.010 |
| [5] | 王斐, 吴晓莉, 周田, 等. 不同Klobuchar模型参数的性能比较[J]. 测绘学报, 2014, 43(11): 1151–1157. WANG Fei, WU Xiaoli, ZHOU Tian, et al. Performance Comparison between Different Klobuchar Model Parameters[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1151–1157. DOI:10.13485/j.cnki.11-2089.2014.0176 |
| [6] | OS-SIS-ICD. European GNSS (Galileo) Open Service Signal in Space Interface Control Document (Issue 1.1)[S].[S.l.]: European Union, 2010. |
| [7] | NAVA B, RADICELLA S M, AZPILICUETA F. Data Ingestion into NeQuick 2[J]. Radio Science, 2011, 46(6). DOI:10.1029/2010RS004635 |
| [8] | BIDAINE B, LONCHAY M, WARNANT R. Galileo Single Frequency Ionospheric Correction: Performances in Terms of Position[J]. GPS Solutions, 2013, 17(1): 63–73. DOI:10.1007/s10291-012-0261-0 |
| [9] | PRIETO-CERDEIRA R, ORUS-PERES R, BREEUWER E, et al. Performance of the Galileo Single-frequency Ionospheric Correction during In-Orbit Validation[J]. GPS World, 2014, 25(6): 53–58. |
| [10] | 杨哲, 宋淑丽, 薛军琛, 等. Klobuchar模型和NeQuick模型在中国地区的精度评估[J]. 武汉大学学报 (信息科学版), 2012, 37(6): 704–708. YANG Zhe, SONG Shuli, XUE Junchen, et al. Accuracy Assessment of Klobuchar Model and NeQuick Model in China[J]. Geomatics and Information Science of Wuhan University, 2012, 37(6): 704–708. |
| [11] | 吴显兵, 阮仁桂. 伽利略电离层改正模型的精度对比分析[J]. 测绘科学, 2015, 40(5): 17–20. WU Xianbing, RUAN Rengui. Accuracy Comparison and Analysis between Galileo Ionospheric Correction Models[J]. Science of Surveying and Mapping, 2015, 40(5): 17–20. |
| [12] | NAVA B, COÏSSON P, RADICELLA S M. A New Version of the NeQuick Ionosphere Electron Density Model[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2008, 70(15): 1856–1862. DOI:10.1016/j.jastp.2008.01.015 |
| [13] | HOQUE M M, JAKOWSKI N. An Alternative Ionospheric Correction Model for Global Navigation Satellite Systems[J]. Journal of Geodesy, 2015, 89(4): 391–406. DOI:10.1007/s00190-014-0783-z |
| [14] | BRUNINI C, AZPILICUETA F J. Accuracy Assessment of the GPS-based Slant Total Electron Content[J]. Journal of Geodesy, 2009, 83(8): 773–785. DOI:10.1007/s00190-008-0296-8 |
| [15] | LI Zishen, YUAN Yunbin, LI Hui, et al. Two-step Method for the Determination of the Differential Code Biases of COMPASS Satellites[J]. Journal of Geodesy, 2012, 86(11): 1059–1076. DOI:10.1007/s00190-012-0565-4 |
| [16] | WANG Ningbo, YUAN Yunbin, LI Zishen, et al. Determination of Differential Code Biases with Multi-GNSS Observations[J]. Journal of Geodesy, 2016, 90(3): 209–228. DOI:10.1007/s00190-015-0867-4 |
| [17] | DACH R, BROCKMANN E, SCHAER S, et al. GNSS Processing at CODE: Status Report[J]. Journal of Geodesy, 2009, 83(3-4): 353–365. DOI:10.1007/s00190-008-0281-2 |
| [18] | WANG Ningbo, YUAN Yunbin, LI Zishen, et al. An Examination of the Galileo NeQuick Model: Comparison with GPS and JASON TEC[J]. GPS Solutions, 2017, 21(2): 605–615. DOI:10.1007/s10291-016-0553-x |
| [19] | NIGUSSIE M, RADICELLA S M, DAMTIE B, et al. TEC Ingestion into NeQuick 2 to Model the East African Equatorial Ionosphere[J]. Radio Science, 2012, 47(5). DOI:10.1029/2012RS004981 |
| [20] | HERNÁNDEZ-PAJARES M, JUAN J M, SANZ J. The IGS VTEC Maps: a Reliable Source of Ionospheric Information Since 1998[J]. Journal of Geodesy, 2009, 83(3-4): 263–275. DOI:10.1007/s00190-008-0266-1 |
| [21] | 张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447–453. ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-Receiver's Differential Code Biases with Uncombined Precise Point Positioning Technique[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 447–453. |
| [22] | ZHANG Baocheng. Three Methods to Retrieve Slant Total Electron Content Measurements from Ground-based GPS Receivers and Performance Assessment[J]. Radio Science, 2016, 51(7): 972–988. DOI:10.1002/2015RS005916 |
| [23] | JEE G, LEE H B, KIM Y H, et al. Assessment of GPS Global Ionosphere Maps (GIM) by Comparison between CODE GIM and TOPEX/Jason TEC Data: Ionospheric Perspective[J]. Journal of Geophysical Research, 2010, 115(A10): A10319. |
| [24] | SCHARROO R, SMITH W H F. A Global Positioning System-based Climatology for the Total Electron Content in the Ionosphere[J]. Journal of Geophysical Research, 2010, 115(A10): A10318. |



