2. 武汉大学国家领土主权与海洋权益协同创新中心, 湖北 武汉 430079
2. Collaborative Innovation Center for Territorial Sovereignty and Maritime Rights, Wuhan University, Wuhan 430079, China
极地是地球气候系统的重要单元, 包含了大气、海洋、陆地、冰雪和生物等多圈层相互作用的全部过程。通过这些相互作用, 地球高纬度地区不断驱动着全球变化, 同时也深受全球变化的影响。极地拥有过去地球系统演变的独特信息, 对认识地球系统及其与人类活动的相互作用具有重要意义。在当下全球变暖、海冰迅速消融的背景下, 对极地冰雪以及冰盖变化的监测对于研究全球气候变化显得格外重要[1-2]。基于此, ESA (European Space Agency) 于2010年4月发射了CryoSat-2卫星, 主要目的是测量冰盖高度变化、评估其对全球海平面变化的影响以及观测两极海冰厚度的季节性变化。通过监测这些变化, CryoSat-2将进一步加深我们对极地地区在地球系统的重要作用的了解[3]。
对于南极而言, 卫星测高技术主要用于构建南极冰盖DEM和监测南极冰盖表面高程变化, 其中DEM是从事地学和环境变化研究重要的基础[4]。随着30多年的发展, 世界各地的极地工作者对南极DEM的研究取得了一定的进展。文献[5—6]分别采用Seasat测高数据和ERS-1卫星测高数据获得了分辨率各异的南极冰盖DEM。2007年, 利用ICESat激光测高数据, 美国国家雪冰数据中心 (NSIDC) 建立了分辨率500 m的南极冰盖DEM[7]。文献[8]利用ICESat测高数据确定了南极冰盖DEM, 并用南极实测GPS数据验证了DEM精度, 大地高差异最大为-10.50 m, 最小为0.27 m, 标准差为5.54 m。文献[9]结合GPS和ICESat数据建立了Dome A区域88 m分辨率的DEM。基于CryoSat-2卫星测高数据, 文献[10]建立了Dome A区域1 km分辨率的DEM。文献[11]利用冰桥计划 (IceBridge) 在西南极Thwaites冰川的机载激光测高数据, 对ICESat卫星测高数据和目前国际常用的4种南极DEM的精度进行了验证分析。但是特殊的地理位置和恶劣的气候条件导致南极大陆存在大面积的实测数据空白区域, 实测数据的稀缺成为建立高精度南极冰盖DEM制约条件之一。
卫星测高数据质量是卫星测高技术应用的基础, 测高卫星精密定轨、测高计硬件延迟、对流层和电离层延迟、海况偏差、地球物理改正和逆气压效应等是影响测高数据精度的重要因素。经过40多年的发展, 这些因素的影响逐渐得到改善或者消除, 测高数据精度达到了厘米量级, 因此卫星测高在开阔深海海域获得了良好应用。然而在包括冰盖在内的非开阔海域, 由于地形、地球物理环境和硬件响应等影响, 卫星测高精度有限, 波形重定方法成为提高测高精度的关键[12-13], 目前国内外已对波形重跟踪技术作了深入的研究。文献[14]对卫星测高技术中的波形重跟踪技术及其算法进行了详细分析讨论, 分析了波形重跟踪中最小二乘解初值及权的确定。文献[15]在阈值法的基础上提出了一种新的波形重跟踪算法—改进阈值法, 并采用了Envisat数据验证了其精度。文献[16]对β参数法进行了改进, 以呼伦湖为例, 发现经波形重定后的结果精度比未重定的GDR结果精度提高近2倍。文献[17]利用TOPEX/POSEIDON (T/P) 测高数据对OCOG、threshold、modified threshold波形重定算法进行了分析比较。文献[18]利用Jason-2卫星测高数据对ocean、ice、threshold, 以及modified threshold波形重定算法进行了比较分析, 利用EGM08验证发现ice波形重定方法最优。文献[19]利用台湾海峡的Topex/Poseidon测高数据对近海测高波形进行分类研究, 并提出了近海测高波形重跟踪的自适应方法。以上研究所选取的研究区域少有极地地区, 对于南极地区, 由于冰盖区域难以到达, 实测数据等精度验证数据较少, 国内外关于卫星测高在冰盖区域波形重定算法的研究不足, 对于最新的卫星测高CryoSat-2的研究更是如此。
坡度误差是陆地测高数据中一项重要的误差, 对格陵兰岛地区的测高数据分析结果显示, 地面坡度在0.1°以下时, 测距误差可达到84±79 cm, 地面坡度在0.7°时, 测距误差则达到10.3±8.4 m[20]。因此, 利用测高确定地面高程的精度主要取决于地面的坡度和起伏[21]。对于冰盖表面, 坡度因素足以引起10 m甚至更大的测距误差, 因此处理卫星数据时有必要对其进行坡度改正。
Dome A是东南极冰盖的最高冰穹, 其所在地区也是南极内陆冰盖海拔最高的地区。作为南极冰盖冰芯钻探理想地点和现代雪冰环境、大气与气象观测等独一无二的科学观测点, 在科学研究中具有无法代替的重要意义[22]。Dome A地区所具有的高海拔、低风速、干燥、低温、少地震等特殊地理和自然条件, 使其成为一系列科学研究的理想之地。它对全球气候变化具有极高的灵敏度, 是监测地球气温变化的理想地区。本文以南极Dome A昆仑站区为例, 利用与CryoSat-2数据时间同步的GPS数据, 对CryoSat-2最新的基线C数据LRM模式下的3种波形重定方法进行比较, 选取精度最高的波形重定方法, 在此基础上评估CryoSat-2精度, 并进行坡度改正处理, 将CryoSat-2与GPS数据进行数据融合, 获取该区域高精度300 m分辨率DEM。
1 数据介绍 1.1 GPS2013年1月, 第29次中国南极科学考察队在Dome A地区以昆仑站为中心30 km×30 km范围内实施了GPS测量, 采用静态和动态相结合的方式获得了该区域大量的GPS采样点 (如图 1(a), 其中静态GPS观测点共46个, 数据采样率为5 s, 空间分辨率为5 km, 持续观测时间均在20 min以上[23], 文中详细给出了这46个点的计算方法、计算过程、结果及其精度, 其高程精度在20 cm以内; 动态GPS在雪地车上实施观测, 采样率为1 s, 动态GPS的求解主要采用TBC软件, 对动态GPS观测点和参考站进行联合求解, 求解基线, 进而获得了动态GPS点的点位, 其中水平方向精度优于10 cm, 高程方向精度优于30 cm。考虑到部分地面软雪层等不确定因素对GPS结果精度影响, 利用46个高精度的静态GPS观测点对动态GPS进行数据约束, 最终使得动态GPS点位的整体高程精度优于20 cm。由于动态GPS数据采样率为1 s, 远高于卫星测高的空间分辨率, 利用GMT软件blockmedian命令对GPS点位信息进行重采样, 获得了1'分辨率的GPS数据, 并将该结果用于评估CryoSat-2高程精度。本文所采用的GPS数据均匀遍布Dome A地区, 可有效提升所建立的DEM精度。

|
| 图 1 数据分布图 Fig. 1 Sketch map of data |
1.2 CryoSat-2
作为最新的测高卫星, CryoSat-2卫星搭载了最新的合成孔径/干涉雷达高度计SIRAL (synthetic aperture interferometric radar altimeter), 该高度计在传统脉冲压缩雷达高度计的基础上, 融合了合成孔径和干涉技术, 使得CryoSat-2能高精度测量冰盖边缘, 系统地监测北极海冰的干舷高度变化。CryoSat-2卫星具备3种测量模式:① 低分辨率模式 (LRM) 主要用于观测海洋和冰盖; ② 合成孔径雷达模式 (SAR) 主要用于观测海冰; ③ 合成孔径雷达干涉测量模式 (SARIn) 主要用于观测冰盖边缘以及海洋浮冰。在南极Dome A地区位于东南极中部, 属于典型的冰盖区域, CryoSat-2在该地区使用低分辨率模式 (LRM) 测量[24]。
CryoSat-2数据产品经过两次变革, 第一次变革始于2012年5月, CryoSat-2数据产品由最初的基线A数据转换到基线B数据, 主要目的是为了提升CryoSat-2海冰观测的数据质量, 与基线A相比, 基线B采用了更精细的栅格间距。第二次变革始于2015年4月由基线B数据转换到基线C数据, 主要区别在于基线C启用新的地面处理系统IPF (Instrument Processing Facility), 升级后的IPF可有效提高CryoSat-2卫星在海洋、冰盖以及海冰上的测量精度。与基线B相比, 基线C修正了约-0.5195 ms、0.673 0 m、0.106 2°和0.052 0°的站偏差、距离偏差、横向和纵向倾角偏差[25], 因此基线C提供更高数据质量的数据产品。此外, 基线C分别为SAR、SARIN和LRM提供了1种、1种和3种波形重定算法对应的高程数据, 由于南极昆仑站区属于LRM模式覆盖, 有3种高程数据可供选择, 选取合适的波形重定算法十分必要。本文选取2010年7月至2013年6月CryoSat-2数据作为试验数据, 采用的改正量包括电离层、干/湿对流层改正、海潮、固体潮和极潮改正, 由此提取出3种波形重定算法对应的高程, CryoSat-2的地面轨迹空间分布如图 1(b)。由于波形重定算法的选取直接关系到高程精度, 下面详细介绍波形重定算法。
卫星测高发射信号, 通过反射面被卫星接收, 形成了随时间变化的能量曲线, 称为回波波形, 如图 2所示。测高卫星所观测的距离是从脉冲发射时刻到回波脉冲最大振幅的一半, 即前缘 (leading edge) 中点。卫星测高计在设计时通常预先设定某个时间点为波形的前缘中点, 该时间点称为预设跟踪门 (tracking gate), 但是回波波形容易受到反射面等因素影响, 致使预设跟踪门与波形前缘中点不一致, 波形重定主要用来确定波形前缘中点和预设跟踪门之间的偏移量, 然后根据公式计算距离改正[26]。CryoSat-2基线C中LRM模式提供3种波形重定算法:OCOG、Ocean CFI model fit以及LIRT (UCL land-ice) 算法, 其中OCOG算法以及CFI算法相较于基线B数据中所采用的波形重定方法均得到了优化, LIRT则是欧空局针对冰盖新研发的波形重定算法[24]。

|
| 图 2 波形重定示意图 Fig. 2 Schematic diagram of waveform retracking |
1.2.1 OCOG
传统的OCOG算法是基于统计规律得到的简单波形重定算法, 其基本思想是找到每个回波波形的重心, 以数值方式统计出波形振幅、宽度与重心位置。通过计算确定矩形的中心和面积与波形本身的重心和面积相同[26]。OCOG算法的数学公式为
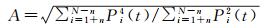 (1)
(1)
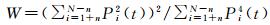 (2)
(2)
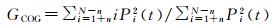 (3)
(3)
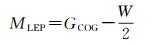 (4)
(4)
式中, N为阀门的总个数; n为波形开始和结束时应剔除的偏差波形采样个数; Pi(t) 为波形的第i个阀门的功率值; A为振幅; W为宽度; GCOG为波形的重心; MLEP为前缘中点。
OCOG算法易受噪声的影响, 有时候会出现重定的前缘中点太靠左。为了降低噪声对波形的影响, 基线C对传统的OCOG算法进行了改进, 在处理回波波形时, 额外添加一个可调控的子窗口以控制噪声的影响[24]。
1.2.2 CFICFI算法可以认为是一个二元的数据库, 所有的操作都在数据库内完成, 并不能提供波形重定方法过程中的细节信息, 因此很难改良和过程控制。基于CFI算法的局限性, 同样采取同OCOG类似改进方法, 相较于在基线B中所使用的CFI算法, 在波形重定过程中添加一个可控制的回波子窗口, 以提升CFI算法的波形重定质量。验证结果表明相对于基线B中的CFI波形重定方法, 利用新的CFI算法进行波形重定后的结果劣质数据更少[24]。
1.2.3 LIRTLIRT算法是欧空局在基线C中针对冰盖新研发的波形重定算法, 其全部参数均可在外部控制, 与CFI算法相比, LIRT算法拥有更强的调控性, 可根据目标区域的特征调整算法[24]。LIRT算法设计的初衷是设计一种可调控的波形重定算法, 以替代原有的CFI波形重定方法。其中, 回波波形符合布朗模型[18], 回波波形的平均功率为
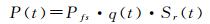 (5)
(5)
式中, P(t) 表示接收机所接收到回波波形的平均功率; Pfs表示平均脉冲响应; q(t) 表示构成散射表面的散射元, 点目标响应Sr(t) 反映雷达系统发射脉冲的包络波形。
2 结果与分析 2.1 重定算法选取与精度验证分别利用2010-07-16至2013-06-30期间CryoSat-2基线C 3种波形重定对应的高程建立对应的300 m分辨率的DEM, 利用GMT软件张力样条插值法内插得到GPS坐标对应的高程值, 与GPS高程求差。由于测高数据不可避免的出现误差, 利用数学统计方法对结果进行数据筛选, 选取差值的3倍标准差作为阈值, 认为超过3倍标准差之外的差值为异常值, 将异常值验证所得到的结果予以剔除。精度验证结果如表 1所示。
| m | |||||
| 数据筛选 前后 |
波形重 定方法 |
最大值 | 最小值 | 平均值 | 标准差 |
| 数据筛选前 | CFI | 47.94 | -2.71 | 1.91 | 1.69 |
| LIRT | 5.86 | -2.30 | 2.41 | 1.06 | |
| OCOG | 1.17 | -3.95 | -0.07 | 0.60 | |
| 数据筛选后 | CFI | 4.04 | -0.28 | 1.88 | 0.72 |
| LIRT | 5.31 | -0.38 | 2.47 | 0.95 | |
| OCOG | 0.78 | -0.61 | 0.08 | 0.23 | |
从验证结果来看, CFI算法的重定效果最差, 差值的平均值为1.91 m, 标准差为1.69 m, 其中差值的最大值出现了异常值; LIRT算法的效果比CFI算法稍好, 但其差值的平均值为2.41 m, 比CFI算法稍大, 标准差为1.06 m, CFI算法的一半; OCOG算法的波形重定效果最优, 差值的平均值为-0.07 m, 标准差为0.60 m。
数据筛选的结果如表 1, 从表中可以看出能提高测高的精度, 3种算法的差值平均值保持不变, 主要差别体现在标准差上, CFI算法标准差从1.77 m提高到0.75 m, 精度提升了约57%;LIRT算法差值从1.09 m提高到0.99 m, 精度提升了约10%;OCOG算法差值从0.60 m减小到0.23 m, 精度提升了约62%。其中, LIRT算法精度提升最小, 这是因为该算法针对冰盖设计, 与其他算法相比, 其波形重定结果出现异常值的概率较小, 因此数据筛选对其波形重定结果精度提升影响不大。综上, 相对于其他两种波形重定方法, 改进的OCOG算法在3种波形重定算法中精度最高, 证明在CryoSat-2基线C的LRM模式中OCOG算法在南极Dome A地区是较为合适的波形重定算法。
2.2 坡度因素与数据精度对于一个倾斜的表面测高仪观测的并不是卫星至星下点的距离, 而是到雷达脉冲覆盖区域中离卫星最近点的距离, 由于坡度因素, 反射点从星下点向上坡偏移, 测得的距离值相对真值偏小, 这种因为坡度所引起的误差叫作距离误差。
为探求坡度因素对CryoSat-2测高数据精度的影响程度, 下面以精度最高的OCOG波形重定高程数据为例, 对坡度与数据精度之间的关系进行分析, 其中坡度的计算方法为4块法[28], 坡度改正方法为直接法[21]。
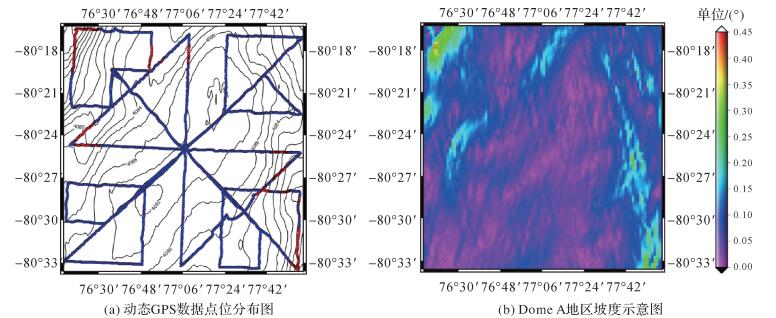
数据筛选中剔除的卫星粗差数据分布呈现出一定的规律性, 主要分布在Dome A地区的西北以及东南区域, 少量数据分布在其他地区, 如图 3(a)所示, 其中点状数据为1'分辨率的GPS数据, 红色点状数据为所剔除的粗差数据。Dome A地区西北以及东南区域地形起伏较大, 坡度较大, 这表明当坡度较大时, 卫星测高高程受坡度影响, 高程精度降低。这与文献[29]给出的结论一致, 即陆地测高波形会受到地形污染。
|
| 图 3 Dome A地区示意图 Fig. 3 Sketch map of Dome A |
利用GMT生成Dome A地区坡度示意图。对比图 3(a)与图 3(b), 可以发现数据筛选中所剔除的数据与坡度分布有较好的一致性, 剔除的粗差数据大多分布在坡度0.15°以上区域, 这说明在坡度较大区域出现粗差的可能性较大。
在数据筛选工作中所剔除的数据受到坡度因素影响成为异常数据, 对该部分异常数据所在的卫星数据做坡度改正, 利用重采样GPS数据对坡度改正前后卫星测高数据插值验证, 结果如表 2所示。为保证坡度改正前后所使用的GPS验证数据一致, 因此没有对验证结果做数据筛选工作。在表 2中可以看出经过坡度改正, 较差平均值得到改善, 从-0.07 m优化为0.03 m; 标准差从0.60 m降为0.37 m, 卫星测高精度约提高了38%。
| m | ||||
| 坡度改正前后 | 最大值 | 最小值 | 平均值 | 标准差 |
| 坡度改正前 | 1.17 | -3.95 | -0.07 | 0.60 |
| 坡度改正后 | 1.99 | -1.91 | 0.03 | 0.37 |
2.3 融合DEM
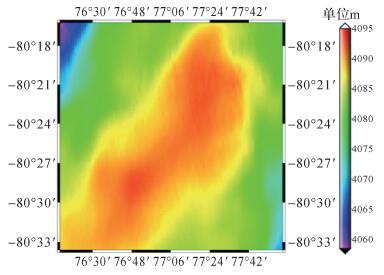
为了结合GPS在数据精度和CryoSat-2在空间分辨率上的优势, 采用数据联合的方法综合两类数据构建南极Dome A地区DEM[30]。即利用静态GPS结果对CryoSat-2数据精度控制, 建立新的DEM (如图 4所示), 所用的插值方法为克里金插值方法。从图 3(a)和图 4中可以看出Dome A地区中部存在东北向的马鞍形地形丘陵, 地形较为平坦, 西北及东南地区地势较低, 高程变化较快, 地形较为陡峭。
|
| 图 4 联合GPS与卫星测高建立的融合DEM Fig. 4 Fusion DEM based on GPS data and CryoSat-2 data |
利用重采样动态GPS数据对融合后的DEM以及国际上常用的两种高精度DEM进行插值验证, 验证结果如表 3所示。相由表可知, 较于单独使用OCOG算法得到的波形重定结果建立DEM, 使用GPS精度控制后的OCOG波形重定结果所建立的DEM精度有明显提升, 标准差仅为0.24 m, 精度约提升了60%, 说明联合GPS与卫星测高的数据融合, 可以提高DEM的精度。此外, 本文建立的融合DEM的精度优于Bamber 1 km DEM和ICESat DEM。这是因为本文在Dome A地区建立DEM时顾及了多种因素, 并采用了大范围、高精度的GPS数据进行精度控制, 这保证了在该区域本文所建立的融合DEM精度。
| m | ||||
| 数据 | 最大值 | 最小值 | 平均值 | 标准差 |
| OCOG波形重定 DEM |
1.17 | -3.95 | -0.07 | 0.60 |
| 融合DEM | 0.70 | -2.41 | -0.06 | 0.24 |
| Bamber 1 km DEM |
3.79 | -3.44 | 1.09 | 0.75 |
| ICESat DEM | 5.25 | -2.89 | 0.28 | 0.84 |
3 结论
本文选取了2010-07-16至2013-06-30期间CryoSat-2基线C卫星测高数据作为研究对象, 研究区域为Dome A地区, 通过3种波形重定方法对CryoSat-2测高数据进行了波形重定处理, 并将重定结果与第29次中国南极科学考察队在Dome A地区采集的GPS结果进行比较分析, 随后分析了坡度因素对卫星测高数据精度的影响, 利用了直接法对卫星测高数据进行了坡度改正处理, 并建立了基于GPS数据的CryoSat-2 Dome A地区DEM, 通过比较分析我们得到以下结论:
(1) 在CryoSat-2基线C LRM模式下提供的3种波形重定算法中, OCOG算法波形重定结果优于LIRT算法和CFI算法, 在南极Dome A地区进行波形重定时应采用优化后的OCOG算法。
(2) 坡度因素对于卫星测高精度的影响不可忽视, 坡度改正有助于卫星测高数据精度的提高。在Dome-A地区的验证结果显示, 考虑坡度改正后, 卫星测高精度约提高了38%。
(3) 联合GPS与卫星测高的数据融合, 可有效提高DEM的精度。与仅利用CryoSat-2卫星数据所建立的DEM、Bamber 1 km DEM和ICESat DEM相比, 联合GPS数据与卫星测高数据所构建的南极Dome A地区融合DEM精度较高, 较差平均值约为-0.06 m, 标准差为0.24 m。
| [1] | 汪汉胜, 张赤军. 南极冰盖部分消融对海平面的影响[J]. 测绘学报, 1996, 25(4): 247–251. WANG Hansheng, ZHANG Chijun. Global Sea Level Rise Caused by Partial Melting of Antarctic Ice Sheet[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(4): 247–251. |
| [2] | 杨磊, 常晓涛, 郭金运, 等. ENVISAT雷达高度计后向散射系数的极区海冰分布特性[J]. 测绘学报, 2013, 42(5): 676–681. YANG Lei, CHANG Xiaotao, GUO Jinyun, et al. Research on Distribution Characteristics of Polar Sea Ice by ENVISAT Altimetry Backscatter Coefficient[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 676–681. |
| [3] | BOUFFARD J, FEMENIAS P, PARRINELLO T, et al. CryoSat Data Quality Assessment and Product Evolutions[C]//EGU General Assembly. Vienna, Austria: EGU, 2015. |
| [4] | 张胜凯, 鄂栋臣, 周春霞, 等. 南极数字高程模型研究进展[J]. 极地研究, 2006, 18(4): 301–309. ZHANG Shengkai, E Dongchen, ZHOU Chunxia, et al. Progress on the Antarctic Digital Elevation Model[J]. Chinese Journal of Polar Research, 2006, 18(4): 301–309. |
| [5] | ZWALLY H J, BINDSCHADLER R A, BRENNER A C, et al. Surface Elevation Contours of Greenland and Antarctic Ice Sheets[J]. Journal of Geophysical Research, 1983, 88(C3): 1589–1596. DOI:10.1029/JC088iC03p01589 |
| [6] | BAMBER J L. A Digital Elevation Model of the Antarctic Ice Sheet Derived from Ers-1 Altimeter Data and Comparison with Terrestrial Measurements[J]. Annals of Glaciology, 1994, 20(1): 48–54. DOI:10.3189/172756494794586934 |
| [7] | DIMARZIO J, BRENNER A, SCHUTZ R, et al. GLAS/ICESat 500 m Laser Altimetry Digital Elevation Model of Antarctica[R]. Boulder, Colorado, USA: National Snow and Ice Data Center (Digital Media), 2007. |
| [8] | 李建成, 范春波, 褚永海, 等. ICESAT卫星确定南极冰盖高程模型研究[J]. 武汉大学学报 (信息科学版), 2008, 33(3): 226–228, 248. LI Jiancheng, FAN Chunbo, CHU Yonghai, et al. Using ICESat Altimeter Data to Determine the Antarctic Ice Sheet Elevation Model[J]. Geomatics and Information Science of Wuhan University, 2008, 33(3): 226–228, 248. |
| [9] | 王显威, 程晓, 黄华兵, 等. 结合GPS和GLAS数据生成Dome-A区域DEM[J]. 遥感学报, 2013, 17(2): 439–451. WANG Xianwei, CHENG Xiao, HUANG Huabing, et al. DEM Production for Dome-A Combining GPS and GLAS Data[J]. Journal of Remote Sensing, 2013, 17(2): 439–451. DOI:10.11834/jrs.20132036 |
| [10] | 张胜凯, 肖峰, 李斐, 等. 基于CryoSat-2测高数据的南极局部地区DEM的建立与精度评定[J]. 武汉大学学报 (信息科学版), 2015, 40(11): 1434–1439. ZHANG Shengkai, XIAO Feng, LI Fei, et al. DEM Development and Precision Analysis in Two Local Areas of Antarctica, Using CryoSat-2 Altimetry Data[J]. Geomatics and Information Science of Wuhan University, 2015, 40(11): 1434–1439. |
| [11] | 黄科伟, 李斐, 张胜凯, 等. 南极冰盖DEM机载测高验证与分析——以西南极Thwaites冰川为例[J]. 测绘学报, 2016, 45(5): 544–551. HUANG Kewei, LI Fei, ZHANG Shengkai, et al. Validation and Analysis of the Antarctic Digital Elevation Models Based on Airborne Altimetry——A Case Study of Thwaites Glacier, West Antarctica[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 544–551. DOI:10.11947/j.AGCS.2016.20150290 |
| [12] | 郭金运, 高永刚, 黄金维, 等. 沿海雷达卫星测高波形重定多子波参数方法和重力异常恢复[J]. 中国科学D辑:地球科学, 2010, 53(4): 610–616. GUO Jinyun, GAO Yonggang, HWANG Jinwei, et al. A Multi-Subwaveform Parametric Retracker of the Radar Satellite Altimetric Waveform and Recovery of Gravity Anomalies over Coastal Oceans[J]. Science China Earth Sciences, 2010, 53(4): 610–616. |
| [13] | 郭金运, 常晓涛, 孙佳龙, 等. 卫星雷达测高波形重定及应用[M]. 北京: 测绘出版社, 2013. GUO Jinyun, CHANG Xiaotao, SUN Jialong, et al. Waveform Retracking of Satellite Radar Altimeter and Applications[M]. Beijing: Surveying and Mapping Press, 2013. |
| [14] | 褚永海, 李建成, 张燕, 等. ENVISAT测高数据波形重跟踪分析研究[J]. 大地测量与地球动力学, 2005, 25(1): 76–80. CHU Yonghai, LI Jiancheng, ZHANG Yan, et al. Analysis and Investigation of Waveform Retracking Data of ENVISAT[J]. Journal of Geodesy and Geodynamics, 2005, 25(1): 76–80. |
| [15] | 鄂栋臣, 杨元德. 卫星测高波形重跟踪算法在南极应用的比较[J]. 大地测量与地球动力学, 2007, 27(1): 45–49. E Dongchen, YANG Yuande. Comparison among Several Altimetry Waveform Retracking Algorithms Applied in Antarctic[J]. Journal of Geodesy and Geodynamics, 2007, 27(1): 45–49. |
| [16] | 高永刚, 岳建平, 郭金运, 等. 卫星测高波形重定方法的改进研究[J]. 测绘通报, 2008(11): 7–9. GAO Yonggang, YUE Jianping, GUO Jinyun, et al. Improved Waveform Retracking Method of Satellite Altimeter[J]. Bulletin of Surveying and Mapping, 2008(11): 7–9. |
| [17] | KAO H C, KUO C Y, LEE H, et al. Hydrology Study in Rivers and Rice Fields Using Waveform Retracking of Satellite Altimeter[C]//EGU General Assembly. Vienna, Austria: EGU, 2010, 12: 83-85. |
| [18] | LEE H, SHUM C K, EMERY W, et al. Validation of Jason-2 Altimeter Data by Waveform Retracking over California Coastal Ocean[J]. Marine Geodesy, 2010, 33(S1): 304–316. |
| [19] | 汪海洪, 罗志才, 杨元德, 等. 基于波形分类的近海卫星测高数据自适应重跟踪方法[J]. 测绘学报, 2012, 41(5): 729–734. WANG Haihong, LUO Zhicai, YANG Yuande, et al. An Adaptive Retracking Method for Coastal Altimeter Data Based on Waveform Classification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 729–734. |
| [20] | BAMBER J L, EKHOLM S, KRABILL W. The Accuracy of Satellite Radar Altimeter Data over the Greenland Ice Sheet Determined from Airborne Laser Data[J]. Geophysical Research Letters, 1998, 25(16): 3177–3180. DOI:10.1029/98GL01594 |
| [21] | 汪海洪, 刘玉春, 王文波. 卫星雷达测高数据的坡度改正方法比较[J]. 大地测量与地球动力学, 2013, 33(3): 68–71. WANG Haihong, LIU Yuchun, WANG Wenbo. Comparison of Slope Correction Methods for Satellite Radar Altimeter Data[J]. Journal of Geodesy and Geodynamics, 2013, 33(3): 68–71. |
| [22] | 刘吉英, 温家洪, 王亚凤, 等. 南极冰盖最高冰穹Dome A数字高程模型的建立与初步应用[C]//中国地理学会2006年学术年会论文摘要集. 兰州: 中国地理学会, 2006. LIU Jiying, WEN Jiahong, WANG Yafeng, et al. Establishment and Preliminary Application of Antarctica Highest Dome-Dome A Digital Elevation Model[C]//Abstracts of the 2006 Annual Meeting of Chinese Geographical Society. Lanzhou: Chinese Geographical Society, 2006. |
| [23] | YANG Yuande, BO Sun, WANG Zemin, et al. GPS-derived Velocity and Strain Fields around Dome Argus, Antarctica[J]. Journal of Glaciology, 2014, 60(222): 735–742. DOI:10.3189/2014JoG14J078 |
| [24] | BOUFFARD J, FEMENIAS P, PARRINELLO T, et al. CryoSat Level-2 Product Evolutions and Quality Improvements in Baseline C[C]//EGU General Assembly. Vienna, Austria: EGU, 2015. |
| [25] | SCAGLIOLA M, FORNARI M, DI GIACINTO A, et al. CryoSat Level1b SAR/SARin BaselineC: Product Format and Algorithm Improvements[C]//EGU General Assembly. Vienna, Austria: EGU, 2015. |
| [26] | WINGHAM D J, RAPLEY C G, GRIFFITHS H D. New Techniques in Satellite Altimeter Tracking Systems[C]//IGARSS 86 Symposium. Zurich: [s.n.], 1986. |
| [27] | BROWN G. The Average Impulse Response of a Rough Surface and Its Applications[J]. IEEE Transactions on Antennas and Propagation, 1977, 25(1): 67–74. DOI:10.1109/TAP.1977.1141536 |
| [28] | 黄培之. 利用地面数字高程模型解求地面坡度值的方法及其评述[J]. 铁道勘察, 1989(1): 19–23. HUANG Peizhi. Method and Its Review for Calculating Ground Slope Value by Using Digital Elevation Model[J]. Railway Investigation and Surveying, 1989(1): 19–23. |
| [29] | SANTORO M, ASKNE J I H, WEGMULLER U, et al. Observations, Modeling, and Applications of ERS-ENVISAT Coherence over Land Surfaces[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(8): 2600–2611. DOI:10.1109/TGRS.2007.897420 |
| [30] | 王泽民, 熊云琪, 杨元德, 等. 联合ERS-1和ICESAT卫星测高数据构建南极冰盖DEM[J]. 极地研究, 2013, 25(3): 211–217. WANG Zemin, XIONG Yunqi, YANG Yuande, et al. Antarctic Digital Elevation Model from ERS-1 and ICESat Data[J]. Chinese Journal of Polar Research, 2013, 25(3): 211–217. |



