2. 西南交通大学高速铁路运营安全空间信息技术国家地方联合工程实验室, 四川 成都 610031;
3. 西南交通大学“2011计划”轨道交通安全协同创新中心, 四川 成都 610031
2. State-Province Joint Engineering Laboratory of Spatial Information Technology for High-speed Railway Safety, Southwest Jiaotong University, Chengdu 610031, China;
3. Collaborative Innovation Center for Rail Transport Safety, Ministry of Education of the People's Republic of China, Southwest Jiaotong University, Chengdu 610031, China
数字高程模型 (digital elevation model, DEM) 是地表形态的数字化表达,是重要的国家基础地理数据之一,在地貌、水文、土壤、灾害、规划等领域广泛应用[1-2],如利用外部DEM辅助高分辨率雷达影像地形制图[3],基于参考DEM的机载InSAR无人工靶标的干涉定标[4]等。在DEM运用过程中常需要进行数据尺度转换、地形简化、重采样等方面的数据处理,例如由30 m分辨率DEM生成90 m分辨率DEM的重采样过程中,需要进行栅格数据的聚合计算处理。DEM格网聚合是根据指定的聚合策略对输入栅格进行重采样,获得更为粗糙分辨率的栅格,最终获得计算处理后的新栅格单元高程值[5]。目前,一些GIS软件提供了总和、最小值、最大值、平均值、中位数的聚合策略以及通过双线性插值法等方法对原始DEM格网进行重采样聚合[6]。聚合计算过程实际上是聚合窗口内格网点属性权重分配的过程,即聚合值是聚合窗口内格网点高程向量的一种线性组合[7]。如果能够根据数学模型找到聚合窗口内的所有格网点高程属性间的某种数学关系,从而得到每个格网点高程值的权重系数,那么就可以根据这种权重系数来计算新格网点的高程聚合值。数理统计中的主成分分析方法可以揭示变量之间的关系,并能够化简数据,把原来多个指标减少为少数几个相互独立且包含原始指标绝大部分信息的综合指标[8-9],它广泛应用于特征提取、数据简化等领域[10]。该方法较多应用于遥感影像处理与分析,并取得了较好的效果,如结合主成分分析实现遥感影像分类[11]、研究SAR图像相干斑抑制方法[12],用小波域主成分分析提取检测窗口内图像特征向量[13]等。根据主成分分析方法的特点,可以运用主成分变换模型来构建聚合窗口中各个格网属性间的相互关系,得到各格网属性的权重,从而可计算出聚合窗口的属性聚合值。
为了评价格网聚合效果,有必要对聚合重构DEM误差进行分析。DEM误差分析与精度评定的目的是期望得到高质量、高精度的DEM产品,以便准确地反映地表起伏变化规律。DEM误差相关研究成果阐明了DEM整体误差包括原始数据传递过来的误差和DEM计算模型误差两部分[14-15],且均视为随机误差,用DEM中误差来描述[16]。传统的DEM误差研究主要利用经验公式或误差模型来表达原始数据、内插模型、地形形态特性和地形表达方法引起的误差[17-18],DEM误差分布的形态没有受到太大重视[15]。用少量的检查点来评估整个DEM质量,其取样有效性值得商榷[19],虽然整体上DEM误差较小,但不同位置的局部误差可能较大[20]。研究表明DEM误差分布具有空间相关性[21-22]。地统计分析、回归分析等方法可用于分析DEM误差的空间格局、变异特性以及空间相关性[16],相关研究主要有采用条件随机模型模拟DEM误差的空间分布[23],利用半变异函数描述DEM误差的空间分布结构[24],利用空间相关分析法、线性回归图和剖面图等技术,研究DEM误差与高程的空间关系[25]。在研究基于DEM提取流域网络算法时考虑了误差空间分布特征[26]。此外,利用随机过程构建的精度场模型适用于评价任意插值方式生成的格网DEM的精度[27]。从上面分析可知,DEM误差既具有随机性,又具有空间结构性。因此,除了比较验证DEM误差的随机性外,还需进一步研究DEM误差的空间结构信息。
本文将基于主成分变换模型研究DEM格网聚合原理,以均值聚合和双线性重采样聚合重构DEM为比较对象,从聚合前后检查点的高程偏差的统计描述、空间变异、空间自相关性,以及等高线套合差异方面分析3种聚合策略下重构DEM的误差特性,并分析评价主成分聚合重构DEM的质量效果,探索一种既能保证较高精度,又较好地保持地形形态特征的DEM格网聚合新方法。
1 基于主成分模型的DEM格网聚合原理主成分分析可以将p个变量的大部分变差由比p小得多的k个主成分来概括。这k个主成分均是原变量的特殊线性组合,且包含在这k个主成分中的信息与原来p个变量的信息几乎一样多,可以用这k个主成分代替原p个变量[9]。因此, p个变量的n次观测样本就可简化为k个主成分的n次观测样本,这里k≤p。基于主成分分析模型,将DEM格网聚合窗口内各格网点高程作为样本观测值,能够建立聚合窗口内各格网点高程数据间的相关关系。
设聚合窗口 (图 1) 大小为p行、p列,把聚合窗口每列作为一个变量对待,每一行作为一组观测样本,则有p个变量:x1, x2, …, xp;p组观测值。主成分的综合变量设为y1, y2, …, yk;k≤p。根据主成分变换模型,则存在一个p行、p列的正交变换U,使得式 (1) 成立
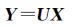 (1)
(1)

|
| 图 1 聚合窗口示意图 Fig. 1 A diagram of aggregation window |
式中,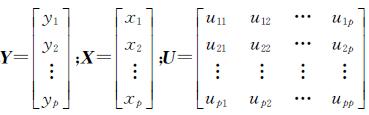
式中, X为p个原变量的向量矩阵;Y为p个主成分综合变量的向量矩阵;U为p行、p列的正交变换矩阵。将矩阵公式 (1) 展开,得到方程组如式 (2) 所示
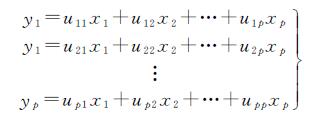 (2)
(2)
设第i个主成分的贡献率用Ci表示,i=1, 2, …, p,则Ci的计算如式 (3) 所示
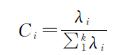 (3)
(3)
式中,λi为第i主成分的方差。
设第i主成分与第j个变量xj的相关系数估计值用ρij表示。相关系数ρij称为第j个变量xj在第i个主成分上的负荷量,也称为因子负荷量,它反映了原变量xj与第i个主成分之间的相关关系。根据聚合窗口格网高程值可计算出相关系数的样本估计值,ρij的计算如式 (4) 所示
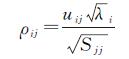 (4)
(4)
式中,λi为第i主成分的方差;uij为正交变换矩阵U的第i行、第j列元素;Sjj为第j个变量xj的样本方差;i=1, 2, …, p; j=1, 2, …, p。
根据各主成分与原变量间的相关系数,以及各主成分的贡献率构建聚合格网属性值的计算模型。设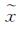
 (5)
(5)
式中,i=1, 2, …, k; j=1, 2, …, p。聚合计算时,取k=p,即在主成分累计贡献率为100%的情况下进行计算。先对第i主成分与各变量xj的相关系数做归一化处理,然后计算第i主成分下各变量加权平均值,并乘以第i主成分贡献率Ci,得到第i主成分下各变量系数;依次计算所有主成分下各变量系数并求和。
综上,基于主成分变换模型格网聚合 (简称主成分聚合) 的基本思路为:先根据第i主成分与p个变量之间的相关系数计算p个变量的加权平均值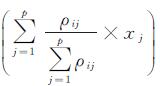
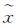
以30 m分辨率DEM转换为90 m分辨率DEM为例,对30 m分辨率DEM分别利用主成分聚合、均值聚合和双线性插值重采样进行3×3窗口移动聚合计算,得到各聚合策略下90 m分辨率的重构DEM。然后将主成分聚合计算得到的重构DEM与均值聚合和双线性插值重采样聚合得到的重构DEM进行比较,以原始DEM为参照,分析3种聚合策略下重构DEM格网点相对于原始DEM的高程偏差的统计描述特性、空间分布与自相关性,并采用等高线套合法定性与定量分析各聚合策略下重构DEM所表达的地形形态特征吻合效果。
3种聚合策略的计算方法分别是:主成分聚合方法是根据上文推导出的聚合模型计算聚合值;均值聚合方法是将聚合计算窗口内各格网点高程值的算术平均值作为聚合值;双线性插值重采样聚合方法是基于窗口内4个最邻近的格网中心的加权平均距离进行双线性插值计算聚合值。主成分聚合计算根据推导的聚合模型通过编程实现;均值聚合和重采样聚合计算均采用GIS软件平台提供的功能模块完成。
分析和评定聚合模型的计算效果时,仅考虑聚合模型带来的误差。从3个方面分析聚合重构DEM的误差。
(1) 分别从高程均值差、高程中误差以及聚合前后检查点高程偏差的离散程度、分布形态等方面进行统计描述分析。高程均值差是聚合策略下重构DEM所有格网点高程算术平均值与原始DEM所有格网点高程算术平均值的差值。高程中误差和聚合前后格网点高程偏差采用检查点法来评定。该方法是在试验样区布设若干检验点,分别获取检查点的实际高程和重构DEM上相应位置上的高程值,然后计算两者差值,得到各个检查点的高程偏差[28]。假设检查点的实际高程为zk,在重构DEM上对应这些点的高程为Zk, n为布设检查点的个数,则聚合前后检查点高程的均方根误差 (root mean square error,RMSE) 计算如式 (6) 所示
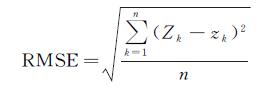 (6)
(6)
为了提高定量评定各聚合策略下重构DEM精度的准确性,将聚合计算得到的90 m分辨率重构DEM的所有格网点作为检查点。分别从原始30 m分辨率DEM、3种聚合策略下获得的90 m分辨率重构DEM上提取检查点对应的高程值,聚合重构DEM上检查点高程值减去原始DEM上检查点高程值得到高程偏差,计算检查点高程偏差的均方根误差来定量评定聚合重构DEM的精度,并对检查点高程偏差进行统计描述分析。
(2) 分析各聚合策略下重构DEM误差的空间变异与自相关性。所有检查点高程偏差作为样本,利用普通克里金插值方法建立误差场,基于半变异函数模型探索DEM误差的空间变异与空间自相关性,分析聚合重构DEM误差的空间分布规律。
(3) 采用等高线套合分析法评价DEM误差的总体状况和聚合重构DEM与原始地形的吻合程度.根据各聚合策略重构DEM生成等高线, 并将它与原始DEM生成的等高线叠加, 检查同名等高线套合的差异情况.这种差异能定性和定量评价聚合重构DEM误差总体状况以及它与原始地形的吻合程度.把原始等高线与聚合重构DEM回放等高线进行叠加构面空间运算, 生成一系列的差异图斑, 用差异图斑的面积变量来量化反映回放等高线与原始等高线之间的差异程度.设试验样区面积为A, 共有n个差异图斑, 第i个差异图斑的面积为αi, 所有差异图斑面积与试验样区面积的比值用ε表示, 它表示回放等高线与原始等高线间整体差异程度, 称为差异率, 计算公式如式 (7)
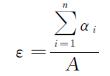 (7)
(7)
用p表示试验样区回放等高线与原始等高线的套合率, 计算公式如式 (8)
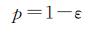 (8)
(8)
同时,还对试验样区所有的差异图斑面积进行描述性统计分析,以期发现等高线套合率与差异图斑面积变量间的关系。
此外,为了试验论证上述模型与方法,选择了四川雅安部分区域作为试验样区。样区总面积约66 km2,最小高程846 m,最大高程1994 m,平均坡度20.7°,地表形态较为复杂。样区试验数据为下载的SRTM的30 m分辨率DEM数据。
3 主成分聚合效果对比分析与评价以ArcGIS提供的均值聚合和双线性插值重采样聚合重构DEM为比较对象,分析主成分聚合重构DEM的误差特性。分别从高程误差统计分析、空间变异分析和等高线套合对比分析3方面分析评价3种聚合策略下重构DEM的误差。
3.1 聚合重构DEM高程误差统计分析高程均值差从整体上反映了聚合重构DEM与原始DEM地形吻合的差异程度。高程均值差绝对值越小,说明聚合重构DEM相对于原始DEM的地形重构总体偏差越小,反之地形重构总体偏差则越大。利用ArcGIS栅格计算器获得的检查点高程偏差如表 1所示。从表 1统计数据可以看出,高程均值差绝对值由小到大的聚合方法依次是重采样聚合、主成分聚合和均值聚合。相对于均值聚合,主成分聚合能够较好地保持地形特征。从高程中误差统计数据可看出,主成分聚合和均值聚合重构DEM的精度基本一致,且均高于重采样聚合重构DEM的精度。
| m | ||||
| 主成分聚合 | 均值聚合 | 重采样聚合 | ||
| 高程均值差 | -1.246 | -1.377 | 0.908 | |
| 高程中误差 | 13.447 | 13.447 | 22.024 | |
| 检查 点高 程偏 差 | 均值 | -0.483 | -0.587 | -0.529 |
| 标准偏差 | 13.439 | 13.435 | 22.019 | |
| 最小值 | -67.000 | -67.890 | -98.000 | |
| 1/4分位数 | -7.000 | -7.333 | -14.000 | |
| 中位数 | 1.000 | 0.667 | 4.000 | |
| 3/4分位数 | 8.000 | 7.667 | 13.000 | |
| 最大值 | 51.000 | 52.000 | 79.000 | |
| 偏度 | -0.580 | -0.618 | -0.543 | |
| 峰度 | 1.376 | 1.416 | 0.681 | |
从检查点高程偏差的各统计量分析可知,高程偏差均值绝对值由小到大的聚合方法依次为主成分聚合、均值聚合和重采样聚合,说明主成分聚合重构DEM从整体上更逼近原始地形。主成分聚合与均值聚合重构DEM的高程偏差的标准差非常接近,且远小于重采样聚合重构DEM的高程偏差的标准差,说明主成分聚合与均值聚合重构DEM的误差分布较为集中,而重采样聚合重构DEM的误差分布更为离散。高程偏差的极差,即高程偏差最大值与最小值的差值,可粗略地测定高程偏差的离散程度。主成分聚合重构DEM的高程偏差的极差略小于均值聚合重构DEM的高程偏差的极差,重采样聚合重构DEM的高程偏差的极差最大,说明主成分聚合重构DEM的高程偏差数据相对要集中。
分位数、偏度和峰度反映了聚合重构DEM高程偏差样本数据分布状况。可用四分位差,即第3四分位到第1四分位之间距离的一半,来分析高程偏差样本数据的离散程度。从四分位差计算结果看,主成分聚合与均值聚合重构DEM的高程偏差的四分位差均是7.50 m,重采样聚合重构DEM的高程偏差的四分位差是13.5 m;相对于重采样聚合,主成分聚合重构DEM的高程偏差分布更为集中。峰度统计量描述了检查点高程偏差样本分布形态陡缓程度。峰度绝对值越大,则高程偏差样本数据分布形态的陡缓程度与正态分布形态的差异程度越大。峰度统计数据分析表明,3种聚合策略重构DEM高程偏差样本数据的峰度均大于0,样本数据分布比正态分布形态更为陡峭;主成分聚合重构DEM高程偏差样本数据的峰度值比均值聚合重构DEM高程偏差样本数据的峰度值小;与均值聚合重构DEM比较,主成分聚合重构DEM高程偏差样本数据分布形态更接近于正态分布形态。偏度统计量描述了高程偏差样本数据分布的对称性。偏度绝对值越大,其分布形态的偏斜程度越大。偏度数据分析表明,3种聚合策略重构DEM高程偏差样本数据分布形态均为负偏,且偏斜程度由小到大的聚合方法依次是重采样聚合、主成分聚合和均值聚合。
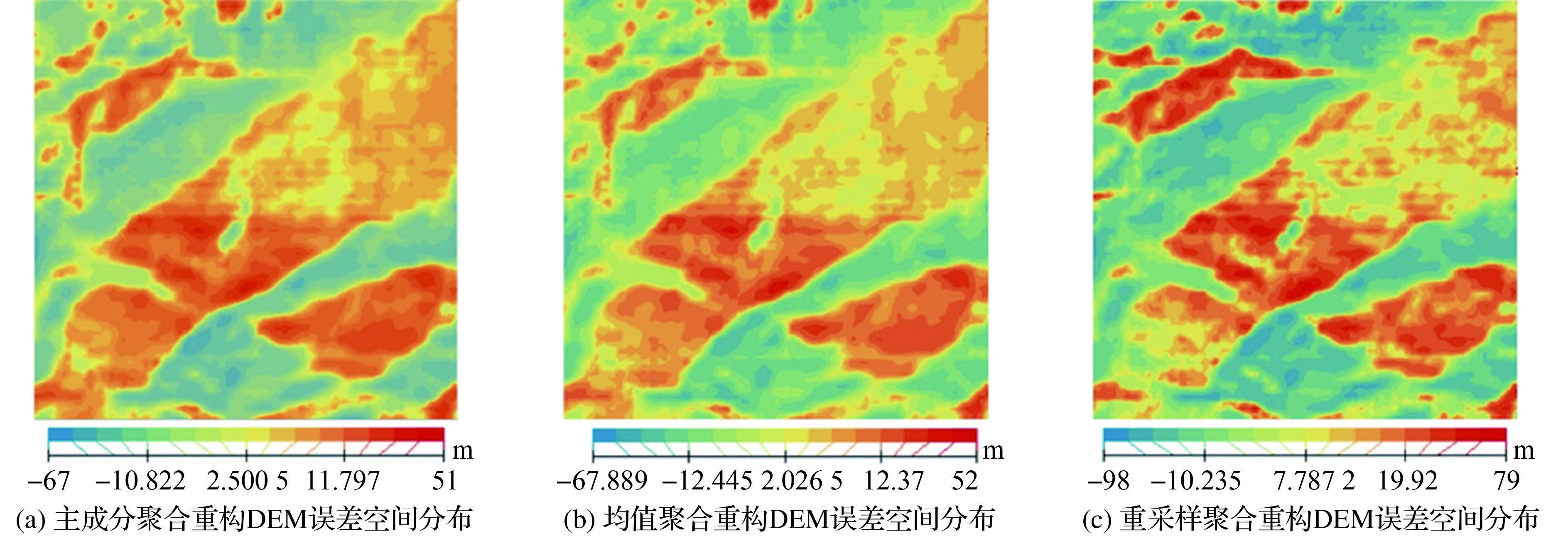
3.2 聚合重构DEM高程误差空间变异与空间自相关性分析从重构DEM高程误差的空间分布图 (图 2) 可以看出,3种聚合策略下重构DEM的不同级别的高程误差的分布与空间位置相关,不同位置的高程误差差异较大,且地形复杂地区的高程误差较地形平坦地区的高程误差要大,所以不能单独只用高程中误差指标来衡量重构DEM的误差大小,还需要进一步分析高程误差空间分布与空间自相关特性。
|
| 图 2 聚合重构DEM高程误差空间分布 Fig. 2 Spatial distribution of DEM elevation error |
半变异函数可分析高程误差的空间变异与空间自相关性。在半变异函数曲线图中有两个重要的点:距离间隔为0的点和函数趋近于平稳时的点,由这两个点产生了块金值、变程、基台值等参数。通过这些参数可以定量分析聚合重构DEM高程误差的空间变异与空间自相关特性。
理论上,当采样点间的距离为0时,半变异函数值应为0,但由于存在测量误差和空间变异,使得两采样点非常接近时,其半变异函数值不为0,此时的函数值即为块金值。基台值反映了当采样点间的距离增大时半变异函数从初始的块金值达到相对稳定值的函数值的变化情况,当半变异函数值超过基台值时,空间相关性不再存在。变程则可测度采样点的空间相关性的作用范围,在变程范围内,采样点间的距离越小,空间相关性越大,但当采样点间距离大于变程时,空间相关性不再存在。
聚合重构DEM高程误差空间相关性强弱可由偏基台值与基台值的比值来度量,比值越大,空间相关性越强,反之则相关性越弱。用基底效应参数,即块金值与基台值的比值,来描述聚合重构DEM高程误差样本间的变异特征,该比值越大,则说明样本间的变异更多是由随机因素引起。
表 2列出了分析聚合重构DEM高程误差空间变异的半变异函数的相关参数。从变程参数可知,聚合重构DEM高程误差的空间相关性作用范围由大到小的聚合方法依次是均值聚合、主成分聚合和重采样聚合。由偏基台值与基台值的比值参数分析可知,聚合重构DEM高程误差的空间相关性强度由强到弱的聚合方法依次为重采样聚合、均值聚合和主成分聚合。从基底效应参数分析,同均值聚合相比,主成分聚合重构DEM高程误差的块金值与基台值的比值略大,即随机因素引起的空间变异稍微大些。重采样聚合重构DEM高程误差的块金值为0,说明高程误差场中当两采样点非常接近时其空间变异和误差非常小。
| 主成分聚合 | 均值聚合 | 重采样聚合 | |
| 块金值/m | 49.680 | 39.757 | 0.000 |
| 偏基台值/m | 146.563 | 157.459 | 527.385 |
| 基台值/m | 196.243 | 197.216 | 527.385 |
| 偏基台值/基台值 | 0.747 | 0.798 | 1.000 |
| 块金值/基台值 | 0.253 | 0.202 | 0.000 |
| 变程/m | 1 710.927 | 1 783.900 | 1 536.499 |
3.3 等高线套合对比定性分析与定量评价
等高线套合分析作为一种定性的误差分析方法,通过目视检查方式逐条对比同名等高线的偏差,并判断其大小和分布[16]。图 3是3种聚合策略下等高线套合差异图斑分布结果。从图中的同名等高线差异图斑分布可以看出,3种聚合策略下重构等高线与原始等高线吻合程度均较高,整体地形结构特征保持了较好的一致性;等高线弯曲度较大的地方,同名等高线差异图斑面积相对较大,即同名等高线偏离程度相对较大,而等高线较平滑的地方,同名等高线差异图斑面积相对较小,即同名等高线偏离程度相对较小。

|
| 图 3 3种聚合策略下等高线套合差异 Fig. 3 The difference between contours with same name generated respectively from original DEM and reconstructed DEM using aggregation strategies |
同名等高线不吻合区域形成的差异图斑面积大小可测度同名等高线的偏离程度[16],从而可定量评价回放等高线与原始等高线间的吻合情况。表 3列示了3种聚合策略下同名等高线差异图斑的数量、平均面积、总面积,图斑面积的最大值、最小值、标准差以及差异率、套合率等统计数据。从等高线套合率定量分析可知,聚合重构DEM回放等高线与原始等高线吻合程度从高到低的聚合方法依次为重采样聚合、主成分聚合和均值聚合。这也从另一方面证实了3.1节中高程均值差反映出的地形形态特征整体上的吻合情况。对比分析3种聚合策略下差异图斑统计指标发现,差异图斑总数量、图斑面积极差与等高线吻合程度成正相关关系;差异图斑的平均面积、总面积、图斑面积标准差与等高线吻合程度成负相关关系。
| 均值聚合 | 主成分聚合 | 重采样聚合 | |
| 计数/个 | 2177 | 2427 | 3033 |
| 最小值/m2 | 0.001 | 0.003 | 0.001 |
| 最大值/m2 | 21 908.453 | 22 284.242 | 25 390.160 |
| 总面积/m2 | 2 533 100.107 | 2 392 817.160 | 1 916 372.000 |
| 平均面积/m2 | 1 163.574 | 985.916 | 631.841 |
| 标准差 | 2 073.409 | 1 852.207 | 1 240.101 |
| 差异率/(%) | 5.4 | 5.1 | 4.1 |
| 套合率/(%) | 94.6 | 94.9 | 95.9 |
4 结束语
DEM格网聚合模型的优劣会影响到地形简化、尺度变换等方面的处理效果。基于主成分变换模型构建的DEM格网聚合策略,实际上是确定聚合窗口内各格网点的权值,通过加权平均求解格网聚合值,具有较强的数理统计理论根据。3种聚合策略重构DEM误差的对比分析结果表明,重采样聚合重构DEM虽然能很好地保持地形形态特征,但其精度相对而言要低很多;均值聚合重构DEM具有较好的精度,但其地形形态特征没有主成分聚合重构DEM所保持的地形形态特征好;从高程中误差分析结果可知,主成分聚合重构DEM与均值聚合重构DEM精度基本一致,且远高于重采样聚合重构DEM的精度;结合高程均值差和等高线套合率两个统计量分析可知,同均值聚合重构DEM相比,主成分聚合重构DEM能够更好地保持地形形态特征。从DEM误差的空间分布格局分析来看,主成分聚合重构DEM格网点高程偏差的空间相关性作用范围与空间相关性强度、重构等高线与原始等高线吻合程度均介于均值聚合和重采样聚合试验结果之间,且3种策略下聚合重构DEM高程误差均具有空间分布变异和空间自相关特性。综合试验分析表明,同均值聚合和双线性重采样聚合相比较,本文提出的基于主成分变换模型构建的DEM格网聚合方法,在保持聚合重构DEM较高精度的前提下,能更好地保持地形形态特征。
由于仅选用了一个样区进行试验验证,没有针对不同地貌类型区进行聚合重构DEM的试验,本文提出的基于主成分变换模型的DEM格网聚合方法对不同地貌类型是否具有普适性,有待进一步研究。此外,也可继续探索聚合窗口尺度对聚合重构DEM高程误差的统计特性、空间相关性与分异特征、地形形态特征保持程度的影响。
| [1] | LI Zhilin, ZHU Qing, GOLD C. Digital Terrain Modeling:Principles and Methodology[M]. Boca Raton, FL: CRC Press, 2004: 1-7. |
| [2] | 汤国安. 我国数字高程模型与数字地形分析研究进展[J]. 地理学报, 2014, 69(9): 1305–1325. TANG Guo'an. Progress of DEM and Digital Terrain Analysis in China[J]. Acta Geographica Sinica, 2014, 69(9): 1305–1325. |
| [3] | 卢丽君, 张继贤, 王腾. 一种基于高分辨率雷达影像以及外部DEM辅助的复杂地形制图方法[J]. 测绘学报, 2011, 40(4): 459–463. LU Lijun, ZHANG Jixian, WANG Teng. A DEM Mapping Method Assisted by External DEM with High Resolution InSAR Data in Complex Terrain Area[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 459–463. |
| [4] | 云烨, 曾琪明, 焦健, 等. 基于参考DEM的机载InSAR定标方法[J]. 测绘学报, 2014, 43(1): 74–82. YUN Ye, ZENG Qiming, JIAO Jian, et al. Calibration of Airborne Interferometric SAR Data Based on Reference DEM[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 74–82. DOI:10.13485/j.cnki.11-2089.2014.0011 |
| [5] | 白燕, 廖顺宝, 孙九林. 栅格化属性精度损失的评估方法及其尺度效应分析——以四川省1:25万土地覆被数据为例[J]. 地理学报, 2011, 66(5): 709–717. BAI Yan, LIAO Shunbao, SUN Jiulin. Evaluating Methods and Scale Effects of Attribute Information Loss in Rasterization:A Case Study of 1:250 000 Land Cover Data of Sichuan[J]. Acta Geographica Sinica, 2011, 66(5): 709–717. |
| [6] | 陈永刚, 汤国安, 祝士杰. DEM重采样误差空间分布格局及差异性分析[J]. 中国矿业大学学报, 2011, 40(4): 653–659. CHEN Yonggang, TANG Guo'an, ZHU Shijie. Spatial Point Pattern of DEM Resampling Error and Difference Analysis of Influence Factor[J]. Journal of China University of Mining & Technology, 2011, 40(4): 653–659. |
| [7] | 卢华兴, 刘学军, 王永君, 等. 插值条件下格网DEM坡度计算模型的噪声误差分析[J]. 测绘学报, 2012, 41(6): 926–932. LU Huaxing, LIU Xuejun, WANG Yongjun, et al. Noise Error Analysis of Slope Algorithms Based on Grid DEM Derived from Interpolation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 926–932. |
| [8] | 顾绍红, 王永生, 王光霞. 主成分分析模型在数据处理中的应用[J]. 测绘科学技术学报, 2007, 24(5): 387–390. GU Shaohong, WANG Yongsheng, WANG Guangxia. Application of Principal Component Analysis Model in Data Processing[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2007, 24(5): 387–390. |
| [9] | ABDI H, WILLIAMS L J. Principal Component Analysis[J]. Wiley Interdisciplinary Reviews:Computational Statistics, 2010, 2(4): 433–459. DOI:10.1002/wics.v2:4 |
| [10] | 赵丽红, 孙宇舸, 蔡玉, 等. 基于核主成分分析的人脸识别[J]. 东北大学学报 (自然科学版), 2006, 27(8): 847–850. ZHAO Lihong, SUN Yuge, CAI Yu, et al. Face Recognition Based on Kernel PCA[J]. Journal of Northeastern University (Natural Science), 2006, 27(8): 847–850. |
| [11] | 杨红磊, 彭军还, 李淑慧, 等. 基于对数-主成分变换的EM算法用于遥感影像分类[J]. 测绘学报, 2010, 39(4): 378–382. YANG Honglei, PENG Junhuan, LI Shuhui, et al. Log-principal Component Transformation Based EM Algorithm for Remote Sensing Classification[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 378–382. |
| [12] | 王文波, 赵攀, 张晓东. 利用经验模态分解和主成分分析的SAR图像相干斑抑制[J]. 测绘学报, 2012, 41(6): 838–843. WANG Wenbo, ZHAO Pan, ZHANG Xiaodong. Research on SAR Image Speckle Reduction Using EMD and Principle Component Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 838–843. |
| [13] | 宦若虹, 杨汝良. 一种基于特征分类辨识的SAR图像目标检测方法[J]. 测绘学报, 2009, 38(4): 324–329. HUAN Ruohong, YANG Ruliang. A Target Detection Method for SAR Image Based on Feature Classification Discrimination[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 324–329. |
| [14] | AGUILAR F J, AGUILAR M A, AGVERA F, et al. The Accuracy of Grid Digital Elevation Models Linearly Constructed from Scattered Sample Data[J]. International Journal of Geographical Information Science, 2006, 20(2): 169–192. DOI:10.1080/13658810500399670 |
| [15] | OKSANEN J, SARJAKOSKI T. Uncovering the Statistical and Spatial Characteristics of Fine Toposcale DEM Error[J]. International Journal of Geographical Information Science, 2006, 20(4): 345–369. DOI:10.1080/13658810500433891 |
| [16] | 吴艳兰, 胡海, 胡鹏, 等. 数字高程模型误差及其评价的问题综述[J]. 武汉大学学报:信息科学版, 2011, 36(5): 568–574. WU Yanlan, HU Hai, HU Peng, et al. A Review on the Issues in DEM Error and DEM Quality Assessment[J]. Geomatics and Information Science of Wuhan University, 2011, 36(5): 568–574. |
| [17] | ÖSTMAN A. Accuracy Estimation of Digital Elevation Data Banks[J]. Photogrammetric Engineering and Remote Sensing, 1987, 53(4): 425–430. |
| [18] | LI Zhilin. A Comparative Study of the Accuracy of Digital Terrain Models (DTMS) Based on Various Data Models[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1994, 49(1): 2–11. DOI:10.1016/0924-2716(94)90051-5 |
| [19] | WISE S. Assessing the Quality for Hydrological Applications of Digital Elevation Models Derived from Contours[J]. Hydrological Processes, 2000, 14(11-12): 1909–1929. DOI:10.1002/(ISSN)1099-1085 |
| [20] | HOLMES K W, CHADWICK O A, KYRIAKIDIS P C. Error in a USGS 30-meter Digital Elevation Model and Its Impact on Terrain Modeling[J]. Journal of Hydrology, 2000, 233(1-4): 154–173. DOI:10.1016/S0022-1694(00)00229-8 |
| [21] | BONIN O, ROUSSEAUX F. Digital Terrain Model Computation from Contour Lines:How to Derive Quality Information from Artifact Analysis[J]. Geoinformatica, 2005, 9(3): 253–268. DOI:10.1007/s10707-005-1284-2 |
| [22] | LÓPEZ C. Improving the Elevation Accuracy of Digital Elevation Models:A Comparison of Some Error Detection Procedures[J]. Transactions in GIS, 2000, 4(1): 43–64. DOI:10.1111/1467-9671.00037 |
| [23] | CARLISLE B H. Modelling the Spatial Distribution of DEM Error[J]. Transactions in GIS, 2005, 9(4): 521–540. DOI:10.1111/tgis.2005.9.issue-4 |
| [24] | KYRIAKIDIS P C, SHORTRIDGE A M, GOODCHILD M F. Geostatistics for Conflation and Accuracy Assessment of Digital Elevation Models[J]. International Journal of Geographical Information Science, 1999, 13(7): 677–707. DOI:10.1080/136588199241067 |
| [25] | SAN B T, SUZEN M L. Digital Elevation Model (DEM) Generation and Accuracy Assessment from Aster Stereo Data[J]. International Journal of Remote Sensing, 2005, 26(22): 5013–5027. DOI:10.1080/01431160500177620 |
| [26] | 刘学军, 王永君, 龚健雅, 等. DEM流域网络提取算法的误差特性分析[J]. 测绘学报, 2007, 36(2): 224–230. LIU Xuejun, WANG Yongjun, GONG Jianya, et al. Error Analysis of Drainage Network Algorithms Based on Digital Elevation Model (DEM)[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 224–230. |
| [27] | 卢华兴, 刘学军, 晋蓓. 基于随机过程的格网DEM精度场模型[J]. 测绘学报, 2012, 41(2): 273–277. LU Huaxing, LIU Xuejun, JIN Bei. Stochastic Process Based Accuracy Field Model for Grid DEM[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 273–277. |
| [28] | 董有福, 汤国安. 利用地形信息强度进行DEM地形简化研究[J]. 武汉大学学报 (信息科学版), 2013, 38(3): 353–357. DONG Youfu, TANG Guo'an. Research on Terrain Simplification Using Terrain Significance Information Index from Digital Elevation Models[J]. Geomatics and Information Science of Wuhan University, 2013, 38(3): 353–357. |


