2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
3. 中国测绘科学研究院, 北京 100830
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. Chinese Academy of Surveying and Mapping, Beijing 100830, China
空间目标匹配就是找出两个数据集中在地理空间位置上具有同等分布格局的实体。我国系列基本比例尺地理空间数据库逐步建成,而城市化发展带来道路网数据变化更新周期缩短,对这些不同尺度、不同精度的道路网数据进行高效管理已成为空间数据库技术的研究热点。有效解决这个问题的关键之一是对不同版本空间数据中的同名要素进行自动识别,并建立它们之间的匹配关系。因此,不同比例尺下同名实体间匹配关系的准确、快速识别与建立是后续道路数据更新、集成与融合的基础,具有重要意义[1]。
国内外学者对道路网匹配算法已有比较深入研究,匹配算法主要分为:基于拓扑结构的匹配[2-8]、基于几何相似度的匹配[9-18]和基于数学模型的匹配[19-22]。基于拓扑结构的匹配算法中,文献[7]的算法首先进行节点、弧段的粗匹配,然后利用节点和弧段拓扑关系的相似性和离散Fréchet距离进行精确匹配。基于几何相似度的匹配算法中,文献[15]提出了基于格网索引的“折线—节点”距离匹配算法,将复杂的折线与折线之间的几何相似度计算转换为求节点到折线距离的匹配方法,降低了计算复杂度,并通过建立格网索引来提高计算效率。文献[16]提出了一种基于概率理论的匹配模型,该模型在线目标匹配中融合多种匹配指标计算实体匹配概率大小来确定匹配实体。基于数学模型的算法中,文献[20]提出了一种基于概率松弛方法的道路网匹配算法。文献[22]通过多个几何指标衡量匹配对之间的几何特征差异,构建道路网回归匹配模型,并利用此模型对待匹配目标对进行匹配。
然而,由于制图综合的原因,再加上道路数据采集过程中,不同制图员会对空间抽象有着各自的理解,在制作不同比例尺的地图时,拓扑变化的规律具有不定性,不同比例尺道路网的匹配会出现一些特殊情况:
(1) 当比例尺变小时,道路网中的环会变成点、正方形或三角形道路;立交桥附属结构可能消失等情况。
(2) 当数据存在更新变化时,某一条道路在小比例尺地图上为连贯的空间目标,但在大比例尺图上可能因为道路的整改、变迁,该道路可能已经分裂成两条道路,或在道路形态结构上发生了很大的改变。
(3) 当道路网稠密时,小比例尺某条道路很可能会在大比例尺匹配数据集中找到多条长度、方向、形状等多个指标都基本一致的候选匹配对象,这就需要改进空间场景结构的评价方法。
(4) 在不同尺度下还会存在单行线变双行线、两车道变4车道等情况。
综上所述,单一匹配技术难以在不同比例尺道路网的匹配中得到较好的匹配效果。因此,本文试图融合stroke技术、多因子几何相似度计算、空间索引技术、正反双向匹配、改进的空间场景结构相似性评价方法以及stroke整体匹配与部分匹配相结合等多种技术进行不同比例尺道路网匹配。
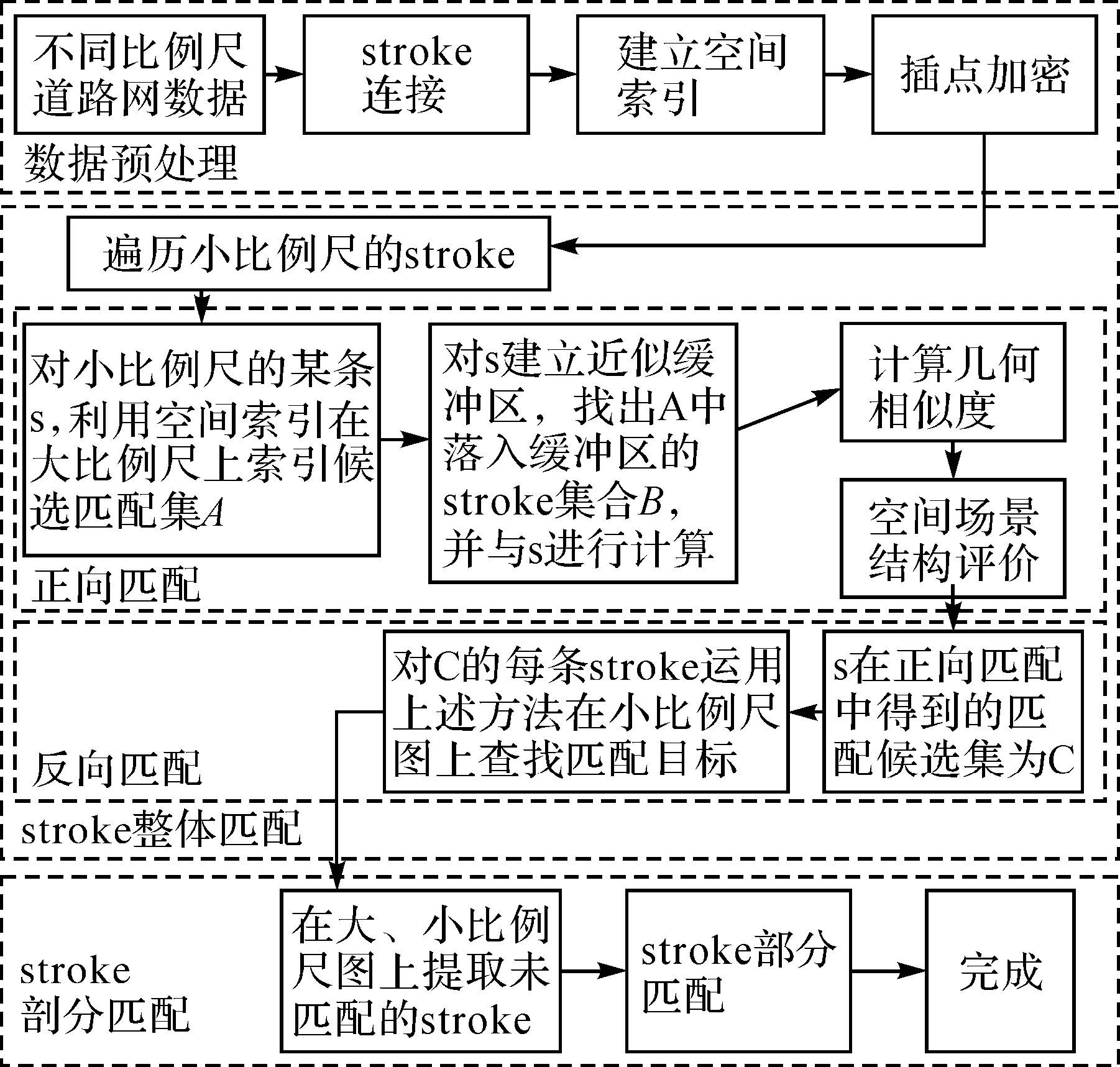
1 不同比例尺道路网匹配的思路不同比例尺的道路网匹配的数据处理流程如图 1所示,主要分为数据预处理、stroke整体匹配和stroke部分匹配3个部分。数据预处理部分主要完成不同比例尺道路内部节点加密、stroke连接以及空间格网索引的建立。在stroke整体匹配过程中,主要完成不同比例尺道路在几何形态和拓扑结构都相似的道路匹配。对于未匹配成功的道路,可利用stroke部分匹配,最大限度地搜查同名目标的匹配关系。
|
| 图 1 不同比例尺道路网匹配的数据处理流程 Fig. 1 Procedure of road networks matching at different scales |
为了提高目标匹配的计算效率,算法中对多种基础几何算法进行了改进,包括近似的缓冲区代替精密缓冲区。对于克服单一几何相似度衡量指标的局限性,本文利用多个几何相似度衡量指标计算空间目标的几何相似度S(s1, s2),计算见式 (1)
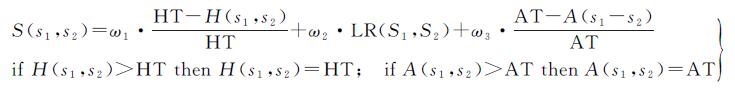 (1)
(1)
式中,ω1、ω2和ω3均为经验权值 (ω1、ω2和ω3均为正数,ω1+ω2+ω3=1);s1和s2表示两条stroke;H(·) 为文献[23]的所提出的Hausdorff距离修正计算方法;HT为Hausdorff距离阈值;LR (·) 为两个stroke长度之比计算函数,长度比越接近1,表明相似度越高;A(·) 是两个stroke之间的夹角 (范围在0~π之间) 计算函数,在计算过程中,两个stroke之间的夹角被抽象成由stroke首末节点所连成的线段之间的夹角;AT为夹角阈值。
根据Hausdorff距离的公式定义,若两空间目标在几何形态结构上差异较大,则两空间目标靠得再近,相互之间的Hausdorff距离也会较大。因此Hausdorff距离除了可以衡量目标之间的空间距离,还可以一定程度上衡量相互之间的几何形态结构相似度。此外,算法还融合了空间索引技术以及文献[24]的正反双向匹配。
2 空间场景结构的相似性评价全局一致性评价是指将待匹配空间场景与候选匹配空间场景进行整体相似性评价,既评价个体相似性,同时也评价空间场景结构特征的相似性[25]。个体相似性的衡量可利用相似度计算公式 (1) 完成,而空间场景结构的相似性则需要对stroke所处的空间分布格局进行评价。一条stroke的空间场景结构由与其首、末节点相连的stroke所构成,当需要比较两条stroke之间的空间场景结构相似度时,利用两个空间场景中相互匹配成功的stroke匹配对来计算[25]。但是,不同比例尺道路网的抽象程度会有所不同,例如在表示同一地区的两幅不同比例尺地图上的道路数量可能存在差别,同名stroke的空间场景结构就有可能不同,导致在空间场景结构评价中出现误判断的情况。
在制图综合中,连通度、长度等被作为衡量一条道路重要性的常用指标,如果某条道路长度较长,则通常是一条具有“主干”“动脉”特点的道路,在制图综合中不易被剔除,也不容易因为时间的变化而出现消失、缩短等情况。基于这样地图制图规则,本文改进的空间场景结构评价方法如下:
(1) 对于两条可能存在匹配关系的stroke道路s(小比例尺) 和m(大比例尺),设s的首、末节点分别为ss和se;m的首、末节点分别为ms和me。为了能保证stroke道路整体匹配中首、末节点相对应,需要先确定s与m的首、末节点对应关系。因为不同比例尺下两个同名空间目标的首末端点可能会有不同的对应关系 (若两道路的空间数据采集方向相同,则s与m的首、末节点相互对应;否则,可能是s的首节点与m的末节点相对应)。本文直接采用s与m的首、末节点相互之间的最小欧氏距离来确定节点的对应关系。若两道路首末节点走向一致,则得到两个节点对P1(ss与ms) 和P2(se与me),否则,两个节点对为P1(ss与me) 和P2(se与ms)。
(2) 这里,设两个节点对为P1(ss与ms) 和P2(se与me)。对于节点对P1,设与ss相连的stroke集合为A,与ms相连的stroke集合为B。若集合A不为空,则选出A中最长的stroke道路,记为Ai,同理在B中选出最长的Bj,转步骤 (3)(对于另外一种节点对情况可以进行类似处理)。
(3) 设Ai和Bj之间计算的几何相似度为Ss。若A和B都为空集,则Ss=1;若A、B中只有一个空集,则Ss=0;否则,利用式 (1) 进行计算Ss=S(Ai, Bj)。
(4) 得到Ss后,利用相同原理转步骤 (2),对P2中的节点对计算Se。
(5) 最终的空间结构场景相似度为Ss与Se的平均值Ss, e,若Ss, e大于给定的阈值,则认为匹配成功;否则匹配失败。
3 stroke部分匹配 3.1 算法提出的背景当道路空间数据出现变化时,若只利用式 (1) 进行匹配,将会得到非常低的相似度。如图 2(a)所示,在小比例尺图上有s_Str1(由弧段s2和s3组成) 和s_Str2(由弧段s1组成) 两条stroke。在数据出现更新变化的大比例尺图上则有m_Str1(由弧段m3组成) 和m_Str2(由弧段m1和m2组成),如图 2(b)所示。此时,小比例尺图上弧段s1与s2并没有连接成一条stroke,因而无法与大比例尺图上的m_Str2相匹配。从图 2(c)可以看出,不同比例尺的道路之间存在匹配情况,但是若只是判断stroke是否整体匹配,则无法识别弧段s3与m3的匹配以及弧段s2与m2的匹配。很明显,s_Str1与m_Str1以及s_Str1与m_Str2之间只存在部分匹配的情况。
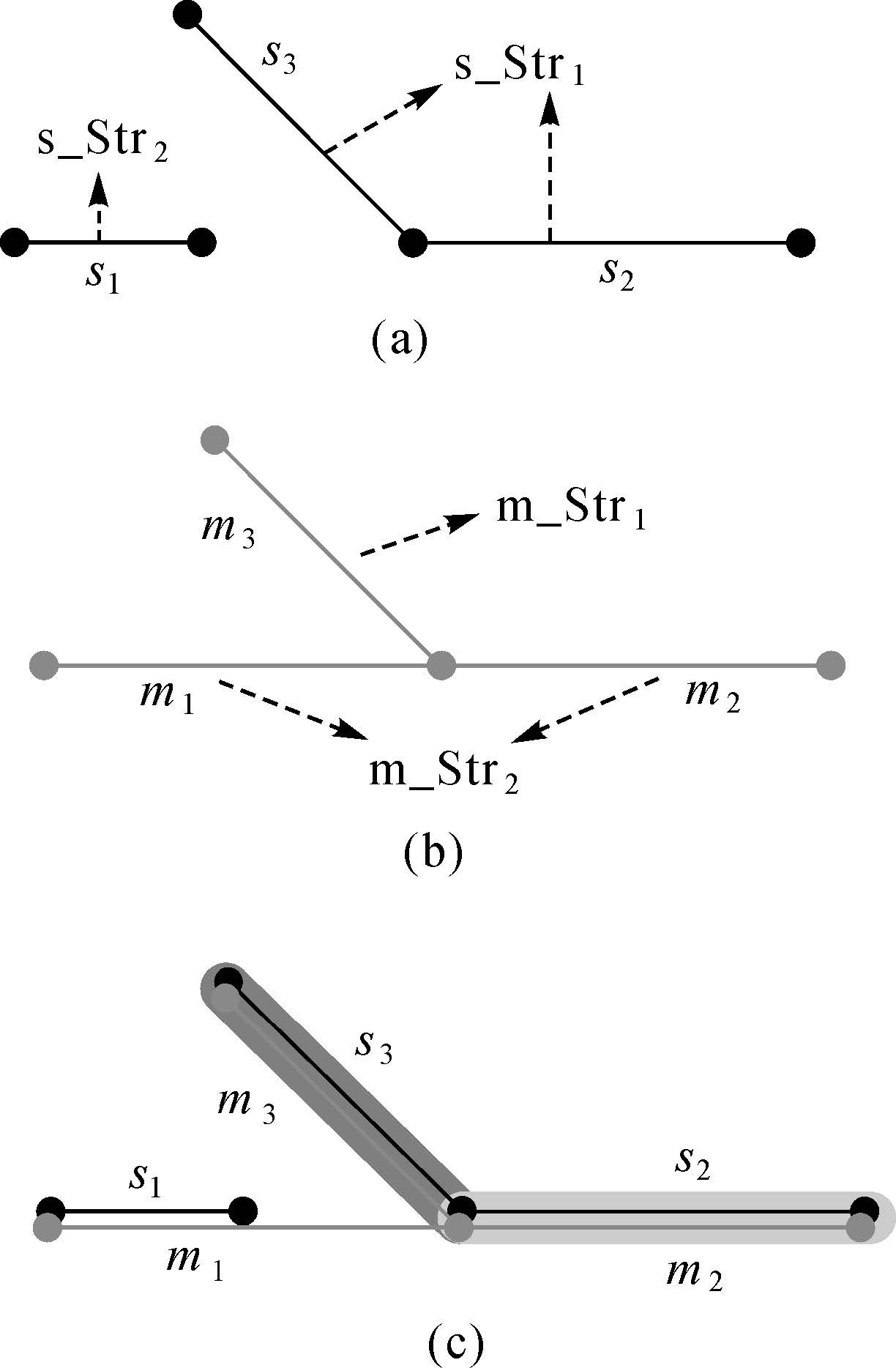
|
| 图 2 存在stroke部分匹配的情况 Fig. 2 Examples of partial stroke matching |
3.2 算法描述
在经过stroke整体匹配后,设未能匹配上的小比例尺的stroke集合为S(共有n条),大比例尺的stroke集为L。本文提出的stroke部分匹配的算法如下:
(1) 若集合S和L不同时为空,则遍历集合S,对集合S中每条stroke道路Si(其中Si∈S; i=0, 1, …, n),利用格网空间索引和近似缓冲区在集合L中搜索出候选匹配集为M;否则结束。若集合M为空,则将Si从集合S中剔除,继续遍历S中的stroke;否则,设M共有m条stroke,对M的每一条stroke道路Mj(其中Mj∈M; j=0, 1, …, m) 进行遍历处理。
(2) 设Si的弧段数为NSi,每条弧段表示为Si, q(其中,q=0, 1, …, NSi);设T为Hausdorff距离阈值。利用文献[21]提出的SM_HD算法计算Si中的每一条弧段Si, q与Mj的Hausdorff距离Hq。若Hq>T,则设Si, q的属性值HBi, q为false,否则HBi, q为true。这样就可以得到Si各个弧段相对于Mj的Hausdorff距离是否满足阈值的一个布尔型集合PSi
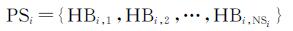
同理,设Mj的弧段数为NMj,反过来计算Mj中每一条弧段Mj, p(其中,p=0, 1, …, NMj) 与Si的Hausdorff距离Hp,同理可得到HBj, p并形成布尔型集合PMj
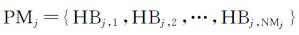
若PSi或PMj其中之一的元素全为false,则继续对集合M的下一个stroke元素Mj+1进行处理;否则,转到步骤 (3)。
(3) 对PSi和PMj的元素值分别进行对比分析,若元素值从左到右连续的都为true值,则组成一个匹配体。PSi中第k个匹配体可以表示为PkSi=[Si, k′, Si, k″](其中k′、k″≤NSi,且k′、k″之间连续),这说明在Si中,从Si, k′到Si, k″之间的所有弧段的HB属性值均为true,且所有弧段在Si中连续 (依次相连)。
(4) 对PSi和PMj中的每个下标k一致的匹配体进行组合,形成一个“匹配对”,得到“匹配对”集合P。
(5) 遍历P,对每个“匹配对”中所包含的Si中的弧段和Mj中的弧段分别重新连接成stroke。
(6) 对新生成的stroke进行长度比值和夹角计算。若长度比值和夹角都符合阈值条件,则认为部分匹配成功,将部分匹配成功的所有弧段标志为已匹配。若长度比值或夹角其中之一不符合阈值条件,则对较长的stroke按照顺序 (从首至末) 剔除一条弧段后,将所剩下的弧段生成新stroke,再与“匹配对”中较短的stroke进行长度比值和夹角的计算,直至符合阈值条件或弧段全部剔除完,继续遍历P,若P已遍历完毕,转至步骤 (7),否则转至步骤 (5)。
(7) 检查M是否被遍历完毕。若遍历完毕,则对Si的下一元素Si+1进行处理,转至步骤 (1);否则,对Mj的下一元素Mj+1进行处理,转至步骤 (2)。
4 试验与分析为了校验本文所提出的算法对不同比例尺下的道路网匹配的有效性,选择了VS2010(C#) 进行了算法的设计与实现。
4.1 比例尺变化较小的试验试验选取了南昌市某地区两幅比例尺分别为1:5000和1:2.5万的道路网数据。其中,大比例尺地图中弧段数、stroke数和总长度分别为739条、502条和1 027.4 km。而小比例尺地图中弧段数、stroke数和总长度分别为301条、176条和634.8 km。试验中,设插入点距离、Hausdorff距离阈值以及近似缓冲半径均为150 m。两种数据叠加后的情况如图 3所示。
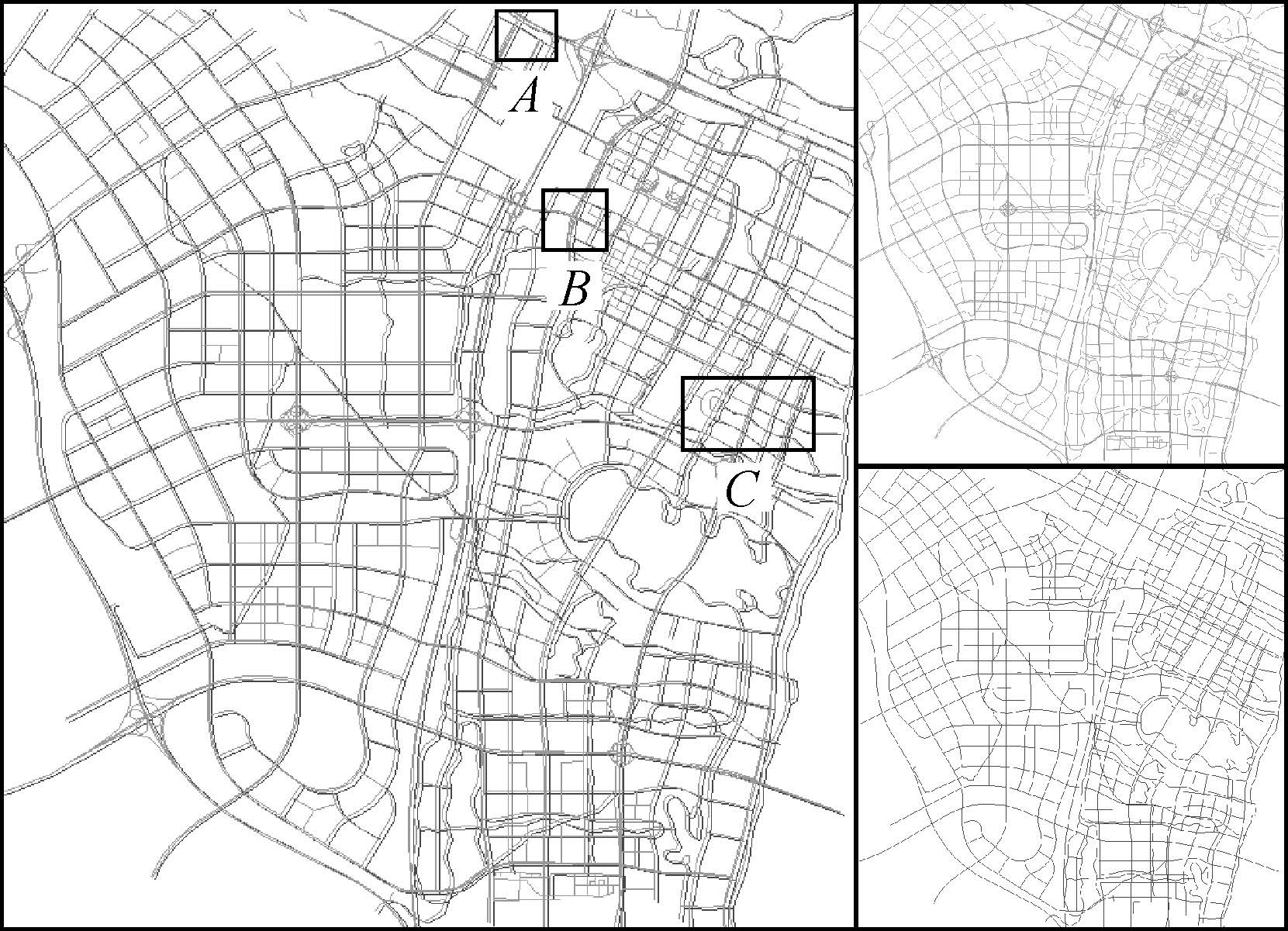
|
| 图 3 试验1的道路网 Fig. 3 Road networks used in experiment 1 |
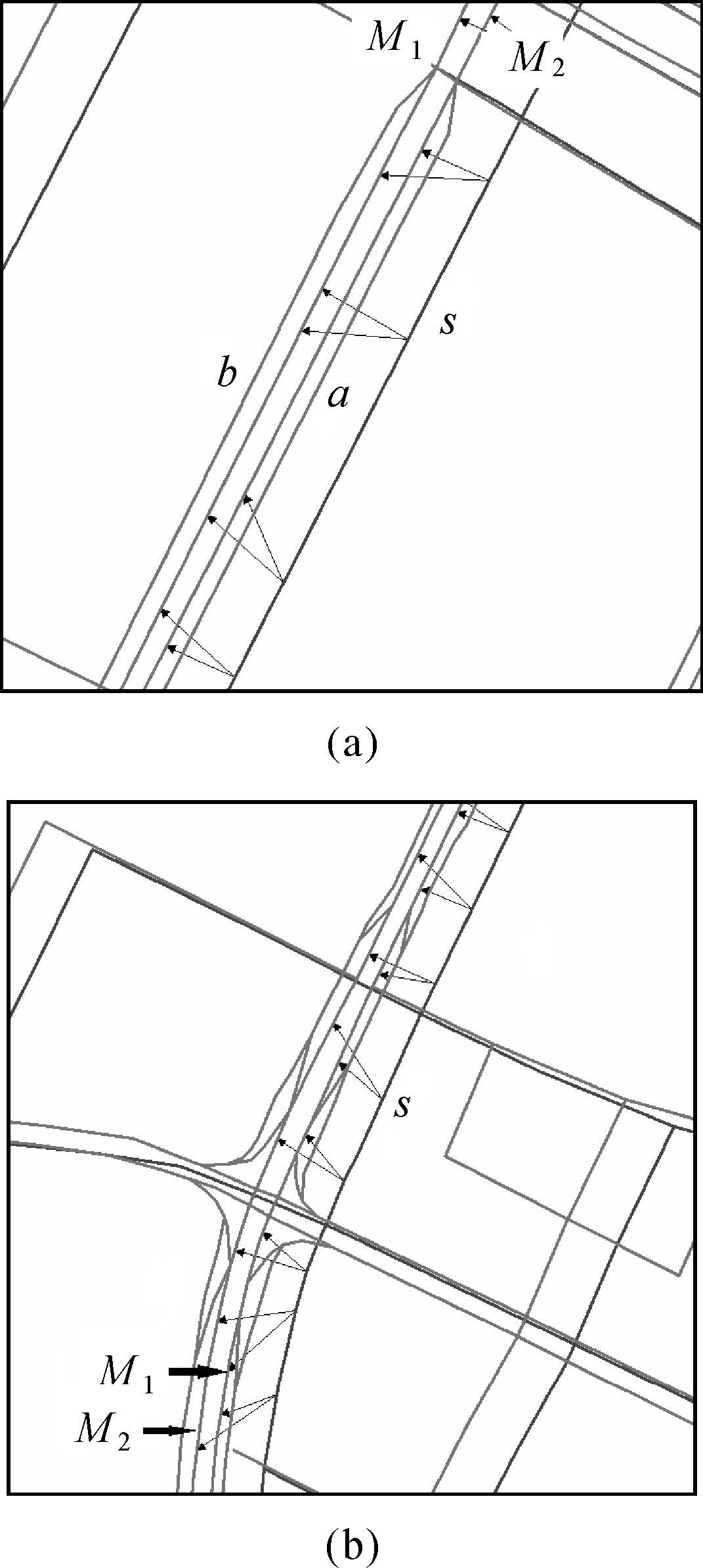
在图 3中的A区域放大后如图 4(a)所示,大比例尺图上原为双行道 (M1和M2),在道路某处拓宽为4车道 (增加a和b),但在小比例尺图中抽象为一条道路S。图 3的B区域放大后为图 4(b)所示,大比例尺图上有纵横交叉的道路所构成的十字路口,在十字路口处还存在一些道路附属结构,使得道路交叉口处道路十分稠密,但在小比例尺地图上,抽象简化为纵横交叉的两条相交道路。
在匹配处理后,得到图 4(a)中S与M1、M2匹配,但并没有把a和b纳入为匹配对象。所以,本算法在处理多车道目标匹配问题时,只选择最佳匹配的对象,因为抽象而退化的附属结构目标不参与匹配。图 4(b)中也是如此, S与M1、M2匹配,十字交叉路口的附属结构道路没有被纳入匹配对象。
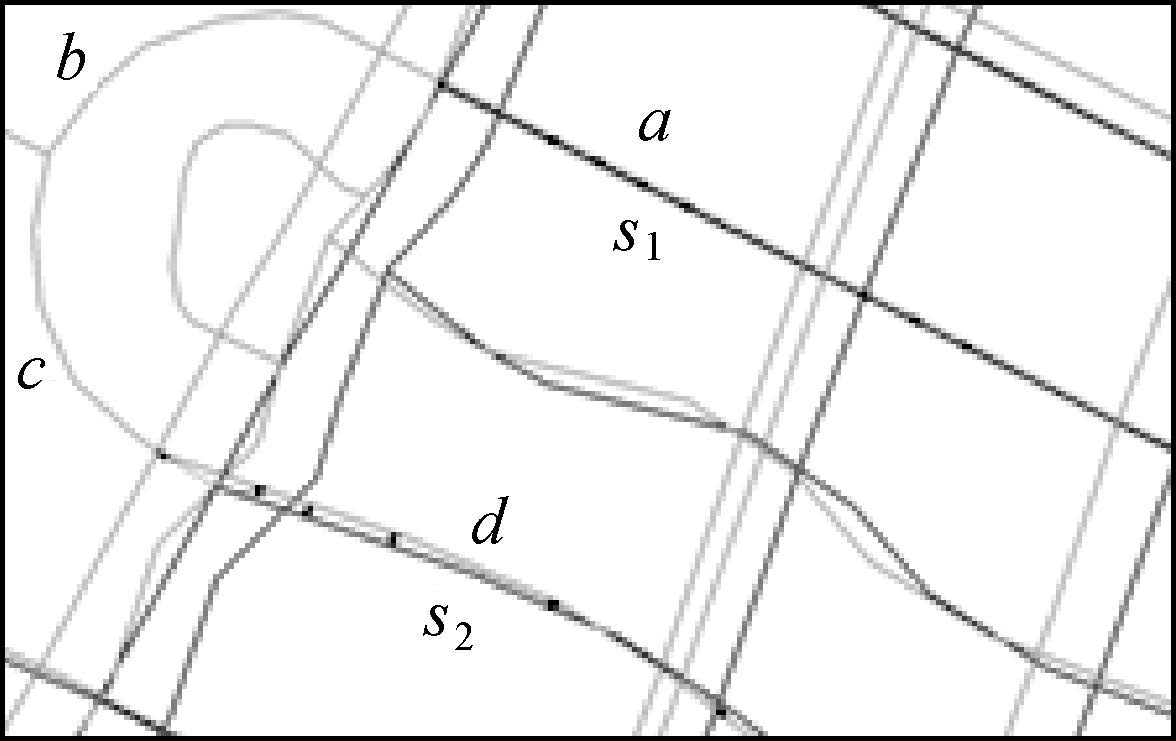
图 3上的C区域放大后如图 5所示,在大比例尺地图上弧段a、b、c和d组成一条stroke (m_stroke),但在小比例尺地图上,由于道路结构发生了变化,在小比例尺上不再存在与弧段b、c相匹配的目标,即大比例地图上的m_stroke在小比例尺地图上缺少圆弧部分,分成s1和s2两条stroke。在进行stroke部分匹配过程中,计算得到s1与a的几何相似度为0.990,s2与d的几何相似度为0.905。此两个匹配对都符合匹配阈值要求。
4.2 比例尺变化较大的试验
试验数据为合肥市某地区的比例尺变化较大的两幅地图数据 (1:5000和1:10万)。小比例尺数据与大比例尺数据在道路形态和测量精度上都有较大的差异。其中,大比例尺地图中弧段数、stroke数和总长度分别为1945条、1294条和1 308.7 km。而小比例尺地图中弧段数、stroke数和总长度分别为359条、143条和629.5 km。试验中,设插入点距离为150 m,Hausdorff距离阈值为200 m,近似缓冲半径300 m。两种数据叠加后的情况如图 6所示。
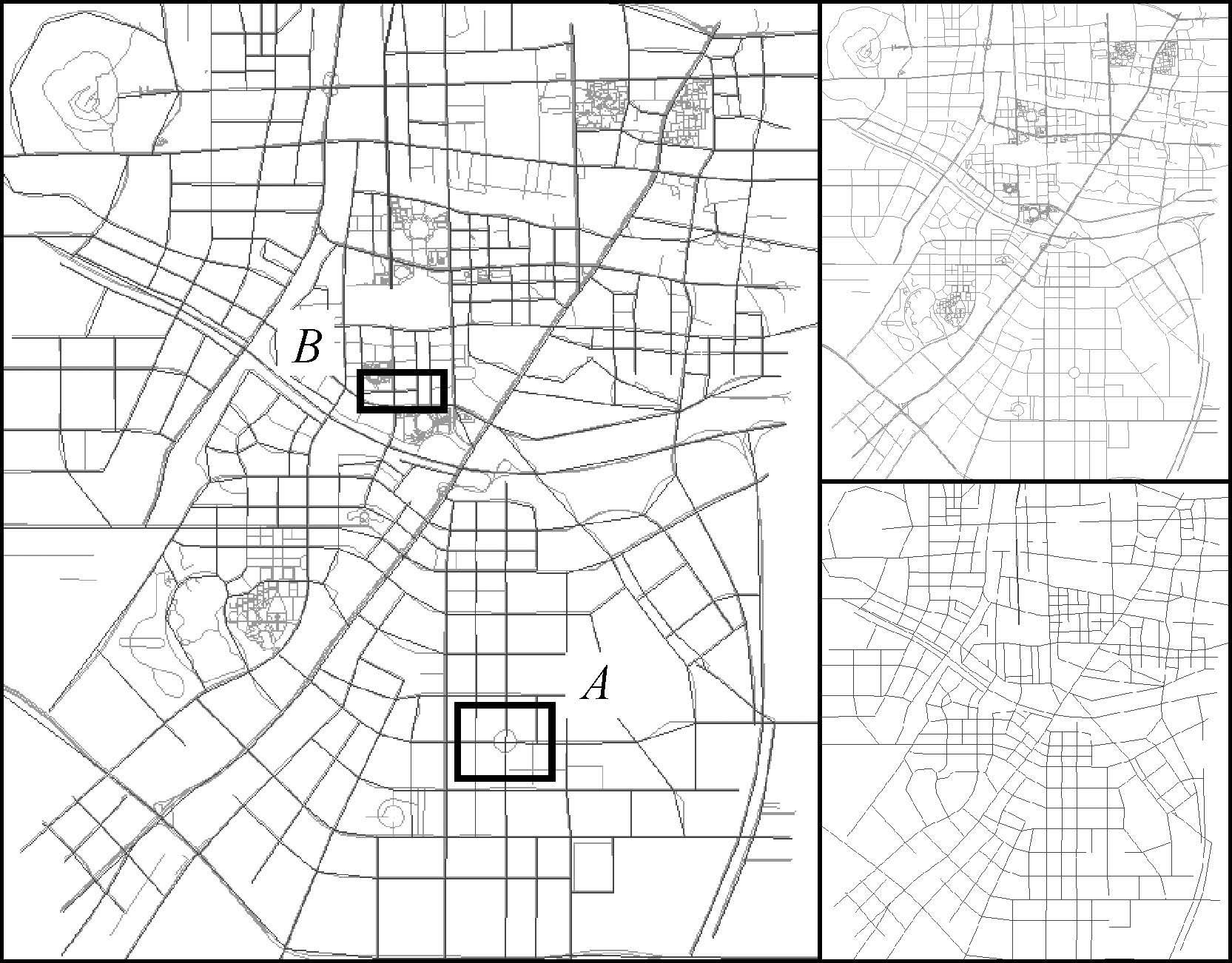
|
| 图 6 试验2的道路网 Fig. 6 Road networks used in experiment 2 |
图 6中的区域A放大后如图 7所示,大比例尺的环形道路结构变为小比例尺图上的十字路口。在进行stroke匹配时,小比例尺的弧段a′和c′会连接成s_stroke1,弧段b′和d′会连接成s_stroke2。而在大比例尺道路中,因为弧段a、b、c和d与环连接,所以它们各自成一条stroke。在匹配过程中,s_stroke1与弧段a所在的stroke和弧段b所在的stroke的几何相似度分别是0.562和0.517,空间场景结构相似度均为0。所以,需要进行stroke部分匹配,s_stroke1的a′弧段形成的stroke与弧段a形成的stroke的几何相似度为0.934,c′弧段所在的stroke与弧段c形成的stroke的几何相似度为0.942,说明这两个“匹配对”的匹配成功。
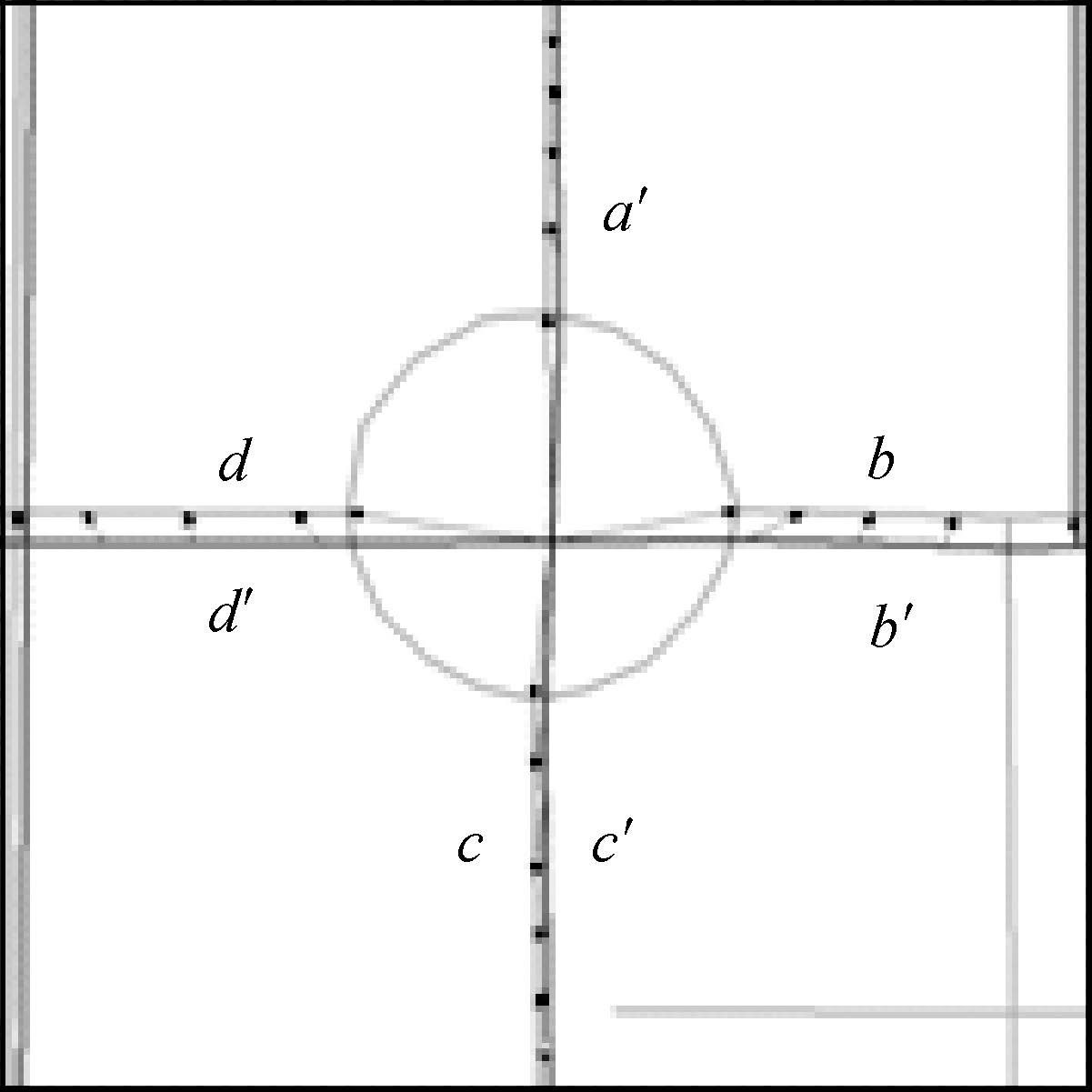
|
| 图 7 环形结构的匹配结果 Fig. 7 Matching result of ring structure |
图 6中B区域放大后如图 8所示,在复杂的道路连接口处,在大比例尺图上为横向分布的两条道路连接纵向分布的双行道,并在连接口处出现分叉的连接结构。而在小比例尺图上,因为比例尺度跨度较大的原因,直接抽象成十字交叉路。经过stroke整体匹配和stroke部分匹配算法处理后,弧段a与弧段a′匹配,弧段b与弧段b′匹配。而双行道c在几何形态和空间场景结构都与c′相似度高,无需进行stroke部分匹配算法就可完成匹配过程。
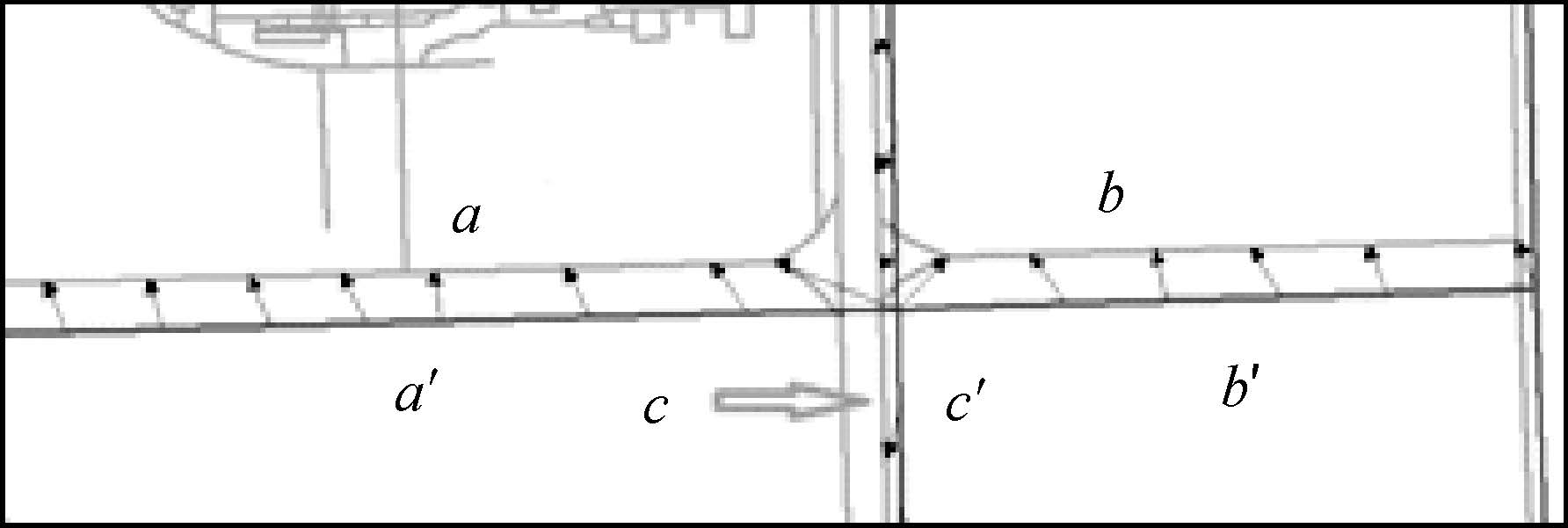
|
| 图 8 有拓扑结构变化的匹配结果 Fig. 8 Matching result of road networks with topological change |
4.3 城郊接合部与乡村道路的试验
以上两个试验主要针对城市道路网的匹配,为了验证本算法的高适应性,选取了城郊接合部 (武汉市某地区,试验3) 和乡村道路 (佛山市某地区,试验4) 作为试验数据,这两类数据的大小比例尺都分别为1:5000和1:2.5万。两次试验都设插入点距离、Hausdorff距离阈值以及近似缓冲半径均为150 m。其中,城郊接合部大比例尺地图中弧段数、stroke数和总长度分别为258条、211条和20.5 km。而小比例尺地图中弧段数、stroke数和总长度分别为144条、100条和15.9 km。城郊接合部的数据在比例尺变化不大时较少存在拓扑结构发生变化的匹配情况,利用stroke整体匹配即可取得较好的匹配效果。
乡村道路的试验数据中,大比例尺地图中弧段数、stroke数和总长度分别为133条、77条和14.3 km。而小比例尺地图中弧段数、stroke数和总长度分别为70条、26条和11.9 km。乡村道路的数据与城郊接合部数据特点相似,但乡村道路数据变化更新频繁,部分区域的匹配需要stroke部分匹配算法进行处理。
4.4 试验结果对比分析为了对匹配效果进行评价, 采用人工方式对试验匹配结果进行了检查, 并利用文献[21]的评价公式对结果进行评估, 见式 (2)
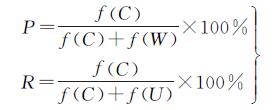 (2)
(2)
式中, P为匹配准确率;R为匹配召回率;f(C) 为正确匹配数;f(W) 为错误匹配数;f(U) 为漏匹配数。前后4次试验结果的统计信息如表 1所示。表中除试验3外各个试验中f(C)+f(W)+f(U) 都大于相应试验数据中的小比例尺的stroke数目。其原因是在匹配过程中,一部分小比例尺的stroke会在部分匹配中由一条stroke分成了若干条stroke形成若干匹配对。
| 试验 | f(C) | f(W) | f(U) | P/(%) | R/(%) | 耗时/s |
| 试验1 | 174 | 2 | 1 | 98.9 | 99.4 | 2.59 |
| 试验2 | 151 | 2 | 0 | 98.7 | 100.0 | 2.45 |
| 试验3 | 95 | 0 | 5 | 100.0 | 95.0 | 0.03 |
| 试验4 | 27 | 0 | 1 | 100.0 | 96.4 | 0.05 |
根据试验结果的统计信息,本算法有着较高的匹配准确率和召回率。按照“数据集总长度/耗时”计算匹配速度,得到试验1至试验4的匹配速度分别是641.8 km/s、791.1 km/s、1 213.3 km/s和524 km/s。在试验1中匹配速度之所以低于试验2,是因为试验2中比例尺变化较大,在大比例尺道路网中存在大量没有匹配对象的细小stroke,从而减轻了计算压力。而试验3和试验4因为数据复杂度较低、路网稀疏,匹配速度较高。
5 结语本文通过分析不同比例尺下的道路网匹配所存在的问题和技术难点,提出了一种融合多种道路网匹配技术的策略。同时,对空间场景结构的评价方法进行了改进,针对整体stroke匹配不能适应存在数据变化的道路网匹配情况,提出了stroke部分匹配方法。试验表明,本文所提出的方法具有较高的匹配准确率、召回率和运行效率,且在处理不同比例尺道路网中的拓扑结构变化时也能有很好的适应性,可适用于不同比例尺的国家基本比例尺地理空间数据库的道路网匹配。但是,阈值和权重这些参数目前都是通过人为经验设定的。在今后的研究工作中,将研究如何根据具体的数据自动设定阈值和权重,以进一步确保匹配的效果和质量。
| [1] | QUDDUS M A, OCHIENG W Y, NOLAND R B. Map Matching Algorithms for Intelligent Transport Systems Applications[C]//Proceedings of the 13th World Congress on Intelligent Transport Systems Services. London:ITRD, 2006. |
| [2] | DOYTSHER Y, FILIN S. The Detection of Corresponding Objects in a Linear-based Map Conflation[J]. Surveying and Land Information Systems, 2000, 60(2): 117–128. |
| [3] | MANTEL D, LIPECK U. Matching Cartographic Objects in Spatial Databases[C]//Proceedings of the 20th ISPRS Congress, Commission 4. Istanbul, Turkey:ISPRS, 2004. |
| [4] | ZHANG Meng, SHI Wei, MENG Liqiu. A Generic Matching Algorithm For Line Networks of Different Resolutions[C]//Proceedings of the 8th ICA Workshop on Generalisation and Multiple Representation. A Coruña, Spain:[s.n.], 2005. |
| [5] | ZHANG Meng, SHI Wei, MENG Liqiu. A Matching Approach Focused on Parallel Roads and Looping Crosses in Digital Maps[C]//International Symposium of Theoretical Cartography and Geo-Information Science. Wuhan, China:[s.n.], 2006. |
| [6] | ZHANG Meng, MENG Liqiu, BOBRICH J. A Road-network Matching Approach Guided by "Structure"[J]. Annals of GIS, 2010, 16(3): 165–176. DOI:10.1080/19475683.2010.513154 |
| [7] | 安晓亚, 孙群, 尉伯虎. 利用相似性度量的不同比例尺地图数据网状要素匹配算法[J]. 武汉大学学报 (信息科学版), 2012, 37(2): 224–228. AN Xiaoya, SUN Qun, WEI Bohu. Feature Matching from Network Data at Different Scales Based on Similarity Measure[J]. Geomatics and Information Science of Wuhan University, 2012, 37(2): 224–228. |
| [8] | 刘闯, 钱海忠, 王骁, 等. 顾及上下级空间关系相似性的道路网联动匹配方法[J]. 测绘学报, 2016, 45(11): 1371–1383. LIU Chuang, QIAN Haizhong, WANG Xiao, et al. A Linkage Matching Method for Road Networks Considering the Similarity of Upper and Lower Spatial Relation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(11): 1371–1383. DOI:10.11947/j.AGCS.2016.20160062 |
| [9] | WALTER V, FRITSCH D. Matching Spatial Data Sets:A Statistical Approach[J]. International Journal of Geographical Information Systems, 1999, 13(5): 445–473. DOI:10.1080/136588199241157 |
| [10] | ZHANG Meng, MENG Liqiu. An Iterative Road-matching Approach for the Integration of Postal Data[J]. Computers, Environment and Urban Systems, 2007, 31(5): 597–615. DOI:10.1016/j.compenvurbsys.2007.08.008 |
| [11] | ZHANG Meng, MENG Liqiu. Delimited Stroke Oriented Algorithm-working Principle and Implementation for the Matching of Road Networks[J]. Annals of GIS, 2008, 14(1): 44–53. DOI:10.1080/10824000809480638 |
| [12] | ZHANG M. Methods and Implementations of Road-network Matching[D]. Munich, Germany:Technical University of Munich, 2009. |
| [13] | VOLZ S. An Iterative Approach for Matching Multiple Representations of Street Data[C]//Proceedings of ISPRS Workshop on Multiple Representation and Interoperability of Spatial Data. Hanover, Germany:ISPRS, 2006:101-110. |
| [14] | DENG MIN, LI ZHILIN, CHEN XIAOYONG. Extended Hausdorff Distance for Spatial Objects in GIS[J]. International Journal of Geographical Information Science, 2007, 21(4): 459–475. DOI:10.1080/13658810601073315 |
| [15] | 陈玉敏, 龚健雅, 史文中. 多尺度道路网的距离匹配算法研究[J]. 测绘学报, 2007, 36(1): 84–90. CHEN Yumin, GONG Jianya, SHI Wenzhong. A Distance-based Matching Algorithm for Multi-scale Road Networks[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 84–90. DOI:10.3321/j.issn:1001-1595.2007.01.015 |
| [16] | 童小华, 邓愫愫, 史文中. 基于概率的地图实体匹配方法[J]. 测绘学报, 2007, 36(2): 210–217. TONG Xiaohua, DENG Susu, SHI Wenzhong. A Probabilistic Theory-based Matching Method[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 210–217. DOI:10.3321/j.issn:1001-1595.2007.02.017 |
| [17] | 赵东保, 盛业华. 全局寻优的矢量道路网自动匹配方法研究[J]. 测绘学报, 2010, 39(4): 416–421. ZHAO Dongbao, SHENG Yehua. Research on Automatic Matching of Vector Road Networks Based on Global Optimization[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 416–421. |
| [18] | HACKELOEER A, KLASING K, KRISP J M, et al. Road Network Conflation:An Iterative Hierarchical Approach[M]//GARTNER G, HUANG Haosheng. Progress in Location-based Services 2014. Switzerland:Springer, 2015:137-151. |
| [19] | SONG Wenbo, KELLER J M, HAITHCOAT T L, et al. Relaxation-based Point Feature Matching for Vector Map Conflation[J]. Transactions in GIS, 2011, 15(1): 43–60. DOI:10.1111/tgis.2011.15.issue-1 |
| [20] | 张云菲, 杨必胜, 栾学晨. 利用概率松弛法的城市路网自动匹配[J]. 测绘学报, 2012, 41(6): 933–939. ZHANG Yunfei, YANG Bisheng, LUAN Xuechen. Automated Matching Urban Road Networks Using Probabilistic Relaxation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 933–939. |
| [21] | TONG Xiaohua, LIANG Dan, JIN Yanmin. A Linear Road Object Matching Method for Conflation Based on Optimization and Logistic Regression[J]. International Journal of Geographical Information Science, 2014, 28(4): 824–846. DOI:10.1080/13658816.2013.876501 |
| [22] | 付仲良, 杨元维, 高贤君, 等. 道路网多特征匹配优化算法[J]. 测绘学报, 2016, 45(5): 608–615. FU Zhongliang, YANG Yuanwei, GAO Xianjun, et al. An Optimization Algorithm for Multi-characteristics Road Network Matching[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 608–615. DOI:10.11947/j.AGCS.2016.20150388 |
| [23] | 张良国, 吴江琴, 高文, 等. 基于Hausdorff距离的手势识别[J]. 中国图象图形学报, 2002, 7(11): 1144–1150. ZHANG Liangguo, WU Jiangqin, GAO Wen, et al. Hand Gesture Recognition Based on Hausdorff Distance[J]. Journal of Image and Graphics, 2002, 7(11): 1144–1150. |
| [24] | 邵世维. 基于几何特征的多尺度矢量面状实体匹配方法研究与应用[D]. 武汉: 武汉大学, 2011: 89-94. SHAO Shiwei. Researches and Applications on Polygon Entity Matching for Multi-scale Vector Data Based on Geometric Features[D]. Wuhan:Wuhan University, 2011:89-94. |
| [25] | 翟仁健. 基于全局一致性评价的多尺度矢量空间数据匹配方法研究[D]. 郑州: 信息工程大学, 2011: 51-79. ZHAI Renjian. Research on Automated Matching Methods for Multi-Scale Vector Spatial Data Based on Global Consistency Evaluation[D]. Zhengzhou:Information Engineering University, 2011:51-79. |