2. 武汉大学地球空间信息技术协同创新中心, 湖北 武汉 430079;
3. 西南交通大学, 四川 成都 610031
2. Collaborative Innovation Center for Geospatial Technology, Wuhan University, Wuhan 430079, China;
3. Southwest Jiaotong University, Chengdu 610031, China
低空倾斜影像能为三维影像城市重建提供丰富的地物三维信息和纹理影像,已逐步成为城市三维场景重建与更新的重要手段。一套基于倾斜影像的完整三维影像城市重建方案包括相机标定、密集点云重建、三维网格表面模型生成和纹理映射等核心技术。目前,从多视倾斜影像到三角网格表面模型的建立已经有了比较可靠的方法[1-6];而在三维影像城市大场景的无缝纹理映射方面,由于大量倾斜影像存在拍摄角度不一致、环境光照差异和透视遮挡等因素的影响,导致重建的三维纹理模型存在映射错误、色彩不一致和大量拼接缝等问题。因此,如何在地物三角网格表面模型的基础上,实现三维影像城市大场景的无缝纹理映射是亟待解决的关键问题之一。对此,国际上已存在一些相关的研究进展,如文献[7]利用影像已知的粗略内、外方位元素,通过二维影像和三维模型上对应线段的匹配结果,综合考虑影像遮挡情况、分辨率和模型法向量等,尝试了高质量的纹理模型重建。文献[8]结合深度缓存遮挡检测判断算法,通过视角法对小型无人机获取的倾斜影像进行筛选用于纹理提取。文献[9-10]通过对来自不同影像的纹理源进行纹理加权实现纹理色彩的一致性过渡,但这种方法在很多情况下并不能得到令人满意的结果。文献[11]将确定三角网格表面模型中每个三角面纹理的过程看作一个马尔科夫随机场 (MRF) 下的优化问题,以尽量保证相邻三角面纹理来自同一幅纹理影像,并将纹理的灰度和梯度同时用来构造网格表面的分布连续函数,在一定程度上减轻了纹理接缝的问题,取得了优于文献[9-10]基于灰度空间的Blending效果;文献[12]先利用MRF对相邻三角面的纹理选取进行优化,以避免因几何误差导致的纹理错位问题,然后通过约束三角纹理边缘的梯度逐面片利用Poisson Blending[13]方法重新计算纹理的每个像素值进一步改善了局部纹理的接缝误差现象,但是文献[11-12]面向的都是室内近景小物体的三维纹理重建,也没有详细阐述基于MRF的最小能量函数构造与优化求解过程,且使用的优化求解模型主要是Belief Propagation (BP) 和α swap图割算法,计算代价较大,效率较低。通过以上文献综述和分析,可知城市无缝纹理模型重建的问题还没有一种完美的方法可以解决,但可以从以下3个方面进行考虑:①对获取的影像进行必要的预处理,并通过遮挡检测,对三角面进行适当处理与分类;②利用有效的纹理优化选择策略,为每个三角面选择一张最优纹理;③通过图像融合算法构建局部或全局色彩变换方程,重新对每个像素赋值,优化无缝纹理模型重建。本文主要围绕前两个问题进行了有效处理。首先,对获取的纹理影像进行了辐射预处理,解决了部分匀色问题;接着,通过遮挡处理和一定的纹理筛选原则,为三角网格表面模型的地物三角面片建立了具有候选优先级的纹理列表;最后,提出基于MRF框架下的图割纹理优化与聚类策略。
1 三角网格表面模型本文按以下流程完成三角网格表面模型重建。首先,对相机检校,解算出相机的内方位元素和相机镜头畸变参数;接着,利用检校结果,对获取的倾斜影像进行自动空中三角测量获取精确的影像外方位元素;然后,结合CMVS (cluster multi-view stereo) 方法,对同一地物多视角的多幅影像采用PMVS (patch-based multi-view stereo) 技术重建出地物的三维密集点云[3-4];最后,通过泊松优化构网算法构建出用于纹理映射的城市三维网格表面模型[1]。图 1为重建的试验区地物三角网格表面模型。
|
| 图 1 试验区三角网格表面模型 Fig. 1 3D model sketch of experimental area |
2 建立可视纹理列表
在对三角网格表面模型进行纹理映射前,首先需要知道模型中每个三角面在哪些影像上可见。即需要根据倾斜摄影在三维空间中的深度信息从二维观测影像中得到它们之间的遮挡关系。对于这个问题,本文参考Z-Buffer[14-15]的思路,将Z-Buffer中的处理单元变为文中地物三角面,并为加快遮挡检测中对地物三角面的遍历,引入稀疏网格法纹理探测进行遮挡面片的处理[16]。接着,根据文献[17]的纹理筛选思想,将地物纹理的遮挡面积、法向量、距离和分辨率等特性作为评价标准,构建候选纹理优先级评价原则,对影像进行进一步筛选,建立待优化的三角面可视纹理列表,为后续基于图割的纹理优化提供基础。
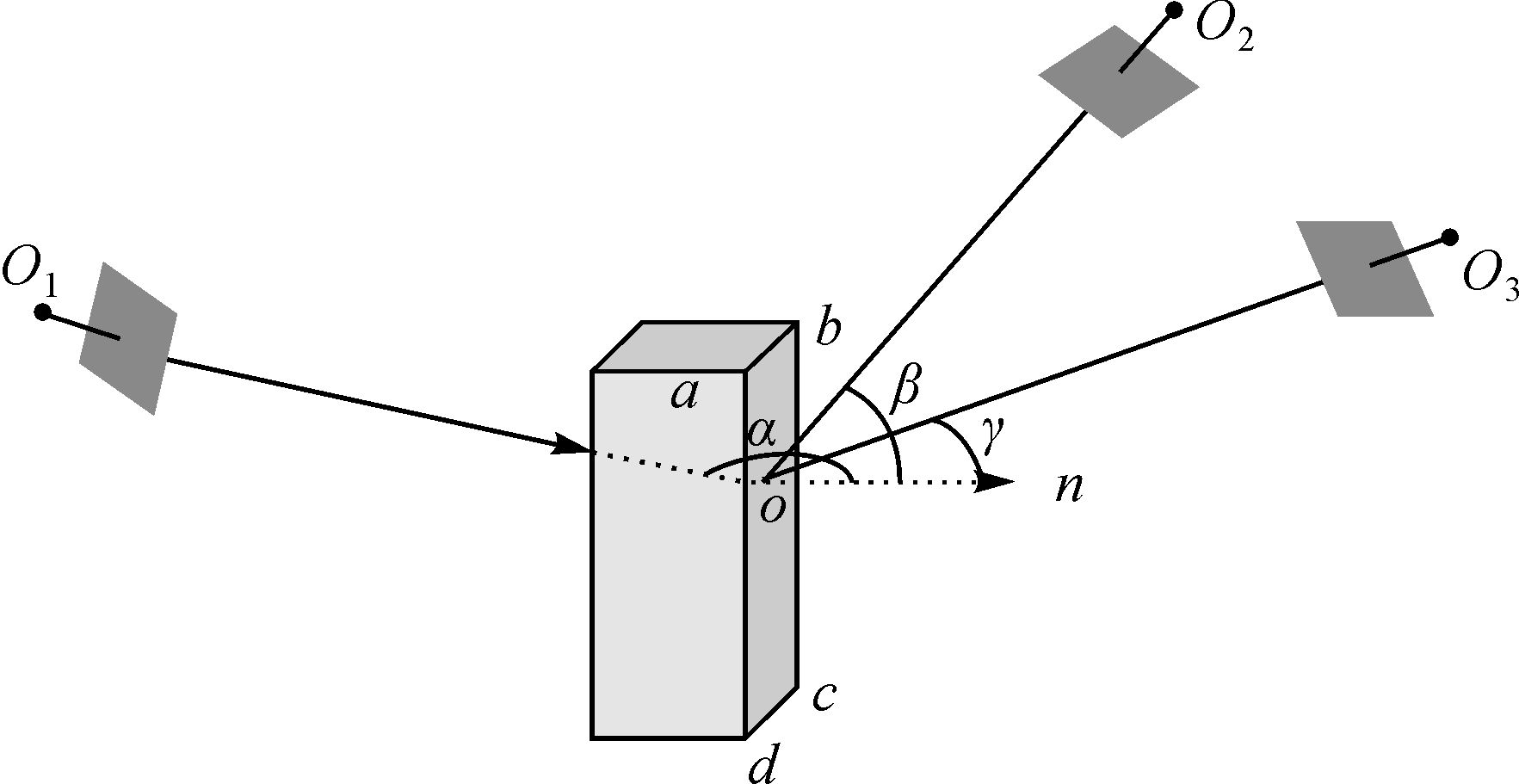
2.1 纹理优先级列表建立原则本文的纹理优先级列表按以下3个原则建立:①面积最大原则,选择非遮挡面积最大的影像作为候选纹理;②交角最小原则,在无遮挡摄影中,纹理影像的变形与摄影光线和地物法线n所成夹角成正比,如图 2,影像O1对于地物中abcd面为遮挡影像,对于物方面元abcd的纹理影像选取中,影像O3比O2更适合作为纹理源;③纹理自动裁剪原则,为了减少纹理存储中因计算机对纹理的重采样导致的时间消耗,在存储纹理时将其尺寸裁剪为2的指数倍。
|
| 图 2 影像遮挡情况示意 Fig. 2 Sketch of image occlusion conditions |
2.2 自适应三角剖分
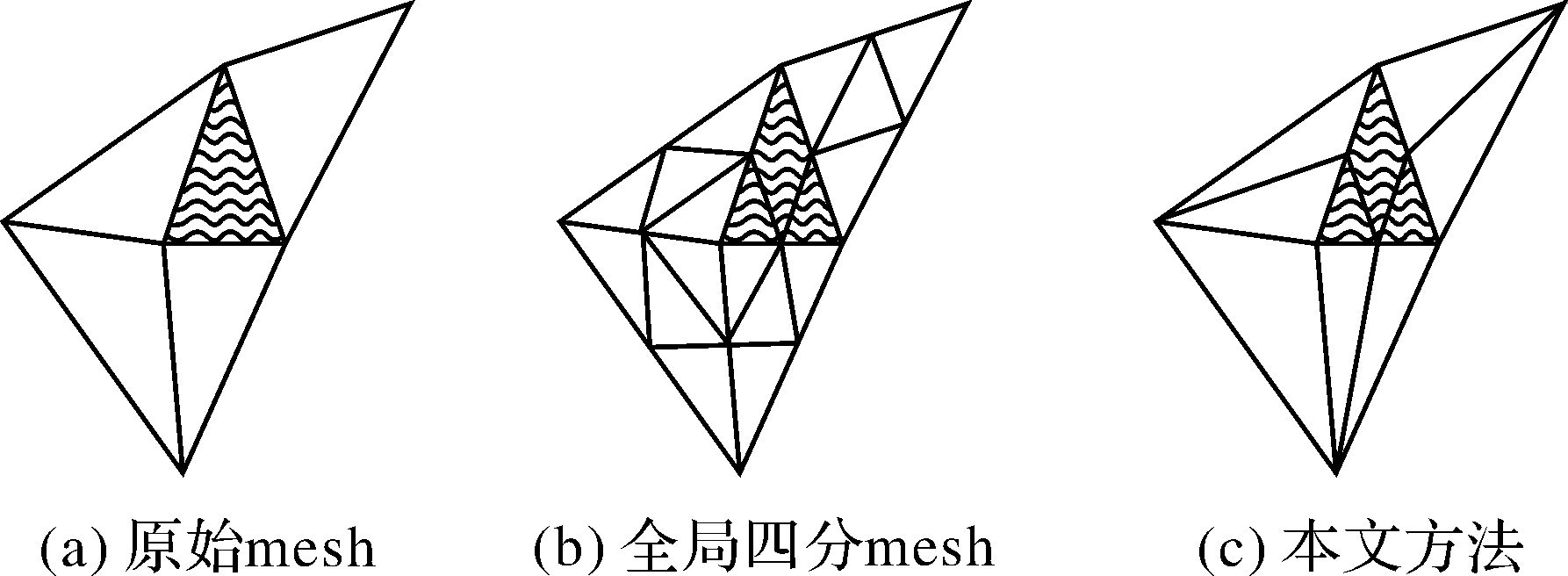
经过遮挡检测和筛选建立的纹理优先级列表中的影像,包括完全可见影像和部分可见影像。对于列表中的部分遮挡纹理影像,如果不做处理,则可能由于构建的三角网格表面模型不够细腻,而出现纹理不一致的现象。为了解决这个问题,加大单个纹理三角面中非遮挡信息的占有率,本文提出了局部四分法的纹理剖分优化策略,即只四分部分遮挡的地物三角面,而对邻接的三角面进行简单的二分法 (图 3)。这样既能保证部分遮挡三角面的高效细分,也能尽可能减少对非遮挡三角面进行分割增加处理时间和数据量。该方法不仅适合大数据三维模型的半遮挡纹理处理,而且能保证三角网格表面模型网形的半边数据结构不变和流行表面的性质。
|
| 图 3 三角网格剖分示意图 Fig. 3 Sketch of triangle mesh subdivision |
图 3中阴影部分为存在部分遮挡的三角形,图 3(c)为本文算法的细分结果。与图 3(b)全局四分法结果相比,本文算法只有在最坏的情况下才与其剖分得到的三角形数据量相等;而一般情况下,本文方法产生的三角形个数为4b+6b≤4a,其中b为三角网中部分遮挡三角形个数, a为三角网中全部三角形个数。
3 基于图割的纹理优化经过以上处理,为每个三角面建立了一个可视纹理影像优先级列表。那么从列表中的哪一幅影像提取其纹理是最优的?当然,这里的最优是指在一定标准下的最好,本文希望每个局部三角面片选取的纹理清晰、细节丰富。在这个标准下,为每个三角面从其可见纹理优先级列表选择一张最优的影像作为其纹理来源本质上是一个MRF下的优化问题。因此,本文提出了一种基于MRF下的图割纹理优化算法,以解决因光照等条件引起的纹理拼接痕迹问题。
3.1 构建标记图图是对现实世界的一种直观表述,由一个点集V与节点间按照某种规则相连的边E所组成,可以表示为G=〈V, E〉;图的一个割就是图G中E的集合的一个子集。图割是一个二标记问题,它使能量函数的极小值与一个含有源和汇的图的最小割对应,在计算机视觉中,图割是马尔科夫随机场框架下求解能量函数最小化模型最有效的方法之一[18-19]。在本文构建的图中,由于影像与三角面的遮挡影响,所以每张影像不一定是每个三角面的候选纹理源,即地物三角面与影像的映射关系不是完全图,这个问题必须在标记图构建中加以考虑。
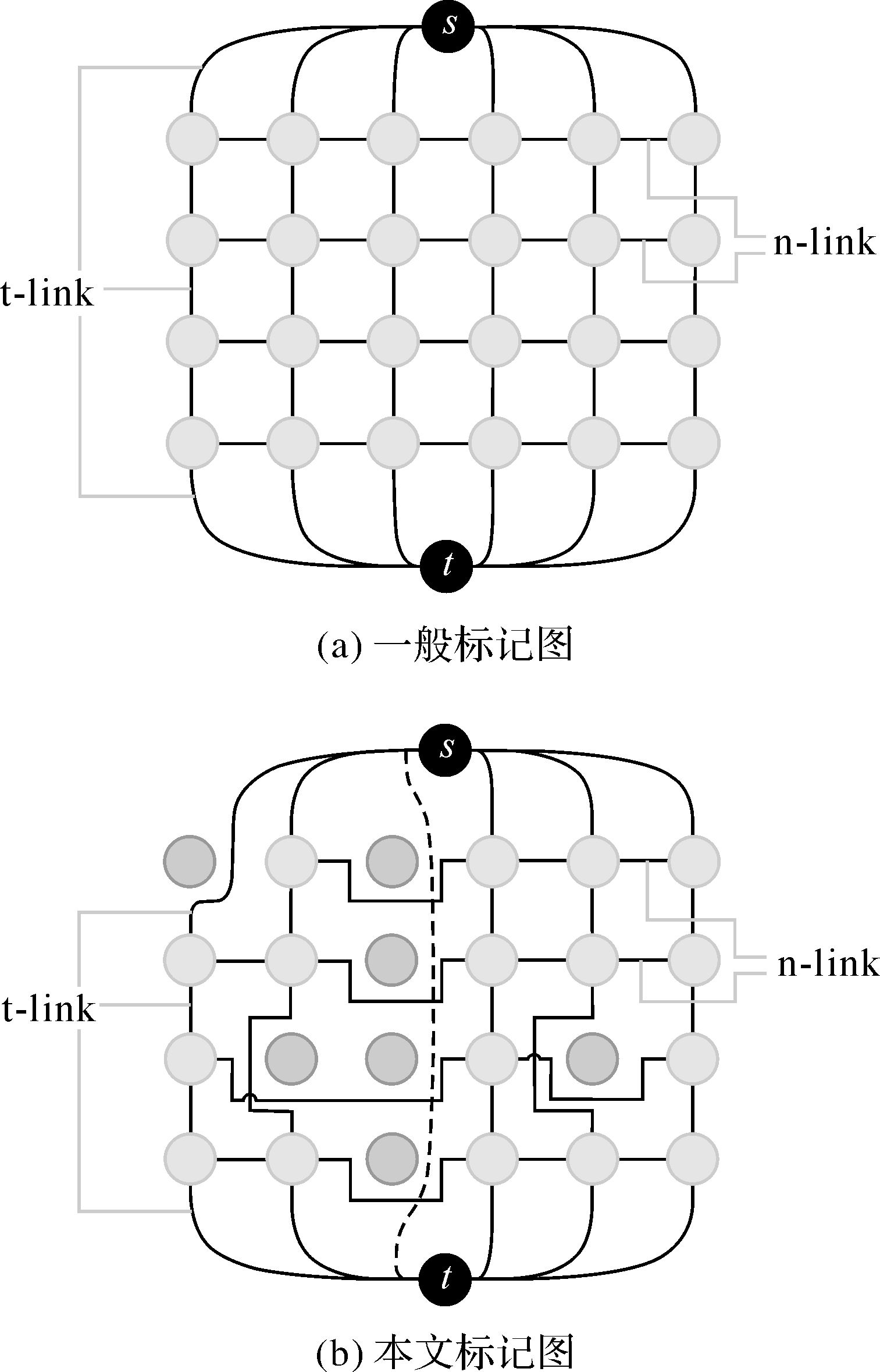
如图 4所示,图 4(a)为一般标记图,其中上下两个特殊的黑色终端节点为图的源s和汇t,其余的节点为每个三角面在不同标记中的节点,节点之间由t-link和n-link边相连,每个边都有相应的能量权重来衡量具体的概率关系。t-link是连接源点、汇点与其他节点的边,为不同标记间的能量关系;n-link是连接标记中节点的边,为相同标记中相邻节点间的能量关系,这种关系主要反映相邻节点选择相同纹理标记的概率的大小,这些节点共同构成了标记空间,且在同一标记层的面具有相同的纹理源;图 4(b)是本文构建的标记图,相比图 4(a),出现了部分有色的空节点,它们表示对应的纹理节点在这一层的纹理空间中不可取,故节点间的连接都需要避开这些空节点,这样可以有效地降低参与图割算法的数据量,从而提高算法的整体效率。
|
| 图 4 两种类型标记 Fig. 4 Two types of labeled graph |
3.2 构建能量函数
图割的能量函数为实际问题的数学表达方式,是图割理论与具体问题的桥梁,一般能量函数由以下两部分组成,即数据项与平滑项,其与图割边的权重一一对应。在本文中数据项代表某节点选择某标记的概率的大小;而平滑项表明相邻节点纹理平滑性,需要综合考虑节点的拓扑信息和不同标记的差异评价标准。图割中的最小割与能量函数的最小值等价,且往往相差一个常数项C,如式 (1) 所示
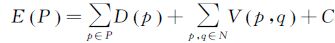 (1)
(1)
本文将三角网格表面模型中的每个三角面看作图G的节点,每两个具有公共边的相邻三角面对应的图G中的节点之间建立一条边,这样就构建了本文需要的图G(V, E)。每个节点有一个含有k个元素的label集,优化算法将为每个节点从其label集中选择一个最佳的label。为了确保图割优化算法在有效的实数范围内计算,并具有对大数据的并行处理能力,本文的能量函数构造需要满足以下3个原则:①能量函数具有上下界;②能量函数的取值范围不超过参与数据个数的有限性倍;③能量函数的数据项与平滑的值及其波动数值影响范围应为同一数量级。本文使用候选影像自身的固有属性 (影像的均值与方差) 来构建能量函数表达式的数据项与平滑项
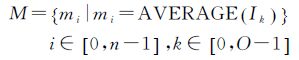 (2)
(2)
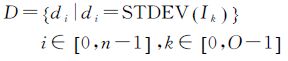 (3)
(3)
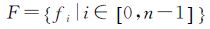 (4)
(4)
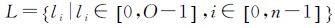 (5)
(5)
式 (2)—式 (5) 分别为影像的均值M、方差D、地物三角面F和标记值域L的表达式, O为影像数, n为地物面。式 (6) 为本文构建的能量函数表达式,其中α与β分别为数据项D(L) 与平滑项N(L) 的控制系数;式 (7)、式 (8) 分别为能量函数的数据项D(L) 与平滑项N(L) 的数学表达式,其中αd与βd为数据项中内部系数,αn与βn为平滑项内部系数,Vfili为地物三角面fi与对应影像li的夹角;Wfili为其对应的可视比值,即影像可见面积与真实面积的比值
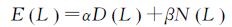 (6)
(6)
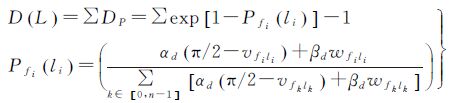 (7)
(7)
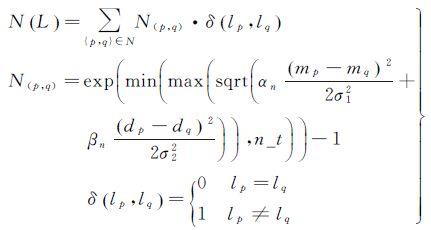 (8)
(8)
本文建立的能量函数满足正态分布数学特性。上述等式中的部分参数在试验中的取值为:α=0.8,β=0.2;αd=0.8,βd=0.2;αn=βn=0.5,且它们直接控制着影像均值与方差的影响;n_t为平滑项的阈值,此处为n_t=1。
3.3 能量最小化求解本文使用α-β swap优化算法来求解能量函数,它是一种有效的图割二分优化算法,不仅可对初始标记的数据集进行优化分割,而且能将多维有向图变为二维简单有向图,从而避免了多维有向图中对t-link与n-link容量值的限定不确定性[18-21]。它的基本思想为:假定已知标记集合L与被分割集合P,若有α、β∈L,交换α和β标记集合,使之形成新的标记集合Lnew,并且确保在新的标记集合下,对应图割的割比原始的小,就把新的标记集合赋值于L;依次循环直至图割中的最小割出现。任何对集合P分割的标记集合L,都可以无差异的等价为P={Pl|l∈L},其中L为标记集合的定义域,Pl={p∈P|lp=l}为集合P中标记为l的子集。给定一组标记α与β,对其作α-β交换操作,即意味着Pα与Pβ的交换,形成新的被分割集合Pnew,其余l≠α、β的集合保持不变。
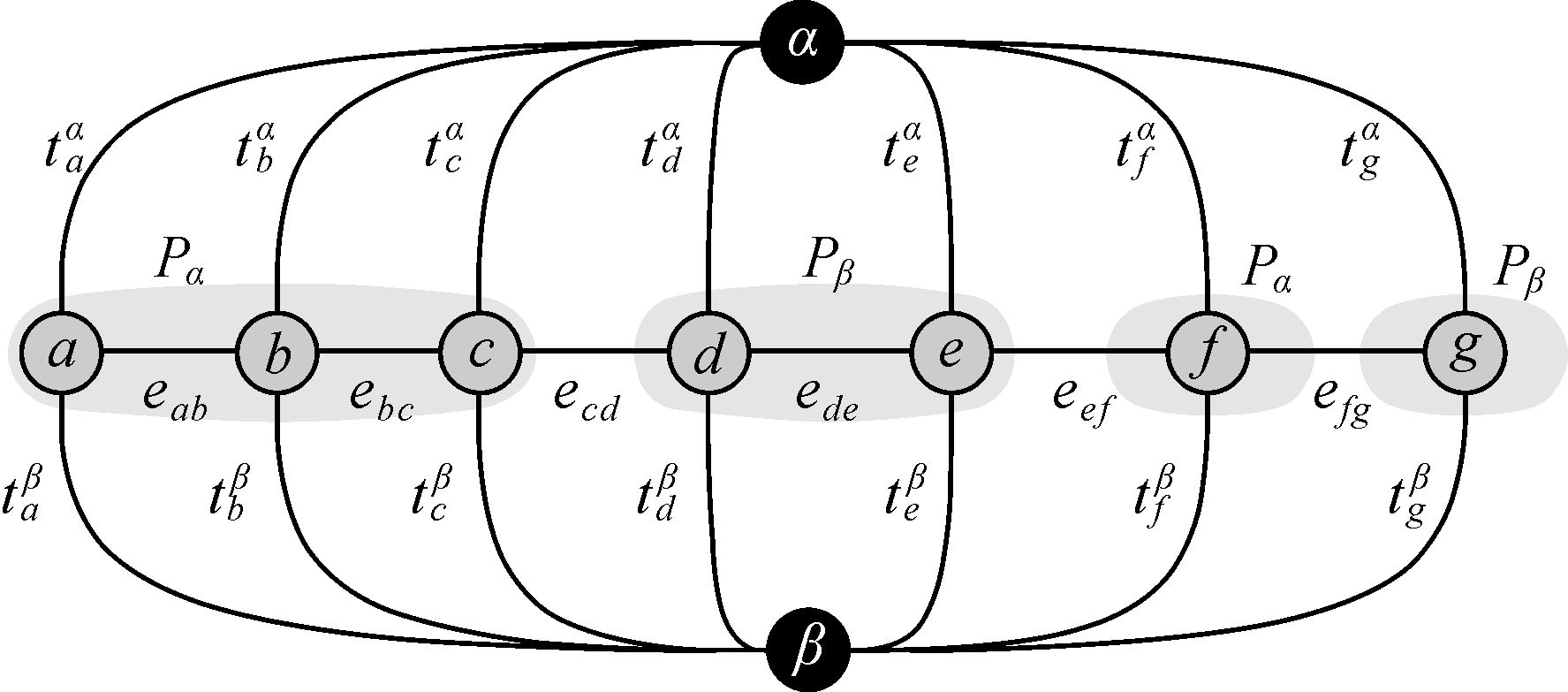
α-β图建立方式如图 5所示,α-β图终端α、β与每个Pα、Pβ集合相连,令Pαβ=Pα∪Pβ,并定义其对应的t-link和n-link权重值,表 1是α-β图的权重。其中,Np为节点p的邻域,Dp(·) 为其标记不相似度;V (·) 为邻域节点的差异度量。前者对图割对应的能量函数空间具有引导作用,而后者具有平滑作用。
|
| 图 5 α-β图示意 Fig. 5 The sketch of graph cuts |
| edge | Weight wp | for |
| tpα | Dp(α)+∑q∈Np, q∉PαβV (α, Lq) | p∈Pαβ |
| tpβ | Dp(β)+∑q∈Np, q∉PαβV (β, Lq) | p∈Pαβ |
| ep, q | V (α, β) | {p, q}∈N, p, q∈Pαβ |
4 试验与结果分析 4.1 试验数据与环境
为了直观地展示和验证评价本文所提算法和策略的优越性与有效性,文中选取了某地区真实倾斜影像数据生成的部分三角网格表面模型数据进行测试,该简化模型有3117个三角面片。本文的计算机试验环境为:Windows7操作系统,内存32 GB,Intel core7 3.6 GHZ,4核。此外,在进行纹理优化前还对试验影像进行了预处理,即引入了文献[22]提出的基于暗通道方法与Wallis方法[23-24],解决了因倾斜影像场景深度不一致导致的影像环境辐射问题,并使用201曲线库DoRF (Database of Real-world camera response Function),通过构建求解相机响应函数的优化函数[25-26],改正了影像的系统辐射误差。
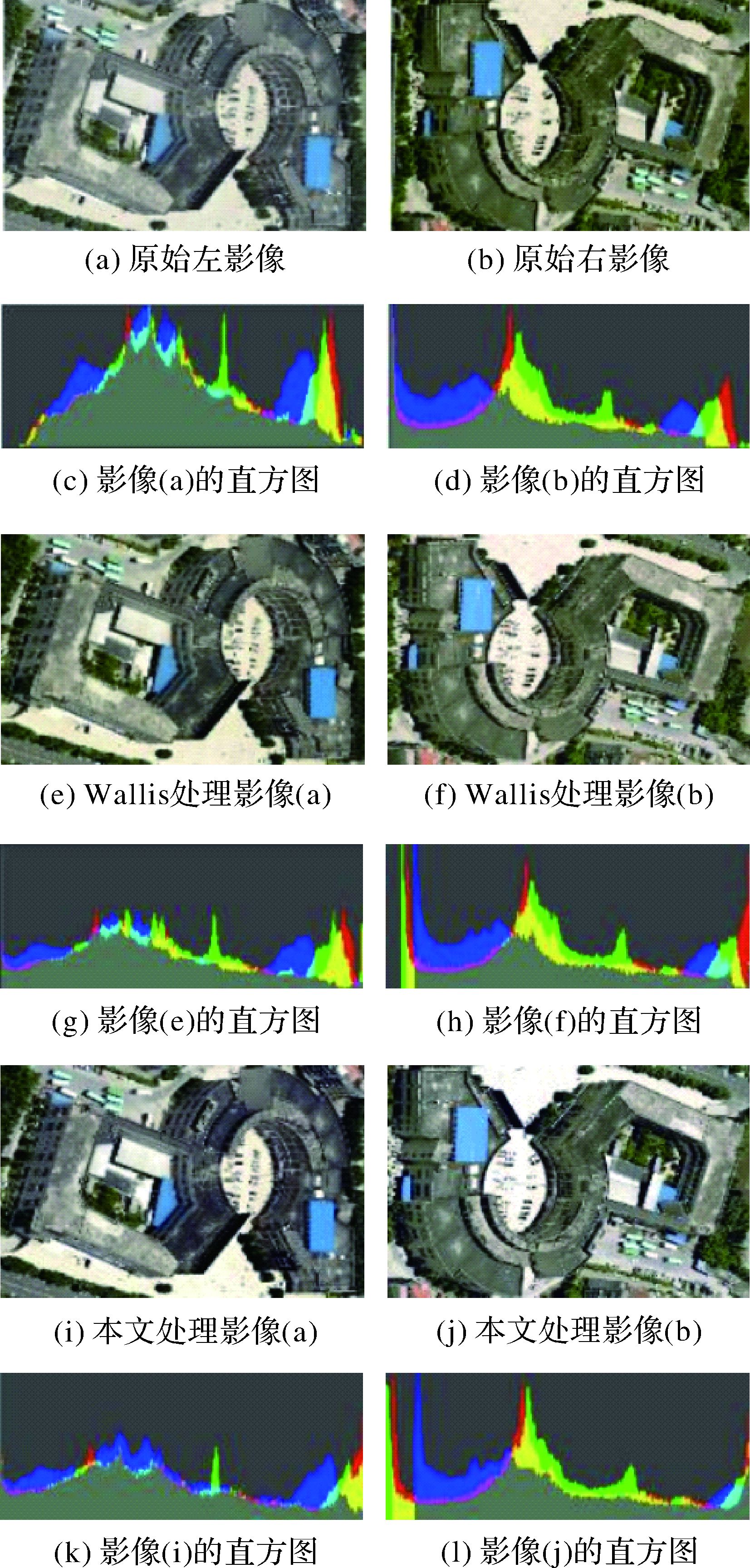
4.2 试验效果对比 4.2.1 影像预处理效果对比图 6是一组左右试验倾斜影像在不同方法下的预处理结果对比,可以发现本文预处理方法与仅使用Wallis方法相比,不仅起到了类似于直方图均衡化的效果,最大限度地维持了影像的高对比度,而且影像的饱和度也有所提高,白平衡处理也更突出。这说明经过环境辐射改正与系统误差纠正后,获得了更真实的纹理影像均值与方差。
|
| 图 6 环境辐射处理局部效果对比 Fig. 6 Effect of preprocessed images |
4.2.2 遮挡探测结果对比
倾斜影像存在建筑物间的相互遮挡问题需要解决。如图 7左侧红框内为未进行遮挡处理的映射结果,而图 7中右侧红框内为经过本文遮挡检测后的映射结果,可见已消除了遮挡现象,更好地确保了纹理的视角与尺度一致性,实现了纹理的连贯性表达。

|
| 图 7 遮挡处理结果对比 Fig. 7 Contrast of occlusion detection |
4.2.3 纹理聚类效果对比
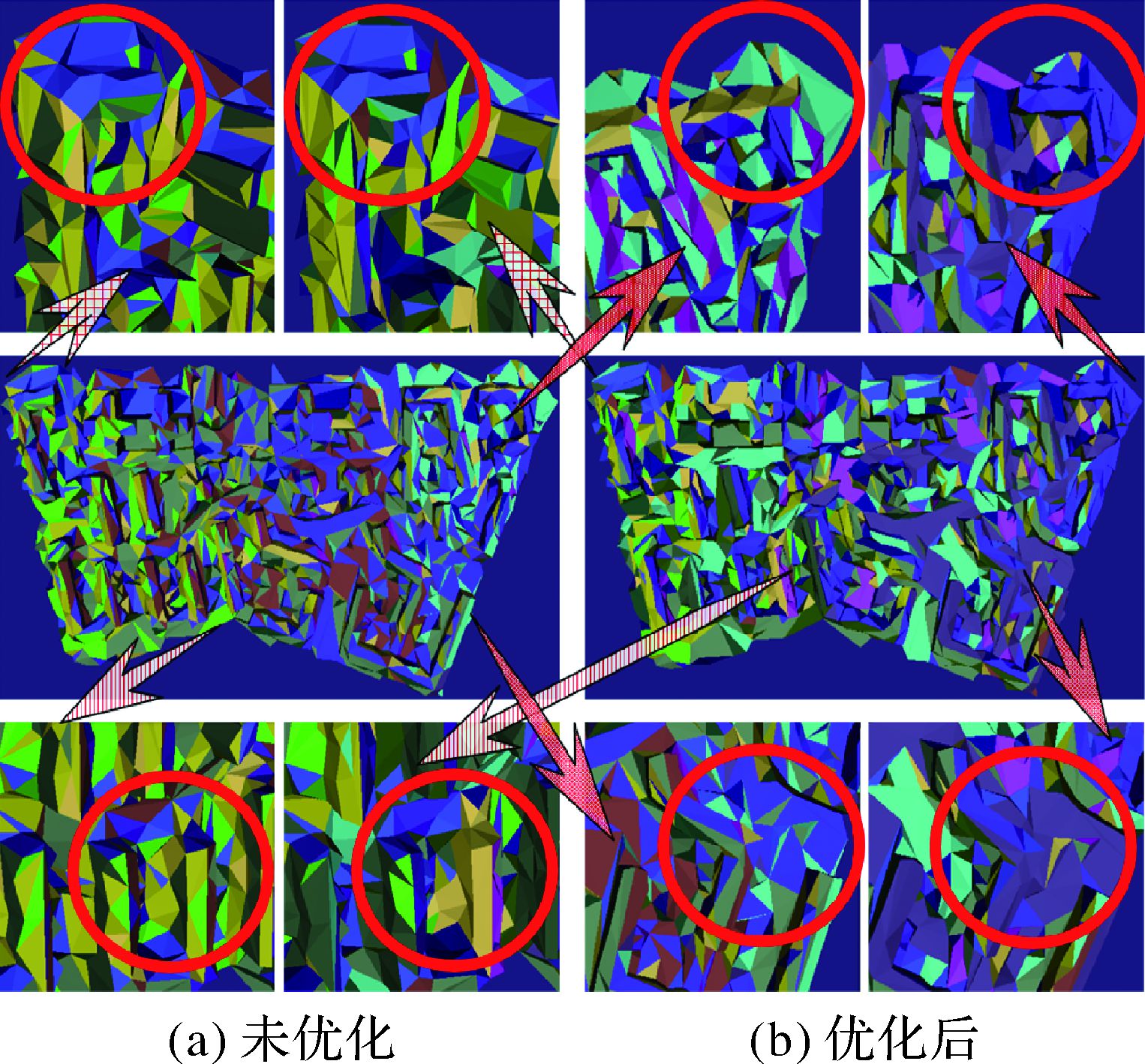
基于MRF的图割纹理选择与聚类可以加强纹理在视觉上的连续性与一致性效果。本文利用纹理影像的固有属性,通过构建并求解最小能量函数实现了相邻三角面的纹理空间标记取值的平滑,实现了纹理映射优化。图 8为试验结果,其中,图 8(a)是未进行优化选择与聚类的效果,图 8(b)是本文方法优化后的效果,图中四角为局部放大图;图中不同的颜色代表三角面纹理取自不同的纹理源,通过图中对比可以看出,经过纹理优化后,三角网格表面模型中更多相邻的三角面被赋予了相同的纹理源,实现了纹理优化选择;同时,在纹理映射操作过程中,还可以利用这个结果,使同一个聚类纹理块一次性取得相应的纹理,从而减少纹理后操作时间,加速纹理映射过程。
|
| 图 8 纹理优化选择与聚类效果对比 Fig. 8 Optimal textures contrast |
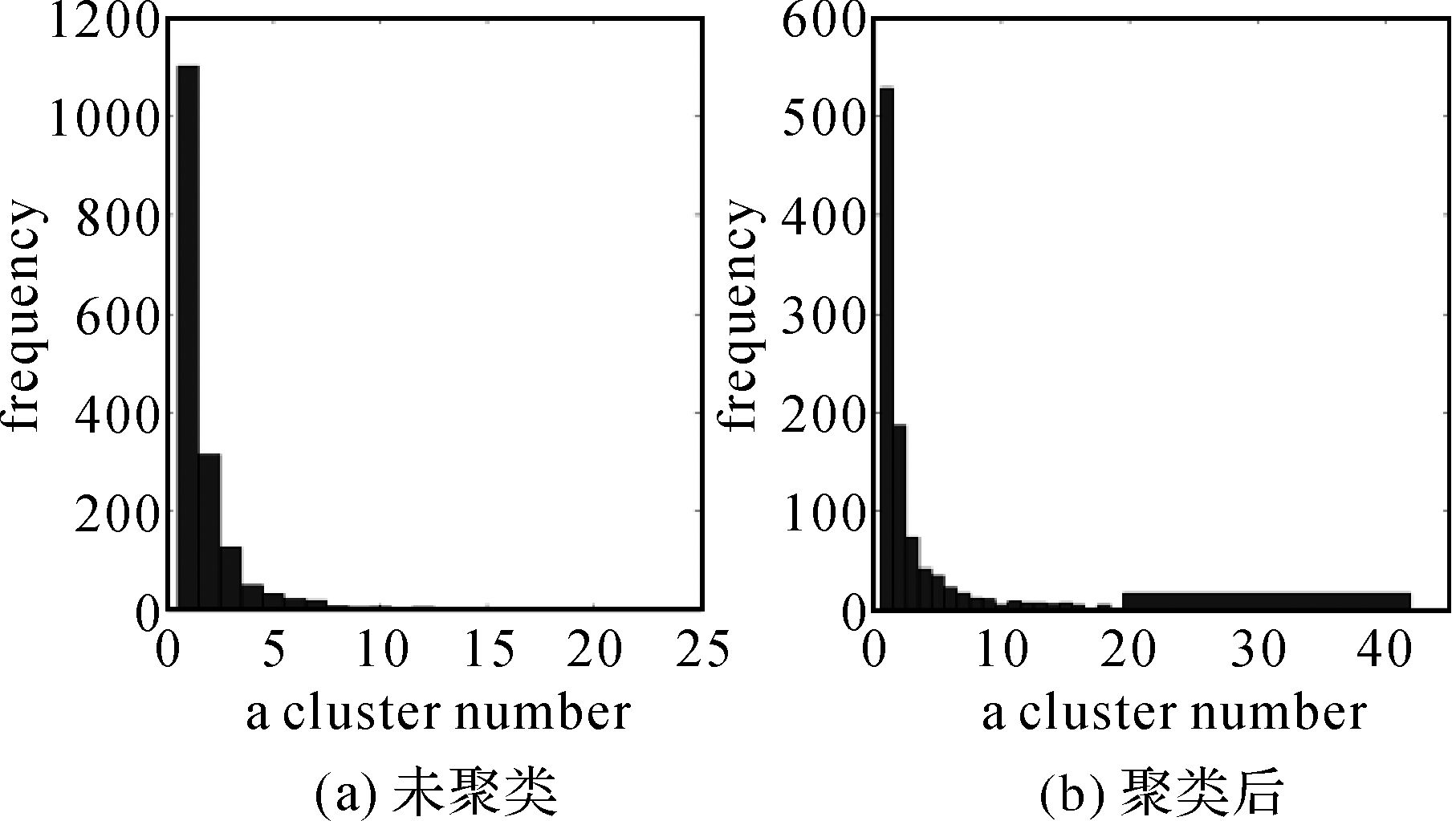
图 9为试验的简化三角网格表面模型3117个三角面片的聚类统计数值分析。其中,图 9(a)为未聚类前相邻三角面的纹理选择分布,图 9(b)是优化后效果。从其统计结果来看,未聚类前孤立的聚类结果 (聚类容量为1的聚类为孤立聚类) 约占总数量的33%,且最大聚类容量不到20;而聚类后孤立的聚类结果只约占总数量的17%,且最大聚类容量大于40,这说明基于MRF的图割纹理聚类效果显著。
|
| 图 9 优化前后统计结果对比 Fig. 9 Optimal result contrast of before and after |
4.2.4 纹理模型重建效果对比
为了更直观地展示本文算法的整体效果和优越性,在此将试验区简化模型的纹理重建结果与使用著名的三维重建软件Photomodeler实现的纹理重建结果进行对比。图 10为试验区纹理模型重建结果对比,其中,图 10上半部分为Photomodeler重建效果,下半部分为本文效果,从图中左侧的整体效果可以看出,Photomodeler与本文方法都十分关注纹理映射中的平滑处理,但是从图中右侧的局部放大图可以容易地发现本文方法不仅保留了更多的纹理细节,而且有效地解决了纹理重建中的部分匀色匀光问题,重建效果真实、清晰,色彩与亮度处理更加自然。

|
| 图 10 纹理模型重建效果对比 Fig. 10 A contrast figure of texture reconstruction |
图 11为试验区重建纹理模型的3组局部放大效果对比图。其中,图左侧为未经本文方法处理的结果,可以看到图中箭头所指处有大量纹理不一致、映射错误和拼接缝的存在,而图右侧经过纹理优化选择与聚类后,极大地减少,甚至消除了这些问题,体现出了本文算法的有效性和优越性。
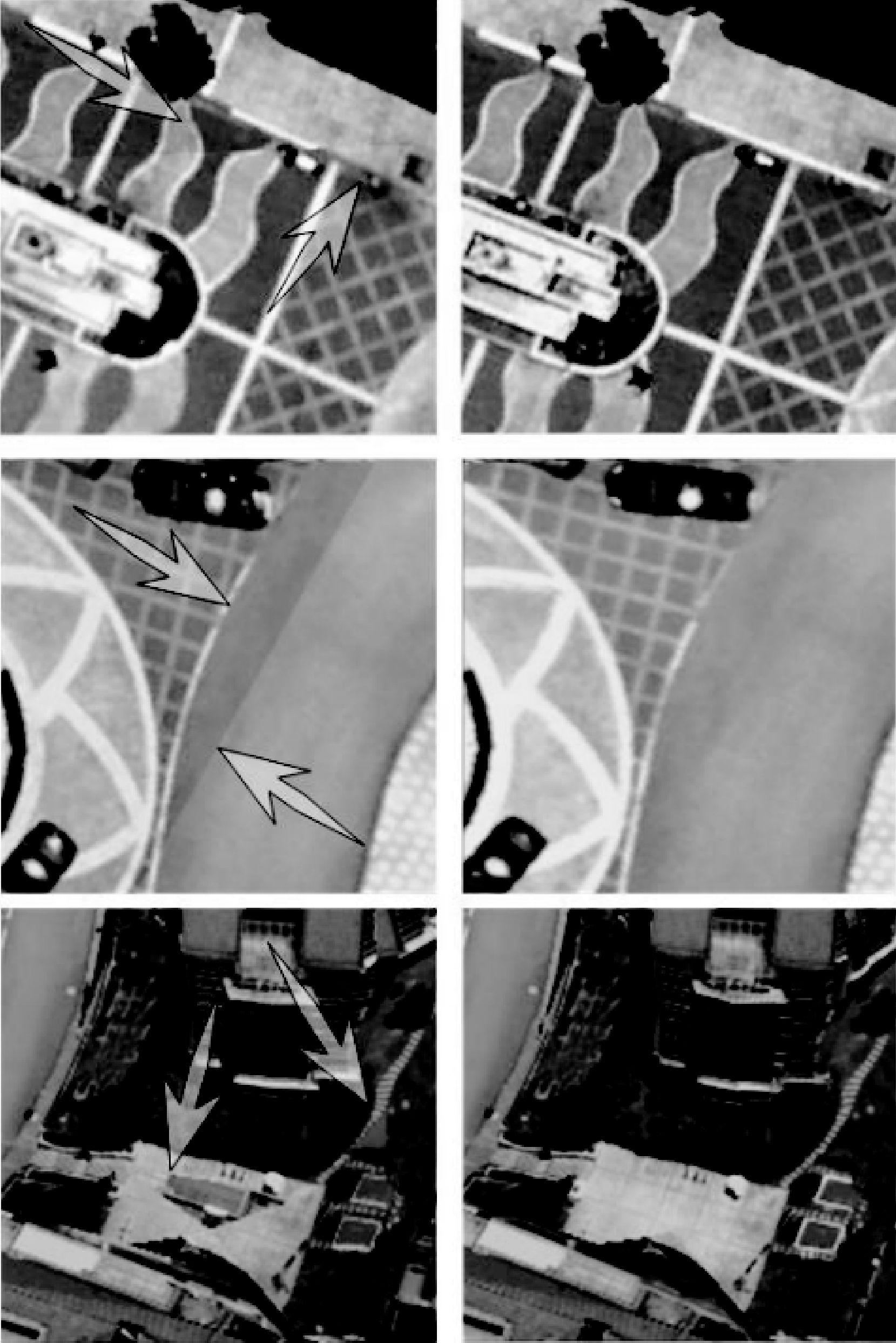
|
| 图 11 纹理模型局部效果对比 Fig. 11 Zoom effect in contrast |
5 结论
本文基于低空倾斜影像,针对三维影像城市重建中的无缝纹理映射问题,提出了一种有效的纹理优化选择方法。该方法在建立城市地面三角网格表面模型和空中三角测量的基础上,计算模型与影像之间的投影关系,并使用稀疏构网法实现了高效的遮挡探测;在纹理优化选择过程中,本文利用影像的固有属性和纹理对应三角面片的拓扑信息,把纹理的优化选择看作一个马尔科夫随机场问题,提出了基于图割的最小能量函数优化求解方案,实现了映射纹理的优化选择与聚类。试验结果表明本文方法可以有效地提高纹理的聚类表达与辐射一致性效果,能显著地减少三维纹理映射中的拼接缝和纹理碎片的产生。
| [1] | KAZHDAN M, BOLITHO M, HOPPE H. Poisson Surface Reconstruction[C]//Proceedings of the Fourth Eurographics Symposium on Geometry Processing. Switzerland:Eurographics Association Aire-la-Ville, 2006. |
| [2] | SEITZ S M, CURLESS B, DIEBEL J, et al. A Comparison and Evaluation of Multi-view Stereo Reconstruction Algorithms[C]//Proceedings of 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York, NY:IEEE, 2006. |
| [3] | FURUKAWA Y, PONCE J. Accurate, Dense, and Robust Multiview Stereopsis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(8): 1362–1376. DOI:10.1109/TPAMI.2009.161 |
| [4] | SCHÖNING J, HEIDEMANN G. Evaluation of Multi-view 3D Reconstruction Software[M]//AZZOPARDI C, PETKOV N. Computer Analysis of Images and Patterns:Lecture Notes in Computer Science. Switzerland:Springer International Publishing, 2015. |
| [5] | 王竞雪, 朱庆, 王伟玺. 多匹配基元集成的多视影像密集匹配方法[J]. 测绘学报, 2013, 42(5): 691–698. WANG Jingxue, ZHU Qing, WANG Weixi. A Dense Matching Algorithm of Multi-view Image Based on the Integrated Multiple Matching Primitives[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 691–698. |
| [6] | PARK J S. Interactive 3D Reconstruction from Multiple Images:a Primitive-based Approach[J]. Pattern Recognition Letters, 2005, 26(16): 2558–2571. DOI:10.1016/j.patrec.2005.05.009 |
| [7] | FRUEH C, JAIN S, ZAKHOR A. Data Processing Algorithms for Generating Textured 3D Building Facade Meshes from Laser Scans and Camera Images[J]. International Journal of Computer Vision, 2005, 61(2): 159–184. DOI:10.1023/B:VISI.0000043756.03810.dd |
| [8] | 崔红霞, 林宗坚, 孙杰. 大重叠度无人机遥感影像的三维建模方法研究[J]. 测绘科学, 2005, 30(2): 36–38. CUI Hongxia, LIN Zongjian, SUN Jie. Research on the 3-Dimensional Modeling Method for Remote Sensing Images of Big Degree of Overlap Acquired by Unmaned Aerial Vehicle[J]. Science of Surveying and Mapping, 2005, 30(2): 36–38. |
| [9] | BERNARDINI F, MARTIN I M, RUSHMEIER H, et al. High-quality Texture Reconstruction from Multiple Scans[J]. IEEE Transactions on Visualization and Computer Graphics, 2001, 7(4): 318–332. DOI:10.1109/2945.965346 |
| [10] | BAUMBERG A. Blending Images for Texturing 3D Models[C]//Marshall D, ROSIN L. Proceedings of the British Machine Vision Conference.[S.l.]:BMVA Press, 2002. |
| [11] | LEMPITSKY V, IVANOV D. Seamless Mosaicing of Image-based Texture Maps[C]//Proceedings of 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, MN:IEEE, 2007. |
| [12] | GAL R, WEXLER Y, OFEK E, et al. Seamless Montage for Texturing Models[J]. Computer Graphics Forum, 2010, 29(2): 479–486. DOI:10.1111/j.1467-8659.2009.01617.x |
| [13] | PERÉZ P, GANGNET M, BLAKE A. Poisson Image Editing[J]. ACM Transactions on Graphics, 2003, 22(3): 313–318. DOI:10.1145/882262 |
| [14] | GREENE N, KASS M, MILLER G. Hierarchical Z-buffer Visibility[C]//Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques. New York:ACM, 1993. |
| [15] | PARKER S, SHIRLEY P, LIVNAT Y, et al. Interactive Ray Tracing for Isosurface Rendering[C]//Proceedings of 1998 International Conference on Visualization. Los Alamitos, CA:IEEE, 1998. |
| [16] | 张春森, 张卫龙, 郭丙轩, 等. 倾斜影像的三维纹理快速重建[J]. 测绘学报, 2015, 44(7): 782–790. ZHANG Chunsen, ZHANG Weilong, GUO Bingxuan, et al. Rapidly 3D Texture Reconstruction Based on Oblique Photography[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 782–790. DOI:10.11947/j.AGCS.2015.20140341 |
| [17] | HARTLEY R, ZISSERMAN A. Multiple View Geometry in Computer Vision[M]. 2nd ed. London: Cambridge University Press, 2003. |
| [18] | BOYKOV Y, VEKSLER O, ZABIH R, et al. Fast Approximate Energy Minimization via Graph Cuts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(11): 1222–1239. DOI:10.1109/34.969114 |
| [19] | SCHMIDT M, ALAHARI K. Generalized Fast Approximate Energy Minimization via Graph Cuts:α-Expansion β-Shrink Moves[C]//Proceedings of 27th Conference on Uncertainty in Artificial Intelligence. Barcelona, Spain:[s.n.], 2011. |
| [20] | ZUREIKI A, DEVY M, CHATILA R. Stereo Matching and Graph Cuts[M]. Vienna, Austria: I-Tech Education and Publishing, 2008: 349-372. |
| [21] | HUSSMANN S, RINGBECK T, HAGEBEUKER B. A Performance Review of 3D TOF Vision Systems in Comparison to Stereo Vision Systems[M]. Vienna, Austria: InTech, 2008. |
| [22] | HE Kaiming, SUN Jian, TANG Xiaoou. Single Image Haze Removal Using Dark Channel Prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(12): 2341–2353. DOI:10.1109/TPAMI.2010.168 |
| [23] | 罗思. 基于Wallis原理改进的匀光算法[J]. 测绘科学技术, 2015, 3(3): 51–58. LUO Si. Improved Dodging Algorithm Based on Wallis Principle[J]. Geomatics Science and Technology, 2015, 3(3): 51–58. DOI:10.12677/GST.2015.33008 |
| [24] | 李德仁, 王密, 潘俊. 光学遥感影像的自动匀光处理及应用[J]. 武汉大学学报 (信息科学版), 2006, 31(9): 753–756. LI Deren, WANG Mi, PAN Jun. Auto-dodging Processing and Its Application for Optical RS Images[J]. Geomatics and Information Science of Wuhan University, 2006, 31(9): 753–756. |
| [25] | KIM S J, POLLEFEYS M. Robust Radiometric Calibration and Vignetting Correction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(4): 562–576. DOI:10.1109/TPAMI.2007.70732 |
| [26] | D'ANGELO P. Radiometric Alignment and Vignetting Calibration[C]//Proceedings of the 2007 ICVS Workshop on Camera Calibration Methods for Computer Vision System. Bielefeld, Germany:Applied Computer Science Group, Bielefeld University, 2007. |



