2. 成都理工大学地球科学学院, 四川 成都 610051
2. College of Earth Science, Chengdu University of Technology, Chengdu 610051, China
BDS (BeiDou Navigation Satellite System) 应用于我国GNSS测量已成一种必然趋势,但因其起步晚,国际国内市场目前仍以GPS为主导[1]。因此,BDS+GPS组合卫星资源的利用成为BDS逐步进入市场的一个过程。已有大量试验研究分析表明,BDS+GPS融合定位能显著提高单系统模糊度解算的固定率和可靠性,能明显改善单系统定位精度[2-9]。虽然近年来大量文献证明了BDS+GPS较单系统具有明显优势,但大部分证明均从试验数据结果分析得出,仅少量文献从理论模型角度分析BDS+GPS的优势所在。文献[10]仿真分析了BDS+GPS对单系统PNT (positioning, navigation and timing) 的DOP (dilution of precision) 理论值改善。文献[11-12]分别从模糊度精度因子ADOP (ambiguity dilution of precision) 和位置精度因子PDOP (position dilution of precision) 出发,论证了BDS+GPS对单系统定位模糊度固定成功率和位置解算精度的提高,未考虑GNSS信号空间传播误差的影响。然而,在GNSS中长距离精密相对定位中,空间传播误差是不容忽略的。文献[13]提出的广义精度因子 (generalised dilution of precision, G-DOP),分析了信号空间传播误差对多系统融合DOP的影响,未对各类误差展开具体分析。本文针对BDS/GPS中长距离精密相对定位中对流层和电离层误差的影响,展开了具体分析。引入对流层精度因子 (troposphere dilution of precision,TrDOP)、电离层精度因子 (Ionosphere Dilution of Precision,IDOP),与相对几何精度因子 (Relative Geometric Dilution of Precision,RGDOP)[14-15]一起构成相对定位精度因子 (Relative Positioning Dilution of Precision, RPDOP)。文献[16-18]中定义的相对定位精度因子RPDOP,又称RGDOP,仅考虑了几何模型参数,而本文在考虑大气模型参数后,提出了新的RPDOP定义。
另外,本文从GNSS相对定位涉及的4项精度因子ADOP、RGDOP、TrDOP、IDOP出发,分析BDS+GPS对定位精度和时间效率的影响。首先,分析延长观测时间,ADOP值减小,模糊度能够更加快速固定;RGDOP和TrDOP值减小,定位精度提高。其次,分析引入BDS卫星,ADOP、RGDOP、TrDOP值均减小,达到与延长观测时间相当的效果;最后,分析引入BDS三频数据,IDOP值的变化及对电离层参数估计的影响。此外,通过5 km km km实测基线数据分析验证了本文理论推导的正确性,并证明了BDS+GPS能够提高相对定位精度和时间效率。
1 顾及大气影响的相对定位精度因子GNSS相对定位主要包括整周模糊度固定和相对位置求解两步[19-20],需求解的未知参数主要包含整周模糊度向量N、相对位置向量为X、对流层参数T、电离层参数I。下面针对这4个基本未知参数分别对应的精度因子ADOP、RGDOP、TrDOP、IDOP展开研究,并分析其对定位精度与时间效率的影响。
GNSS相对定位的观测方程线性化[21]如下所示
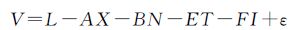 (1)
(1)
式中, L表示观测值向量;X表示三维空间直角坐标下的相对位置向量 (x, y, z);N表示n×1维双差整周模糊度向量 (n为双差载波观测值个数);T表示1个双差天顶对流层湿延迟参数;I表示s×1维电离层参数向量 (s为卫星个数,电离层参数指第一个频率双差观测量的电离层延迟量);A、B、E、F表示系数阵;V表示残差向量;ε表示噪声。
对式 (1) 进行最小二乘平差,通过分块求解方法消除X、T、I,求解模糊度浮点解及其协因数阵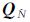
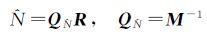 (2)
(2)
式中, M和R为与L、A、B、E、F相关的表达式[21]。
求解出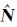



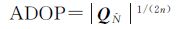 (3)
(3)
式中, n表示方差阵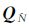
整周模糊度固定后,即可进行高精度位置参数求解。消除整周模糊度的误差方程表示为
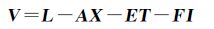 (4)
(4)
同上,分块求解X、T、I及其方差阵QX、QT、QI
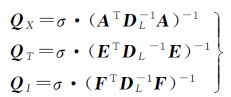 (5)
(5)
式中,σ=(VTDL-1V)/r表示验后方差因子;r为多余观测数;DL-1表示观测值权阵。
根据上述函数模型,可知相对定位几何精度因子RGDOP为[14-16]
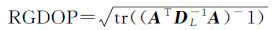 (6)
(6)
式中,tr (·) 表示矩阵的迹。
另外,为了考虑大气影响,笔者提出对流层精度因子TrDOP和电离层精度因子IDOP,分别定义如下
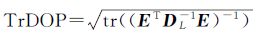 (7)
(7)
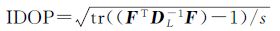 (8)
(8)
式中,对流层精度因子定义与几何精度因子定义类似,对流层参数为天顶对流层湿延迟,参数个数不变,且虽属于时变因子,但在约2 h范围内也可认为值不变。式 (8) 中,电离层未知参数个数为非参考卫星个数s,随卫星升降而变化,故此处IDOP定义为平均电离层精度因子。
根据上述3个精度因子,笔者定义相对定位精度因子RPDOP为
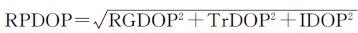 (9)
(9)
由式 (4)—(9) 可知,仅当X、T、I解算精度均较高时,才能使得残差V较小,相对定位精度较高。
2 多历元相对定位精度因子分析一般GNSS测量通过延长卫星观测时间,来获得高精度定位结果。设采用t个历元求解模糊度 (相位周跳已修复),每个历元模糊度维数相同,则模糊度方差阵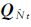
 (10)
(10)
式中,M1、M2、…、Mt为式 (2) 中单历元模糊度固定的中间矩阵。因这些矩阵均为正定矩阵,故存在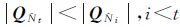
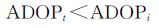 (11)
(11)
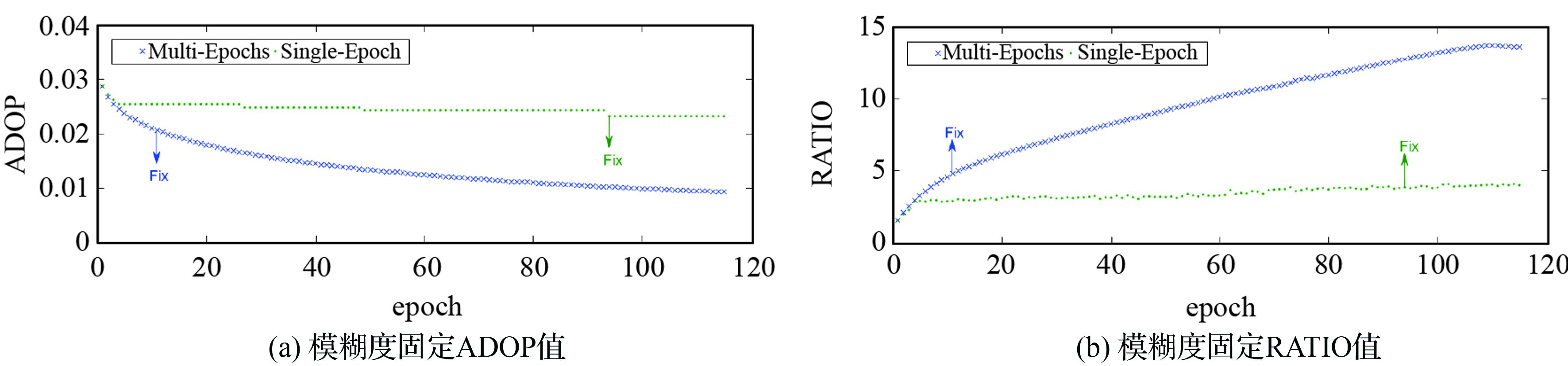
图 3列出了5 km短基线双差模糊度固定过程中的ADOP值和RATIO值。其中,双差模糊度固定采用多历元 (multi-epochs) 和单历元 (single-epochs) 两种方式,单历元方法采用单个历元观测量估计位置参数和浮点模糊度,然后利用LAMBAD方法固定;多历元方法通过历元累加不断滤波估计位置参数和浮点模糊度,直至模糊度固定。图 1(a)给出了模糊度固定时的ADOP值,图 1(b)列出了RATIO值。从图 1可明显看出,随着时间的累积,多历元ADOP值减小,RATIO值增加,累积11个历元模糊度固定 (Fix);单历元ADOP值和RATIO值随时间变化均非常缓慢,直至94个历元模糊度才固定 (RATIO限值根据F分布设定)。显然,相比单个历元,多个历元时间累积,模糊度解算的ADOP值显著减小,能够提高固定的时间效率。
|
| 图 1 模糊度固定ADOP和RATIO值随观测历元的变化 Fig. 1 The variations of ADOP and RATIO values over epochs |
采用t个历元求解基线相对位置参数,则其相对定位精度因子为
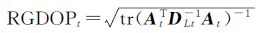 (12)
(12)
式中,AtTDLt-1At=A1TDL1-1A1+A2TDL2-1A2+…+AtTDLt-1At。矩阵AiTDLi-1Ai为正定矩阵,则tr ((AtTDLt-1At)-1)<tr ((AiTDLi-1Ai)-1),i<t因此可知
 (13)
(13)
静态控制测量中,估计的位置参数为常数,对流层随时间变化缓慢,其天顶湿延参数在约2 h范围内可认为常数。因此,理论上可认为对流层精度因子值随着时间增加而减小
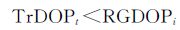 (14)
(14)
然而,由于大气参数的过程噪声与大气的真实情况并不完全一致,尤其是电离层,从而会导致TrDOP随时间的变化与理论推导式 (14) 存在差异,IDOP值随时间累积而减小的趋势不明显。
图 2列出了滤波解算43 km基线的RGDOP、TrDOP、IDOP值。43 km中长基线解算模式是对双差原始伪距和载波观测值,利用Kalman滤波估计位置参数、模糊度浮点解 (浮点解滤波过程中包含未知双差整周模糊度)、对流层和电离层大气参数 (单位为m)。图 2(a)、图 2(c)、图 2(e)表示前164个历元浮点解过程中3个精度因子的变化,图 2(b)、图 2(d)、图 2(f)表示整周模糊度固定后,固定解滤波2 h左右3个精度因子的变化。浮点解滤波过程中,RGDOP、TrDOP和IDOP值随时间累积,均呈明显减小趋势,表明模糊度的逐渐收敛,将提高位置、对流层和电离层的解算精度;固定解滤波1.5 h过程中,RGDOP和TrDOP值随着定位历元的累积呈明显减小的趋势,而IDOP值随时间累积而减小的趋势不明显,与式 (13)、式 (14) 理论推导基本一致 (图中非趋势性波动,受随机模型影响,因而并不完全一致)。据式 (9) 可知,随观测时间的累积,相对定位精度因子RPDOP将减小,可提高相对定位精度。

|
| 图 2 相对定位RGDOP、TrDOP和IDOP值随观测历元的变化 Fig. 2 The variations of RGDOP、TrDOP and IDOP values over epochs |
3 BDS+GPS相对定位精度因子分析
由第2节分析可知,延长观测时间,ADOP和RPDOP值减小,模糊度固定成功的概率和相对定位的精度得到了提高。若采用其他手段,精度因子ADOP、RGDOP、TrDOP、IDOP减小,也有助于改善定位的精度,从而提高时间效率。下文研究引入BDS卫星后,BDS/GPS融合定位各项精度因子的变化。
根据文献[22]定义,设BDS与GPS系统模糊度精度因子近似相等:ADOPB≈ADOPG≈ADOP*,且两系统观测值个数近似相等:fBSB≈fGSG,给出BDS+GPS与独立系统ADOP间的近似关系
 (15)
(15)
式中, B和G分别表示BDS和GPS系统;*表示其中某一系统;
式 (15) 中,因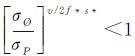

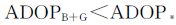 (16)
(16)
另外,根据ADOP*的定义[11]可知,ADOP*正比与
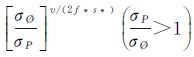
上述ADOP相关定义及分析表明,增加观测频率、增加卫星个数或增加观测系统,ADOP值将减小。利用ADOP值,从理论上能够估计出模糊度固定的成功概率PADOP[25-26]
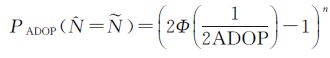 (17)
(17)
式中,函数Φ(·) 为标准正态累积分布函数;n表示模糊度的维数。
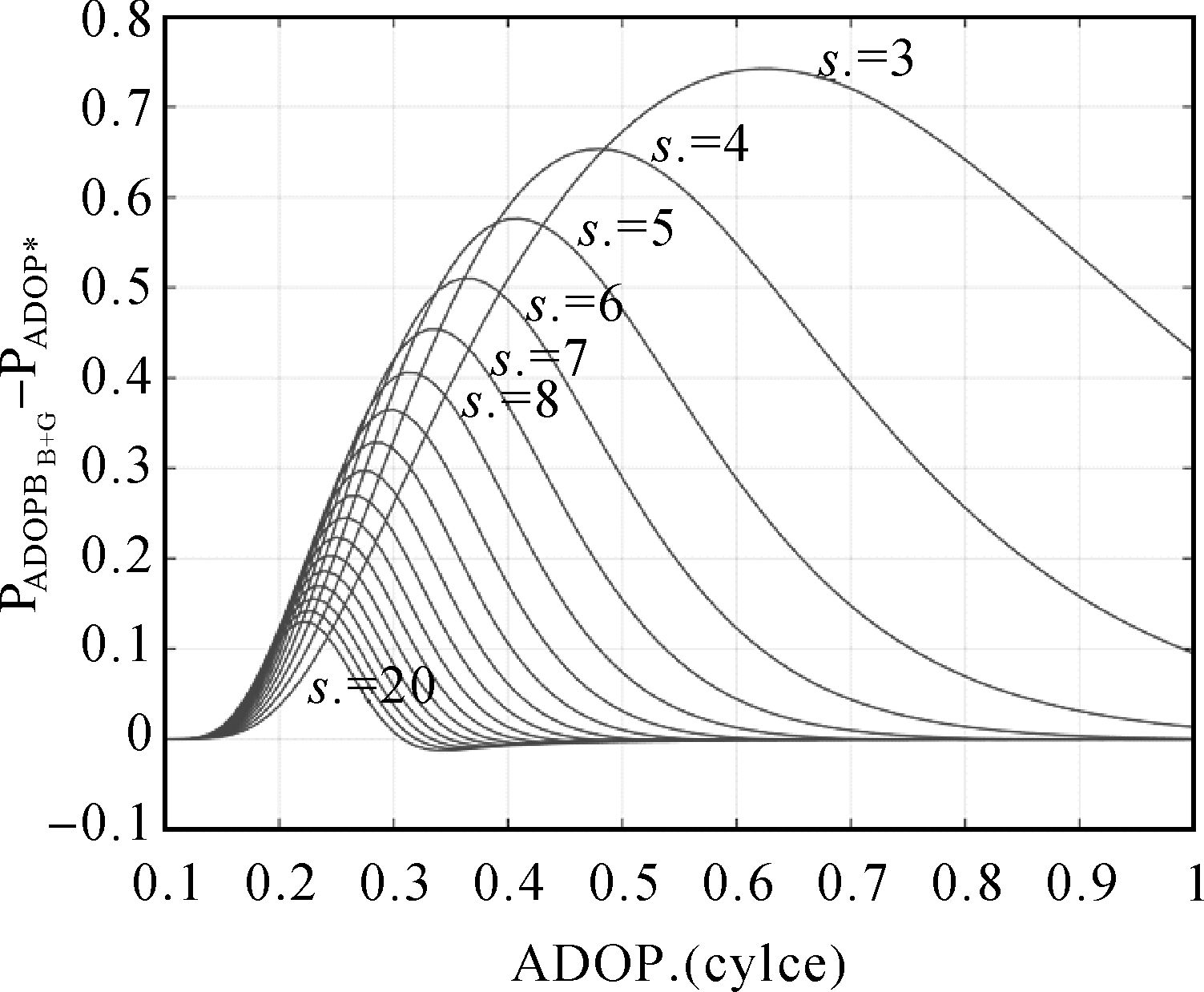
根据ADOP值的变化,分析BDS+GPS对模糊度固定成功概率的影响,如图 3所示。设BDS和GPS为双频观测量,非参考卫星个数均为s*,双系统相同未知数 (x, y, z) 为3,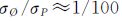
|
| 图 3 BDS+GPS与单系统模糊度固定成功概率的差值PADOPB+G-PADOP* Fig. 3 Difference of PADOPB+G and PADOP* in fixing integer ambiguity |
在本文研究中,设观测值权阵DL-1能准确反映观测值精度,故忽略不同系统随机模型影响,仅分析函数模型相关的系数阵影响 (式 (1) 中系数阵:A、E、F)。据式 (6) 定义,BDS+GPS与独立系统RGDOP可分别表示为式 (18) 和式 (19)
 (18)
(18)
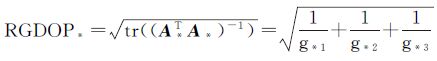 (19)
(19)
式 (18) 和式 (19) 中,gB1、gB2、gB3为正定矩阵ABTAB的特征值;gG1、gG2、gG3为正定矩阵AGTAG的特征值,均大于0,故
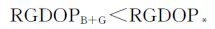 (20)
(20)
同理,BDS+GPS与独立系统TrDOP间的关系为
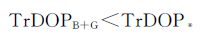 (21)
(21)
据式 (8),忽略随机模型DL-1影响,BDS+GPS与独立系统IDOP分别表示为式 (22) 和式 (23)
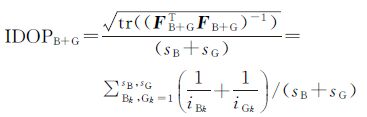 (22)
(22)
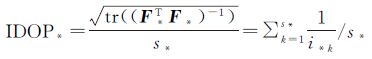 (23)
(23)
式 (22) 和式 (23) 中,iBk, k=1,2,…,sB为正定矩阵FBTFB的特征值,iGk, k=1, 2, …, sG为正定矩阵FGTFG的特征值。若BDS与GPS独立系统电离层参数求解精度一致,则
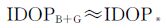 (24)
(24)
因F*是一个f**s*行、s*列的矩阵;f*卫星频率个数。F*TF*中的值等于矩阵F*对应行与列的乘积,f*个数增加时,矩阵行数增加,F*TF*中的值均变大,其特征值也随之变大。故
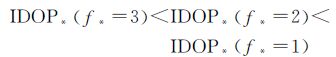 (25)
(25)
目前,BDS卫星均有三频数据,而GPS仅少量卫星有三频,因此,引入BDS,IDOP值将减小。
由式 (20)、式 (21)、式 (24)、式 (25) 可知,BDS+GPS与独立系统相对定位精度因子间的关系可表示为
 (26)
(26)
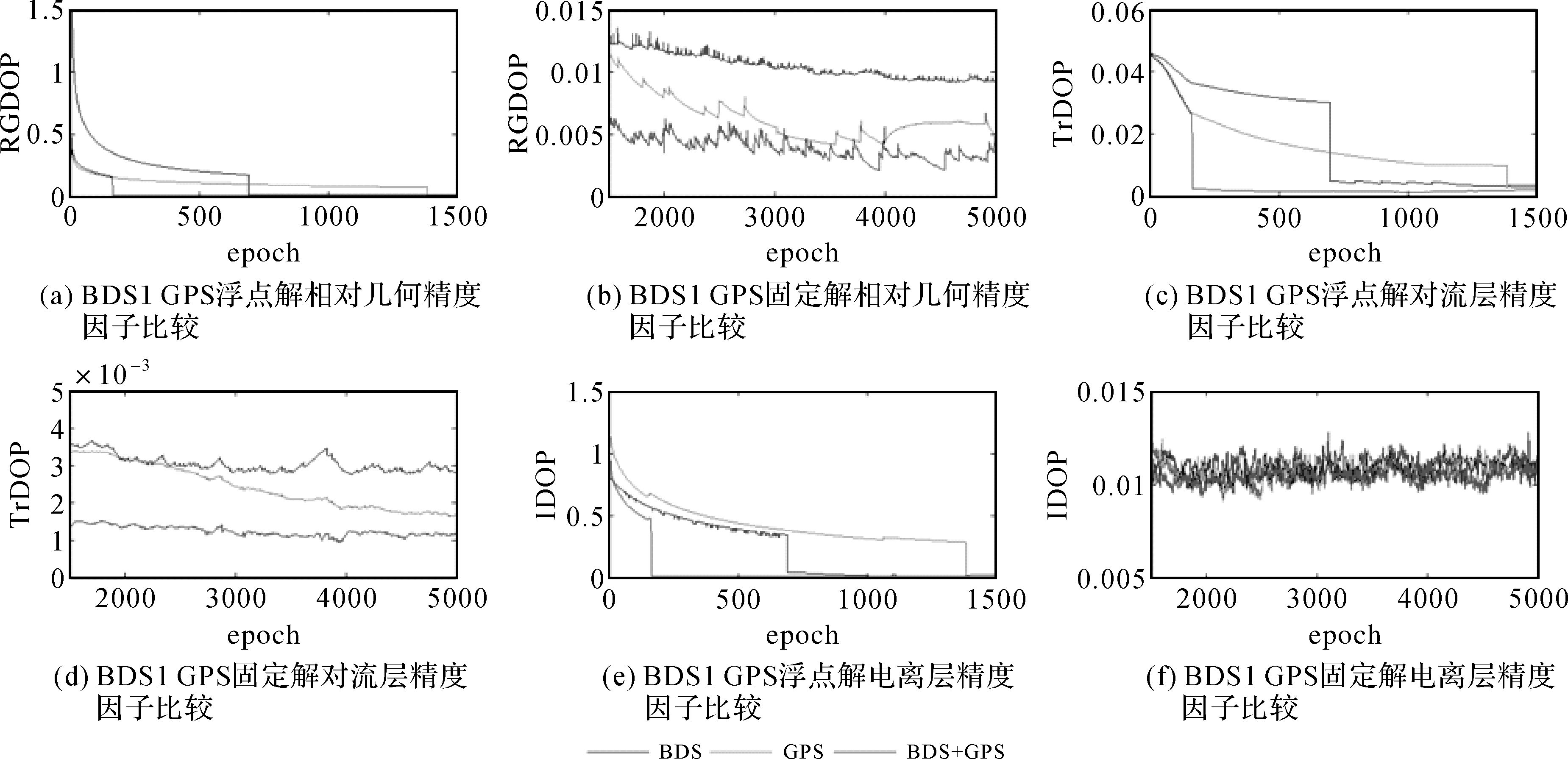
图 4列出了BDS与GPS融合前后,25 km基线处理RGDOP、TrDOP、IDOP值的变化,数据处理采用上述43 km中长基线处理模式。其中 (a)、(c)、(e) 表示前1500个历元,反映浮点解过程中精度因子的变化;(b)、(d)、(f) 表示1500~5000个历元,反映整周模糊度固定后精度因子的变化。浮点解滤波过程中,BDS+GPS于第160个历元固定,BDS于第680个历元固定,GPS于第1388个历元固定,BDS+GPS明显提高了模糊度固定的时间效率。固定解滤波过程中,BDS+GPS的RGDOP和TrDOP值的小于独立系统,IDOP值约等于独立系统,与式 (20)、式 (21)、式 (24) 理论推导一致 (图中不完全一致之处,因实际计算考虑了随机模型,而理论推导未考虑随机模型影响)。
|
| 图 4 BDS、GPS、BDS+GPS相对定位RGDOP、TrDOP和IDOP值 Fig. 4 RGDOP, TrDOP and IDOP values in BDS, GPS and BDS+GPS relative positioning |
图 5比较了BDS三频与双频数据频估计电离层的IDOP值,可看出增加观测频率,IDOP值存在一定幅度的减小,与式 (25) 理论推导一致 (图中不完全一致之处,因实际计算考虑了随机模型,而理论推导未考虑随机模型影响引起)。
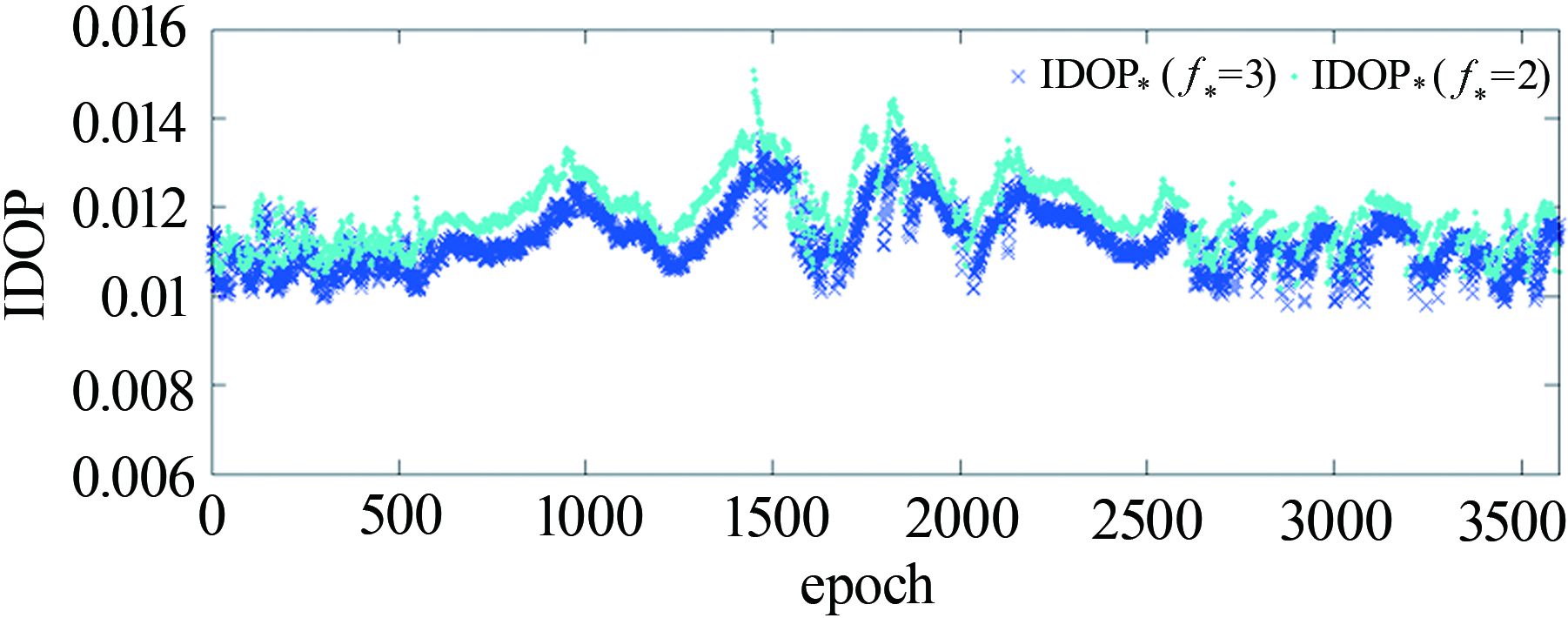
|
| 图 5 BDS双频和三频相对定位IDOP值 Fig. 5 IDOP values in double-frequency and triple-frequency BDS relative positioning |
4 结论
本文从相对定位中模糊度固定和相对位置求解的4类因子 (ADOP、RGDOP、TrDOP、IDOP) 出发,重新定义了相对定位精度因子RPDOP,并论证了BDS+GPS对单系统定位精度与时间效率的影响,得到如下结论:
(1) 相比单系统,BDS+GPS ADOP值减小,模糊度固定成功的概率提高,特别在单系统卫星个数较少时,提高概率可达70%以上。因此,系统融合能够更加快速地固定模糊度,显著提高模糊度固定的时间效率。
(2) 相比单系统,BDS+GPS RGDOP、TrDOP减小,IDOP近似不变 (双频BDS+GPS) 或者减小 (三频BDS+GPS)。通过TrDOP和IDOP值分析,可知BDS/GPS系统融合能够提高大气参数估计精度。
(3) 相比单系统,BDS/GPS系统融合后ADOP、RGDOP、TrDOP减小,达到与单系统延长观测时间相当的效果;根据RGDOP、TrDOP、IDOP对相对定位精度因子RPDOP的重新定义可知,相比单系统,BDS/GPS系统融合后RPDOP减小,相对定位内符合精度明显提高。总体上,在一定测量精度的前提下,BDS/GPS系统融合能够有助于提高单系统测量的内符合精度和时间效率。
致谢: 感谢西南交通大学周乐韬副教授的指导,香港理工大学提供的数据支持。
| [1] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [2] | 高星伟, 过静珺, 程鹏飞, 等. 基于时空系统统一的北斗与GPS融合定位[J]. 测绘学报, 2012, 41(5): 743–748. GAO Xingwei, GUO Jingjun, CHENG Pengfei, et al. Fusion positioning of Compass/GPS Based on Spatio Temporal System Unification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 743–748. |
| [3] | ODOLINSKI R, TEUNISSEN P J G, ODIJK D. Quality Analysis of a Combined COMPASS/BeiDou-2 and GPS RTK Positioning Model[C]//International Global Navigation Satellite Systems Society. Outrigger Gold Coast, Qld Australia:[s.n.], 2013:25-48. |
| [4] | DENG Chenlong, TANG Weiming, LIU Jingnan, et al. Reliable Single-Epoch Ambiguity Resolution for Short Baselines Using Combined GPS/BeiDou System[J]. GPS Solutions, 2014, 18(3): 375–386. DOI:10.1007/s10291-013-0337-5 |
| [5] | 杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 44(1): 72–81. YANG Yuanxi, Li Jinlong, WANG Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J]. Science China Earth Sciences, 2014, 44(1): 72–81. |
| [6] | ODOLINSKI R, ODIJK D, TEUNISSEN P J G. Combined GPS and BeiDou Instantaneous RTK Positioning[J]. Navigation, 2014, 61(2): 135–148. DOI:10.1002/navi.61 |
| [7] | ODOLINSKI R, TEUNISSEN P J G, ODIJK D. First Combined COMPASS/BeiDou-2 and GPS Positioning Results in Australia. Part Ⅱ Single-and Multiple-Frequency Single-Baseline RTK Positioning[J]. Journal of Spatial Science, 2014, 59(1): 25–46. DOI:10.1080/14498596.2013.866913 |
| [8] | HE Haibo, LI Jinlong, YANG Yuanxi, et al. Performance Assessment of Single-and Dual-Frequency BeiDou/GPS Single-Epoch Kinematic Positioning[J]. GPS Solutions, 2014, 18(3): 393–403. DOI:10.1007/s10291-013-0339-3 |
| [9] | 李金龙. 北斗/GPS多频实时精密定位理论与算法[J]. 测绘学报, 2015, 44(11): 1297. LI Jinlong. BDS/GPS Multi-frequency Real-time Kinematic Positioning Theory and Algorithms[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1297. DOI:10.11947/j.AGCS.2015.20150254 |
| [10] | 杨元喜, 李金龙, 徐君毅, 等. 中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(21): 1734–1740. YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Science Bulletin, 2011, 56(21): 1734–1740. |
| [11] | TEUNISSEN P J G, ODIJK D. Ambiguity Dilution of Precision:Definition, Properties and Application[C]//Proceedings of the 10th International Technical Meeting of the Satellite Division of the Institute of Navigation. Kansas City, MO:ION Publications, 1997:891-899. |
| [12] | ODIJK D, TEUNISSEN P J G. ADOP in Closed form for a Hierarchy of Multi-Frequency Single-Baseline GNSS Models[J]. Journal of Geodesy, 2008, 82(8): 473–492. DOI:10.1007/s00190-007-0197-2 |
| [13] | YANG Yuanxi, LI Jinlong, TANG Junyi, et al. Generalised DOPs with Consideration of the Influence Function of Signal-in-Space Errors[J]. The Journal of Navigation, 2011, 64(S1): S3–S18. DOI:10.1017/S0373463311000415 |
| [14] | 李建文, 李作虎, 周巍, 等. 卫星导航中几何精度衰减因子最小值分析及应用[J]. 测绘学报, 2011, 40(S1): 85–88. LI Jianwen, LI Zuohu, ZHOU Wei, et al. Study on the Minimum of GDOP in Satellite Navigation and Its Applications[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 85–88. |
| [15] | MENG Fanchen, ZHU Bocheng, WANG Shan. A New Fast Satellite Selection Algorithm for BDS-GPS Receivers[C]//Proceedings of the 2013 IEEE Workshop on Signal Processing Systems. Taipei China:IEEE, 2013:371-376. |
| [16] | NIELSEN R O. Relationship between Dilution of Precision for Point Positioning and for Relative Positioning with GPS[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(1): 333–338. DOI:10.1109/7.570809 |
| [17] | TEUNISSEN P J G. A Proof of Nielsen's Conjecture on the GPS Dilution of Precision[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(2): 693–695. DOI:10.1109/7.670364 |
| [18] | PARK C, KIM I. Comments on "Relationships between Dilution of Precision for Point Positioning and for Relative Positioning with GPS"[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(1): 315–316. DOI:10.1109/7.826336 |
| [19] | MISRA P, ENGE P. Global Positioning System:Signals, Measurements and Performance[M]. 2nd ed. Lincoln, MA:Ganga-Jamuna Press, 2006:238-255. |
| [20] | 黄丁发, 张勤, 张小红, 等. 卫星导航定位原理[M]. 武汉: 武汉大学出版社, 2015: 203-219. HUANG Dingfa, ZHANG Qin, ZHANG Xiaohong, et al. Satellite Navigation and Positioning[M]. Wuhan: Wuhan University Press, 2015: 203-219. |
| [21] | Xu Guochang. GPS:Theory, Algorithms and Applications[M]. Berlin Heidelberg: Springer-Verlag, 2007: 133-150. |
| [22] | TEUNISSEN P J G, ODOLINSKI R, ODIJK D. Instantaneous BeiDo+GPS RTK Positioning with High Cut-Off Elevation Angles[J]. Journal of Geodesy, 2014, 88(4): 335–350. DOI:10.1007/s00190-013-0686-4 |
| [23] | CHANG X W, YANG X, ZHOU T. MLAMBDA:A Modified LAMBDA Method for Integer Least-Squares Estimation[J]. Journal of Geodesy, 2005, 79(9): 552–565. DOI:10.1007/s00190-005-0004-x |
| [24] | VERHAGEN S, LI Bofeng, TEUNISSEN P J G. Ps-LAMBDA:Ambiguity Success Rate Evaluation Software for Interferometric Applications[J]. Computers & Geosciences, 2013, 54: 361–376. |
| [25] | TEUNISSEN P J G. Success Probability of INTEGER GPS Ambiguity Rounding and Bootstrapping[J]. Journal of Geodesy, 1998, 72(10): 606–612. DOI:10.1007/s001900050199 |
| [26] | TEUNISSEN P J G. Mixed Integer Estimation and Validation for Next Generation GNSS[M]//FREEDEN W, NASHED M Z, SONAR T.Handbook of Geomathematics. Berlin Heidelberg:Springer, 2015:2373-2403. |



