2. 武汉大学测绘学院, 湖北 武汉 430079;
3. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 江西 南昌 330013
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASG, Nanchang 330013, China
大地测量反演主要是通过大地测量观测手段获得地表形变值求解地球物理模型参数的过程,在震源机制研究中,位错模型是反演震源参数的有效模型[1],也是最常用的模型之一。利用弹性半空间均匀矩形位错模型[2]反演地震震源参数,通常包括非线性反演断层几何参数和线性反演滑动分布两个过程,在确定断层位置等几何参数后,滑动参数与形变观测值为线性关系,此时滑动参数模型的系数矩阵即为格林函数矩阵。系数矩阵的元素通常是由剖分得到的每个子断层块的单位滑动引起的地表点的位移构成,矩阵中的元素与模型本身、模型的几何参数、观测点位等因素有关,地壳的复杂性、模型参数求解存在的不确定性及形变导致的观测点的坐标误差等都会引起系数矩阵的变化,可以将这部分影响看成系数矩阵存在误差,并考虑系数矩阵误差对滑动参数解的影响。目前在求解滑动参数时,通常都是采用普通最小二乘法,即只考虑了观测形变量的误差影响;若采用同时顾及系数矩阵和观测向量误差的总体最小二乘方法[3-6]来求解滑动参数,显然更具合理性。而国内外未见相关研究发表。
基于大地测量观测资料 (如InSAR、GPS数据等) 反演同震滑动分布是研究震源参数的重要手段,国内外许多学者利用InSAR或GPS等数据对同震滑动分布进行了研究[7-12],研究结果充分体现了采用InSAR或GPS数据进行滑动分布反演的优越性。
本文研究中,首先给出滑动分布反演的总体最小二乘函数模型,考虑到系数矩阵的病态性,借助拉普拉斯二阶平滑得到了正则化矩阵,通过正则化法解决病态情形下总体最小二乘问题。模拟滑动分布反演试验,并利用Envisat卫星升降轨数据约束同震地表形变场研究2009年意大利拉奎拉 (L’Aquila) Mw6.3级地震滑动分布,研究了同时顾及系数矩阵误差和观测值误差对滑动分布反演结果的影响。
1 滑动分布反演的总体最小二乘方法 1.1 滑动分布总体最小二乘函数模型及算法采用Okada矩形位错模型反演同震滑动分布,首先需要确定断层的位置、走向等几何参数,这些参数可以利用非线性最优化方法反演获得。当这些参数确定后,有
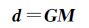 (1)
(1)
式中, d为同震形变观测值;M为滑动参数;G为格林函数矩阵,定义为[12]
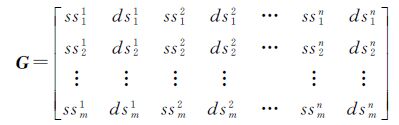 (2)
(2)
矩阵G中ss、ds分别表示断层子块单位走滑和倾滑引起的地表位移,上标表示断层的编号;下标表示同震形变观测值个数。
同时考虑观测值d和系数矩阵G含有误差的情况,得到
 (3)
(3)
式中, e为观测向量的误差向量;EG为系数矩阵G的误差矩阵。
精细滑动分布反演时,将断层面离散化为均匀的小断层片,此时矩阵G是严重病态 (秩亏) 的,即为病态情形下的总体最小二乘参数估计,国内外许多学者开展了相关研究,主要方法包括Tikhonov正则化法[13-14]、广义正则化法[15]、岭估计法[16]、虚拟观测法[17]等。本文采用Tikhonov正则化解法[14]来反演滑动分布。滑动分布反演时,为克服系数矩阵的病态性,对参数施加拉普拉斯二阶平滑约束,使得
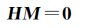 (4)
(4)
式中, H为拉普拉斯平滑矩阵,而R=HTH视为正则化矩阵。
根据Tikhonov正则化理论[18],得到估计准则为
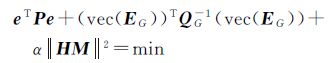 (5)
(5)
式中, P为观测值的权阵;QG为系数矩阵误差 (即EG) 的协因数阵,且假设QG满足QG=Q0⊗QM,Q0为2n×2n阶方阵,QM为m×m阶方阵;α为正则化参数,即平滑因子,其意义是用来平衡模型参数分辨率和数据误差,这里可以通过拟合残差 (d-GM)T(Qd+(MTQ0M)·QM)-1(d-GM) 和粗糙度||HM||22之间的折中曲线来确定,前者等价于eTPe+(vec (EG))TQG-1(vec (EG))。
结合同震滑动分布参数反演,采用病态加权总体最小二乘正则化解法来迭代求解式 (5),具体如下:
(1) 通过最小二乘法得到参数最初估计值
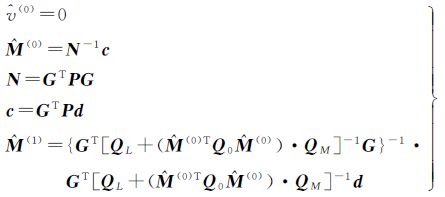 (6)
(6)
(2) 更新待定参数解
 (7)
(7)
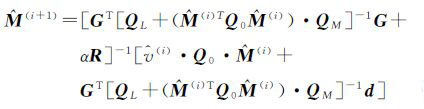 (8)
(8)
(3) 迭代求解第 (2) 步,满足条件
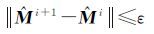 (9)
(9)
时,计算结束。
值得注意的是,在滑动分布反演算法中,由于系数矩阵G是严重秩亏的,因此式 (6) 中的N需使用广义逆N+。
1.2 权阵P及协因数阵QG的确定权阵P可通过观测数据的误差来确定,本文认为观测数据是独立且不相关的;假设QG=Q0⊗QM,必须确定Q0和QM,Q0表示系数矩阵每一列元素只存在数量因数不同且互不相关;QM表示系数矩阵每一行元素只存在数量因数不同且互不相关[4]。本文假设Q0为单位阵,即Q0=I2n,对于QM,进行如下分析。
根据位错模型,地表某一点的形变量di(i=1, 2, …, m) 是断层破裂面上每一个子块断层的走滑地表响应dsj(j=1, 2, …, n) 和倾滑地表响应ddj(j=1, 2, …, n) 的总和,即
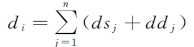 (10)
(10)
故可以假设系数矩阵每一行元素的协因数为
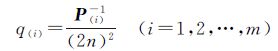 (11)
(11)
即有
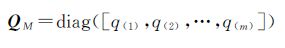 (12)
(12)
为验证总体最小二乘方法反演滑动分布的有效性,本文首先对模拟滑动分布进行反演,分别采用总体最小二乘法和最小二乘法反演最优滑动分布。
假定断层破裂面的几何参数为:断层面中心位置X=0 km,Y=0 km,断层上底深度MinDep=0 km,长度L=36 km,宽度W=16 km,走向角α=90°,倾角Dip=70°。共模拟了328个GPS地表形变观测点。将断层面均匀剖分为2 km×2 km的矩形单元,模拟的断层面的滑动分布见图 1(a),其中最大滑动量为1.426 8 m,平均滑动量为0.303 9 m。结合位错模型正演得到地表形变位移,分别给形变位移观测量和系数矩阵元素施加随机误差,水平位移误差为N(0,32 mm2),垂直位移误差为N(0,52 mm2),相应的系数矩阵元素误差分别为N(0,32/(2n)2mm2) 及N(0, 52/(2n)2mm2)。总体最小二乘法、最小二乘法及两者的残差结果分别如图 1(b)、图 1(c)及图 1(d)所示。

|
| 图 1 模拟试验的震源滑动分布反演结果 Fig. 1 Slip distribution inversion results of simulation |
模拟不同的观测数据,基于蒙特卡罗误差传递法估计公式[19]给出了参数的均方根误差 (root mean square error,RMSE) 作为估计参数的精度水平。RMSE的计算公式如下
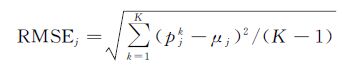 (13)
(13)
式中, K为模拟反演的次数;pjk为第k次模拟反演的第j个参数的估计值;μj为第j个参数的真值。
反演时总体最小二乘法和最小二乘法所选取的最优滑动因子分别为0.01、0.1。从图 1及表 1的结果可以看出,总体最小二乘解与最小二乘解的结果非常接近,其中总体最小二乘结果中最大滑动量及平均滑动量分别为1.344 5 m、0.243 3 m,误差的最大值和平均值分别为0.148 6 m、0.038 1 m,残差中误差 (RMS) 为4.7 mm,最小二乘反演结果的最大滑动量、平均滑动量及RMS与总体最小二乘结果一致,误差最大值和平均值分别为0.148 7 m、0.038 8 m。总体最小二乘与最小二乘滑动分布解的差别最大量级在10-4,说明此时系数矩阵误差对滑动参数解有一定影响,但影响程度有限。
| 分布解 | 滑动量 | 误差 (RMSE) | RMS /mm | |||
| 最大值 /m | 平均值 /m | 最大值 /m | 平均值 /m | |||
| TLS解 | 1.344 5 | 0.313 2 | 0.148 6 | 0.038 1 | 4.7 | |
| LS解 | 1.344 5 | 0.313 2 | 0.148 7 | 0.038 8 | 4.7 | |
2.2 意大利拉奎拉地震震源滑动分布反演
2009年4月6日发生在意大利中部拉奎拉地区的Mw6.3级地震,据美国地质调查局 (USGS) 网站发布,地震震中位置为 (13.334°E,42.334°N),震源深度为8.8 km。地震造成一千余人的伤亡,大量的房屋被损毁或破坏[20]。地震发生后,许多研究机构通过不同手段对震源机制进行了较详细的研究。其中,文献[21—22]分别通过GPS数据反演了地震震源参数,认为此次地震的主断层为西南走向的正断层。文献[20]通过ASAR数据反演断层的几何参数和滑动分布,结果也表明该断层为正断层。文献[23]利用不同的InSAR数据集反演比较后获得了最优震源模型。文献[11]则结合拉奎拉地区的地形特点,联合Envisat卫星的升降轨数据、ALOS卫星数据及GPS形变观测数据,提供比较完整的震区三维形变场,反演得到断层几何模型参数及滑动分布。
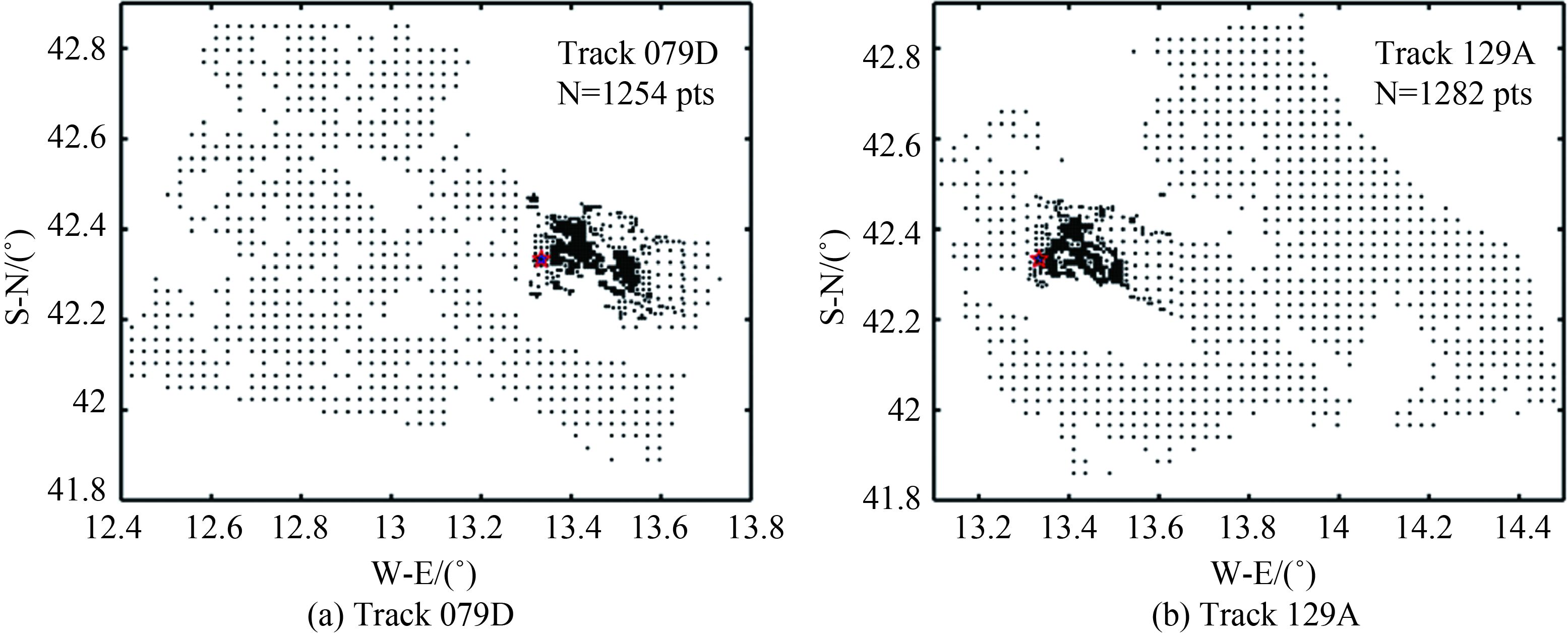
本文研究该地震的InSAR数据来源于文献[11]:项目组对获取的ASAR数据采用二通法对影像进行干涉差分处理后得到地表同震形变场;使用瑞士的Gamma软件处理,分别采用了ESA和JAXA提供的DOR精密轨道和精密轨道用于修正轨道误差,并利用90 m分辨率的SRTM DEM去除地形影响;采用基于能量谱的局部自适应滤波方法对干涉图进行了滤波处理;最后采用枝切法进行相位解缠,得到差分干涉相位。本文研究选用了其中Envisat卫星降轨Track097和升轨Track129两幅影像的数据,而没有采用数据误差较大的ALOS卫星数据,通过对远场数据进行均匀采样,对近场数据进行四叉树采样,获得了降轨数据1254个,升轨数据1282个 (见图 2),能有效约束断层滑动参数的反演。
|
| 图 2 InSAR采样后的点位分布 (五角星为震中位置) Fig. 2 The distribution of InSAR samples points (The star is the epicenter) |
首先利用多峰值颗粒群算法 (MPSO)[24-25]反演得到拉奎拉地震单一均匀滑动断层的走向、倾角及断层矩形中心位置等几何参数 (见表 4),在此基础上,将断层破裂面沿走向、倾向将长度、宽度分别拓展至30 km、26 km,并将破裂面延伸至地表,然后将拓展后的破裂面均匀剖分为2 km×2 km的矩形单元,共得到195个矩形断层单元。采用上述的总体最小二乘方法进行滑动分布的反演研究。
关于反演涉及的观测值和系数矩阵元素定权问题,根据InSAR观测值的先验中误差确定观测值的权阵P,由式 (11)、式 (12) 可以确定协因数阵QM,Q0仍为单位阵,进而可以确定协因数阵QG(此时n=390)。总体最小二乘算法和最小二乘算法最优滑动分布解对应的最优滑动因子分别为0.36和0.6,反演结果如图 3所示。

|
| 图 3 拉奎拉地震的滑动分布、误差分布及TLS解与LS解的残差 Fig. 3 Slip and its error distribution of L'Aquila earthquake, the residuals of TLS-LS |
从图 3可以看出,震源滑动分布总体最小二乘法反演结果表明,滑动主要发生在4~15 km的深度范围内,总体最小二乘法的平均滑量为0.22 m,最大滑动量为0.95 m,滑动角为-96.4°,深度位于6~8 km的范围,总体最小二乘与最小二乘结果几乎一致。反演得到此次地震的地震级3.63×1018N·m,对应的矩震级为Mw6.34。滑动分布解的最大误差为0.17 m,分布在断层面下部边缘,不在主要的滑动区域,平均误差为0.05 m,反演模型比较稳定。
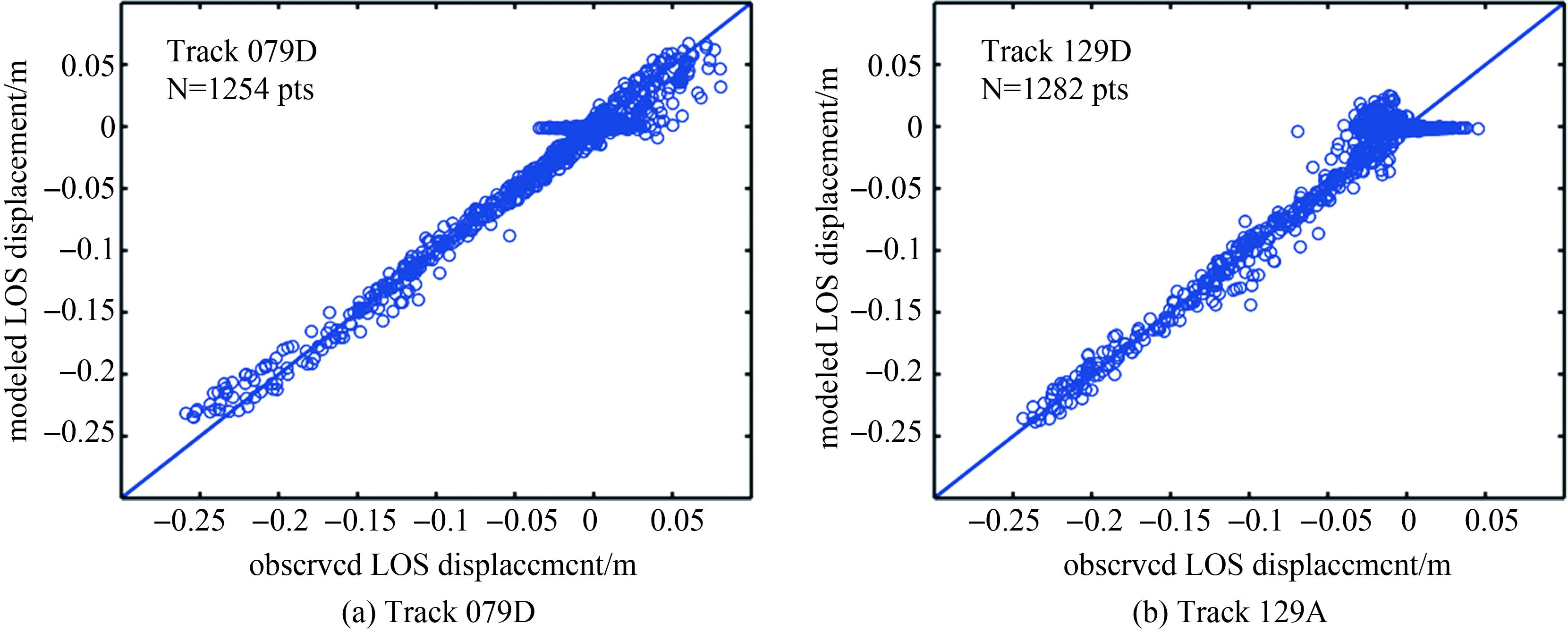
为验证滑动分布模型与观测数据的拟合程度,图 4给出了升降轨观测数据与滑动分布模型预测数据的散点分布。观测数据拟合残差的总体中误差为1.26 cm,其中降轨、升轨数据拟合残差中误差分别为1.19 cm、1.33 cm,小于均匀滑动的残差中误差 (数据总体拟合中误差、降轨及升轨拟合中误差分别为1.43 cm、1.37 cm、1.48 cm)。从图 4可以看出,总体上升降轨数据都拟合得较好,只有少数远场数据未能很好拟合,这是由于这些远场数据点形变值很小且数据受到断层模型简化、大气延迟误差等影响。
|
| 图 4 拉奎拉地震观测位移值和滑动分布模型预测值位移的散点分布 Fig. 4 Scatter points of the observed and the distribution slip modeled displacement in L'Aquila earthquake |
从总体最小二乘解、最小二乘解及误差可以看出,差别并不明显。表 2及表 3比较了两者的反演结果,最大滑动量、平均量、RMSE最大值及平均值都几乎一致,总体最小二乘法与最小二乘法的滑动分布平均差值量级为10-4,误差分布平均差值量级为10-5。
| 滑动量/m | RMSE/m | 滑动角 /(°) | Mo/Mw 1018 N·m/- | ||||
| 最大值 | 平均值 | 最大值 | 平均值 | ||||
| TLS | 0.950 9 | 0.222 2 | 0.171 3 | 0.054 0 | -96.413 2 | 3.63/6.34 | |
| LS | 0.950 8 | 0.222 1 | 0.171 5 | 0.054 1 | -96.414 5 | 3.63/6.34 | |
| m | ||||
| SlipTLS-LS | RMSETLS-LS | |||
| 最大值 | 平均值 | 最大值 | 平均值 | |
| 3.29×10-4 | 1.25×10-4 | 2.26×10-4 | 7.81×10-5 | |
为了分析系数矩阵误差对系数矩阵元素的影响,通常借助系数矩阵的信噪比来分析。文献[26]将系数矩阵的信噪比定义为系数矩阵的量级||A||与系数矩阵元素中误差的量级σA的比值,即信噪比SN=||A||/σA。研究表明[26],EIV模型中参数最小二乘估计值的相对偏差与系数矩阵信噪比的二次方成反比。本文模拟试验的系数矩阵量级||A||约为10-3,系数矩阵中误差量级σA由式 (11) 估计约为10-5,则系数矩阵的信噪比约为102,那么同震滑动分布估计值的相对偏差则约为10-4;而拉奎拉地震滑动分布反演时,系数矩阵的量级A约为10-4,系数矩阵中误差量级σA约为10-6,则系数矩阵的信噪比约为102,此时同震滑动分布估计值的相对偏差则约为10-4。以上结论与本文计算所得结果相符,同时较好地解释了导致总体最小二乘解与最小二乘解出现这一差别的原因。根据系数矩阵的信噪比,可以近似估计系数矩阵误差对滑动分布估计值的影响。
表 4列举了此次地震震源参数的部分研究成果。可以看出,本文确定的断层走向、倾角、滑动角等参数与USGS机构得到的机制解 (走向122°,倾角53°,滑动角-122°) 很相似,只是走向相差了22°,余震分布显示出该发震断层为NW-SE结构及SW倾向的正断层[11],参数反演结果印证了此结论。本文方法得到的最大滑动量为0.95 m,平均滑动量为0.22 m,地震矩为3.63×1018 N·m,对应的矩震级为Mw6.34,而均匀滑动反演的滑动量、矩张量及矩震级分别为0.70 m、2.68×1018 N·m、Mw6.34。文献[11]联合了不同波长、不同入射角的Enviast和ALOS卫星差分干涉数据,并联立了震区部分GPS三维形变数据,通过弹性三角位错模型,反演得到滑动分布的最大滑动量为1.07 m,平均滑动量为0.34 m,给出的矩张量矩震级分别为3.43×1018 N·m、Mw6.32;其最大滑动量大于本文的结果,这可能与约束地表的数据源有关。文献[20]联合ASAR数据反演得到的断层滑动量为0.66 m,给出的矩张量2.80×1018 N·m;利用L’Aquila震中附近的GPS观测站数据,文献[22]研究了此次地震的同震滑动分布和震后的余震滑动分布,得到的最大滑动量为1.1 m,矩张量为3.90×1018 N·m。
| 来源 | 走向 /(°) | 倾角 /(°) | 滑动角 /(°) | 经度 /(°) | 纬度 /(°) | 滑动量 /m | 长度 /km | 顶深 /km | 底深 /km | 地震矩 (1018 N·m) | 震级 /Mw |
| 均匀滑动 | 144.37 | 59.06 | -103.94 | 13.436 2 | 42.335 7 | 0.70 | 12.86 | 3.31 | 11.84 | 2.68 | 6.25 |
| 0.08 | 0.47 | 0.41 | 0.000 6 | 0.000 5 | 0.01 | 0.07 | 0.01 | 0.15 | |||
| TLS | 144.37 | 59.06 | -96.4 | 13.436 2 | 42.335 7 | 0.95 | 30 | 0 | 22.30 | 3.63 | 6.34 |
| LS | 144.37 | 59.06 | -96.4 | 13.436 2 | 42.335 7 | 0.95 | 30 | 0 | 22.30 | 3.63 | 6.34 |
| 文献[11] | 143.9 | 51.5 | -102.8 | 13.480 8 | 42.361 5 | 1.07 | 30 | 0 | 20 | 3.43 | 6.32 |
| 文献[20] | 144 | 54 | -105 | 13.449 | 42.333 | 0.66 | 13.45 | 3.0 | 11.7 | 2.8 | 6.23 |
| 文献[21] | 140 | 55.3 | -98 | 13.42 | 42.32 | 0.49 | 13.42 | 0 | 12.9 | 3.2 | 6.32 |
| 文献[22] | 135.8 | 50.4 | -98.5 | 13.469 | 42.358 | 1.1 | 13.47 | 0.6 | 14.0 | 3.90 | 6.36 |
| USGS | 122 | 53 | -122 | 13.37 | 42.40 | — | — | — | — | 3.4 | 6.29 |
野外地质调查结果发现,拉奎拉地震在地表附近区域发生了7~10 cm的破裂,已有的GPS数据[21-22]、InSAR数据[20, 27]反演结果都表明在断层接近地表处没有滑动的迹象,本文研究结果也验证了这一结论,只有部分接近地表处的滑动在10 cm左右,此地表破裂可能是由地下的滑动能量传递到地表脆性区域造成[11]。许多研究者认为,Paganica断层与相邻断层比较,其地形活动表现更弱,而来自遥感观测结果却揭示此次地震就发生在Paganica断层带,Paganica断层正好位于两个主要的活动断层之间的位置[22, 28]。此次观测对于该地震区域和与之相似地质条件的区域确定潜在的危险断层显得更为重要,有必要提高观测手段对地震震后及震间的应变积累进行更为细致和长久的研究。
3 结论地震同震滑动分布反演是分析地震发震机理,研究活动断层破裂扩展、震后形变、岩石圈应力变化及后期地震危险性评估的基础。本文研究了顾及格林函数矩阵的误差的同震滑动分布反演。研究表明,滑动分布反演时顾及格林函数矩阵误差是合理的,但系数矩阵元素与系数矩阵元素中误差的比值 (信噪比) 较大,导致总体最小二乘与最小二乘反演结果差别仅在10-4以内的量级,即本文同震滑动分布反演中格林函数矩阵含有的随机误差对参数估计的影响很有限。
本文利用总体最小二乘法研究了2009年意大利拉奎拉 (L’Aquila) Mw6.3级地震,反演结果表明,发震断层的走向为144.37°,倾角为59.04°,倾向为SW,是一次以正倾滑为主兼少量右旋滑动事件,滑动分布的最大滑动量为0.95 m,平均滑动量为0.22 m,主要滑动深度范围为4~15 km。研究表明,此次地震的发震断层Paganica断层正好位于两个主要的活动断层之间的位置。因此,应该对地震震后及震间的应变积累进行更为细致和长久的研究。
| [1] | 许才军, 尹智. 利用大地测量资料反演构造应力应变场研究进展[J]. 武汉大学学报 (信息科学版), 2014, 39(10): 1135–1146. XU Caijun, YIN Zhi. Progress in Inversion for Tectonic Stress-strain Fields Using Geodetic Data[J]. Geomatics and Information Science of Wuhan University, 2014, 39(10): 1135–1146. |
| [2] | OKADA Y. Surface Deformation DUE to Shear and Tensile Faults in a Half-space[J]. Bulletin of the Seismological Society of America, 1985, 75(4): 1135–1154. |
| [3] | VAN HUFFEL S, VANDEWALLE J. The Total Least Squares Problem:Computational Aspects and Analysis[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1991. |
| [4] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415–421. DOI:10.1007/s00190-007-0190-9 |
| [5] | 王乐洋. 基于总体最小二乘的大地测量反演理论及应用研究[J]. 测绘学报, 2012, 41(4): 629. WANG Leyang. Research on Theory and Application of Total Least Squares in Geodetic Inversion[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 629. |
| [6] | WANG Leyang, XU Guangyu. Variance Component Estimation for Partial Errors-in-Variables Models[J]. Studia Geophysica et Geodaetica, 2016, 60(1): 35–55. DOI:10.1007/s11200-014-0975-2 |
| [7] | FUNNING G J, PARSONS B, WRIGHT T J, et al. Surface Displacements and Source Parameters of the 2003 Bam (Iran) Earthquake from Envisat Advanced Synthetic Aperture Radar Imagery[J]. Journal of Geophysical Research:Solid Earth, 2005, 110(B9): B09406. |
| [8] | 许才军, 刘洋, 温扬茂. 利用GPS资料反演汶川Mw7.9级地震滑动分布[J]. 测绘学报, 2009, 38(3): 195–201. XU Caijun, LIU Yang, WEN Yangmao. Mw7.9 Wenchuan Earthquake Slip Distribution Inversion from GPS Measurements[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 195–201. |
| [9] | 张国宏, 屈春燕, 宋小刚, 等. 基于InSAR同震形变场反演汶川Mw7.9地震断层滑动分布[J]. 地球物理学报, 2010, 53(2): 269–279. ZHANG Guohong, QU Chunyan, SONG Xiaogang, et al. Slip Distribution and Source Parameters Inverted from Co-seismic Deformation Derived by InSAR Technology of Wenchuan Mw7.9 Earthquake[J]. Chinese Journal of Geophysics, 2010, 53(2): 269–279. |
| [10] | JIANG Zaisen, WANG Min, WANG Yanzhao, et al. GPS Constrained Coseismic Source and Slip Distribution of the 2013 Mw6.6 Lushan, China, Earthquake and Its Tectonic Implications[J]. Geophysical Research Letters, 2014, 41(2): 407–413. DOI:10.1002/2013GL058812 |
| [11] | 温扬茂, 何平, 许才军, 等. 联合Envisat和ALOS卫星影像确定L'Aquila地震震源机制[J]. 地球物理学报, 2012, 55(1): 53–65. WEN Yangmao, HE Ping, XU Caijun, et al. Source Parameters of the 2009 L'Aquila Earthquake, Italy from Envisat and ALOS Satellite SAR Images[J]. Chinese Journal of Geophysics, 2012, 55(1): 53–65. |
| [12] | 李志才, 张鹏, 金双根, 等. 基于GPS观测数据的汶川地震断层形变反演分析[J]. 测绘学报, 2009, 38(2): 108–113. LI Zhicai, ZHANG Peng, JIN Shuanggen, et al. Wenchuan Earthquake Deformation Fault Inversion and Analysis Based on GPS Observations[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(2): 108–113. |
| [13] | GOLUB G H, HANSEN P C, O'LEARY D P. Tikhonov Regularization and Total Least Squares[J]. SIAM Journal on Matrix Analysis and Applications, 1999, 21(1): 185–194. DOI:10.1137/S0895479897326432 |
| [14] | 鲁铁定. 总体最小二乘平差理论及其在测绘数据处理中的应用[D]. 武汉: 武汉大学, 2010. LU Tieding. Research on the Total Least Squares and Its Applications in Surveying Data Processing[D]. Wuhan:Wuhan University, 2010. |
| [15] | 葛旭明, 伍吉仓. 病态总体最小二乘问题的广义正则化[J]. 测绘学报, 2012, 41(3): 372–377. GE Xuming, WU Jicang. Generalized Regularization to Ⅲ-posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 372–377. |
| [16] | 王乐洋, 许才军, 鲁铁定. 病态加权总体最小二乘平差的岭估计解法[J]. 武汉大学学报 (信息科学版), 2010, 35(11): 1346–1350. WANG Leyang, XU Caijun, LU Tieding. Ridge Estimation Method in Ill-posed Weighted Total Least Squares Adjustment[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1346–1350. |
| [17] | 王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575–581. WANG Leyang, YU Dongdong. Virtual Observation Method to Ill-posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575–581. DOI:10.13485/j.cnki.11-2089.2014.0091 |
| [18] | TIKHONOV A N. Regularization of Incorrectly Posed Problems[J]. Soviet Mathematics Doklady, 1963, 4(1): 1624–1627. |
| [19] | DAWSON J, TREGONING P. Uncertainty Analysis of Earthquake Source Parameters Determined from InSAR:A Simulation Study[J]. Journal of Geophysical Research:Solid Earth, 2007, 112(B9): B09406. |
| [20] | WALTERS R J, ELLIOTT J R, D'AGOSTINO N, et al. The 2009 L'Aquila Earthquake (Central Italy):A Source Mechanism and Implications for Seismic Hazard[J]. Geophysical Research Letters, 2009, 36(17): L17312. DOI:10.1029/2009GL039337 |
| [21] | ANZIDEI M, BOSCHI E, CANNELLI V, et al. Coseismic Deformation of the Destructive April 6, 2009 L'Aquila Earthquake (Central Italy) from GPS Data[J]. Geophysical Research Letters, 2009, 36(17): L17307. DOI:10.1029/2009GL039145 |
| [22] | CHELONI D, D'AGOSTINO N, D'ANASTASIO E, et al. Coseismic and Initial Post-seismic Slip of the 2009 Mw6.3 L'Aquila Earthquake, Italy, from GPS Measurements[J]. Geophysical Journal International, 2010, 181(3): 1539–1546. |
| [23] | 冯万鹏, 李振洪, 李春来. 利用InSAR确定2009年4月6日Mw6.3拉奎拉 (Italy) 地震最优震源模型[J]. 地球物理学进展, 2010, 25(5): 1550–1559. FENG Wanpeng, LI Zhenhong, LI Chunlai. Optimal Source Parameters of the 6 April 2009 Mw6.3 L'Aquila, Italy Earthquake from InSAR Observations[J]. Progress in Geophysics, 2010, 25(5): 1550–1559. |
| [24] | 冯万鹏, 李振洪. InSAR资料约束下震源参数的PSO混合算法反演策略[J]. 地球物理学进展, 2010, 25(4): 1189–1196. FENG Wanpeng, LI Zhenhong. A Novel Hybrid PSO/Complex Algorithm for Determining Earthquake Source Parameters Using InSAR Data[J]. Progress in Geophysics, 2010, 25(4): 1189–1196. |
| [25] | 温扬茂, 许才军, 刘洋, 等. 升降轨InSAR数据约束下的2007年阿里地震反演分析[J]. 测绘学报, 2015, 44(6): 649–654. WEN Yangmao, XU Caijun, LIU Yang, et al. The 2007 Ali Earthquake Inversion from Ascending and Descending InSAR Observations[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 649–654. DOI:10.11947/j.AGCS.2015.20140349 |
| [26] | 曾文宪. 系数矩阵误差对EIV模型平差结果的影响研究[D]. 武汉: 武汉大学, 2013. ZENG Wenxian. Effect of The Random Design Matrix on Adjustment of an EIV Model and Its Reliability Theory[D]. Wuhan:Wuhan University, 2013. |
| [27] | ATZORI S, HUNSTAD I, CHINI M, et al. Finite Fault Inversion of DInSAR Coseismic Displacement of the 2009 L'Aquila Earthquake (Central Italy)[J]. Geophysical Research Letters, 2009, 36(15): L15305. |
| [28] | BONCIO P, LAVECCHIA G, PACE B. Defining a Model of 3D Seismogenic Sources for Seismic Hazard Assessment Applications:The Case of Central Apennines (Italy)[J]. Journal of Seismology, 2004, 8(3): 407–425. DOI:10.1023/B:JOSE.0000038449.78801.05 |


