2. 北京环球信息应用开发中心, 北京 100094;
3. 信息工程大学地理空间信息学院, 河南 郑州 450001
2. Beijing Global Information Application and Development Center, Beijing 100094, China;
3. Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450001, China
我国的北斗混合星座具有多GNSS时代的多卫星类型特征[1-2]。目前,以轨道几何参数表征轨道短期变化的卫星广播星历,以GPS标准导航电文NAV (GPS navigation) 和增强的民用导航电文CNAV (civil navigation) 为主。这两套星历参数,都能很好地拟合北斗近圆中高轨卫星MEO和IGSO,但是对于北斗GEO,仅顾及了小偏心率近圆轨道,忽略了小倾角特性,因此,即使人为旋转5°倾角,星历参数拟合仍有潜在的奇异性,导致直接拟合算法不稳定或者少数拟合参数出现超限现象[3]。此外,用户计算卫星位置时还需要反向旋转5°倾角以恢复GEO轨道的正确定向[3-5]。因此从完整流程来看,GEO的广播星历模型与IGSO和MEO并非完全一致。
针对GEO的小偏心率和小倾角,文献[6—7]引进了第2类无奇点根数及其根数摄动,设计了无奇点广播星历,并且可以同时适用于MEO和IGSO。但是,无奇点参数目前尚不普及,卫星位置计算公式也需要较大改动。文献[8]提出以第1类无奇点根数为拟合参数再转换为星历参数的两步法,也不用旋转倾角,但是仿真结果表明,该拟合算法不能很好地适应小倾角情况。
针对星历拟合参数的变化范围超出导航电文接口设计门限的参数超限问题,文献[3]介绍了GEO卫星广播星历参数超限的现象和规律,基于轨道动力学特性分析了Δn参数超限的原因,并提出了固定Δn参数+参数岭估计+调整拟合弧长的综合策略。该策略能解决参数超限,但是嵌套判断和调用多种算法过于复杂和繁琐,其中岭估计需要经验确定岭参数。
本文在文献[8]的基础上,进一步分析了无需人为旋转5°倾角的GEO星历参数拟合算法。首先,拟合参数集基于第1类无奇点根数,以消除小偏心率引起的数学奇异。其次,从摄动运动方程出发,讨论了3个长期摄动参数由于小倾角导致的系数放大。最后,针对GEO的参数超限时段,引进缩减参数拟合法。试验分析了包含地影期在内的北斗GEO星历数据拟合和卫星位置计算,结果表明,在不改变现有导航电文的参数接口设计条件下,统一北斗混合星座的星历拟合算法和用户算法是可行的,拟合精度优于5 cm。
1 GEO的两步法星历参数算法卫星在惯性系下的轨道运动描述常采用3种轨道根数,即开普勒根数、第1类和第2类无奇点根数[9]。其中,第1类无奇点根数是专用于描述小偏心率轨道及其轨道变化的无奇点根数,并已长期用于近圆轨道卫星的轨道描述,如GPS的星历参数等[10]。
1.1 近圆轨道和第一类无奇点根数经典开普勒根数 (a, e, i, Ω, ω, M) 分别表示轨道半长轴、偏心率、轨道倾角、升交点赤经、近点角距和平近点角。
在小偏心率情况下,用开普勒轨道根数描述近圆轨道具有奇异性。由于椭圆的拱线 (即近地点和远地点连线) 几何意义模糊,近点角距ω和平近点角M难以分离,两参数具有强负相关性。为此,引进了第1类无奇点根数σ1=[ae1iΩu],其与开普勒根数的关系为[7]
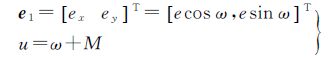 (1)
(1)
式中,二维偏心率矢量e1的大小等于偏心率,方向指向近点,并且椭圆运动方向的快变量采用新的组合量u,组合量去除了ω和M的负相关性。
在理想无摄运动条件下,描述同一轨道的3类轨道根数可以直接转换。在各种摄动力作用下,轨道的变化还对应了轨道根数的摄动。通常轨道根数的摄动变化依据时变特性分为3类,即长期项、长周期项和短周期项。但是,若仅仅描述数小时内的轨道星下点的运动特性,并保证拟合算法的稳健性和节省发播电文数据,通常要求用有限数量的参数表征主要的轨道变化,同时用户仍能够采用简便的解析公式计算卫星的受摄位置向量。
以16参数的GPS广播星历参数为例,虽然GPS卫星轨道具有小偏心率特点,但是却采用了开普勒根数和第1类无奇点根数的综合表示法[11]
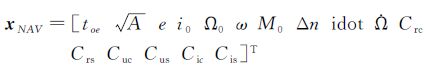
(1) 轨道参数采用开普勒根数形式。其中将升交点赤经Ω修改为升交点经度Ωe=Ω-θg(θg表示Greenwich恒星时),由于吸收了一阶地球自转效应,反映了星下点的运动特征。
(2) 摄动参数利用了第1类无奇点根数u。在数小时拟合弧段中,考虑了径向、沿迹方向和外法向上的主要摄动项,包括一阶长期摄动项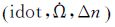
若直接拟合GPS广播星历参数,由于近圆轨道中开普勒根数 (ω, M0) 的强负相关性,拟合算法的法矩阵严重病态,从而影响拟合迭代收敛速度和拟合精度。
1.2 无奇点拟合参数集文献[8]提出先计算第1类无奇点根数形式的拟合参数再转换为标准广播星历参数的两步法,既保证了拟合算法的稳定性,同时具有转换简单的优点。该算法在MEO和IGSO卫星的星历参数拟合中均获得验证。
16参数NAV和18参数CNAV广播星历,除了星历参考时刻toe,基于第1类无奇点根数及其摄动的无奇点拟合参数集为[8, 12-14]
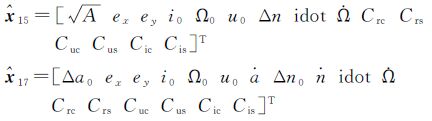
式中, 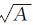
与星历参数相比,拟合参数没有修改任何摄动参数,仅针对开普勒根数修改并引进了3个无奇点轨道参数,即ex, ey, u0。拟合参数解算得到后,可方便地通过式 (1) 将无奇点拟合参数ex, ey, u0转换到星历参数 (e, ω, M0)。此外,还需要把惯性系ECI的升交点赤经转换为地心地固系ECEF的升交点经度或与参考值之差,具体公式这里略去。
拟合算法需要给出ECEF下卫星位置向量R对3个无奇点轨道参数ex, ey, u0的偏导数,即
 (2)
(2)
式中,Rz(Θ) 表示ECEF转换至地心惯性系的地球自转旋转矩阵;Θ是toe时刻之后的格林尼治恒星时角
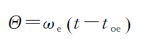 (3)
(3)
式中,ωe是地球自转角速度;n为卫星平均角速度;r和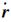
星历参数作为导航电文的数据内容,需要根据各参数变化范围进行接口设计,并在接口控制文档 (interface control document,ICD) 中按照规定的格式表示成二进制比特流的形式。为讨论方便起见,表 1仅列出了NAV和CNAV的摄动星历参数的参数适用范围指标[11-13]。
| 摄动参数 | NAV 适用范围 | CNAV 适用范围 | 单位 | |
| 长期 摄动 参数 | 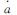 | — | ±8 | m/s |
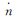 | — | ±2.910 4e-011 | π/s2 | |
| idot | ±9.313 2e-010 | ±9.313 2e-010 | π/s | |
| (Δ*) | ±9.536 7e-007 | ±3.725 3e-009 | π/s | |
| Δn(Δn0**) | ±3.725 3e-009 | ±3.725 3e-009 | π/s | |
| 短周 期摄 动参 数 | Cuc | ±6.103 5e-005 | ±9.765 6e-004 | rad |
| Cus | ±6.103 5e-005 | ±9.765 6e-004 | rad | |
| Crc*** | ±1024 | ±32 768 | m | |
| Crs*** | ±1024 | ±32 768 | m | |
| Cic | ±6.103 5e-005 | ±3.051 8e-005 | rad | |
| Cis | ±6.103 5e-005 | ±3.051 8e-005 | rad | |
注:*CNAV参数相对于参考值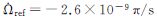 的差值;**CNAV参数符号不同,含义相同;*** BDS的Crc和Crs的适用范围是±2048 的差值;**CNAV参数符号不同,含义相同;*** BDS的Crc和Crs的适用范围是±2048 | ||||
从表 1可以看出,CNAV在NAV接口设计基础上,调整了大部分摄动参数的适用范围,仅有idot和Δn(CNAV中称为Δn0) 保持不变。此外,北斗导航电文与NAV相比,有两个摄动参数有变化,即Crc和Crs的适用范围放大了一倍[15]。
星历参数的变化范围必须控制在其设计的适用范围内,否则在编码导航电文时超过了系统设计分配给该参数的比特位限制,即参数超限[3]。
1.3.2 星历摄动参数的超限分析小偏心率的近圆轨道有e≈0,若仅考虑保守力的摄动影响,并保留至e的一阶小量,可以写出3个长期摄动参数
 (4)
(4)
式中, R表示摄动位。
由于GEO轨道的小倾角,式 (4) 的3个方程都有小分母问题。即使预先实施了旋转5°倾角,假定i=5°,有1/sin i≈11.5,cos i≈1,代入式 (4) 可知:
(1) 与IGSO卫星 (i=55°) 相比,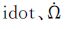
(2) 
长期的GEO星历拟合表明,只有Δn有星历超限现象,且通常出现在月球摄动引起的半月周期变化的峰值附近[3]。
1.3.3 参数超限的抑制新方法在不能修改参数接口设计的条件下,文献[5]提出了几种抑制超限的方法,即固定Δn参数+参数岭估计+调整拟合弧长的综合策略。对于Δn出现超限的特定拟合时段,首先采用固定Δn参数,如接近门限的某数值,从而不参与解算,其实质是一种缩减参数的拟合算法。对于仍然超限的拟合时段,采用岭估计方法,通过压缩待估计参数的模,在保证拟合误差的前提条件下,将参数控制在接口范围门限以内。此外,还需要适当增加拟合时段长度对参数变化范围进行调控。
本文利用摄动参数间的动力学运动关系,提出一种改进的超限抑制方法。该方法采用单一的缩减参数拟合法,无需岭估计,也不需要反复改变拟合时段长度。
根据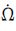

 (5)
(5)
组合参数Q消除了i≈0的小分母问题。因此,尽管拟合方程病态程度较强,导致两个线性相关的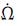
因此,缩减参数的改进思路是,首先,采用缩减一个参数的拟合法,即为Δn选用一个不超限的固定值Δn。由于Q的小变化范围限制,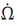

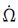
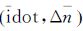

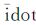
改进的超限抑制方法,流程如下:
(1) 采用无奇点参数拟合算法,判断Δn是否超限。
(2) 对于Δn超限的时段,固定Δn,重新拟合,并判断idot是否超限。
(3) 对于idot超限的时段,固定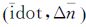
(4) 统一将无奇点拟合参数转换为星历参数。
需要注意的是,取固定值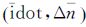
采用北斗混合星座的5颗GEO卫星G1~G5进行两步法星历拟合试验。地固系卫星位置向量来自精密星历的轨道外推结果,外推10~11 d,并根据地球自转参数EOP转换至地固系,具体力模型设置参见文献[10]。非地影期的试验数据从2016年4月底开始,其中G4卫星由于轨道出现问题,缺少精密星历。地影期数据时段从2013年春分日开始,GEO每年两次的地影季分别在春分日和秋分日附近,每次持续46 d[16-20];地影季期间,GEO卫星每天有约1 h位于地影内。
为适应每小时的星历更新模式,将10 d左右的连续轨道数据逐小时分组,每组分别包含2 h和3 h时段,时段内数据点间隔300 s。参数解算采用最小二乘拟合,当前后两次拟合的残差均方差 (RMS) 的相对偏差小于0.001时,迭代结束。GEO的轨道半长轴的参考值aref取为42 165 760 m[15]。
轨道参数化的误差常借助于URE进行表征,称为拟合URE[6]。URE是计算星历和钟差误差对定位影响的一个重要评价指标[1, 21]。URE的来源主要是外推的轨道和钟差误差,此外还包括星历参数拟合和钟参数拟合的拟合误差。这里仅分析星历参数拟合的单项影响,即将事后精密星历数据作为轨道位置真值,因此评定的星历计算和URE均是数学意义上的拟合精度,不包括轨道和钟差自身的计算和预报误差。拟合URE是轨道位置分量均方差的加权平均[4-5],即

式中,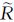
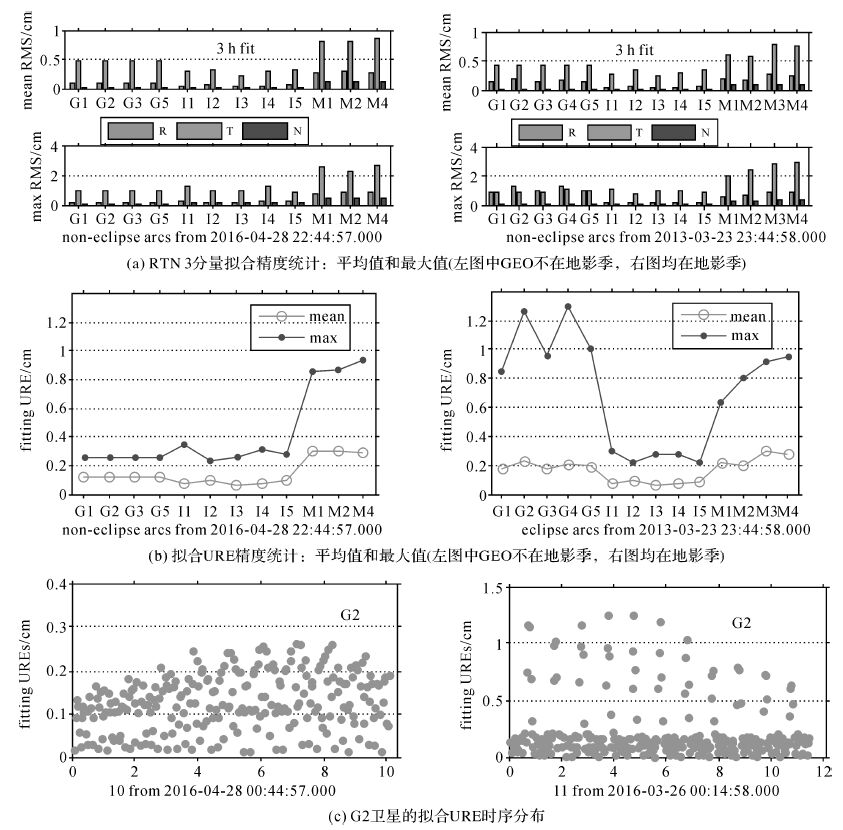
分别对地影期和非地影期数据时段进行拟合,图 1给出了2 h拟合时段的NAV星历拟合统计结果,图 2给出了3 h拟合时段的CNAV星历拟合统计结果。为了对比混合星座的3类轨道,图 2给出了CNAV星历对北斗混合星座的14颗GEO/IGSO/MEO卫星的结果。

|
| 图 1 NAV星历拟合结果 (非地影季 (左) 和地影季 (右)) Fig. 1 NAV-ephemeris fit results during non-eclipse (left) and eclipse (right) seasons |
|
| 图 2 CNAV星历拟合结果 (非地影季 (左) 和地影季 (右)) Fig. 2 CNAV-ephemeris fit results during non-eclipse (left) and eclipse (right) seasons |
(1) GEO的拟合成功率均为100%,拟合迭代次数均稳定为3或4次。可以看出,虽然基于第1类无奇点根数的拟合参数对小倾角轨道描述有数学奇异问题,导致解算法方程存在潜在的病态性,但是各试验数据段均没有出现迭代发散的现象。
(2) 地影数据对GEO径向拟合精度影响最为显著,因而直接反映到拟合URE。对比图 1(a)和图 2(a)的左右两图,尤其是图 2(a)的3 h CNAV拟合,径向拟合RMS的最大值达到甚至超过沿迹方向。
(3) GEO拟合URE统计平均值均稳定优于3 mm (图 1(b)和图 2(b));非地影期的最大值优于6 mm,地影期间可超过1 cm。
(4) 过地影数据会影响3~5个连续时段的GEO拟合URE。图 1(c)和图 2(c)的右图分别给出了G2星的时序拟合URE,每天1 h的进出地影期间,光压摄动力消失,引起轨道不平稳变化,导致卫星每天相关的2 h或3 h拟合时段出现连续一致的跳变现象,比无地影时高出2~4倍。
(5) GEO卫星的位置拟合精度与其他两类卫星量级相当 (图 2(a))。由于2 h对应GEO和IGSO的1/12轨道弧段,对应MEO则约1/6弧长,因此MEO的拟合精度略低些,尤其是沿迹向。
2.2 NAV星历摄动参数的变化范围图 3列出了5颗GEO卫星的NAV星历摄动参数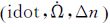
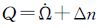

|
图 3
GEO的NAV星历参数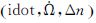 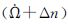 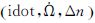 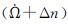 |
(1) 小倾角导致GEO卫星的3个摄动参数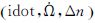
(2) NAV星历参数Δn出现大幅超限现象,其限差为±3.725 3e-009,对应图中的两条直线。5个GEO卫星的多个10 d试验数据统计中,超限时段共计913组,占总时段的40%,见表 2。
| 轨道 | 拟合时段 | 全参数拟 合后Δn超 限时段 | 单参数缩 减拟合后 idot超限时段 | 双参数缩 减拟合后 超限时段 |
| 非地影期 | 968 | 285 | 4 | 0 |
| 地影期 | 1331 | 628 | 13 | 0 |
(3) 对于近赤道卫星,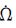
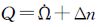
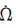

5颗GEO卫星数据拟合的CNAV摄动参数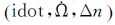
为满足参数接口设计,采用固定超限参数取值的缩减参数拟合算法。首先,对Δn超限时段采用单参数缩减重新拟合;其次,对仍超限的剩余时段采用双参数缩减重新拟合。固定值方案为
(1) 单参数缩减方案:固定Δn的取值为略低于其最大适用范围,Δn=±3.725e-009。
(2) 双参数缩减方案:同时固定idot和Δn,dot=0, Δn=±3.725e-009。
表 2列出了超限时段的统计。采用单参数缩减的拟合算法,将占40%总时段的Δn超限时段减少到17个,再对这不到1%的超限时段进行双参数缩减的拟合计算,即可完全消除超限问题。
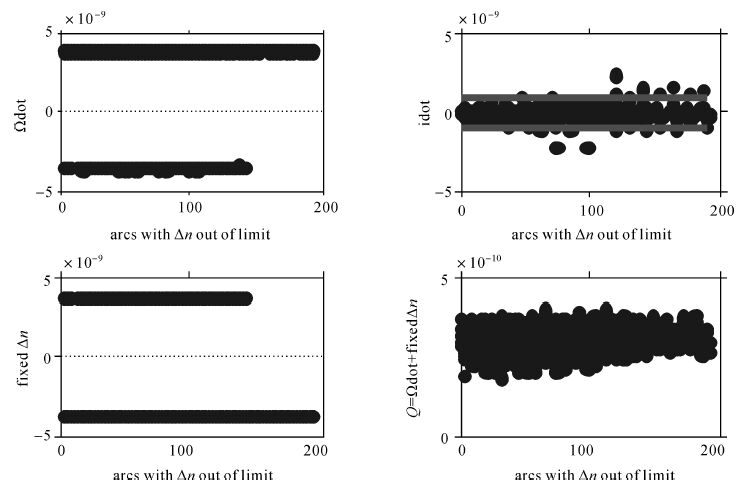
图 4列出了全部Δn超限时段的单参数缩减的拟合结果。横坐标是超限时段个数,每颗星的拟合参数值进行了叠加,与图 3相比可知:
|
图 4
固定Δn的NAV星历参数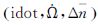 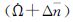  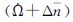 |
(1) 采用了e-9量级的Δn固定值,与之强相关的拟合值也控制在合理的同量级变化范围内,从e-8量级减少到e-9量级。
(2) 组合参数
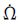
(3) 少量时段由于固定Δn出现了idot的超限现象。这是因为,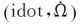
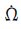
对于idot的超限时段,采用同时固定Δn和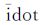
图 5是缩减参数拟合法的卫星位置R/T/N分量误差统计和拟合URE分布。左边是固定Δn的结果,右边是同时固定Δn和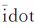

|
| 图 5 Δn超限和idot超限的NAV星历拟合结果 Fig. 5 NAV-ephemeris fit results with Δn and idot out of limit |
2.4 CNAV超限抑制算法
GPS的CNAV针对NAV参数接口缩小了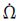

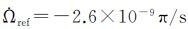
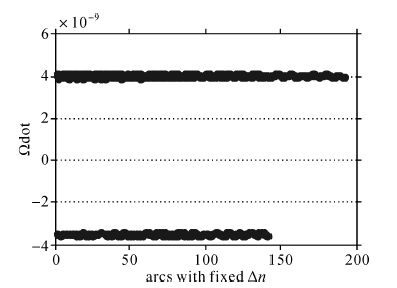
对于GEO卫星,图 6列出了固定Δn时的缩减参数拟合得到的
|
| 图 6 固定Δn的CNAV星历参数的变化范围 Fig. 6 Ranges of CNAV-ephemeris parmeter with a fixed Δn |
3 结语
实现北斗混合星座的用户算法通用性,需要对GEO卫星采用无人为倾角旋转的星历拟合算法。已有文献提出采用基于第1类无奇点根数的MEO和IGSO星历参数拟合算法,但是没有针对GEO进行广泛的拟合验证和分析。本文选取了北斗的5颗GEO卫星在地影季和非地影季的10 d轨道数据,就GEO拟合精度、成功率和星历参数接口设计开展试验分析,并对比了MEO和IGSO的拟合结果。通过16参数NAV和18参数CNAV的星历拟合试验,初步结果表明:
(1) 基于第1类无奇点根数的星历参数拟合算法,能够适用于GEO的星历拟合,并且能够反映出地影数据对轨道拟合的显著影响。GEO的拟合URE精度与MEO和IGSO的结果相当,拟合URE统计平均值均稳定优于3 mm,最大值优于5 cm。
(2) GEO卫星有星历参数Δn(或Δn0) 的超限现象。超限拟合时段达到总时段的40%,其根源是第1类无奇点根数对GEO轨道描述的奇异性。
(3) 缩减参数拟合法能够解决GEO参数超限问题。拟合参数的减少导致轨道面外法向位置分量的拟合误差变大,但是能够满足拟合URE的精度要求。
致谢: 特别感谢国家留学基金委对笔者在德国地学研究中心公派访学的资助。
| [1] | 杨元喜. 综合PNT体系及其关键技术[J]. 测绘学报, 2016, 45(5): 505–510. YANG Yuanxi. Concepts of Comprehensive PNT and Related Key Technologies[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 505–510. DOI:10.11947/j.AGCS.2016.20160127 |
| [2] | 杨元喜, 陆明泉, 韩春好. GNSS互操作若干问题[J]. 测绘学报, 2016, 45(3): 253–259. YANG Yuanxi, LU Mingquan, HAN Chunhao. Some Notes on Interoperability of GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 253–259. DOI:10.11947/j.AGCS.2016.20150653 |
| [3] | 何峰, 王刚, 刘利, 等. 地球静止轨道卫星广播星历参数拟合与试验分析[J]. 测绘学报, 2011, 40(S): 52–58. HE Feng, WANG Gang, LIU Li, et al. Ephemeris Fitting and Experiments Analysis of GEO Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S): 52–58. |
| [4] | 陈刘成, 韩春好, 陈金平. 广播星历参数拟合算法研究[J]. 测绘科学, 2007, 32(3): 12–14. CHEN Liucheng, HAN Chunhao, CHEN Jinping. The Research of Satellites Broadcast Ephemeris Parameters Fitting Arithmetic[J]. Science of Surveying and Mapping, 2007, 32(3): 12–14. |
| [5] | 阮仁桂, 贾小林, 吴显兵, 等. 关于坐标旋转法进行地球静止轨道导航卫星广播星历拟合的探讨[J]. 测绘学报, 2011, 40(S): 145–150. RUAN Rengui, JIA Xiaolin, WU Xianbing, et al. Broadcast Ephemeris Parameters Fitting for GEO Satellites Based on Coordinate Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S): 145–150. |
| [6] | 张中凯, 杜兰, 刘利, 等. GEO广播星历参数设计的无奇点根数法[J]. 测绘学报, 2014, 43(5): 452–457. ZHANG Zhongkai, DU Lan, LIU Li, et al. Parameter Design of GEO Broadcast Ephemeris Based on the Nonsingular Orbital Elements[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(5): 452–457. DOI:10.13485/j.cnki.11-2089.2014.0076 |
| [7] | DU Lan, ZHANG Zhongkai, ZHANG Jin, et al. An 18-element GEO Broadcast Ephemeris Based on Non-singular Elements[J]. GPS Solutions, 2015, 19(1): 49–59. DOI:10.1007/s10291-014-0364-x |
| [8] | 韩星远, 向开恒, 王海红. 第一类无奇点变量的广播星历参数拟合算法[J]. 航天器工程, 2011, 20(4): 54–59. HAN Xingyuan, XIANG Kaiheng, WANG Haihong. Research on Broadcast Ephemeris Parameters Fitting Algorithm Based on the First Class of no Singularity Variables[J]. Spacecraft Engineering, 2011, 20(4): 54–59. |
| [9] | 刘林, 胡松杰, 王歆. 航天动力学引论[M]. 南京: 南京大学出版社, 2006. LIU Lin, HU Songjie, WANG Xin. An Introduction of Astrodynamics[M]. Nanjing: Nanjing University Press, 2006. |
| [10] | 杜兰, 张中凯, 刘利, 等. GEO卫星广播星历的拟合参数设计[J]. 中国空间科学技术, 2013, 33(3): 46–51. DU Lan, ZHANG Zhongkai, LIU Li, et al. Fitting Parameters Design for GEO Broadcast Ephemeris[J]. Chinese Space Science and Technology, 2013, 33(3): 46–51. |
| [11] | IS-GPS-200G (2012) Navstar GPS Space Segment/Navigation User Interface[EB/OL].[2012-07-18]. Global Positioning System Wing, Space and Missile Systems Center. http://www.navcen.uscg.gov. |
| [12] | IS-GPS-800C (2012) Navstar GPS Space Segment/User Segment L1C Interface[EB/OL].[2012-08-31]. Global Positioning System Wing, Space and Missile Systems Center. http://www.navcen.uscg.gov. |
| [13] | IS-GPS-705C (2012) Navstar GPS Space Segment/User Segment L5 Interfaces[EB/OL].[2012-07-18]. Global Positioning System Wing, Space and Missile Systems Center. http://www.navcen.uscg.gov. |
| [14] | 黄华, 刘林, 周建华, 等. 18参数广播星历分析研究[J]. 飞行器测控学报, 2012, 31(3): 80–84. HUANG Hua, LIU Lin, ZHOU Jianhua, et al. Research on 18 Elements Broadcast Ephemeris Model[J]. Journal of Spacecraft TT & C Technology, 2012, 31(3): 80–84. |
| [15] | BDS-SIS-ICD (2016) BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B1I-2.1[EB/OL].[2016-08-31]. Administrator Office of China Satellite Navigation. http://www.beidou.gov.cn. |
| [16] | 李恒年. 地球静止卫星轨道与共位控制技术[M]. 北京: 国防工业出版社, 2010. LI Hengnian. Geostationary Satellite Orbital Analysis and Collocation Strategies[M]. Beijing: National Defense Industry Press, 2010. |
| [17] | KUZNETSOV E D. The Effect of the Radiation Pressure on the Orbital Evolution of Geosynchronous Objects[J]. Solar System Research, 2011, 45(5): 433–446. DOI:10.1134/S0038094611050078 |
| [18] | SOOP E M. Handbook of Geostationary Orbits[M]. WANG Zhengcai, trans. Beijing: National Defense Industry Press, 1999. |
| [19] | XU Guochang. GPS:Theory, Algorithms, and Applications[M]. Berlin: Springer-Verlag, 2007. |
| [20] | MONTENBRUCK O, GILL E. Satellite Orbits:Models, Methods, and Applications[M]. Berlin: Springer-Verlag, 2000. |
| [21] | TAPLEY B D, SCHUTZ B E, BORN G H. Statistical Orbit Determination[M]. New York: Elsevier Academic Press, 2004. |


