2. 武汉大学中国南极测绘研究中心, 湖北 武汉 430079
2. Chinese Antarctic Center of Surveying and Mapping, Wuhan University, Wuhan 430079, China
深空探测是解答地球起源与演化、行星和太阳系形成与演化、人类是否是宇宙中的唯一生命等科学问题的手段,同时也蕴涵了巨大的经济价值[1]。国际上深空探测活动主要集中在美国、欧洲、俄罗斯、日本等一些强国。我国自开展“嫦娥探月工程”以来,已相继成功发射嫦娥一号 (CE-1)、嫦娥二号 (CE-2)、嫦娥三号 (CE-3)、嫦娥五号试验星 (CE-5T),攻克了一系列难题,积累了丰富的经验,并取得了众多科学成果[2-3]。在此基础上,我国自主火星探测任务正式立项,预计2020年发射,未来也将开展形式更加丰富多样的深空探测活动。
在深空探测中,探测器的定轨定位是任务成败的关键,也是各种科学任务顺利进行的前提。探测器的精密轨道是进行行星地形地貌测绘以及重力场解算的基础数据,而探测器精密轨道的计算完全依赖于定轨软件平台的支撑,因此,行星探测器精密定轨软件系统的研制在深空探测中是必不可少一个环节,具有重要的工程和科学意义,其研制一直受到国内外科研机构的重视。
对于地球卫星的精密定轨,国内外已有众多优秀软件,如喷气推进实验室JPL的GIPSY、麻省理工学院MIT的GAMIT、瑞士伯尔尼天文学院的Bernese、CSR的Utopia、武汉大学自主开发的卫星导航数据综合处理软件平台PANDA[4]、西安测绘研究所的SPODS[5]等。但是对于深空探测器而言,其距离遥远,信号传播路径环境也比地球卫星复杂,相对论效应显著,定轨几何差,探测器的动力学的精度不如地球卫星的精度。深空探测器精密定轨技术要比传统的地球卫星精密定轨复杂,实现难度也更大[6],因此深空探测器精密定轨技术主要集中在欧美一些大的航天机构如JPL、GSFC、ESA等,具有代表性的软件包括JPL的DPTRAJ/ODP[7-8]和MONTE[9],GSFC的GEODYN-Ⅱ[10],CNES的GINS[11]软件系统,ESOC的AMFIN[12-13]。除此之外,为处理欧空局的MEX和Rosatta数据,Andert也开发了自己的定轨软件系统[14],通过MEX 2006年和2008年两次飞掠火卫Phobos的跟踪数据成功解算了Phobos的质量[15]。针对ESA的BepiColombo任务,意大利比萨大学和意大利航天局ASI合作开发了自主的定轨软件系统ORBIT14[16],并针对水星探测器的相对论时延进行了详细的讨论[17]。文献 [18-19]根据天体力学研究方法,将BERNESE GNSS软件系统功能拓展至月球,通过处理DSN Doppler跟踪数据和GRAIL的KBRR星间测速数据,解算了200阶次的月球重力场模型。
作为我国深空探测任务的飞行控制中心,北京航天飞行控制中心开展了月球、火星探测器定轨技术的研究,研制了BODAS (BACC orbit determination and analysis software) 软件系统[6],成功应用于我国嫦娥系列任务中[20-21]。为适应我国“萤火一号”火星探测计划,上海天文台也自主研发了其火星卫星定轨软件MarsODP[22]。针对探月二期,基于动力学统计定轨法和运动学统计定轨法,上海天文台研发了月球探测器定轨定位综合软件,运用于“嫦娥三号”的定轨和定位中[23-24]。
尽管目前有国外一些机构的精密定轨与重力场解算软件系统可以使用,但这些软件并不能完全适应我国深空探测的需求。从长远来讲,随着我国深空探测的稳步推进,行星测地学的研究必将进一步深入,攻克行星探测器精密定轨的具体细节技术,开发具有完全自主知识产权的深空探测器精密定轨与重力场解算软件系统势在必行,这也是WUDOGS研发的根本出发点。
本文简要介绍了WUDOGS设计思路、主要功能及其开发测试过程,并以我国“嫦娥一号”和欧空局的火星快车 (MEX) 的精密定轨为例,重点讨论了WUDOGS与国际上领先水平的行星探测器精密定轨软件系统GEODYN-Ⅱ的交叉验证测试结果。最后对WUDOGS的下一步发展进行了讨论和展望,以此作为WUDOGS研发的阶段性总结。
1 WUDOGS系统概述深空探测器精密定轨与重力场解算软件系统WUDOGS,全称Wuhan University deep-space orbit determination and gravity recovery system,是武汉大学行星探测器精密定轨与重力场研究团队独立设计、开发、测试与维护的一套具有完全自主知识产权的精密定轨与重力场解算软件系统[25-31]。
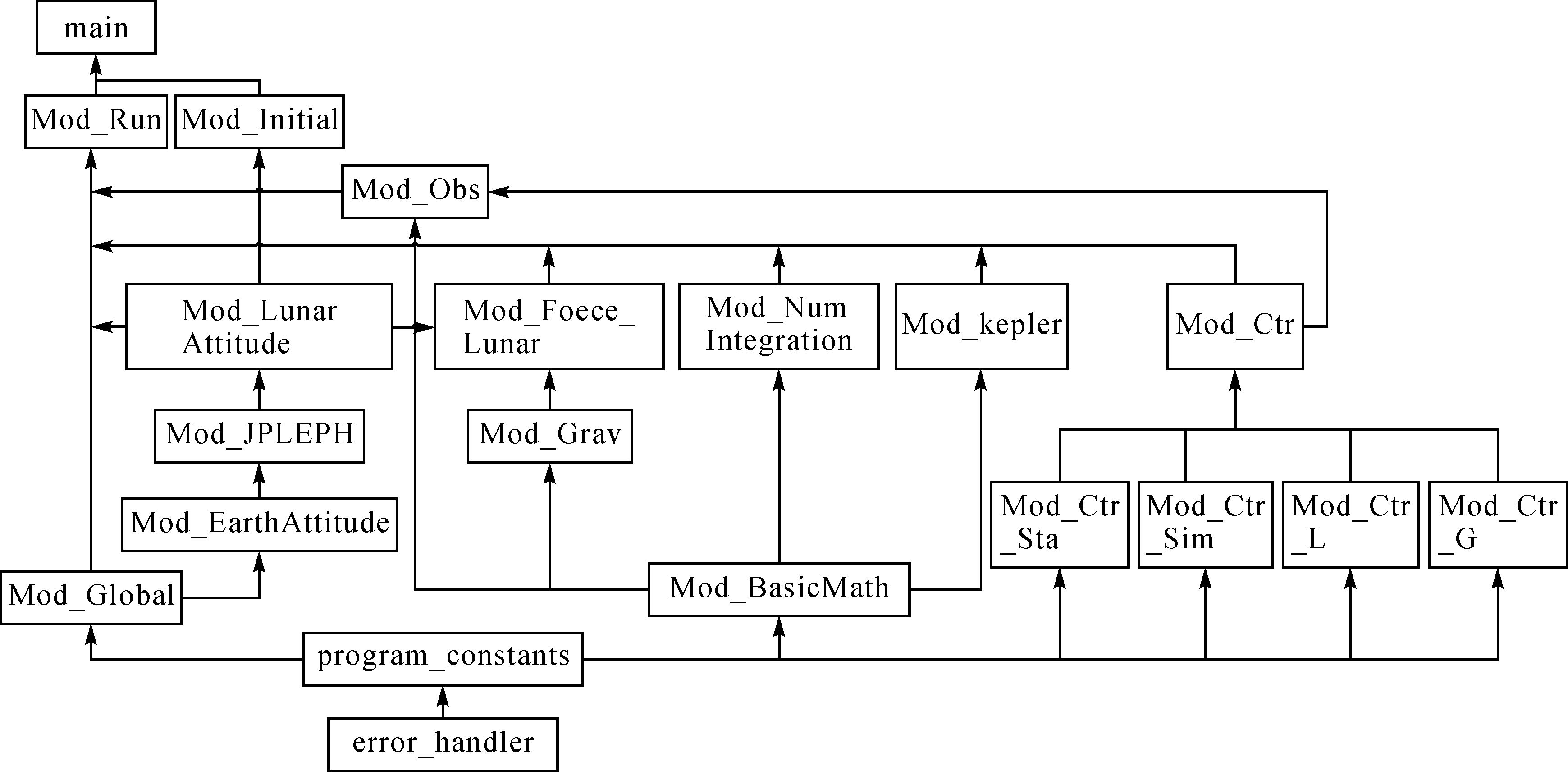
WUDOGS的设计主要是为了满足解算行星重力场模型和相关动力学参数的需求,同时也具备行星探测器轨道预报和观测值模拟功能。为实现上述3项功能,软件采用自上而下、逐步求精的设计原则,将需求划分成更细小的单位模块。软件核心代码采用了Fortran 95语言开发,充分利用了其Module的语法属性,将功能类似的函数放在一个Module中,实现封装。除主程序外,主要包括14大模块:容错模块、常数模块、输入参数总控制模块 (具体包含测站控制参数、模拟控制参数、局部参数和全局参数控制4个部分)、基本数学函数模块、地球及行星定向参数模块、行星历表模块、重力场模块、精密力模型模块、数值积分器模块、开普勒二体问题模块、观测值模型模块、全局变量池模块、初始化模块、运行模块[29]。主要模块之间的关系如图 1所示。除了上述的核心计算模块外,同时开发了其他的辅助工具,包括数据预处理工具、数据格式的转换、计算结果的分析比较、成图以及重力场可视化工具等。
|
| 图 1 WUDOGS主要模块框架 Fig. 1 Schematic view of the main modules in WUDOGS |
WUDOGS采用经典的动力法进行精密定轨,一步法恢复重力场及其他动力学参数。具体步骤为:给定探测器的初始状态,利用12阶Adams预估较正方法数值积分动力学方程和变分方程,得到探测器的星历、状态转移矩阵和参数敏感矩阵;结合测站信息和观测几何模型得到计算值C,与观测值O作差,形成单弧段法方程,采用经典加权最小二乘方法求得单弧段局部参数解;然后联合多个单弧段法方程,利用批处理方法求解得到重力场位系数及其他动力学参数等全局参数改正数,通过迭代处理,得到最终收敛解。
经过4年的独立开发与系统严格测试,WUDOGS目前已初具规模,积累核心代码6万余行。目前软件支持传统的单程测速/测距、双程测速/测距、三程测速/测距、四程测速、VLBI时延/时延率和同波束时延等,并新增了基于着陆器-轨道器的四程中继跟踪测量类型[30],可实现月球、火星探测器以及着陆器的精密定轨和定位。可以解算的参数包括初始轨道根数、太阳光压系数、大气阻力系数、经验加速度、测站偏差等局部参数,以及重力场模型位系数、固体潮Love数、行星着陆器位置等全局参数。WUDOGS已经初步具备了月球、火星重力场解算功能,目前正在进行进一步的完善和优化。同时,由于设计时充分考虑了未来我国其他行星探测器的精密定轨和重力场解算的需求,扩展性良好,可快速拓展至水星、金星等其他行星。
2 WUDOGS的开发与测试过程对于深空探测器精密定轨软件系统而言,除了系统的开发、测试等步骤外,还需要进行外符合精度测试,如和已有的成熟软件进行交叉验证测试 (CVT, cross verification tests),并经过几次实际深空任务的检验,才能逐步走向成熟。ESA/ESOC的深空定轨软件和JPL的新一代深空导航软件系统MONTE均经历了此过程[9, 32]。
WUDOGS的开发按照图 1中的模块自下而上,循序渐进,在开发中进行了大量的试验、分析与比对。WUDOGS的验证选择了国际上领先水平的且较为成熟的GEODYN-Ⅱ作为比对软件,进行了系统严格的测试。测试过程包括如下6个步骤:
(1) 单元测试。对每一个具体的函数输入输出进行测试,并和相关成熟工具进行对比。例如WUDOGS中的时间系统转换、坐标系转换可以和SPICE进行对比。
(2) 各个模块测试。这一步重点是对WUDOGS中的积分器和力模型模块进行测试。关于积分器的测试有众多的方法,如通过二体问题比对、能量法以及和已有的成熟积分器的对比测试等。特别地,对于非球形引力及其偏导数的计算展开详细的研究,分析比较了不同计算方法的精度和效率[33]。
(3) 轨道预报对比测试。通过探测器轨道预报的交叉验证测试,可以测试软件系统的输入输出模块、时空坐标系统、积分器模块和力模型模块及其之间的集成。
(4) 模拟观测值对比测试。该步骤相对于第3步,可对软件系统的测量模型模块进行验证,保证软件中的光行时计算的准确性。
(5) 仿真定轨测试。通过软件系统生成仿真观测值,进行仿真定轨,是软件系统各个模块的第一次全面综合,可以保证软件系统的自洽性。
(6) 实测数据的处理。该步是软件系统设计的最终目的,通过和已有成熟软件进行对比,进一步测试整个系统的正确性、稳定性、健壮性等。
以上各步骤是循序渐进,不断发现错误与修正错误、反复迭代升级的过程。
对于探测器轨道预报和模拟观测值的计算,对WUDOGS设置的基线 (baseline) 为:探测器2 d轨道预报和GEODYN-Ⅱ相差低于1 mm;软件系统的双程测距、双程测速的理论计算值C的精度必须比观测量O的精度至少高一个数量级,即至少达到100 mm、0.01 mm/s的精度水平。事实上,对WUDOGS的测试更加严格,甚至到了苛刻的地步。
在对WUDOGS与GEODYN-Ⅱ的轨道预报和模拟观测值进行的对比分析表明:对于探测器的轨道预报,WUDOGS与GEODYN-Ⅱ一个月位置最大差值小于0.3 mm,2 d位置差值小于5×10-3 mm;对于双程测距、双程测速的理论计算值和GEODYN-Ⅱ的差值分别在0.06 mm、0.002 mm/s的水平,均超过预期的基线。上述测试结果表明WUDOGS在探测器轨道预报、观测值计算方面具备了与GEODYN-Ⅱ较为一致的精度,为下述实测数据的处理打下基础。
3 WUDOGS实测数据的精密定轨试验分析为进一步测试WUDOGS定轨精度,分别以我国“嫦娥一号”和欧空局火星快车号MEX的精密定轨为例,对WUDOGS实测数据处理能力进行验证测试。
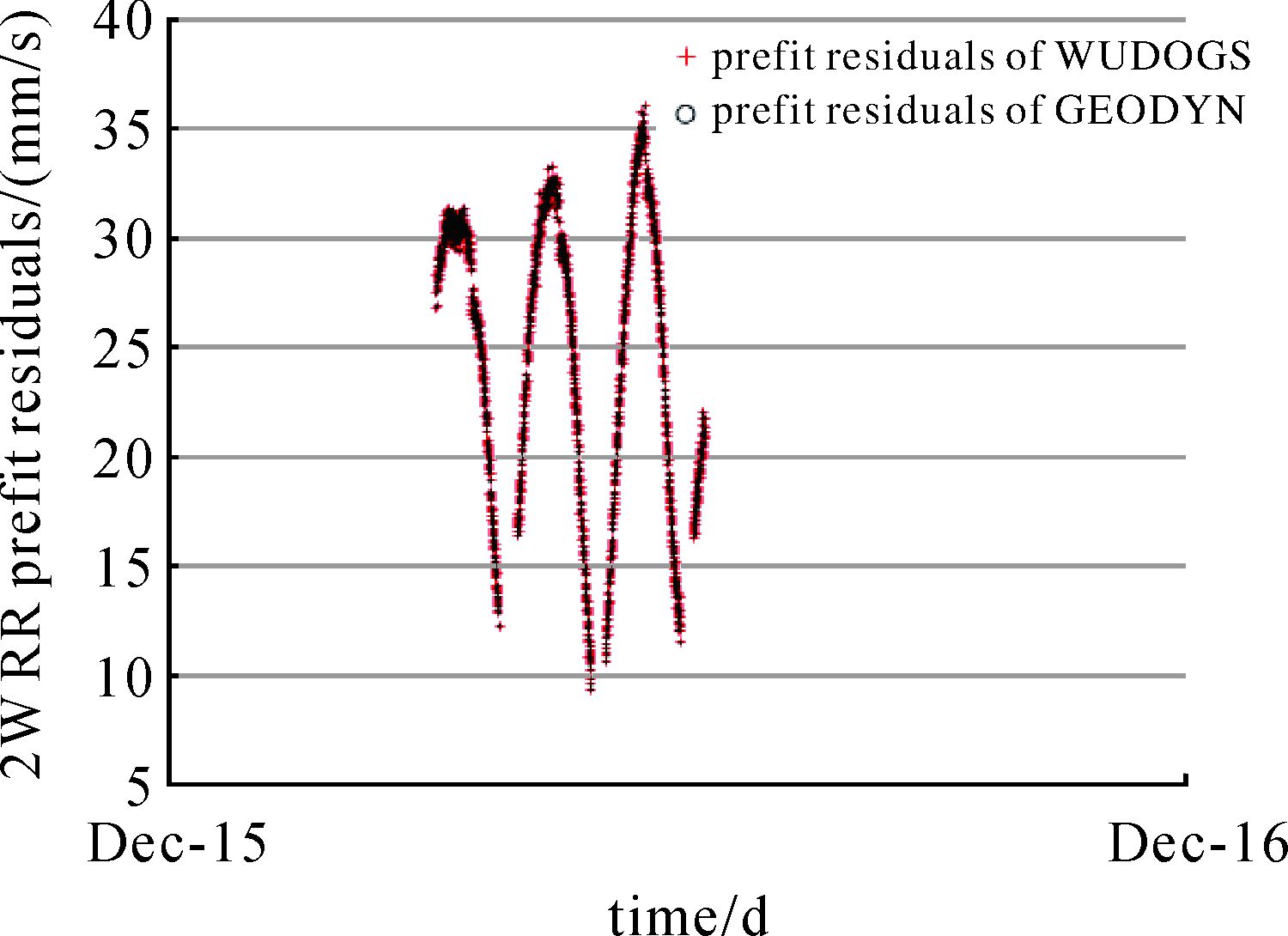
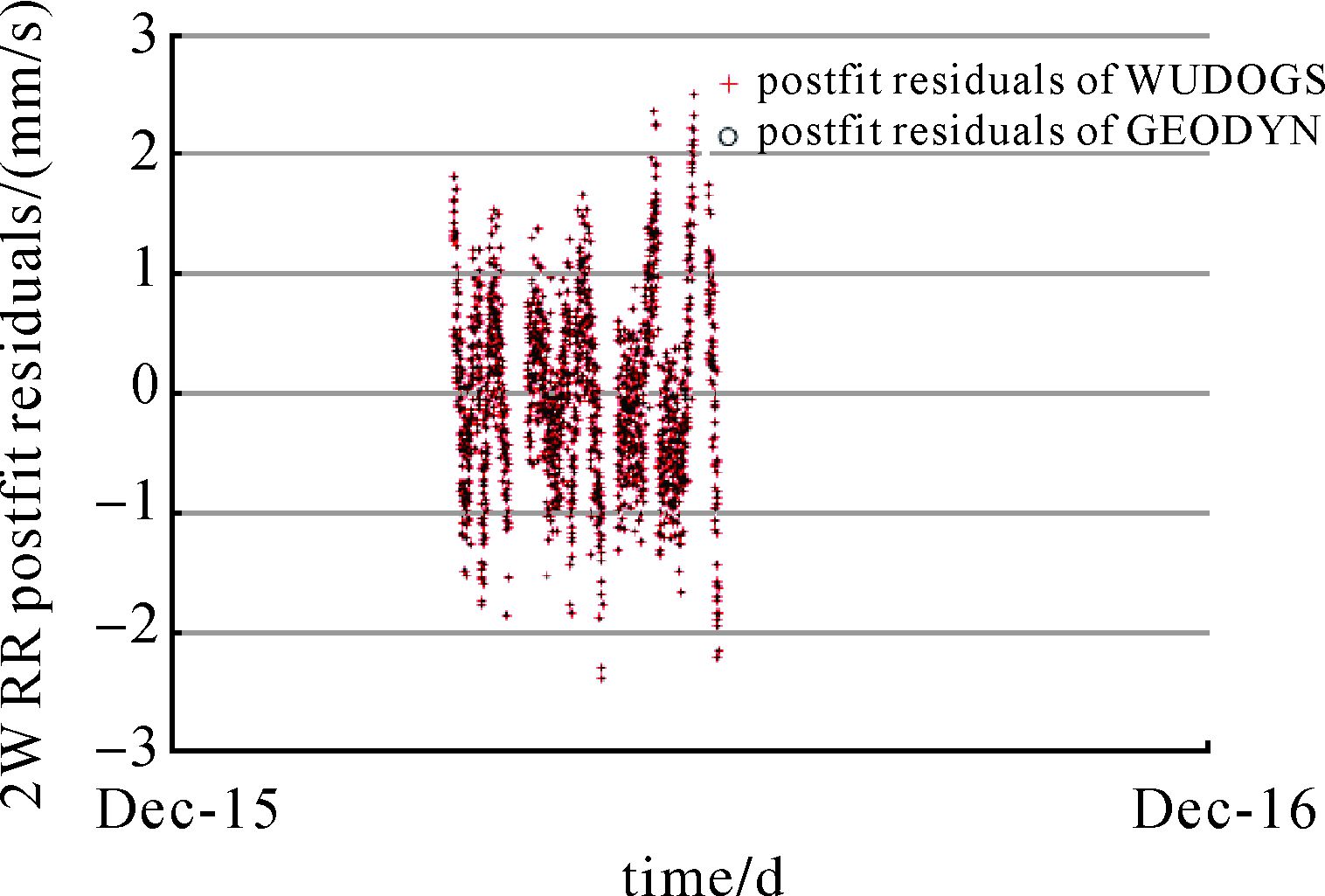
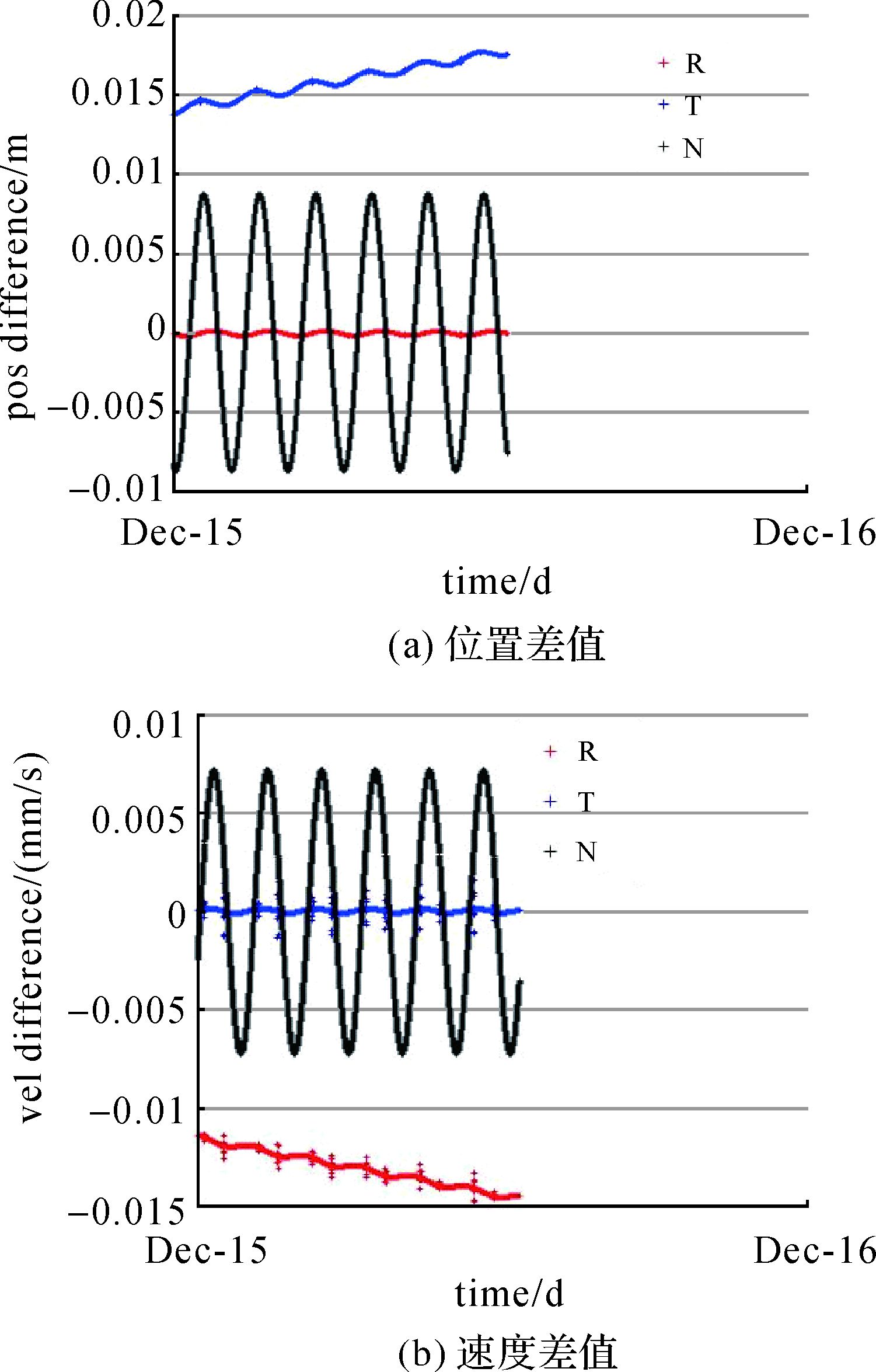
3.1 “嫦娥一号”探测器的精密定轨采用“嫦娥一号”2007年12月期间的双程测速数据,用WUDOGS与GEODYN-Ⅱ分别进行精密定轨,对两套软件系统采用完全一致的定轨策略和输入参数,主要目的是检验WUDOGS对实测数据的定轨能力。表 1给出了“嫦娥一号”精密定轨采用的策略。鉴于GEODYN-Ⅱ软件系统的成熟性,本文将WUDOGS的定轨输入结果与GEODYN-Ⅱ进行了详细的比对,可认为是外符合精度。表 2给出2007-12-15弧段两者的解算结果,从中可以看出无论是第1次迭代结果还是最终收敛结果,两者解算的改正量均较为一致,残差RMS和观测精度相符。图 2为第1次迭代结束后 (pre-fit残差) 两者的残差分布图,图 3为收敛后两者的残差分布图,图 4为两者事后精密轨道在月心J2000中R、T、N方向的差值。由图 2和图 3可以看出,WUDOGS和GEODYN-Ⅱ计算的残差非常接近,在图中几乎重叠。图 4表明事后精密轨道位置最大差值小于2 cm,速度差值小于0.002 mm/s。其他弧段的解算结果和弧段2007-12-15的解算精度类似。
| 项目 | 类型 | 具体说明 |
| 弧长 | 取1~2 d,根据动量轮卸载时间确定 | |
| 力 模 型 | 非球形引 力摄动力 | GRGM660PRIM[34-35],截断至500阶次 |
| N体摄动力 | 太阳、地球及其他太阳系行星 | |
| 月球固体 潮摄动力 | K2项,K2=0.027 | |
| 地月扁率 摄动力 | 月球J2间接摄动力 地球J2直接摄动力和间接摄动力 | |
| 相对论摄 动力 | 点质量摄动+测地岁差 | |
| 光压摄 动力 | 固定面质比、考虑地月锥形阴影 | |
| 月球辐射 反照力 | ||
| 测 量 模 型 | 测站 | 青岛站、喀什站 截止高度角5° |
| 介质改正 | 对流层改正模型采用Hopfield模型+CfA2.2映射函数 | |
| TDB-TT 计算模型 | 采用Moyer1982模型 | |
| 地球自转 模型 | IAU1976/1980岁差章动模型极移参数取自IERS C04采用双线性插值方法 | |
| 月球自转 模型 | 采用DE421历表包含的天平动参数 | |
| 测量数据 预处理 | 观测数据进行了平滑滤波处理扣除了电离层和中性大气的影响 | |
| 观测值 | 双程测速,权值取10 mm/s | |
| 待估参数 | 卫星6个初始轨道根数 | |
| 每弧段的常值系统偏差 | ||
| 太阳光压系数 | ||
| 经验加速度 |
| 项目 | 类型 | GEODYN-Ⅱ
解算结果 | WUDOGS 解算结果 |
| 第1次迭 代结果 | 总共观测值个数 | 1857 | 1857 |
| 剔除数据个数 | 69 | 69 | |
| 加权观测值个数 | 1788 | 1788 | |
| 加权RMS/(cm/s) | 2.573 8 | 2.573 8 | |
| x改正值/m | 312.683 | 312.689 | |
| y改正值/m | 316.399 | 316.404 | |
| z改正值/m | 322.707 | 322.712 | |
| xdot改正值/(m/s) | 0.090 9 | 0.090 9 | |
| ydot改正值/(m/s) | 0.266 9 | 0.266 9 | |
| zdot改正值/(m/s) | -0.281 5 | -0.281 5 | |
| 常数测量偏差1/(m/s) | 0.022 9 | 0.022 9 | |
| 常数测量偏差2/(m/s) | 0.022 8 | 0.022 8 | |
| 常数测量偏差3/(m/s) | 0.021 9 | 0.021 9 | |
| 常数测量偏差4/(m/s) | 0.029 0 | 0.029 0 | |
| 2007-12-15 弧段经过 5次迭代 后收敛, 收敛结果 | 加权RMS/(cm/s) | 0.073 6 | 0.073 6 |
| x改正值/m | 311.410 | 311.418 | |
| y改正值/m | 315.019 | 315.027 | |
| z改正值/m | 321.264 | 321.272 | |
| xdot改正值/(m/s) | 0.090 5 | 0.090 5 | |
| ydot改正值/(m/s) | 0.265 6 | 0.265 6 | |
| zdot改正值/(m/s) | -0.280 3 | -0.280 3 | |
| 常数测量偏差1/(m/s) | 0.022 98 | 0.022 98 | |
| 常数测量偏差2/(m/s) | 0.022 80 | 0.022 80 | |
| 常数测量偏差3/(m/s) | 0.021 89 | 0.021 89 | |
| 常数测量偏差4/(m/s) | 0.029 06 | 0.029 06 |
|
| 图 2 弧段2007-12-15的pre-fit残差 Fig. 2 The pre-fit residuals of arc 2007-12-15 |
|
| 图 3 弧段2007-12-15的post-fit残差 Fig. 3 The post-fit residuals of arc 2007-12-15 |
|
| 图 4 弧段2007-12-15的事后精密轨道R、T、N方向的差值 Fig. 4 The differences of reconstructed orbit on 2007-12-15 in R, T, N directions |
3.2 欧空局火星快车号MEX的精密定轨
MEX是ESA的首颗火星探测器,于2003年6月发射,12月进入环火星轨道,次年1月进入工作轨道。比利时皇家天文台利用法国空间局CNES的GINS软件,以7 d观测数据为一个弧段,解算了MEX两年的跟踪数据,得到平均精度20~25 m的MEX精密轨道[36]。
采用欧空局MEX双程观测数据,使用WUDOGS对MEX 2009-08-07弧段进行精密定轨,并将定轨结果与比利时皇家天文台MEX的精密轨道相比较。表 3给出了MEX精密定轨采用的策略,表 4给出精密定轨的解算结果,从中可以看出初轨改正值与MEX精密轨道相差非常小,差距小于25 m。图 5为post-fit残差分布图。图 6为两组MEX事后精密轨道在火星天球J2000中R、T、N方向的差值。图 6表明事后精密轨道位置最大差值小于25 m,速度差值小于10 mm/s,均在MEX精密轨道误差范围之内。
| 项目 | 类型 | 具体说明 |
| 弧长 | 一个弧段,根据动量轮卸载时间确定 | |
| 力模型 | 非球形引 力摄动力 | MRO120D 120阶重力场模型 |
| N体摄动力 | 太阳、地球及其他太阳系行星 | |
| 火星固体 潮摄动力 | K2项,K2=0.169 | |
| 相对论摄 动力 | 点质量摄动+测地岁差 | |
| 光压摄动力 | 固定面质比 | |
| 测量模型 | 测站 | 新诺舍站 截止高度角5° |
| 介质改正 | 对流层改正模型采用Hopfield模型+CfA2.2映射函数 | |
| TDB-TT 计算模型 | 采用Moyer1982模型 | |
| 地球自转 模型 | IAU1976/1980岁差章动模型极移参数取自IERS C04采用双线性插值方法 | |
| 火星自转 模型 | Pathfinder火星定向模型 | |
| 测量数据 预处理 | 观测数据进行了平滑滤波处理扣除了电离层和中性大气的影响 | |
| 观测值 | 双程测速,权值取1 mm/s | |
| 待估参数 | 卫星6个初始轨道根数 | |
| 太阳光压系数 |
| 类型 | 解算结果 |
| 总共观测值个数 | 3452 |
| 剔除数据个数 | 22 |
| 加权观测值个数 | 3430 |
| 加权RMS/(mm/s) | 0.068 |
| x改正值/m | 7.058 0 |
| y改正值/m | -9.367 1 |
| z改正值/m | 18.080 4 |
| xdot改正值/(m/s) | 0.002 3 |
| ydot改正值/(m/s) | -0.001 2 |
| zdot改正值/(m/s) | -0.001 2 |
| Cr改正值 | 0.000 048 |

|
| 图 5 弧段2009-08-07的post-fit残差 Fig. 5 The post-fit residuals of arc 2009-08-07 |

|
| 图 6 弧段2009-08-07的事后精密轨道R、T、N方向的差值 Fig. 6 The differences of reconstructed orbit on 2009-08-07 in R, T, N directions |
4 结论与展望
武汉大学深空探测器精密定轨与重力场解算软件WUDOGS的系统架构目前已经搭建完毕,取得初步成果。通过与GEODYN-Ⅱ严格地交叉验证测试表明对于探测器的轨道预报,WUDOGS与GEODYN-Ⅱ一个月位置最大差值小于0.3 mm,2 d位置差值小于5×10-3 mm;对于双程测距、双程测速的理论计算值和GEODYN-Ⅱ的差值分别在0.06 mm、0.002 mm/s的水平。对“嫦娥一号”和MEX的精密定轨试验表明WUDOGS已完全具备月球、火星探测器的精密定轨能力,并具有了较高的精度水平。
该软件的研发将为我国行星测地学界提供一套具有自主知识产权的高精度、高可靠性的科研型软件平台,满足我国后续行星测地学特别是行星重力场方面的研究需求。WUDOGS下一步发展将以科学目标为导向,重点从以下几个方面进行完善:
(1) 完善和优化WUDOGS系统的重力场解算模块。通过处理我国嫦娥系列跟踪数据,进一步挖掘嫦娥系列轨道跟踪数据的科学价值,探讨通过融合嫦娥系列数据优化现有月球重力场模型低阶项的可能性。
(2) 进一步完善WUDOGS中的精密动力学模型和测量模型。对于月球和火星探测器,分别以GRAIL和MGS的精密定轨技术为突破口,使WUDOGS数据处理能力早日达到国外成熟综合定轨软件的精度水平,同时为我国即将到来的火星探测任务提供精密定轨与重力场方面的技术储备。
(3) 紧密结合我国未来深空探测的需求,将WUDOGS的功能拓展至其他行星。
致谢: 感谢北京航天飞行控制中心、上海天文台提供相关研究数据。特别感谢胡松杰研究员、陈明博士、曹建峰博士、黄勇研究员、简念川博士等在软件研制和数据处理过程中提供的宝贵意见。感谢欧空局提供MEX跟踪数据。
| [1] | 中国科学院月球与深空探测总体部. 月球与深空探测[M]. 广州: 广东科技出版, 2014. Department of Lunar and Deep Space Exploration, CAS. Lunar and Deep Space Exploration[M]. Guangzhou: Guangdong Science and Technology Press, 2014. |
| [2] | 欧阳自远, 李春来. 绕月探测工程科学目标专题研究[M]. 北京: 科学出版社, 2015. OUYANG Ziyuan, LI Chunlai. Monographic Study on Scientific Objectives of Lunar Explorer Project[M]. Beijing: Science Press, 2015. |
| [3] | 欧阳自远, 李春来. 绕月探测工程月球科学与探测技术研究[M]. 北京: 科学出版社, 2015. OUYANG Ziyuan, LI Chunlai. Research on Lunar Science and Exploration Technology in Lunar Explorer Project[M]. Beijing: Science Press, 2015. |
| [4] | 赵齐乐. GPS导航星座及低轨卫星的精密定轨理论和软件研究[D]. 武汉: 武汉大学, 2004. ZHAO Qile. Research on Precise Orbit Determination Theory and Software of GPS Navigation Constellation and LEO Satellite[D]. Wuhan:Wuhan University, 2004. |
| [5] | 魏子卿, 阮仁桂, 贾小林, 等. 卫星定位定轨系统SPODS:理论与测试[J]. 测绘学报, 2014, 43(1): 1–4. WEI Ziqing, RUAN Rengui, JIA Xiaolin, et al. Satellite Positioning and Orbit Determination System SPODS:Theory and Test[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 1–4. DOI:10.13485/j.cnki.11-2089.2014.0001 |
| [6] | 胡松杰, 唐歌实. 北京中心深空探测器精密定轨与分析软件系统[J]. 飞行器测控学报, 2010, 29(5): 69–74. HU Songjie, TANG Geshi. BACC Orbit Determination and Analysis Software for Deep-space Explorers[J]. Journal of Spacecraft TT & C Technology, 2010, 29(5): 69–74. |
| [7] | MOYER T D. Mathematical Formulation of the Double Precision Orbit Determination Program (DPODP)[R]. JPL-TR 32-1527. Pasadena, CA:Jet Propulsion Lab, 1971. |
| [8] | MOYER T D. Formulation for Observed and Computed Values of Deep Space Network Data Types for Navigation[M]. Hoboken: John Wiley & Sons, 2003. |
| [9] | EVANS S, TABER W, DRAIN T, et al. Monte:The Next Generation of Mission Design & Navigation Software[C]//Proceedings of the 6th International Conference on Astrodynamics Tools and Techniques (ICATT). Darmstadt, Germany:[s.n.], 2016. |
| [10] | PAVLIS D E, WIMERT J, MCCARTHY J J. GEODYN Ⅱ System Description[R]. Greenbelt, MD:SGT Inc, 2013:1-5. |
| [11] | MEYER U, CHARLOT P, BIANCALE R. GINS:A New Multi-technique Software for VLBI Analysis[C]//International VLBI Service for Geodesy and Astrometry 2000 General Meeting Proceedings.[S.l.]:NASA, 2000(1):324-328. |
| [12] | BUDNIK F, MACKENZIE R. Orbit Determination Software at ESOC Flight Dynamics[C]//MORE Relativity Meeting. Rome, Italy:[s.n.], 2009. |
| [13] | MACKENZIE R, BUDNIK F. Orbit Determination Software Design at ESOC[C]//MORE Relativity Meeting. Rome, Italy:[s.n.], 2009. |
| [14] | ANDERT T P. Masses of Small Bodies:Mass Estimation of Small Solar System Bodies Using Radio Science Data from Close Flybys[D]. Köln:Universität zu Köln, 2010. |
| [15] | ANDERT T P, ROSENBLATT P, PÄTZOLD M, et al. Precise Mass Determination and the Nature of Phobos[J]. Geophysical Research Letters, 2010, 37(9): L09202. |
| [16] | CICALÒ S, SCHETTINO G, DI RUZZA S, et al. The BepiColombo MORE Gravimetry and Rotation Experiments with the Orbit14 Software[J]. Monthly Notices of the Royal Astronomical Society, 2016, 457(2): 1507–1521. DOI:10.1093/mnras/stw052 |
| [17] | TOMMEI G, MILANI A, VOKROUHLICKY D. Light-time Computations for the BepiColombo Radio Science Experiment[J]. Celestial Mechanics and Dynamical Astronomy, 2010, 107(1-2): 285–298. DOI:10.1007/s10569-010-9273-7 |
| [18] | BERTONE S, ARNOLD D, JÄGGI A, et al. GRAIL Gravity Field Determination Using the Celestial Mechanics Approach-status Report[C]//AGU Fall Meeting Abstracts.[S.l.]:AGU, 2014. |
| [19] | ARNOLD D, BERTONE S, JÄGGI A, et al. GRAIL Gravity Field Determination Using the Celestial Mechanics Approach[J]. Icarus, 2015, 261: 182–192. DOI:10.1016/j.icarus.2015.08.015 |
| [20] | 曹建峰, 刘磊, 刘勇, 等. 嫦娥二号再拓展试验测定轨精度研究[J]. 飞行器测控学报, 2012, 31(4): 84–89. CAO Jianfeng, LIU Lei, LIU Yong, et al. Orbit Determination Analysis for CE-2 Second Extended Mission[J]. Journal of Spacecraft TT & C Technology, 2012, 31(4): 84–89. |
| [21] | 曹建峰, 张宇, 胡松杰, 等. 嫦娥三号着陆器精确定位与精度分析[J]. 武汉大学学报 (信息科学版), 2016, 41(2): 274–278. CAO Jianfeng, ZHANG Yu, HU Songjie, et al. An Analysis of Precise Positioning and Accuracy of the CE-3 Lunar Lander Soft Landing[J]. Geomatics and Information Science of Wuhan University, 2016, 41(2): 274–278. |
| [22] | 黄勇, 胡小工, 曹建峰, 等. 上海天文台火星卫星定轨软件系统[J]. 飞行器测控学报, 2009, 28(6): 83–89. HUANG Yong, HU Xiaogong, CAO Jianfeng, et al. The Mars Satellite Orbit Determination Software at Shanghai Astronomical Observatory[J]. Journal of Spacecraft TT & C Technology, 2009, 28(6): 83–89. |
| [23] | 黄勇, 昌胜骐, 李培佳, 等. "嫦娥三号"月球探测器的轨道确定和月面定位[J]. 科学通报, 2014, 59(23): 2268–2277. HUANG Yong, CHANG Shengqi, LI Peijia, et al. Orbit Determination of Chang'E-3 and Positioning of the Lander and the Rover[J]. Chinese Science Bulletin, 2014, 59(23): 2268–2277. |
| [24] | 李培佳. 我国月球探测工程中的定轨和定位[D]. 上海: 中国科学院上海天文台, 2013. LI Peijia. Researches on the Orbit Determination and Positioning of the Chinese Lunar Exploration Program[D]. Shanghai:Shanghai Astronomical Observatory, Chinese Academy of Sciences, 2013. |
| [25] | 李斐, 鄢建国. 月球重力场的确定及构建我国自主月球重力场模型的方案研究[J]. 武汉大学学报 (信息科学版), 2007, 32(1): 6–10. LI Fei, YAN Jianguo. Principle and Method of Lunar Gravity Field Determination and Project on Self-determinational Lunar Gravity Field[J]. Geomatics and Information Science of Wuhan University, 2007, 32(1): 6–10. |
| [26] | 李斐, 郝卫峰, 鄢建国, 等. 空间跟踪技术的发展对月球重力场模型的改进[J]. 地球物理学报, 2016, 59(4): 1249–1259. LI Fei, HAO Weifeng, YAN Jianguo, et al. Advancement of Lunar Gravity Model due to the Development of Space Tracking Techniques[J]. Chinese Journal of Geophysics, 2016, 59(4): 1249–1259. |
| [27] | 鄢建国, 李斐, 平劲松, 等. 利用LP多普勒数据解算月球重力场模型的分析[J]. 测绘学报, 2009, 38(1): 6–11. YAN Jianguo, LI Fei, PING Jinsong, et al. Lunar Gravity Field Recovery Based on LP Doppler Data[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 6–11. |
| [28] | 鄢建国, 李斐, 平劲松. 基于MGS测图段部分弧段的精密定轨及火星重力场模型解算[J]. 测绘学报, 2010, 39(5): 484–490. YAN Jianguo, LI Fei, PING Jinsong. Precision Orbit Determination of MGS Mapping Phase Arcs and Martian Gravity Field Model Solution[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 484–490. |
| [29] | 叶茂. 月球探测器精密定轨软件研制与四程中继跟踪测量模式研究[J]. 测绘学报, 2016, 45(9): 1132. YE Mao. Development of Lunar Spacecraft Precision Orbit Determination Software System and Research on a Four-way Relay Tracking Measurement Mode[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1132. DOI:10.11947/j.AGCS.2016.20160339 |
| [30] | LI Fei, YE Mao, YAN Jianguo, et al. A Simulation of the Four-way Lunar Lander-orbiter Tracking Mode for the Chang'E-5 Mission[J]. Advances in Space Research, 2016, 57(11): 2376–2384. DOI:10.1016/j.asr.2016.03.007 |
| [31] | YE Mao, YAN Jianguo, LI Fei, et al. Preliminary Results of LUGREAS and Its CVT with GEODYN-Ⅱ[C]//International Symposium on Lunar and Planetary Science. Wuhan:ISLPS, 2016. |
| [32] | BUDNIK F, MORLEY T A, MACKENZIE R A. ESOC's System for Interplanetary Orbit Determination:Implementation and Operational Experience[C]//Proceedings of the 18th International Symposium on Space Flight Dynamics. Munich, Germany:[s.n.], 2004, 548:387. |
| [33] | 叶茂, 肖驰, 李斐, 等. 三种关于引力位及其一、二阶导数计算方法的比较与分析研究[J]. 地球物理学进展, 2015, 30(6): 2581–2588. YE Mao, XIAO Chi, LI Fei, et al. Analysis and Comparison of Three Different Calculational Methods for Gravitational Potential and Its Derivatives[J]. Progress in Geophysics, 2015, 30(6): 2581–2588. |
| [34] | LEMOINE F G, GOOSSENS S, SABAKA T J, et al. High-degree Gravity Models from GRAIL Primary Mission Data[J]. Journal of Geophysical Research:Planets, 2013, 118(8): 1676–1698. DOI:10.1002/jgre.v118.8 |
| [35] | 叶茂, 李斐, 鄢建国, 等. GRAIL月球重力场模型定轨性能分析[J]. 武汉大学学报 (信息科学版), 2016, 41(1): 93–99. YE Mao, LI Fei, YAN Jianguo, et al. Orbit Determination Ability Analysis of the GRAIL Gravity Model[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 93–99. |
| [36] | ROSENBLATT P, LAINEY V, LE MAISTRE S, et al. Accurate Mars Express Orbits to Improve the Determination of the Mass and Ephemeris of the Martian Moons[J]. Planetary and Space Science, 2008, 56(7): 1043–1053. DOI:10.1016/j.pss.2008.02.004 |



