在全球导航卫星系统中,斜路径对流层延迟量约为2 m至20 m[1],是一个必须考虑的误差源[2],因此提高对流层延迟改正精度是多频多模GNSS精密定位的前提[3]。GNSS观测中信号路径的大气延迟量通常是由接收机的天顶对流层延迟 (zenith tropospheric delay,ZTD) 通过映射函数投影得到的[4],传统的Hopfield、Saastamoinen、Black等对流层延迟模型[5-7]计算时需要已知测站实测气象参数,改正精度可达厘米或分米级。文献[8]为美国广域增强导航系统 (WAAS) 的推广应用建立了UNB模型,其在北美区域的适用性较好[9]。EGNOS模型[10-12]是欧洲星基广域增强系统EGNOS采用的天顶对流层延迟改正模型[13]。文献[14]基于球谐函数建立了GZTD模型,之后对其模型进行改进,建立了GZTD-6 h模型,有效提高ZTD估值的时间分辨率[15]。但是随着对地观测网络的完善和观测数据的增加,对流层延迟改正从依赖简单封闭的数据模型向依赖大量外部数据的改正模型过渡[1],利用气象观测的数值预报资料也成为计算ZTD的一种有效手段[16]。如根据欧洲中尺度天气预报中心 (The European Center for Medium-Range Weather Forecasts,ECMWF) 提供的分析资料和美国国家环境预报中心 (The United States National Centers for Environmental Prediction,NCEP) 提供的再分析资料和预报资料等[17],文献[18]评估了亚洲地区ECMWF/NCEP资料计算ZTD的精度,研究结果表明该资料可用于高精度的ZTD研究和应用。IGS融合多个分析中心的结果发布了全球对流层天顶延迟产品,其精度可达4 mm,应用范围较广[19],但是无法实时发布。GGOS (Global Geodetic Observing System) Atmosphere项目中,维也纳科技大学基于ECMWF的数值气象资料并结合Marini[20]投影函数,发布了VMFG系列的全球对流层天顶延迟产品:VMFG、VMFG_FC[21]。文献[3]评估比较VMFG、UNBVMFG、VMFG_FC在中国范围内的计算精度、差异和适用性,并分析了各种产品对北斗导航应用的影响,各对流层产品在伪距单点定位和相对定位中相对于传统的Saastamoinen等经验改正模型能有效提高导航定位精度。不同国际机构发布了高精度的全球对流层天顶延迟产品,由于采用的数据源和计算方法不同,导致其应用精度和适用性不同[2],尽管全球对流层延迟产品在各自建模所用的数据源区域能取得良好的改正效果[9],但是至今对各种对流层产品在全球的精度及适用性方面的研究较少。
GGOS对流层产品全球覆盖,分布均匀,可提供实时对流层产品,空间分辨率高,且数据连续,但是时间分辨率仅仅为6 h,无法反映出ZTD的半日周期变化特征。更可靠的对流层延迟模型有助于改善空间大地测量技术的精度[1],因此研究GGOS-ZTD与IGS-ZTD之间的系统差,有利于确定对流层延迟多源数据模型建立时源数据的权比,根据系统差模型提高GGOS-ZTD产品的精度,增强其在导航定位等大地测量技术中的适用性。
本文对GGOS Atmosphere对流层数据资料在全球范围内的精度进行了系统评估,研究分析了GGOS Atmosphere对流层延迟产品与IGS发布ZTD资料之间的系统差,将经过系统差修正后的GGOS-ZTD产品应用到PPP中,取得了较好的结果。
1 不同对流层产品差异的时空特征分析 1.1 数据介绍本文的研究选取了2015年全年GGOS Atmosphere的全球对流层延迟产品,以及2015年发布的全球343个IGS测站的对流层延迟数据。
1.1.1 GGOS Atmosphere ZTD数据GGOS Atmosphere基于ECMWF的数据资料发展出对流层模型[22],用少量的系数为广大区域、时间和高度角范围内的GNSS用户提供更加直接的对流层产品用于延迟改正。这种方法有效减少了计算量并且能提供全球范围内的有效修正。GGOS Atmosphere提供的对流层延迟参数有ZHD、ZWD以及投影函数VMF1的系数,这些参数均是以空间分辨率为2.5°×2°(经度×纬度)、时间分辨率为6 h的全球格网形式提供。将格网点上的ZHD和ZWD相加即可得到天顶对流层延迟ZTD。
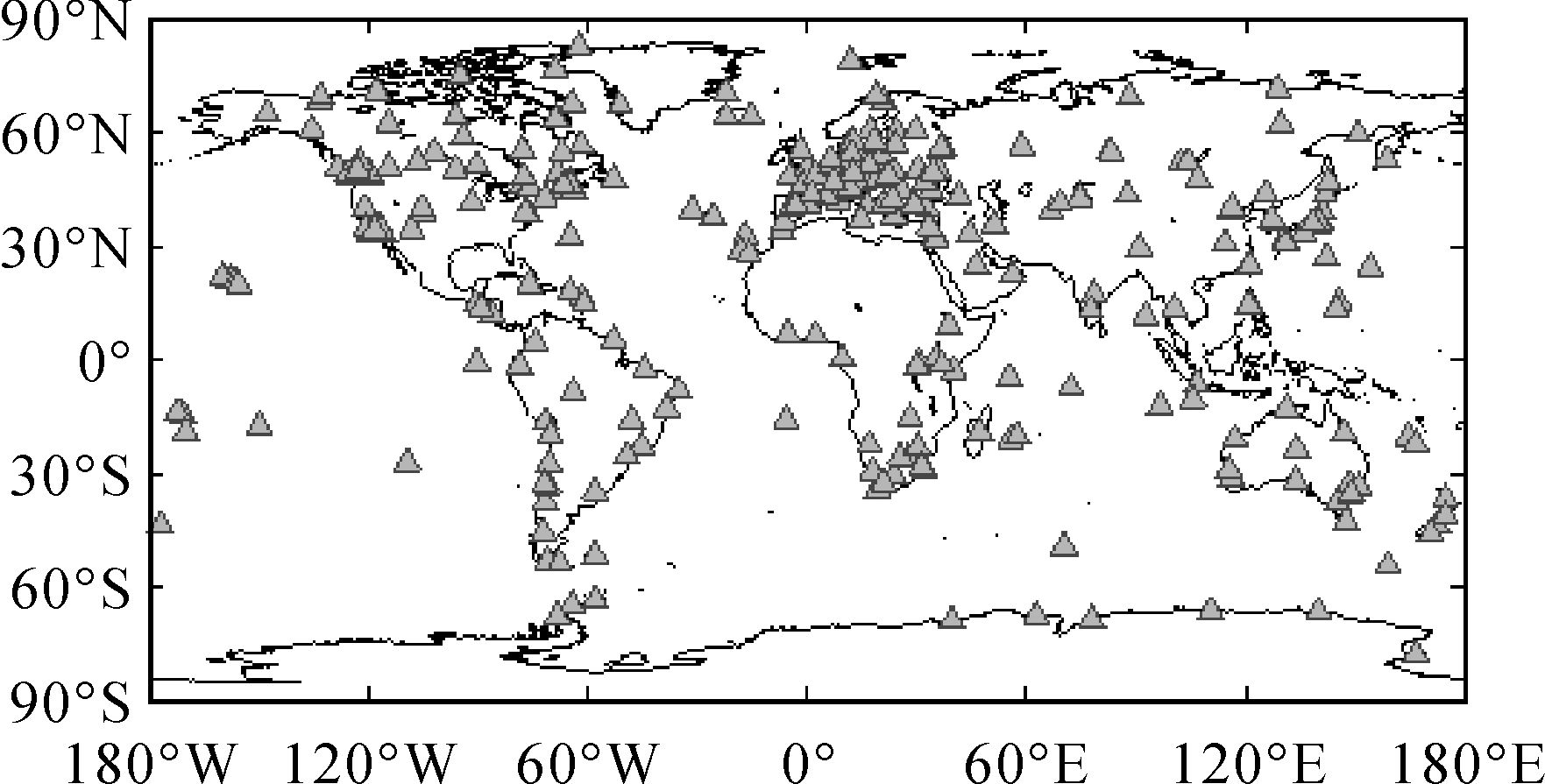
1.1.2 IGS站ZTD数据IGS产品包含全球各跟踪站的对流层天顶延迟。它是由全球的7个分析中心采用6套不同的软件,将天顶延迟作为待定参数,随观测资料一起估计,再通过加权平均算得的,IGS产品具有很高的精度[23]。其中,IGS发布的全球ZTD产品精度可达4 mm,可作为评估其他ZTD产品的标准。本文选取了全球343个IGS站的ZTD时间序列,各站点位置如图 1所示。表 1给出了两种ZTD产品在时间、空间分辨率和连续性的统计信息。
|
| 图 1 IGS站全球分布 Fig. 1 The distribution of stations |
| 数据源 | 时间分辨率 | 空间分辨率 | 连续性 |
| GGOS Atmosphere | 6 h | 经差2.5°、纬差2°,全球13 104个格网点 | 1979—2013年不间断 |
| IGS | 5 min | 全球现有约470个测站,分布不均,欧洲较为密集,海洋上较少 | 站点逐年增加,部分站点不连续,缺多天数据 |
1.1.3 数据预处理
对IGS测站时间序列进行粗差探测,对343个IGS测站ZTD数据进行预处理,如果ZTD日均值大于3 m或者标准差大于3.5 mm,则剔除当天数据,提高数据质量和可靠性。
1.2 分析方法由于GGOS产品的格网点与IGS测站位置不一致,为了将GGOS-ZTD日均值与IGS-ZTD日均值进行对比,先计算GGOS各个格网点的ZTD日均值,然后根据文献[14]得到的高度归算系数采用指数函数进行高度归算和双线性内插得出IGS测站位置的ZTD日均值,最后进行比较分析。
以全球343个IGS测站ZTD时间序列为标准参考值,与GGOS资料计算出来的IGS测站位置的ZTD进行比较,求其残差,计算各IGS测站上年平均bias和RMS及月平均bias和RMS,计算方法如下式 (1),统计结果见表 2,然后对其时空分布特性进行详细分析。
 (1)
(1)
| cm | ||||||
| bias | RMS | |||||
| mean | min | max | mean | min | max | |
| -0.54 | -3.60 | 3.18 | 1.31 | 0.45 | 3.60 | |
式中,ZTDiGGOS是GGOS对流层产品计算得到的该测站第i天的ZTD日均值;ZTDiIGS是IGS发布的该测站当天ZTD日均值;N表示参与统计的总天数。平均偏差bias衡量GGOS-ZTD与IGS-ZTD的平均偏离程度,均方根误差RMS衡量GGOS对流层产品相对于IGS-ZTD产品的精度。
1.3 bias和RMS在时空上的分布特点从表 2可以看出,相对于IGS-ZTD,GGOS-ZTD的bias和RMS平均值分别为-0.54 cm和1.31 cm。空间大地测量技术主要使用无线电信号进行距离测量,对流层延迟是许多空间大地测量技术的主要误差源,当前广域增强系统所用的对流层延迟模型精度为4 cm左右,本文参与统计的各测站GGOS-ZTD相对于IGS-ZTD的偏差和RMS均未超过4 cm,因此格网化的GGOS对流层产品足以满足广大GNSS导航定位用户对流层延迟改正的需要,在其他大地测量技术中的对流层延迟改正也具有广阔的应用前景,也可用于高精度ZTD研究和应用。
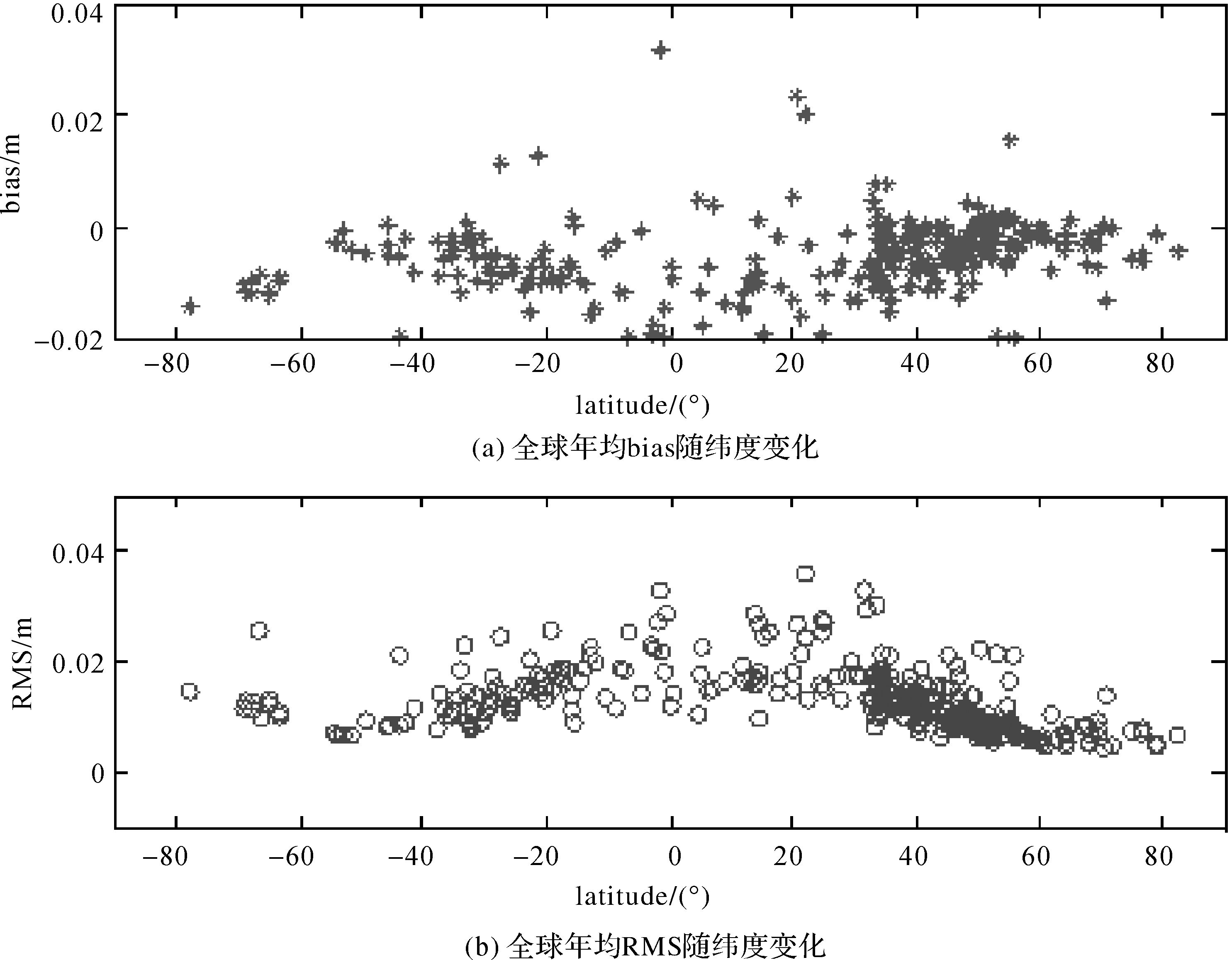
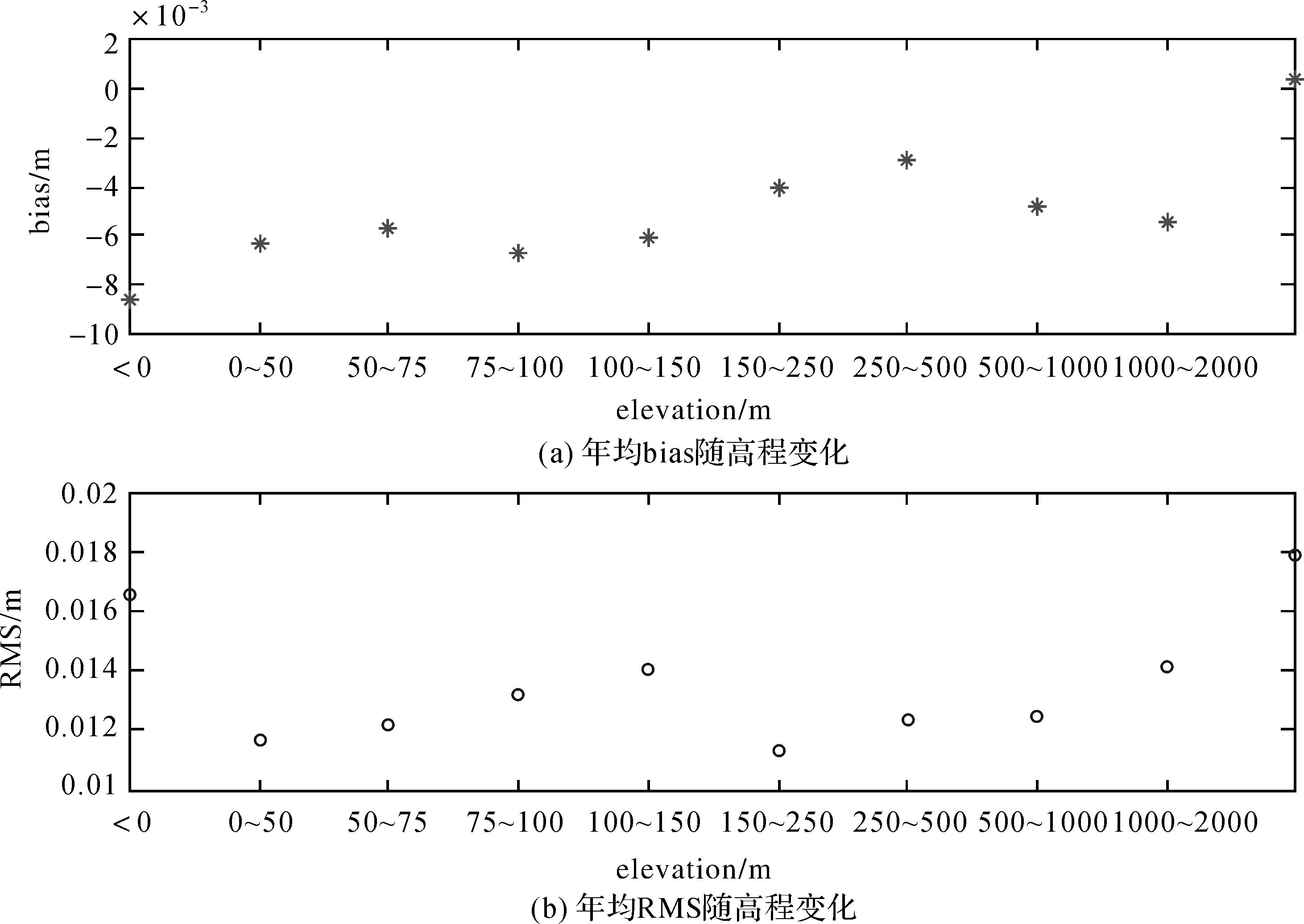
为分析GGOS-ZTD相对于IGS-ZTD的bias和RMS在季节上的变化特点,把343个IGS测站的bias和RMS按月进行统计,如图 2所示。由图 2可知,bias和RMS均有明显的季节效应。夏季气候复杂多变,夏季bias和RMS整体较冬季更大。全球范围内ZTD空间分布主要与纬度相关[14]。图 3给出了bias和RMS随纬度的变化情况。bias随纬度变化趋势不是很明显;RMS在南北半球呈现近似对称现象。图 4给出了bias和RMS随高度的分布特点。bias随高度增加呈现波浪形分布。RMS随高度的变化趋势较明显,随高度增加而增大。这是由于ZTD本身分布与高度有密切关系,同时高度归算系数的不精细所带来的影响随高度的增加而增加。

|
| 图 2 月平均bias和RMS变化情况 Fig. 2 The variation of monthly average bias and RMS |
|
| 图 3 年均bias和RMS随纬度变化图 Fig. 3 The variation with latitude of annual average bias and RMS |
|
| 图 4 年均bias和RMS在各个高度范围的变化趋势 Fig. 4 The variation of annual average bias and RMS in each sectional elevation |
2 GGOS-ZTD产品与IGS-ZTD产品的系统差确定
下面对GGOS Atmosphere对流层延迟产品与IGS估计的ZTD之间的系统差进行建模,更进一步分析GGOS Atmosphere对流层延迟产品的精度,为建立多源对流层延迟模型过程中GGOS-ZTD与其他对流层延迟产品的融合提供参考依据。
2.1 线性拟合设每个IGS测站观测的ZTD数值为Y,用GGOS Atmosphere资料内插计算出的该位置ZTD值为X,根据公式Y=aX+b对每个测站2015年一年的数据进行线性拟合,解算出343个测站的拟合系数,包括比例误差a、固定误差b。通过F检验,系数显著,说明两种数据源存在一定的区分度,两者之间存在显著的系统差,需要进一步估算。
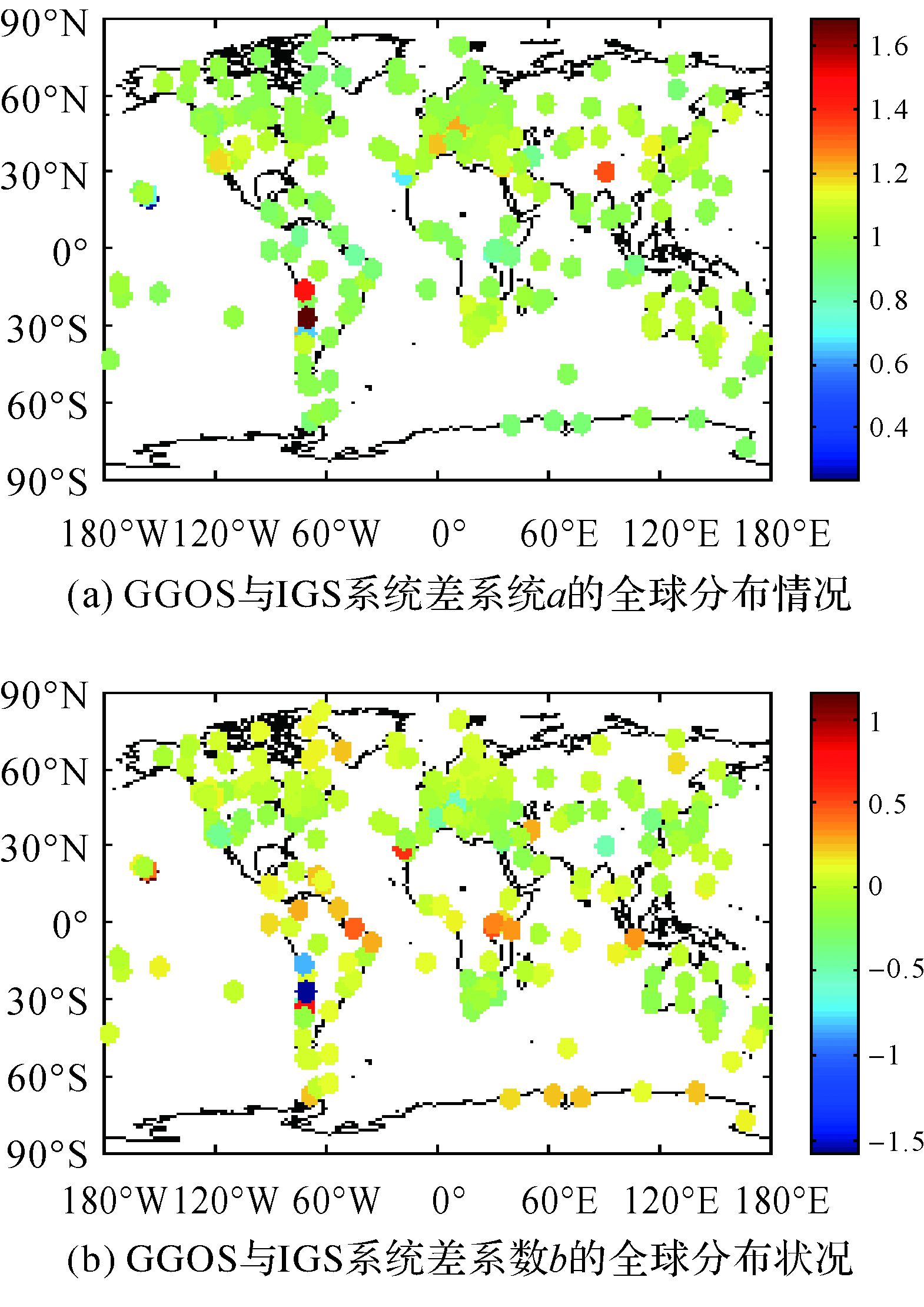
2.2 系统差系数 (比例误差及固定误差) 的分布特征图 5给出了系统差系数a、b的全球分布情况。从图中可以看出,赤道附近a值基本小于1,高纬度地区a的变化不大,基本都在1左右,中纬度地区a的差异比较明显。两个显著大于1的地方可能与测站高程有关。海洋及海陆交界处特别是南美洲西岸、喜马拉雅地区, a值异常高于1或低于1。这些地区ZTD变化存在不规则的扰动,其来源可能与较复杂的地形以及活跃的气候变化有关,具体的原因需要进一步研究。系数b的分布现象与a对应。
|
| 图 5 GGOS与IGS系统差系数a、b的全球分布状况 Fig. 5 The global distribution of systematic difference coefficient a and b between GGOS and IGS |
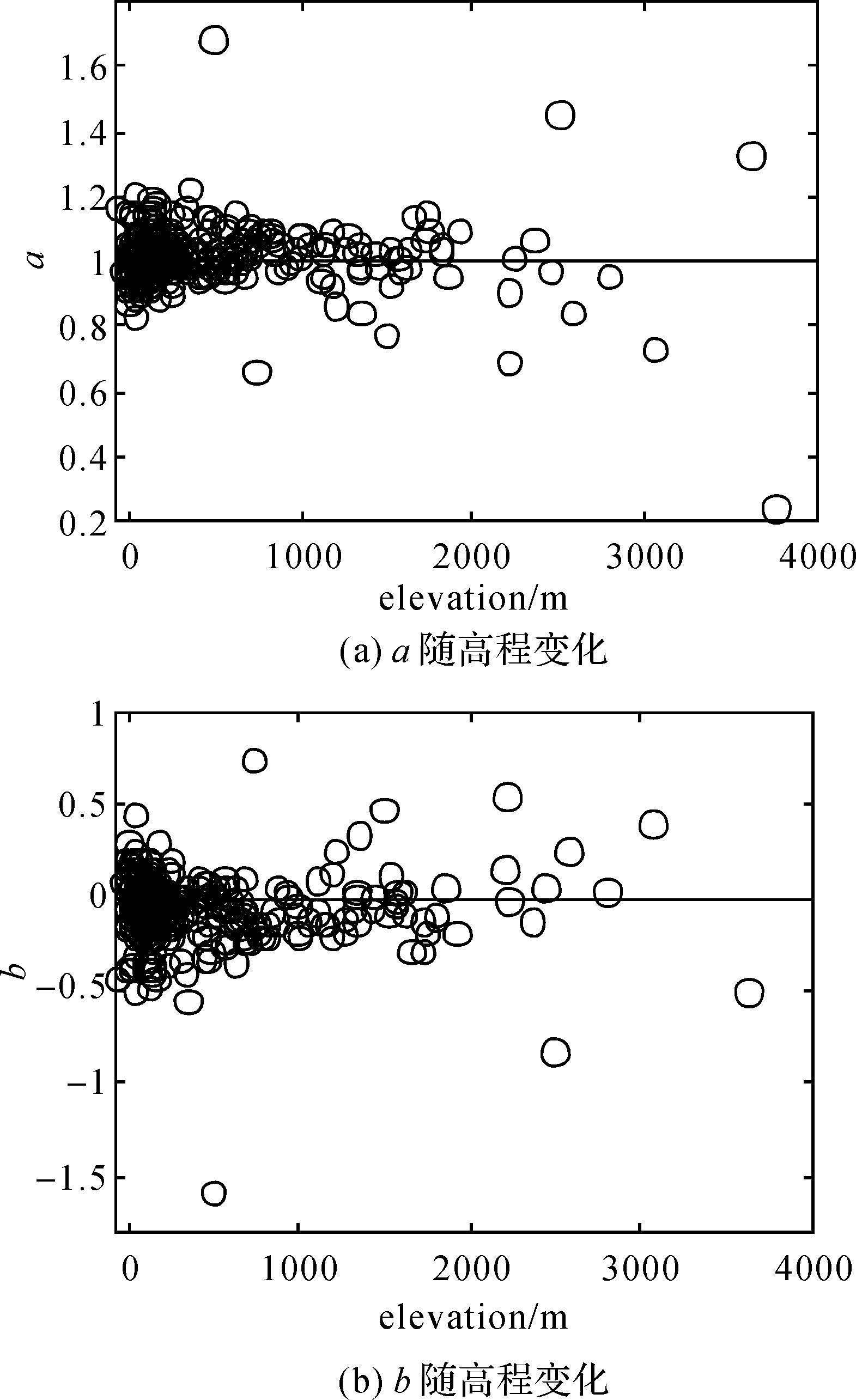
ZTD的大小与高度的变化有关,为分析系统差系数a在高度上的分布特点,图 6给出了a值、b值随高度的变化。由图知, a值、b值2000 m以下随机分布,2000 m以上测站较少异常值较多,整体上随高程变化没有规律性特征。
|
| 图 6 系统差系数a、b的高度分布 Fig. 6 The distribution with elevation of a and b |
2.3 系统差系数 (比例误差a、固定误差b) 的球谐拟合
文献[21]首次使用9阶9次球谐函数建立全球地表温度和气压经验模型 (GPT模型),取得良好效果。文献[24]采用球谐函数方法对全球大气加权平均温度进行建模 (GWMT模型),在减少模型参数数量的同时达到了GNSS气象学中反演水汽的精度要求。这说明球谐函数在表征球面物理参量方面具有极大的优势和应用前景[24]。本文采用类似的思想建立球谐函数模型,根据式 (2) 把系统差系数a、b展开成位置的函数。
 (2)
(2)
式中,Pnm为勒让德多项式:ψ和λ分别为纬度和经度。
对于全球343个测站位置处的GGOS-ZTD相对于IGS-ZTD的系统差系数a、b,为了达到精度要求又不过多引入参数,用11阶11次球谐函数对a、b系数进行位置 (经度λ,纬度θ) 拟合,通过线性回归方法求解系数Anm、Bnm,即可计算全球任意位置GGOS-ZTD与IGS-ZTD之间的系统差系数a、b,并运用于GGOS对流层延迟改正的系统差消除。
利用球谐函数反算IGS 343个测站的系统差系数a、b,与每个测站线性拟合得到的a、b对比,统计两者bias和RMS,结果见表 3。
| 系数 | bias | RMS | ||
| mean | max | min | ||
| A | 0.000 0 | 0.158 6 | -0.164 6 | 0.034 2 |
| B | 0.000 0 | 0.388 9 | -0.335 1 | 0.076 8 |
由表 3可知,球谐模型计算的各测站系统差系数与拟合得到系统差系数符合度很好,平均bias可忽略不计,比例误差和固定误差的RMS分别为0.034 2和0.076 8,说明所建立的11阶系统差球谐模型精度非常高,可用于全球系统差改正。
3 GGOS Atmosphere对流层延迟产品的PPP应用效果PPP是实现全球精密实时动态定位与导航的关键技术,也是GNSS定位方面的前沿研究方向[25]。将对流层延迟模型产品用于PPP定位,是当前的一个研究热点。本文尝试将结合系统误差修正后的GGOS Atmosphere对流层延迟产品用于PPP定位,并检验其效果。
采用GGOS对流层产品计算得到试验台站 (选择IGS测站ALBH站、DEAR站、ISPA站、PALM站、ADIS站、WUHN站、陆态网测站YNMH) 位置未经系统差修正的ZTD和系统差修正后的ZTD,在传统PPP中,在每个测站试验时段引入天顶对流层延迟参数GGOS-ZTD作为初始近似值,在获取其与IGS-ZTD的RMS前提下,运用RMS进行外部约束,观测方程和约束方程如式 (3)、式 (4),通过平差计算来估计其精确值,以进行精密单点定位,并与采用Saastamoinen模型对流层延迟的定位结果进行比较,分析GGOS对流层延迟产品的应用效果。
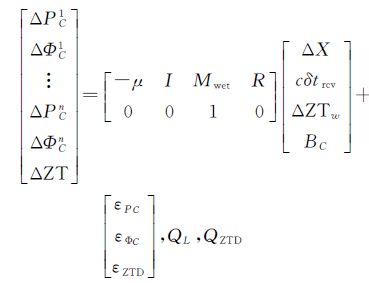 (3)
(3)
 (4)
(4)
式中,ZTrvir表示ZTD的虚拟观测值; εZTD是相应的噪声;QZTD是ZTrvir的随机模型。
3.1 对流层延迟改正计算选取分布于全球不同半球及不同纬度的IGS测站ALBH站、DEAR站、ISPA站、PALM站、ADIS站及陆态网测站YNMH站 (2015年Doy1、90、180、270) 和WUHN站 (2015年DOY3(晴)、90(晴)、121(雨)、146(雨)),分别计算各个测站周围4个格网点当天的GGOS天顶对流层延迟日均值,运用指数函数高度归算和双线性内插,将格网点ZTD归算到测站位置处;再运用前述的系统差球谐模型计算3个测站的系统差系数a、b,对ZTD进行系统差改正,分别用Saastamoinen模型 (策略1)、附加系统差修正的GGOS-ZTD (策略2) 和未经系统差修正的GGOS-ZTD (策略3) 对4个测站数据进行对流层延迟改正和精密单点定位。
3.2 精密单点定位结果分析进行精密单点定位结果分析,将收敛条件设为:连续30个历元各方向误差小于10 cm,以此比较不同对流层延迟处理策略的收敛速度。
表 4、表 5为ALBH测站、DEAR测站、ISPA测站、PALM测站、ADIS测站、YNMH测站、WUHN测站3种对流层延迟处理策略定位U方向收敛时间。由于U方向通常收敛时间最慢,因此此处仅分析各站各天U方向收敛效果。ALBH测站、DEAR测站、ISPA站、PALM站、ADIS站、YNMH站系统差模型对ZTD分别平均修正0.67 cm和1.64 cm、0.86 cm、1.87 cm、0.33 cm、7.12 cm。未经系统差修正的GGOS-ZTD定位收敛速度比附加系统差修正GGOS-ZTD约束一般定位慢,部分天数收敛速度较Saastamoinen模型更差,这与GGOS-ZTD取日均值偏离0:00时刻真实值有关,而加附加系统差修正GGOS-ZTD约束定位收敛速度与Saastamoinen模型相比, U方向收敛速度分别提高10.58%和31.68%、15.96%、43.89%、51.46%、14.69%。本文试验验证附加系统差改正的GGOS对流层产品在全球不同地区进行GNSS定位的可用性。
| Doy | 策略 | ALBH-收敛 时间 | 收敛速度 提升量/(%) | DEAR-收敛 时间 | 收敛速度 提升量/(%) | ISPA-收敛 时间 | 收敛速度 提升量/(%) | PALM-收敛 时间 | 收敛速度 提升量/(%) |
| 1 | 1 | 00:15:30 | — | 00:20:00 | — | 00:40:00 | — | 00:14:00 | — |
| 2 | 00:15:30 | 0 | 00:15:30 | 22.50 | 01:05:00 | -62.50 | 00:11:30 | 17.86 | |
| 3 | 00:15:00 | 3.22 | 01:00:00 | -200 | 00:55:00 | -37.50 | 00:05:30 | 60.71 | |
| 90 | 1 | 01:26:00 | — | 00:29:30 | — | 00:30:00 | — | 00:20:00 | — |
| 2 | 01:29:30 | -4.07 | 00:20:00 | 32.20 | 00:19:00 | 36.67 | 00:05:00 | 75.00 | |
| 3 | 01:44:30 | -21.51 | 00:10:30 | 66.10 | 00:25:00 | 16.67 | 00:20:30 | -2.50 | |
| 180 | 1 | 00:25:30 | — | 00:50:00 | — | 01:14:30 | — | 00:06:00 | — |
| 2 | 00:14:30 | 43.14 | 00:29:30 | 41 | 00:35:00 | 53.02 | 00:05:30 | 8.33 | |
| 3 | 00:35:00 | -37.25 | 00:50:00 | 0 | 00:40:00 | 46.31 | 00:13:00 | -116.67 | |
| 270 | 1 | 00:15:30 | — | 00:29:00 | — | 00:30:00 | — | 00:19:30 | — |
| 2 | 00:15:00 | 3.23 | 00:20:00 | 31.03 | 00:19:00 | 36.67 | 00:05:00 | 74.36 | |
| 3 | 00:15:00 | 3.23 | 00:20:30 | 29.31 | 00:18:00 | 40.00 | 00:09:00 | 53.85 |
由表 5知WUHN测站3种对流层延迟处理策略U方向收敛时间。系统差模型对ZTD平均修正1.01 cm,未经系统差修正的GGOS-ZTD相较于Saastamoinen模型整体收敛速度平均提高10.65%,加附加系统差修正的GGOS-ZTD约束定位收敛速度与Saastamoinen模型相比,在晴天即使收敛时间相对稍慢,但是整体偏差曲线波动趋势较小,更接近0,解算结果更加稳定;下雨天U方向收敛效果明显优于Saastamoinen模型,整体收敛速度平均提高18.40%。由于在降雨等复杂天气状况时,利用Saastamoinen等经典模型很难细致的刻画对流层延迟,但GGOS对流层产品融合了各种观测数据,计算的对流层延迟更精准。本文试验同时也验证附加系统差改正的GGOS对流层产品在不同天气情况下进行GNSS定位的可用性。
| Doy | 策略 | ADIS-收敛 时间 | 收敛速度 提升量/(%) | YNMH-收敛 时间 | 收敛速度 提升量/(%) | WUHN-收敛 时间 | 收敛速度 提升量/(%) |
| 3 | 1 | 06:30:00 | — | 00:18:00 | — | 00:13:30 | — |
| 2 | 06:09:00 | 36.67 | 00:14:00 | 22.22 | 00:15:30 | -14.81 | |
| 3 | 06:09:00 | 36.67 | 00:14:00 | 22.22 | 00:15:00 | -11.11 | |
| 90 | 1 | 00:50:00 | — | 00:15:30 | — | 00:16:30 | — |
| 2 | 00:10:00 | 80.00 | 00:15:30 | 0 | 00:21:00 | -27.27 | |
| 3 | 00:10:00 | 80.00 | 00:16:00 | -3.2 | 00:23:00 | -39.39 | |
| 121 | 1 | 00:26:00 | — | 00:25:00 | — | 00:23:00 | — |
| 2 | 00:15:00 | 34.62 | 00:15:00 | 40 | 00:10:00 | 56.52 | |
| 3 | 00:20:00 | 23.08 | 00:30:00 | -20 | 00:16:00 | 30.43 | |
| 146 | 1 | 00:33:00 | — | 00:14:30 | — | 01:11:00 | — |
| 2 | 00:15:00 | 54.55 | 00:15:00 | -3.45 | 00:29:00 | 59.15 | |
| 3 | 00:14:00 | 57.58 | 00:11:00 | 24.13 | 00:26:30 | 62.68 |
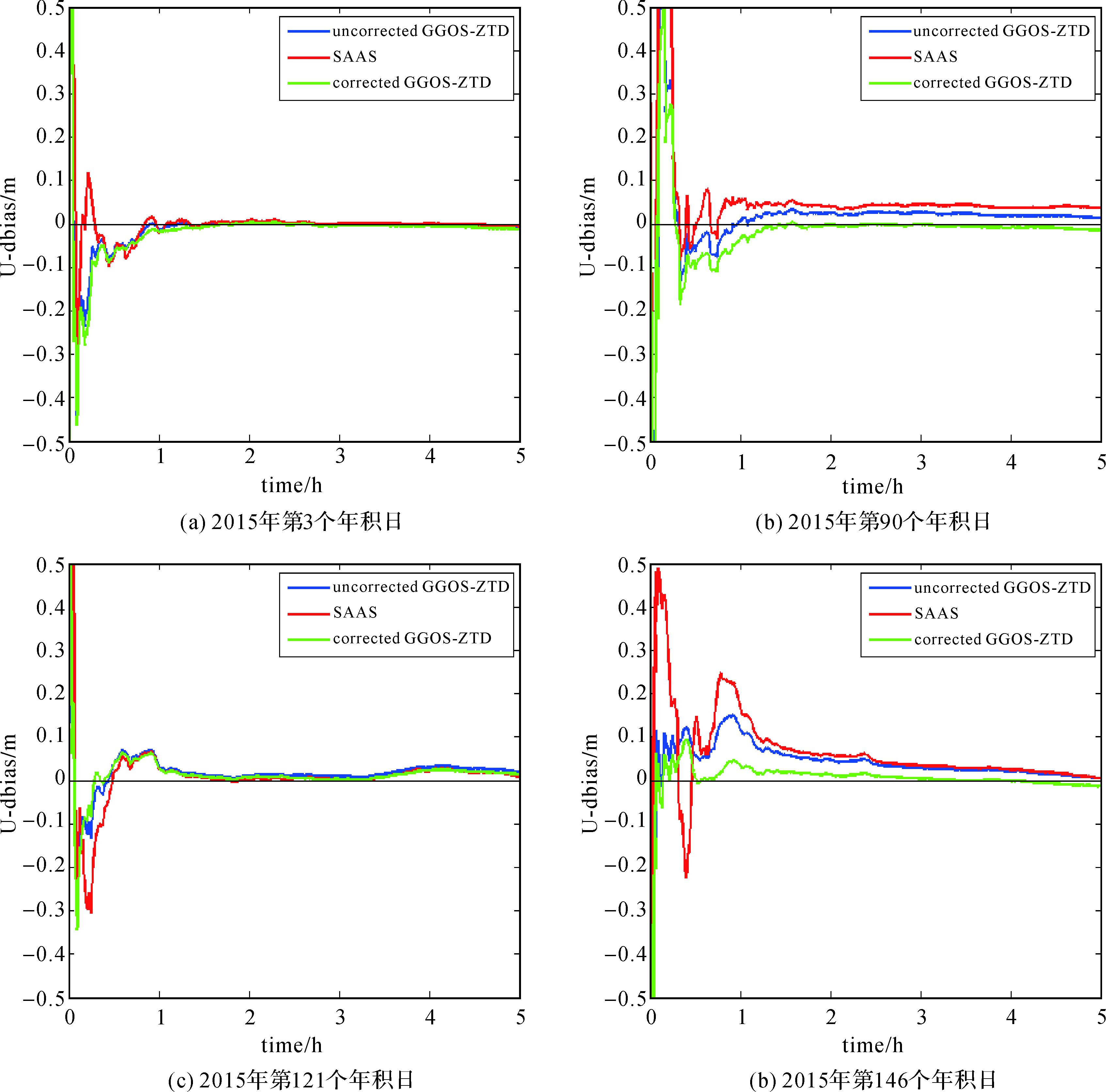
图 7给出了WUHN测站2015年第3、90、121、146个年积日通过3种对流层延迟处理方法U方向进行精密单点定位得到的坐标结果。
|
| 图 7 WUHN站3种对流层延迟处理策略DOY3、DOY90、DOY121、DOY146定位精度对比 Fig. 7 The comparison of positioning precision between three ZTD processing strategies at WUHN site in DOY3, DOY90, DOY121 and DOY146 |
4 结论
本文以分布于全球的343个IGS测站2015年全年发布的ZTD资料为基准,分析评估了GGOS Atmosphere基于ECMWF的数据资料发展出的对流层产品的精度,分析了bias和RMS的时空分布特点,对GGOS Atmosphere对流层延迟产品与IGS-ZTD资料之间的系统差进行建模,对其应用于GNSS导航定位的效果进行了评估。结论如下:
(1) 相对于IGS发布的ZTD资料,GGOS Atmosphere计算的ZTD的bias和RMS平均值分别为-0.54 cm和1.31 cm,说明GGOS Atmosphere的ZTD产品足以满足广大GNSS实时导航定位用户对流层延迟改正的需要,在空间大地测量技术中的对流层延迟改正方面有广阔应用前景。
(2) 分析了GGOS-ZTD相对于IGS-ZTD的bias和RMS的季节性变化特征,发现它们的月均值呈现明显的季节性变化,总体上呈现夏季大,冬季小。受海洋气候和夏季气候影响,夏季GGOS-ZTD产品误差相对较大。
(3) GGOS-ZTD相对于IGS-ZTD的bias在空间分布上随着纬度的变化不明显,但RMS在高纬度地区和赤道附近相对较小,中低纬度地区值相对较大;bias随高度的增加有先增大后减小的趋势,RMS随高度变化趋势不明显。
(4) GGOS与IGS的ZTD数据存在一定的区分度。对系统差系数a、b进行球谐拟合,通过全球IGS测站检验,模型内符合精度较高。
(5) 系统差系数a、b的地理分布特征明显,赤道地区和高纬度地区的变化不大,基本分别在1和0左右;中纬度地区和海陆交界处的差异比较明显。a、b随高程变化没有明显特征。
(6) GGOS对流层延迟产品运用于GNSS定位的效果良好。精密单点定位中使用附加系统差修正的GGOS-ZTD产品相对未经系统差修正的GGOS-ZTD产品及传统Saastamoinen模型的定位结果更精准、更稳定,且大多数情况收敛速度更快,对U方向收敛速度的改进尤其明显。
本文评估GGOS对流层延迟产品的精度并建立系统差模型,可用于大地测量中导航定位等应用,由于解算站数和时间跨度的限制,PPP应用结果可能不太稳定,更精确的RMS确定和更全面的定位应用如广域增强、SLR、VLBI等应用研究是下一步的研究工作。
| [1] | 殷海涛, 黄丁发, 熊永良, 等. GPS信号对流层延迟改正新模型研究[J]. 武汉大学学报 (信息科学版), 2007, 32(5): 454–457. YIN Haitao, HUANG Dingfa, XIONG Yongliang, et al. New Model for Tropospheric Delay Estimation of GPS Signal[J]. Geomatics and Information Science of Wuhan University, 2007, 32(5): 454–457. |
| [2] | 陈瑞琼, 刘娅, 李孝辉. 卫星导航系统中对流层改正模型分析[J]. 测绘通报, 2015(3): 12–15. CHEN Ruiqiong, LIU Ya, LI Xiaohui. Analysis of Tropospheric Correction Models in Navigation Satellite System[J]. Bulletin of Surveying and Mapping, 2015(3): 12–15. DOI:10.13474/j.cnki.11-2246.2015.0064 |
| [3] | 王苗苗, 李博峰, 沈云中, 等. 全球对流层延迟产品评估及其在北斗导航中应用[C]//第五届中国卫星导航学术年会论文集. 南京: 中国卫星导航系统管理办公室学术交流中心, 2014. WANG Miaomiao, LI Bofeng, SHEN Yunzhong, et al. Assessment of Global Troposphere Delay Products and ItsApplication to BeiDou Navigation[C]//China Satellite Navigation Conference, CSNC. Nanjing:China Satellite Navigation System Management Office Academic Exchange Center, 2014. |
| [4] | MENDES V B. Modeling the Neutral-atmosphere Propagation Delay in Radiometric Space Techniques[D]. Brunswick:University of New Brunswick, 1999. |
| [5] | HOPFIELD H S. Two-quartic Tropospheric Refractivity Profile for Correcting Satellite Data[J]. Journal of Geophysical Research, 1969, 74(18): 4487–4499. DOI:10.1029/JC074i018p04487 |
| [6] | SAASTAMOINEN J. Contributions to the Theory of Atmospheric Refraction[J]. Bulletin Géodésique (1946-1975), 1972, 105(1): 279–298. DOI:10.1007/BF02521844 |
| [7] | BLACK H D. An Easily Implemented Algorithm for the Tropospheric Range Correction[J]. Journal of Geophysical Research, 1978, 83(B4): 1825–1828. DOI:10.1029/JB083iB04p01825 |
| [8] | COLLINS J P, LANGLEY R B. A Tropospheric Delay Model for the User of the Wide Area Augmentation System[R]. Final Contract Report for Nav Canada, Department of Geodesy and Geomatics Engineering Technical Report No. 187. Fredericton, NB:University of New Brunswick, 1997. |
| [9] | 李博峰, 王苗苗, 沈云中, 等. 不同全球对流层天顶延迟产品在中国区域的比较[J]. 同济大学学报 (自然科学版), 2014, 42(8): 1267–1272. LI Bofeng, WANG Miaomiao, SHEN Yunzhong, et al. Comparison of Different Global Troposphere Zenith Path Delay Products in China[J]. Journal of Tongji University (Nature Science), 2014, 42(8): 1267–1272. |
| [10] | DODSON A H, CHEN Wu, BAKER H C, et al. Assessment of EGNOS Tropospheric Correction Model[C]//Proceedings of the 12th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1999). Nashville, TN:[s.n.], 1999:1401-1408. |
| [11] | PENNA N, DODSON A, CHEN Wu. Assessment of EGNOS Tropospheric Correction Model[J]. The Journal of Navigation, 2001, 54(1): 37–55. DOI:10.1017/S0373463300001107 |
| [12] | UENO M, HOSHINOO K, MATSUNAGA K, et al. Assessment of Atmospheric Delay Correction Models for the Japanese MSAS[C]//Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2001). Salt Lake City, UT:[s.n.], 2001:2341-2350. |
| [13] | MOPS W. Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment[R]. Documentation No. RTCA DO-229B. Washington, DC:RTCA Ine, 1999:6. |
| [14] | 姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218–2227. YAO Yibin, HE Changyong, ZHANG Bao, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2218–2227. |
| [15] | 姚宜斌, 胡羽丰, 余琛. 一种改进的全球对流层天顶延迟模型[J]. 测绘学报, 2015, 44(3): 242–249. YAO Yibin, HU Yufeng, YU Chen. An Improved Global Zenith Tropospheric Delay Model[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 242–249. DOI:10.11947/j.AGCS.2015.20140089 |
| [16] | EMARDSON T R, ELGERED G, JOHANSSON J M. Three Months of Continuous Monitoring of Atmospheric Water Vapor with a Network of Global Positioning System Receivers[J]. Journal of Geophysical Research, 1998, 103(D2): 1807–1820. DOI:10.1029/97JD03015 |
| [17] | BROMWICH D H, WANG S H. Evaluation of the NCEP-NCAR and ECMWF 15-and 40-yr Reanalyses Using Rawinsonde Data from Two Independent Arctic Field Experiments[J]. Monthly Weather Review, 2005, 133(12): 3562–3578. DOI:10.1175/MWR3043.1 |
| [18] | 陈钦明, 宋淑丽, 朱文耀. 亚洲地区ECMWF/NCEP资料计算ZTD的精度分析[J]. 地球物理学报, 2012, 55(5): 1541–1548. CHEN Qinming, SONG Shuli, ZHU Wenyao. An Analysis of the Accuracy of Zenith Tropospheric Delay Calculated from ECMWF/NCEP Data over Asian Area[J]. Chinese Journal of Geophysics, 2012, 55(5): 1541–1548. |
| [19] | BYUN S H, BAR-SEVER Y E. A New Type of Troposphere Zenith Path Delay Product of the International GNSS Service[J]. Journal of Geodesy, 2009, 83(3-4): 1–7. DOI:10.1007/s00190-008-0288-8 |
| [20] | MARINI J W. Correction of Satellite Tracking Data for an Arbitrary Tropospheric Profile[J]. Radio Science, 1972, 7(2): 223–231. DOI:10.1029/RS007i002p00223 |
| [21] | BOEHM J, HEINKELMANN R, SCHUH H. Short Note:A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679–683. DOI:10.1007/s00190-007-0135-3 |
| [22] | BÖHM J, SCHUH H. Atmospheric Effects in Space Geodesy[M]. Berlin: Springer, 2013. |
| [23] | 史先领. 利用IGS产品推算对流层延迟湿分量[J]. 北京测绘, 2009(3): 6–9. SHI Xianling. Calculating Wet Component of Tropospheric Propagation Delay Using IGS Products[J]. Beijing Surveying and Mapping, 2009(3): 6–9. |
| [24] | YAO Yibin, ZHU Shuang, YUE Shunqiang. A Globally Applicable, Season-specific Model for Estimating the Weighted Mean Temperature of the Atmosphere[J]. Journal of Geodesy, 2012, 86(12): 1125–1135. DOI:10.1007/s00190-012-0568-1 |
| [25] | 李征航, 黄劲松. GPS测量与数据处理[M]. 2版.武汉: 武汉大学出版社, 2010. LI Zhenghang, HUANG Jinsong. GPS Surveying and Data Processing[M]. 2nd ed. Wuhan: Wuhan University Press, 2010. |


