在影像匹配过程中,经常会存在一些误匹配点对,这时可以通过匹配提纯的方法对误匹配点对进行剔除。一般的提纯思路是寻找一个恰当的匹配点对约束模型,估计出正确的模型参数,利用约束模型进行匹配点对提纯。在匹配点对约束模型中,通常使用变换约束矩阵作为估计模型,其一般包括平移变换、刚体变换、相似性变换、仿射变换、射影变换、极线几何基本矩阵变换等。现行的变换约束矩阵模型已经能够很好地进行匹配点对间的几何约束,因此大多数学者更加倾向于模型参数估计方法的研究。
在模型参数估计中,常用的方法有稳健回归估计和随机参数估计等。对于稳健回归估计方法,如M-估计[1-2],其核心思想是采用迭代加权最小二乘估计回归系数,但其仅能适应误匹配率较小的情况。对于随机参数估计方法,如LMedS(least median of squares)算法[3-4]、MLESAC(maximum likelihood estimation sample and consensus)算法[5]和RANSAC(random sample consensus)算法[6]等,其核心思想是随机选择样本子集,迭代挑选出最佳模型参数。其中,RANSAC算法能够在存在大量外点的数据中找到内点,因而得到广泛应用并派生出一系列改进算法[7-9]。改进的RANSAC方法主要从两个方面进行了优化。一方面是速度优化,如P-RANSAC(preemptive RANSAC)[10-11]和R-RANSAC(randomized RANSAC)[12-13]等;一方面是提纯率的优化,如M-RANSAC(multi RANSAC)[7]等。然而这些算法都需要选择一个合适的初始内点集,提纯结果容易陷入局部最优解,造成部分正确匹配点对遗漏;在误匹配率增大时,成功选择内点集的试验次数也急剧增大。除了以上的约束模型及参数估计方法,近期也有一些其他的研究成果[14-17]。文献[14]提出通过统计模板的旋转角度直方图来剔除误匹配,但其依赖角度区间的划分,仅适用于对精度要求不高的情况;文献[15]提出一致性函数(correspondence function)模型,通过学习匹配点对一致性函数来拒绝误匹配;文献[17]提出通过Hough变换求解模型参数来进行匹配点对提纯,然而仅适用于模型参数较少的情况。由此,在匹配点对约束模型选定的情况下,本文对如何求解模型参数整体最优解,实现稳健匹配点对提纯的问题进行了研究。
主成分分析(principal components analysis,PCA)[18-20]是一种有效的多元统计方法,在信号处理、统计学等领域有重要应用。类似于信号处理过程中利用主成分分析方法进行噪声去除,可将主成分分析思想引入匹配点对提纯的过程,逐步剔除噪声点,实现匹配点对的提纯。为了方便阐述与试验,文中以奇异值分解作为主成分分析的具体实现方法,并以此为基础对提纯方法进行了推导与论述。奇异值分解[21-22](singular value decomposition,SVD)是矩阵分析中正规矩阵酉对角化的推广,是一种重要的主成分分析实现方法,能够进行并行化计算[23-24],可用于最小二乘求解[25-26],已被广泛应用于各个领域。
本文分析了奇异值分解中奇异值的对应含义,并将其引用到匹配点对提纯过程中。首先,用特定模型来描述匹配点对之间的变换关系,建立模型误差方程;其次,对含有匹配点对信息的系数矩阵进行奇异值分解,重构大奇异值对应的矩阵,得到差分矩阵;然后,剔除可能的误匹配点对,构造降阶矩阵,进行模型求解;最后,利用求解的模型参数,进行匹配点对约束,达到匹配点对提纯的目的。
1 匹配点对提纯模型与算法 1.1 主成分分析与奇异值分解模型经典的主成分分析算法通过计算输入数据的协方差矩阵及其特征向量来实现数据主成分的提取。当数据规模较大时,这一途径的计算代价非常昂贵。而奇异值分解与主成分分析都是特征正交分解(proper orthogonal decomposition,POD),具有等价性[27],在实际应用中处理效果相似[28]。奇异值分解无需计算协方差矩阵,无需进行均值化处理,计算量少,能避免计算协方差矩阵的舍入误差,相对误差较小,因此计算主成分最优的方法是使用奇异值分解[29]。
定义一个秩为r的m×n维矩阵A,则A的奇异值分解形式为
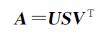 (1)
(1)
式中,U为m×m维正交矩阵;V为n×n维正交矩阵,S为m×n维对角阵。U的列向量ui称为矩阵A的左奇异向量;V的列向量vi称为矩阵A的右奇异向量;S的对角线元素σi称为矩阵A的奇异值,且以递减顺序排列,即σ1≥σ2≥…≥σr。
由矩阵A的前t个奇异值重新组成对角阵St×t=diag[σ1,σ2,…,σt],由奇异值对应的左、右奇异向量重新组成矩阵Um×t=[u1,u2,…,ut]和Vt×n=[v1,v2,…,vt],利用式(1)可重构矩阵A,得到
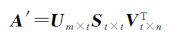 (2)
(2)
对式(2)进行化简可得
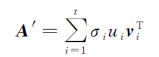 (3)
(3)
A′为A的近似矩阵,由矩阵A的主奇异值重构而成,包含了矩阵A的主要信息。两矩阵间的差分矩阵ΔA为
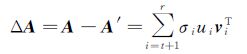 (4)
(4)
可以发现,A与A′间仅相差小奇异值对应的部分。研究表明,大的奇异值对应的重构矩阵A′包含更多的主要信息,小的奇异值对应的差分矩阵ΔA包含更多的噪声信息[30-32]。基于这种思想,ΔA则反映了矩阵A中噪声信息的大体分布情况。因此,可依据差分矩阵ΔA进行矩阵A中的噪声剔除,得到更为合理的降阶矩阵B,这也是本文主成分分析思想研究的关键。
1.2 主成分分析思想下的提纯模型随着特征点提取与匹配技术的不断发展,硬件计算能力的日益增长,现行的匹配算法已使匹配精度达到一个较高的水平。但由于算法本身的缺陷,不可避免地存在一些误匹配点对,这时就需要利用一些技术手段将其剔除。在此背景下,本文以“正确匹配点对占据匹配中的主要成分”为先验条件,结合现有的数据分析技术,尝试在匹配点对提纯中引入主成分分析思想,从而求解出较优的提纯结果。
假设点集Φ=Ρii=0,1,…,n中包含n个点,匹配点对间的约束模型为Ψ。为了求解Ψ的模型参数,可通过数据Φ,得到m个误差方程。对所有误差方程进行主成分分析,得到正确匹配点对对应的误差方程,然后求解出模型参数,最后依据精准的模型进行匹配点对的约束提纯。在此过程中使用整体点对信息进行参数求解,相比于RANSAC方法大大减少了迭代次数,避免了RANSAC方法随机采样造成的多次运行结果可能不一致的现象,从而增加了求解的稳定性。由于主成分分析是一个非精准的过程,以上过程需迭代进行,如图 1所示。
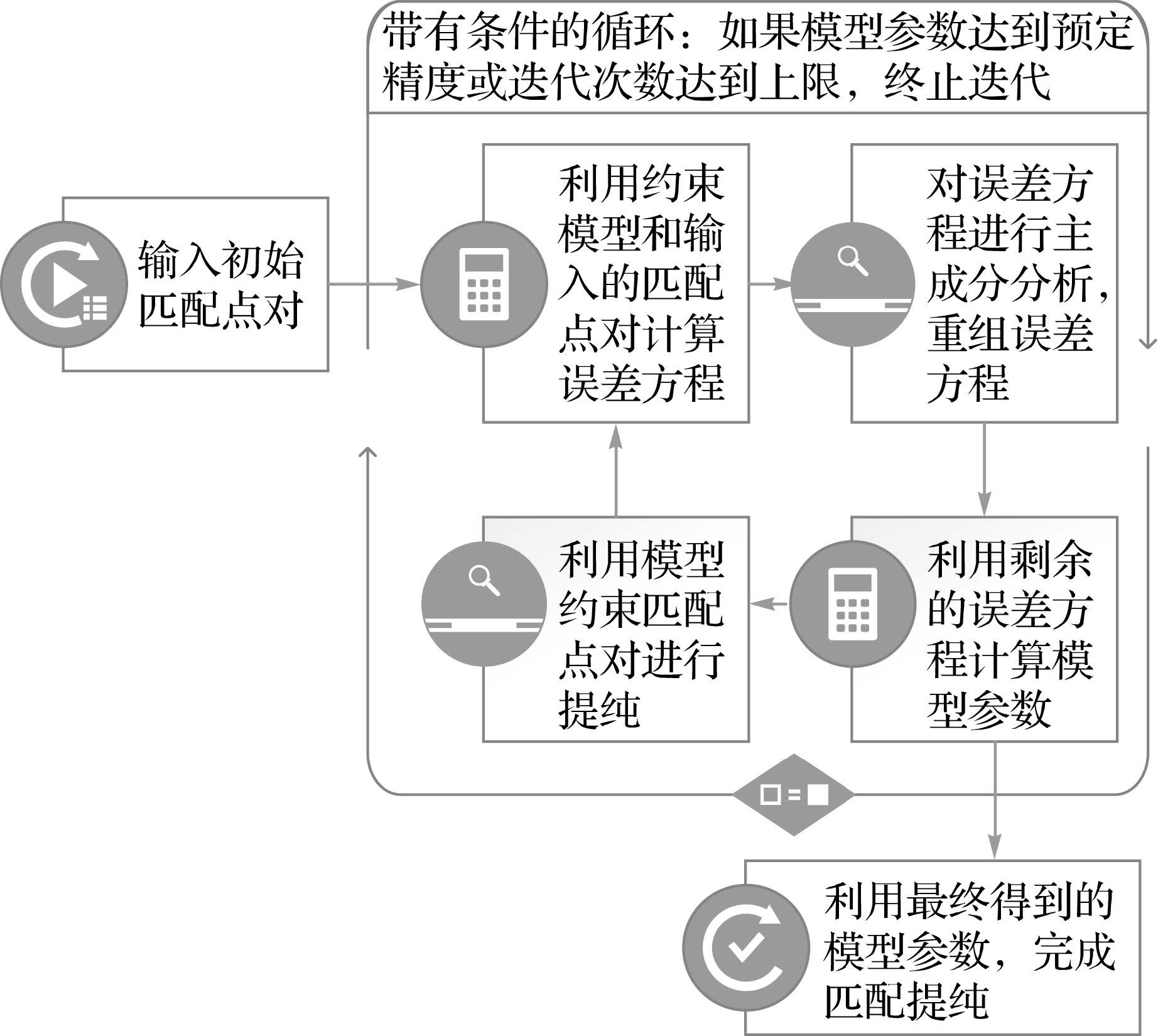
|
| 图 1 主成分分析思想下的提纯流程 Fig. 1 The process of purification based on principal component analysis |
为了具体说明提纯方法,下文以奇异值分解作为主成分分析的具体实现方法,以基本矩阵模型作为约束模型,对以上过程进行详细推导。
1.3 基于奇异值分解的匹配点对提纯算法匹配点对提纯应遵循两个原则:一是正确匹配点对被剔除的概率应尽量小,即“弃真”错误少发生;二是误匹配点对被接受的概率应尽量小,即“取伪”错误少发生。前者避免了提纯算法过于严格,后者避免了提纯算法过于宽松。两者相互作用,避免了提纯结果陷入局部最优解,确保了提纯过程的稳健性。匹配提纯的实质是匹配点对间模型参数的确定,选择合适的模型以及适当的参数,使其满足提纯的两个原则,即可实现匹配点对间的提纯操作。这里使用基本矩阵模型进行求解推导。
影像间匹配点对一般满足极线几何约束,即对应匹配点应在对应极线上。这一约束可通过基本矩阵描述为
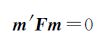 (5)
(5)
式中,m=(x,y,1)T、m′=(x′,y′,1)T分别为匹配点对齐次坐标;F为基本矩阵。令F=(fij),则式(5)可写为如下形式
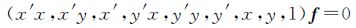 (6)
(6)
式中,f=[f11 f12 f13 f21 f22 f23 f31 f32 f33]T。将式(6)作为模型,f作为待解参数,可进行匹配点对的提纯。给定n对匹配点对可以得到线性方程组
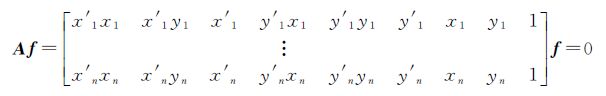 (7)
(7)
式中,A为n×9维的系数阵。对A进行奇异值分解,利用前t个奇异值得到其对应的差分矩阵ΔA,则每一匹配点对对应的近似误差值为φi=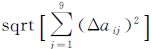
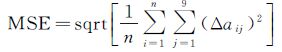 (8)
(8)
式中,Δaij为ΔA中的元素。以近似均方误差作为阈值,对每一匹配点对误差方程进行筛选,得到约束后的匹配点对误差方程,然后再次重新组成系数矩阵,得到降维矩阵B。对矩阵B再次进行奇异值分解,求解f的最小二乘解,并进行秩2约束,得到最终的模型参数解f。利用求解的参数及相应的模型,对匹配点对进行约束,得到提纯点对。利用提纯后的点对迭代进行以上步骤,直到求解的模型参数f趋于稳定。整个算法流程如图 2所示。
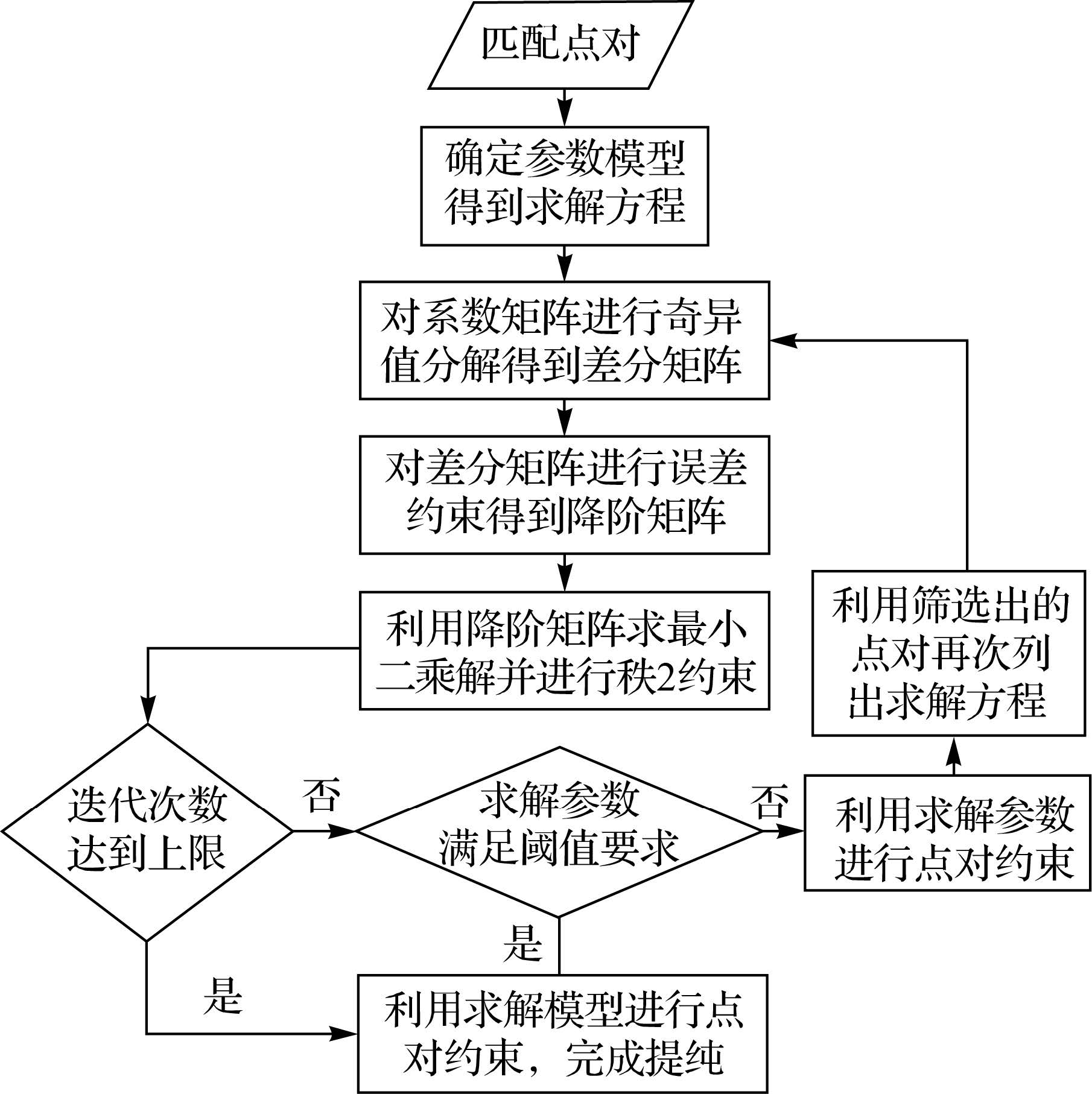
|
| 图 2 匹配点对提纯流程 Fig. 2 Matching points purification |
2 试验及其结果分析
上述算法中,重要的一步是计算重构矩阵时奇异值个数t的确定。一个恰当的t应能使计算的重构矩阵A′中的正确匹配点对部分,与原始矩阵A中对应的正确匹配点对部分尽量相似,而对应的误匹配部分尽量相差较大。即ΔA中正确匹配点对的近似误差值尽量小,而误匹配点对的近似误差值尽量大。
利用多幅影像进行试验,这里选取某幅影像中的1000对正确匹配点对进行说明。如图 3所示,对前100对匹配点对加入随机误差,分别在t=1,2,…,8的条件下求解差分矩阵,计算每一匹配点对对应的近似误差,得到如图 4所示的结果。

|
| 图 3 匹配点对示意图 Fig. 3 Matching points diagram |
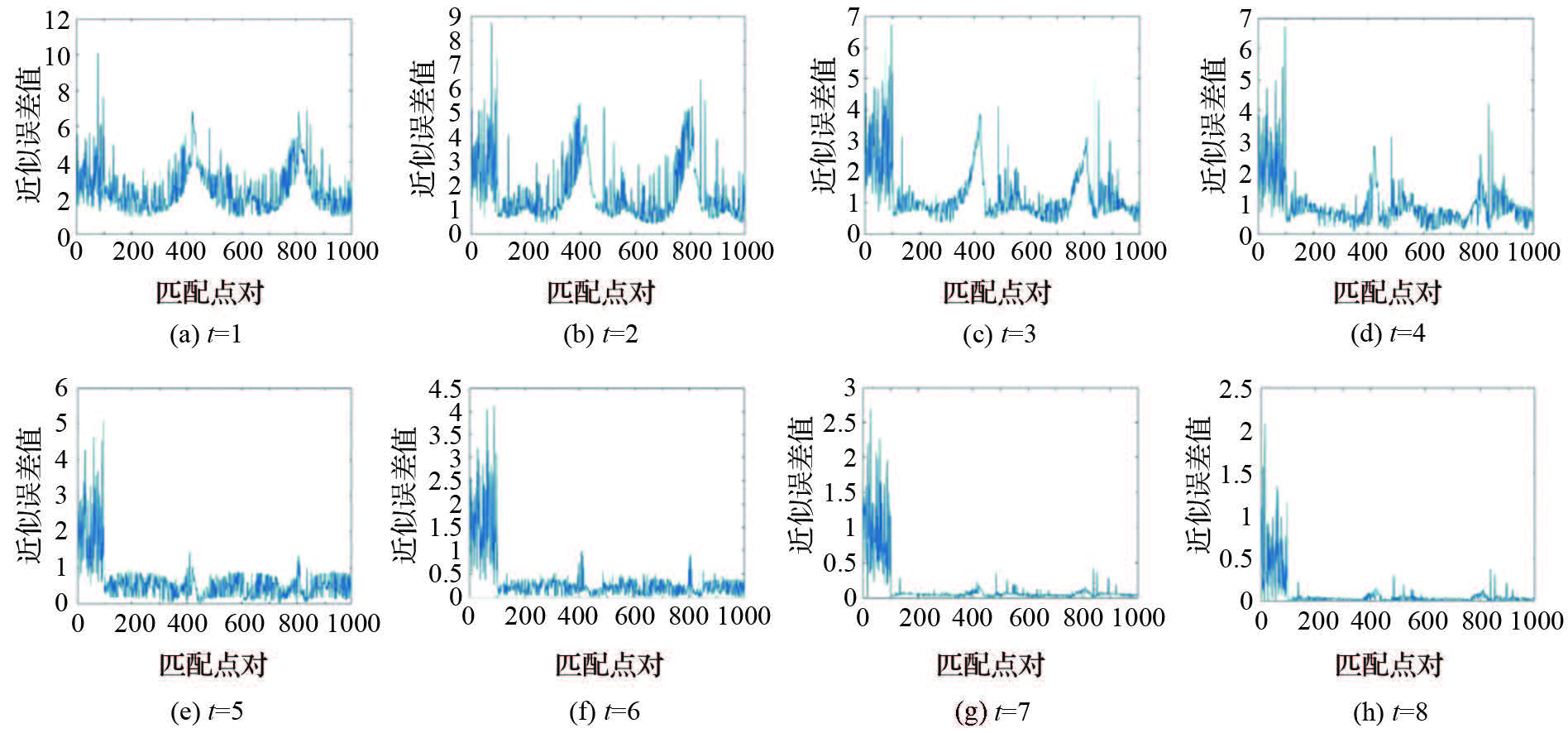
|
| 图 4 取值误差示意图 Fig. 4 Value of the error diagram |
图 4中横轴表示匹配点对,纵轴表示对应的近似误差值,其中前100个为误匹配点对,可以看出当t值取5时,已经能够很好地区别正确匹配点对与误匹配点对,当t值增大时,虽然这种区别更加明显,但计算量也随之而增长。在实际操作中取t=5。
在得到恰当的t值后,为了进一步验证本文算法的实际效果,对含有不同误点率的影像匹配点对进行了试验,截取其中6对试验影像,如图 5至图 10所示。其中,每幅图中(a)图表示原始像对图,(b)图表示加入误匹配点对后的像对图,(c)图表示利用本文方法进行点对提纯后的像对图。

|
| 图 5 经过本文方法提纯后,误点率由13.85%降到0 Fig. 5 The mismatch percentage is reduced from 13.85% to 0 |

|
| 图 6 经过本文方法提纯后,误点率由33.33%降到0 Fig. 6 The mismatch percentage is reduced from 33.33% to 0 |

|
| 图 7 经过本文方法提纯后,误点率由36.94%降到0 Fig. 7 The mismatch percentage is reduced from 36.94% to 0 |

|
| 图 8 经过本文方法提纯后,误点率由50.00%降到0 Fig. 8 The mismatch percentage is reduced from 50% to 0 |

|
| 图 9 经过本文方法提纯后,误点率由71.00%降到2.03% Fig. 9 The mismatch percentage is reduced from 71.00% to 2.03% |

|
| 图 10 经过本文方法提纯后,误点率由78.33%降到0.77% Fig. 10 The mismatch percentage is reduced from 78.33% to 0.77% |
图 5至图 7为手机拍摄影像,图 8至图 9为普通相机拍摄影像,图 10为航拍影像。可以看出,在不同场景中随着误匹配率的不断提升,本文方法仍能保持着优良的提纯率,反映了本文方法较好的稳健性。同时,为了比较本文算法的效率与全局求解的优势,将上述像对分别用经典RANSAC算法进行处理,统计每次的运算耗时与实际迭代次数,统计如表 1所示。其中,设置RANSAC算法迭代上限为2000次,本文算法迭代上限为50次,编号1—编号6数据分别对应图 5—图 10。
| 编号 | 试验数据 | 时间/ms | 迭代次数 | |||||
| 总点数 | 误点率
/(%) | 本文
方法 | RANSAC | 本文
方法 | RANSAC | |||
| 1 | 65 | 13.85 | 11 | 3 | 5 | 36 | ||
| 2 | 60 | 33.33 | 10 | 4 | 4 | 92 | ||
| 3 | 111 | 36.94 | 12 | 13 | 4 | 240 | ||
| 4 | 200 | 50.00 | 13 | 26 | 3 | 446 | ||
| 5 | 500 | 71.00 | 40 | 205 | 10 | 2000 | ||
| 6 | 6000 | 78.33 | 2170 | 1430 | 30 | 2000 | ||
表 1中时间栏为多次试验的平均耗时。同时,本文认为试验中处理时间差异在10 ms以内的两种方法处于相同的耗时水平。由表 1可以看出不同情况下本文方法迭代次数皆远小于RANSAC方法的迭代次数。由于全局求解的优势,本文方法在数次迭代后便可得到最优解,而RANSAC方法由于随机抽样的特性,在大数据量与高误点率的情况下,迭代次数骤然上升。试验中编号为5和6的数据试验结果表明RANSAC方法在此种情况下已达到迭代次数上限。同时,由表 1也可以看出在低误点率情况下,本文方法与RANSAC方法时间消耗相当,在中误点率的情况下,本文方法时间消耗少于RANSAC方法,而在高误点率的情况下,本文方法耗时多于RANSAC方法。这种特性是由奇异值分解过程的耗时与迭代次数上限的设置共同造成的。单次奇异值分解的耗时大于单次随机采样求解的耗时,在低误点率的情况下,RANSAC方法迭代次数多于本文方法,总体而言时间消耗相当;在中误点率的情况下,RANSAC方法迭代次数骤然增加,而本文方法迭代次数增加缓慢,总体而言本文方法耗时相对较少;在高误点率的极端情况下,由于RANSAC方法迭代次数已达到上限,而本文方法的迭代次数继续增加,耗时相对较多。在实际应用中可通过奇异值分解算法的并行求解与GPU加速缩短单次求解时间,优化整体耗时。
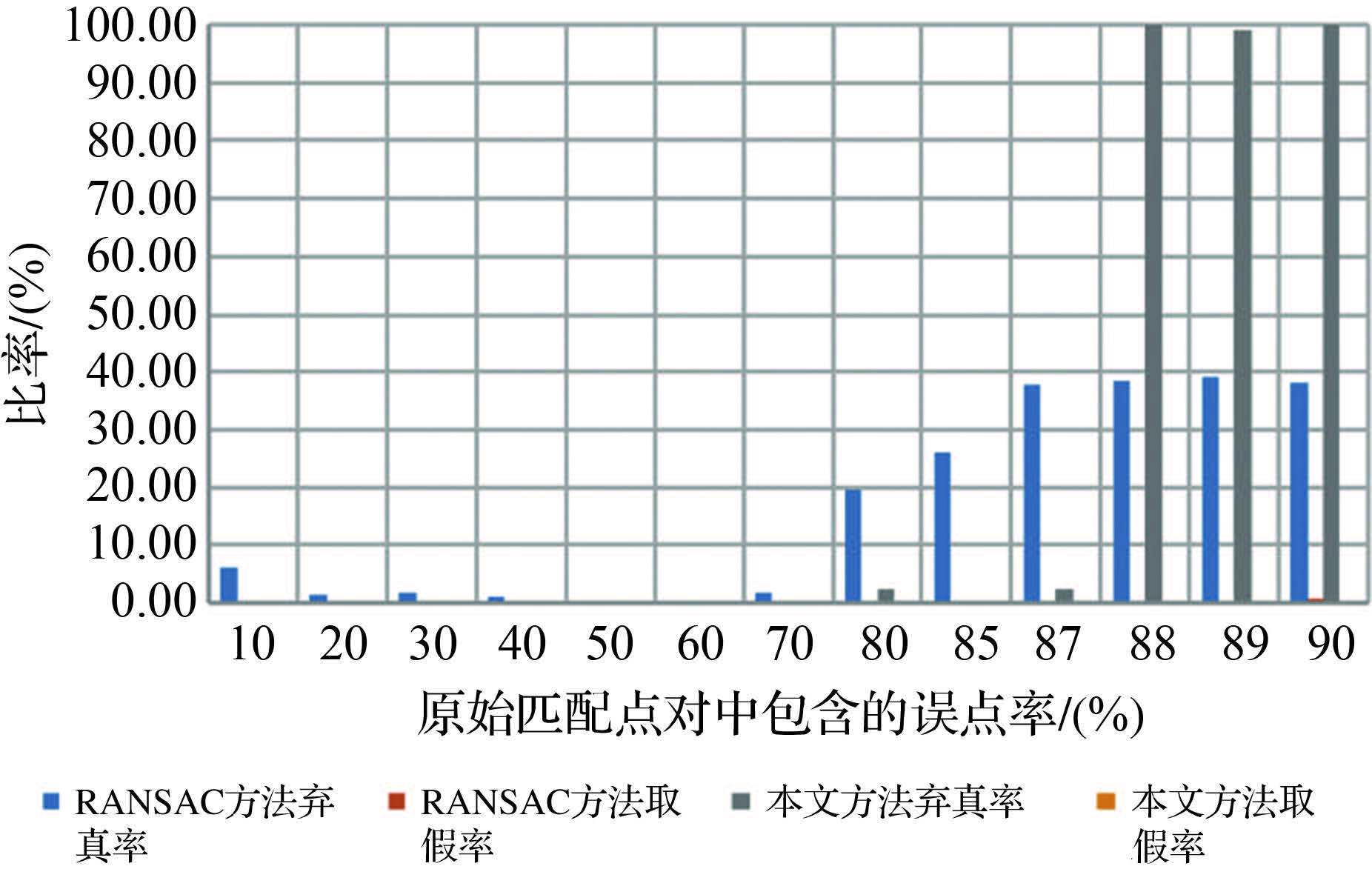
为了进一步验证本文算法与现有算法间的性能优劣,取1000对正确匹配点对逐步加入随机误差,分别用经典RANSAC算法和本文算法对匹配点对进行提纯,得到结果如表 2和图 11所示。
| 原始匹配点 | RANSAC方法 | 本文方法 | |||||||||
| 原始总
点数 | 原始误
点数 | 提纯总
点数 | 提纯误
点数 | 弃真率
/(%) | 取假率
/(%) | 提纯总
点数 | 提纯误
点数 | 弃真率
/(%) | 取假率
/(%) | ||
| 1000 | 100 | 848 | 0 | 6.13 | 0.00 | 900 | 0 | 0.00 | 0.00 | ||
| 1000 | 200 | 789 | 0 | 1.38 | 0.00 | 800 | 0 | 0.00 | 0.00 | ||
| 1000 | 300 | 689 | 0 | 1.57 | 0.00 | 700 | 0 | 0.00 | 0.00 | ||
| 1000 | 400 | 593 | 0 | 1.17 | 0.00 | 600 | 0 | 0.00 | 0.00 | ||
| 1000 | 500 | 500 | 0 | 0.00 | 0.00 | 500 | 0 | 0.00 | 0.00 | ||
| 1000 | 600 | 401 | 1 | 0.00 | 0.17 | 401 | 1 | 0.00 | 0.17 | ||
| 1000 | 700 | 295 | 0 | 1.67 | 0.00 | 300 | 0 | 0.00 | 0.00 | ||
| 1000 | 800 | 164 | 3 | 19.50 | 0.38 | 195 | 0 | 2.50 | 0.00 | ||
| 1000 | 850 | 115 | 4 | 26.00 | 0.47 | 154 | 4 | 0.00 | 0.47 | ||
| 1000 | 870 | 84 | 3 | 37.69 | 0.34 | 129 | 2 | 2.31 | 0.23 | ||
| 1000 | 880 | 77 | 3 | 38.33 | 0.34 | 0 | 0 | 100.00 | 0.00 | ||
| 1000 | 890 | 70 | 3 | 39.09 | 0.34 | 2 | 1 | 99.09 | 0.11 | ||
| 1000 | 900 | 68 | 6 | 38.00 | 0.67 | 1 | 1 | 100.00 | 0.11 | ||
|
| 图 11 试验结果对比 Fig. 11 Comparison of experimental results |
试验中,RANSAC算法和本文算法的最终阈值约束都设置为3。根据之前提到的两个原则,定义弃真率的计算公式为PT=nt1/nt,nt1表示未能被提取出来的正确匹配点对个数,nt表示总共的正确匹配点对个数;定义取假率的计算公式为PF=nf1/nf,nf1表示被提取出来的误匹配点对的个数,nf表示总共的误匹配点对个数。图11中横轴表示原始匹配点对中的误匹配率值,纵轴表示比率值。表 2中括号内的数据表示误匹配点对的个数。由表 2和图 11中数据可以发现,在不同的原始误匹配率下,RANSAC方法始终带有一定的弃真率,这是由求解的模型参数陷入局部极值造成的。而本文方法,在原始误匹配率达到87%之前,都保持着较低的弃真率与取假率,尤其是在误匹配率达到50%之前,有着理想的弃真率与取假率,具有稳健的模型参数解,相对优于RANSAC方法,符合预期结果。但在误匹配率达到87%之后,本文方法的弃真率急剧上升,RANSAC方法弃真率则保持在38%左右。这是由于本文方法引入的主成分分特性所造成的,当误匹配率极大时,正确信息被湮没在噪声信息之中造成了正确主成分提取失败。但在实际应用过程中,原始误匹配率达到80%的情况不易发生,本文方法在弃真率与取假率方面总体而言优于RANSAC方法。
3 结 语经典的RANSAC方法将随机挑选的小部分点对作为输入,计算模型参数,然后验证全部点对,留下能够满足大多数点对的模型参数作为结果,是一种“由小到大”的思想。本文方法首先将全部点对作为输入,利用主成分分析思想,剔除可能的误匹配点对,计算模型参数,然后验证全部点对,迭代求解出稳健的模型参数,是一种“由大到小”的思想。RANSAC方法由于这种随机抽选的特性,使得其容易陷入局部极大值,求解不出最优的模型参数。针对这种不足,本文方法将整体匹配点对作为输入,避免了局部极值的弊端,能够求解出相对稳定的模型参数。试验表明,在中、低原始误匹配率的情况下,本文方法迭代次数较少,总体耗时较短,弃真率与取假率较低,相对优于RANSAC方法;在高原始误匹配率的极端情况下,本文方法相对劣于RANSAC方法。同时,本文在试验中推导并采用了奇异值分解模型和基本矩阵模型,在实际应用中可根据情况更换模型。
| [1] | HUBER P J. Robust Statistics[M]//LOVRIC M. International Encyclopedia of Statistical Science. Berlin:Springer, 2011. |
| [2] | STEWART C V. Robust Parameter Estimation in Computer Vision[J]. SIAM Review, 1999, 41(3): 513–537. DOI:10.1137/S0036144598345802 |
| [3] | HAWKINS D M. The Feasible Set Algorithm for Least Median of Squares Regression[J]. Computational Statistics & Data Analysis, 1993, 16(1): 81–101. |
| [4] | ROUSSEEUW P J. Least Median of Squares Regression[J]. Journal of the American Statistical Association, 1984, 79(388): 871–880. DOI:10.1080/01621459.1984.10477105 |
| [5] | TORR P H S, ZISSERMAN A. MLESAC:A New Robust Estimator with Application to Estimating Image Geometry[J]. Computer Vision and Image Understanding, 2000, 78(1): 138–156. DOI:10.1006/cviu.1999.0832 |
| [6] | FISCHLER M A, BOLLES R C. Random Sample Consensus:A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381–395. DOI:10.1145/358669.358692 |
| [7] | 王亚伟, 许廷发, 王吉晖. 改进的匹配点提纯算法mRANSAC[J]. 东南大学学报(自然科学版), 2013, 43(S1): 163–167. WANG Yawei, XU Tingfa, WANG Jihui. Improved Matching Point Purification Algorithm mRANSAC[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(S1): 163–167. |
| [8] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [9] | MOREL J M, YU Guoshen. ASIFT:A New Framework for Fully Affine Invariant Image Comparison[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 438–469. DOI:10.1137/080732730 |
| [10] | NISTÉR D. Preemptive RANSAC for Live Structure and Motion Estimation[J]. Machine Vision and Applications, 2005, 16(5): 321–329. DOI:10.1007/s00138-005-0006-y |
| [11] | CHUM O, MATAS J. Matching with PROSAC-progressive Sample Consensus[C]//Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, CA:IEEE, 2005, 1:220-226. |
| [12] | MATAS J,CHUM O.Randomized RANSAC[R]. Prague:Center for Machine Perception, Czech Technical University, 2001. |
| [13] | CHUM O, MATAS J. Optimal Randomized RANSAC[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(8): 1472–1482. DOI:10.1109/TPAMI.2007.70787 |
| [14] | 钟金荣, 杜奇才, 刘荧, 等. 特征提取和匹配的图像倾斜校正[J]. 中国图象图形学报, 2013, 18(7): 738–745. ZHONG Jinrong, DU Qicai, LIU Ying, et al. Robust Method of Skew Correction Based on Feature Points Matching[J]. Journal of Image and Graphics, 2013, 18(7): 738–745. |
| [15] | LI Xiangru, HU Zhanyi. Rejecting Mismatches by Correspondence Function[J]. International Journal of Computer Vision, 2010, 89(1): 1–17. DOI:10.1007/s11263-010-0318-x |
| [16] | PAUL V C H.Method and Means for Recognizing Complex Patterns:U.S., 3,069,654[P]. 1962-12-18. |
| [17] | 谢亮, 陈姝, 张钧, 等. 利用Hough变换的匹配对提纯[J]. 中国图象图形学报, 2015, 20(8): 1017–1025. XIE Liang, CHEN Shu, ZHANG Jun, et al. Purifying Algorithm for Rough Matched Pairs Using Hough Transform[J]. Journal of Image and Graphics, 2015, 20(8): 1017–1025. |
| [18] | GROTH D, HARTMANN S, KLIE S, et al. Principal Components Analysis[M]//REISFELD B, MAYENO A N. Computational Toxicology:Methods in Molecular Biology.[S.l.]:Humana Press, 2013, 930:527-547. |
| [19] | 王俊淑, 江南, 张国明, 等. 融合光谱-空间信息的高光谱遥感影像增量分类算法[J]. 测绘学报, 2015, 44(9): 1003–1013. WANG Junshu, JIANG Nan, ZHANG Guoming, et al. Incremental Classification Algorithm of Hyperspectral Remote Sensing Images Based on Spectral-spatial Information[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(9): 1003–1013. DOI:10.11947/j.AGCS.2015.20140388 |
| [20] | 王文波, 赵攀, 张晓东. 利用经验模态分解和主成分分析的SAR图像相干斑抑制[J]. 测绘学报, 2012, 41(6): 838–843. WANG Wenbo, ZHAO Pan, ZHANG Xiaodong. Research on SAR Image Speckle Reduction Using EMD and Principle Component Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 838–843. |
| [21] | DE LATHAUWER L, DE MOOR B, VANDEWALLE J. A Multilinear Singular Value Decomposition[J]. SIAM Journal on Matrix Analysis and Applications, 2000, 21(4): 1253–1278. DOI:10.1137/S0895479896305696 |
| [22] | 林东方, 朱建军, 宋迎春, 等. 正则化的奇异值分解参数构造法[J]. 测绘学报, 2016, 45(8): 883–889. LIN Dongfang, ZHU Jianjun, SONG Yingchun, et al. Construction Method of Regularization by Singular Value Decomposition of Design Matrix[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 883–889. DOI:10.11947/j.AGCS.2016.20150134 |
| [23] | 周伟, 戴宗友, 袁广林, 等. CPU-GPU协同计算的并行奇异值分解方法[J]. 计算机科学, 2015, 42(6A): 549–552. ZHOU Wei, DAI Zongyou, YUAN Guanglin, et al. Parallelized Singular Value Decomposition Method with Collaborative Computing of CPU-GPU[J]. Computer Science, 2015, 42(6A): 549–552. |
| [24] | LAHABAR S, NARAYANAN P J. Singular Value Decomposition on GPU Using CUDA[C]//Proceedings of the 2009 IEEE International Symposium on Parallel & Distributed Processing. Rome:IEEE, 2009:1-10. |
| [25] | GOULUB G H, REINSCH C. Singular Value Decomposition and Least Squares Solutions[J]. Numerische Mathematik, 1970, 14(5): 403–420. DOI:10.1007/BF02163027 |
| [26] | 徐文华, 孙学栋. 奇异值分解求线性最小二乘解的理论分析[J]. 贵阳学院学报(自然科学版), 2010, 4(4): 1–4. XU Wenhua, SUN Xuedong. A Theoretical Analysis of Linear Least Square Based on Singular Value Decomposition[J]. Journal of Guiyang College (Natural Sciences), 2010, 4(4): 1–4. |
| [27] | 吴春国, 梁艳春, 孙延风, 等. 关于SVD与PCA等价性的研究[J]. 计算机学报, 2004, 27(2): 286–288. WU Chunguo, LIANG Yanchun, SUN Yanfeng, et al. On the Equivalence of SVD and PCA[J]. Chinese Journal of Computers, 2004, 27(2): 286–288. |
| [28] | 聂振国, 赵学智. PCA与SVD信号处理效果相似性与机理分析[J]. 振动与冲击, 2016, 35(2): 12–17. NIE Zhenguo, ZHAO Xuezhi. Similarity of Signal Processing Effect between PCA and SVD and Its Mechanism Analysis[J]. Journal of Vibration and Shock, 2016, 35(2): 12–17. |
| [29] | 数据科学自媒体. 解码数据降维:主成分分析(PCA)和奇异值分解(SVD)[EB/OL]. (2015-10-23).[2016-01-20].http://www.wtoutiao.com/p/T5431a.html. Data Science We Media. Decoding Data Dimension Reduction:Principal Component Analysis (PCA) and the Singular Value Decomposition (SVD)[EB/OL]. (2015-10-23).[2016-01-20]. http://www.wtoutiao.com/p/T5431a.html. |
| [30] | 钱征文, 程礼, 李应红. 利用奇异值分解的信号降噪方法[J]. 振动、测试与诊断, 2011, 31(4): 459–463. QIAN Zhengwen, CHENG Li, LI Yinghong. Using Singular Value Decomposition of the Signal Noise Reduction Method[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(4): 459–463. |
| [31] | 王建国, 李健, 刘颖源. 一种确定奇异值分解降噪有效秩阶次的改进方法[J]. 振动与冲击, 2014, 33(12): 176–180. WANG Jianguo, LI Jian, LIU Yingyuan. An Improved Method for Determining Effective Order Rank of SVD Denoising[J]. Journal of Vibration and Shock, 2014, 33(12): 176–180. |
| [32] | VU V. A Simple SVD Algorithm for Finding Hidden Partitions[EB/OL]. (2014-04-07).[2016-01-30]. http://adsabs.harvard.edu/abs/2014arXiv1404.3917v. |



