2. 中国测绘科学研究院, 北京 100039
2. Chinese Academy of Surveying and Mapping, Beijing 100039, China
直线提取是计算机视觉及航空遥感图像处理领域中一个关键的问题[1-2]。作为图像中一种规则离散点集,线特征相比于点特征能够提供更加明确、丰富的结构信息,其方向、长度、端点及直线间的拓扑关系等信息在图像压缩、目标识别、图像匹配等领域具有重要的应用价值[3-6]。但如何构建一种直线提取模型,从不规则离散边缘点集中获取有意义的直线信息,具有相当大的难度[7]。
自顶而下方法是直线提取的一个有效策略,该类方法是将图像中具有一定空间关系的边缘点进行聚类,寻找解析形式获取直线参数信息。其中以Hough变换方法最为典型,该方法具有抗噪性好的优点,并且对共线短直线连接具有较好的稳健性。缺点是复杂度高、参数难以选择、缺乏局部特性、直线端点定位难度大,易产生虚假直线及漏检问题[8-11]。
直线提取的另外一种策略是自下而上方法,该类方法采用一定的约束准则跟踪边缘点,并对跟踪编组后的边缘点集进行直线拟合。其中以边缘链码与相位编组方法为典型代表,前者通过直线几何约束准则进行边缘链码编组,利用合并或分裂方法完成对直线的提取[12]。该类方法原理比较简单,计算量小同时适合实时处理,但也存在直线易断裂、无意义直线较多等缺点[13-15]。究其原因在于以下4点:①链码跟踪受限于起始点的位置;②几何约束准则是以45°为基准方向码,这并不能满足实际直线角度要求;③多边缘交叉点处易引发其他方向边缘的断裂,这主要是由于边缘图细化程度不够,交叉点无法准确定义,难以建立有效边缘补偿机制;④对形成直线的边缘点缺乏相位约束机制,难以避免由不同相位边缘点构成无效直线问题的发生。与链码编组方法不同的是,边缘点相位是相位编组方法进行链码跟踪的主要约束准则,因而这类方法检测的有效直线产出率高[16],但也是受到边缘点相位的约束,局部白噪声、起始点相位、相位分组阈值等因素均会引发相位交错分组的问题,使得直线提取效果的完整性较差[17-19]。
针对自下而上直线提取方法中存在的问题,论文提出一种链码跟踪与相位验证相结合的直线提取方法。该方法首先建立细化规则对边缘图进行完全细化;其次通过检测端点进行链码跟踪直线拟合,同时在跟踪过程中建立的动态链码主方向,以精确链码直线几何约束准则;最后利用边缘点相位进行直线有效性约束,以此解决在相位编组方法中出现的断裂问题以及链码跟踪方法中的直线有效性验证问题,获取更好的直线拟合效果,实现利用直线分析影像结构信息的目的。
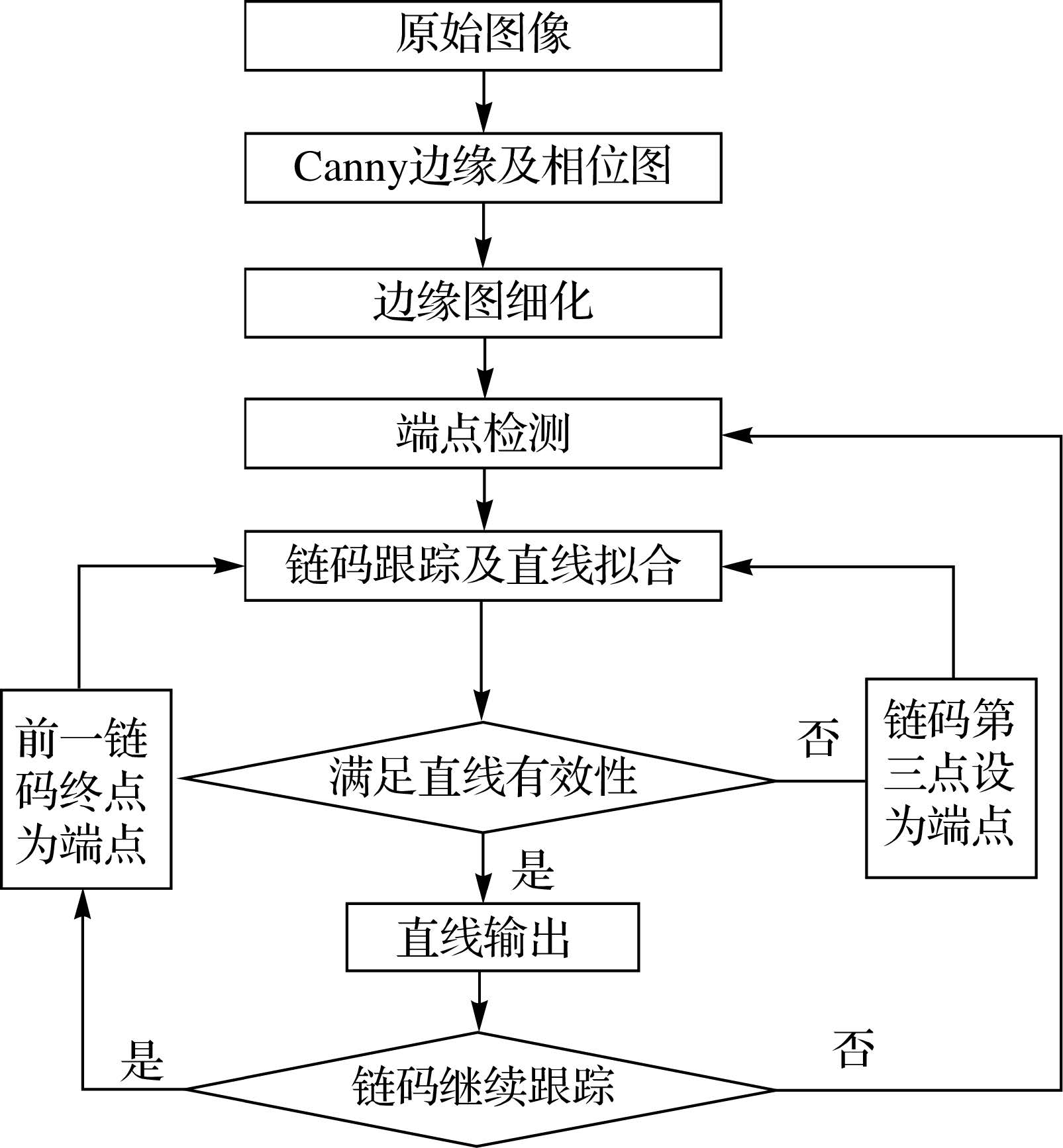
1 方 法如图 1所示为本文方法的流程图。该方法充分结合了链码跟踪与相位编组的优点:首先,利用链码跟踪几何约束准则,避免局部白噪声所引起的直线断裂问题;其次,对链码跟踪的直线进行相位验证,防止无效直线的产生。
|
| 图 1 方法流程 Fig. 1 Flowchart of the proposed method |
具体步骤如下:
(1) 利用Canny方法提取边缘图及其相位图。
(2) 采用论文所提出的细化规则对边缘图进行完全细化处理,以避免多边缘交叉点处引发的直线断裂问题。
(3) 遍历搜索边缘端点,以此作为链码起始点进行跟踪。
(4) 以端点为起始点,利用论文所提的链码跟踪方法进行边缘点编组,在编组结束后对边缘点进行直线拟合。
(5) 对拟合后的直线进行有效性判断,不满足要求则表明当前起始端点出现错误,进入步骤(6);满足要求则输出直线,同时判断当前链码是否可以继续跟踪,满足要求则进入步骤(7);不满足要求则进入步骤(3)。
(6) 以当前提取的边缘链码为基础,按照跟踪顺序确定第3个边缘点作为端点进入步骤(4),前面2个边缘点删除。
(7) 以当前链码终点为端点,进入步骤(4)。
1.1 边缘提取Canny方法是效果较优的一种边缘检测算子,该方法通过建立梯度图,利用高低两个阈值来提取图像中的边缘信息。由于充分考虑了图像中的梯度幅值与局部结构信息,因此具有较强的实用性[20]。在这里仅对传统Canny方法部分步骤进行修改,包括以下内容:
(1) 在进行影像滤波处理时,选择16×1的高斯滤波器。
(2) 梯度检测以x向梯度图为例,先对原图像y向滤波,然后进行x向梯度检测;对y向梯度图检测,则先对原图像x向滤波,然后进行y向梯度检测。
(3) 边缘点相位计算。这里借鉴文献[17]中对边缘点的相位计算方法,其公式如下
 (1)
(1)
式中,i为图像y向坐标;j为图像x向坐标;ang(i,j)是坐标为(i,j)的边缘点相位;gx(i,j)为x向梯度检测值;gy(i,j)为y向梯度检测值。
Canny方法在边缘提取过程中采取了非极大值抑制处理,但由于抑制方向为目标点的梯度方向,通常该方向对比梯度幅值来源于相邻两像素梯度插值,故难以避免多像素宽度边缘、毛刺等现象的发生,而这可能导致以下3个问题的出现:
(1) 链码跟踪起始端点很难清晰定义。
(2) 链码可能会向非边缘方向跟踪,造成链码的断裂,降低了直线提取的完整性。
(3) 边缘交叉点判断条件很难设计,进而导致在边缘交叉处直线发生断裂。
因而,对Canny边缘图必须进行细化处理。
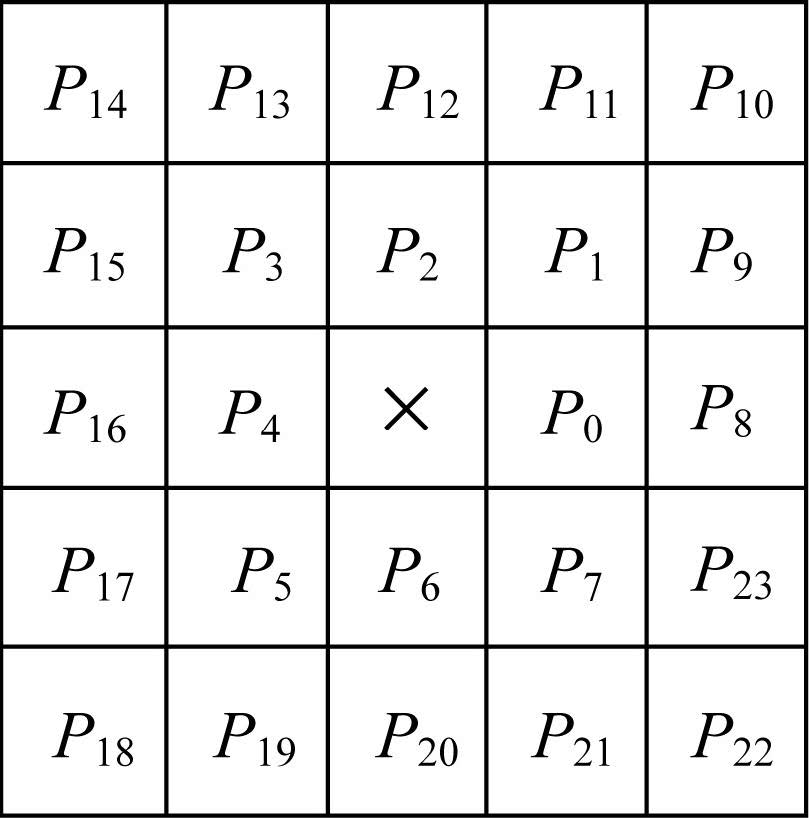
1.2 边缘细化细化作为二值图像处理中的一种基本方法,目的是减少图像成分,保留区域的最基本信息,便于图像进行识别和分析。经典细化方法有ZS方法[21-22]、HSCP方法[23-24]、OPTA方法[25]等,这些方法通过大量试验验证均存在细化程度不足、细化过度、毛刺点大量存在等问题,无法满足链码跟踪要求。因此本文依据Canny提取的边缘图,基于最大限度保留直线信息的原则,提出一种新的细化规则。如图 2所示为边缘邻域方向模板。
|
| 图 2 邻域方向模板 Fig. 2 Neighbor direction template ×为当前待处理目标点;P0-P23表示相对于×点的不同方向邻点;P0-P7为点×的八邻域点;P8-P23为八邻域外点。 |
依据Canny方法处理后的边缘图像,分别对不同情形下目标点进行细化处理:
(1) 八邻域内无边缘点,直接对目标点进行消除处理。
(2) 当八邻域内仅有1个边缘点时,这表明目标点可能为毛刺点也可能为端点。
(a) 假定八邻域内边缘点为四角点。例如P1为边缘点,对P1八邻域进行判断,由于P0、P2为非边缘点,×无需判断,即只需对P8、P9、P10、P11、P12 5点进行判断。
若上述5点中3点以上为边缘点,则×点必然为毛刺点,进行消除处理。
若2点为边缘点,则根据×点与P0点方向形成主方向进行判断,若1点与主方向相同,另外1点与主方向相邻,即2点为P9和P10或P10和P11,则目标点保留;其他情况下目标点进行消除处理。
仅有1个边缘点,则保留当前目标点。
(b) 假定边缘点为四邻点。假定P0为边缘点,判断其八邻域,由于P1、P2、P6、P7为非边缘点,即需对P8、P9、P23 3点进行分析:
若3点为边缘点,则×点为毛刺点,进行消除处理。
若2点为边缘点,则根据×点与P0点方向形成主方向进行判断,若2点为P8、P23时目标点保留;其余情况目标点进行消除处理。
仅有1个边缘点,当前目标点保留。
(3) 当八邻域内存在2个边缘点时,如2点不存在连通性,例如2点为P0和P23,当前目标点予以保留。而当2点存在连通性时:
(a) 当2点为P0和P2类似对角关系时,若P0和P2在其八邻域内除×点外均存在边缘点,则目标点消除;
(b) 当两点为P0和P1类似四连通关系时,若P0和P1在其八邻域内均有边缘点,除仅有P8、P9、P8和P9为边缘点3种情况外,可消除当前目标点,其余情况下目标点均予以保留。
(4) 当目标点八邻域内存在3个边缘点时,如3点之间存在八连通关系,则当前目标点消除。
(5) 八邻域内存在4个边缘点时,如4点均存在四连通关系,消除当前目标点。
(6) 八邻域内存在5个边缘点时,如5点间存在连通关系,消除当前目标点。
在论文中,通常图像细化需要进行2~3次处理,以达到边缘图完全细化的目的。
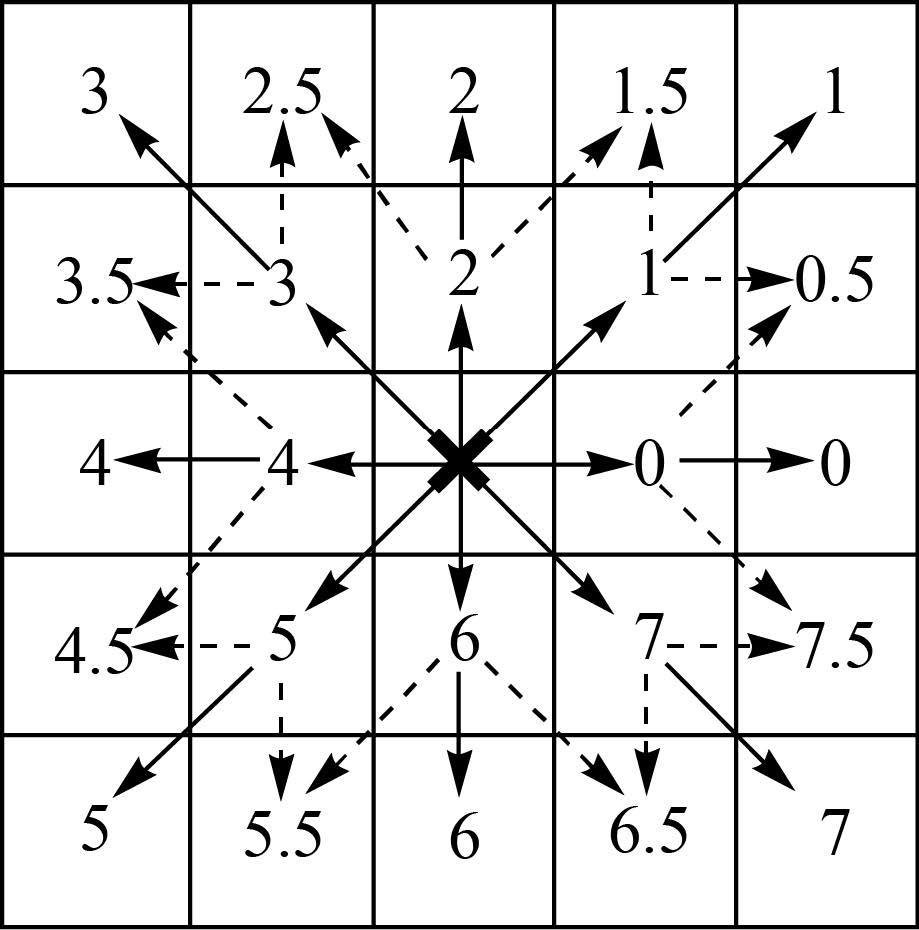
1.3 边缘链码直线提取采用论文细化方法可将边缘线条宽度降为单像素,便于边缘链码跟踪。论文首先确定链码起始端点,其次设计动态跟踪约束主方向,依据主方向采取先八邻域点后八邻域外点方式进行链码跟踪,并对链码跟踪结果进行动态直线化分析,最终利用相位验证的方式输出有效直线。在链码方向码的设计中,与传统方向码不同,论文引入非整数的方向码,以精细确定链码跟踪的方向。如图 3所示,中心点为当前链码跟踪点,八邻域为0—7方向码,0—7外延对应的是链码八邻域外方向码,其中八邻域外方向码为相对于中心点的非整数方向码。
|
| 图 3 链码方向码示意图 Fig. 3 Sketch map of chain code direction |
具体关键步骤及相关说明如下:
(1) 链码起始端点检测。起始端点检测是链码跟踪的基础,伪端点必然引发链码断裂、方向发生偏转等问题。如图 4所示为自然图像边缘局部放大图,如果仅采用由左至右、由上至下遍历方式定义端点,那么灰色虚框边缘点必然首先被遍历为链码起始端点,以此为基础链码向右侧跟踪,导致完整链码断裂,而左侧分裂后的链码也可能因长度过低而被过滤掉。因此在论文中,起始端点是指单端点(八邻域内存在1个边缘点)与环状端点(八邻域内存在2个边缘点)。环状端点主要存在于房屋、田块等闭合地物场景中,其检测方式可以依据其八邻域内两边缘点间存在对角关系进行判断。为防止环状端点检测对链码跟踪构成干扰,本文采取先单端点后环状端点的顺序进行链码跟踪,进入步骤(2)。

|
| 图 4 边缘局部放大图 Fig. 4 Partial enlarged detail of edge |
(2) 动态链码主方向(Main_Orient)确定。传统链码跟踪过程中,直线链码约束准则通常由链码起始跟踪方向或链码组最后跟踪点方向确定,这将引发两方面的问题:一方面以45°为基准的方向码很难清晰表达链码的直线特性;另一方面过少点确定的链码方向极易受到异常点的干扰,促使链码发生断裂。因此,本文在设计直线链码约束时,建立的动态链码主方向是随链码变化而不断发生变化的,这符合链码的整体直线特性,排除了链码跟踪受到起始端点和局部异常点干扰的可能性,并且主方向不再受限于8个方向,更加符合实际直线角度。本文首先将起始端点作为链码起点,搜索与起始端点连通的下一边缘点,将链码初始方向记录为Orient,然后进入步骤(3)。具体计算公式如下
 (2)
(2)
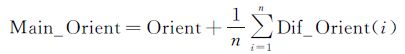 (3)
(3)
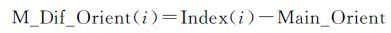 (4)
(4)
式中,Index(i)为第(i+2)个边缘点相对于第(i+1)个边缘点方向码;Dif_Orient(i)为Index(i)与起始方向链码的差值,取值范围为[-4,4];M_Dif_Orient(i)为Index(i)与链码主方向差值,取值范围为[-4,4];n为当前链码组除前两个点外其他边缘点数量。
(3) 链码跟踪方式。首先判断当前点八邻域是否存在边缘点,如果存在,采用八邻域内跟踪,转到步骤(4),否则采用八邻域外跟踪,转到步骤(5)。
(4) 八邻域跟踪。判断当前点八邻域内边缘点数量:
八邻域内仅有1个边缘点时,依据式(3)分析当前跟踪方向与链码主方向差异M_Dif_Orient(i),若差值为-4或4,这表明链码方向发生剧烈变形,则链码断裂进入步骤(7);其他情况下,进入步骤(6)。
若边缘点不唯一时,当前目标点通常为边缘交叉点,根据式(4)计算不同边缘点方向码与主方向码差值,选择最小绝对差值方向码作为当前链码跟踪方向,进入步骤(6);同时在当前链码跟踪结束后对边缘交叉点进行边缘补偿,即将边缘交叉点单独设为边缘点。以防止链码形成直线后,原有链码内全部边缘点非边缘化,进而导致下一边缘直线的断裂。
(5) 八邻域外跟踪。判断链码是否存在过度离散化问题,即链码中八邻域外连接点数量(计入即将跟踪点)与当前链码边缘点数量之间的比值是否低于阈值δ,若是则直接进入步骤(7);如高于阈值δ,则判断八邻域外最接近Main_Orient、Main_Orient-0.5和Main_Orient+0.5方向上是否存在边缘点,如果是转到步骤(6);如果不存在,转到步骤(7)。
(6) 链码直线化分析。为确保获取最佳链码终点,分别对步骤(4)和步骤(5)加入的边缘点进行以下判断:
(a) 链码方向检测。每次加入的新点i均进行检测,即当M_Dif_Orient(i)、M_Dif_Orient(i-1)、M_Dif_Orient(i-2)均为同一符号,并且累计绝对值大于3.0以上时,这表明当前链码发生明显偏转,必将改变拟合直线方向,因此链码立即断裂,进入步骤(7)。
(b) 链码点与拟合直线距离检测。当加入边缘点数量n为3的倍数时,进行直线最小二乘拟合,对链码中的点进行抽样计算与直线垂直距离,若距离超过垂直距离阈值ε时,链码断裂进入步骤(7)。
通过上述两种检测后,利用式(2)和式(3)更新Main_Orient,进入步骤(3)。
(7) 对获取的边缘链码进行相位编组验证,通过最小二乘方法求取直线方向,接着对边缘点进行相位验证。该方法首先统计链码中边缘点相位符合直线方向的数量(相位与直线方向之间差异不超过π/4弧度),其次将该数量与链码组边缘点总数量进行对比,判断比值是否低于阈值θ:
(a) 若低于阈值θ,判断直线长度是否达到阈值τ,满足要求则直接输出直线,接着以当前链码终点为端点进入步骤(3);不满足要求则按照链码跟踪顺序,将第3点边缘点视为端点,进入步骤(3)。
(b) 若当前链码高于阈值θ并且链码中存在交叉点,则按照链码跟踪顺序,将前两个边缘点删除,链码中其余点恢复为边缘点后进入步骤(1),防止影响交叉点处其他直线的提取。
(c) 若当前链码高于阈值θ且不存交叉点,同时这种情况是由步骤(4)和步骤(6)链码产生断裂所产生,则按照链码跟踪顺序,将前两个边缘点删除,其余点按照原来链码顺序由前两点建立Orient,后续点依次更新Main_Orient,进入步骤(3);如当前链码由步骤(5)进入,则转入步骤(1)。
2 试验结果及分析为了深入验证论文方法关键步骤的试验效果,论文分别对边缘细化结果与直线提取效果进行讨论。
2.1 图像细化结果试验分析为验证论文提出细化方法的实际效果,以VS2010作为处理平台,分别对论文细化方法、HSCP方法和ZS方法进行编程实现,并通过大量图像对3种方法的处理性能进行比较。
为清晰展示边缘细化结果,图 5给出了3种方法边缘图局部细化对比结果。首先由图 5(b)局部图像中可以看出Canny边缘图中存在像素冗余、毛刺等多种问题,细化处理十分必要。如图 5(d)所示HSCP方法处理结果明显有信息丢失的现象发生,并且数据的冗余问题依然没有得到较好的解决,同时毛刺问题仍然存在;而ZS方法相对于HSCP方法局部信息丢失较少,但毛刺现象依然没有根除。如图 5(c)所示,论文方法细化结果比较光滑,不存在毛刺现象,同时基本完整保存原有边缘连通信息。利用人工对论文方法细化后的Lena边缘图进行全面细致观察,边缘毛刺、冗余现象已完全消除,得到了保持8连接、完全细化的边缘图。而在运行效率方面,3种方法的耗时基本都在0.1 s左右,相差不大。

|
| 图 5 不同方法的细化效果比较 Fig. 5 Thinning results of different algorithms |
2.2 直线拟合结果与分析
在对直线试验效果进行评价时,论文基于以下原则对直线提取效果进行评价:①提取直线的有效性,即直线是否位于真实地物边缘上;②直线的拟合长度,对同一边缘应尽量采用少量的较长直线进行拟合,以降低机器对图像信息的理解难度;③直线提取方法的运行时间。一个良好的直线提取方法应定义为,在保证直线提取正确率情况下,最大化拟合直线的同时提高方法运行速度。
2.2.1 参数分析由于本文方法涉及一些阈值参数,因此需要对这些参数进行讨论分析:
(1) 八邻域外连接点数量与链码组边缘点数量比例阈值δ,该阈值是为防止链码由多个八邻域外点组成,进而导致虚假直线现象的发生,另外也是为了避免由异常点所引发的链码断裂问题。因此论文从以上两方面考虑,将δ设定为0.2。
(2) 边缘点与拟合直线垂直距离阈值ε。通过该阈值可对链码进行直线几何约束,防止链码出现曲线化的倾向,因此该阈值设定不宜过大。但由于在跟踪过程中链码不断更新主方向,并且链码方向检测已起到了部分直线几何约束的作用,同时直线长度较大时阈值ε过小将导致直线断裂。故论文综合考虑将ε阈值设为3像素。
(3) 相位验证阈值θ。该参数一方面是为了降低白噪声对链码跟踪的影响,另一方面也是避免无效直线的产生,因此该阈值不宜过小,故将其设为0.9。
(4) 直线长度阈值τ。在图像处理中,通常认为直线长度越大其信息量越大,而过短的直线不仅意义不大,同时也会影响机器对图像的认知,因此论文设定τ为8像素。
以上参数是通过对多幅光学图像的测试所确定,如果图像中存在强烈干扰性噪声或者SAR图像,则上述参数需重新设定。
2.2.2 直线提取结果对比分析为了充分验证论文方法的有效性,分别利用文献[10]方法、文献[15]方法、LSD(line segment detector)方法[17]及EDlines(edge drawing lines)方法[18]等具有典型性的直线提取方法进行对比,其中文献[10]方法、文献[15]方法、LSD方法分别对应于Hough变换、链码跟踪及相位编组方法。在试验中,文献[10]方法和文献[15]方法采用Canny边缘图,并利用ZS方法对边缘图进行细化处理。而LSD方法及EDlines方法则直接下载相应论文网站提供的开源代码,将其放入VS2010平台进行处理。
如图 6(a)所示,首先论文选取一幅近景图像(638×638像素),其中包含数量较少的清晰线性信息,便于对不同方法试验效果进行人工检查,其精度评定的依据是直线评价效果原则①。从图 6试验结果可以看出,5种方法均可清晰检测出图像大致线性轮廓信息。但对图 6(c)和图 6(d)直线检测的结果进行详细观察可以发现,文献[10]和文献[15]方法由于没有进行完全细化及端点检测,因此提取的直线长度过短并且数量过多,在连续边缘线(例如窗口边缘及墙角处)附近存在大量的断裂直线,这不符合直线评价原则②的要求。而相对于另外两种方法,图 6(b)论文方法试验结果具有线状特征更加简洁的优点,这在窗户外沿与左侧墙体的连接处有清晰呈现结果。如表 1所示,对多种方法直线检测的精度结果分析表明,论文方法、文献[10]和文献[15]方法不存在错误直线,而LSD和EDlines方法所检测的错误直线主要出现在图像的四周,图像边缘效应可能是出现这一问题的主要原因。对比直线提取的拟合长度可以看到,论文方法直线数量最小,但拟合长度却最大,这说明论文方法所采用的细化方法和跟踪方法是有效的,直线的完整性提取效果优势非常明显。

|
| 图 6 近景图像不同直线提取效果 Fig. 6 Line extraction results with different algorithms for close range image |
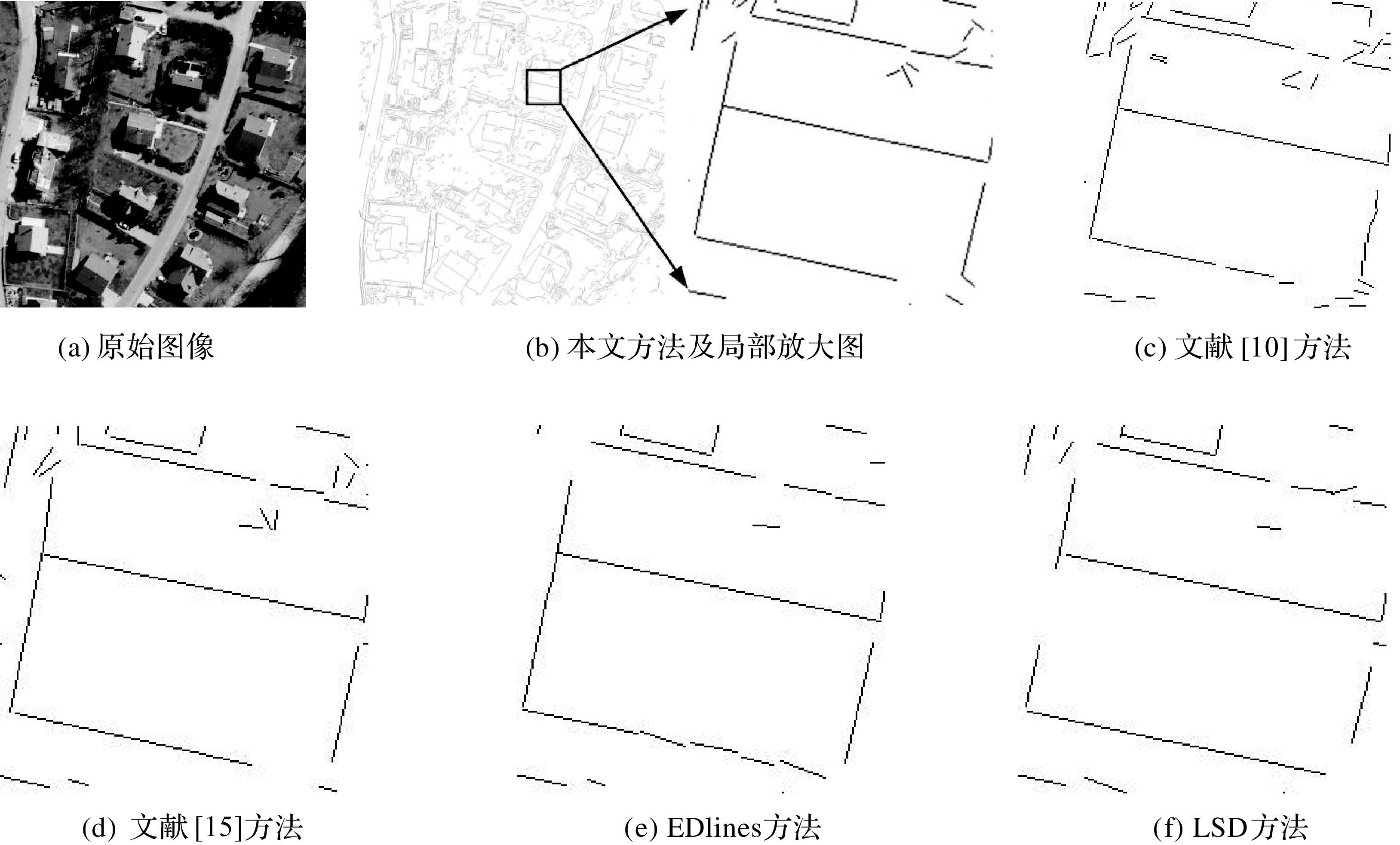
其次,如图 7(a)所示,为了验证本文方法在航空图像上的效果,对ISPRS官方网站提供的1800×1800像素航空数据进行分析。由于航片图幅较大,直线信息过多,一方面人工检查直线效果难度较大,没有标准直线检测对比图;另一方面论文方法直线提取效果精度较高,这一点在图 6中有定量验证,因此本文并未对后续图像的5种方法试验效果进行精度检验,仅对直线效果评价原则②和③进行探讨。为了对试验效果进行详细观察,如图 7(b)所示,本文对图像黑色框内中建筑物直线信息进行局部放大分析,可以看到文献[15]方法和本文方法所提取直线拟合效果较好,而文献[10]、LSD、EDlines方法则存在直线断裂的问题,其原因在于:文献[10]方法采用聚类方法进行峰值检测,连续性边缘由于聚类不一致导致直线破裂;LSD和EDlines方法则与相位交错编组及白噪声有关。而相比于文献[15]方法,本文方法提取直线更加清晰有效,并具有更好的连续性。由此可以表明,本文方法采用链码形式进行跟踪,利用先直线检测后相位验证的方式,可以有效解决白噪声造成的直线破裂问题。本文方法也存在屋顶右下侧直线信息漏检的问题,这一问题取决于Canny边缘图效果,选取较低的高低阈值则右下侧直线必然出现,但同时也会产生过多的无意义直线,例如图像中树木阴影所形成的直线信息,这将加大机器对图像理解的难度,如何解决这一矛盾也是未来进一步需要探讨的问题。
|
| 图 7 航空图像不同直线提取效果 Fig. 7 Line extraction results with different algorithms for aerial image |
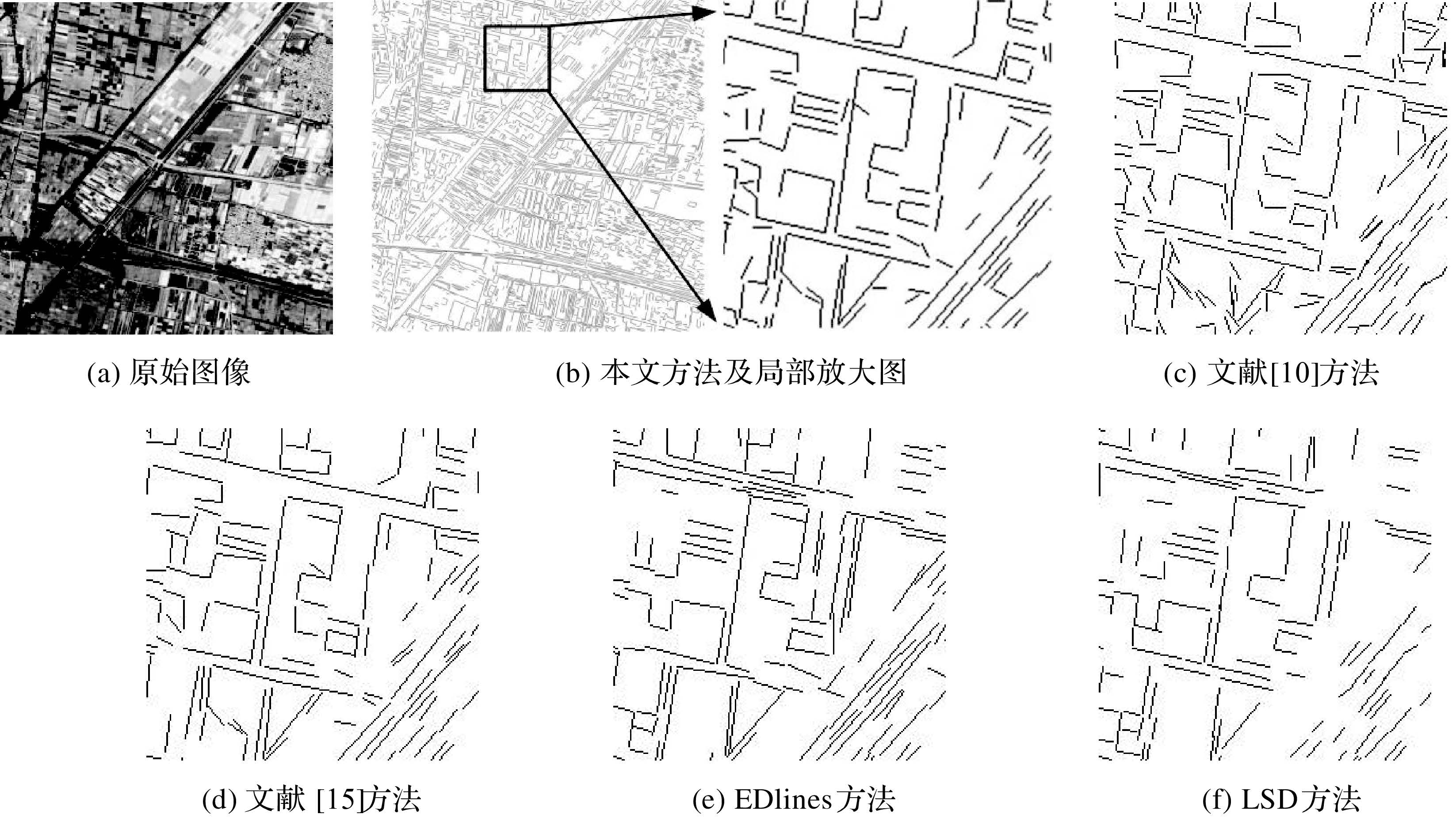
最后,本文尝试对噪声更多、模糊度更大的IKONOS光学卫星全色图像进行实验,以进一步探讨论文方法的抗噪性。如图 8(a)所示,图像大小为1024×1024像素,覆盖区域为城市近郊,区域内中包含房屋、梯田、道路等多种线性特征信息。通过5种方法局部直线提取效果对比分析表明:除了文献[10]方法外,其余4种方法均能较好地提取建筑物轮廓线,但LSD方法存在一定的直线断裂,本文方法、EDlines方法、文献[15]方法则很少出现这一问题;而相对于EDlines方法和文献[15]方法,本文方法连贯度更好,但也存在部分直线没有检测的问题。
|
| 图 8 光学卫星图像不同直线提取效果 Fig. 8 Line extraction results with different algorithms for optical satellite image |
如表 1和表 2所示对比方法耗时,可以看到本文方法明显优于文献[10]方法,但远低于EDlines方法。由于EDlines方法网站不提供源代码,只能采用其封装动态链接库,具体单进程运行效果无法有效预测,因此可比性不强。而本文方法耗时长于文献[15]和LSD方法的原因在于,本文方法是链码跟踪与相位验证的结合,需要进行迭代分析验证。而文献[15]和LSD方法分别是链码跟踪与相位编组的改进,不需进行迭代计算,因而计算速度较快。
3 结 语
本文提出一种链码跟踪与相位验证相结合的直线拟合方法,相对于其他方法,具有以下几个创新之处:
(1) 提出一种边缘细化方法,实现了边缘图的完全细化。这使得链码起始端点更加易于定义,多边缘交叉处便于进行边缘补偿,有利于链码的完整性提取。
(2) 改进了链码跟踪方法。对动态链码主方向进行了定义,并给出了相应的计算公式,使得链码跟踪不再受到起始端点、局部异常点及45°基准方向码的限制。
(3) 相位验证与链码跟踪相结合。对链码跟踪获取的直线进行相位验证,解决了链码直线提取方法中缺乏相位约束机制问题;同时先进行链码跟踪后进行相位验证的方法,也解决了局部白噪声、起始点相位、相位分组阈值等因素对相位编组直线提取方法的限制问题。
通过试验的对比与分析,验证了本文方法的优越性。但其不足之处在于本文方法暂时仅能在噪声相对较小的光学图像中实现直线的检测任务,还无法在强噪声及SAR图像中进行直线的提取,并且本文方法中的一些阈值参数尚需人工设定,这些问题都将是今后工作研究的重点。
| [1] | 董银文, 苑秉成, 王航宇, 等. 一种有效的航拍图像中直线提取算法[J]. 武汉大学学报(信息科学版), 2012, 37(2): 160–164. DONG Yinwen, YUAN Bingcheng, WANG Hangyu, et al. An Effective Algorithm for Line Extraction in Aerial Image[J]. Geomatics and Information Science of Wuhan University, 2012, 37(2): 160–164. |
| [2] | BALTSAVIAS E P. Object Extraction and Revision by Image Analysis Using Existing Geodata and Knowledge:Current Status and Steps towards Operational Systems[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 58(3-4): 129–151. DOI:10.1016/j.isprsjprs.2003.09.002 |
| [3] | ZHENG Yefeng, LI Huiping, DOERMANN D. A Parallel-line Detection Algorithm Based on HMM Decoding[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 27(5): 777–792. |
| [4] | 周绍光, 陈超, 岳建平. 形状先验和图割的高分辨率遥感影像道路段提取[J]. 测绘学报, 2014, 43(1): 60–65. ZHOU Shaoguang, CHEN Chao, YUE Jianping. Extracting Roads from High-resolution RS Images Based on Shape Priors and Graph Cuts[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 60–65. DOI:10.13485/j.cnki.11-2089.2014.0009 |
| [5] | 曹金山, 龚健雅, 袁修孝. 直线特征约束的高分辨率卫星影像区域网平差方法[J]. 测绘学报, 2015, 44(10): 1100–1107. CAO Jinshan, GONG Jianya, YUAN Xiuxiao. A Block Adjustment Method of High-resolution Satellite Imagery with Straight Line Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1100–1107. DOI:10.11947/j.AGCS2.0152.0150023 |
| [6] | 王竞雪, 宋伟东, 王伟玺. 同名点及高程平面约束的航空影像直线匹配算法[J]. 测绘学报, 2016, 45(1): 87–95. WANG Jingxue, SONG Weidong, WANG Weixi. Line Matching Algorithm for Aerial Image Based on Corresponding Points and Z-plane Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 87–95. DOI:10.11947/j.AGCS.2016.20140527 |
| [7] | 徐胜华, 朱庆, 刘纪平, 等. 基于预存储权值矩阵的多尺度Hough变换直线提取算法[J]. 测绘学报, 2008, 37(1): 83–88. XU Shenghua, ZHU Qing, LIU Jiping, et al. Straight Line Extraction via Multi-scale Hough Transform Based on Pre-storage Weight Matrix[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 83–88. |
| [8] | 文贡坚, 王润生. 一种稳健的直线提取算法[J]. 软件学报, 2001, 12(11): 1660–1666. WEN Gongjian, WANG Runsheng. A Robust Approach to Extracting Straight Lines[J]. Journal of Software, 2001, 12(11): 1660–1666. |
| [9] | CHUNG K L, CHEN T C, YAN Wenming. New Memory and Computation-efficient Hough Transform for Detecting Lines[J]. Pattern Recognition, 2004, 37(5): 953–963. DOI:10.1016/j.patcog.2003.09.008 |
| [10] | 王竞雪, 朱庆, 王伟玺, 等. 结合边缘编组的Hough变换直线提取[J]. 遥感学报, 2014, 18(2): 378–389. WANG Jingxue, ZHU Qing, WANG Weixi, et al. Straight Line Extraction Algorithm by Hough Transform Combining Edge Grouping[J]. Journal of Remote Sensing, 2014, 18(2): 378–389. |
| [11] | XU Zezhong, SHIN B S, KLETTE R. Accurate and Robust Line Segment Extraction Using Minimum Entropy with Hough Transform[J]. IEEE Transactions on Image Processing, 2015, 24(3): 813–822. DOI:10.1109/TIP.2014.2387020 |
| [12] | FREEMAN H. Boundary Encoding and Processing[C]//LIPKIN B S, ROSENFELD A. Proceedings of Picture Processing and Psychopictorics. New York:Academic Press, 1970:241-266. |
| [13] | 尚振宏, 刘明业. 运用Freeman准则的直线检测算法[J]. 计算机辅助设计与图形学学报, 2005, 17(1): 49–53. SHANG Zhenhong, LIU Mingye. Line Detection Algorithm Using Freeman Criteria[J]. Journal of Computer-Aided Design & Computer Graphics, 2005, 17(1): 49–53. |
| [14] | 赵丽科, 宋伟东, 王竞雪. Freeman链码优先级直线提取算法研究[J]. 武汉大学学报(信息科学版), 2014, 39(1): 42–46. ZHAO Like, SONG Weidong, WANG Jingxue. Straight Line Extraction Algorithm of Freeman Chain Code Priority[J]. Geomatics and Information Science of Wuhan University, 2014, 39(1): 42–46. |
| [15] | 王竞雪, 宋伟东, 赵丽科, 等. 改进的Freeman链码在边缘跟踪及直线提取中的应用研究[J]. 信号处理, 2014, 30(4): 422–430. WANG Jingxue, SONG Weidong, ZHAO Like, et al. Application of Improved Freeman Chain Code in Edge Tracking and Straight Line Extraction[J]. Journal of Signal Processing, 2014, 30(4): 422–430. |
| [16] | BURNS J B, HANSON A R, RISEMAN E M. Extracting Straight Lines[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(4): 425–455. |
| [17] | VON GIOI R G, JAKUBOWICZ J, MOREL J M, et al. LSD:A Fast Line Segment Detector with a False Detection Control[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(4): 722–732. DOI:10.1109/TPAMI.2008.300 |
| [18] | AKINLAR C, TOPAL C. EDLines:A Real-time Line Segment Detector with a False Detection Control[J]. Pattern Recognition Letters, 2011, 32(13): 1633–1642. DOI:10.1016/j.patrec.2011.06.001 |
| [19] | 王竞雪, 朱庆, 张云生, 等. 叠置分区辅助的相位编组直线提取算法[J]. 测绘学报, 2015, 44(7): 768–774. WANG Jingxue, ZHU Qing, ZHANG Yunsheng, et al. Phase Grouping Line Extraction Algorithm Using Over-lapped Partition[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 768–774. DOI:10.11947/j.AGCS.2015.20140234 |
| [20] | CANNY J. A Computational Approach to Edge Detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(6): 679–698. |
| [21] | ZHANG T Y, SUEN C Y. A Fast Parallel Algorithm for Thinning Digital Patterns[J]. Communications of the ACM, 1984, 27(3): 236–239. DOI:10.1145/357994.358023 |
| [22] | 韩建峰, 宋丽丽. 改进的字符图像细化算法[J]. 计算机辅助设计与图形学学报, 2013, 25(1): 62–66. HAN Jianfeng, SONG Lili. An Improved Thinning Algorithm for Character Image[J]. Journal of Computer-Aided Design & Computer Graphics, 2013, 25(1): 62–66. |
| [23] | HOLT C M, STEWART A, CLINT M, et al. An Improved Parallel Thinning Algorithm[J]. Communications of the ACM, 1987, 30(2): 156–160. DOI:10.1145/12527.12531 |
| [24] | 许宏科, 秦严严, 潘勇. 一种改进的边缘细化方法[J]. 激光与红外, 2014, 44(3): 319–324. XU Hongke, QIN Yanyan, PAN Yong. Improved Edge Thinning Method[J]. Laser & Infrared, 2014, 44(3): 319–324. |
| [25] | CHIN R T, WAN H K, STOVER D L, et al. A One-pass Thinning Algorithm and Its Parallel Implementation[J]. Computer Vision, Graphics, and Image Processing, 1987, 40(1): 30–40. DOI:10.1016/0734-189X(87)90054-5 |



