2. 地理信息工程国家重点实验室, 陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China
作为影像的基本特征,线特征包含了丰富的信息,且比较稳定,所以线特征匹配方法相对于传统的灰度匹配和点特征匹配[1-3]方法在稳定性上有很大的优势,对影像间的视角及亮度差异具有更好的稳定性[4],得到了研究者的广泛关注。影像中的线特征主要包括直线特征等可用数学解析式表达的特征和自由形状线特征两类。因较容易进行表达,前者最早被加以利用,也应用得更广泛,针对这类特征的匹配可分为单直线匹配[5]、直线组合的匹配[6-7]以及直线与特征点组合的匹配[8],这些方法在城区高分辨遥感影像的匹配以及建筑物三维重建等应用中发挥着重要作用。但在自然场景中,线特征更多的表现形式却是自由形状的,如海岸线、道路等,这类特征由一系列连续无规律的边缘点组成,难以通过数学模型解析表达,在处理过程中很难被直接利用[9],所以针对这类特征的研究也相对较少。
文献[10]提出一种经典的自由形状曲线匹配方法——迭代最邻近点法(iterative closest point,ICP),匹配过程中所有点均参与匹配,通过搜索最邻近点确定对应点,能达到较高的匹配精度,但其对匹配的初始条件要求较高,计算量也较大。
目前,对自由形状线特征的匹配研究大体可分为两类:一类是采用描述子对自由形状线特征进行表达后匹配,包括曲率尺度空间的方法、链码、Zernike矩[11]以及对仿射变换具有较好稳定性的傅里叶描述子[12]、Helmholtz描述子[13-14]等,这些方法对图形间的仿射变形具有一定的稳定性,但对线特征的连续性要求较高,匹配的稳定性很大程度上依赖于线特征的稳定性,往往对边缘断裂等问题难以克服,此外,描述子对一些形状较复杂线特征的适应性有待提升[14],且采用描述子进行表达会使曲线变得平滑从而导致部分曲线偏离原始位置,影响匹配精度;另一类则是提取线特征中的部分信息进行匹配,即利用线特征的特征进行匹配,如线特征的角点、闭合线的重心等特征[15-16],这些特征的提取对成像条件的变化有较好的稳定性,但对特征信息量有很大程度的舍弃,难以保证匹配方法达到较高的匹配精度。为较好地解决线特征丰富信息的充分利用与对线特征的有效描述这一对矛盾,本文提出一种利用分级匹配策略的基于自由形状线特征的影像匹配方法。
1 研究方法本文方法包括自由形状线特征提取、匹配所用特征提取、粗匹配和精匹配等主要步骤,整体流程如图 1所示。基本思想是:首先对影像进行亚像素边缘检测并对离散边缘点进行跟踪、精化,得到连续性较好的自由形状线特征;然后分别从中提取用于粗匹配和精匹配的特征;粗匹配时,将根据相似性测度确定的待选同名特征进行两两组合后,依次基于几何信息、模型参数分布剔除误匹配,进而确定精匹配的初始变换参数;最后采用二维ICP法,依次利用由低到高采样率的亚像素边缘点进行精匹配。
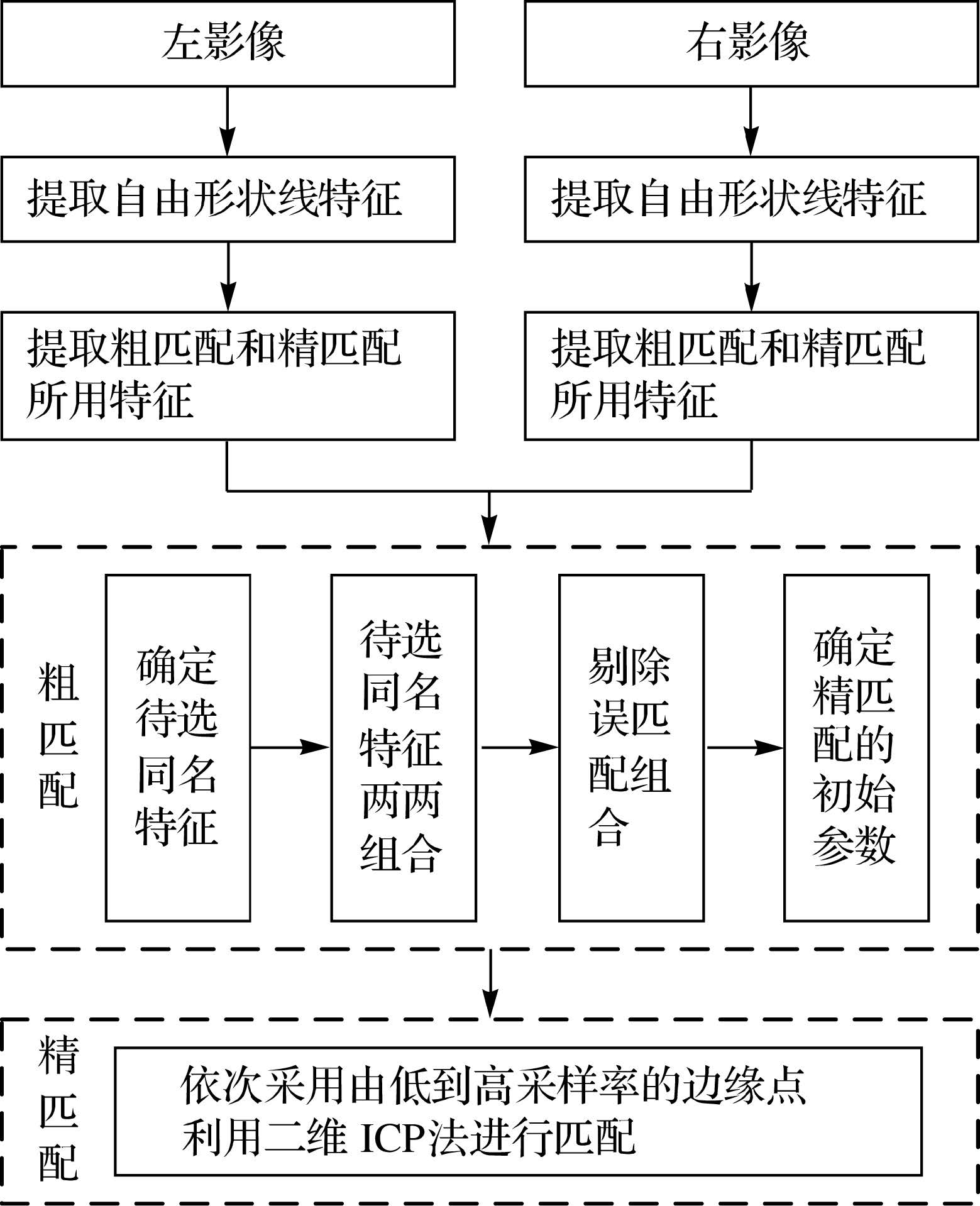
|
| 图 1 自由形状线特征匹配流程 Fig. 1 Flowchart of free-form linear features matching |
1.1 自由形状的亚像素线特征提取
自由形状线特征的提取包括边缘检测和边缘跟踪与精化两个主要步骤,提取的精度直接影响着最终匹配的精度。近年来,随着计算机视觉技术在各领域的应用不断深入,亚像素边缘检测受到了研究者们的广泛关注[17-18]。为了保证本文方法的匹配精度,本文采用文献[18]提出的利用极值梯度的亚像素边缘检测方法对影像中的边缘进行检测。该方法对不同类型的边缘都能较好地检测,具有较好的通用性,并且对包括角点在内的边缘均有较高的定位精度。
极值梯度包括正梯度和负梯度两部分,分别是各像点灰度值增加最大和减少最大的梯度。大小由当前像点与其八邻域像点的灰度差值极值确定,方向为当前像点指向差值极值所对应的邻域像点。通过计算各点的极值梯度,即可得到由局部灰度增加最大和减少最大的两类像点共同组成的初始边缘,再根据初始边缘的特点,分别利用建立的不同边缘类型的亚像素定位模型确定边缘点的精确位置。
边缘检测的结果是离散的边缘点,在对其进行利用前还需进行有效的跟踪。通常,自由形状边缘的形状较复杂且存在相交的情况,加之噪声等因素使得部分边缘断裂、不平滑,而目前大部分的跟踪算法并未对这些情况加以充分的讨论,使得难以对边缘特征进行完整有效的提取,一定程度上制约着自由形状线特征的应用。
针对上述问题,文献[19]提出一种亚像素边缘提取方法,在保持边缘检测高定位精度的基础上,该方法能有效提取连续性较好且平滑的自由形状线特征,在此采用该方法对所检测的边缘点进行跟踪及精化等后处理。为尽可能完整地记录自由形状边缘,根据边缘点的实际分布情况,以边缘连通块为单元对边缘进行跟踪记录;再采用一种双角度长度控制的扩展连接法以尽量恢复边缘的连续性,同时也可避免连接不相关的边缘;最后利用基于曲线内在表示的平滑算法对二维的自由形状线特征进行平滑处理。
1.2 粗匹配所用特征的提取 1.2.1 闭合线特征通过判断起点和终点相同的线特征即可确定闭合线特征。为了使所选取特征具有更好的稳定性,本方法仅将面积大于阈值Ts的闭合线特征用于粗匹配,Ts应不小于30像素,并将利用二阶和三阶中心矩构造的可以描述闭合区域形状特点的7个不变矩作为其匹配实体,这7个不变矩对旋转、平移和缩放都具有较好的不变性。
1.2.2 线特征交点1.1节中所采用的跟踪方法,对线特征进行了较完整的提取,通过判断各边缘点的记录次数是否超过两次即可确定线特征交点。由于多于3个线特征分支的线特征交点的提取容易受噪声的影响,且数量较少,故仅选择包含3个分支且各分支方向较稳定的交点用于匹配,并将各分支之间的3个夹角作为其匹配实体,最大夹角的平分线所在方向记为主方向。
为了保证线特征交点的匹配实体具有更好的唯一性,按如下规则排列3个夹角:从最大的夹角开始且按顺时针排列。各分支间夹角的顺时针排列可通过各分支的方向向量的顺时针排列来实现。通过分析可知,起点相同的3个向量的任意排列只包括顺时针和逆时针排列两种,并且交换后两个向量的顺序即可实现两种方式的互换(如图 2所示,图中数字表示各分支的排列序号)。因此,在计算过程中,通过比较各方向向量的横纵分量判断其排列方式,若是逆时针排列则交换后两个向量的顺序,进而可计算相邻向量间的夹角,最后从最大夹角开始,按顺时针依次记录各夹角即可得到交点的匹配实体。
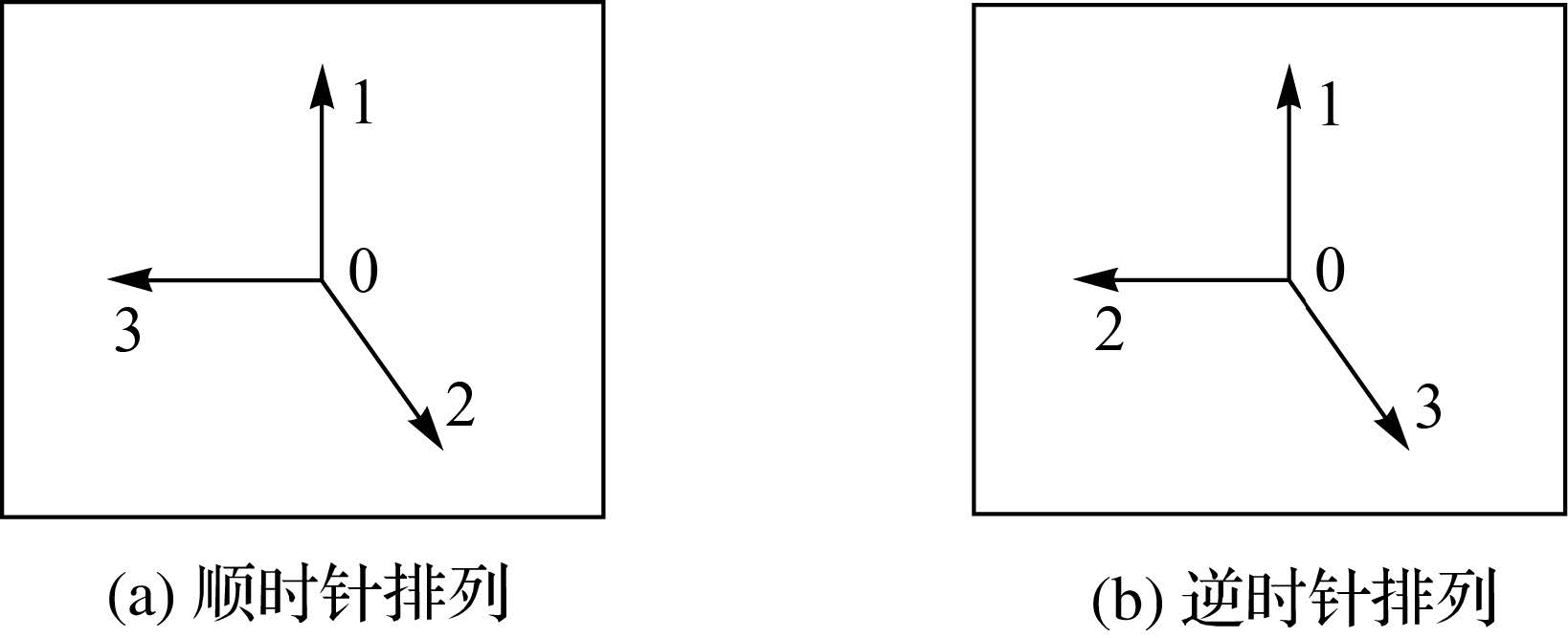
|
| 图 2 3个方向向量的两种排列顺序示意图 Fig. 2 Two arrangement types of three direction vectors |
1.2.3 线特征角点
Douglas-Peucker(DP)法是从整体到局部确定曲线的特征点,对平移、旋转具有不变性,计算效率高,但其阈值不易确定。阈值较大时,易造成过度压缩;反之则对噪声引起的突刺较敏感,易得到错误的特征点。文献[20]提出的基于绝对链码和之差的角点提取方法具有较好的信息压缩能力和抗干扰能力,此处利用该方法对DP法提取的待选角点进行可靠性和准确性检验,下面结合图 3对基本原理进行简要介绍。
设点O是待选角点(即DP法确定的特征点),处理时同时考虑点O及其两侧相邻的两个边缘点Ai、Bi(i=1,2):首先判断点O、点A1、B1的绝对链码和之差是否大于阈值Tc(Tc取3~4),若只有点O满足,则该点为正确的角点;若点A1、B1至少有一点满足,则比较该点与点O作为角点的可靠性,将可靠性最大的点作为角点;若上述3个点均不满足,则进一步对点A2、B2进行判断,当至少有一点满足时,将其与点O可靠性较大的点作为角点;否则将点O作为虚假角点进行剔除。其中,某点作为角点的可靠性根据式(1)进行确定。
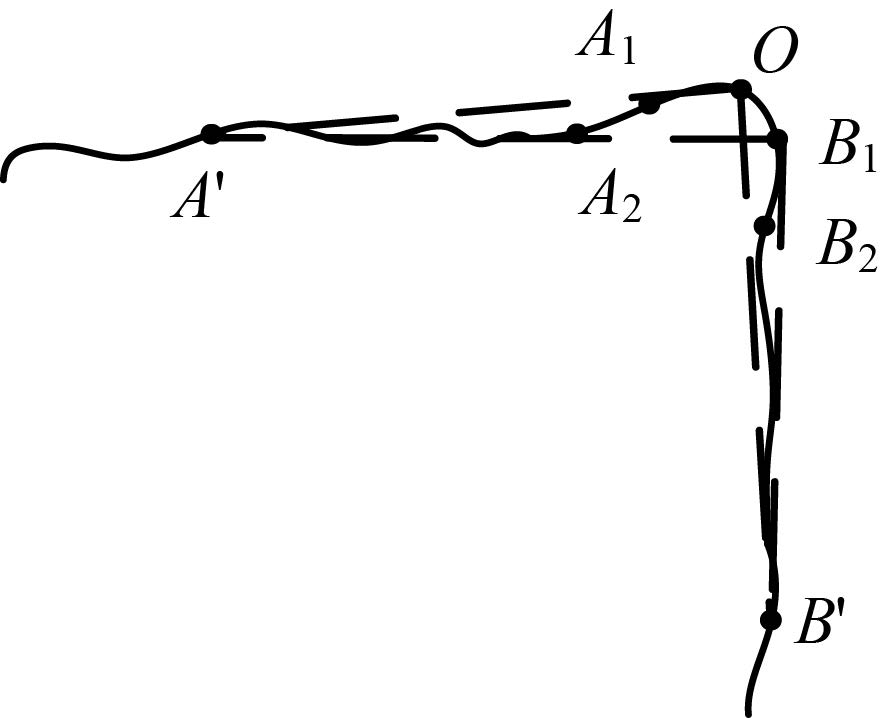
|
| 图 3 角点检验的基本原理 Fig. 3 Basic inspection principle of the LFC |
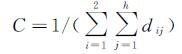 (1)
(1)
式中,d1j和d2j分别表示Pj和Qj到直线l1和l2的距离;li(i=1,2)是待选角点(如图中点O)与其某侧分支上间隔h点的边缘点(如点A′,B′)之间的连线(如OA′,OB′);Pj、Qj(j=1,2,…,h)分别为这两侧分支上的第j个边缘点。
为得到分布均匀、数量适中的角点,仅利用线特征上分支方向稳定且与同一线特征上相邻角点的间隔大于阈值Td的角点,Td应不小于10像素。将角点两侧分支方向向量之间的夹角作为其匹配实体,并将夹角平分线所在方向记为主方向。
1.3 精匹配所用边缘点的提取ICP法被认为是基于纯粹几何模型的三维物体匹配算法,可直接对三维物体无关表面的数据进行处理,无需对物体的特征进行假设和分割,得到了广泛的应用。ICP法在点集精度较高时能得到较高的匹配精度,但其易受噪声点的干扰,鲁棒性较差,并且当点集数量较大时效率较低。
此外,点集的采样率也对该方法的匹配结果有影响。如图 4所示,图 4(a)中3个实心圆点、5个圆点分别为左影像中曲线的两种采样率所包含的数据点,十字叉代表右影像中对应的数据点,图 4(b)、4(c)分别为两种采样率数据点的匹配结果,这表明在数据点具有同等精度的条件下,采样率越高,越可能得到更准确的匹配结果[10]。
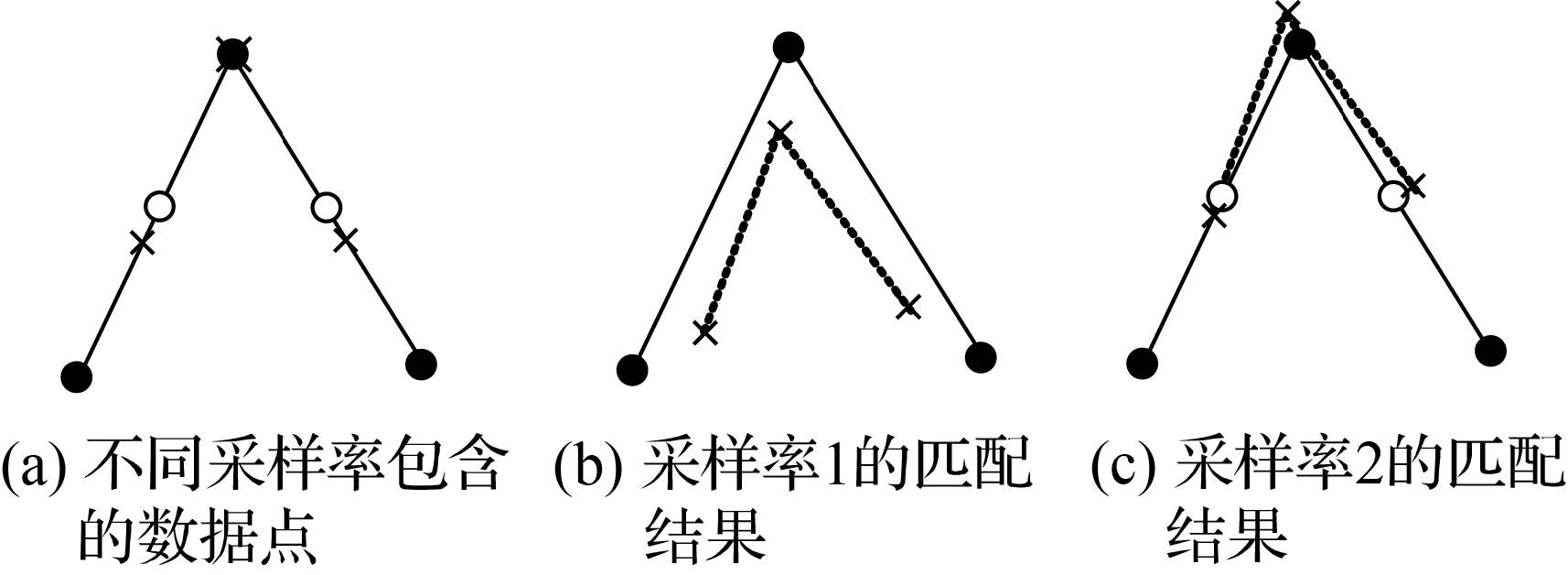
|
| 图 4 曲线不同采样率对匹配结果的影响 Fig. 4 Influence of different sampling rate on matching result |
基于上述分析,对1.1节中提取的自由形状线特征进行下述两步处理,以提取用于精匹配的边缘点,需要说明的是,此处对所有提取的线特征均加以利用,包括闭合的、不闭合单条的以及不闭合存在相交的所有1.1节中提取到的各类线特征。
(1) 结合角点进行线特征平滑处理,减小噪声的影响。考虑到地物特别是人工地物的边缘曲线通常比较光滑,同时为了保持具有较高精度和较好稳定性的角点,在进行1.1节中的线特征平滑处理时,若其中有1.2节中提取的角点,则对这些角点进行保持,仅对各角点之间的边缘曲线进行平滑处理。
(2) 在原始边缘点(1.1节中所提线特征中的边缘点)的基础上分别进行降采样和内插处理,建立边缘点金字塔。降采样时每两个相邻的边缘点保留一个点,并且对其中的线特征角点也进行保留;内插处理则是在所有相邻的两个边缘点中线性内插增加一个点。因此,建立的边缘点金字塔共3层,顶层为经降采样处理后所保留的边缘点,第2层为原始边缘点,底层为原始边缘点和内插增加的点。
1.4 利用多种边缘特征的粗匹配 1.4.1 确定待选同名特征对于闭合线特征,由于其匹配实体的7个不变矩之间的数量级差异较大,采用如式(2)所示的归一化相关算法来度量各闭合线特征之间的相似度
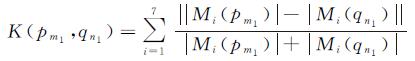 (2)
(2)
式中,Mi(·)表示闭合线特征的第i个不变矩;p·、q·分别代表左、右影像中的闭合线特征,i=1,2,…,7,m1=1,2,…,MCLF,n1=1,2,…,NCLF,MCLF、NCLF分别为左、右影像中闭合线特征数。
依次计算两影像中各闭合线特征之间的相似度,可得矩阵K=(kij)MCLF×NCLF,其中元素kij即为闭合线特征pi和qj之间的相似度K(pi,qj),根据式(3)将每行和每列最小且小于阈值Tk的元素对应的闭合线特征作为待选的同名闭合线特征。
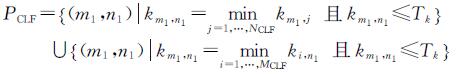 (3)
(3)
对于线特征交点、角点,分别利用式(4)、式(5)确定待选的同名特征。
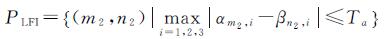 (4)
(4)
式中,α·,i、β·,i分别表示左、右影像中线特征交点匹配实体的第i个角,i=1,2,3;m2=1,2,…,MLFI;n2=1,2,…,NLFI;MLFI、NLFI分别为左、右影像中线特征交点数。
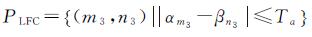 (5)
(5)
式中,α·、β·分别表示左、右影像中线特征角点的匹配实体,m3=1,2,…,MLFC;n3=1,2,…,NLFC;MLFC;NLFC分别为左、右影像中线特征角点数。
为保证方法对仿射变形的适应性及抗噪性,阈值Tk和Ta取值稍大,取值范围分别为4.2~4.9、10°~20°。
1.4.2 待选同名特征的两两组合在遥感图像处理中,二维(或三维)的相似变换可近似代替许多二维(或三维)的变换,并因其变换参数较少,可独立求解而得到广泛应用,本文便将二维相似变换作为粗匹配的变换模型。
由于经过相似变换的特征之间只存在缩放、旋转和平移,故两影像中各特征的面积和特征间的距离有相同的缩放比例,特征的主方向和特征之间的连线则应有相同角度的旋转。此外,利用两对同名特征即可求解一组二维相似变换参数,根据两对正确同名特征组成的组合(简称“正确组合”)确定的参数会比较接近真实值,即各正确组合所确定的参数分布相对集中,而其中至少有一对待选同名特征不是正确同名特征组成的组合(简称“误匹配组合”)所确定参数则会存在较大的差异。
因此,在确定待选同名特征后,将各类特征分别进行两两组合,得到若干组待选同名特征组合(简称“待选组合”),并根据上述待选组合的特点,对误匹配组合进行剔除。
1.4.3 剔除误匹配组合根据1.4.2 节中分析的待选组合所具有的特点,剔除误匹配组合主要包括基于几何信息和基于模型参数分布两个步骤,流程如图 5所示。
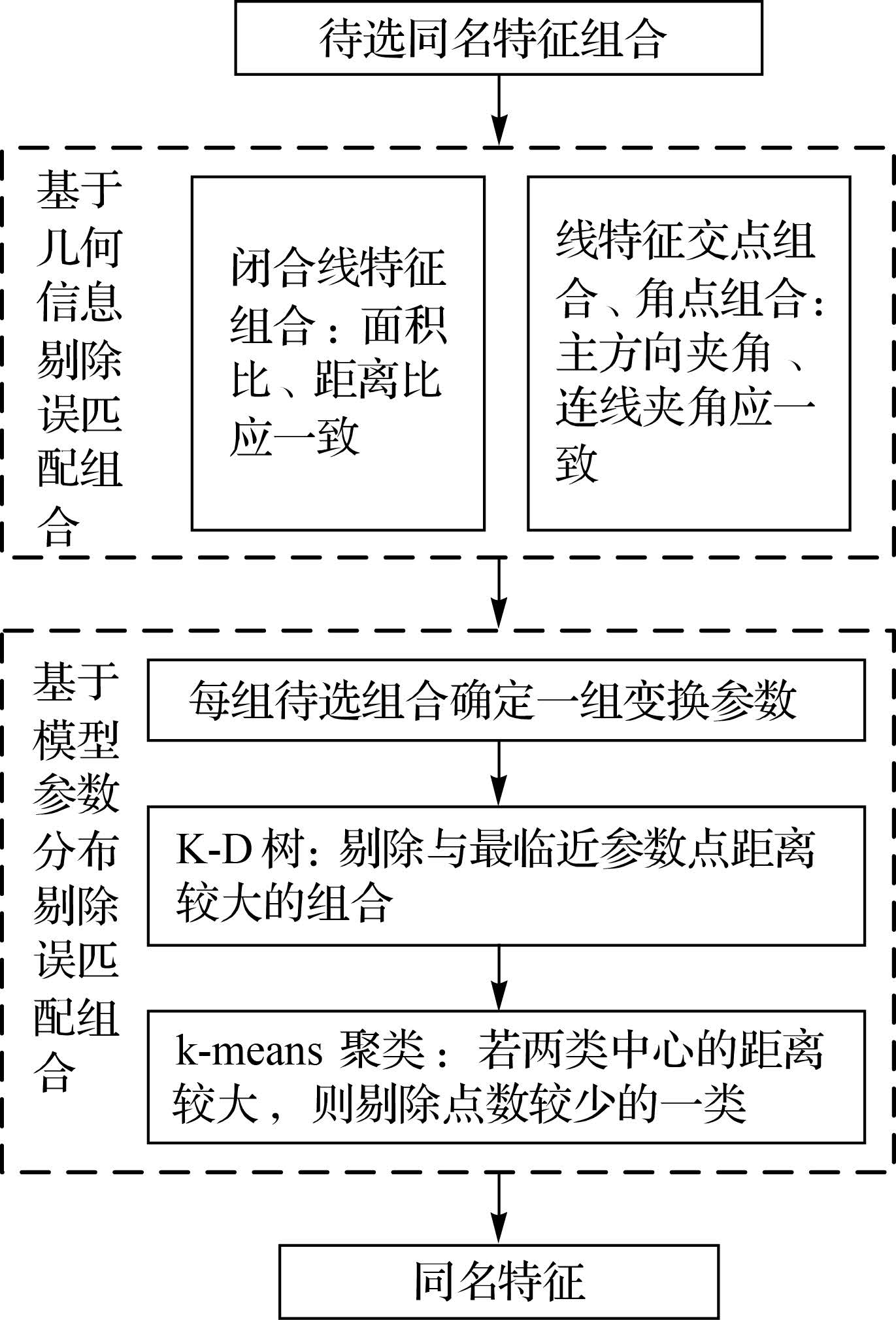
|
| 图 5 剔除误匹配组合流程 Fig. 5 Flowchart of elimination false matching combinations |
基于几何信息剔除误匹配组合的基本原理为:
(1) 对于闭合线特征,两影像中待选同名特征的面积比、特征组合之间的距离比应保持一致,比值差异大于阈值Tdr的则判定为误匹配组合。
若两影像中的闭合线特征分布如图 6所示,设N1(p2,q1)、N2(p2,q2)、N3(p3,q3)和N4(p4,q4)是根据相似性测度确定的4对待选同名特征,其中N1为误匹配,将其进行两两组合得到N1N2、N1N3、N1N4、N2N3、N2N4、N3N4共6种待选组合,依次计算如式(6)所示的各组合的最大比例差异度量dR(式(6)以组合N1N3为例),并将dR大于阈值Tdr的组合判定为误匹配组合进行剔除,Tdr取0.08~0.12。
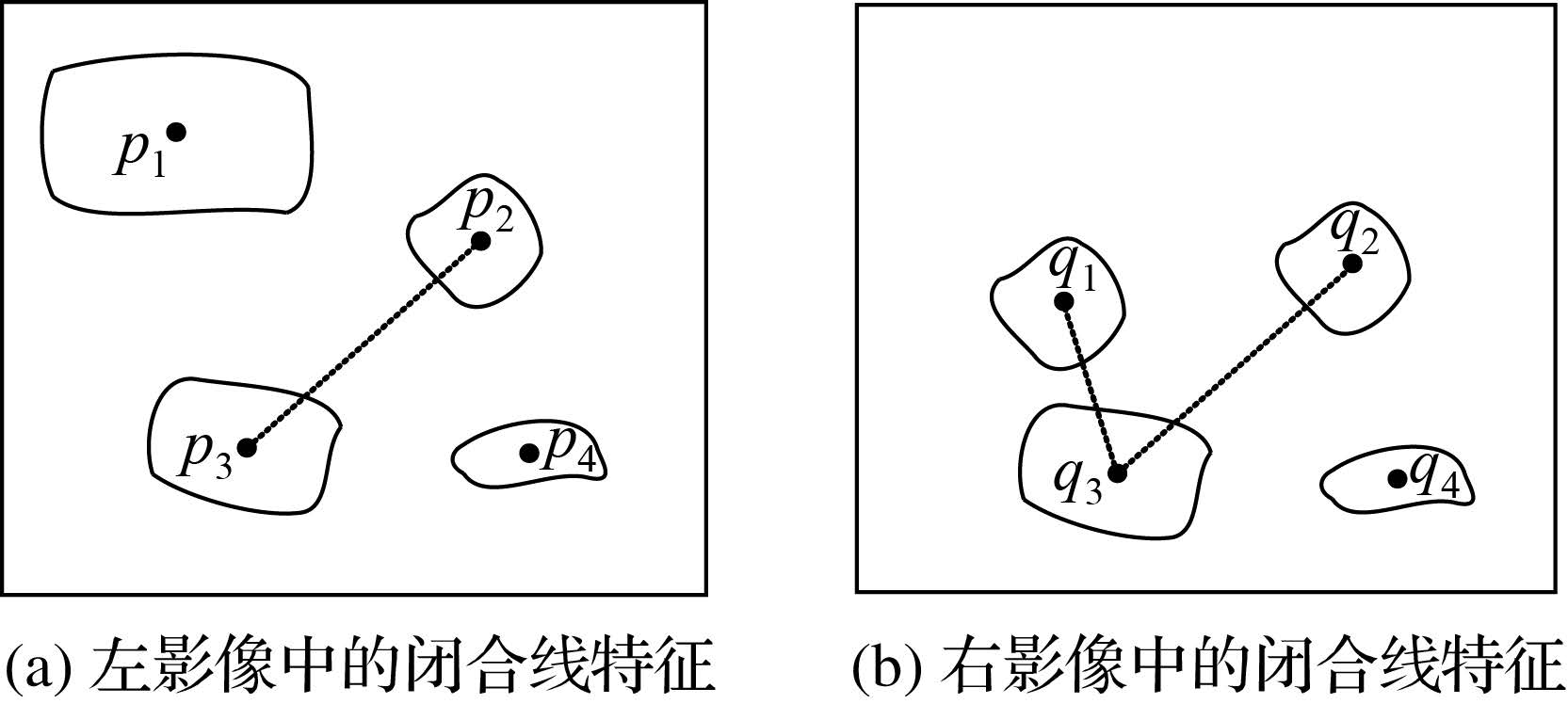
|
| 图 6 利用几何信息剔除误匹配组合的原理 Fig. 6 False matching combinations elimination principle based on geometric information |
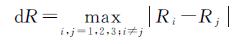 (6)
(6)
式中,
(2) 对于特征交点和角点,根据待选同名特征主方向之间的夹角、特征组合连线之间的夹角一致的原则进行判断,将角度差异较大的判定为误匹配组合。
下面再根据变换参数的分布特点进一步剔除误匹配组合。利用剩余的各待选组合均可确定一组变换参数,将这些参数视为高维空间(R4)中的点,进行下面两步处理:
(1) 利用各空间点建立K-D树,并搜索各点的最邻近点(即差异最小的变换参数),剔除与最邻近点的距离超过阈值Tkd的空间点对应的组合,Tkd取[0.08~0.12,5°~7°,6~10像素,6~10像素]T。
(2) 利用k-means法将剩余点分为两类,若两类点的中心的距离小于阈值Tkm,则认为剩余点已相对集中,根据剩余的待选组合确定同名特征;否则保留点数较多的一类继续利用k-means法进行分类,直至两类点中心的距离满足阈值要求或者剩余点少于3,对于后一种情形,则认为未找到同名特征,Tkm取Tkd~2Tkd。
通过分析和试验验证可知,闭合线特征数量适中、性能稳定,为保证效率,粗匹配时首先仅匹配闭合线特征,当有3对以上的正确同名特征实现匹配时,将其作为先验信息确定同名交点和角点;否则再利用上述方法确定同名交点和角点。
1.5 采用多层次二维ICP法的精匹配精匹配利用式(7)来表达两影像间的变换关系,该模型通常在两影像间变换模型较复杂或未知时选用[21]
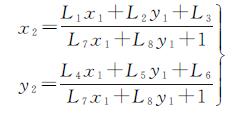 (7)
(7)
式中,L=[L1L2L3L4L5L6L7L8]T是投影变换参数;(x1,y1)为左影像中边缘点的像坐标;(x2,y2)为边缘点(x1,y1)经变换后在右影像中最邻近的边缘点坐标。
在方程两侧同时乘以分母,对其进行线性化可得
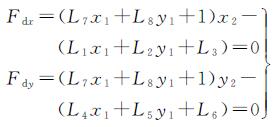 (8)
(8)
因此,利用二维ICP法进行迭代计算时的误差方程和法方程分别如式(9)和式(10)所示
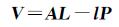 (9)
(9)
式中,
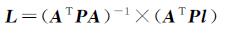 (10)
(10)
式中,P是权矩阵,权值根据同名点之间的距离确定。
根据上文分析可知,精匹配时按从顶层到底层的顺序依次对各层边缘点进行匹配可兼顾匹配的效率和精度,具体流程如图 7所示。
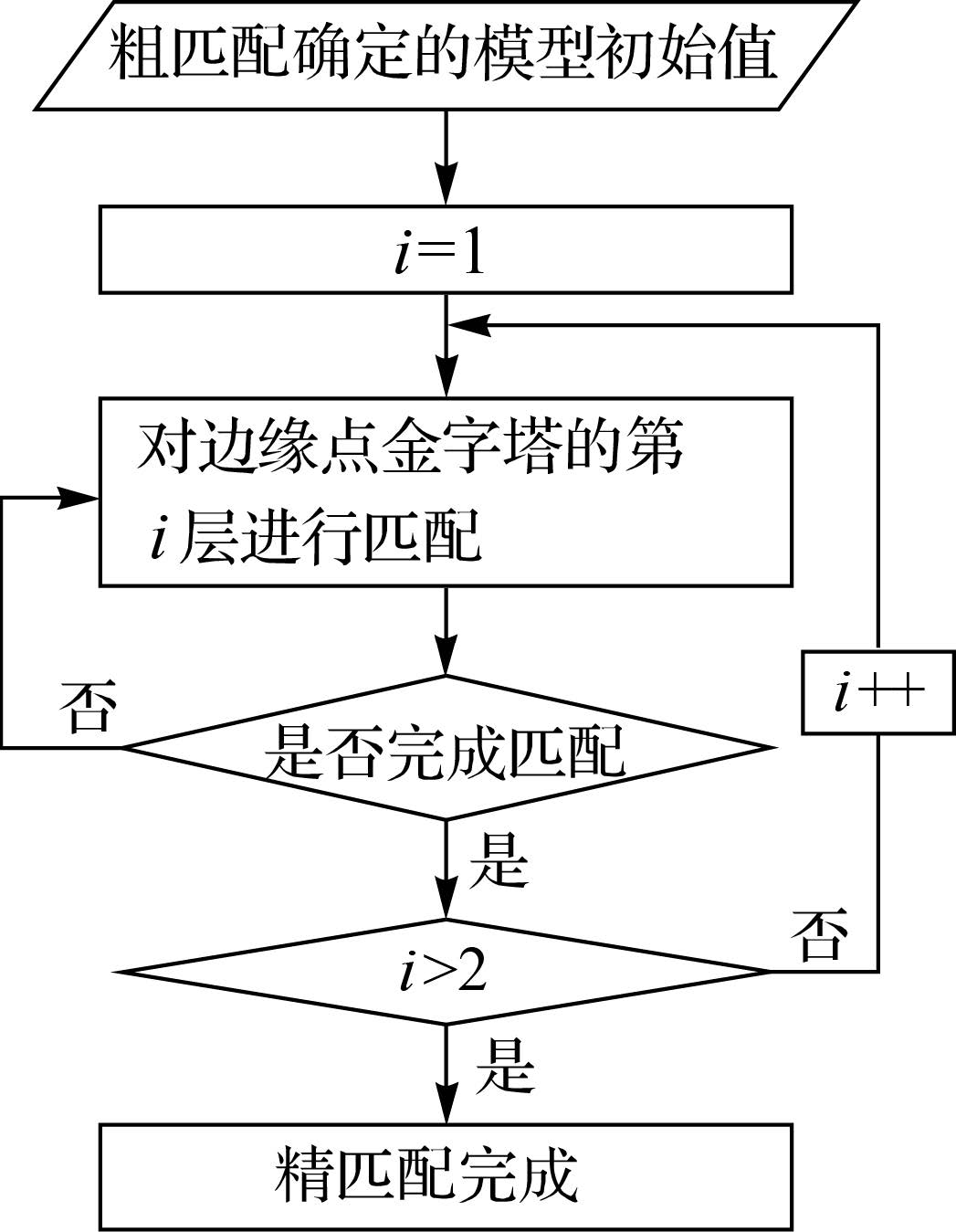
|
| 图 7 精匹配流程 Fig. 7 Flowchart of accurate matching |
匹配时上一层边缘点匹配确定的变换参数作为下一层边缘点匹配的初始值,底层确定的变换参数则为最终确定的变换参数。各层边缘点进行匹配时,首先根据变换参数将左影像中的边缘点变换至右影像中,并利用K-D树搜索各变换点的最邻近边缘点,对应点即为同名点;然后利用同名点按上述计算模型改正变换参数;最后判断是否完成该层边缘点的匹配(变换参数的改正值小于阈值Tdl),若是则对下一层边缘点进行匹配;反之,则按照上述迭代计算模型继续对变换参数进行改正。
2 试验结果与分析 2.1 试验1:利用模拟数据验证粗匹配的稳定性及精度为验证本文方法提取的用于粗匹配的各类特征的稳定性以及粗匹配方法的正确率和精度,设计了具有不同旋转角度和缩放系数的影像间的匹配试验。选取某城区航空影像的局部区域(图 8(a))作为基准影像,大小为339×353像素,利用两组相似变换参数(见表 2)得到如图 8(b)、8(c)所示的两幅模拟影像,两幅影像分别包含较小和较大角度的旋转以及一定程度的缩放。

|
| 图 8 基准影像和经相似变换生成的模拟影像 Fig. 8 Reference image and simulated images generated by the similarity transformation |
利用本文方法分别将两幅模拟影像与基准影像进行粗匹配试验,根据前文给出的各阈值的参考取值范围,各阈值设置情况如下:Ts=30像素,Tc=3,Td=10像素,Tk=4.5、Ta=15°,Tdr=0.10、Tkd=[0.10,6°,8像素,8像素]T、Tkm=1.5Tkd,Tdl=[0.0010.0010.050.0010.0010.050.0010.001]T,试验2、3所设参数相同。提取的各类特征及匹配结果如表 1所示,第1列表示从基准影像中提取的特征数,模拟影像对应的3列数据分别为从模拟影像中提取的特征数(提取)、所提取特征中有同名特征的特征数(实际)、粗匹配确定的同名特征数(匹配)及其中正确的同名特征数(括号内的数字)。根据粗匹配确定的同名特征计算的相似变换参数如表 2所示。
| 统计参数 | 基准影像 | 模拟影像1 | 模拟影像2 | |||||
| 提取 | 实际 | 匹配 | 提取 | 实际 | 匹配 | |||
| 闭合线特征 | 11 | 11 | 4 | 4(4) | 16 | 6 | 6(6) | |
| 线特征交点 | 8 | 14 | 0 | 0(0) | 10 | 1 | 1(1) | |
| 线特征角点 | 64 | 123 | 33 | 33(33) | 92 | 35 | 33(33) | |
| 参数 | 模拟影像1 | 模拟影像2 | |||
| 实际参数 | 粗匹配结果 | 实际参数 | 粗匹配结果 | ||
| s | 1.200 0 | 1.200 4 | 1.100 0 | 1.101 0 | |
| α/(°) | 20.000 0 | 19.997 8 | 170.000 0 | 170.010 8 | |
| tx/像素 | 180.000 0 | 179.917 5 | 450.000 0 | 450.087 6 | |
| ty/像素 | 30.000 0 | 29.867 4 | 400.000 0 | 400.268 5 | |
为定量评价匹配精度,从基准影像中选取在行列方向上均间隔10像素的点作为检查点(共计1155个),分别利用实际变换参数和匹配确定的变换参数计算各检查点在模拟影像中的理论坐标和计算坐标,通过对检查点两种坐标的差值进行分析从而评价匹配精度。这些检查点均匀分布于整幅影像,利用其可以对匹配精度进行较好的评价,两幅模拟影像与基准影像的匹配试验中检查点在列方向(x)、行方向(y)以及整体(xy)误差的统计结果如表 3所示。
| 像素 | |||||||||||
| 影像 | x | y | xy | ||||||||
| |min| | |max| | RMSE | |min| | |max| | RMSE | |min| | |max| | RMSE | |||
| 模拟影像1 | 0.00 | 2.40 | 0.70 | 0.03 | 1.11 | 0.48 | 0.06 | 2.42 | 0.85 | ||
| 模拟影像2 | 0.01 | 1.36 | 0.44 | 0.02 | 1.54 | 0.57 | 0.05 | 1.56 | 0.71 | ||
由表 1可知,本文方法从影像中提取的闭合线特征数量适中,线特征角点最多,这两类特征对旋转、缩放变换以及噪声具有较好的稳定性,从变换前后的影像中能提取到适量的同名特征;提取的线特征交点及对应的同名特征均较少,这主要是由于重采样、噪声等原因使得线特征提取时在这些位置较难在各个分支方向仍然保持较好的连续性,任意一个分支未完整提取均会造成该点不能检测为特征性交点。由匹配结果可知,本文方法对各类特征的同名特征均能实现较好的匹配:匹配的准确率高,漏匹配率低,且没有误匹配。由表 2和表 3可知,粗匹配确定的变换参数与实际变换参数很接近,检查点在行方向和列方向上的中误差均较小,整体中误差小于±1个像素,这表明本方法的粗匹配即具有较高的匹配精度。
综上可知,粗匹配所选取的各类特征稳定可靠,利用它们进行粗匹配切实可行,粗匹配方法具有较高的准确率和精度,且能保持较低的误匹配率和漏匹配率,稳定性较好,可为精匹配提供准确可靠的初始值。
2.2 试验2:利用仿射变换生成的模拟数据验证本方法的精度本试验利用通过仿射变换生成的模拟影像与基准影像进行匹配,并与SIFT[1]、ASIFT[2]、MSER[3]等经典点特征匹配方法以及最小二乘影像匹配(least square matching,LSM)的精度进行比较,以验证本文方法的精度以及对仿射变形的适应性。
利用如图 9(a)、9(d)所示的两幅影像进行模拟试验:第1幅影像为长江流域某段的天绘一号全色影像,分辨率为5 m,影像大小为560×750像素,该区域包括河流、池塘、道路等地物,其中的边缘特征多为自由形状;第2幅影像为德黑兰广场的QuickBird全色影像,分辨率为0.61 m,影像大小为930×1000像素,该区域主要包括道路以及不规则形状的草坪等地物。模拟影像分别由原始影像根据表 4中的两组仿射变换参数变换得到,如图 9(b)、9(e)所示。
| 参数 | a11 | a12 | a13 | a21 | a22 | a23 |
| 变换参数1 | 1.020 0 | -0.050 0 | 35.000 0 | 0.010 0 | 1.050 0 | 15.000 0 |
| 变换参数2 | 1.050 0 | 0.100 0 | 10.000 0 | -0.050 0 | 1.120 0 | 70.000 0 |

|
| 图 9 存在仿射变换关系的影像间的匹配 Fig. 9 Matching results between affine deformation image and original image |
两组数据的匹配结果如图 9(c)、9(f)所示,由于精匹配确定的同名点较多,未对同名点进行连线。利用与试验1相同的方法对各种方法的匹配精度进行评价,检查点的中误差统计结果如表 5所示。
| 像素 | |||||||
| 方法 | 影像1 | 影像2 | |||||
| x | y | xy | x | y | xy | ||
| SIFT | 0.07 | 0.15 | 0.17 | 0.15 | 0.07 | 0.16 | |
| ASIFT | 0.05 | 0.17 | 0.17 | 0.69 | 0.10 | 0.69 | |
| MSER | 0.08 | 0.19 | 0.21 | 0.02 | 0.03 | 0.03 | |
| SIFT+LSM | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 粗匹配 | 0.19 | 0.50 | 0.53 | 0.17 | 0.22 | 0.28 | |
| 精匹配 | 0.02 | 0.00 | 0.02 | 0.01 | 0.01 | 0.01 | |
由试验结果可知,粗匹配的精度与SIFT、ASIFT等经典的点特征匹配方法在一个数量级,可为精匹配提供较准确的初始值;精匹配时有大量定位精度较高的亚像素边缘点参与匹配,匹配精度高,检查点在行、列方向的误差以及整体误差的最大值均小于±0.10像素,整体中误差优于±0.02像素,与LSM精度相当(整体中误差优于±0.01像素),即本文方法可达到与LSM相当的亚像素级匹配精度。试验影像的覆盖范围内包括河流、道路等典型的具有自由形状线特征的地物,由图 9中的匹配结果可知,各类地物的边缘点都得到了充分的利用,同时试验影像涵盖了米级和亚米级的高分辨率卫星影像,这些均表明本文方法对不同场景、不同分辨率的遥感影像具有较好的适应性。此外,试验结果还表明本文方法对仿射变换也具有一定的适应性,当影像间存在的仿射变形不严重时,利用本文方法仍然能实现高精度的匹配。
2.3 试验3:遥感立体影像的匹配试验本试验利用美国加州圣塔芭芭拉分校(UCSB)提供的该校区的IKONOS影像,该区域内包含建筑物、海域、湖泊等地物类型,影像大小分别为1024×1024像素,1064×1172像素,试验影像和匹配结果如图 10所示,由图 10(c)可知,建筑物、道路、湖泊等具有不同边缘形状特点的地物的边缘都得到了较充分的利用。
下面对匹配精度进行定量评价。理论分析以及试验2的结果均表明LSM具有很高的匹配精度,可达±0.10~±0.01像素,甚至更高;此外,由于本文方法与LSM的基本原理不同,两种方法的精度高低不存在相关性,所以本文试验中将SIFT+LSM确定的变换参数视为实际变换参数,并用于确定检查点在待匹配影像中的理论坐标,参照前两组试验的定量评价方法对各种方法的匹配精度进行比较,各种方法所确定的同名特征数及检查点中误差统计结果如表 6所示。

|
| 图 10 IKONOS影像的匹配结果 Fig. 10 Matching result between IKONOS satellite images |
| 数据 | SIFT | ASIFT | MSER | 粗匹配 | 精匹配 |
| 同名特征数 | 2981 | 905 | 208 | 39 | 26 852 |
| RMSE_x(像素) | 0.35 | 0.14 | 0.08 | 0.12 | 0.02 |
| RMSE_y(像素) | 0.52 | 0.44 | 0.02 | 0.18 | 0.01 |
| RMSE_xy(像素) | 0.62 | 0.46 | 0.08 | 0.22 | 0.02 |
从图 10和表 6可知,本方法对只有部分重叠的高分辨率航天影像也能实现较好的匹配,粗匹配能达到与SIFT、ASIFT、MSER等经典的点特征匹配方法相当的精度,精匹配与LSM的精度相当,与试验2的结果一致。因此,本文试验进一步验证了本文方法的匹配特征性能稳定,匹配策略切实可行,具有较高的匹配正确率和精度。
3 结 语在自由形状线特征的匹配研究中,特征中丰富信息的充分利用与有效描述是一对矛盾,这在一定程度上制约着这类方法的发展。此外,正是由于仅有线特征被利用,这类方法对线特征中的误差更敏感,最终匹配的可靠性和精度很大程度上依赖于线特征的可靠性和精度。为较好地解决上述问题,本文提出一种利用分级匹配策略的基于自由形状线特征的遥感影像匹配方法。试验结果表明,本文方法选取的用于粗匹配的特征性能稳定可靠,粗匹配具有较高的正确率和精度,能为精匹配提供较好的初值,精匹配能达到与最小二乘影像匹配相当的亚像素级精度。此外,本方法对较小的仿射变形也具有较好的稳定性。需要说明的是,尽管本方法涉及较多的阈值参数,但都具有较广的适用性,文中针对不同分辨率、不同场景的航空航天遥感影像的几组试验都采用同一组阈值取值,均能得到较稳定、准确的匹配结果,因此,参数较多并不影响本方法的自动化水平。后续研究中,一方面提高线特征提取方法抗噪能力等方面的性能,以得到连续性更好的自由形状线特征;另一方面则试图对自由形状线特征中具有较好仿射不变性的特征进行研究,以进一步提高匹配方法的抗仿射能力。
| [1] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [2] | MOREL J M, YU Guoshen. ASIFT:A New Framework for Fully Affine Invariant Image Comparison[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 438–469. DOI:10.1137/080732730 |
| [3] | MATAS J, CHUM O, URBAN M, et al. Robust Wide-baseline Stereo from Maximally Stable Extremal Regions[J]. Image and Vision Computing, 2004, 22(10): 761–767. DOI:10.1016/j.imavis.2004.02.006 |
| [4] | VASSILAKI D I, IOANNIDIS C C, STAMOS A A. Multitemporal Data Registration through Global Matching of Networks of Free-form Curves[C]//FIG Working Week 2009:Surveyors Key Role in Accelerated Development. Eilat, Israel:FIG, 2009:TS 6B 1-18. |
| [5] | 王竞雪, 宋伟东, 王伟玺. 同名点及高程平面约束的航空影像直线匹配算法[J]. 测绘学报, 2016, 45(1): 87–95. WANG Jingxue, SONG Weidong, WANG Weixi. Line Matching Algorithm for Aerial Image Based on Corresponding Points and Z-plane Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 87–95. DOI:10.11947/j.AGCS.2016.20140527 |
| [6] | KIM H, LEE S. Simultaneous Line Matching and Epipolar Geometry Estimation Based on the Intersection Context of Coplanar Line Pairs[J]. Pattern Recognition Letters, 2012, 33(10): 1349–1363. DOI:10.1016/j.patrec.2012.03.014 |
| [7] | ZHANG Li.Automatic Digital Surface Model (DSM) Generation from Linear Array Images[D]. Zurich, Switzerland:Institute of Geodesy and Photogrammetry, Swiss Federal Institute of Technology, ETH, 2005. |
| [8] | SAEEDI P, MAO M. Two-edge-corner Image Features for Registration of Geospatial Images with Large View Variations[J]. International Journal of Geosciences, 2014, 5(11): 1324–1344. DOI:10.4236/ijg.2014.511109 |
| [9] | VASSILAKI D I, IOANNIDIS C C, STAMOS A A. Automatic ICP-based Global Matching of Free-form Linear Features[J]. The Photogrammetric Record, 2012, 27(139): 311–329. DOI:10.1111/phor.2012.27.issue-139 |
| [10] | ZHANG Zhenyou. Iterative Point Matching for Registration of Free-form Curves and Surfaces[J]. International Journal of Computer Vision, 1994, 13(2): 119–152. DOI:10.1007/BF01427149 |
| [11] | CHEN Zen, SUN Shukuo. A Zernike Moment Phase-based Descriptor for Local Image Representation and Matching[J]. IEEE Transactions on Image Processing, 2010, 19(1): 205–219. DOI:10.1109/TIP.2009.2032890 |
| [12] | EKOMBO P L E, ENNAHNAHI N, OUMSIS M, et al. Application of Affine Invariant Fourier Descriptor to Shape-based Image Retrieval[J]. International Journal of Computer Science and Network Security, 2009, 9(7): 240–247. |
| [13] | ZULIANI M, BERTELLI L, KENNEY C S, et al. Drums, Curve Descriptors and Affine Invariant Region Matching[J]. Image and Vision Computing, 2008, 26(3): 347–360. DOI:10.1016/j.imavis.2006.12.001 |
| [14] | 张桂梅, 马珂, 储珺. 基于薄膜振动模型的曲线匹配方法[J]. 电子学报, 2013, 41(10): 1917–1925. ZHANG Guimei, MA Ke, CHU Jun. A New Curve Matching Method Based on Membrane Vibration Model[J]. Acta Electronica Sinica, 2013, 41(10): 1917–1925. |
| [15] | NG E S, KINGSBURY N G. Matching of Interest Point Groups with Pairwise Spatial Constraints[C]//Proceedings of the 17th IEEE International Conference on Image Processing. Hong Kong:IEEE, 2010:2693-2696. |
| [16] | WU Bo, ZHANG Yunsheng, ZHU Qing. Integrated Point and Edge Matching on Poor Textural Images Constrained by Self-adaptive Triangulations[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 68: 40–55. DOI:10.1016/j.isprsjprs.2011.12.005 |
| [17] | DA Feipeng, ZHANG Hu. Sub-pixel Edge Detection Based on an Improved Moment[J]. Image and Vision Computing, 2010, 28(12): 1645–1658. DOI:10.1016/j.imavis.2010.05.003 |
| [18] | 陈小卫, 徐朝辉, 郭海涛, 等. 利用极值梯度的通用亚像素边缘检测方法[J]. 测绘学报, 2014, 43(5): 500–507. CHEN Xiaowei, XU Zhaohui, GUO Haitao, et al. Universal Sub-pixel Edge Detection Algorithm Based on Extremal Gradient[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(5): 500–507. DOI:10.13485/j.cnki.11-2089.2014.0073 |
| [19] | 陈小卫, 张保明, 郭海涛, 等. 一种亚像素边缘提取方法[J]. 测绘科学技术学报, 2014, 31(6): 624–629. CHEN Xiaowei, ZHANG Baoming, GUO Haitao, et al. An Edge Curve Extraction Method Based on Sub-pixel Edge[J]. Journal of Geomatics Science and Technology, 2014, 31(6): 624–629. |
| [20] | 李富裕, 李言俊, 张科. 链码技术在景象图像特征提取中的应用[J]. 中国图象图形学报, 2008, 13(1): 114–118. LI Fuyu, LI Yanjun, ZHANG Ke. The Use of the Chain-code Technique in Extracting Feature Point in Scene Image[J]. Journal of Image and Graphics, 2008, 13(1): 114–118. |
| [21] | 季顺平, 袁修孝. 基于RFM的高分辨率卫星遥感影像自动匹配研究[J]. 测绘学报, 2010, 39(6): 592–598. JI Shunping, YUAN Xiuxiao. Automatic Matching of High Resolution Satellite Images Based on RFM[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 592–598. |


