2. 武汉大学遥感信息工程学院, 湖北 武汉 430079;
3. 北京中测智绘有限责任公司, 北京 100830
2. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China;
3. Smart Mapping Technology Inc., Beijing 100830, China
区域网平差是遥感数据几何处理,特别是解析空中三角测量中的关键技术之一。经过几十年的发展,其理论方法已较为成熟,应用也十分广泛,几乎涉及与遥感数据几何处理相关的各个应用领域,如航空航天摄影测量,基于影像的城市三维建模等;在计算机视觉领域,区域网平差同样是三维重建,虚拟现实中的十分重要的技术。传统的区域网平差方法主要是采用列文伯格-马夸尔特法(levenberg marquardt,LM)[1]模型,逐点构建误差方程,构建法方程以及改化法方程,通过对法方程系数矩阵求逆,计算法方程的解(未知数改正数),更新未知数,通过反复迭代直到收敛,即可最终得到未知数(内外方位元素)的解。上述模型对于处理传统的规则航空摄影影像十分有效,然而随着科技的发展,大量新兴传感器不断涌现,数据获取方式和来源发生了巨大的变化,如倾斜摄影、无人机摄影、车载相机摄影、普通手持相机摄影等,相应的,也有很多学者对这些新数据进行了大量的研究[1-4],提出了一些新的方法,但平差效率问题仍然存在。与传统的规则航空摄影相比,新的数据呈现出不同的特点,如排列不规则、重叠度的方向和大小不一等。而随着地理空间信息逐步进入大数据时代[5],平差的大数据量问题也日益凸显,新的数据源给区域网平差带来了新的难题和挑战。
针对传统的LM区域网平差模型,很多学者研究了法方程的存储和运算问题,例如,如何优化法方程系数矩阵的最小带宽,以减少法方程系数矩阵的内存需求[6-9],这些研究均是基于影像排列的规律性,如果影像的排列呈随机性,法方程系数矩阵的结构不满足带状条件,则必须存储整个法方程。此时法方程系数矩阵将会耗费大量内存,即便现代计算机性能已经得到大幅提升,但是当影像数超过5000张时,普通计算机仍然会面临内存不足的问题,因此必须寻找其他替代方法来解决上述难题。
如前所述,法方程(改化法方程,对法方程的改化是常用办法,为了便于表达,若无特殊说明,下文中法方程均是仅含有外方位元素未知数的改化法方程)的存储和求逆是两大难题,为了解决这两大难题,可以引入一种迭代求解大型线性方程组的算法,用于替代传统的直接求逆方法。最为典型的迭代求解方法包括最速下降法(steepest descent method)[10]、共轭梯度算法等。共轭梯度算法是由文献[1]在1952年提出[11],该算法采用迭代逼近的方法求解法方程,迭代次数与法方程系数矩阵的条件数密切相关。法方程系数矩阵的条件数越大,所需的迭代次数越大。为了减少迭代次数,可引入预条件矩阵,通过将该矩阵左乘于法方程等式两边,减少法方程系数矩阵的条件数,从而加快迭代收敛速度。预条件矩阵的选择必须是构造简单、易于求逆,且左乘法方程系数矩阵之后,可以降低法方程系数矩阵的条件数。常用的预条件矩阵有雅可比预条件矩阵(Jacobi)[12-15]、对称逐次超松弛(symmetric successive over-relaxation,SSOR)预条件矩阵[14-15]、基于QR分解的预条件矩阵[14]、平衡不完全分解(balanced incomplete factorization,BIF)预条件矩阵[16]、多尺度预条件矩阵[17]等。其中Jacobi预条件矩阵是最常用且最稳定的预条件矩阵。引入预条件矩阵在一定程度上减少了共轭梯度法迭代次数,但当法方程系数矩阵较大时,其迭代次数仍可达到数百次[18],为了进一步减少迭代次数,本文引入一种基于共轭梯度的不精确牛顿解法(inexact/truncated newton method),其基本思想是在共轭梯度法迭代求解法方程过程中,改变迭代收敛条件,提前终止迭代。该方法用一组强制序列系数(forcing sequence)来替代共轭梯度法迭代中的残差向量,每次迭代分别计算一次该系数,当强制序列系数小于某个阈值时即终止迭代,此时得到的法方程解称为它的一组不精确牛顿解[12, 14]。由于整个区域网平差本身也是一个迭代近似逼近的过程,因此用不精确牛顿解替代法方程的精确解,在一定程度上是可行的,经过测试表明,在保证最终精度的同时,可以大幅减少共预条件轭梯度法迭代次数。
预条件共轭梯度法避免了对法方程系数矩阵的直接求逆,在迭代求解的过程中,每次只需要计算一次法方程系数矩阵与向量的乘积即可。但该方法仍面临法方程的存储问题,如果不存储法方程,则必须在每一次共轭梯度法迭代中对法方程进行实时计算一次,这将是一个非常耗时的过程,此时可考虑引入GPU高性能并行计算方法。文献[19]介绍了一种GPU并行区域网平差方法,使得平差的效率得到了提升,但受限于GPU的单精度运算能力,其平差精度还是不如CPU方法。本文选择CPU方法进行研究,提出一种对法方程系数矩阵压缩存储格式。常用的矩阵压缩格式是稀疏行压缩法(compressed sparse row,CSR)[20],它是一种以行为单位来进行压缩存储的格式,对普通稀疏矩阵较为适用。其他的压缩方法还有如对角压缩法(diagonal,DIA)[21]、ELLPACK/ITPACK(ELL)[22]等,但这些压缩方法均破坏了法方程系数矩阵的块状结构(每组外方位元素未知数对应着一个6×6大小的块),因此实际的压缩和恢复操作较为复杂,本文使用一种分块压缩方法对法方程系数矩阵进行压缩存储,在法方程系数矩阵中,以每一组外方位元素未知数所构成的6×6小区域为一个分块,仅存储非零块,并建立索引,且由于法方程的对称性,仅需要存储上三角矩阵中的非零块即可。在进行矩阵-向量积运算时,当需要某个分块的数据时,则通过索引从内存中取出对应的分块,然后乘以向量中对应的位置,将结果累加至结果向量中,在所有分块处理完毕之后,即可得到矩阵-向量积的结果向量。
综上所述,本文引入预条件共轭梯度法及其不精确牛顿解法至区域网平差流程中,建立全新的区域网平差技术流程,同时使用一种分块压缩方法对法方程系数矩阵进行压缩存储和运算[18],以应对区域网平差中大数据带来的内存和计算效率问题。通过分别采用本方法、传统办法以及国际上其他同类方法对总共10组真实数据进行试验,验证本文方法相较于传统发方法在内存需求以及计算效率方面的优越性,并检查本文提出方法的平差精度。
1 理论与方法 1.1 区域网平差区域网平差的主要目标是恢复每张影像的内外方位元素,从而得到像点坐标与物方点坐标之间的相互转换关系,其基本理论方法已经十分成熟,在共线条件方程的基础上,对所有像点观测值列出一个误差方程组,然后法化得到法方程,通过求解法方程得到未知数改正数,更新未知数并重新进入下一次迭代,直到满足退出条件为止。以传统的区域网平差为例,若不考虑内方位元素作为未知数的情况,即内方位元素为给定值,在平差之前已经做好了检校工作,误差方程表达形式如式(1)所示
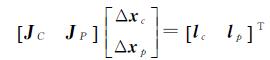 (1)
(1)
式中,JC、JP分别对应误差方程系数中的外方位元素部分和地面点未知数部分;lc、lp分别代表误差方程常数项向量中外方位元素部分和地面点未知数部分;Δxc、Δxp分别对应未知数改正数向量中外方位元素部分和地面点未知数部分。
将上述误差方程法化,从而得到法方程,如式(2)所示
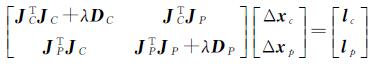 (2)
(2)
式中,λDC、λDP分别对应外方位元素未知数和地面点未知数的阻尼系数(damping value),对于没有控制点的测区,阻尼系数有助于控制未知数改正数的变化幅度,避免因为法方程系数矩阵的奇异性造成不稳定解的情况[17,19,23]。将式(2)简化之后得到式(3)
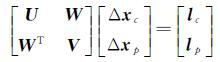 (3)
(3)
式中,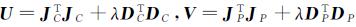
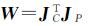
通过对法方程中的地面点未知数进行消元处理,得到改化的法方程,如式(4)所示
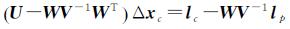 (4)
(4)
此时,通过解算式(4)可以得到外方位元素未知数改正数,再将其回代至式(5)中求解得到地面点坐标未知数
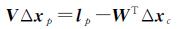 (5)
(5)
但在实际处理中,地面点未知数往往通过利用新的外方位元素进行前方交会得到。
1.2 预条件共轭梯度法共轭梯度法是一种迭代求解大型线性方程组的方法,给定一个线性方程组(6)
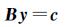 (6)
(6)
式中,B是线性方程组的系数矩阵;y是未知数向量;c是常数项向量。
共轭梯度法求解的基本思想是,给定线性方程组(6)的初始解x0,然后根据线性方程组系数矩阵,常数项向量,计算共轭梯度法迭代的残差向量,方向向量,然后计算线性方程组的新解x1,重复上述过程,直到其方向向量的模小于给定的阈值,也即线性方程组的解的改变量小于给定阈值,即可退出迭代,此时的解xn即为线性方程组的最终解。
理论上共轭梯度法收敛的次数与线性方程组系数矩阵的条件数密切相关,条件数越大,需要迭代的次数越多.因此,为了减少迭代次数,则需要降低线性方程组系数矩阵的条件数.可以在线性方程组(6)两端分别左乘一个预条件矩阵M-1,得到式(7)
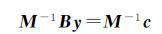 (7)
(7)
此时,系数矩阵变为M-1B,其迭代次数也相应变为矩阵M-1B的条件数,通过选取合适预条件矩阵M,可以有效降低线性方程组的条件数,从而减少解算时的迭代次数。预条件矩阵M的选取需要满足一定的原则,即构造简单且易于求逆,同时与系数矩阵相乘后可以减少系数矩阵的条件数。本文采用应用范围较广,且计算简单,效果稳定的块状Jacobi预条件矩阵。其他的一些预条件矩阵可能效果更好,但是计算复杂且稳定性差[18]。
在区域网平差计算中,可以对法方程(4)采用预条件共轭梯度法迭代求解,块状Jacobi预条件矩阵则是由法方程系数矩阵中对角线上的块状子矩阵构成,其结构示意图如图 1所示。

|
| 图 1 块状Jacobi预条件矩阵的结构示意图 Fig. 1 Structure of the block Jacobi preconditioner matrix 图中每一个子块由3×3个元素组成(本文中每组外方位元素有6个元素,对应的块状Jacobi预条件矩阵是由对角线上的6×6大小的子块组成)。 |
如前所述,引入预条件矩阵的目的是为了在共轭梯度法求解法方程的过程中,减少系数矩阵的条件数,从而减少共轭梯度法的迭代次数。块状Jacobi预条件矩阵是构造最为简单,易于求逆,且效果最为稳定的预条件矩阵,满足预条件矩阵的选取原则,因此本文选择块状Jacobi预条件矩阵来进行处理。
预条件共轭梯度法的具体技术流程如下所示:
针对线性方程组(6),给定初始参数:y0=0,r0=c-By0,d0=M-1r0,k=0;
Do
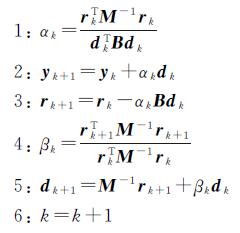
While(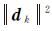
如图 2所示,本文算法包括两种迭代过程,一种是区域网平差迭代,一种是预条件共轭梯度法迭代求解法方程,后者被包含于前者当中,预条件共轭梯度法迭代的目的是求得法方程的解,然后利用这组解继续进行区域网平差迭代。由于两种迭代都是近似逼近的过程,对预条件共轭梯度法迭代而言,该迭代过程只有在前几次迭代会对未知数有较大的改进,后面的若干次迭代对未知数的改进并不大,而这后面的若干次迭代仍然会消耗大量的计算资源和时间,因此可以考虑提前结束预条件共轭梯度法迭代,此时虽然只得到了一组法方程的不精确解,但如果使用这组不精确的解继续进行区域网平差迭代,不影响区域网平差的最终精度,则可认为提前结束预条件共轭梯度法是可行的,此时,只需要确定在何时停止迭代即可。
本文引入一种不精确牛顿解法,其基本思想是引入新的迭代收敛条件(判断强制序列系数Forcing sequence是否小于指定阈值),通过设定强制系数的阈值,提前终止迭代,用法方程的一种不精确解替代其精确解,从而达到减少迭代次数的目的。强制序列系数ηk的计算方法如式(8)所示
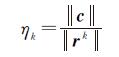 (8)
(8)
式中,k为迭代次数;
由于区域网平差解算本身就是一种近似逼近的过程,因此用法方程不精确解替代精确解是可行的,在不影响平差的最终精度的情况下,可以大幅降低共轭梯度法迭代次数,本文试验部分将对此方法的有效性进行试验验证。引入不精确牛顿解后,1.1节预条件共轭梯度法流程中的迭代退出条件应该由“While(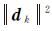
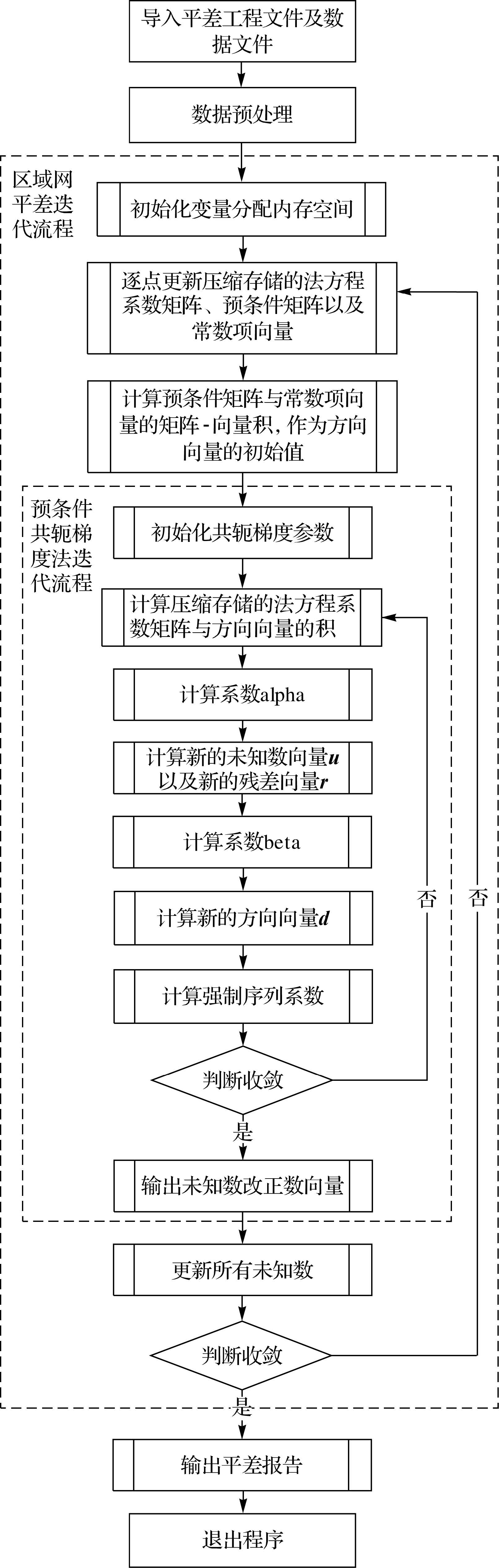
引入预条件共轭梯度法、不精确牛顿解以及法方程系数矩阵的压缩存储方法后,传统的区域网平差流程需要进行彻底的改变,传统的逐点生成法方程后,更新法方程时,必须根据索引找到该点生成子块在压缩后法方程中的位置,然后取出对应的子块,并与当前子块累加,然后将结果更新至压缩存储的法方程中,求解法方程时,不再需要对法方程进行求逆运算,而是区域按照1.2节中的步骤,通过预条件共轭梯度法迭代求解法方程。全新的区域网平差技术流程如图 2所示。
|
| 图 2 基于预条件共轭梯度法的区域网平差技术流程 Fig. 2 The whole workflow of the bundle adjustment with PCG algorithm |
1.5 法方程系数矩阵的压缩存储与计算
一般来讲,在传统区域网平差中,如果采用算法对法方程系数矩阵进行压缩,由于改变了法方程的存储结构,则在对压缩的法方程求逆时,其操作非常复杂,而本文采用预条件共轭梯度法迭代求解法方程,无须对法方程系数矩阵进行直接求逆运算,求解过程中只需要每次迭代时计算法方程系数矩阵与某个向量的乘积即可,因此该方法为法方程系数矩阵的压缩存储提供可能,同时,为了适应区域网平差中法方程系数矩阵的块状结构,本文使用一种分块矩阵压缩方法[18]。该方法的基本思想是以每一个子块矩阵为单元(每个子块对应两组外方位元素的协方差,即每个子块大小为6×6),仅存储非零子块,舍去为零的子块,将法方程系数矩阵中的上三角部分(由于法方程是对称矩阵,因此只需要存储其上三角矩阵:图 3中的黑色填充块)的非零子块按照从左到右,从上到下的顺序依次存储至一个一维存储结构,如图 4所示。同时记录每个子块在原始法方程中的位置和大小,即图 4中的第2行,其具体存储方法如图 3和图 4所示。

|
| 图 3 待压缩的系数块状矩阵 Fig. 3 The uncompressed block matrix |
从图 3和表 1可以看出,本文使用的法方程系数矩阵压缩存储方法的最小操作单位是一个子块矩阵,该子矩阵对应一组外方位元素未知数,由于对法方程系数矩阵的运算均是以子块矩阵为单位,因此本压缩算法可以继承法方程的块状结构,保留了法方程系数矩阵在构建,存储以及运算过程中的块状结构特性。同时,本文采用预条件共轭梯度法求解法方程,无需对法方程系数矩阵进行直接求逆运算,仅需要计算法方程系数矩阵与某个向量的乘积,因此可以考虑将矩阵与向量的乘积,分解为各个子块矩阵分别与向量对应位置的乘积,然后累加。由于压缩算法保留了块状结构,因此压缩存储后,可以方便地进行矩阵向量积运算。本算法的压缩效率与法方程系数矩阵的稀疏程度密切相关,法方程系数矩阵越稀疏,则其压缩效率越高,反之亦然。
| 子块序号 | 0 | 1 | 2 | 3 | … | 13 | 14 |
| 子块信息 | (0,0,6,6) | (0,5,6,6) | (1,1,6,6) | (1,6,6,6) | … | (8,8,6,6) | (9,9,6,6) |
| 子块数据 | Sub-block1 | Sub-block2 | Sub-block3 | Sub-block4 | … | Sub-block13 | Sub-block14 |
2 试验结果与分析 2.1 数据及试验环境
采用10组数据对本文提出的方法进行试验,这10组数据中,一部分是由数码相机以及手机拍摄得到,还有一部分是直接从网络上下载的拍摄同一区域的影像[12],这些影像从拍摄角度、距离、分辨率以及相机的焦距等各不相同,影像的分布呈随机性,不满足规则排列。为了验证本文提出的方法在内存使用效率,计算效率以及平差精度等个方面的性能,并与传统的算法在上述各个方面进行全方位对比。本文使用的数据信息如表 2所示。
| 数据 | 来源 | 影像数 | 地面点 | 影像点 |
| 1 | 手机 | 40 | 8272 | 23 681 |
| 2 | 网络 | 52 | 64 063 | 347 143 |
| 3 | 无人机 | 84 | 127 939 | 560 900 |
| 4 | 网络 | 88 | 64 298 | 383 937 |
| 5 | 无人机 | 228 | 249 829 | 895 702 |
| 6 | 网络 | 394 | 100 368 | 534 408 |
| 7 | 网络 | 961 | 187 103 | 1 692 975 |
| 8 | 网络 | 1936 | 649 673 | 5 213 733 |
| 9 | 网络 | 4585 | 1 324 582 | 9 125 125 |
| 10 | 网络 | 13 682 | 4 456 117 | 28 972 841 |
表 2中,地面点是指匹配得到的地面连接点数量,影像点则是这些地面点对应于不同影像上的同名像点。另外,除了第3组数据中存在少量地面控制点,用于检查控制点平差精度,其余测区由于均不是来自于常规航空摄影,大多为网络下载的影像,因此基本上无地面控制点数据可用。所有测区平差均采用无控制点自由网平差方式,第3组数据则额外进行带控制点平差,用于检查控制点平差精度,具体结果见2.5节。除了网络下载的影像外(网络下载影像数据由Sameer在其个人网站公开的数据,且带有已经匹配好的连接点数据)[12],其余测区的连接点数据均由本课题组研发的空三匹配软件匹配得到,所使用的平差软件是由作者自主开发的区域网平差软件。本文中所有试验使用的硬件配置为Inter (R) Core(TM) i5-33320M CPU 2.60GHz,8.00GB RAM,软件环境为Windows 10操作系统。
2.2 权策略在区域网平差中,观测值权的选择可以在一定程度上削弱粗差对平差系统的影响,本文的给观测值的初始权均为1,在每次区域网平差迭代之后,根据各观测值的残差重新计算各观测值的权值,若观测值的残差大于给定的阈值,则给该观测值一个较小的权,若观测值的残差小于给定的阈值,则观测值的权保持不变。未知数的权为单位1,如1.1节所述,由于在法方程中加入了阻尼项(damping term),因此可以约束未知数的改正数,使其在特定的范围变化,以避免平差系统因为没有控制点而发生迭代不收敛的情况。
2.3 内存使用对比对10组试验数据,分别统计传统算法以及本文提出算法的内存使用情况,该内存包括了整个算法中各个数据项占用内存的总和(包括原始数据,法方程系数矩阵,常数项向量,其他变量等),也即算法程序运行的实际内存,其结果如表 3所示。
| 数据 | 影像数 | 传统方法/MB | 本文方法/MB |
| 1 | 40 | 2.0 | 1.5 |
| 2 | 52 | 15.7 | 13.2 |
| 3 | 84 | 16.3 | 14.4 |
| 4 | 88 | 17.0 | 14.9 |
| 5 | 314 | 57.7 | 30.8 |
| 6 | 394 | 63.6 | 19.93 |
| 7 | 961 | 313.7 | 134.5 |
| 8 | 1936 | 1 214.1 | 509.6 |
| 9 | 4585 | 5 959.5 | 1 363.2 |
| 10 | 13 682 | 52 939.2 | 3 202.6 |
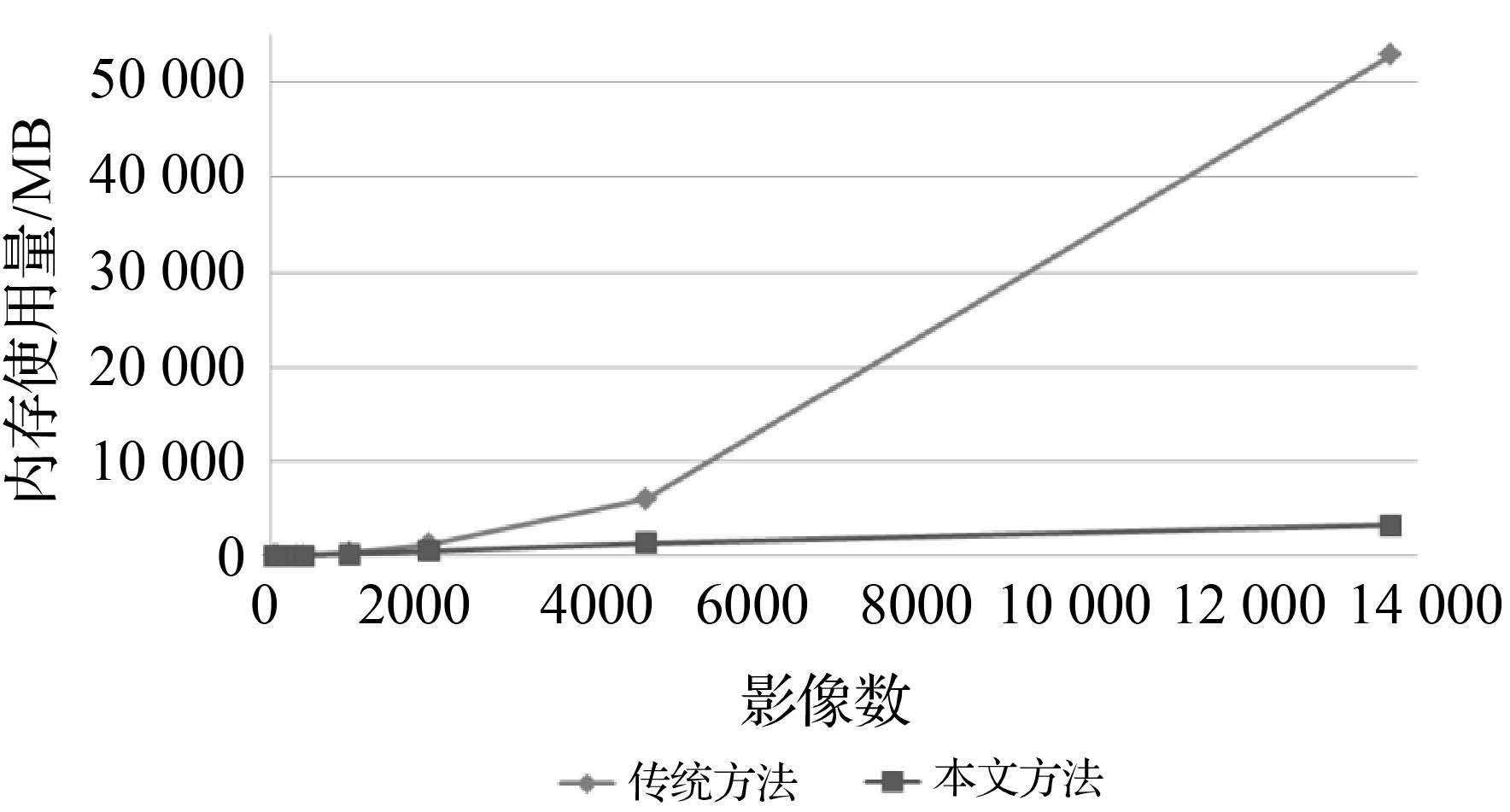
从表 3和图 4中可以看出,本文方法对内存的需求明显低于传统办法的内存需求,传统的方法对内存的需求随着影像数的增加呈近似指数式增长,而本文方法则仅呈现线性增长。当影像数增加到13 682时,传统的办法需要至少53 GB内存,才能进行运算,而本文方法则只需要约3 GB内存即可。
|
| 图 4 传统方法与本文方法的内存使用对比图 Fig. 4 Comparison of memory requirement of conventional method and proposed method |
2.4 平差效率对比
分别使用传统的方法和本文方法对10组试验数据进行区域网平差处理(图 5),并记录每组数据采用不同平差方法所使用的时间,如表 4所示。
| 数据 | 影像数 | 地面点/s | 传统方法/s | 本文方法/s |
| 1 | 40 | 8272 | 1.0 | 0.968 |
| 2 | 52 | 64 063 | 42.3 | 39.6 |
| 3 | 84 | 127 939 | 21.5 | 22.0 |
| 4 | 88 | 64 298 | 55.4 | 50.1 |
| 5 | 228 | 249 829 | 103.3 | 64.7 |
| 6 | 394 | 100 368 | 501.9 | 38.7 |
| 7 | 961 | 187 103 | 1 422.1 | 444.6 |
| 8 | 1936 | 649 673 | 10 301.8 | 1 368.4 |
| 9 | 4585 | 1 324 582 | N/A | 935.5 |
| 10 | 13 682 | 4 456 117 | N/A | 5 766.7 |
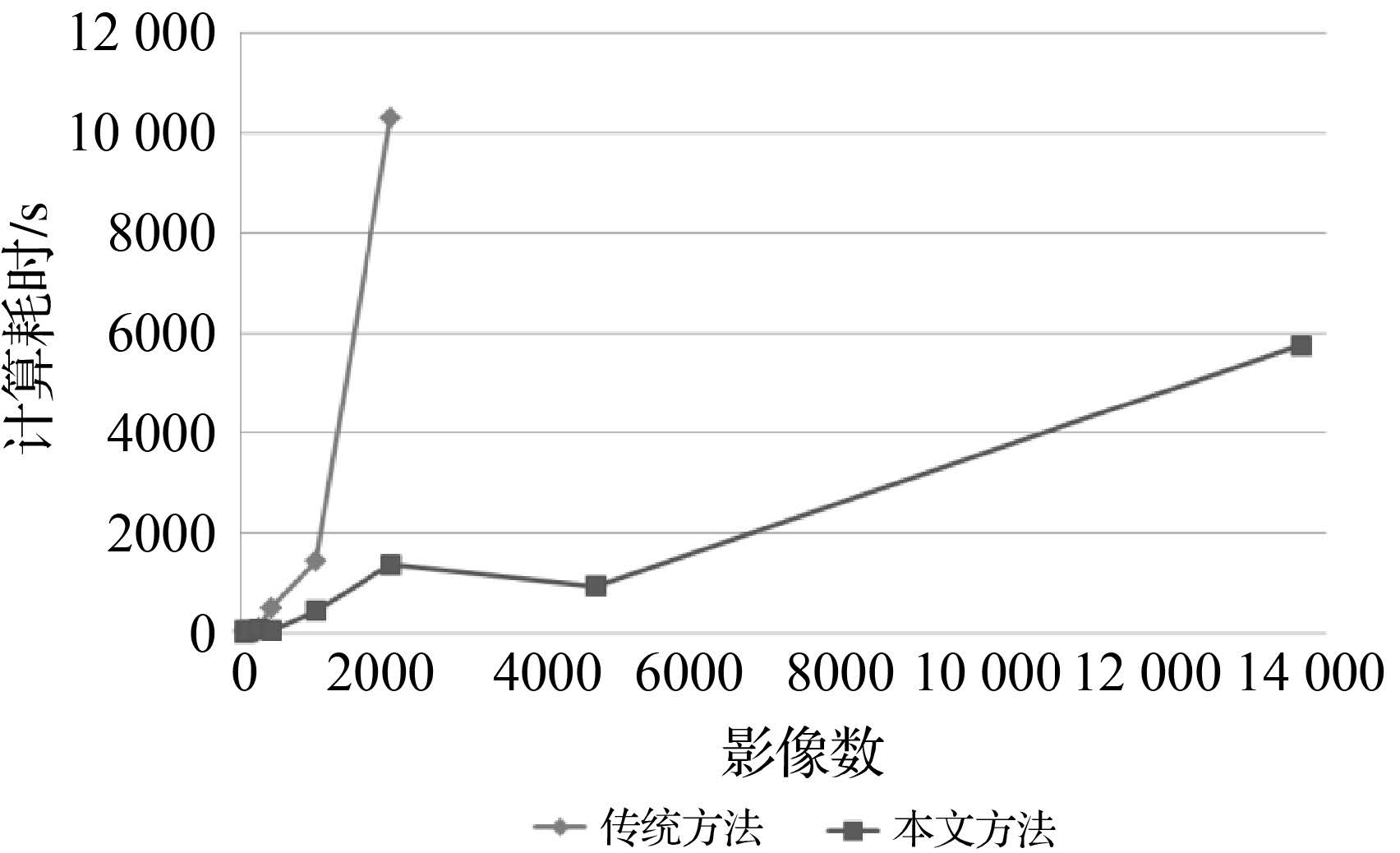
|
| 图 5 不同算法的计算耗时对比 Fig. 5 The computation time for different methods |
从表 4和图 5可以看出,传统方法平差的计算耗时也随着影像数的增加呈指数式增加,而本文算法则随着影像数的增加呈近似的线性增长趋势。当影像数较小时,本文算法和传统的算法计算耗时相当,无明显区别,而随着影像数逐渐增加至200以上时,本文算法逐渐显现出其优越性,继续增加影像数,本文算法的优势更加明显,计算速度可提升3~10倍。值得指出的是,当影像数达到4585及以上时,传统的算法由于受到内存大小的限制,无法进行平差,而本文算法由于采用了法方程系数矩阵压缩存储算法,仍然可以正常进行平差处理,且计算耗时在可接受范围内。此时的计算速度比影像数为1936时的计算速度还要快,这是由于在本文的预条件共轭梯度法迭代求解法方程过程中,其迭代次数根据不同观测网型结构、粗差数量以及内外方位元素初始值的准确度的不同而有明显区别,因此出现影像数较大的测区比影像数较小的测区平差所需时间要少的情况是可能的。在传统算法中,影响平差系统计算速度的主要是法方程的求逆运算,而随着影像数增加,法方程的大小呈指数级增长,因而其计算耗时也呈指数级增长。本文算法采用预条件共轭梯度算法求解法方程,无需对法方程系数矩阵进行直接求逆运算,且由于采用了法方程系数矩阵压缩算法,平差系统的耗时大大降低,仅随着影像数的增加而呈线性增长。
2.5 平差精度对比本文算法在内存使用和计算效率方面均优于传统的算法,为了全方位验证本文方法的优越性,还需要比较本文算法与传统算法在平差精度方面的表现。还是对上述10组数据分别采用传统算法和本文算法进行处理,并将其精度指标进行对比分析(本文由于没有使用控制点和检查点,因此精度指标用相对精度来衡量,即用像点残差来表示)。具体精度统计信息如表 5所示。
| 像素 | ||||||
| 数据 | 影像数 | 传统算法 | 本文算法 | |||
| x | y | x | y | |||
| 1 | 40 | 0.479 | 0.624 | 0.443 | 0.553 | |
| 2 | 52 | 0.751 | 0.564 | 0.750 | 0.563 | |
| 3 | 84 | 0.457 | 0.195 | 0.458 | 0.193 | |
| 4 | 88 | 0.685 | 0.689 | 0.525 | 0.547 | |
| 5 | 314 | 0.282 | 0.247 | 0.282 | 0.247 | |
| 6 | 394 | 0.644 | 0.601 | 0.644 | 0.601 | |
| 7 | 961 | 0.732 | 0.639 | 0.732 | 0.639 | |
| 8 | 1936 | 0.817 | 0.809 | 0.818 | 0.809 | |
| 9 | 4585 | N/A | N/A | 0.819 | 0.740 | |
| 10 | 13 682 | N/A | N/A | 0.781 | 0.746 | |
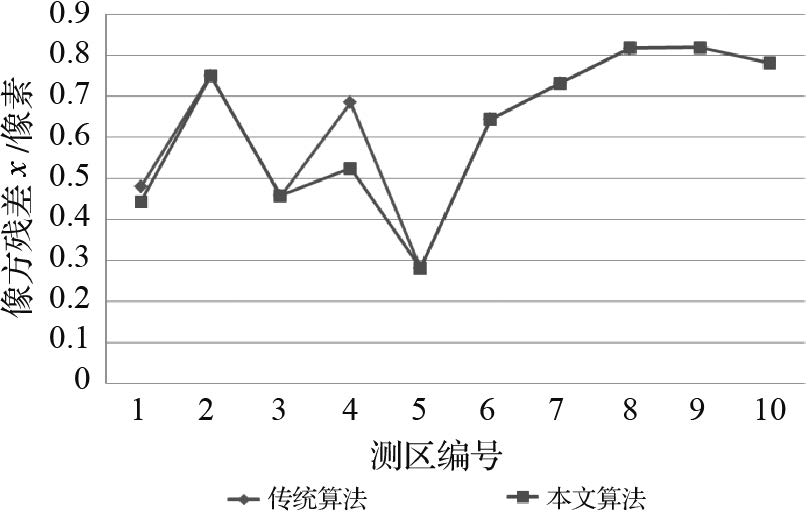
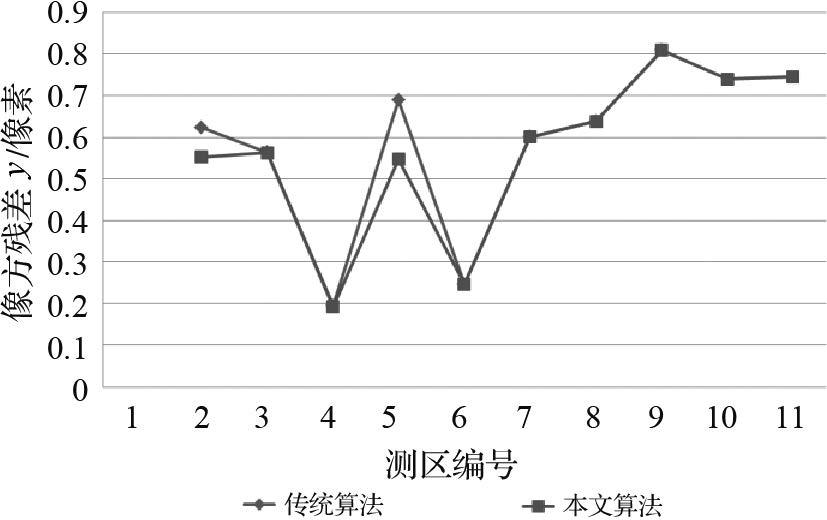
如表 5和图 6、7所示,本文算法在平差精度上与传统算法相当,二者的精度差异在实际应用中可忽略不计。
|
| 图 6 本文算法与传统算法x方向的残差对比 Fig. 6 The comparison of reprojection error of the conventional method and proposed method in x direction |
|
| 图 7 本文算法与传统算法y方向的残差对比 Fig. 7 The comparison of reprojection error of the conventional method and proposed method in y direction |
以上试验均是不带控制点进行的自由网区域网平差,为了验证本算法在有控制点情况下的平差精度,本文在第3个测区采用共27个外业测量点,其中13个点作为控制点,剩余点作为检查点。采用带控制点进行平差后,如表 6所示,在像点残差和检查点残差方面本文方法与传统方法仍然具有相当的精度水平。
| 数据 | 影像数 | 传统算法 | 本文算法 | |||||||||||
| 像点残差/像素 | 检查点残差/m | 像点残差/像素 | 检查点残差/m | |||||||||||
| x | y | X | Y | Z | x | y | X | Y | Z | |||||
| 3 | 84 | 0.457 | 0.195 | 0.14 | 0.14 | 0.8 | 0.448 | 0.201 | 0.15 | 0.18 | 0.81 | |||
2.6 与同类方法对比
文献[22]也是用预条件共轭梯度法进行区域网平差,其使用的数据大部分也来自于本文从网上下载的数据(由Sameer在其个人网站公开的数据),但使用的是GPU并行区域网平差,在求解的过程中,法方程系数矩阵是没有以任何形式存储在法方程中的,只是在需要的时候,利用GPU实时计算出来的,其计算速度因而比本文算法要快。从该文献中找到了与本文中相同的3组试验数据,并将其试验精度结果与本文的精度结果进行对比,如表 7所示。
| 数据 | 来源 | 影像数 | 地面点 | 影像点 | 像点残差/像素 | |
| Wu的方法 | 本文方法 | |||||
| 1 | 网络 | 52 | 64 063 | 347 143 | >1.0 | 0.625 |
| 2 | 网络 | 88 | 64 298 | 383 987 | >1.8 | 0.536 |
| 3 | 网络 | 13 682 | 891 224 | 5 801 328 | >1.9 | 0.907 |
文献[22]中的精度没有用具体的数字以表格的形式给出,而是给出了几张对比图形,但是可以通过图形中刻度值得到其精度的大概范围。该方法由于使用了GPU并行计算,其计算速度也因此比本文的方法要快,但如表 7所示,其计算精度普遍较差,可见该方法虽然有很快的计算速度,但是由于GPU的单精度浮点运算,其计算精度明显低于本文的方法。
综上所示,本文算法不仅节省了内存使用量,提高了计算速度,同时还保证了平差的最终精度几乎无损,因此本算法非常适合于除了规则航空摄影以外的其他摄影测量区域网平差问题。传统算法和本文算法的高程精度相当,但都不是理想的高程精度,可能是由于没有对内方位元素做自检校,即没有对相机主光轴倾角,镜头畸变等系统误差进行有效补偿,仅解算了外方位元素。本文方法虽不如GPU并行计算方法效率高,但是在精度上却有明显的优势。
3 结 论针对各类新型传感器给摄影测量数据源带来的多源性、随机性、大数据等方面的挑战,本文引入预条件共轭梯度法以及不精确牛顿解法求解区域网平差中的法方程,使用一种有效的法方程系数矩阵压缩格式,并在此基础之上建立了全新的区域网平差方法流程,使之在保证计算精度的同时,可以节省内存使用量,并提高计算速度。本文共使用了10组真实数据,包括无人机影像、倾斜影像、手机影像以及网络下载的影像分别进行对比试验。通过对试验数据的对比分析,可以得出以下结论:①本文算法相较于传统的算法可以节省3~15倍内存空间,影像数越大,压缩效率越高;②本文算法的计算速度比传统算法大幅提升,且数据量越大,计算速度提升倍率越高;③本文算法保证了精度与传统算法相当。
本算法虽然在一定程度上节省了内存空间,提高了计算速度,但是由于本算法使用预条件共轭梯度法以及不精确牛顿解法迭代求解法方程,因此本算法的稳定性仍需要大量真实数据进行测试验证。本文仅解算外方位元素,内方位元素是在平差之前进行检校的,因此无需解决内外方位元素之间的相关性这一传统的平差难题,但如果内外方位元素同时求解,也可以使用本文的算法提高平差的效率,节省内存空间,只是本文算法对于内外方位元素的相关性问题,也并没有明确的优势。另外,本算法存储了法方程,当影像数大于15 000并继续增大时,本文算法所需的内存仍会继续增加,且最终一定会超过普通电脑甚至是专业工作站的内存,因此需要研究新的方法,彻底解决法方程系数矩阵的内存需求问题,即不存储法方程系数矩阵,而是在平差迭代过程中实时计算法方程系数矩阵,此时需要高性能的计算设备,引入GPU并行计算和大型服务器并行计算是可能的方法,同时还要解决引入GPU后,仅使用单精度浮点运算带来的精度损失问题,本文后续将进一步研究此类方法。
| [1] | MARQUARDT D W. An Algorithm for Least-squares Estimation of Nonlinear Parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431–441. DOI:10.1137/0111030 |
| [2] | 陈驰, 杨必胜, 彭向阳. 低空UAV激光点云和序列影像的自动配准方法[J]. 测绘学报, 2015, 44(5): 518–525. CHEN Chi, YANG Bisheng, PENG Xiangyang. Automatic Registration of Low Altitude UAV Sequent Images and Laser Point Clouds[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(5): 518–525. DOI:10.11947/j.AGCS.2015.20130558 |
| [3] | 闫利, 费亮, 叶志云, 等. 大范围倾斜多视影像连接点自动提取的区域网平差法[J]. 测绘学报, 2016, 45(3): 310–317. YAN Li, FEI Liang, YE Zhiyun, et al. Automatic Tie-points Extraction for Triangulation of Large-scale Oblique Multi-view Images[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 310–317. DOI:10.11947/j.AGCS.2016.20140673 |
| [4] | 季顺平, 史云. 车载全景相机的影像匹配和光束法平差[J]. 测绘学报, 2013, 42(1): 94–100. JI Shunping, SHI Yun. Image Matching and Bundle Adjustment Using Vehicle-based Panoramic Camera[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 94–100. |
| [5] | 李德仁. 展望大数据时代的地球空间信息学[J]. 测绘学报, 2016, 45(4): 379–384. LI Deren. Towards Geo-spatial Information Science in Big Data Era[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 379–384. DOI:10.11947/j.AGCS.2016.20160057 |
| [6] | 王祥, 张永军, 黄山, 等. 旋转多基线摄影光束法平差法方程矩阵带宽优化[J]. 测绘学报, 2016, 45(2): 170–177. WANG Xiang, ZHANG Yongjun, HUANG Shan, et al. Bandwidth Optimization of Normal Equation Matrix in Bundle Block Adjustment in Multi-baseline Rotational Photography[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 170–177. DOI:10.11947/j.AGCS.2016.20150282 |
| [7] | 林诒勋. 稀疏矩阵计算中的带宽最小化问题[J]. 运筹学学报, 1983, 2(1): 20–27. LIN Yixun. Bandwidth Minimization Problem in Sparse Matrix Computations[J]. Chinese Journal of Operations Research, 1983, 2(1): 20–27. |
| [8] | GIBBS N E, POOLE JR W G, STOCKMEYER P K. An Algorithm for Reducing the Bandwidth and Profile of a Sparse Matrix[J]. SIAM Journal on Numerical Analysis, 1976, 13(2): 236–250. DOI:10.1137/0713023 |
| [9] | 郑志镇, 李尚健, 李志刚. 稀疏矩阵带宽减小的一种算法[J]. 华中理工大学学报, 1998, 26(1): 43–45. ZHENG Zhizhen, LI Shangjian, LI Zhigang. A New Algorithm for Reducing Bandwidth of Sparse Matrix[J]. Journal of Huazhong University of Science & Technology, 1998, 26(1): 43–45. |
| [10] | FRADSEN P E, JONASSON K, NIELSEN H B, et al. Unconstrained Optimization[M/OL]. 3rd ed. Denmark:Informatics and Mathematical Modelling, Technical University of Denmark, 2004. http://www.imm.dtu.dk/courses/02611/uncon.pdf. |
| [11] | HESTENES M R, STIEFEL E. Methods of Conjugate Gradients for Solving Linear Systems[J]. Journal of Research of the National Bureau of Standards, 1952, 49(6): 409–436. DOI:10.6028/jres.049.044 |
| [12] | AGARWAL S, SNAVELY N, SEITZ S M, et al. Bundle Adjustment in the Large[M]//DANIILIDIS K, MARAGOS P, PARAGIOS N. Computer Vision-ECCV 2010. Berlin Heidelberg:Springer, 2010:29-42. |
| [13] | AGARWAL S, FURUKAWA Y, SNAVELY N, et al. Building Rome in a Day[J]. Communications of the ACM, 2011, 54(10): 105–112. DOI:10.1145/2001269 |
| [14] | BYRÖ D M, ÅSTRÖ M K. Conjugate Gradient Bundle Adjustment[M]//DANIILIDIS K, MARAGOS P, PARAGIOS N. Computer Vision-ECCV 2010. Berlin Heidelberg:Springer, 2010, 6312:114-127. |
| [15] | JIAN Y D, BALCAN D C, DELLAERT F. Generalized Subgraph Preconditioners for Large-scale Bundle Adjustment[C]//Proceedings of IEEE International Conference on Computer Vision. Barcelona:IEEE, 2011:295-302. |
| [16] | BRU R, MARÍN J, MAS J, et al. Balanced Incomplete Factorization[J]. SIAM Journal on Scientific Computing, 2008, 30(5): 2302–2318. DOI:10.1137/070696088 |
| [17] | BYRÖ D M, ÅSTRÖ M K. Bundle Adjustment using Conjugate Gradients with Multiscale Preconditioning[C]//Proceedings of 2009 British Machine Vision Conference. London:BMVC, 2009. |
| [18] | ZHENG Maoteng, ZHANG Yongjun, ZHOU Shunping, et al. Bundle Block Adjustment of Large-Scale Remote Sensing Data with Block-based Sparse Matrix Compression Combined with Preconditioned Conjugate Gradient[J]. Computers & Geosciences, 2016, 92: 70–78. |
| [19] | WU Changchang, AGARWAL S, CURLESS B, et al. Multicore Bundle Adjustment[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI:IEEE, 2011:3057-3064. |
| [20] | BELL N, GARLAND M. Implementing Sparse Matrix-Vector Multiplication on Throughput-Oriented Processors[C]//Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis. Portland, OR:IEEE, 2009:1-11. |
| [21] | SAAD Y. Iterative Methods for Sparse Linear Systems 2nd ed.[M]. Philadelphia, PA: SIAM, 2003. |
| [22] | GRIMES R G, KINCAID D R, YOUNG D M. ITPACK 2.0 User's Guide[R]. Technical Report CNA-150. Austin, TX:Center for Numerical Analysis, University of Texas, 1980. |
| [23] | NIELSEN H B, Damping Parameter in Marquardt's Method[R]. Technical Report IMM-REP-1999-05[J]. Denmark:Technical University of Denmark, 1999. |

