遥感影像几何定位模型通常以构建影像坐标与物方坐标之间的映射关系为主要任务,遥感影像几何定位通常分严密物理模型和通用模型两大类。严密模型通常根据传感器成像机理和传感器本身的结构为基础构建成像几何关系,而通用模型通常避开了成像机理和传感器几何结构实现影像坐标与物方坐标的函数拟合。共线方程和距离-多普勒方程分别是光学影像和雷达影像使用得最为广泛的严密构像方程,有理函数模型RFM是目前卫星影像使用得最为广泛的通用模型。2002年文献[1-2]在ASCM-APSRS年会上发表,同时提出通过在像方坐标以低阶多项式补偿方式实现RFM影像高精度定向,此后,像方定向即成为RFM定向的主流方法。相关研究内容主要集中在不同卫星影像RPC参数的计算、RFM定位方法等内容上。近几年,国内基于RFM进行几何定位的研究也非常活跃,相关成果也代表了国际上该领域的水平。文献[3]以SPOT-5 HRS为研究对象,通过对长条带影像的区域网平差解决了西部测图稀少控制难点;文献[4]对卫星线阵影像RFM近似核线生成进行了研究;文献[5-6]对RFM代替卫星光学与SAR影像严密模型的方法与精度进行了研究;文献[7]通过CCD虚拟成像技术对原影像进行重成像,降低因原始传感器像元排列不规则引起的RFM拟合误差,提升了资源三号卫星影像RPC的拟合精度。
在构像模型基础上,精化定向参数是影像定位的重要内容。内外定向参数初值及其精度信息的利用,使得严密模型在稀少或无地面控制点定位中能够实现遥感影像定位定向参数的精确稳健求解。在多源影像联合定位数据处理中,不同传感器影像在区域网影像的定向参数求解中起着主次不同的作用。与严密模型相比,RFM模型对定向参数精度信息几乎没有挖掘和利用,使得严密模型的上述优点在RFM模型中并没有得到体现。
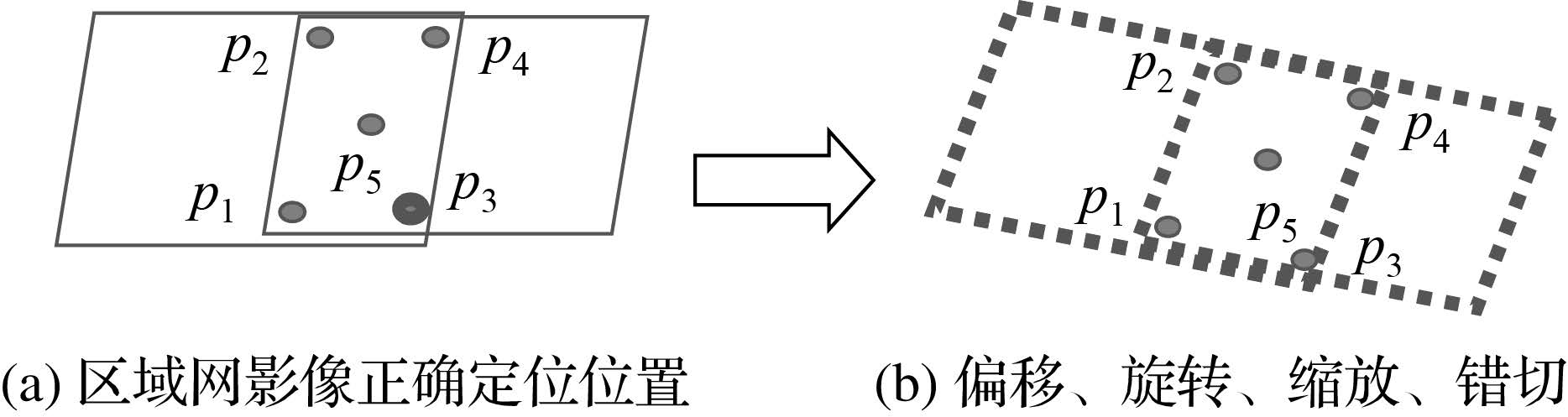
基于像方仿射变换的定向方法根据控制点数目的不同,选用常数项、一次项等不同的定向参数,避免影像定向参数因控制点不足而无法求解。完全无地面控制点条件的自由网平差技术,至目前为止相关研究并不多。在直接使用传统RFM模型时,在完全无地面控制点条件下,通过连接点约束的自由网平差仅以连接点间的误差最小二乘为条件,而影像定位可能会完全偏离实际结果。图 1描述了经过像方仿射变换模型定向后,影像和定位结果失真情况下,连接点间几何关系仍保持良好的情况。
|
| 图 1 仅有连接点的自由网平差失真示意图 Fig. 1 Distortion only with tie points in free-net |
RFM由于其传感器无关的特点,是多源卫星影像联合定位的优选模型,文献[8-9]对基于RFM模型的多源影像联合定位进行了研究。完全无地面控制点的卫星影像测图是航天摄影测量的方向,也是当前难点之一。同轨多线阵立体光学影像如SPOT-5 HRS、P5、资源三号、天绘卫星影像等具有良好的同轨立体,是目前1∶10 000~1∶100 000比例尺测图的主要卫星影像源。它们虽然具有立体测图的先天优势,但无控制点自主定位精度还难以直接达到制图规范要求,如SPOT-5影像的精度在50 m左右[10],国产资源三号影像的精度为10~40 m[7]。国际上一些无控制点条件下高精度自主定位卫星如TerraSAR-X、WorldView-2、GeoEye等影像,自主定位精度可达10 m内[11-13]。特别是TerraSAR-X聚束式成像影像,该类影像在ITRF2008框架下,角反射器自主定位精度可达分米甚至是厘米级别[13-14]。国内研究也表明,聚束模式影像角反射器绝对定位精度优于1.5 m水平[15-16]。这些高精度自主定位影像在专业测图上也存在一定的不足,如影像不容易获取理想的立体条件,影像分辨率很高而导致影像覆盖范围很小,价格昂贵等。如果将两类影像进行联合定位,发挥自主定位精度高的影像在区域网影像中的控制作用,发挥立体测图卫星影像覆盖范围广、内部相对几何精度良好、立体几何结构合理稳定的特点,一起促进无控制点区域网影像的定位精度,无疑是一种值得探索的技术。
1 考虑影像自主定位精度信息的RFM区域网平差在RFM模型中,RPC原始参数通过严密模型转换获得[5-6]。当直接利用原始RPC参数进行定位时,等同像方定向参数同时取0值。RFM与严密模型有同等无控制定位精度,意味着像方定向参数隐含了精度信息。挖掘出像方定向参数的初值和精度信息,就可以以像方定向参数作为虚拟观测值,参考严密模型中轨道、姿态测量值与影像量测值的联合平差处理,构建考虑定向参数精度信息的RFM模型。主要思路和步骤为:①构建影像像点观测值的误差方程,并对其定权;②构建像方定向参数虚拟观测值的误差方程,并根据误差传播理论,由影像原始参数定位先验精度信息计算像方定向参数的精度和权;③联合影像观测值和虚拟观测值的误差方程,通过带权最小二乘实现定向参数和地面点坐标的求解;④将定向参数解与其先验精度δ值比较(通常3δ作为解阈值),判断定向未知数解以及影像原始RPC值的合理性。
RFM几何模型通过归一化地面点坐标的三元三次多项式的比值来表达归一化影像坐标的函数。其形式为
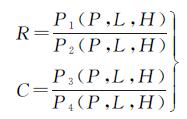 (1)
(1)
式中,P(P,L,H)为纬度P、经度L和高程H的三元三次多项式,形式为
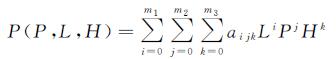 (2)
(2)
式中,aijk为RPC参数中的有理多项式系数;m1、m2、m3为多项式的阶数,一般均取值为3。
区域网平差各影像像点坐标误差方程的建立,未知数除条带影像的像方定向参数(a0,a1,a2,b0,b1,b2)外,还包括地面点坐标增量未知数(dL,dP,dH),误差方程可写为
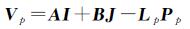 (3)
(3)
式中,Vp为量测像点坐标误差向量[VR VC]T;I为像方定向参数增量未知数向量[da0 da1 da2 db0 db1 db2]T;J为地面点三维坐标和平面坐标增量未知数向量[ΔL ΔP ΔH]T;A为定向参数未知数向量I的系数矩阵;B为地面点三维坐标增量未知数向量J的系数矩阵;Lp为像点坐标误差方程常数项向量[lR lC]T;Pp为相应误差方程的权矩阵,其矩阵值PR、PC直接根据像点的量测精度(通常不大于1像素)来计算。
高分辨率线阵CCD传感器具有飞行高度高、成像光束窄、接近平行投影的特点,其定向参数之间存在很强的相关性。例如,传感器在飞行方向的瞬时成像位置与传感器俯仰角、侧摆角具有强相关性,但这些参数的误差均主要引起影像像点坐标的整体平移。在RFM模型中,平差参数b0将吸收星载传感器位置和姿态误差所引起飞行方向上的影像行坐标误差,平差参数a0吸收所有星载传感器位置和姿态误差所引起的影像列方向上的误差;而参数a1、a2、b1、b2则吸收因内定向参数误差所引起的影像误差[3]以及航偏角误差引起的影像定位旋转误差、影像内部线性飘移误差等。像方仿射变换模型参数虽然不代表影像几何变换具体影响因素,但各参数与相关的主要影响因素间的联系是清楚的,即传感器定轨和定姿精度决定了影像自主定位精度、影像自主定位精度决定了RFM模型定向参数的a0、b0精度。不同传感器影像定向参数值统计量与相关传感器仍然存在密切联系,为构建考虑影像自主定位精度信息的RFM模型提供基础。
有理函数模型参数通过拟合严密模型计算得到。轨道、姿态以及传感器检校参数初值属于独立观测值,根据严密模型利用独立观测误差的传播定律不难计算影像的自主对地定位精度。同时,每种影像的自主定位精度在相当长的时间内是相对平稳的,也可以通过先验值或一些公开文献如文献[17]获得。因此,将a0、b0作为虚拟观测值,其精度ma0/mb0与沿轨、垂轨向自主定位精度mX/mY和分辨率RX/RY的关系有
 (4)
(4)
在仅知道影像自主定位平面先验精度m的情况下,可认为沿轨和垂轨精度等同,有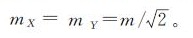
由于定向模型一次项参数主要修正影像旋转缩放(成像时线性漂移导致的)误差,而影像定位此类误差主要来源于姿态航偏角误差、影像沿轨向或垂轨向线性飘移测量误差等,它们对影像内部相对形变最大影响量通常不超过若干像素(设最大精度改变量为M像素),根据误差传播理论,ma1、ma2、mb1、mb2可根据M和影像宽度Wimg计算
 (5)
(5)
根据其精度信息,即可方便对一次项参数定权。因此,对于像方仿射变换参数,可建立相应的误差方程
 (6)
(6)
式中,VI为定向参数误差向量[va0 va1 va2 vb0 vb1 vb2]T;I为定向参数增量未知数向量[da0 da1 da2 db0 db1 db2]T;LI为定向参数误差方程常数项向量[la0 la1 la2 lb0 lb1 lb2]T;E为单位系数矩阵;PI为相应定向参数虚拟观测值的权矩阵,可根据相应参数的精度计算。
联合式(3)和式(6),即可组成考虑定向参数精度信息的RFM型基础误差方程组,通过带权最小二乘解算,即可得出定向参数精化值以及地面点坐标。则误差方程(3)、(6)构建的法方程NX=U的第i个未知数xi的精度δi可以按下式计算[16]
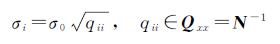 (7)
(7)
试验数据位于喜马拉雅山东麓,地理位置见图 2,区域网覆盖区高程为450~5500 m,属于典型的高山区域地形。试验数据包括:
(1) 6对SPOT-5 HRS长条带立体影像A、B、C、D、E、F(如图 2),其影像分辨率为10 m×5 m,影像获取于2002年12月-2007年11月,影像覆盖区面积约18万km2,各立体条带影像长度如表 1所示。
| 像素 | ||||||
| 条带号 | A | B | C | E | F | G |
| 影像长度 | 114 584 | 50 800 | 50 456 | 60 000 | 52 304 | 53 816 |
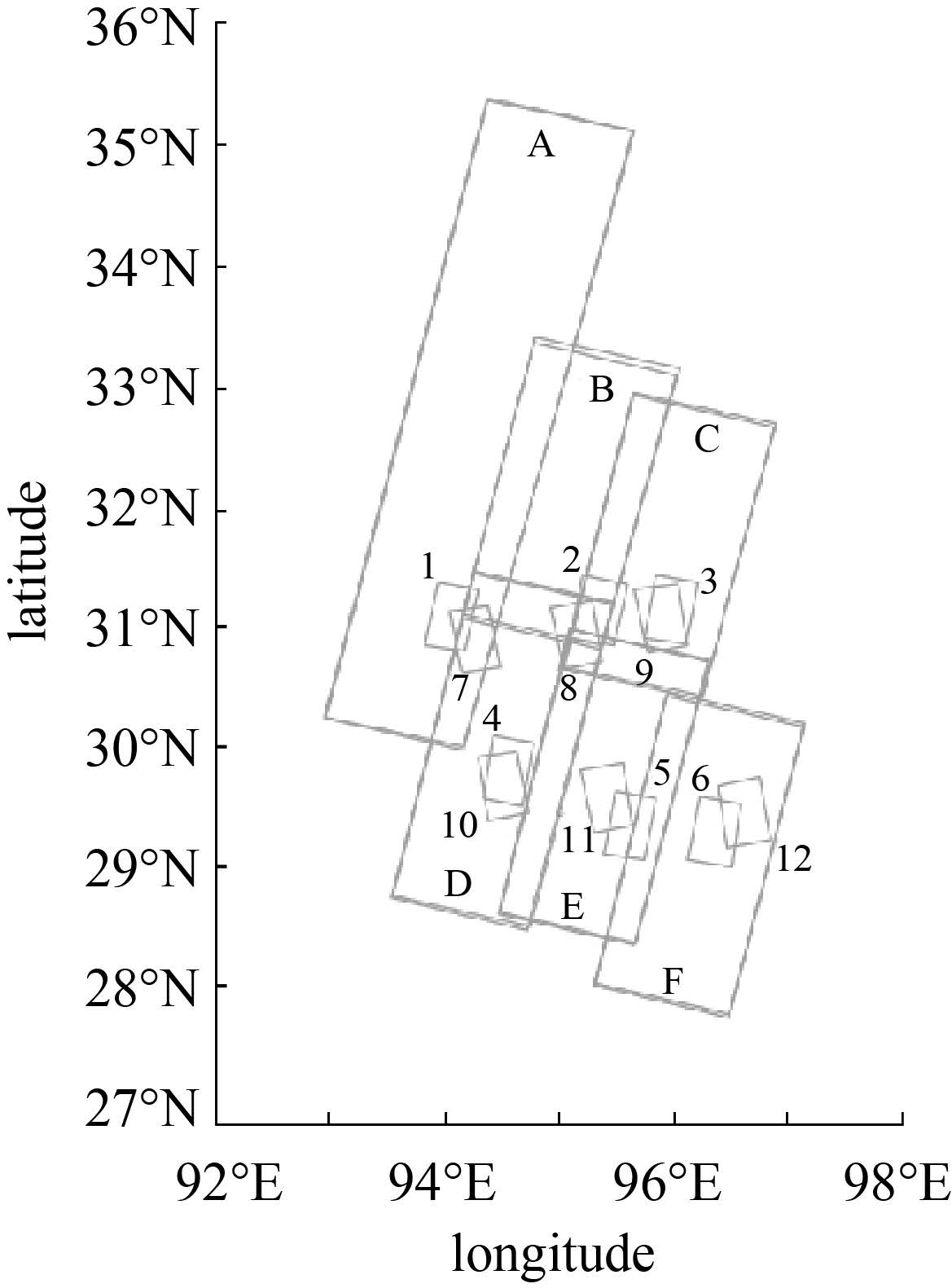
(2) 12标准景TerraSAR-X影像(如图 2),获取时间为2008年11月-2009年11月,条带模式成像,该方式成像的影像质量和自主定位精度会略低于聚束模式。试验包括6景升轨影像(图 2中编号7-12)和6景降轨影像(图 2中编号1-6),升轨和降轨SAR影像之间构成了6对立体像对,中心点的地面入射角和分辨率信息统计于表 2。HRS条带像和TerraSAR-X影像之间的位置关系则如图 2所示。
| 影像编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 入射角/(°) | 39.2 | 28.7 | 41.1 | 33.3 | 41.0 | 35.4 | 46.1 | 37.3 | 42.8 | 46.1 | 37.1 | 28.7 |
| 方位分辨率/m | 1.38 | 2.0 | 1.99 | 1.82 | 1.99 | 1.99 | 2.01 | 2.02 | 2.18 | 2.14 | 1.69 | 2.00 |
| 距离分辨率/m | 1.36 | 0.90 | 1.36 | 1.36 | 1.36 | 1.36 | 1.36 | 1.36 | 1.36 | 1.36 | 1.36 | 0.90 |
(3) 测区影像覆盖范围内有地面实测GPS点218个,采用WGS-84大地坐标和椭球高,所有外业GPS地面点由专业测绘技术人员在立体环境下量测到HRS影像,同时在HRS与SAR影像之间、HRS影像之间、SAR影像之间也由专业技术人员人工量测获取足量同名连接点。
试验前,利用SPOT-5 HRS影像和TerraSAR-X影像的星历数据将定向数据转换成RPC参数,转换方法参考文献[3, 5-6]。由于SPOT-5轨道控制DORIS系统和TerraSAR-X的星历数据为ITRF坐标框架下的值,因此,根据RFM模型无控制点定位计算得到的定位结果也是ITRF坐标框架下的值转换成大地坐标的结果。
2.2 试验与分析分别从定向参数精度信息配置的偏离度对定位精度的影响,SAR影像数量、分布、轨道方向等差异对定位精度的影响进行两组试验。区域网平差影像定位精度信息可以根据式(7)或地面检查点误差统计得出,在定向参数先验精度给定准确的前提下,理论上两者有相近的结果[18],但通过检查点获得的精度仍然是各国生产应用中认可的高可靠性指标[19]。
|
| 图 2 HRS影像与SAR影像分布 Fig. 2 Distribution of HRS and SAR images |
由于两种方式结果均与平差参数的配置相关,配置与真实值偏离时,精度计算值也可能失真,因此,定向参数精度信息的精确获取是定位模型和精度公式应用的关键。本文试验在于测试模型的可行性与发现定向参数先验精度误差对定位精度影响的规律,利用足量检查点统计得到的定位精度比式(7)计算值应有更好的真实性。
2.2.1 试验1:精度信息配置偏差对联合定位精度的影响本文模型所采用的精度信息是影像定位先验精度或过往影像的统计精度出发来进行定权的,在区域网影像数量足够多的情况下,经过良好检校的影像的实际定位系统误差分布是以均值为0的正态分布值。但由于实际应用中所使用的影像数量有限,测区影像的自主定位实际精度与先验精度可能会存在较大差异。本试验在平差参数配置值与实际值存在差异时,对定位结果的影响进行测试,试验数据包括所有HRS像对和SAR影像。
试验1.1:定向参数常数项精度配置对定位精度的影响。一次项配置上SAR影像给定4.0、HRS影像给定0.5情况下,常数项精度SAR影像按自主定位精度0.1~60 m、HRS影像按自主定位精度10~560 m进行转换配置,对检查点进行统计,得到的平面/高程定位结果统计于表 3中。
| m | ||||||||
| 参数配置与定位结果 | 10.0 | 60.0 | 110.0 | 160.0 | 260.0 | 360.0 | 560.0 | |
| 0.1 | 精度 | 8.8/3.8 | 6.0/4.4 | 6.0/4.5 | 6.0/4.5 | 6.0/4.5 | 6.0/4.5 | 6.0/4.5 |
| 最大误差 | 32.9/8.5 | 17.3/8.3 | 17.1/8.4 | 17.1/8.4 | 17.0/8.4 | 17.0/8.4 | 17.0/8.4 | |
| 1.0 | 精度 | 9.1/3.8 | 6.0/4.3 | 6.0/4.4 | 6.0/4.4 | 6.1/4.4 | 6.1/4.4 | 6.1/4.4 |
| 最大误差 | 33.2/8.4 | 16.3/8.1 | 16.2/8.2 | 16.2/8.3 | 16.2/8.3 | 16.2/8.3 | 16.2/8.3 | |
| 2.0 | 精度 | 9.7/3.9 | 6.2/4.4 | 6.3/4.4 | 6.3/4.4 | 6.3/4.4 | 6.3/4.4 | 6.3/4.4 |
| 最大误差 | 33.9/8.5 | 16.7/8.3 | 16.5/8.4 | 16.5/8.4 | 16.5/8.4 | 16.5/8.4 | 16.5/8.4 | |
| 3.0 | 精度 | 10.3/4.0 | 6.4/4.4 | 6.5/4.5 | 6.6/4.5 | 6.6/4.5 | 6.6/4.5 | 6.6/4.5 |
| 最大误差 | 34.5/8.7 | 17.2/8.5 | 17.0/8.6 | 16.98/8.60 | 16.95/8.62 | 16.95/8.62 | 16.95/8.62 | |
| 5.0 | 精度 | 11.2/4.2 | 6.8/4.5 | 6.9/4.5 | 7.0/4.5 | 7.0/4.5 | 7.0/4.5 | 7.0/4.5 |
| 最大误差 | 35.4/9.0 | 18.0/8.9 | 17.9/8.9 | 17.9/9.0 | 17.9/9.0 | 17.9/9.0 | 17.9/9.0 | |
| 8.0 | 精度 | 11.8/4.4 | 7.2/4.6 | 7.4/4.6 | 7.4/4.5 | 7.5/4.5 | 7.5/4.5 | 7.5/4.5 |
| 最大误差 | 36.0/9.4 | 18.7/9.3 | 18.7/9.2 | 18.7/9.2 | 18.7/9.2 | 18.7/9.2 | 18.7/9.2 | |
| 11.0 | 精度 | 12.0/4.6 | 7.5/4.6 | 7.7/4.6 | 7.7/4.5 | 7.8/4.5 | 7.8/4.5 | 7.8/4.5 |
| 最大误差 | 36.2/9.6 | 19.0/9.4 | 19.1/9.3 | 19.2/9.3 | 19.2/9.3 | 19.2/9.3 | 19.2/9.3 | |
| 25.0 | 精度 | 12.4/4.9 | 8.4/4.8 | 8.2/4.6 | 8.3/4.6 | 8.4/4.5 | 8.5/4.5 | 8.5/4.5 |
| 最大误差 | 36.5/10.2 | 20.5/9.7 | 19.2/9.6 | 19.8/9.5 | 20.2/9.4 | 20.4/9.4 | 20.5/9.4 | |
| 60.0 | 精度 | 12.5/5.1 | 11.3/5.1 | 9.1/4.9 | 8.5/4.7 | 8.4/4.5 | 8.5/4.5 | 8.6/4.4 |
| 最大误差 | 36.6/10.5 | 25.8/10.3 | 20.9/10.0 | 19.6/9.8 | 20.4/9.6 | 20.7/9.5 | 21.0/9.5 | |
试验1.2:像方仿射变换定向模型常数项参数SAR影像按自主定位精度1.0 m、HRS影像按自主定位精度60.0 m进行转换配置,而一次项精度SAR影像按100~0.1、HRS影像按100~0.1分别进行配置,得到的平面/高程定位结果统计于表 4中。
| m | ||||||||||
| 精度配置/×10-5 | 0.1 | 0.5 | 1.0 | 2.0 | 4.0 | 10.0 | 20.0 | 50.0 | 100.0 | |
| 0.1 | 精度 | 6.3/5.4 | 5.5/5.9 | 5.4/6.2 | 5.8/6.6 | 6.5/7.1 | 6.8/7.2 | 7.0/7.3 | 7.0/7.3 | 7.0/7.3 |
| 误差 | 15.7/10.1 | 15.4/13.2 | 16.1/14.3 | 16.5/14.5 | 18.4/14.9 | 19.9/15.9 | 20.4/16.2 | 20.6/16.2 | 20.6/16.3 | |
| 0.5 | 精度 | 6.7/5.1 | 5.6/5.5 | 5.5/5.8 | 5.9/6.2 | 6.7/6.8 | 7.1/7.0 | 7.2/7.1 | 7.3/7.1 | 7.3/7.1 |
| 误差 | 17.0/9.9 | 15.2/11.3 | 15.5/12.8 | 16.6/13.3 | 19.7/15.5 | 21.3/16.6 | 21.8/16.9 | 22.0/17.0 | 22.0/17.0 | |
| 1.0 | 精度 | 7.0/4.9 | 5.7/5.0 | 5.5/5.3 | 5.9/5.8 | 6.8/6.5 | 7.2/6.7 | 7.4/6.8 | 7.4/6.8 | 7.5/6.8 |
| 误差 | 18.1/9.8 | 15.8/9.1 | 15.9/10.4 | 17.1/11.8 | 20.5/16.0 | 22.3/17.4 | 22.9/17.7 | 23.1/17.9 | 23.1/17.9 | |
| 2.0 | 精度 | 7.2/4.8 | 5.9/4.6 | 5.5/4.9 | 5.9/5.4 | 7.0/6.3 | 7.5/6.6 | 7.8/6.7 | 7.8/6.7 | 7.8/6.8 |
| 误差 | 18.8/9.7 | 16.3/8.5 | 16.2/9.6 | 17.5/12.1 | 21.4/17.2 | 23.6/19.1 | 24.4/19.7 | 24.6/19.8 | 24.6/19.8 | |
| 4.0 | 精度 | 7.3/4.6 | 6.0/4.3 | 5.5/4.6 | 5.9/5.1 | 7.2/6.1 | 8.1/6.7 | 8.4/6.9 | 8.6/7.0 | 8.6/7.0 |
| 误差 | 18.9/9.6 | 16.3/8.1 | 15.9/9.3 | 17.3/11.7 | 21.8/18.3 | 24.8/21.3 | 26.0/22.4 | 26.4/22.7 | 26.5/22.7 | |
| 10.0 | 精度 | 7.3/4.5 | 6.0/4.2 | 5.5/4.5 | 5.8/4.9 | 7.3/5.9 | 8.4/6.7 | 8.8/7.0 | 9.0/7.1 | 9.0/7.1 |
| 误差 | 18.9/9.6 | 16.4/8.0 | 16.0/8.9 | 16.8/10.9 | 21.4/17.8 | 25.1/21.9 | 26.7/23.5 | 27.2/23.9 | 27.3/24.0 | |
| 20.0 | 精度 | 7.3/4.4 | 6.0/4.2 | 5.4/4.4 | 5.8/4.8 | 7.3/5.8 | 8.5/6.7 | 9.0/7.1 | 9.1/7.2 | 9.2/7.3 |
| 误差 | 18.9/9.6 | 16.4/7.9 | 15.8/8.8 | 16.5/10.4 | 21.0/17.3 | 25.1/22.0 | 27.0/24.0 | 27.6/24.6 | 27.7/24.7 | |
| 100 | 精度 | 7.3/4.4 | 6.0/4.1 | 5.4/4.4 | 5.8/4.7 | 7.3/5.7 | 8.5/6.7 | 9.0/7.1 | 9.2/7.3 | 9.3/7.3 |
| 误差 | 18.9/9.5 | 16.4/7.9 | 15.8/8.6 | 16.3/10.2 | 20.8/17.0 | 25.1/22.0 | 27.1/24.2 | 27.8/24.9 | 28.0/25.0 | |
分析试验1,可以得到如下结论:
(1) 从表 3可以看出,对于常数项参数精度SAR影像配以0.1~3.0,HRS影像配以50~560 m时,能够得到稳定、良好的平面和高程定位结果。参考两者的先验精度分别为3 m和50 m,表明了自主定位精度是常数项参数配置的重要依据和参考,同时表明在影像数量有限的情况下,高精度自主定位SAR影像精度可以适当提高,低精度自主定位HRS影像精度可以降低,区域网平差参数配置有一定的范围自由度。
(2) 由表 4可以看出,在一次项SAR与HRS精度分别配以0.1和1.0时平面精度最优5.4 m,100和0.5时高程精度达到最优4.1 m,综合考虑SAR配以0.5~100、HRS配以0.5~1.0时能够得到较优的平面和高程定位精度。当HRS影像一次项定向参数值达到0.5时,对于影像条带长度为114 584像素大小的影像,一次项定向参数对影像内部相对精度最大影响理论上小于3.3像元(以影像中心为参考),这与HRS影像较好的内部质量[20]也是相符的。同时在降低SAR影像一次项精度配置条件下,有利于降低SAR与HRS的同名点选点误差对HRS长条带影像内部相对几何关系的干扰。
2.2.2 试验2:不同SAR组合对影像定位精度不同控制点及其分布对影像定位产生直接影响,高精度影像的数目与分布对低精度影像的控制是否与地面控制类似?为此,本文试验以6对条带立体计12景HRS影像分别与不同的TerraSAR-X影像组合,试验时仿射变换的定向参数一次项精度SAR与HRS分别按4.0和0.5进行配置,常数项配置TerraSAR-X按1.0 m、SPOT-5 HRS影像按60 m定位精度进行转换配置。试验包括以下11个方案。
T2.0:无SAR影像,不考虑定向参数精度信息的传统模型,每景6个定向参数。
T2.1:无SAR影像,利用原始定向参数的直接定位。
T2.2:无SAR影像,考虑定向精度信息的本文模型。
T2.3:12景SAR影像,包括6景降轨影像(1)-(6)和6景升轨影像(7)-(12)。
T2.4:6景降轨SAR影像(1)-(6)。
T2.5:6景升轨SAR影像(7)-(12)。
T2.6:6景SAR影像,包括3景降轨影像(1)、(3)、(5)和3景降轨影像(7)、(9)、(11),构成3个有重叠区域的SAR立体像对。
T2.7:6景SAR影像,包括3景降轨影像(1)、(3)、(5)和3景升轨影像(8)、(10)、(12),SAR影像之间无重叠。
T2.8:3景SAR影像,两景降轨影像(1)、(3)和一景升轨影像(11),SAR影像之间无重叠。
T2.9:2景SAR影像,包括一景降轨影像(2)和一景升轨影像(8),SAR影像之间有重叠,构成立体,且在区域网中心位置。
T2.10:2景SAR影像,包括一景降轨影像(1)和一景升轨影像(12),两者距离较远。
以上试验中,试验2.0解算发散,其余试验定位精度统计如表 5。
| m | |||||
| 试验编号 | 精度 | 最大误差 | |||
| 平面 | 高程 | 平面 | 高程 | ||
| T2.0 | 解发散 | 解发散 | 解发散 | 解发散 | |
| T2.1 | 35.0 | 6.6 | 71.9 | 12.7 | |
| T2.2 | 15.2 | 4.9 | 31.1 | 11.8 | |
| T2.3 | 6.0 | 4.3 | 16.3 | 8.1 | |
| T2.4 | 16.6 | 6.0 | 30.3 | 11.1 | |
| T2.5 | 7.3 | 5.2 | 20.2 | 11.9 | |
| T2.6 | 6.9 | 6.6 | 16.9 | 16.6 | |
| T2.7 | 6.8 | 4.7 | 17.7 | 9.7 | |
| T2.8 | 8.4 | 4.2 | 19.6 | 13.0 | |
| T2.9 | 7.8 | 4.2 | 18.9 | 11.7 | |
| T2.10 | 12.8 | 4.0 | 27.9 | 9.0 | |
图 3(a)-(e)分别是T2.1、T2.3、T2.7、T2.8和T2.10获得的各地面检查点的误差矢量图。每个点有两个矢量,蓝色竖直方向表示高程误差,向上表示正误差,向下表示负值;非竖直方向的矢量表示该点在平面内的误差矢量。

|
| 图 3 SAR影像控制下的HRS影像定位残差示意图 Fig. 3 Error vectors of HRS image positioning controlled by TerraSAR-X images |
分析试验2可以得到如下结论:
(1) 在不考虑定向参数精度信息时,求解发散,属于秩亏自由网。秩亏自由网平差通常需要一定约束条件下获得稳健解。传统RFM模型仅使用了定向参数的初值信息,在将定向参数作为未知数情况下仅用作迭代初值的作用,精度信息利用的缺失使得无控定位模型中约束条件缺失,试验2.0结果体现了传统RFM定向存在的不足。
(2) 由图 3(a)可以看出,利用原始定向参数进行HRS影像直接定位,对于平面误差,各立体条带内的像点定位带有明显的系统性,条带间系统误差差异也较大;对于高程误差,区域网内高程误差系统性较强,条带间系统误差差异较小。表明不同条带影像带有的定向参数系统误差有明显差异,但立体条带前后景影像间的相对几何关系仍然比较稳定。
(3) 图 3(b)-(e)表明,随着SAR影像数目的增多,覆盖范围的增大,HRS影像定位精度会越高,定向残差的系统性和规则性越弱,图 3(b)中残差规则性比图 3(e)的规则性明显。在HRS区域网影像的下部,受到SAR影像的直接控制,定位残差相对较小,在HRS区域网影像上部,由于缺少SAR影像,其定位残差整体上要大于下部。表明高精度控制影像的数目和分布对区域网影像定位精度的影响与经典的地面控制点有类似的作用。
(4) 对照试验T2.3、T2.4、T2.5以及SAR影像的入射角表明,在多源影像联合定位中,尽管HRS影像的像点有较好的前方交会角,SAR与HRS影像像点间的交会角也比较理想,但高精度自主定位SAR影像之间的交会角大小对区域网影像的控制强度有重要的作用。在90°范围内交会角越大,意味着有更大的基高比,越有利于区域网精度的提升。同时表明,SAR影像之间非重叠非立体时与同等交会条件下有重叠的立体SAR对区域网有同等的控制效果,这对高精度SAR影像的选取赋予了更大的自由度。
本文模型定位结果与1∶5万和1∶10万摄影测量内业规范国标要求相比,SAR影像控制下的HRS影像定位,平面定位精度容易达到1∶5万测图精度要求,但对于高程,很多方案下达到4.2 m,但最大误差最优值7.9 m(表 4最后一行中)仍略大于1∶5万高山地区测图规范对高程限差7.0 m的要求[3]。虽然高程限差接近而没有达到5万测图精度要求,对于采用本文方法进行全球无控制点1∶5万测图的可行性,仍存在以下几点需要考虑:①定位点用作加密点测图,还需要考虑坐标系统和高程基准的转换,GPS测量所依据的坐标参考基准,是由IERS所提供的ITRF国际参考框架,与我国制图采用CGCS2000坐标系和84国家高程基准间存在坐标系和高程基准差异,坐标和高程的转换会可能导致精度进一步损失;②考虑到在HRS上部分缺少SAR控制影像,在SAR影像分布数量和均匀性进一步提升情况下,HRS影像的定位精度有望进一步提升;③本文采用了分辨率为10 m×5 m、自主定位在50 m左右的光学立体HRS影像,与当前高分立体测图卫星影像如ZY-3分辨率和自主定位精度存在差距,TerraSAR-X成像采用的是条带模式,与聚束成像模式在影像分辨率与自主定位精度上也存在差异,如果采用分辨率和自主定位精度均高于本文试验数据的影像,对于联合定位精度提升,应有较大的空间。
3 结 论随着对全球地理信息需求的加速,“一带一路”国家战略的提出和实施,对全球测图提出了迫切需求。而绝大多数卫星影像尤其是我国卫星影像的综合质量还难以实现完全无控制点测图要求。通过后处理技术实现完全无控制点条件下的影像高精度定位,是当前实现全球测图最为核心的技术之一。本文提出的考虑影像自主定位精度信息的RFM模型,不仅能够实现两类影像重叠部分的联合定位,也显著提升了无地面控制点条件下HRS光学立体卫星影像定位求解的稳健性和精度,发挥了TerraSAR-X影像在区域网影像中的主导作用。本文给出的依赖影像自主定位先验精度信息的RFM模型定向参数精度信息的配置方法是可行的,定向参数精度信息的最优配置可根据实际应用情况作适应性调整,定位结果对定向参数精度配置在一定的区间内有较好的容忍度。
由于考虑了相应传感器影像自主定位精度信息,本文模型不具有传感器无关性,但模型并不失通用性。本文研究在以下两个方面仍需进一步深入:①利用国际上一些高精度自主定位卫星影像与国产立体测图卫星ZY-3、天绘影像的联合处理仍有待进一步测试;②本文方法虽然可以非常显著提升无控制点定位精度,但适用于不同应用定向参数的最优化配置仍需进一步研究。它们是发挥本文模型应用价值的重要内容。
| [1] | TAO C V, HU Y, SCHNICK S. Photogrammetric Exploitation of IKONOS Imagery Using the Rational Function Model[C]//Proceedings of ASCM-APSRS Annual Convention. Washington, DC:CDROM, 2002. |
| [2] | DIAL G, GRODECKI J. Block Adjustment with Rational Polynomial Camera Models[C]//Proceedings of ASCM-APSRS Annual Convention. Washington, DC:CDROM, 2002. |
| [3] | 张力, 张继贤, 陈向阳, 等. 基于有理多项式模型RFM的稀少控制SPOT5卫星影像区域网平差[J]. 测绘学报, 2009, 38(4): 302–310. ZHANG Li, ZHANG Jixian, CHEN Xiangyang, et al. Block-adjustment with SPOT-5 Imagery and Sparse GCPs Based on RFM[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 302–310. |
| [4] | 张永军, 丁亚洲. 基于有理多项式系数的线阵卫星近似核线影像的生成[J]. 武汉大学学报(信息科学版), 2009, 34(9): 1068–1071. ZHANG Yongjun, DING Yazhou. Approximate Epipolar Image Generation of Linear Array Satellite Stereos with Rational Polynomial Coefficients[J]. Geomatics and Information Science of Wuhan University, 2009, 34(9): 1068–1071. |
| [5] | 张过, 费文波, 李贞, 等. 用RPC替代星载SAR严密成像几何模型的试验与分析[J]. 测绘学报, 2010, 39(3): 264–270. ZHANG Guo, FEI Wenbo, LI Zhen, et al. Analysis and Test of the Substitutability of the RPC Model for the Rigorous Sensor Model of Spaceborne SAR Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(3): 264–270. |
| [6] | 张过, 李德仁. 卫星遥感影像RPC参数求解算法研究[J]. 中国图象图形学报, 2007, 12(12): 2080–2088. ZHANG Guo, LI Deren. The Algorithm of Computation RPC Model's Parameters for Satellite Imagery[J]. Journal of Image and Graphics, 2007, 12(12): 2080–2088. |
| [7] | 唐新明, 张过, 祝小勇, 等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报, 2012, 41(2): 191–198. TANG Xinming, ZHANG Guo, ZHU Xiaoyong, et al. Triple Linear-array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191–198. |
| [8] | 秦绪文. 基于拓展RPC模型的多源卫星遥感影像几何处理[D]. 北京:中国地质大学(北京), 2007. QIN Xuwen. Geometry Processing for Remote Sensing Image Based on Expanded RPC Model[D]. Beijing:China University of Geosciences (Beijing), 2007. http://d.wanfangdata.com.cn/Thesis/Y1784679 |
| [9] | 吴颖丹, 明洋. 基于有理函数模型的多源SAR遥感影像区域网平差[J]. 测绘科学, 2012, 37(2): 49–51. WU Yingdan, MING Yang. Multi-source SAR Remote Sensing Imagery Block Adjustment Based on Rational Function Model[J]. Science of Surveying and Mapping, 2012, 37(2): 49–51. |
| [10] | BOUILLON A, BRETON E,DE LUSSY F,et al. SPOT5 HRG and HRS First In-flight Geometric Quality Results[C]//Proceedings of SPIE 4881, Sensors, Systems, and Next-generation Satellites VI. Crete, Greece:SPIE, 2003:212-223. |
| [11] | AGUILAR M A, SALDAÑ A M D M, AGUILAR F J. Assessing Geometric Accuracy of the Orthorectification Process from GeoEye-1 and WorldView-2 Panchromatic Images[J]. International Journal of Applied Earth Observation and Geoinformation, 2013, 21: 427–435. DOI:10.1016/j.jag.2012.06.004 |
| [12] | STABEN G W, PFITZNER K, BARTOLO R, et al. Calibration of Worldview-2 Satellite Imagery to Reflectance Data Using an Empirical Line Method[C]//Proceedings of the 34th International Symposium on Remote Sensing of Environment. Sydney, Australia:[s.n.], 2011. |
| [13] | EINEDER M, FRITZ T, MITTERMAYER J, et al. TerraSAR-X Ground Segment, Basic Product Specification Document[R]. ADA515513, 2008. |
| [14] | GISINGER C, BALSS U, PAIL R, et al. Precise Three-dimensional Stereo Localization of Corner Reflectors and Persistent Scatterers With TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 1782–1802. DOI:10.1109/TGRS.2014.2348859 |
| [15] | 周晓, 曾琪明, 焦健. TerraSAR-X传感器定标精度及其应用分析[J]. 遥感信息, 2014, 29(2): 33–37. ZHOU Xiao, ZENG Qiming, JIAO Jian. Analysis of Terrasar-X Sensor Calibration Accuracy and Its Application[J]. Remote Sensing Information, 2014, 29(2): 33–37. |
| [16] | 张过, 李贞. 基于RPC的TerraSAR-X影像立体定向平差模型[J]. 测绘科学, 2011, 36(6): 146–148. ZHANG Guo, LI Zhen. RPC-based Adjustment Model for TerraSAR-X Stereo Orientation[J]. Science of Surveying and Mapping, 2011, 36(6): 146–148. |
| [17] | JACOBSEN K. DEM Generation from High Resolution Satellite Imagery[J]. Photogrammetrie-Fernerkundung-Geoinformation, 2013(5): 483–493. |
| [18] | 李德仁, 袁修孝. 误差处理与可靠性理论[M]. 武汉: 武汉大学出版社, 2002. LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan: Wuhan University Press, 2002. |
| [19] | U.S. Department of the Interior. Map Accuracy Standards[R]. Fact Sheet FS-171-99, 1999. |
| [20] | 张永军, 张勇. SPOT5 HRS立体影像无(稀少)控制绝对定位技术研究[J]. 武汉大学学报(信息科学版), 2006, 31(11): 941–944. ZHANG Yongjun, ZHANG Yong. Direct Georeferencing of SPOT 5 HRS Imagery without (or with a Few) Ground Control Point[J]. Geomatics and Information Science of Wuhan University, 2006, 31(11): 941–944. |

