2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 湖北 武汉 430077
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China
陆地水包含地表水体(冰雪、冻土、湖泊、水库、河流等)、土壤湿度和地下水等,是全球水循环的重要组成部分。陆地水储量时空变化起因于气候变化、工业用水、生活用水和农业用水等自然和人为因素。有关研究表明陆地水储量变化对全球海平面上升的贡献率高达42%[1],而印度西北部的地下水持续减少则可能造成农业减产甚至饮用水短缺[2]。因此,了解陆地水储量时空变化对全球变化以及人类社会活动和经济发展有着重要的意义。
重力卫星GRACE(gravity recovery and climate experiment)自发射以来已对全球重力场变化进行了十余年的连续观测。由于其数据的高精度和高时空分辨率且全球覆盖,GRACE观测已成为监测陆地水变化的有效手段。目前,GRACE数据已广泛应用于监测陆地水储量的季节性[3-4]和年际变化[5-8]。
但在北欧北美等地区,GRACE监测陆地水变化受到了冰川均衡调整(GIA)严重的制约[9]。因为这些地区在末次盛冰期基本上被巨厚的冰盖所覆盖,尽管古冰盖从约二万年前开始消融,约六至八千年前消融殆尽,然而由于地幔的黏滞性,GIA过程现今仍在持续,这主要表现为地壳回弹,地幔高密度物质回流,导致重力增加,从而使GRACE的水文监测受到强烈的干扰。一般的,可利用模型对GRACE观测重力变化进行GIA信号改正。文献[10]根据GIA模型ICE-5G(VM2)[11]进行改正,利用GRACE研究了北美马更些河流域的陆地水变化。但是现今GIA模型又强烈地依赖地幔黏滞度和古冰盖的历史变化等参数,具有较大的不确定性,因此GIA模型不能提供精密的改正。为了避免使用GIA模型引入的巨大不确定性,文献[12]根据GIA重力和垂直位移在球谐域的近似理论线性关系[13],联合利用GRACE的RL04数据和GPS垂直位移数据定量揭示了北美和北欧GIA近场地区的陆地水储量变化,但没有对Wahr的理论近似关系的不确定性及其对所得结果的影响进行深入研究。与文献[12]的方法类似,文献[14]利用GRACE的RL04数据研究了北美纳尔逊河流域的陆地水变化情况,但利用了实测的GIA重力和垂直位移线性关系。那么,能否利用实测数据研究北欧地区的陆地水弱信号、实测的GIA重力和垂直位移线性关系与Wahr理论值的差别以及使用质量较高的GRACE RL05数据所得结果与RL04数据的有何差异是本文探讨的几个主要问题。
自2012年以来,GRACE数据处理中心(GFZ、CSR和JPL等)发布了RL05数据。该数据使用了新的海洋、大气、潮汐等背景模型,其观测精度和空间分辨率较之前的RL04数据都有所提高[15]。因此利用该数据所得的观测结果预期有较高的可靠性。
本文联合利用绝对重力、GPS和GRACE重力卫星RL05实测数据,研究北欧斯堪的纳维亚半岛的陆地水储量变化的线性趋势,并根据观测数据的不确定性完整估算了研究结果的不确定性,并与两种广泛使用的水文学模型做了对比分析。
1 研究方法与相关公式 1.1 GRACE重力变化根据GRACE重力场球谐系数,可由下式计算地面任一点的重力变化速率[16]
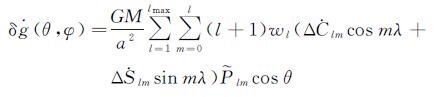 (1)
(1)
式中,θ、λ分别为地心余纬和经度;a为地球平均半径,GM为引力常数与地球质量的乘积,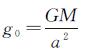
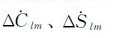

在斯堪的纳维亚等GIA近场地区,GRACE观测的重力变化速率同时包含了GIA和陆地水储量变化两种信号,且GIA信号占主导。如何扣除GIA重力信号是利用GRACE研究这些地区陆地水储量变化的关键。
本文利用的斯堪的纳维亚的绝对重力和GPS并址观测数据主要反映了GIA过程引起的重力和垂直位移变化,水文的影响很小,相关研究结果表明水文因素可以忽略[17-20]。所以,可以利用绝对重力和GPS并址观测数据得到斯堪的纳维亚半岛的重力-垂直位移比值,其比值写为A。那么,利用北欧GPS网BIFROST(baseline inferences for fennoscandian rebound observations sea level and tectonics)[21-22]观测的垂直位移速率场[23]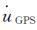
 (2)
(2)
根据GRACE观测的重力变化速率扣除上述“观测的”GIA重力变化速率,所得的剩余重力变化速率就只反映了研究区域的陆地水储量变化速率,可表示为
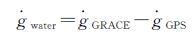 (3)
(3)
为了估算陆地水储量变化,剩余重力速率可用等效水柱高(EWT)速率表示为[24]
 (4)
(4)
式中,地球的平均密度
本文方法研究GIA近场的陆地水变化,能够避开常规方法中需要借助于GIA模型而造成结果的不确定较大且难以定量估计的弊端。
1.3 陆地水储量变化不确定性估计本文研究方法所得陆地水变化速率的不确定性主要来源于剩余重力变化速率的不确定性。根据误差传播定律,由式(3),剩余重力变化速率的不确定性又与GRACE重力速率不确定性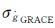

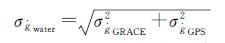 (5)
(5)
根据式(2),GIA重力变化速率不确定性与GPS垂直位移速率场的不确定性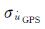
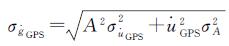 (6)
(6)
将式(6)代入式(5)即可得到剩余重力变化速率的不确定性。再将此不确定性与重力转换为等效水柱高的比例因子24.3 mm/μGal[14]相乘,就可以计算出研究区域陆地水储量变化速率的不确定性。
2 观测数据及其处理 2.1 GRACE观测数据本文采用德国地学中心(GFZ)发布的GRACE卫星2003年1月—2011年3月时段共97个月的RL05数据,其球谐截断阶数为90阶。虽然RL05数据较之前的RL04数据在空间分辨率和精度上都有所提高,“条带”误差明显减小[27],但还需要数据后处理来提高信噪比以满足研究需要。笔者使用人卫激光测距观测的C20项[28]替代了GRACE的相应项并加回了地心改正项[29]。
GRACE数据后处理分为“去相关”和空间平滑两个步骤[30]。首先,本文采用文献[31]提出的p3m10方法对GRACE重力场系数进行去相关处理;然后,利用对真实信号影响较小[32]的高斯滤波[24]对去相关后的数据进行空间平滑,用于压制GRACE数据中的高阶误差。由于GRACE为近极轨道,其在中高纬度地区观测数据较密集,分辨率及精度较低纬度地区高。因此,对于斯堪的纳维亚半岛(53°N—72°N),采用滤波半径为200 km的高斯滤波就可以很好地达到抑制误差和保留信号的目的。
根据式(1)计算了斯堪的纳维亚半岛0.5°×0.5°重力变化时间序列,扣除周年变化、半年变化以及161 d变化等周期项后,就可得到GRACE的重力变化速率分布,如图 1所示。由图 1可知,GRACE重力变化速率分布的整体走向为西南—东北走向,最大值位于波的尼亚湾中部,幅值约为1.65 μGal/a,这主要反映了GIA的信号。但是,位于维纳恩湖附近的地方呈现明显的正重力速率,表明GRACE观测信号还包含了陆地水变化的信息。

|
| 图 1 GRACE观测的重力变化速率 Fig. 1 Gravity change rates observed from GRACE |
2.2 并址站数据及GIA重力与垂直位移实测比值
根据相关文献[19-20, 22-23, 33],笔者搜集了位于斯堪的纳维亚半岛的绝对重力和GPS并址共13个站的观测数据,两种数据都进行了潮汐、大气、极移效应等改正。需要说明的是,本文利用相应观测站的GPS垂直位移速率对绝对重力变化速率扣除了不反映地表质量变化的自由空气重力贡献。表 1列出了具体台站的位置和观测数据情况。这些观测台站位于斯堪的纳维亚半岛GIA隆升区的中心地带,绝对重力和GPS垂直位移速率主要反映了此地区的GIA信号。由于观测时段基本都在10年以上,使得这些台站所得的长期线性速率受周围环境(陆地水等)的季节性变化影响很小,可以忽略不计,相关问题已在前人的文献中有过深入的研究[12, 14]。
| 站点 | 经度/(°E) | 纬度/(°N) | dg/dt(AG)/(μGal/a) | dh/dt(GPS)/(mm/a) |
| Tromsø | 18.938 | 69.663 | 0.51±0.3 | 2.30±0.49 |
| Stavanger | 5.599 | 59.018 | 0.26±0.3 | 1.18±0.51 |
| Trysil | 12.382 | 61.423 | 1.74±0.1 | 9.20±0.34 |
| Onsala AS | 11.926 | 57.395 | 0.12±0.1 | 2.66±0.31 |
| Maårtsbo | 17.259 | 60.595 | 0.88±0.2 | 6.74±0.15 |
| Skellefteå | 21.048 | 64.879 | 1.17±0.2 | 9.61±0.18 |
| Kiruna | 21.060 | 67.871 | 1.14±0.3 | 6.30±0.18 |
| Sodankylä | 26.389 | 67.421 | 0.60±0.3 | 7.12±0.31 |
| Vaasa AA | 21.771 | 62.961 | 0.96±0.3 | 8.62±0.19 |
| Metsaåhovi | 24.395 | 60.217 | 0.81±0.2 | 4.26±0.23 |
| Arjeplog | 18.125 | 66.318 | 1.51±0.2 | 7.70±0.20 |
| Kramfors | 7.907 | 58.083 | 1.70±0.3 | 10.20±0.50 |
| Östersund | 14.858 | 63.443 | 1.10±0.1 | 8.30±0.20 |
通过对13个并址站数据进行线性回归,给出了观测重力速率-垂直位移速率的线性比值线。图 2中,黑色实线表示实测重力-径向位移比率拟合值,比值为A=0.148±0.020 μGal/mm,与文献[13]通过不同粘弹地球模型得到的GIA重力-垂直位移速率的近似理论比值0.154 μGal/mm差异很小(相对差异为4%),文献[34-35]也得到了相似的理论比值。该结果与文献[35]根据模型模拟的结果较为一致。这从实测角度验证了上述的近似理论的可靠性。造成实测值与理论值之间差异的原因[36]有:①理论值估计的近似性;②理论值的近似关系是有频谱限制的,而地面观测数据则包含了全部的频谱信息;③地面观测数据含有误差。

|
| 图 2 绝对重力-GPS垂直位移速率比值 Fig. 2 Ratio of absolute gravity-uplift rates |
2.3 GPS垂直位移速率场及其所得重力速率
本文研究所使用的地表垂直位移速率数据来自于北欧GPS观测网络BIFROST。该观测网工程始建于1993年,其首要科学任务是观测芬诺斯堪的亚(Fennoscandia)的三维地壳形变,从而能够对该地区的GIA过程研究提供强有力的约束[37]。所使用的这些GPS观测数据的最长观测时间跨度已超过13年(1993年8月至2006年12月)。该数据已经扣除了固体潮和大气潮等因素的影响,通过对观测时间序列进行最小二乘回归分析,去除周年项、半年项以及漂移项等,得到了地表垂直位移线性速率。该数据反映了GIA过程引起的地壳隆升[23]。
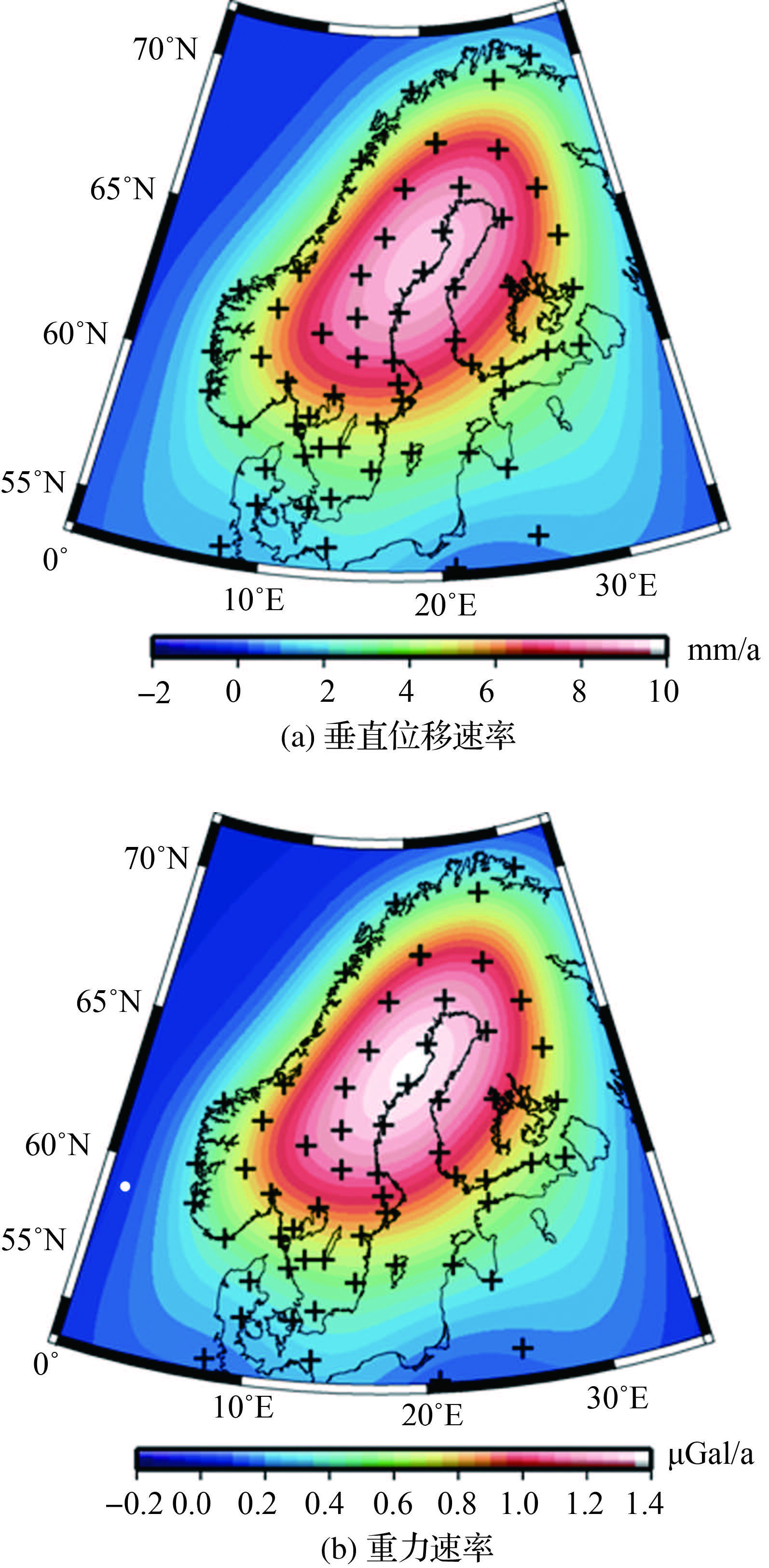
首先,将各站点的GPS垂直位移速度数据内插为0.5°×0.5°格网数据。然后,为了同GRACE的观测数据处理保持一致,对GPS数据采用球谐截断到90阶且使用半径为200 km的高斯滤波平滑处理。处理后的垂直位移速度场如图 3(a)所示,其中的“十字”符号表示GPS站点的位置。
由图 3(a)可知,由于末次盛冰期巨厚冰盖的消融,北欧地区现今地壳存在较快的隆升速率,速率分布大体呈现为东北—西南走向的椭圆状;隆升的中心位于波的尼亚湾中部,说明该地点是古冰盖覆盖的中心地区[38];隆升速率以波的尼亚湾中部向外逐渐减小。
根据式(2),利用GIA重力-垂直位移速率比值A=0.148 μGal/mm,可将GPS垂直位移速率转换为重力变化速率。此重力变化可视为GIA重力信号,如图 3(b)所示。
2.4 水文模型为了与本文研究所得的陆地水变化做比较,采用两个水文模型来进行对比分析。两种水文模型分别是GLDAS(global land data assimilation system)[39]和WGHM(water gap global hydrology model)[40],基于这两个水文模型计算了斯堪的纳维亚半岛的陆地水变化。同样,本文也对这两种水文模型球谐截断到90阶且进行了滤波半径为200 km的空间平滑。
GLDAS模型通过陆地表面建模和数据同化技术,输出陆地表面各项参数(如土壤湿度、土壤温度、蒸发量、降雨、径流和雪量等)。本文采用基于Noah陆地表面模型的GLDAS输出的地表(0~2 m)土壤湿度和雪量数据,每月一值,分辨率为1°×1°。
不同于GLDAS水文模型:①WGHM水文模型输出量更为丰富,除土壤湿度等因素外,WGHM模型还包含了地下水及地表水体(湖泊、湿地等)的信息,并且模拟了人类活动(如农业灌溉)对水文的影响;②WGHM模型空间分辨率为0.5°×0.5°,而GLDAS为1°×1°。
3 结果与分析本节主要介绍利用GRACE和GPS观测数据估算斯堪的纳维亚地区陆地水储量变化的结果,并将本文的研究结果与现今广泛使用的水文学模型做了对比分析。
3.1 陆地水储量变化由GRACE观测所得的重力变化在斯堪的纳维亚同时包含了GIA和陆地水储量变化两种信号。在GRACE重力变化速率(图 1所示)中扣除GIA重力速率(图 3(b))所得的剩余重力即为陆地水储量变化信号,如图 4(a)所示。同时根据式(4)给出了其相应的等效水柱高速率,如图 4(b)所示。由图 4可以看到,该地区的陆地水储量在2003—2011年期间呈现明显的增加趋势(重力正速率);信号中心位于斯堪的纳维亚半岛南端的维纳恩湖和维特恩湖附近,幅值约为12 mm/a的等效水柱高(图 4(b)),对应约0.5 μGal/a的重力变化(图 4(a))。
|
| 图 3 GPS垂直位移速率及所得重力速率 Fig. 3 GPS vertical velocites and derived gravity rates |

|
| 图 4 分离的陆地水信号 Fig. 4 Seperated terrestrial water signal |
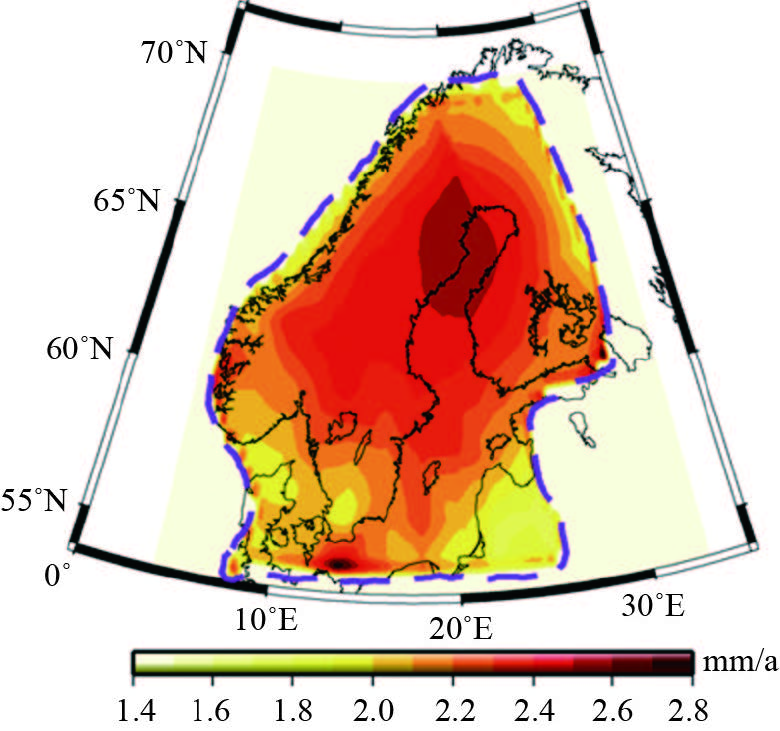
如前所述,本文方法研究所得的陆地水变化的不确定性主要来自于GRACE重力速率和GPS垂直位移速率的观测不确定性。本文使用的GPS垂直位移速率的不确定性在文献[23]中已有详细叙述,GRACE重力速率不确定性较易求得,限于篇幅这里不再逐一图示。根据2.3节中的相关公式,得到了研究区域陆地水储量变化速率的不确定性分布,如图 5所示。总体而言,其不确定性一般不大于2.5 mm/a,相对于斯堪的纳维亚半岛南端陆地水变化的信号而言(图 4(b))很小;较大的不确定性位于波的尼亚湾的东北部,幅值约为2.7 mm/a,远离本文估算的陆地水储量变化的主体信号。
|
| 图 5 陆地水储量变化速率的不确定性 Fig. 5 Uncertainty of terrestrial water storage change rate |
为了定量估算该地区陆地水储量变化情况,本文计算了研究区域内(图 4中紫色虚线所示范围)总体水储量增加情况。2003年1月—2011年3月期间,研究区域内总的陆地水储量增加的速率为4.6±2.1 km3/a,累积增加了38±17 km3的陆地水储量,相当于大约0.11±0.04 mm的海平面变化所需水量。
本文所得的陆地水增加速率要比文献[12]的结果(2.3 km3/a)要大。这主要是由于本文使用了观测精度和分辨率都有提高的RL05卫星重力数据,其球谐截止阶数为90阶,较之前60阶的RL04数据包含了更丰富的高阶信息。再者,对数据质量更高的RL05数据进行了半径较小的高斯滤波处理(滤波半径为200 km),这有利于在压制误差的同时保留更多的观测信号,而文献[12]对其使用的RL04数据进行了滤波半径为340 km的高斯平滑。
3.2 与水文模型的比较为了验证本文研究所得的陆地水储量变化的可靠性,利用WGHM和GLDAS水文模型与本文结果进行了对比分析。
为了与GRACE观测数据保持一致,对两个水文模型2003—2011年期间的数据进行了90阶球谐截断和半径为200 km的高斯滤波空间平滑处理。在扣除周年项和半年项后,得到了两个水文模型在斯堪的纳维亚半岛的变化速率,如图 6所示。图 6(a)和图 6(b)分别给出了WGHM模型和GLDAS模型的结果。

|
| 图 6 水文模型变化速率 Fig. 6 Linear rates of hydrological models |
由图 6可以看到,两个水文模型在斯堪的纳维亚半岛都呈现出非常明显的陆地水储量增加趋势。如2.4节所述,由于输出参数不同,两个模型存在着较为明显的差异。对于WGHM水文模型,其主体信号基本呈西南—东北走向,一直延伸到波的尼亚湾的北端,信号范围和幅值要比本文所得的观测结果(图 4b所示)略大;幅值位于斯堪的纳维亚半岛南部维纳恩湖的东北,大约为13 mm/a,与本文的结果很接近;WGHM水文模型在芬兰南部湖泊密集地区呈现了少量的水量增加趋势,但该区域处于GPS观测网络边缘,数据稀疏,笔者的研究结果没有完全体现出来。对于GLDAS模型,其陆地水储量变化趋势比本文的研究结果明显小得多;除了半岛南端存在水量的增加,在波的尼亚湾北端也呈现明显的水量增加趋势,与我们的结果差异较大。这可能是由于GLDAS水文模型只包含了地表土壤湿度和雪量的信息,而本文结果则反映了该地区总的陆地水储量变化(土壤湿度、地表水体和地下水等)所致。
总体而言,本文观测的斯堪的纳维亚半岛陆地水储量变化与WGHM模型较一致,而与GLDAS模型差异相对较大。为了定量描述本文结果与水文模型的一致性,笔者统计了它们的相关性。本文结果与WGHM模型的相关系数达到了0.69,与GLDAS水文模型的相关系数为0.57。这很好地验证了笔者关于斯堪的纳维亚半岛陆地水储量变化结果的可靠性。
4 结 论利用GPS垂直位移、绝对重力和GRACE卫星的RL05实测数据,本文分离了处于GIA近场的斯堪的纳维亚半岛2003年1月至2011年3月期间的陆地水储量变化,基于观测数据完整的估计了结果的不确定性,揭示了观测期间该地区陆地水储量的空间变化情况以及不确定性的地理分布,并与两种水文模型的结果进行了对比分析,发现具有良好的一致性。主要结论如下:
(1) 通过对斯堪的纳维亚半岛绝对重力和GPS并址站观测数据的回归分析,得到GIA重力-垂直位移实测比值为0.148±0.020 μGal/mm。该结果验证了Wahr的理论近似值且与北美实测的结果非常接近,说明两种方法扣除或分离GIA影响的途径是可行的。
(2) 斯堪的纳维亚半岛呈现明显的陆地水储量增加趋势,信号的主体位于半岛南端的维纳恩湖附近,幅值约为12 mm/a的等效水柱高。研究区域总的陆地水变化增加速率为4.6±2.1 km3/a,数据观测期间的累积增加水量为38±17 km3,相当于大约0.11±0.04 mm的海平面变化。
(3) 通过与两种水文模型对比分析,发现WGHM模型与本文观测结果在幅值和空间分布上都有较好的一致性,相关系数达到0.69;而GLDAS模型的幅值小于观测的陆地水变化速率,两者的相关系数为0.57。
(4) 本文研究方法利用实际观测数据扣除GIA效应,避免了直接采用GIA模型所带来的不确定性,对研究GIA近场地区的陆地水变化提供了借鉴意义。
| [1] | POKHREL Y N, HANASAKI N, YEH P J F, et al. Model Estimates of Sea-level Change due to Anthropogenic Impacts on Terrestrial Water Storage[J]. Nature Geoscience, 2012, 5(6): 389–392. DOI:10.1038/ngeo1476 |
| [2] | RODELL M, VELICOGNA I, FAMIGLITTI J S. Satellite-based Estimates of Groundwater Depletion in India[J]. Nature, 2009, 460(7258): 999–1002. DOI:10.1038/nature08238 |
| [3] | WAHR J, SWENSON S, ZLOTNICKI V, et al. Time-variable Gravity from GRACE:First Results[J]. Geophysical Research Letters, 2004, 31(11): L11501. |
| [4] | 汪汉胜, 王志勇, 袁旭东, 等. 基于GRACE时变重力场的三峡水库补给水系水储量变化[J]. 地球物理学报, 2007, 50(3): 730–736. WANG Hansheng, WANG Zhiyong, YUAN Xudong, et al. Water Storage Changes in Three Gorges Water Systems Area Inferred from GRACE Time-variable Gravity Data[J]. Chinese Journal of Geophysics, 2007, 50(3): 730–736. |
| [5] | FENG Wei, ZHONG Min, LEMOINE J M, et al. Evaluation of Groundwater Depletion in North China Using the Gravity Recovery and Climate Experiment (GRACE) Data and Ground-based Measurements[J]. Water Resources Research, 2013, 49(4): 2110–2118. DOI:10.1002/wrcr.20192 |
| [6] | 卢飞, 游为, 范东明, 等. 由GRACE RL05数据反演近10年中国大陆水储量及海水质量变化[J]. 测绘学报, 2015, 44(2): 160–167. LU Fei, YOU Wei, FAN Dongming, et al. Chinese Continental Water Storage and Ocean Water Mass Variations Analysis in Recent Ten Years Based on GEACE RL05 Data[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 160–167. DOI:10.11947/j.AGCS.2015.20130753 |
| [7] | 文汉江, 黄振威, 王友雷, 等. 青藏高原及其周边地区水储量变化的独立成分分析[J]. 测绘学报, 2016, 45(1): 9–15. WEN Hanjiang, HUANG Zhenwei, WANG Youlei, et al. Independent Component Analysis of Water Storage Changes Interpretation over Tibetan Plateau and Its Surrounding Areas[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 9–15. DOI:10.11947/j.AGCS.2016.20140447 |
| [8] | 罗志才, 李琼, 钟波. 利用GRACE时变重力场反演黑河流域水储量变化[J]. 测绘学报, 2012, 41(5): 676–681. LUO Zhicai, LI Qiong, ZHONG Bo. Water Storage Variations in Heihe River Basin Recovered from GRACE Temporal Gravity Field[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 676–681. |
| [9] | LETTENMAIER D P, FAMIGLIETTI J S. Hydrology:Water from on High[J]. Nature, 2006, 444(7119): 562–563. DOI:10.1038/444562a |
| [10] | MORROW E, MITROVICA J X, FOTOPOULOS G. Water Storage, Net Precipitation, and Evapotranspiration in the Mackenzie River Basin from October 2002 to September 2009 Inferred from GRACE Satellite Gravity Data[J]. Journal of Hydrometeorology, 2011, 12(3): 467–473. DOI:10.1175/2010JHM1278.1 |
| [11] | PELTIER W R. Global Glacial Isostasy and the Surface of the Ice-age Earth:The ICE-5G (VM2) Model and GRACE[J]. Annual Review of Earth and Planetary Sciences, 2004, 32: 111–149. DOI:10.1146/annurev.earth.32.082503.144359 |
| [12] | WANG Hansheng, JIA Lulu, STEFFEN H, et al. Increased Water Storage in North America and Scandinavia from GRACE Gravity Data[J]. Nature Geoscience, 2013, 6(1): 38–42. |
| [13] | WAHR J, HAN Dazhong, TRUPIN A. Predictions of Vertical Uplift Caused by Changing Polar Ice Volumes on a Viscoelastic Earth[J]. Geophysical Research Letters, 1995, 22(8): 977–980. DOI:10.1029/94GL02840 |
| [14] | LAMBERT A, HUANG J, VAN DER KAMP G, et al. Measuring Water Accumulation Rates Using GRACE Data in Areas Experiencing Glacial Isostatic Adjustment:The Nelson River Basin[J]. Geophysical Research Letters, 2013, 40(23): 6118–6122. DOI:10.1002/2013GL057973 |
| [15] | DAHLE C, FLECHTNER F, GRUBER C, et al. GFZ GRACE Level-2 Processing Standards Document for Level-2 Product Release 0005[R]. Potsdam:Deutsches Geo Forschungs Zentrum GFZ, 2012. http://www.oalib.com/references/18990380 |
| [16] | 汪汉胜, 贾路路, WUP, 等. 冰川均衡调整对东亚重力和海平面变化的影响[J]. 地球物理学报, 2010, 53(11): 2590–2602. WANG Hansheng, JIA Lulu, WU P, et al. Effects of Global Glacial Isostatic Adjustment on the Secular Changes of Gravity and Sea Level in East Asia[J]. Chinese Journal of Geophysics, 2010, 53(11): 2590–2602. |
| [17] | MAZZOTTI S, LAMBERT A, COURTIER N, et al. Crustal Uplift and Sea Level Rise in Northern Cascadia from GPS, Absolute Gravity, and Tide Gauge Data[J]. Geophysical Research Letters, 2007, 34(15): L15306. |
| [18] | MAZZOTTI S, LAMBERT A, HENTON J, et al. Absolute Gravity Calibration of GPS Velocities and Glacial Isostatic Adjustment in Mid-continent North America[J]. Geophysical Research Letters, 2011, 38(24): L24311. |
| [19] | STEFFEN H, GITLEIN O, DENKER H, et al. Present Rate of Uplift in Fennoscandia from GRACE and Absolute Gravimetry[J]. Tectonophysics, 2009, 474(1-2): 69–77. DOI:10.1016/j.tecto.2009.01.012 |
| [20] | MVLLER J, NAEIMI M, GITLEIN O, et al. A Land Uplift Model in Fennoscandia Combining GRACE and Absolute Gravimetry Data[J]. Physics and Chemistry of the Earth, Parts A/B/C, 2012, 53(54): 54–60. |
| [21] | JOHANSSON J M, DAVIS J L, SCHERNECK H G, et al. Continuous GPS Measurements of Postglacial Adjustment in Fennoscandia 1. Geodetic Results[J]. Journal of Geophysical Research, 2002, 107(B8): 2157. DOI:10.1029/2001JB000400 |
| [22] | LIDBERG M, JOHANSSON J M, SCHERNECK H G, et al. An Improved and Extended GPS-derived 3D Velocity Field of the Glacial Isostatic Adjustment (GIA) in Fennos-candia[J]. Journal of Geodesy, 2007, 81(3): 213–230. DOI:10.1007/s00190-006-0102-4 |
| [23] | LIDBERG M, JOHANSSON J M, SCHERNECK H G, et al. Recent Results Based on Continuous GPS Observations of the GIA Process in Fennoscandia from BIFROST[J]. Journal of Geodynamics, 2010, 50(1): 8–18. DOI:10.1016/j.jog.2009.11.010 |
| [24] | WAHR J, MOLENAAR M, BRYAN F. Time Variability of the Earth's Gravity Field:Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical Research, 1998, 103(B12): 30205–30229. DOI:10.1029/98JB02844 |
| [25] | WANG Hansheng, WU P, WANG Zhiyong. An Approach for Spherical Harmonic Analysis of Non-smooth Data[J]. Computers & Geosciences, 2006, 32(10): 1654–1668. |
| [26] | 汪汉胜, 许厚泽, 李国营. SNREI地球模型负荷勒夫数数值计算的新进展[J]. 地球物理学报, 1996, 39(S1): 182–189. WANG Hansheng, XU Houze, LI Guoying. Improvement of Computations of Load Love Numbers of SNREI Earth Model[J]. Chinese Journal of Geophysics, 1996, 39(S1): 182–189. |
| [27] | 鞠晓蕾, 沈云中, 张子占. 基于GRACE卫星RL05数据的南极冰盖质量变化分析[J]. 地球物理学报, 2013, 56(9): 2918–2927. JU Xiaolei, SHEN Yunzhong, ZHANG Zizhan. Antarctic Ice Mass Change Analysis Based on GRACE RL05 Data[J]. Chinese Journal of Geophysics, 2013, 56(9): 2918–2927. |
| [28] | CHENG Minkang, TAPLEY B D. Variations in the Earth's Oblateness During the Past 28 Years[J]. Journal of Geophysical Research, 2004, 109(B9): B09402. |
| [29] | SWENSON S, CHAMBERS D, WAHR J. Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output[J]. Journal of Geophysical Research, 2008, 113(B8): B08410. |
| [30] | 贾路路, 汪汉胜, 相龙伟, 等. 冰川均衡调整对南极冰质量平衡监测的影响及其不确定性[J]. 地球物理学报, 2011, 54(6): 1466–1477. JIA Lulu, WANG Hansheng, XIANG Longwei, et al. Effects of Glacial Isostatic Adjustment on the Estimate of Ice Mass Balance over Antarctica and the Uncertainties[J]. Chinese Journal of Geophysics, 2011, 54(6): 1466–1477. |
| [31] | CHAMBERS D P. Evaluation of New GRACE Time-variable Gravity Data over the Ocean[J]. Geophysical Research Letters, 2006, 33(17): L17603. DOI:10.1029/2006GL027296 |
| [32] | STEFFEN H, WU P, WANG Hansheng. Determination of the Earth's Structure in Fennoscandia from GRACE and Implications for the Optimal Post-processing of GRACE Data[J]. Geophysical Journal International, 2010, 182(3): 1295–1310. DOI:10.1111/j.1365-246X.2010.04718.x |
| [33] | PETTERSEN B R. The Postglacial Rebound Signal of Fennoscandia Observed by Absolute Gravimetry, GPS, and Tide Gauges[J]. International Journal of Geophysics, 2011: 957329. |
| [34] | JAMES T S, IVINS E R. Present-day Antarctic Ice Mass Changes and Crustal Motion[J]. Geophysical Research Letters, 1995, 22(8): 973–976. DOI:10.1029/94GL02800 |
| [35] | FANG M, HAGER B H. Vertical Deformation and Absolute Gravity[J]. Geophysical Journal International, 2001, 146(2): 539–548. DOI:10.1046/j.0956-540x.2001.01483.x |
| [36] | 贾路路, 汪汉胜, 相龙伟. 冰川均衡调整重力与径向位移近似关系的不确定性[J]. 地球科学:中国地质大学学报, 2014, 39(7): 905–914. JIA Lulu, WANG Hansheng, XIANG Longwei. Uncertainty of Approximate Relationship between GIA Induced Viscous Gravity and Radial Displacement[J]. Earth Science-Journal of China University of Geosciences, 2014, 39(7): 905–914. DOI:10.3799/dqkx.2014.085 |
| [37] | MILNE G A, DAVIS J L, MITROVICA J X, et al. Space-geodetic Constraints on Glacial Isostatic Adjustment in Fennoscandia[J]. Science, 2001, 291(5512): 2381–2385. DOI:10.1126/science.1057022 |
| [38] | LAMBECK K, PURCELL A, ZHAO J, et al. The Scandinavian Ice Sheet:From MIS 4 to the End of the Last Glacial Maximum[J]. BOREAS, 2010, 39(2): 410–435. DOI:10.1111/bor.2010.39.issue-2 |
| [39] | RODELL M, HOUSER P R, JAMBOR U, et al. The Global Land Data Assimilation System[J]. Bulletin of the American Meteorological Society, 2004, 85(3): 381–394. DOI:10.1175/BAMS-85-3-381 |
| [40] | DÖLL P, KASPAR F, LEHNER B. A Global Hydrological Model for Deriving Water Availability Indicators:Model Tuning and Validation[J]. Journal of Hydrology, 2003, 270(1-2): 105–134. DOI:10.1016/S0022-1694(02)00283-4 |


