2. 地理信息工程国家重点实验室, 陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China
GNSS是以时间测量为基础的系统,星载原子钟作为系统的星上时间基准及核心部件,其性能直接决定导航、定位和授时的质量[1-2]。基于较长时间段的卫星钟差(satellite clock bias,SCB)数据分析星载原子钟的性能是掌握和评估卫星钟性能和运行状况的一种重要手段,在系统的完好性监测[3]、系统性能评估[4]和卫星钟差确定[5]及预报[6-7]等方面具有重要作用。因此,对于GNSS星载原子钟性能的评估,国内外学者进行了大量的研究[2, 8-15]。例如,文献[2]对GPS星载原子钟的性能指标进行了分析,文献[9]对GPS和GLONASS星载原子钟较短时间尺度内的特性进行了对比和分析等。但是从已有的研究成果来看,大部分的工作主要是针对GPS星载原子钟展开的。
北斗卫星导航系统(BeiDou Navigation System,BDS)目前正处于全面建设阶段,开展BDS星载原子钟性能分析的相关研究,对于提升系统的服务性能和下一步系统的建设、维护等具有重要意义。近年针对BDS星载原子钟的性能分析也进行了一些初步探讨[16-22]。文献[16]采用修正阿伦方差计算和分析了BDS的IGSO和GEO星载原子钟的稳定性;文献[17]使用近一个月的钟差数据对4颗BDS卫星的星载原子钟稳定性以及噪声类型进行了计算分析;文献[18]基于近一年的钟差数据分析了BDS卫星钟差数据的周期特性;文献[19]使用300多天的BDS卫星钟差数据分析了BDS星载原子钟的相位、频率、频漂等指标的变化规律;文献[20]基于星载原子钟的最大钟差、钟速及钟漂值对北斗二代卫星钟的性能进行了评估;文献[21]在介绍频率准确度、稳定度和漂移率这几种评估北斗在轨卫星钟性能方法的基础上采用3个月的北斗钟差数据对这些性能指标进行了计算和分析;文献[22]基于8周的钟差数据根据准确度、漂移率和稳定度3个性能指标对BDS与GPS/GLONASS星载原子的性能进行了比较分析。但是与GPS相比,针对BDS星载原子钟性能分析的研究仍十分有限,更重要的是目前的研究成果存在一定的局限性,主要表现在:首先,目前对星载原子钟性能的分析,大多集中在某一特性方面,并没有形成较为全面的星载原子钟性能评价体系;其次,BDS星载原子钟性能分析的研究主要集中在使用一年左右的数据进行较短时间的分析和评估,长期性能分析的相关研究目前鲜有报道。基于此,本文采用2013年1月1日—2015年12月31日共3年的多星定轨联合解算的BDS卫星钟差数据,综合BDS星载原子钟的钟差数据长期变化特点、钟差模型参数长期变化特征、频率稳定性长期变化规律、观测噪声长期变化特性和钟差周期特性等指标较为全面地分析和评估了BDS星载原子钟的长期性能,得到了一些有益的结论。
1 算法原理 1.1 异常钟差数据的预处理方法星载原子钟在长期运行过程中会受到各种不确定因素的影响,因此在获取的卫星钟差数据中经常会出现粗差等数据异常情况。因此,在使用BDS卫星钟差数据时需要进行适当的预处理。考虑较长时间段的卫星钟差数据及其对应的频率数据的数据量相对较大,本文采用具有较好抗差性和时效性的中位数法(MAD)[23]进行粗差探测,即当观测量满足式(1)的形式
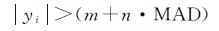 (1)
(1)
时(整数n根据需要确定)就认为是粗差点,式中m=Median(yi),MAD=Median{|yi-m|/0.674 5}。该方法通常只应用于频率数据,本文是将钟差数据一次差分转换为频率数据后再进行异常值探测的。异常值探测出之后,一般是将该异常数据设为0或者通过剩余数据对其进行内插。但是,这两种异常值处理方式都会引入新的数据,从而造成原始数据一定程度上的失真。为了避免这种情况,本文在探测出异常数据后直接将其对应的卫星钟差数据设为空,即这些历元时刻的卫星钟差数据缺失,此即为本文对MAD方法的改进。
1.2 星载铷原子钟钟差模型星载铷原子钟在运行过程中存在着较为显著的频率漂移,所以在构造BDS精密钟差模型时采用包含了表征卫星钟时频特性的相位、频率、频率漂移的二次多项式模型。该模型的表达式为[12]
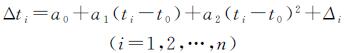 (2)
(2)
式中,Δti是第i历元的卫星钟差(相位);t0为星钟参数的参考时刻;ti表示历元时刻;待估参数a0、a1和a2分别表示参考时刻t0的相位(钟差)、频率(钟速)及频率漂移率(钟漂);Δi为观测误差。当已知钟差数据不少于3个时,便可拟合求得待估参数。
1.3 基于频谱分析的周期项提取在使用频谱分析的方法进行周期项提取时,要求数据序列不宜含有较为明显的趋势项。所以,在提取BDS卫星钟差的周期项时,首先使用二次多项式对每天的卫星钟差进行拟合来消除钟差的趋势项,然后基于拟合残差进行周期项的提取。
对于离散傅里叶级数(DFT)而言,其表达式为[24]
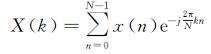 (3)
(3)
式中,X(k)代表k时段的频谱值;x(n)对应于钟差的拟合残差序列;n是残差序列中元素的序号;j表示虚数单位;e是数学常数;N是残差的个数,求解时通常要求满足N=2L,L=0,1,2,…,n,若个数达不到要求则通过增加0元素来满足;通过该式便可求出残差序列中各点对应的频谱值。在实际应用中,对于频谱值可采用快速傅里叶变换(FFT)求解得到。然后,根据残差数列对应的频谱图便可较为容易地确定周期项。
1.4 基于重叠哈达玛方差的频率稳定性计算方法频率稳定性的结果是衡量原子钟性能优劣的重要指标之一。哈达玛系列方差因能够较好地消除原子钟频漂造成的影响,常被用来计算铷原子钟的频率稳定性[1, 23]。同时,在哈达玛系列方差中重叠哈达玛方差具有较高的置信区间、适合计算较短时间的频率稳定度且其公式相对简单,因此本文选用重叠哈达玛方差来计算BDS星载原子钟的频率稳定度。
重叠哈达玛方差通过最大限度地利用已有数据构造所有可能的3次采样来提高计算的置信度。基于相位(钟差)数据的重叠哈达玛方差计算公式为[19, 23]
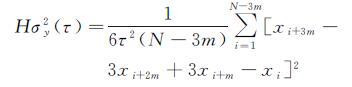 (4)
(4)
式中,τ=mτ0为平滑时间;τ0为相邻钟差数据的采样间隔;xi为钟差数据;N为钟差数据的个数;m为平滑因子,一般取1≤m≤int[(N-1)/3]。
图 1给出了本文分析和评估BDS星载原子钟性能的整个流程。图中加粗的字体表示BDS星载原子钟性能分析时所采用评估指标。
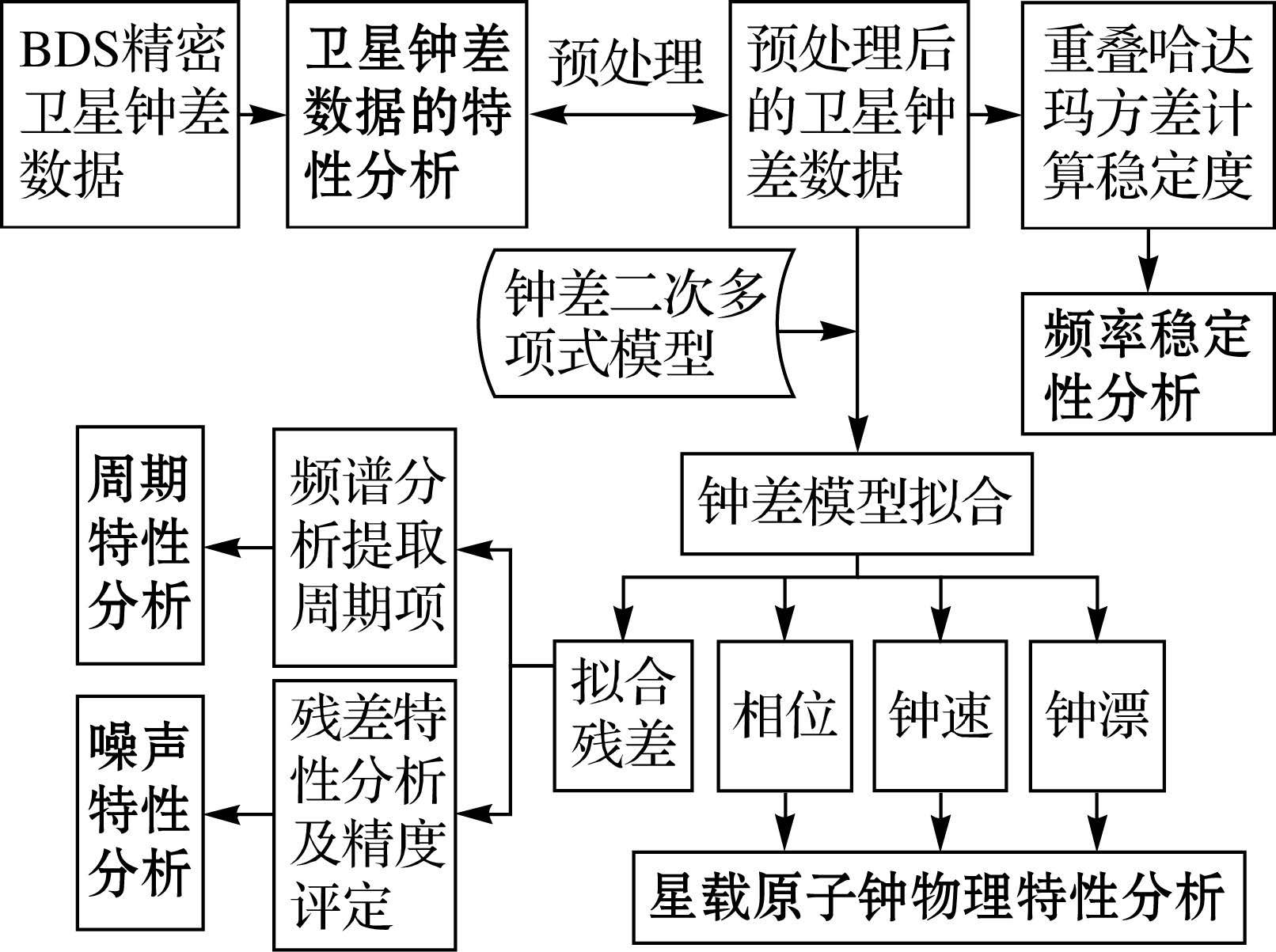
|
| 图 1 BDS星载原子钟性能分析的流程及其所采用的评价指标 Fig. 1 The evaluation indexes and procedures used for analyzing the performance of BDS satellite clocks |
2 BDS卫星钟性能分析
GNSS星载原子钟性能分析和评估大多是基于已知的钟差产品来开展研究的[12]。目前,BDS卫星钟差主要通过两种方式来获取,分别是基于星地双向无线电时间比对确定卫星钟差和通过多星定轨联合解算卫星轨道和钟差[25]。前者是BDS运控方用来进行高精度的星地时间同步,其相关数据尚未公开;后者所得钟差产品为BDS卫星钟相关的研究提供免费、公开的可靠数据源。针对这两种数据产品的相关特性,文献[26]进行了对比分析研究,结果表明两种数据之间存在某种表现为常量的系统误差和以天为周期的周期性误差,但是这两种数据产品均能较好地评价BDS星载原子钟的性能;两种数据计算的频率漂移率和频率准确度具有很好的一致性,两者计算的频率稳定度结果均能达到系统所要求的精度范围;但是后者由于受未完全分离的定轨误差等的影响,频率稳定性的计算结果前者优于后者。
本文BDS星载原子钟性能分析所采用的卫星钟差数据来自IGS多GNSS试验项目(the multi-GNSS experiment,MGEX)中武汉大学GNSS中心通过多星定轨联合解算[25]得到的精密星历钟差产品。该产品自2013年1月1日公开发布,其与北斗轨道产品耦合,数据精度优于0.5 ns,是目前国际上精度相对较好的BDS卫星钟差产品,可以较为客观地用来开展与BDS卫星钟相关的研究和试验[19]。本文数据收集的时间段为2013年1月1日—2015年12月31日共3年,数据的采样间隔为15 min。
2.1 卫星钟差数据预处理对BDS卫星钟差数据进行预处理的具体步骤是:①对3年钟差数据的非空数据进行提取,然后对提取的非空钟差数据进行相邻历元间的一次差分得到其对应的一次差分数据;②将钟差的一次差分数据视为钟差频率数据采用本文所给的改进MAD方法进行处理,得到预处理之后的钟差数据;③在此基础之上,对每天的卫星钟差数采用改进MAD方法进行再次预处理。需要说明的是,本文卫星钟差数据预处理的目的是剔除数据序列中的异常值,提供相对干净的卫星钟差数据。而在基于预处理后的数据计算卫星钟性能指标时,还是要满足具体方法对数据的要求来计算相应的性能指标。例如,在基于频谱分析提取周期项时,数据的个数要满足2L个(L=0,1,2,…,n),若个数达不到要求则通过补充0元素来满足;为了符合公式的要求,在具体的计算中就需要对间断点和序列最后补0填充。
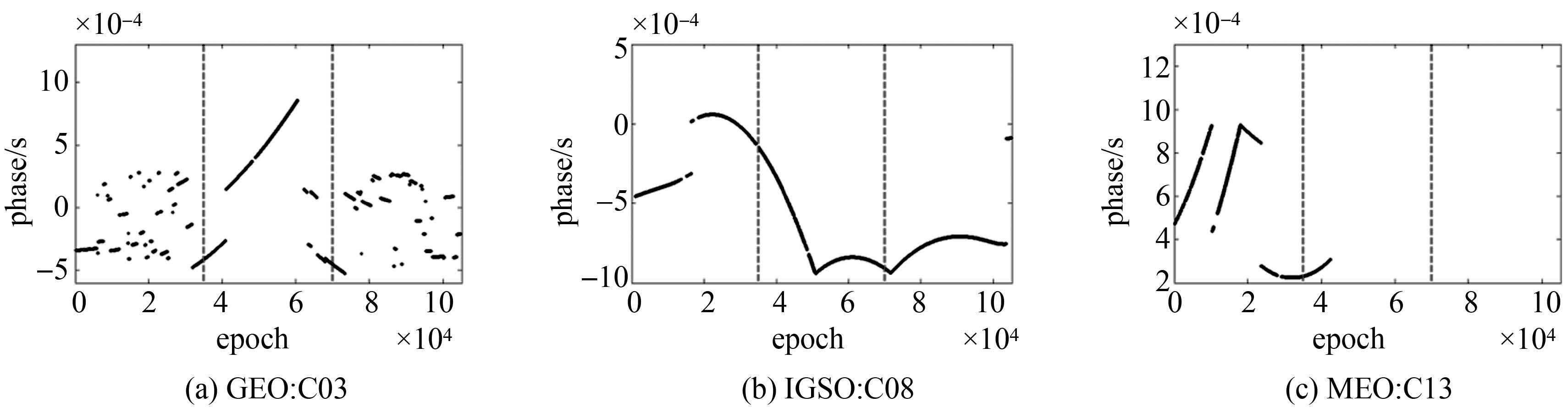
以GEO的C03、IGSO的C08、MEO的C13为例,图 2和图 3分别给出了预处理前后3年时间里这3颗卫星的钟差数据变化情况。图中纵向的两条虚线是对3年数据按照年份的划分,本文接下来的图也是如此。对比图 2和图 3可以看出,预处理后的钟差数据质量有较大程度的提高,特别是C03和C08两颗卫星的钟差数据实际变化过程得到了有效的展示,说明原始的精密卫星钟差数据中存在一定量的异常值,在基于钟差数据开展与星载原子钟相关的研究时需要进行适当的数据预处理。同时,也说明了基于本文数据预处理策略能有效探测并处理数据序列中的异常值。

|
| 图 2 原始的BDS卫星钟差数据 Fig. 2 Original BDS SCB data |
|
| 图 3 预处理后的BDS卫星钟差数据 Fig. 3 Preprocessed BDS SCB data |
2.2 钟差(相位)、钟速(频率)、钟漂(频漂)指标的长期变化规律
采用钟差二次多项式模型对预处理后的卫星钟差数据进行逐天拟合,得到卫星钟的相位、钟速和钟漂参数的长期数据序列,其结果如图 4—图 6所示,此外,图 6还给出了数据按年统计的均方根(RMS)值。RMS的计算公式如式(5)所示
 (5)
(5)
式中,ai为数据序列{ai,i=1,2,…,n}第i个非空元素,n为数据序列非空元素的个数。

|
| 图 4 BDS星载原子钟相位指标的长期变化规律 Fig. 4 Long-term variation of phase index of BDS satellite clocks |
根据图 4的相位指标序列可以发现,BDS星载原子钟在长期运行过程中存在着一定次数的相位跳变,这说明BDS星载原子钟运行期间可能存在多次的调相操作,但是这种频繁的相位调整使得卫星钟差数据的稳定性和连续性变差。而在3类卫星中,GEO卫星相位跳变的次数相对最多,因此,其相位的稳定性和连续性相对最差。此外,在第3年的时候,相位调整的次数明显增多,出现这种情况的主要原因可能是星载原子钟随着运行时间的积累,自身硬件设备出现了一定程度的老化,导致输出相位随时间累计偏差增大得更快,所以为了保证相位的准确性需要进行频繁的切换来予以校准。
|
| 图 5 BDS星载原子钟频率指标的长期变化规律 Fig. 5 Long-term variation of frequency index of BDS satellite clocks |
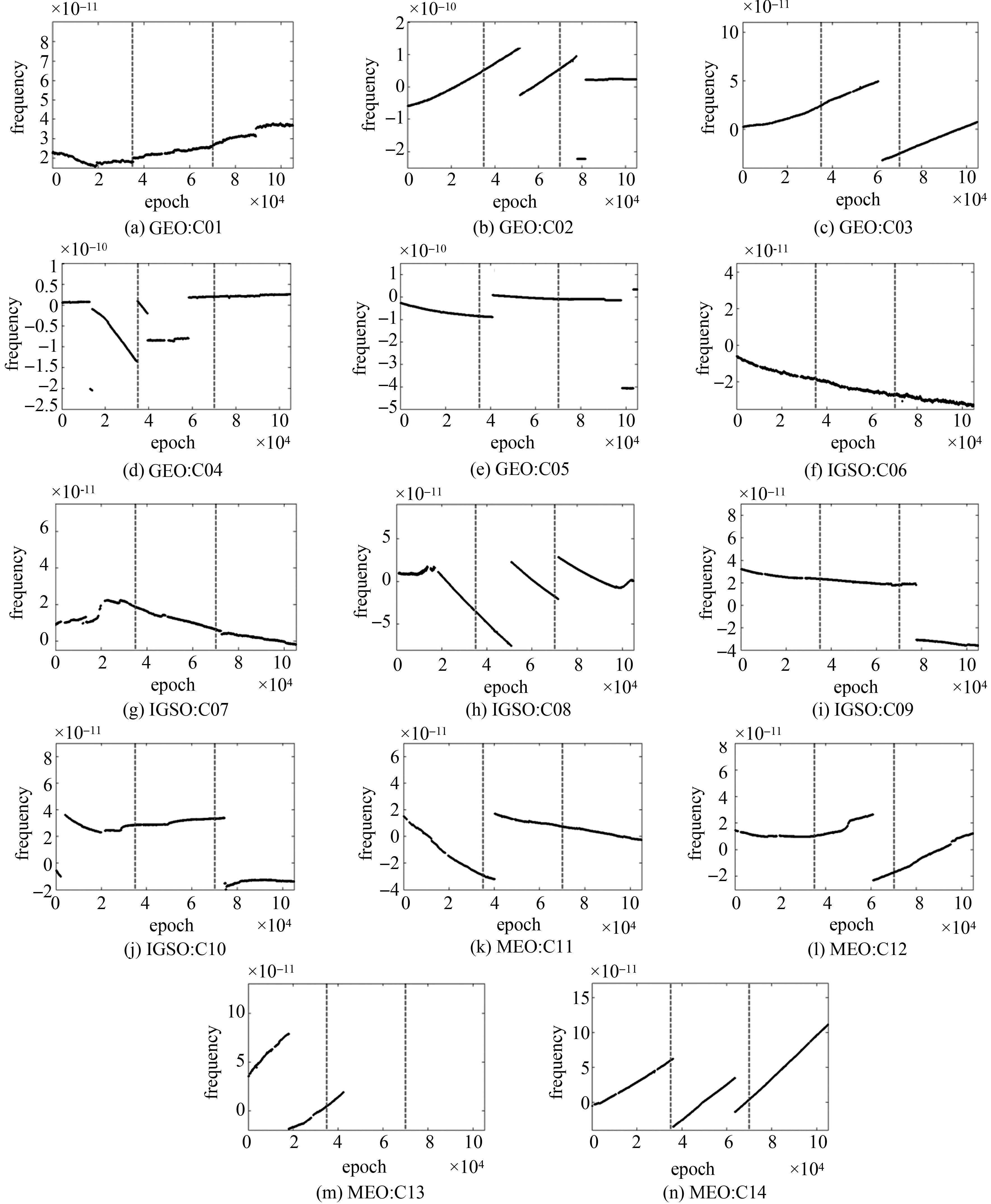
根据图 5的频率序列可看出,BDS在3年的运行过程中所有卫星的星载原子钟也同样存在一定次数的频率跳变(C06卫星在第3年刚开始的阶段出现了一段短时间的频率跳变段),但是其跳变次数比相位跳变的次数要少得多,说明整体而言,频率数据的稳定性和连续性相对较好。同时,在3类卫星中MEO卫星整体上的频率跳变最少,其频率序列的稳定性和连续性相对最好。
根据图 6中各颗卫星钟的频漂序列可以看出,BDS星载原子钟的频漂值都在10-18量级,并且每颗卫星在不同时间的情况各不相同。GEO卫星中的C03卫星、IGSO卫星中的C09卫星、MEO卫星中的C11和C12卫星,其在同类型卫星中的原子钟频漂特性最好,频漂值能够取到10-19量级。同时,可以发现在一定时间段内随着时间的推移频漂会逐渐发散变大,但是,当增大到一定程度的时候,频漂参数又会被调整到相对较好的状态,特别是C04和C08卫星表现得最为显著;这可能是因为当地面监测站监测到星载原子钟频漂不断变大对卫星钟的准确性造成影响时,会对星载原子钟进行一定的处理来校准频漂。此外,从C06和C09的频漂序列可以看出,这两颗卫星的原子钟频漂序列存在近似的周期性变化规律,其周期大约是半年。分析其原因可能是这两颗卫星在基于多星定轨联合解算卫星钟差时,存在对频漂产生周期性影响的系统误差。
|
| 图 6 BDS星载原子钟频漂指标的长期变化规律 Fig. 6 Long-term variation of frequency drift index of BDS satellite clocks |
2.3 钟差模型噪声的长期变化特点
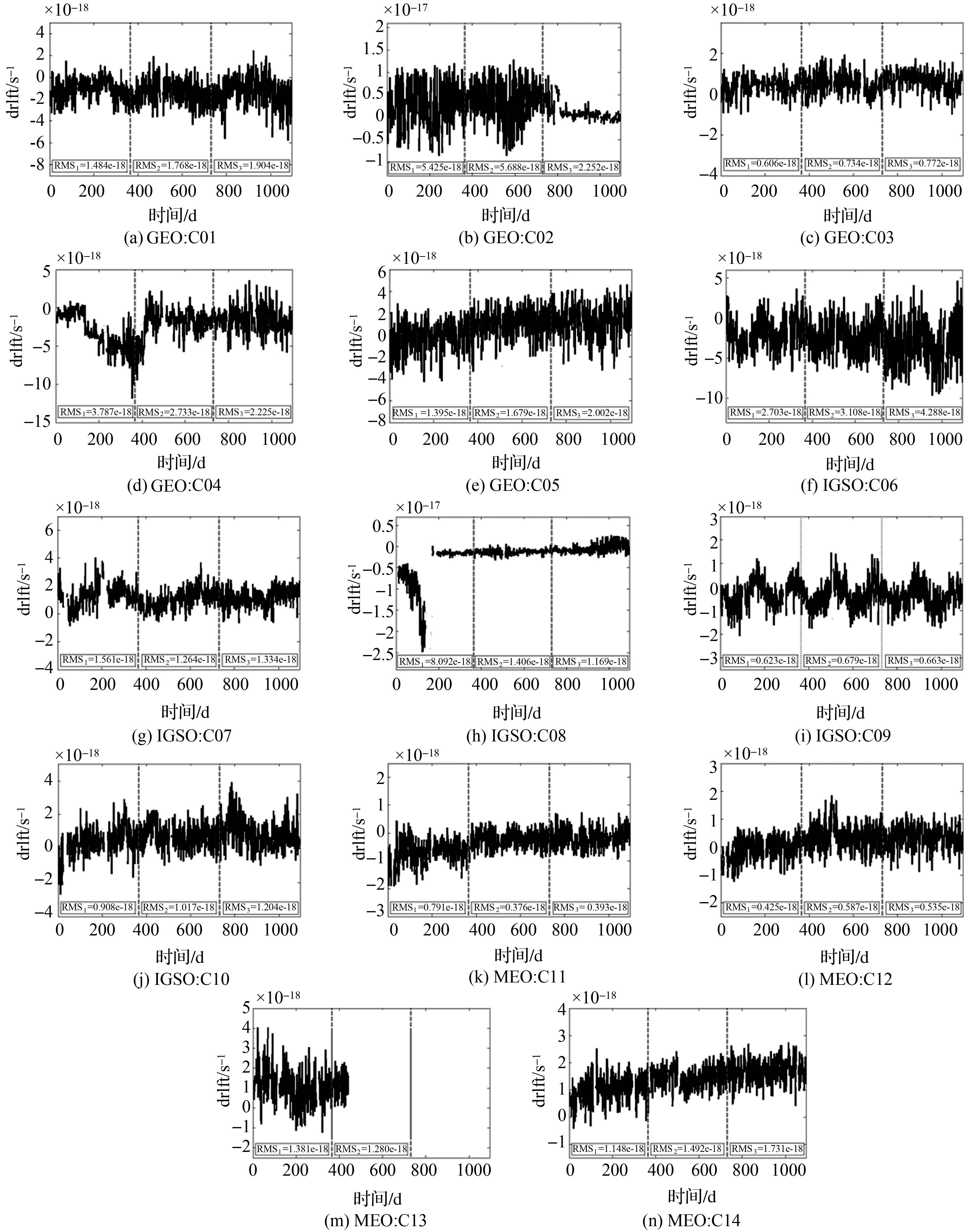
星载原子钟钟差模型的噪声水平决定着钟差实时估计和预报的精度和稳定性[12]。本文将该特性作为反映BDS星载原子钟性能的一项指标。采用钟差二次多项式模型对预处理后的卫星钟差数据进行逐天拟合得到其对应的拟合残差。图 7给出了拟合残差及其按年统计的精度结果。
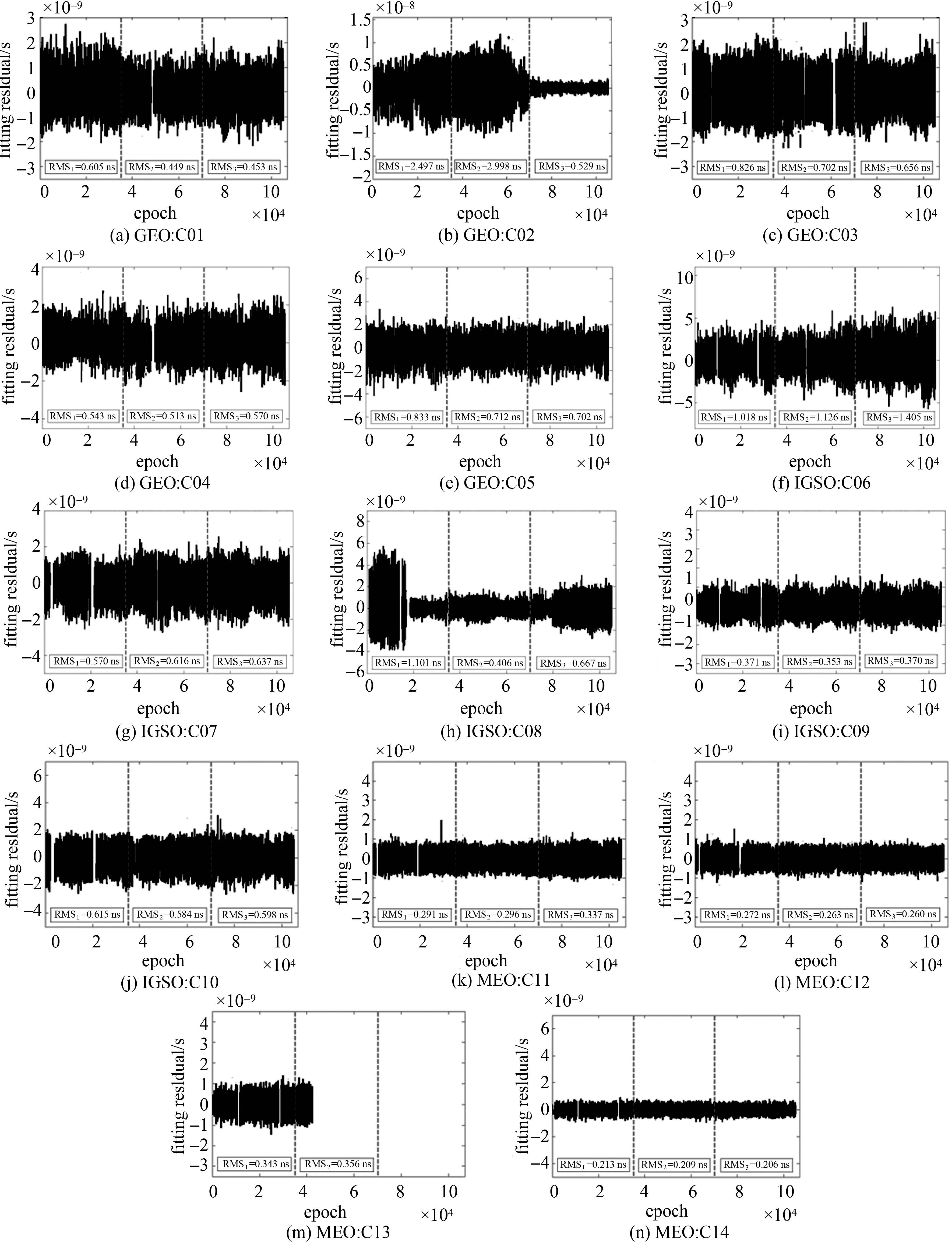
|
| 图 7 BDS星载原子钟钟差模型的噪声水平及其精度统计值 Fig. 7 Model noise level and fitting precision statistics of BDS satellite clocks |
由图 7可知,不论是噪声的随机分布还是噪声水平(RMS),3年时间里MEO星载原子钟都要明显好于GEO和IGSO星载原子钟,并且MEO卫星钟的噪声分布是最为均匀和平稳的,特别是C14卫星,说明MEO卫星钟的噪声特性相对最好。此外,在GEO和IGSO卫星里面,C02卫星钟噪声大小随着时间增加呈现出先逐渐变大后迅速变小并趋于平稳的变化趋势,C08卫星第1年前期原子钟的噪声较大,后续时间段的噪声相对较小,但随着时间增加逐渐变大,C06卫星钟噪声随着时间增加逐渐变大并呈现出一定的周期性,C09卫星钟噪声大小变化相对平稳但却呈现出较为显著的周期特性,可能是C06和C09这两颗卫星在基于多星联合解算卫星钟差时存在周期性影响的系统误差。同时结合图 6,对比MEO卫星钟的频漂和噪声可以看出,即使钟漂随时间增加有间断性的增大趋势,但其卫星钟噪声的波动范围都基本保持在近似相同的水平之内,说明对于该类卫星即使其星载原子钟包含较大噪声时也不会显著影响钟差自身的物理模型参数值。
2.4 钟差周期特性分析星载原子钟钟差的周期特性分析能够精化星载原子钟的钟差模型,并为联合定轨轨道动力学模型的完善提供参考[18]。因此,本文将钟差周期特性分析也作为评估BDS星载原子钟性能的一项重要指标。使用频谱分析的方法对3年的BDS卫星钟差数据进行周期项提取,以C03卫星为例,图 8是其频谱分析的结果图示。由图 8可知其卫星钟差数据中存在着显著的周期项。本文在提取周期项时取到前9项,因为这样既能保留主要的周期项并反映数据真实的周期特性又能避免提取过多周期项导致出现周期项提取不准和避免不必要的工作量。剩余卫星的钟差数据周期项提取与之类似,表 1给出了所有卫星的钟差周期项提取结果。

|
| 图 8 C03卫星的钟差数据频谱分析结果 Fig. 8 The spectral analysis results based on SCB data of satellite C03 |
| h | ||||||||||
| 轨道类型 | 卫星 | 周期1 | 周期2 | 周期3 | 周期4 | 周期5 | 周期6 | 周期7 | 周期8 | 周期9 |
| GEO | C01 | 12 | 24 | 8 | 6 | 4 | 4.8 | 3.428 | 3 | 2.667 |
| C02 | 12 | 24 | 8 | 14.376 | 17.054 | 17.902 | 13.408 | 12.857 | 11.547 | |
| C03 | 12 | 24 | 8 | 6 | 4.8 | 3.428 | 4 | 3 | 2.406 | |
| C04 | 12 | 24 | 4.8 | 6 | 8 | 4 | 3.428 | 3 | 2.667 | |
| C05 | 12 | 24 | 8 | 6 | 4 | 3.428 | 3 | 4.8 | 2.667 | |
| IGSO | C06 | 12 | 24 | 8 | 6 | 4.8 | 4 | 3.428 | 3 | 2.667 |
| C07 | 24 | 12 | 8 | 6 | 4.8 | 4 | 3.429 | 3 | 2.667 | |
| C08 | 12 | 24 | 6 | 8 | 4 | 4.8 | 3.428 | 2.667 | 3 | |
| C09 | 24 | 12 | 8 | 6 | 4.8 | 4 | 3.428 | 3 | 2.667 | |
| C10 | 24 | 12 | 6 | 8 | 4 | 4.8 | 3.428 | 3 | 2.667 | |
| MEO | C11 | 12.908 | 6.443 | 27.928 | 12.826 | 13.186 | 12.562 | 11.994 | 13.964 | 15.217 |
| C12 | 12.908 | 6.443 | 27.928 | 13.964 | 14.616 | 11.994 | 12.379 | 13.313 | 15.252 | |
| C13 | 12.908 | 6.443 | 12.635 | 11.891 | 13.964 | 27.928 | 14.805 | 12.156 | 15.821 | |
| C14 | 6.443 | 12.908 | 13.964 | 11.994 | 12.385 | 14.306 | 14.698 | 13.477 | 17.244 | |
由表 1可知,14颗BDS卫星的长期钟差数据中均存在显著的周期项,并且不同轨道类型的卫星,其钟差周期项不同,而同种轨道类型的卫星其钟差周期项也存在差异。具体表现为:所有的GEO卫星以及IGSO中的C06、C08卫星,其钟差的两个主周期依次是12 h和24 h,剩余的IGSO卫星,其钟差的两个主周期依次是24 h和12 h,MEO卫星中除了C14钟差的两个主周期依次是6.443 h和12.908 h之外,其余卫星钟差的两个主周期依次是12.908 h和6.443 h。
同时,根据表 1中的数据可以发现,GEO和IGSO(轨道周期为23 h 56 min)钟差数据最显著的周期是12 h或者是24 h,MEO(轨道周期为12 h 53 min)钟差数据最显著的周期项是12.908 h(约为12 h 55 min)或6.443 h(约为6 h 27 min),3类卫星的钟差数据主周期分别近似为其卫星轨道周期的1/2倍或1倍。考虑到本文的BDS卫星钟差数据是基于多星联合定轨解算得到的,所以可以认为在同时解算卫星轨道和钟差的过程中一部分的轨道误差被钟差吸收。
此外,GEO和IGSO钟差都含24 h这一主周期项,说明基于多星联合定轨解算得到的卫星钟差除了跟轨道周期耦合之外,还可能与外界昼夜环境变化有一定的联系。而MEO卫星钟差则存在相对较长的周期项27.928 h,但该值接近24 h,可能是在解算卫星轨道和钟差时由于MEO卫星的光压模型摄动力存在昼夜环境变化周期而造成的。
2.5 基于重叠哈达玛方差的频率稳定性长期特性分析频率稳定性是衡量星载原子钟性能最常用和最重要的评估指标之一。本文基于重叠哈达玛方差对每天的卫星钟差数据进行计算,得到各颗卫星3年时间每天的频率稳定度。图 9给出了BDS星载原子钟频率稳定度指标的计算结果及其按年统计的精度值。需要说明的是,在计算稳定度时,只有当这一天的数据连续完整(即不存在数据间断,数据历元个数为96个)时才计算其对应的稳定度值。图 9中的DAYSi(i=1,2,3)表示第i年参与计算稳定度的天数,RMSi(i=1,2,3)表示第i年稳定度稳序列的均方根值。

|
| 图 9 BDS星载原子钟的频率稳定度长期变化指标及其精度统计值 Fig. 9 Long-term variation of frequency stability index and their precision statistics of BDS satellite clocks |
由图 9可知,14颗BDS卫星钟的频率稳定度序列,除了前31天的变化呈近似对钩状的较大波动之外(可能是系统刚开始正式提供服务时,多星定轨条件下的北斗卫星钟差受到解算策略调整等因素的影响而出现这种情况),整体上长期频率稳定性波动相对平稳,其频率稳定性整体保持在10-13量级,个别星载原子钟内部存在着一定程度的显著差异。具体而言,除了C03、C14在3年时间里、C02和C04在第1年其星载原子钟稳定度的RMS值达到了10-14量级,其余星载原子钟稳定度的RMS值都在1.0~3.0×10-13量级。因此,可认为BDS星载原子钟之间的稳定度差异不显著。C08的稳定度变化比较异常,3年时间里出现过两个时间段比较差的稳定度序列,再结合其稳定度统计值,可以看出该卫星的星载原子钟频率稳定性在整个系统中相对最差;而C14的星载原子钟稳定度序列波动最小且3年稳定度的RMS值也相对最小,说明该卫星的星载原子钟频率稳定性在整个系统中相对最好。
最后,统计3年时间每颗卫星的钟差模型拟合残差序列、钟漂序列及稳定度序列的RMS值,同时根据卫星轨道类型计算对应结果的平均值,统计情况如表 2所示。根据表 2中的结果可以看出,在星载原子钟的噪声特性和钟漂特性方面,MEO卫星钟的性能最好,其次是IGSO卫星钟,最差的是GEO卫星钟;所有星载原子钟噪声水平和钟漂的RMS平均值分别为0.677 ns和1.922×10-18;此外,根据MEO星载原子钟的噪声水平和频漂结果,以C14卫星为例,虽然其钟漂值在同类型卫星中最大,但是其钟噪声特性却是最好的,说明对于该类卫星当其星载原子钟含有较大噪声时不会直接影响钟差自身的物理模型参数值。从表 2中的频率稳定性统计结果可以看出,GEO星载原子钟的稳定度最好,其平均值为1.283×10-13;MEO卫星钟次之,其平均值为1.385×10-13;稳定度最差的是IGSO星载原子钟,其稳定度平均值为1.765×10-13;而所有卫星钟稳定度的平均值为1.484×10-13。
| 卫星 | 拟合残差/(ns) | 频漂/(×10-18) | 稳定性/(×10-13) | |
| GEO | C01 | 0.509 | 1.731 | 1.518 |
| C02 | 2.296 | 4.749 | 1.250 | |
| C03 | 0.731 | 0.710 | 0.906 | |
| C04 | 0.543 | 2.973 | 1.150 | |
| C05 | 0.751 | 1.710 | 1.589 | |
| 平均值 | 0.966 | 2.375 | 1.283 | |
| IGSO | C06 | 1.196 | 3.447 | 1.789 |
| C07 | 0.610 | 1.387 | 1.465 | |
| C08 | 0.755 | 4.562 | 2.057 | |
| C09 | 0.365 | 0.656 | 1.202 | |
| C10 | 0.599 | 1.053 | 2.313 | |
| 平均值 | 0.705 | 2.221 | 1.765 | |
| MEO | C11 | 0.308 | 0.554 | 2.098 |
| C12 | 0.265 | 0.522 | 1.118 | |
| C13 | 0.346 | 1.363 | 1.563 | |
| C14 | 0.209 | 1.484 | 0.760 | |
| 平均值 | 0.282 | 0.981 | 1.385 | |
| 总的平均值 | 0.677 | 1.922 | 1.484 | |
3 总 结
基于3年的BDS卫星钟差数据,本文综合分析了北斗星载原子钟的钟差数据特点、钟差模型参数(相位、频率和频漂)长期变化特征、钟模型噪声长期变化特性、钟差周期特性以及星载原子钟频率稳定性长期变化情况,从而实现了对BDS星载原子钟性能较为全面的评估和分析。根据试验结果及其分析得到以下结论:
(1) BDS星载原子钟在长期运行过程中存在一定次数的相位、频率跳变,但频率跳变的次数比相位跳变的次数少。此外,GEO卫星的相位跳变次数相对最多,其相位的稳定性和连续性最差;MEO卫星整体上的频率跳变最少,其频率序列的稳定性和连续性相对最好。
(2) 噪声特性和钟漂特性方面,MEO卫星钟的性能最好,其次是IGSO卫星钟,最差的是GEO卫星钟。BDS星载原子钟噪声水平和频漂的RMS平均值分别为0.677 ns和1.922×10-18。同时,C03、C09、C11和C12在其同类卫星中频漂特性最好,频漂能达到10-19量级;C06和C09的频漂序列存在近似周期为半年的周期性变化。此外,MEO星载原子钟噪声大小不会直接影响钟差自身的物理模型参数值。
(3) BDS卫星钟差序列存在显著的周期项,不同轨道类型的卫星其钟差周期项不同,而同种轨道类型的卫星其钟差周期项也存在差异;3类卫星的钟差主周期分别近似为其卫星轨道周期的1/2倍或1倍。此外,在基于多星联合定轨同时解算卫星轨道和钟差的过程中,部分的轨道误差被钟差吸收;卫星钟差除了跟轨道周期耦合之外还可能与外界昼夜环境变化有一定的联系。
(4) BDS星载原子钟的长期稳定度序列相对稳定,GEO星载原子钟的频率稳定性最好,其平均值为1.283×10-13;MEO卫星钟次之,其平均值为1.385×10-13;频率稳定性最差的是IGSO星载原子钟,其稳定度平均值为1.765×10-13。BDS星载原子钟频率稳定度的平均值为1.484×10-13,其中C08卫星钟的稳定度最差,而C14卫星钟的稳定度最好。
本文所采用的BDS卫星钟差数据是基于多星联合定轨解算轨道和钟差得到的,该数据与定轨精度存在较强的相关性,这在一定程度上影响了对BDS星载原子钟特性的真实完全反映。同时本文分析过程主要侧重数据特性,以后将对BDS在轨星载原子钟的内在特性进行深入分析。
| [1] | 郭海荣. 导航卫星原子钟时频特性分析理论与方法研究[D]. 郑州:信息工程大学, 2006. GUO Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D]. Zhengzhou:Information Engineering University, 2006. |
| [2] | 贾小林, 冯来平, 毛悦, 等. GPS星载原子钟性能评估[J]. 时间频率学报, 2010, 33(2): 115–120. JIA Xiaolin, FENG Laiping, MAO Yue, et al. Performance Evaluation of GPS On-board Clock[J]. Journal of Time and Frequency, 2010, 33(2): 115–120. |
| [3] | 唐升, 刘娅, 李孝辉. 星载原子钟自主完好性监测方法研究[J]. 宇航学报, 2013, 34(1): 39–45. TANG Sheng, LIU Ya, LI Xiaohui. A Study on Onboard Satellite Atomic Clock Autonomous Integrity Monitoring[J]. Journal of Astronautics, 2013, 34(1): 39–45. |
| [4] | 李作虎. 卫星导航系统性能监测及评估方法研究[D]. 郑州:信息工程大学, 2012. LI Zuohu. Research on Monitoring and Assessment of Satellite Navigation System Performance[D]. Zhengzhou:Information Engineering University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-90005-1013161237.htm |
| [5] | GE Maorong, CHEN Junping, DOUŠA J, et al. A Computationally Efficient Approach for Estimating High-rate Satellite Clock Corrections in Realtime[J]. GPS Solutions, 2012, 16(1): 9–17. DOI:10.1007/s10291-011-0206-z |
| [6] | 唐桂芬, 许雪晴, 曹纪东, 等. 基于通用钟差模型的北斗卫星钟预报精度分析[J]. 中国科学:物理学力学天文学, 2015, 45(7): 079502. TANG Guifen, XU Xueqing, CAO Jidong, et al. Precision Analysis for Compass Satellite Clock Prediction Based on a Universal Clock Offset Model[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2015, 45(7): 079502. |
| [7] | 王宇谱, 吕志平, 王宁, 等. 顾及卫星钟随机特性的抗差最小二乘配置钟差预报算法[J]. 测绘学报, 2016, 45(6): 646–655. WANG Yupu, LV Zhiping, WANG Ning, et al. Prediction of Navigation Satellite Clock Bias Considering Clock's Stochastic Variation Behavior with Robust Least Square Collocation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 646–655. DOI:10.11947/j.AGCS.2016.20150569 |
| [8] | 毛悦, 陈建鹏, 戴伟, 等. 星载原子钟稳定性影响分析[J]. 武汉大学学报(信息科学版), 2011, 36(10): 1182–1186. MAO Yue, CHEN Jianpeng, DAI Wei, et al. Analysis of On-board Atomic Clock Stability Influences[J]. Geomatics and Information Science of Wuhan University, 2011, 36(10): 1182–1186. |
| [9] | GRIGGS E, KURSINSKI E R, AKOS D. An Investigation of GNSS Atomic Clock Behavior at Short Time Intervals[J]. GPS Solutions, 2014, 18(3): 443–452. DOI:10.1007/s10291-013-0343-7 |
| [10] | UHLEMANN M, GENDT G, RAMATSCHI M, et al. GFZ Global Multi-GNSS Network and Data Processing Results[M]//RIZOS C, WILLIS P. IAG 150 Years:International Association of Geodesy Symposia. Switzerland:Springer, 2016. |
| [11] | STEIGENBERGER P, HUGENTOBLER U, LOYER S, et al. Galileo Orbit and Clock Quality of the IGS Multi-GNSS Experiment[J]. Advances in Space Research, 2015, 55(1): 269–281. DOI:10.1016/j.asr.2014.06.030 |
| [12] | HUANG G, ZHANG Q, LI H, et al. Quality Variation of GPS Satellite Clocks On-orbit Using IGS Clock Products[J]. Advances in Space Research, 2013, 51(6): 978–987. DOI:10.1016/j.asr.2012.09.041 |
| [13] | SENIOR K L, RAY J R, BEARD R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions, 2008, 12(3): 211–225. DOI:10.1007/s10291-008-0089-9 |
| [14] | HAUSCHILD A, MONTENBRUCK O, STEIGENBERGER P. Short-term Analysis of GNSS Clocks[J]. GPS Solutions, 2013, 17(3): 295–307. DOI:10.1007/s10291-012-0278-4 |
| [15] | MONTENBRUCK O, HUGENTOBLER U, DACH R, et al. Apparent Clock Variations of the Block IIF-1(SVN62) GPS Satellite[J]. GPS Solutions, 2012, 16(3): 303–313. DOI:10.1007/s10291-011-0232-x |
| [16] | STEIGENBERGER P, HUGENTOBLER U, HAUSCHILD A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515–525. DOI:10.1007/s00190-013-0625-4 |
| [17] | 罗璠, 李建文, 黄海, 等. 北斗卫星钟稳定性分析及噪声识别[J]. 测绘科学技术学报, 2014, 31(1): 34–37. LUO Fan, LI Jianwen, HUANG Hai, et al. Frequency Stability Analysis and Noise Identification of BD Satellite Clock[J]. Journal of Geomatics Science and Technology, 2014, 31(1): 34–37. |
| [18] | 周佩元, 杜兰, 路余, 等. 多星定轨条件下北斗卫星钟差的周期性变化[J]. 测绘学报, 2015, 44(12): 1299–1306. ZHOU Peiyuan, DU Lan, LU Yu, et al. Periodic Variations of BeiDou Satellite Clock Offsets Derived from Multi-satellite Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1299–1306. DOI:10.11947/j.AGCS.2015.20150183 |
| [19] | 余航. BDS/Galileo星载原子钟性能及短期预报算法研究[D]. 西安:长安大学, 2015. YU Hang. Research on Prediction and Characteristics of BDS/Galileo Onboard Satellite Atomic Clock[D]. Xi'an:Chang'an University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10710-1015802675.htm |
| [20] | CHEN Maolin, ZHAN Xingqun, DU Gang, et al. Compass/BeiDou-2 Spaceborne Clock Performance Assessment and its Error Detection, Mitigation[J]. IEEE Transactions on Electrical and Electronic Engineering, 2015, 10(4): 438–446. DOI:10.1002/tee.2015.10.issue-4 |
| [21] | 高为广, 蔺玉亭, 陈谷仓, 等. 北斗系统在轨卫星钟性能评估方法及结论[J]. 测绘科学技术学报, 2014, 31(4): 342–346. GAO Weiguang, LIN Yuting, CHEN Gucang, et al. The Performances Assessment Methods and Results of In-Orbit Atomic Clocks of BDS[J]. Journal of Geomatics Science and Technology, 2014, 31(4): 342–346. |
| [22] | 张清华, 王源, 孙阳阳, 等. BDS与GPS/GLONASS星载原子钟性能的比较分析[J]. 海洋测绘, 2015, 35(2): 62–64. ZHANG Qinghua, WANG Yuan, SUN Yangyang, et al. Performance Analysis of Atomic Clocks on Board BDS/GPS/GLONASS Satellites[J]. Hydrographic Surveying and Charting, 2015, 35(2): 62–64. |
| [23] | RILEY W. Handbook of Frequency Stability Analysis[M]. Boulder, CO: NIST Special Publication, 2008. |
| [24] | 黄观文, 张勤, 许国昌, 等. 基于频谱分析的IGS精密星历卫星钟差精度分析研究[J]. 武汉大学学报(信息科学版), 2008, 33(5): 496–499. HUANG Guanwen, ZHANG Qin, XU Guochang, et al. IGS Precise Satellite Clock Model Fitting and Its Precision by Using Spectral Analysis Method[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 496–499. |
| [25] | ZHAO Qile, GUO Jing, LI Min, et al. Initial Results of Precise Orbit and Clock Determination for COMPASS Navigation Satellite System[J]. Journal of Geodesy, 2013, 87(5): 475–486. DOI:10.1007/s00190-013-0622-7 |
| [26] | SHI Xin, LIU Li, YAO Gang, et al. Comprehensive Satellite Clock Performance Evaluation Results Analysis with Multi-data[M]//SUN Jiadong, LIU Jingnan, FAN Shiwei,et al.China Satellite Navigation Conference (CSNC) 2016 Proceedings:Volume Ⅲ. Singapore:Springer, 2016:121-129. |



