2. 西安测绘研究所, 陕西 西安 710054;
3. 中国科学院国家空间科学中心, 北京 100190
2. Xi'an Institute of Surveying and Mapping, Xi'an 710054, China;
3. National Space Science Center, the Chinese Academy of Sciences, Beijing 100190, China
波形重跟踪是当代测高卫星数据处理的关键技术和必要过程,对于获取高精度的海面高及风速、浪高等参数具有重要意义。文献[1]及后来学者提出的Brown-Hayne模型描述了传统雷达高度计回波波形的基本特征,成为传统高度计波形重跟踪的基本理论依据。此后,国内外学者提出了诸如重心偏移法(OCOG)、阈值法、改进阈值方法及β算法等经验函数算法,这些算法的特点各不相同,在不同区域特别是近海区域取得了较好的效果[2-12]。传统雷达高度计技术虽已成熟但在沿轨分辨率、测量精度方面仍有提升空间,因此,合成孔径雷达测高技术(也称延迟多普勒技术)应运而生。在该模式下,沿航迹向的信号历程经过处理都对高度测量作出贡献,且沿航迹向的地面分辨率足迹提高到300 m以内,同时高度计利用了整个波束内的辐射能量,这样在相同信噪比的情况下,可以将传统高度计发射的峰值功率降低,从而提高了高度计的测量精度[13-16]。目前,国内外已经或准备发射的高度计基本上都是合成孔径雷达高度计,如2010年发射的CryoSat-2卫星[17-18]、2016年发射的Sentinel-3A卫星[19],Sentinel-3B卫星预计将于2017年发射。
文献[20]基于三项卷积的回波模型分析了合成孔径雷达技术的优势,并指出与传统高度计技术相比精度有了不同程度的提高。文献[21]利用阈值法对CryoSat-2卫星的波形数据进行了重跟踪分析。文献[22]利用简化的解析回波模型对CryoSat-2卫星、JASON-1卫星数据进行重跟踪并反演获得更高精度的全球海洋重力场数据。考虑到全球广阔海域的波形数据处理,有必要从合成孔径模式下的回波模型出发进行重跟踪处理,然而合成孔径模式下的回波模型较为复杂且国外有关技术细节并未完全公开[23-24]。国内相关单位开展了合成孔径雷达高度计技术的初步研究工作,尤其是获得了仿真条件下的合成孔径波形数据,这对于开展重跟踪分析提供了充分的数据支撑。本文将在初步研究基础上开展波形重跟踪的初步试验与分析,以期为合成孔径技术在海洋测高领域的成熟应用提供参考和借鉴。
1 合成孔径高度计的回波模型从技术原理上来看,合成孔径雷达高度计技术是在传统高度计基础上发展起来的,传统高度计的Brown-Hayne模型为
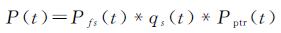 (1)
(1)
式中,t表示测量时间;Pfs(t)表示平坦海面的冲击响应函数;qs(t)是镜像点的海洋面高程概率密度函数;Pptr(t)表示雷达点目标响应函数。式(1)是一个包含三项函数的卷积模型(*表示卷积运算)。
经研究对比发现,合成孔径雷达高度计在收发脉冲过程中和传统高度计并没有本质区别,也就是说二者的工作机理在形式上是一致的。鉴于此,式(1)仍是描述合成孔径雷达高度计波形的基本形式。但模型中的Pfs(t)与传统高度计有所不同[16],这与文献[20]的研究结论是相同的。在合成孔径模式下,高度计的天线波束被锐化成多个子波束,随着卫星的飞行,雷达将用多个子波束依次对某一给定地理网格进行测量,获取多次测量回波。每次测量的回波均不相同,其中第i次测量的回波可以用式(2)表达
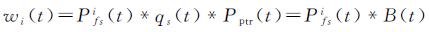 (2)
(2)
对于多视测量回波,则可以用式(3)表达
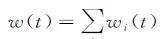 (3)
(3)
在合成孔径雷达高度计回波模型的研究中,平坦表面脉冲响应函数是研究的难点,国外学者大都根据电磁场散射原理推导了表达式,但目前无法确定哪个表达式是最准确的。鉴于此,笔者采用2011年研究得出的平坦表面脉冲响应函数形式[16],具体如下
 (5)
(5)
 (6)
(6)
式中,c表示光速;h表示轨道高;κ表示轨道参数,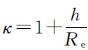
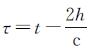
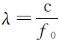
系统点目标响应函数采用与传统高度计回波模型相似的高斯函数来近似表达,见式(7)
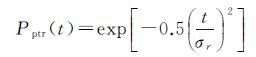 (7)
(7)
这种近似表达会带来一定的误差,需要在未来工作中进行完善。
通过波形重跟踪可以获取3个关键参数:t0表示相对于波形真实跟踪点的时间偏移,该参数可求得星地距离改正值;σ表示合成上升时间,对应有效波高;A0信号幅度,与后向散射系数有关。
为了有效估计回波模型中的典型参数,本文采用迭代最小二乘估计,此时,3个参数的最小二乘解的形式如下
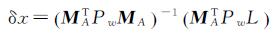 (8)
(8)
式中,δx表示未知参数改正值;MA表示P(t)对待估参数的偏导数在初始值x0处的值;L表示回波波形观测值。
对于传统高度计卷积回波模型而言,经过国外学者的不断研究,给出了较为实用的解析化回波模型。而对于合成孔径模式下的卷积回波模型,目前尚未有公认的解析化模型,如果贸然进行解析化处理,有可能会降低原卷积模型的精度。基于此,笔者从原始模型出发利用傅里叶变换解决卷积的实际计算问题。此外,推导回波波形关于偏天底点角ξ的偏导数是非常复杂的问题,在传统高度计模式下,回波波形关于ξ导数的推导就比其他参数复杂得多[12],因此,为了便于实际计算,考虑到偏天底点角ξ影响较小,将此参数忽略。此时,合成孔径模式下回波波形的模型可用式(9)描述
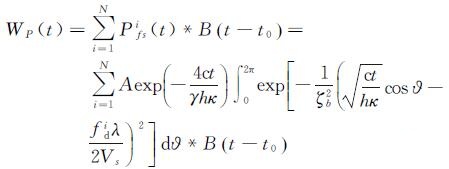 (9)
(9)
式中,B(t-t0)的表达式为
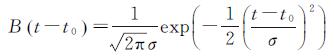 (10)
(10)
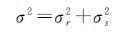 (11)
(11)
给定3个参数的初值t00、A0、σ0,则可得到回波功率的初始值WP(t)0,通过最小二乘估计得到3个参数的改正值δt0、δσs、δσ0。WP(t)关于3个参数的偏导数推导如下
 (12)
(12)
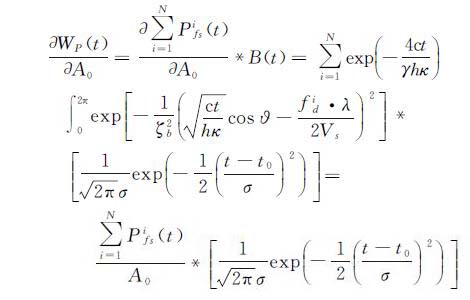 (13)
(13)
 (14)
(14)
在最小二乘估计中,未知参数的系数矩阵MA(m行,3列)如下
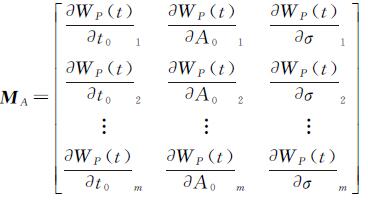 (15)
(15)
仿真试验由西安测绘研究所、中国科学院国家空间科学中心、航天东方红卫星有限公司等单位共同实施。为了尽量使仿真环境接近真实条件,采用了如下模型生成轨道及大气传播、潮汐等仿真环境,见表 1。
| 项 目 | 模 型 |
| 轨道 | 轨道高890 km,太阳同步轨道 |
| 海面 | DNSC08平均海面高+随机海浪模型 |
| 电离层 | 全球电离层模型(GIM) |
| 干对流层 | Saastamoinen模型 |
| 湿对流层 | Saastamoinen模型 |
| 海潮 | CSR4.0模型 |
| 固体潮 | IERS2010推荐模型 |
| 极潮 | IERS2010推荐模型 |
| 海况偏差 | JASON-2四参数模型 |
表 1中卫星轨道数据由STK软件生成,轨道倾角98.9°,轨道周期102.69 min,每天运行圈数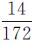
|
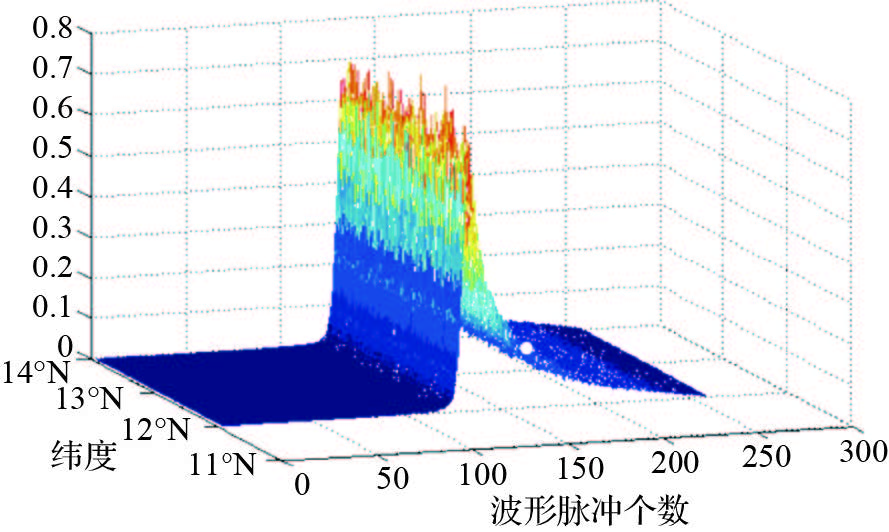
| 图 1 合成孔径雷达高度计的仿真波形(编号GDJ_210) Fig. 1 Simulation waveform of synthetic aperture radar altimeter |
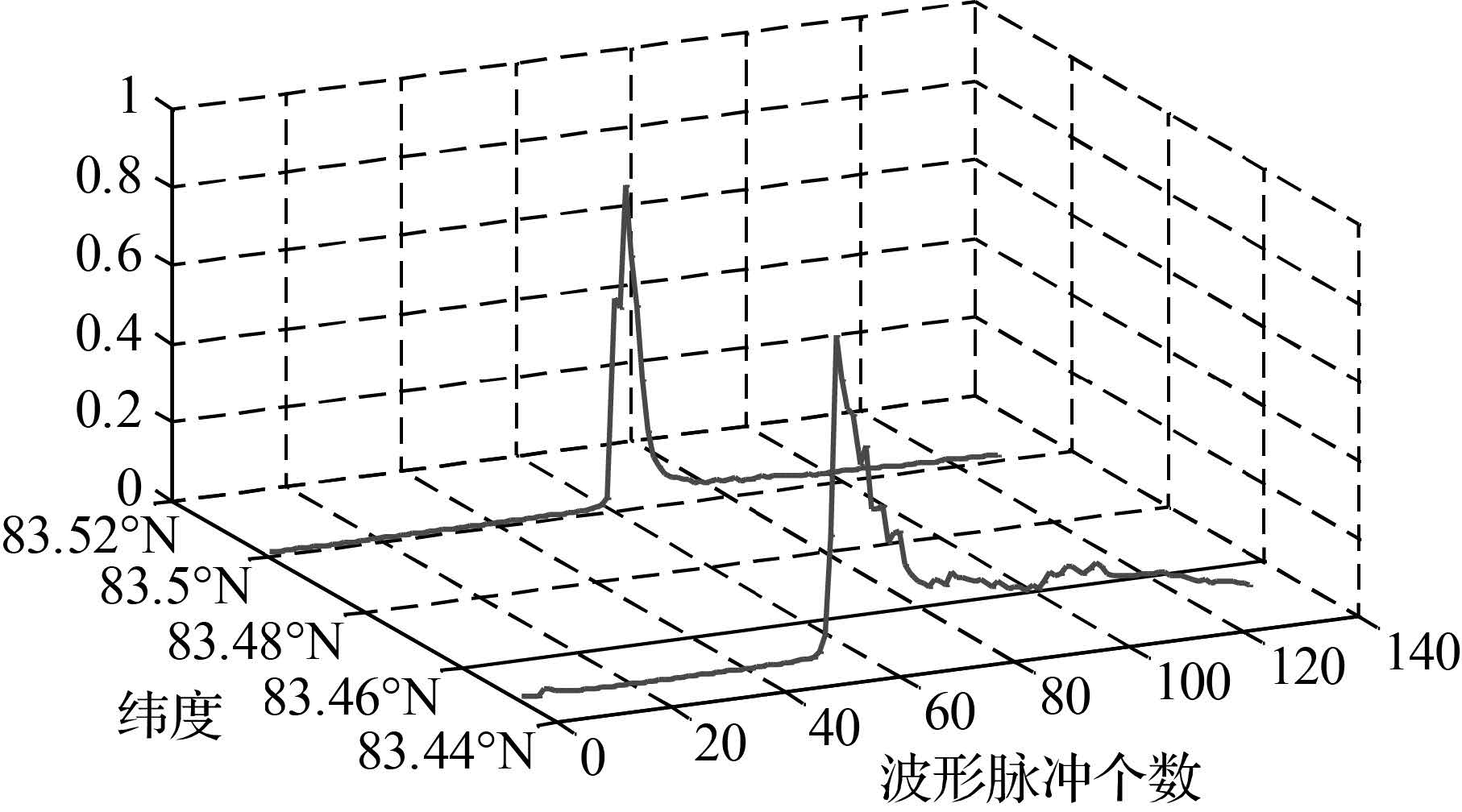
为了与仿真波形进行比较,选择法国空间局发布的2011年CryoSat-2卫星的SAR模式下的L1级数据进行比较。该数据采样频率1 Hz,波形脉冲个数为128个,其中两个波形数据见图 2。
|
| 图 2 CryoSat-2卫星SAR模式下的实测波形 Fig. 2 Measurement waveform of CryoSat-2 under SAR model |
对比CryoSat-2卫星SAR模式下的实测波形(经过归一化处理)与论文仿真生成的波形数据可以看出,两种波形整体趋势一致,波形在初始和末段都较平缓,中间段却呈尖锐的尖峰形状。
实际计算中,首先利用傅里叶变换将卷积计算转换为两个函数的乘积,而后利用逆傅里叶变换得到最终结果[25]。为了避免卷积运算中出现的计算误差,将Pfs(t)、B(t)采样率提升32倍参与计算,计算后再重新降采样获得与正常波形相同采样率的计算值。函数Pfs(t)的求解采用16阶高斯数值积分完成。
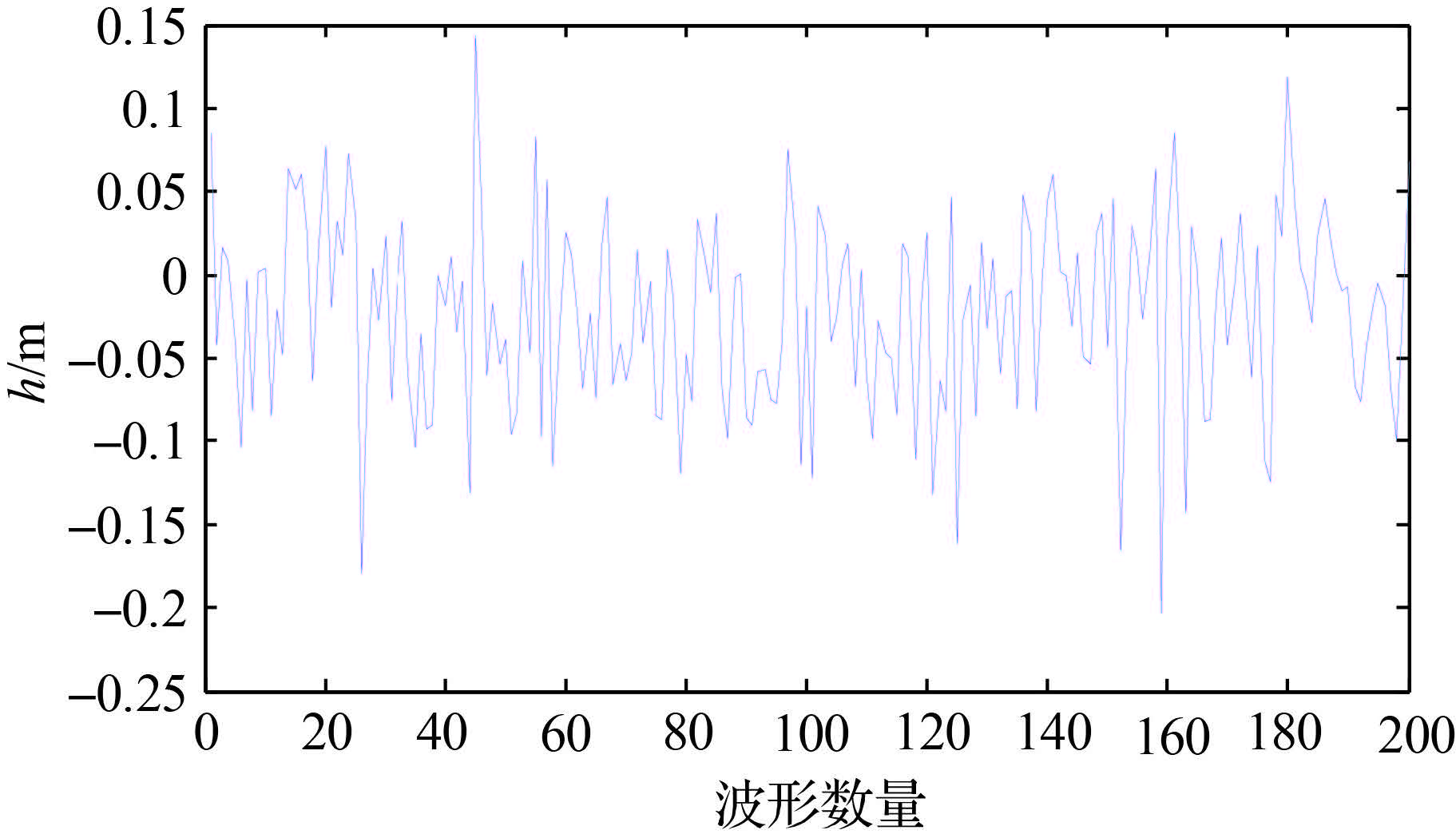
利用前述的模型及重跟踪方法得到“GDJ_210”弧段的结果见图 3。
|
| 图 3 “GDJ_210”弧段合成孔径雷达高度计的重跟踪结果 Fig. 3 The waveform retracking results of synthetic aperture radar altimeter of “GDJ_210” pass |
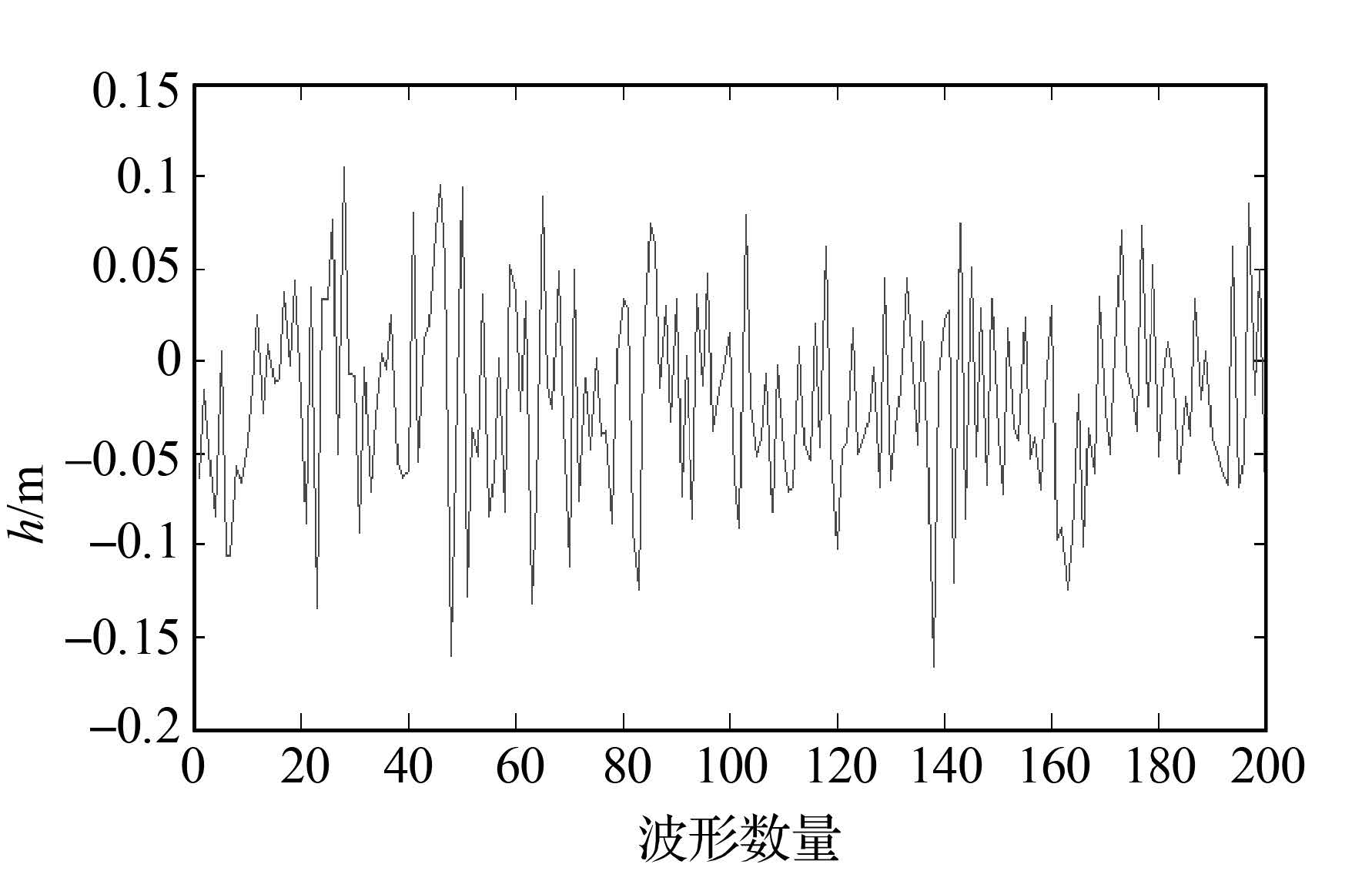
利用第1节的重跟踪方法得到“GDJ_206”弧段的结果见图 4。
|
| 图 4 “GDJ_206”弧段合成孔径雷达高度计的重跟踪结果 Fig. 4 The waveform retracking results of synthetic aperture radar altimeter of “GDJ_206” pass |
对两个弧段的结果进行统计见表 2。
| m | |||||
| 弧段 | 波形数量 | 最大值 | 最小值 | 平均值 | 标准差 |
| GDJ_210 | 200 | 0.143 | -0.201 | -0.017 | 0.053 |
| GDJ_206 | 200 | 0.105 | -0.164 | -0.009 | 0.051 |
在仿真条件下,波形数据认为是没有误差的,重跟踪结果即表明了理论模型所能达到的精度。由表 3可以看出,两条弧段20 Hz(约350 m分辨率)重跟踪结果精度在5 cm左右。文献[26]给出了传统高度计20 Hz仿真条件下(与表 1的仿真条件一致)的重跟踪精度即约7 cm,如果进行对比,则可以看出合成孔径模式下的重跟踪精度要比传统模式高约1.4倍,这也正是合成孔径高度计优越性的具体表现。
3 结 语本文针对合成孔径雷达高度计技术中的波形重跟踪问题开展了初步研究工作。基于三项卷积的合成孔径雷达高度计的回波模型,推导获得在最小二乘估计中合成孔径雷达高度计波形关于时间偏移、合成上升时间、信号幅度3个参数的卷积计算公式。仿真数据试验结果表明,在20 Hz数据条件下,合成孔径模式下的重跟踪精度达到5 cm。通过仿真试验在一定程度上验证了合成模式下三项卷积回波模型的有效性,也验证了模型解算方法的有效性,为雷达高度计的工程化研制提供参考和借鉴,也为测高卫星体系指标设计和论证提供了依据。根据国外学者的研究结果,在不同的环境和不同的参数条件下获得的重跟踪结果是有差异的,且合成孔径模式下的回波模型也有多种形式,因此未来还需要在更多参数条件下进行全面系统的仿真试验,同时对多种回波模型形式进行对比分析(如利用CryoSat-2卫星原始0级数据中的回波波形进行处理和对比)。
| [1] | THIBAUT P, POISSON J C, BRONNER E, et al. Relative Performance of the MLE3 and MLE4 Retracking Algorithms on JASON-2 Altimeter Waveforms[J]. Marine Geodesy, 2010, 33(S1): 317–335. |
| [2] | 郭金运, 常晓涛, 孙佳龙, 等. 卫星雷达测高波形重定及应用[M]. 北京: 测绘出版社, 2013. GUO Jinyun, CHANG Xiaotao, SUN Jialong, et al. Waveform Retracking of Satellite Radar Altimeter and Applications[M]. Beijing: Surveying and Mapping Press, 2013. |
| [3] | 汪海洪, 罗志才, 杨元德, 等. 基于波形分类的近海卫星测高数据自适应重跟踪方法[J]. 测绘学报, 2012, 41(5): 729–734. WANG Haihong, LUO Zhicai, YANG Yuande, et al. An Adaptive Retracking Method for Coastal Altimeter Data Based on Waveform Classification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 729–734. |
| [4] | 鲍李峰, 陆洋, 许厚泽. 浅海区域TOPEX/Poseidon测高卫星数据波形重构方法[J]. 地球物理学报, 2004, 47(2): 216–221. BAO Lifeng, LU Yang, XU Houze. Waveform Retracking of TOPEX/Poseidon Altimeter in Chinese Offshore[J]. Chinese Journal of Geophysics, 2004, 47(2): 216–221. |
| [5] | 常晓涛, 李建成, 郭金运, 等. 一种多前缘多阈值的波形重构算法[J]. 地球物理学报, 2006, 49(6): 1629–1634. CHANG Xiaotao, LI Jiancheng, GUO Jinyun, et al. A Multi-leading Edge and Multi-threshold Waveform Retracker[J]. Chinese Journal of Geophysics, 2006, 49(6): 1629–1634. |
| [6] | 杨乐, 林明森, 张有广, 等. 中国近岸海域高度计JASON-1测量数据的波形重构算法研究[J]. 海洋学报, 2010, 32(6): 91–101. YANG Le, LIN Mingsen, ZHANG Youguang, et al. Improving the Quality of JASON-1 Altimetry Data by Waveform Retracking in Coastal Waters off China[J]. Acta Oceanologica Sinica, 2010, 32(6): 91–101. |
| [7] | 郭金运, 高永刚, 常晓涛, 等. 近岸海域EnviSat卫星测高波形重定的Threshold优化算法[J]. 地球物理学报, 2010, 53(4): 807–814. GUO Jinyun, GAO Yonggang, CHANG Xiaotao, et al. Optimal Threshold Algorithm of EnviSat Waveform Retracking over Coastal Sea[J]. Chinese Journal of Geophysics, 2010, 53(4): 807–814. |
| [8] | 杨元德, 鄂栋臣, 黄金维, 等. GeoSat/GM波形重跟踪反演中国沿海区域重力异常[J]. 武汉大学学报(信息科学版), 2008, 33(12): 1288–1291. YANG Yuande, E Dongchen, HUANG Jinwei, et al. Chinese Coastal Gravity Anomalies from Wave-form Retracked GeoSat/GM Altimetry[J]. Geomatics and Information Science of Wuhan University, 2008, 33(12): 1288–1291. |
| [9] | 褚永海, 李建成, 张燕, 等. EnviSat测高数据波形重跟踪分析研究[J]. 大地测量与地球动力学, 2005, 25(1): 76–80. CHU Yonghai, LI Jiancheng, ZHANG Yan, et al. Analysis and Investigation of Waveform Retracking Data of EnviSat[J]. Journal of Geodesy and Geodynamics, 2005, 25(1): 76–80. |
| [10] | HWANG C, GUO Jinyun, DENG Xiaoli, et al. Coastal Gravity Anomalies from Retracked GeoSat/GM Altimetry:Improvement, Limitation and the Role of Airborne Gravity Data[J]. Journal of Geodesy, 2006, 80(4): 204–216. DOI:10.1007/s00190-006-0052-x |
| [11] | 翟振和, 孙中苗. JASON-2高度计数据在中国四大海域的波形重跟踪与分析[J]. 武汉大学学报(信息科学版), 2015, 40(11): 1499–1503. ZHAI Zhenhe, SUN Zhongmiao. Waveform Retracking Analysis of JASON-2 Altimeter Data in the Four Chinese Sea Area[J]. Geomatics and Information Science of Wuhan University, 2015, 40(11): 1499–1503. |
| [12] | 翟振和, 李晓燕. 解析Brown模型中波形参数的最小二乘估计的实现与验证[J]. 测绘科学与工程, 2015, 35(3): 6–9. ZHAI Zhenhe, LI Xiaoyan. Least Square Estimation of Waveform Parameters of Analytical Brown Model[J]. Geomatics Science and Engineering, 2015, 35(3): 6–9. |
| [13] | RANEY R K. The Delay/Doppler Radar Altimeter[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1578–1588. DOI:10.1109/36.718861 |
| [14] | JENSEN J R. Radar Altimeter Gate Tracking:Theory and Extension[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(2): 651–658. DOI:10.1109/36.752182 |
| [15] | 许可, 王志森, 杨双宝. 小型延时多普勒雷达高度计[J]. 遥感学报, 2007, 11(3): 380–384. XU Ke, WANG Zhisen, YANG Shuangbao. Compact Delay Doppler Radar Altimeter[J]. Journal of Remote Sensing, 2007, 11(3): 380–384. |
| [16] | 史灵卫. 合成孔径雷达高度计的数据处理和精度分析[D]. 北京:中国科学院研究生院, 2011. SHI Lingwei. The Data Processing and Accuracy Analysis of Synthetic Aperture Radar Altimeter[D]. Beijing:Graduate University of Chinese Academy of Science, 2011. http://d.wanfangdata.com.cn/Thesis/Y2248877 |
| [17] | SEPULVEDA H H, QUEFFEULOU P, ARDHUIN F. Assessment of SARAL/AltiKa Wave Height Measurements Relative to Buoy, JASON-2, and CryoSat-2 Data[J]. Marine Geodesy, 2015, 38(S1): 449–465. |
| [18] | 魏鑫, 李斐, 张胜凯, 等. CryoSat-2卫星测高计划及其应用[J]. 极地研究, 2015, 27(4): 446–453. WEI Xin, LI Fei, ZHANG Shengkai, et al. CryoSat-2 Satellite Altimetry and Its Application[J]. Chinese Journal of Polar Research, 2015, 27(4): 446–453. |
| [19] | DINARDO S, LUCAS B, BENVENISTE J. Sentinel-3 STM SAR Ocean Retracking Algorithm and SAMOSA Model[C]//Proceedings of 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Milan:IEEE, 2015:5320-5323. |
| [20] | HALIMI A, MAILHES C, TOURNERET J Y, et al. A Semi-analytical Model for Delay/Doppler Altimetry and Its Estimation Algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4248–4258. DOI:10.1109/TGRS.2013.2280595 |
| [21] | 王立伟, 金涛勇, 张胜军, 等. CryoSat-2卫星海冰区域波形识别及海冰干舷高确定[J]. 大地测量与地球动力学, 2015, 35(4): 722–725. WANG Liwei, JIN Taoyong, ZHANG Shengjun, et al. CryoSat-2 Satellite Sea Ice Area Waveform Recognition and Freeboard Determined[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 722–725. |
| [22] | GARCIA E, SANDWELL D T, SMITH W H F. Retracking CryoSat-2, EnviSat and JASON-1 Radar Altimetry Waveforms for Improved Gravity Field Recovery[J]. Geophysical Journal International, 2014, 196(3): 1402–1422. DOI:10.1093/gji/ggt469 |
| [23] | GOMMENGINGER C, MARTIN-PUIG C, DINARDO S, et al. Improved Altimetric Accuracy of SAR Altimeters over Ocean[C]//Proceedings of Ocean Surface Topography Science Team Meeting. San Diego:[s.n.], 2011. |
| [24] | GOMMENGINGER C, CIPOLLINI P, COTTON P D, et al. Finer, Better, Closer:Advanced Capabilities of SAR Altimetry in the Open Ocean and the Coastal Zone[C]//Proceedings of Ocean Surface Topography Science Team Meeting. Venice-Lido:[s.n.], 2012. |
| [25] | 张登奇, 陈佳. 离散卷积的算法分析及MATLAB实现[J]. 湖南理工学院学报(自然科学版), 2013, 26(2): 48–52. ZHANG Dengqi, CHEN Jia. Analysis of Discrete Convolution Algorithm and Realization Based on MATLAB[J]. Journal of Hunan Institute of Science and Technology (Natural Sciences), 2013, 26(2): 48–52. |
| [26] | 翟振和. 海洋测高卫星数据处理理论及应用方法研究[D]. 郑州:信息工程大学, 2015. ZHAI Zhenhe. Researches on Theories and Algorithms of Data Processing and Application in Altimetry Satellite[D]. Zhengzhou:Information Engineering University, 2015. |


