2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan 430079, China
航空重力测量是以飞机为载体快速地获取分布均匀、精度良好、大面积区域或局部重力场信息的有效方法[1]。目前,航空标量重力测量可提供精度为2 mGal(1 Gal=10-2 m/s2),分辨率为2 km的重力场信息[2-3]。航空矢量重力测量技术与航空标量重力测量技术相比,不仅能获取重力扰动矢量的垂直分量(重力异常),而且也能获取重力扰动矢量的水平分量(垂线偏差)。由于受重力加速度的放大作用,重力扰动矢量的水平分量受姿态误差影响较大,1″的水平姿态误差将会引起约4.75 mGal的水平分量误差[1]。文献[4-5]通过大量试验发现陀螺漂移误差是影响水平姿态误差的主要因素,如果能够在航空矢量重力测量解算过程中估计出陀螺漂移误差并对其补偿,可显著提高重力扰动矢量水平分量估算精度。目前航空矢量重力测量主要是捷联式航空重力测量,葡萄牙波尔图大学研究表明光纤陀螺可用于航空矢量重力测量[1, 6-7]。光纤陀螺漂移主要包含固定漂移和随机漂移[8-9]。固定漂移不随时间变化,可通过实验室标定加以补偿。随机漂移是一个十分复杂的随机、时变过程,不易消除,是影响航空矢量重力测量水平分量精度的关键因素。因此,针对光纤陀螺随机漂移开展研究对于提高航空矢量重力测量系统精度具有重要意义。
国内外研究人员通过各种方法对光纤陀螺随机漂移误差进行了建模和滤波分析。文献[10-13]中用自回归(autoregressive,AR)模型或自回归滑动平均(autoregressive moving average,ARMA)模型建立了光纤陀螺(fiber optic gyroscope,FOG)的随机误差模型,并用卡尔曼滤波器对随机漂移误差进行了滤波,得到了较好的结果。但是,由于ARMA模型要求信号必须为平稳、正态和零均值的时间序列,因此必须首先对陀螺信号进行平稳、正态和零均值处理,才能建立该模型。所以这种建模和滤波方法只适用于对陀螺信号进行事后处理与分析,而不满足捷联式航空矢量重力测量系统初始对准过程的实时性需求。为解决此问题,文献[14-15]通过将陀螺原始采样值中的常值分量作为新的状态变量引入Kalman滤波系统状态方程中,实现了随机漂移的在线估计。但该方法的应用前提是陀螺随机漂移序列满足平稳性假设条件。在实际应用中,陀螺随机漂移误差可能是非平稳的,由该方法形成的Kalman滤波可观性矩阵将具有奇异性,系统不完全可观,无法实现陀螺原始采样值序列中常值分量的分离。因此,该方法同样不适用于陀螺非平稳随机漂移误差的实时在线滤波。
鉴于此,本文基于某型光纤陀螺仪实测数据,详细探讨了光纤陀螺非平稳随机漂移误差的建模过程,引入求和自回归滑动平均模型(autoregressive integrated moving average,ARIMA)。该模型可直接对非平稳随机漂移误差进行建模。在此模型的基础上,本文通过实时平均算法补偿掉陀螺原始采样值序列中由地球自转和零漂引起的常值分量,实现了陀螺随机漂移误差的实时Kalman滤波估计,并对滤波后的数据进行了Allan方差分析。试验结果表明,基于该ARIMA模型的实时Kalman滤波方法能够有效抑制陀螺仪随机漂移误差,将有效提高航空矢量重力测量系统的姿态解算精度。
1 ARIMA原理及建模 1.1 ARIMA模型结构设xk,k=1,2,3,…为一非平稳序列。若其差分序列Δdxk(d为差分阶数)是一个平稳序列,则可用ARIMA(p,d,q)模型来描述[16],即
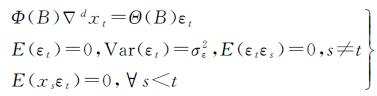 (1)
(1)
式中,B为延迟算子;Φ(B)=1-φ1B-φ2B-…-φpBp,为平稳可逆ARMA(p,q)模型的自回归系数多项式;Θ(B)=1-θ1B-θ2B-…-θqBq,为平稳可逆ARMA(p,q)模型的移动平滑系数多项式。
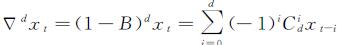 (2)
(2)
将式(1)和式(2)联合,可求出非平稳序列xt表达式为
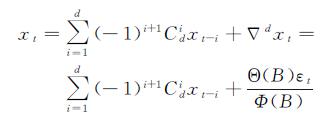 (3)
(3)
由式(3)可知,ARIMA模型的实质就是差分运算与ARMA模型的组合。
1.2 ARIMA模型建模步骤(1) 时间序列预处理(序列平稳性、正态性检验,趋势项提取等);
(2) 根据时间序列模型识别规则(表 1)建立相应模型;
(3) 模型参数估计;
(4) 模型适用性检验,主要诊断残差序列是否为白噪声。
| 模型类别 | AR(p) | MA(q) | ARMA(p,q) |
| 自相关系数ρk | 拖尾 | 截尾(k>q) | 拖尾 |
| 偏相关系数φkk | 截尾(k>q) | 拖尾 | 拖尾 |
2 基于ARIMA模型的光纤陀螺非平稳随机漂移误差建模 2.1 数据预处理
数据预处理主要包括原始信号采集、随机漂移信号提取和序列平稳性分析等步骤。
2.1.1 光纤陀螺随机漂移信号的采集本文以高精度组合导航系统SPAN-FSAS系统中的IMU-FSAS为研究对象,以fs=200 Hz的采样率,采集了3 h的原始陀螺漂移数据,结果如图 1所示。
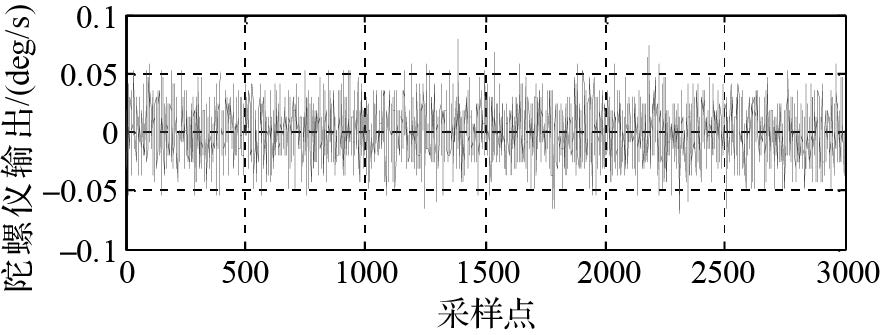
|
| 图 1 某光纤陀螺仪原始漂移信号 Fig. 1 Original drift signals for a certain kind of FOG |
2.1.2 随机漂移信号提取
光纤陀螺的原始信号中包含常值分量和随机分量。图 2为去掉常值分量之后的随机漂移信号。
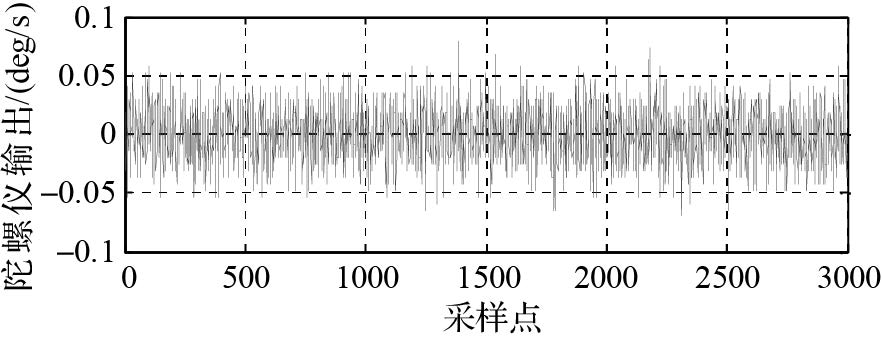
|
| 图 2 光纤陀螺仪随机漂移信号 Fig. 2 Random drift for a certain kind of FOG |
2.1.3 序列平稳性检验
本文采用逆序法来检验陀螺随机漂移数据的平稳性,它通过构造统计量u来检验序列的平稳性[17],具体结果如表 2所示。由表 2可知预处理后的陀螺随机漂移数据的统计值u=-5.875 0。因为u>1.96,故拒绝序列平稳的原假设,认为序列非平稳。
| 数据类型 | 统计数量 | 分组M | A值 | u值 |
| 预处理后数据 | 3 000 | 300 | 17 324 | -5.875 0 |
| 差分数据 | 2 999 | 300 | 22 484 | 0.090 4 |
对数据作一阶差分(图 3),并对差分后数据进行平稳性检验。由表 2可知,差分后统计量u=0.090 4。因|u|<1.96,故在0.05的显著水平下接受平稳性假设,认为差分后数据平稳。
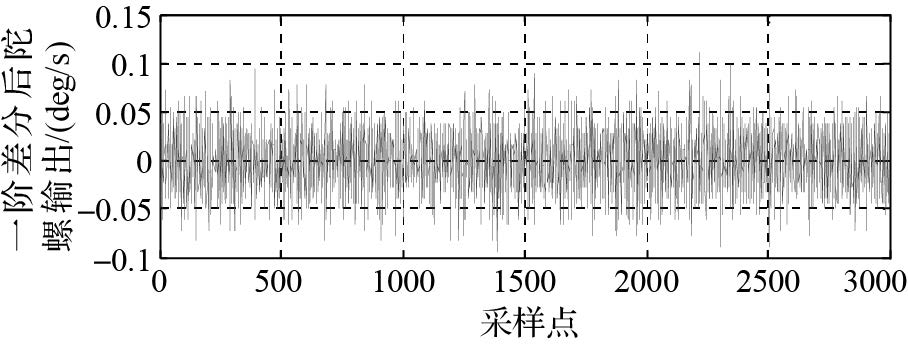
|
| 图 3 一阶差分陀螺随机漂移 Fig. 3 First-order differenced random drift of FOG |
2.2 模型参数识别及优化
根据前文分析可知,陀螺随机漂移序列ωk,k=1,2,3,…作一阶差分后平稳,故差分阶数d=1。接下来利用差分后得到的平稳序列对模型进行识别及优化。
2.2.1 ARIMA(p,d,q)模型识别模型识别的方法很多,使用较广泛的是Box-Jenkins方法。此方法根据时间序列的自相关系数(autocorrelation function,ACF)和偏自相关系数(partial autocorrelation function,PACF)的截尾、拖尾性来识别模型[17-18]。一阶差分后陀螺随机漂移信号的自相关系数和偏自相关系数计算结果如图 4所示。
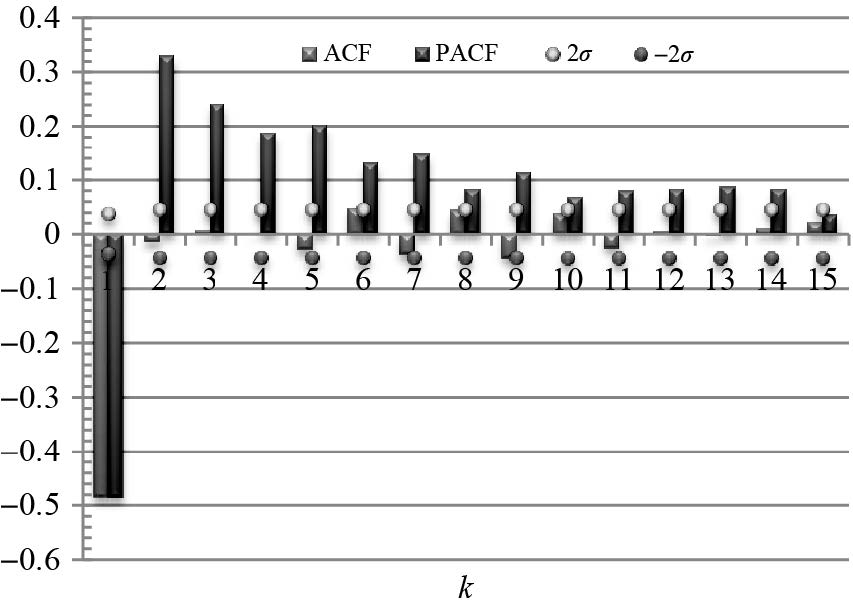
|
| 图 4 一阶差分后序列的自相关系数与偏自相关系数 Fig. 4 ACF and PACF of first-order differenced random drift of FOG |
由图 4可知,自相关系数在滞后阶数为1时显著不为零;在滞后阶数大于1时基本处于±2σ置信带内。偏自相关系数随延迟阶数k的增大逐渐衰减到零,表现出显著的拖尾性。根据表 1中模型的定阶原则,模型应该在滑动平均MA和自回归滑动平均ARMA中选取。
2.2.2 ARIMA(p,d,q)模型优化同一时间序列可由AR、MA和ARMA模型中的一种或多种进行拟合。最优拟合模型可通过BIC信息准则确定[19-20]。利用BIC准则对一阶差分后的陀螺漂移数据进行定阶,各拟合模型的BIC值如表 3所示。
| 模型 | MA(1) | MA(2) | AR(1,1) | ARMA(1,2) | ARMA(2,1) |
| θ1 | 0.983 65 | 0.954 02 | 0.985 01 | 0.004 69 | 0.985 11 |
| θ2 | - | 0.030 48 | - | 0.962 67 | - |
| φ1 | - | - | 0.031 12 | -0.984 76 | 0.031 14 |
| φ2 | - | - | - | - | 0.002 76 |
| BIC值 | -7.604 54 | -7.604 54 | -7.602 25 | -7.622 78 | -7.599 74 |
由表 3中各模型的BIC值可知,一阶差分后陀螺随机漂移序列的最优模型为ARMA(1,2)。但在实际情况中ARMA模型相当于一个最小实现的线性系统,模型中的自回归阶数应大于或等于滑动平均阶数(p≥q),故表 3中满足的模型只有ARMA(1,1)、ARMA(2,1)两种。比较二者的BIC值,选取值较小的ARMA(1,1)模型作为一阶差分后陀螺随机漂移误差模型。
2.3 模型参数估计及适用性检验 2.3.1 ARIMA模型参数估计本文采用最小二乘估计法对差分后平稳模型ARMA(1,1)参数进行估计[21],各模型对应的自回归系数φi(i=1,2)和滑动平均系数θi(i=1,2)的估值如表 3所示。将ARMA(1,1)模型所对应系数代入式(1)得一阶差分后陀螺随机漂移数据模型为
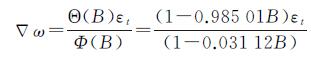 (4)
(4)
结合式(3)和式(4),求出光纤陀螺随机漂移数据的ARIMA(1,1,1)模型为
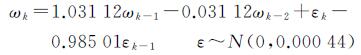 (5)
(5)
本文利用QLB统计量对ARIMA(1,1,1)模型的残差序列进行白噪声检验[17],结果如表 4所示。由表 4可知统计量QLB的P值显著大于显著性水平α,故残差序列为白噪声,拟合模型ARIMA(1,1,1)显著有效。
| autocorrelation check for white noise | ||||||||||
| to lag | chi-square | DF | P | autocorrelations | ||||||
| 6 | 4.69 | 4 | 0.320 5 | 0 | 0.003 | 0.004 | -0.006 | -0.015 | 0.036 | |
3 基于ARIMA模型的陀螺随机漂移误差实时Kalman滤波
Kalman滤波可实现线性最小均方误差估计意义下随机信号的最优线性滤波[22]。在建立了陀螺随机漂移ARIMA(1,1,1)模型后,可采用Kalman滤波对陀螺随机漂移误差进行补偿。根据式(5)建立系统的状态方程
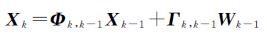 (6)
(6)
式中,状态变量Xk=[ωk ωk-1]T;过程噪声Wk=[εk εk-1]T;状态转移矩阵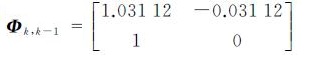

由于式(6)是针对零均值非平稳陀螺随机漂移误差的系统状态方程,要实现陀螺随机漂移误差的在线Kalman滤波估计,需实时补偿掉陀螺原始采样值序列中由地球自转和常值零漂引起的常值部分。本文根据实时平均算法来分离陀螺原始采样值中的常值分量,采用当前时刻及其前9个时刻采样点的平均值作为当前时刻的常值估计值。
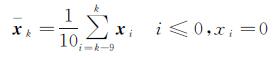 (7)
(7)
利用xk对陀螺原始采样值Zk进行实时补偿,则系统的量测方程转化为
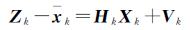 (8)
(8)
式中,Hk=[1 0];Vk为量测误差,可由Vk=Zk-xk求得;xk为模型输出量。求得的量测误差满足Vk~N(0,0.000 940 2)分布。Wk、Vk的统计性质满足以下条件:E(Wk)=0;E(Vk)=0;E(WkWjT)=Qkδkj;E(VkVjT)=Rkδkj;E(WkVjT)=0。
根据系统状态方程(6)和量测方程(8),可得系统的可观测性矩阵为[23-24]
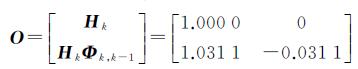 (9)
(9)
由可观性矩阵O的秩rank(O)=2,可知该随机系统是完全可观的,由Kalman滤波能对状态实现最优估计。将实测光纤陀螺原始采样数据作为卡尔曼滤波器输入对陀螺随机漂移误差进行实时在线Kalman滤波估计,滤波处理结果如图 5所示。
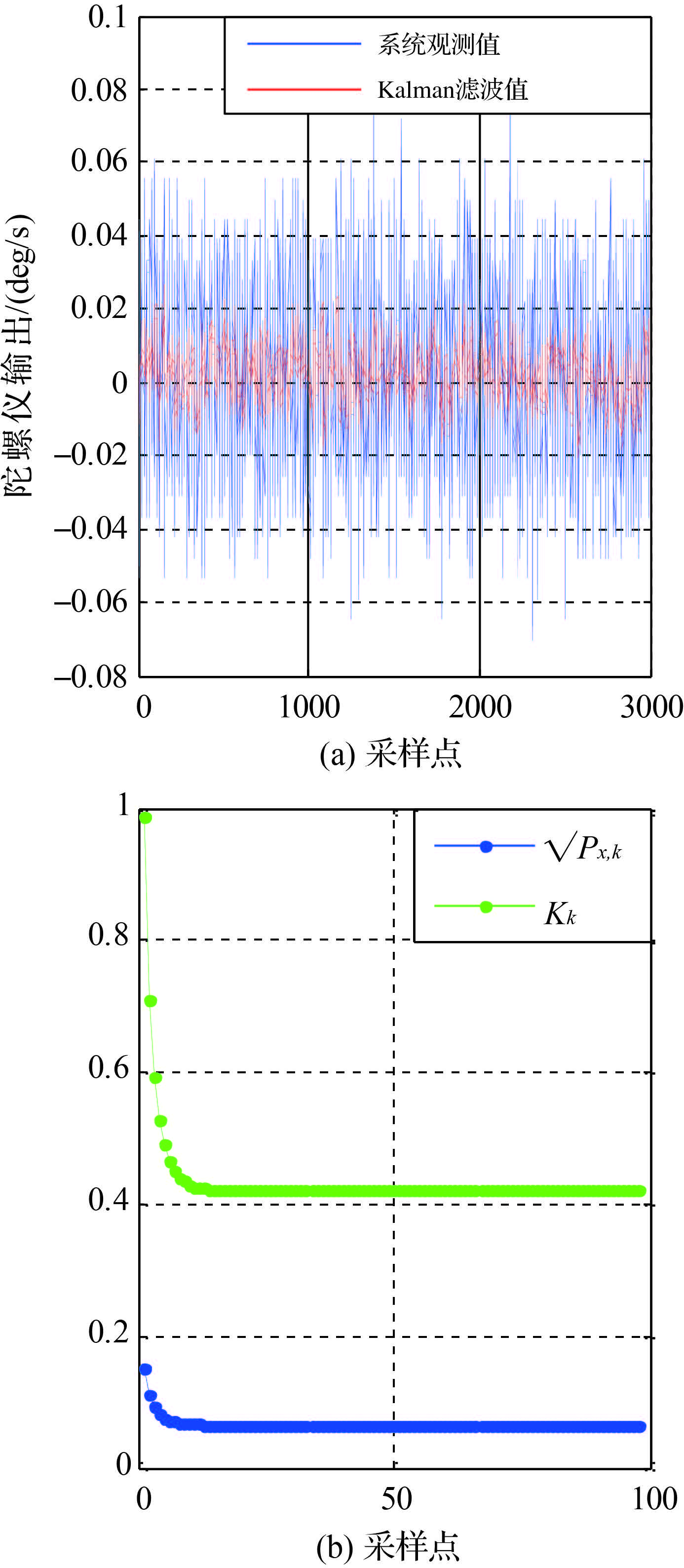
|
| 图 5 基于ARIMA模型的Kalman滤波结果 Fig. 5 Results of Kalman filtering based on the ARIMA model |
从图 5(a)可看出滤波后数据的波动性明显变小,表明经Kalman滤波后陀螺随机误差得到明显抑制。图 5(b)中蓝线和绿线分别对应状态估计均方根误差
由表 5可知,滤波前后数据均值基本一致,其大小约为0.003 54 °/s,因为Kalman滤波属于线性无偏最优滤波。滤波后数据方差较滤波前减小46.5%,说明基于ARIMA模型的实时卡尔曼滤波算法能实现对非平稳随机漂移误差的在线补偿。
| 统计量 | 滤波前 | 滤波后 |
| 均值/(°/s) | 0.003 538 6 | 0.003 541 2 |
| 方差/((°/s)2) | 4.373 8e-004 | 2.340 0e-004 |
4 Allan方差分析
Allan方差法是在时域上对频域特性进行分析的一种方法,最早由美国国家标准局David Allan提出,是IEEE公认的陀螺仪参数辨识的标准方法[25]。图 6给出了Allan方差中频域窗函数|HA(jf)|的幅频响应曲线。由图 6可知,取样时间τ决定了滤波器窗函数的窗口宽度和位置。τ越大,窗口宽度越小,窗口位置越集中于低频段。通过调整τ的大小即可分割出不同的频率成分。本文采用Allan方差法对滤波前后的光纤陀螺随机漂移数据进行了分析,结果如图 7所示。
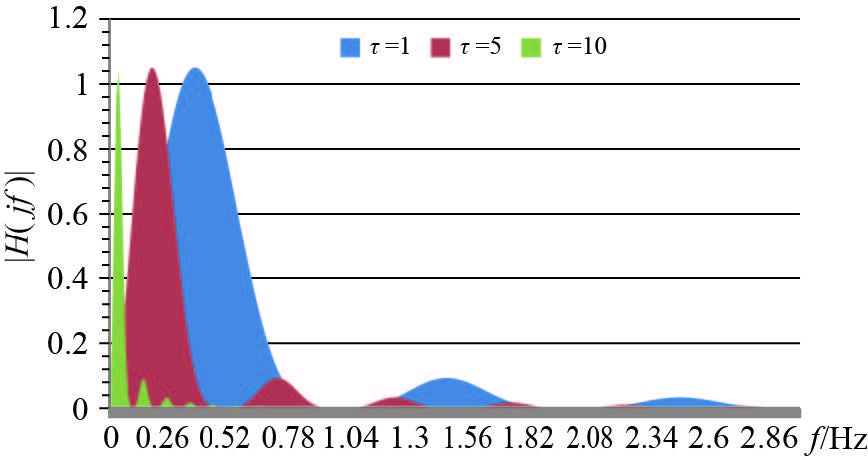
|
| 图 6 |HA(jf)|的幅频特性 Fig. 6 Amplitude-frequency characteristics of |HA(jf)| |

|
| 图 7 光纤陀螺随机漂移数据Kalman滤波前后Allan方差曲线 Fig. 7 Allan-variance results of FOG random drift with and without Kalman filtering |
由图 7可知,光纤陀螺随机漂移误差通过实时Kalman滤波补偿后的Allan方差曲线较原始Allan方差曲线幅值有了明显下降,特别是在高频段下降了一个量级。由图 7中τ-σA(τ)双对数曲线斜率特性可知,该型号光纤陀螺仪的随机漂移误差主要由角度随机游走和角速率随机游走组成,中间有稍弱的零偏稳定性表现出来,具体误差系数分析结果如表 6所示。
| 参数 | 误差系数 | 滤波前 | 滤波后 |
| 角度随机游走/(°/h1/2) | N | 0.103 4 | 0.050 7 |
| 零偏不稳定性/(°/h) | B | 0.079 7 | 0.053 1 |
| 角速率随机游走/(°/h3/2) | K | 0.471 0 | 0.277 9 |
由表 6可知,经Kalman滤波补偿后,光纤陀螺随机漂移误差中的角度随机游走系数N、零偏不稳定性系数B和角速率随机游走系数K都较滤波前显著减小,尤其是角度随机游走系数N和角速率随机游走系数K分别降低了约50%和40%。
5 结 论本文从航空矢量重力测量系统对惯性器件的实际需求出发,针对传统ARMA模型只能对平稳随机漂移误差建模,且模型无法满足实时滤波需求的问题,引入了适用于非平稳随机漂移误差的ARIMA模型,并给出详细的建模过程。在此模型的基础上,基于实时平均算法的Kalman滤波器对陀螺随机漂移误差进行了实时在线滤波与补偿,并对滤波结果进行Allan方差分析。主要结论如下:
(1) 根据光纤陀螺随机漂移误差的统计特性建立了ARIMA(1,1,1)模型,该模型能够较准确地描述陀螺的非平稳随机漂移误差。
(2) 实时平均算法可有效补偿陀螺原始采样序列中由地球自转和零漂引起的常值分量,实现随机漂移误差的实时Kalman滤波与补偿。
(3) 实测数据处理表明,基于本文所提出的方法滤波后随机漂移的主要误差较滤波前明显减小,信号中的高频噪声得到有效抑制,噪声水平降低了46.5%,角度随机游走系数和角速率随机游走系数分别降低了50%和40%。
在实际应用中,可通过约当标准型或可控标准型等方法将光纤陀螺随机漂移误差的ARIMA模型转换为等效的连续状态方程表达式,并扩充到航空矢量重力测量系统的误差方程中,通过Kalman滤波实时补偿来提高航空矢量重力测量系统的姿态解算精度。
| [1] | 蔡劭琨. 航空重力矢量及误差分离方法研究[D]. 长沙:国防科学技术大学, 2014. CAI Shaokun. The Research about Airborne Vector Gravimeter and Methods of Errors Separation[D]. Changsha:National University of Defense Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-90002-1015959238.htm |
| [2] | FORSBERG R, OLESEN A V. Airborne Gravity Field Determination[M]//XU Guochang. Sciences of Geodesy-I. Berlin Heidelberg:Springer, 2010:83-104. |
| [3] | LI X. Examination of Two Major Approximations Used in the Scalar Airborne Gravimetric System-A Case Study Based on the LCR System[J]. Journal of Geodetic Science, 2013, 3(1): 32–39. |
| [4] | GLEASON D M. Gravity Vector Estimation from Integrated GPS/Strapdown IMU Data[J]. Navigation, 1992, 39(2): 237–253. DOI:10.1002/navi.1992.39.issue-2 |
| [5] | JEKELI C. Airborne Vector Gravimetry Using Precise, Position-aided Inertial Measurement Units[J]. Bulletin Géodésique, 1994, 69(1): 1–11. DOI:10.1007/BF00807986 |
| [6] | DEURLOO R A,MARTIN J, BASTOS M L, et al. Comparison of the Performance of Two Types of Inertial Systems for Strapdown Airborne Gravimetry[C]//Proceedings of the IEEE/ION Position Location and Navigation Symposium. 2012. |
| [7] | AYRES-SAMPAIO D, DEURLOO R, BOS M, et al. A Comparison Between Three IMUs for Strapdown Airborne Gravimetry[J]. Surveys in Geophysics, 2015, 36(4): 571–586. DOI:10.1007/s10712-015-9323-5 |
| [8] | 毛奔, 林玉荣. 惯性器件测试与建模[M]. 哈尔滨: 哈尔滨工程大学出版社, 2008. MAO Ben, LIN Yurong. Testing and Modelling of Inertial Device[M]. Harbin: Harbin Engineering University Press, 2008. |
| [9] | 严恭敏, 李四海, 秦永元. 惯性仪器测试与数据分析[M]. 北京: 国防工业出版社, 2012. YAN Gongmin, LI Sihai, QIN Yongyuan. Testing and Data Analysis of Inertial Instruments[M]. Beijing: National Defense Industry Press, 2012. |
| [10] | ORAVETZ A S, SANDBERG H J. Stationary and Nonstationary Characteristics of Gyro Drift Rate[J]. AIAA Journal, 1970, 8(10): 1766–1772. DOI:10.2514/3.5988 |
| [11] | CHEN Xiyuan. Modeling Random Gyro Drift by Time Series Neural Networks and by Traditional Method[C]//Proceedings of the 2003 International Conference on Neural Networks and Signal Processing. Nanjing, China:IEEE, 2003, 1:810-813. |
| [12] | 吴富梅, 杨元喜. 基于高阶AR模型的陀螺随机漂移模型[J]. 测绘学报, 2007, 36(4): 389–394. WU Fumei, YANG Yuanxi. Gyroscope Random Drift Model Based on the Higher-order AR Model[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 389–394. |
| [13] | 白俊卿, 张科, 卫育新. 光纤陀螺随机漂移建模与分析[J]. 中国惯性技术学报, 2012, 20(5): 621–624. BAI Junqing, ZHANG Ke, WEI Yuxin. Modeling and Analysis of Fiber Optic Gyroscope Random Drifts[J]. Journal of Chinese Inertial Technology, 2012, 20(5): 621–624. |
| [14] | 王立冬, 张春熹. 高精度光纤陀螺信号的在线建模与滤波[J]. 光电工程, 2007, 34(1): 1–3. WANG Lidong, ZHANG Chunxi. On-line Modeling and Filter of High-precise FOG Signal[J]. Opto-Electronic Engineering, 2007, 34(1): 1–3. |
| [15] | 李家垒, 许化龙, 何婧. 光纤陀螺随机漂移的实时滤波方法研究[J]. 宇航学报, 2010, 31(12): 2717–2721. LI Jialei, XU Hualong, HE Jing. Real-time Filtering Methods of Random Drift of Fiber Optic Gyroscope[J]. Journal of Astronautics, 2010, 31(12): 2717–2721. |
| [16] | BOX G E P, JENKINS G M. Time Series Analysis:Forecasting and Control[M]. San Francisco: Holden-day Press, 1970. |
| [17] | 杨叔子, 吴雅, 轩建平. 时间序列分析的工程应用[M]. 2版. 武汉: 华中科技大学出版社, 2007. YANG Shuzi, WU Ya, XUAN Jianping. Time Series Analysis in Engineering Application[M]. 2nd ed. Wuhan: Huazhong University of Science and Technology Press, 2007. |
| [18] | GOODWIN G C, PAYNE R L. Dynamic System Identification:Experiment Design and Data Analysis[M]. New York: Academic Press, 1977. |
| [19] | AKAIKE H. Fitting Autoregressive Models for Prediction[J]. Annals of the Institute of Statistical Mathematics, 1969, 21(1): 243–247. DOI:10.1007/BF02532251 |
| [20] | AKAIKE H. A Bayesian Extension of the Minimum AIC Procedure of Autoregressive Model Fitting[J]. Biometrika, 1979, 66(2): 237–242. DOI:10.1093/biomet/66.2.237 |
| [21] | ANSLEY G F. An Algorithm for the Exact Likelihood of a Mixed Autoregressive-moving Average Process[J]. Biometrika, 1979, 66(1): 59–65. DOI:10.1093/biomet/66.1.59 |
| [22] | KALMAN R E. A New Approach to Linear Filtering and Prediction Problems[J]. Journal of Basic Engineering, 1960, 82(1): 35–45. DOI:10.1115/1.3662552 |
| [23] | TSIEN H S. Engineering Cybernetics[M]. New York: McGraw-Hill, 1954. |
| [24] | CANON M D, CULLUM C D JR, POLAK E. Theory of Optimal Control and Mathematical Programming[M]. New York: McGraw-Hill, 1970. |
| [25] | IEEE Std. 952-1997 IEEE Standard Specification Format Guide and Test Procedure for Single-axis Interferometric Fiber Optic Gyros[S].[S.l.]:IEEE, 1998. http://www.doc88.com/p-98733672437.html |


