2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079;
3. 地球空间信息技术协同创新中心, 湖北 武汉 430079;
4. 武汉大学中国南极测绘研究中心, 湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China;
3. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China;
4. Chinese Antarctic Center of Surveying and Mapping, Wuhan University, Wuhan 430079, China
现今多GNSS技术得到了快速发展和广泛应用,越来越多的卫星系统相继建立,主要包括美国的GPS、中国的北斗导航卫星系统BDS、俄罗斯的GLONASS、欧盟的伽利略(Galileo)以及一些区域导航系统,如日本的QZSS(Quasi-Zenith Satellite System),印度的IRNSS(India Regional Navigation Satellite System)[1-3]。其中,BDS是中国自主研发的新一代卫星导航系统,整个系统将于2020年全部组网完成。现阶段,BDS由5颗GEO(geostationary earth orbit)卫星,4颗MEO(medium earth orbit)卫星和5颗IGSO(inclined geosynchronous satellite orbit)卫星组成,并且能够提供亚太大部分地区定位精度优于10 m的免费公开服务[4]。
在卫星端导航信号从产生到发射完成,或在接收机端从天线接收导航信号到数字中频输出这一过程会产生时间延迟,通常称为硬件延迟,其中前者称为卫星硬件延迟,后者称为接收机硬件延迟[5-6]。由于卫星(或接收机)终端通过不同通道发射(或接收)不同频率的导航信号,而不同频率的导航信号在卫星或接收机内部的硬件延迟会有差值,该差值通常称为硬件延迟偏差,或频间偏差。对测距码来说,该频间偏差就是所谓的差分码偏差(differential code bias,DCB)[7]。
卫星和接收机DCB可以达到几纳秒甚至几十纳秒的量级,是影响高精度电离层总电子含量(total electron content,TEC)求解精度的重要误差源,同时也是影响用户定位和授时精度的重要因素[8-12]。文献[5]详细地研究了GPS卫星DCB对定位的影响,发现对DCB进行改正后,可以将单频接收机的垂直方向定位精度提高20%~30%。文献[11]研究了GPS民用广播星历中ISC参数(ISC参数本质上是DCB参数)对导航定位精度的影响,发现经由ISC改正后,GPS L2C单频标准单点定位(SPP)的位置精度提高了30.6%,L1C/A+L2C双频SPP的位置精度提高了12.2%。在不出现硬件变更的情况下,卫星和接收机DCB的日变化较为稳定,其中卫星DCB的变化在0.5 ns内,接收机DCB的变化在1 ns内[8, 13]。尽管卫星发射前和接收机出厂前一般都进行DCB的标定,但由于设备所处环境的变化以及设备老化等原因,DCB的稳定性会受影响,工作一段时间后,DCB会产生漂移[14],因此实际工作期间需要根据地面跟踪站的数据对其重新测定。由于电离层是耗散介质,即电离层效应与频率是相关的,因此DCB可以利用GNSS双频观测值估计得到[3]。一般来说,GNSS的DCB通过对TEC建模的方式,利用卡尔曼滤波或最小二乘等方法求解电离层模型系数并同时估计卫星和接收机DCB,求解过程中使用“零均值”基准约束将卫星和接收机DCB分离[15-20]。
随着BDS的快速发展,人们迫切地需要对北斗卫星和接收机的DCB进行连续监测和评估,以满足空间环境监测和电离层延迟改正等需求。但由于目前受到BDS系统卫星的分布以及地面跟踪站数量的限制等,全球范围内BDS电离层穿刺点较少而且分布不均,利用BDS单系统很难建立高精度的电离层模型,获得的BDS DCB精度有限[21-22]。自1998年6月以来,IGS电离层工作组开始对外以IONEX(ionosphere exchange)的格式发布稳定、可靠的全球电离层图(global ionosphere maps,GIM),包括最终、快速和预报产品,精度分别为:2~8 TECU、2~9 TECU、2~11 TECU(http://www.igs.org/products)。基于以上考虑,一些学者在现有“零均值”基准约束下(即所有BDS卫星DCB之和为0),用GIM和多GNSS观测值来估计北斗DCB,并对其进行评估,得出了一些有益的结论。文献[21]利用欧洲定轨中心(center for orbit determination in Europe,CODE)的GIM和中国境内的5个跟踪站对北斗卫星DCB进行评估发现,卫星DCB的精度优于1 ns,C09 DCB精度最高(优于0.2 ns),并认为测站数量的改变对卫星DCB的估计精度有影响。文献[1]利用全球MGEX(multi-GNSS experiment)观测数据计算了BDS卫星DCB,发现BDS卫星DCB日变化的标准差为0.2 ns(最大值为0.5 ns),其稳定性比GPS卫星稍差,认为这可能与BDS测站和卫星数目有限等有关。文献[3]利用2013—2014年MGEX和BETS(BeiDou experimental tracking stations)的GNSS观测数据对GPS/BDS的DCB进行计算,发现BDS卫星和GPS卫星的DCB RMS都优于0.3 ns(除了BDS GEO卫星),认为BDS GEO卫星观测值质量较差,会影响其他卫星DCB的稳定性
以上方法在添加“零均值”基准约束时,认为所有BDS卫星DCB稳定性是一样或相近的,而事实并非如此,本文顾及BDS卫星DCB的稳定性差异,对BDS卫星采用两种不同的约束方案,基于CODE GIM和MGEX的BDS三频观测数据,采用附有限制条件的间接平差求解卫星和接收机DCB。
1 处理方法联合无几何组合(geometry free,GF)的伪距和相位观测值,利用相位平滑伪距的方式可获取高精度的电离层TEC[15, 19]
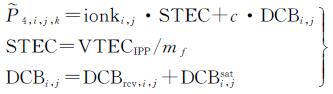 (1)
(1)
式中,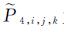
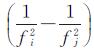
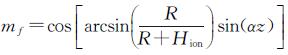
假设伪距和相位观测值不相关,则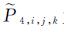
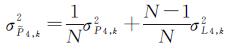 (2)
(2)
式中,σP4,k2和σL4,k2分别为伪距和相位GF观测量的方差;N是该卫星弧段的平滑历元数。
另外,本文使用的GIM是由CODE分析中心提供的时空分辨率为1 h×2.5°(纬度)×5°(经度)的VTEC,在使用时需要将GIM在时间域和空间域内插,得到相应时刻穿刺点处的VTECIPP。VTECIPP的方差σVTECIPP2可根据GIM提供的格网点处的精度信息,利用误差传播定律确定。
同时,为减弱观测噪声以及投影函数误差的影响,卫星截止高度角设置为20°,按照高度角定权的方式(PELE=1/(1+cos2ELE),ELE是卫星高度角)得到观测值的方差σELE2。
根据式(1)以及电离层观测值的精度信息(如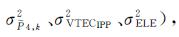
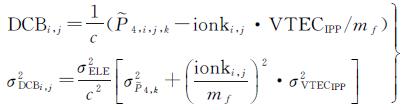 (4)
(4)
将上述DCBi,j和σDCBi,j2写成矩阵的形式
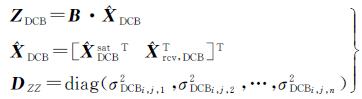 (4)
(4)
式中,ZDCB=[DCBi,j,1DCBi,j,2…DCBi,j,n]T是各个卫星与接收机的DCB组合值构成的列向量,可将其视为卫星与接收机DCB之和的观测值;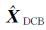
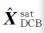
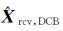
由于接收机与卫星的DCB参数列相关,需要提供一个附加的参考基准,才可实现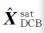
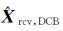
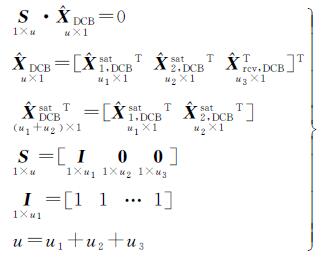 (5)
(5)
式中,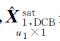
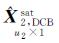
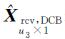
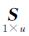
方案1:采用与GPS卫星类似的“零均值”基准,将14颗BDS卫星的DCB之和假定为0,即u1=14,u2=0。
方案2:考虑到BDS空间段采用GEO/IGSO/MEO混合的星座架构,建设初期很难保证各类BDS卫星DCB的稳定性相同,且各种类型卫星的空间分布、不同轨道高度处的外部环境、观测值质量等可能不同,如GEO卫星仅在亚太地区赤道上空可见,多路径效应严重,电离层观测值质量差,由此引起的误差会通过“零均值”基准污染所有卫星DCB参数的估值[1-3, 18, 23],而IGSO和MEO卫星稳定性较高,因此将稳定性较高的IGSO和MEO卫星的DCB之和假定为0,即u1=9,u2=5。
结合式(4)和式(5),根据附有限制条件的间接平差,可得到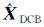
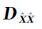
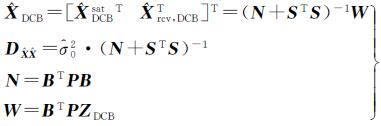 (6)
(6)
式中,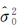
上述两种约束方案采用的卫星参考基准不同,使用时需要将不同的卫星参考基准转换到统一的基准后再进行比较,具体转换方法可参考文献[11]。
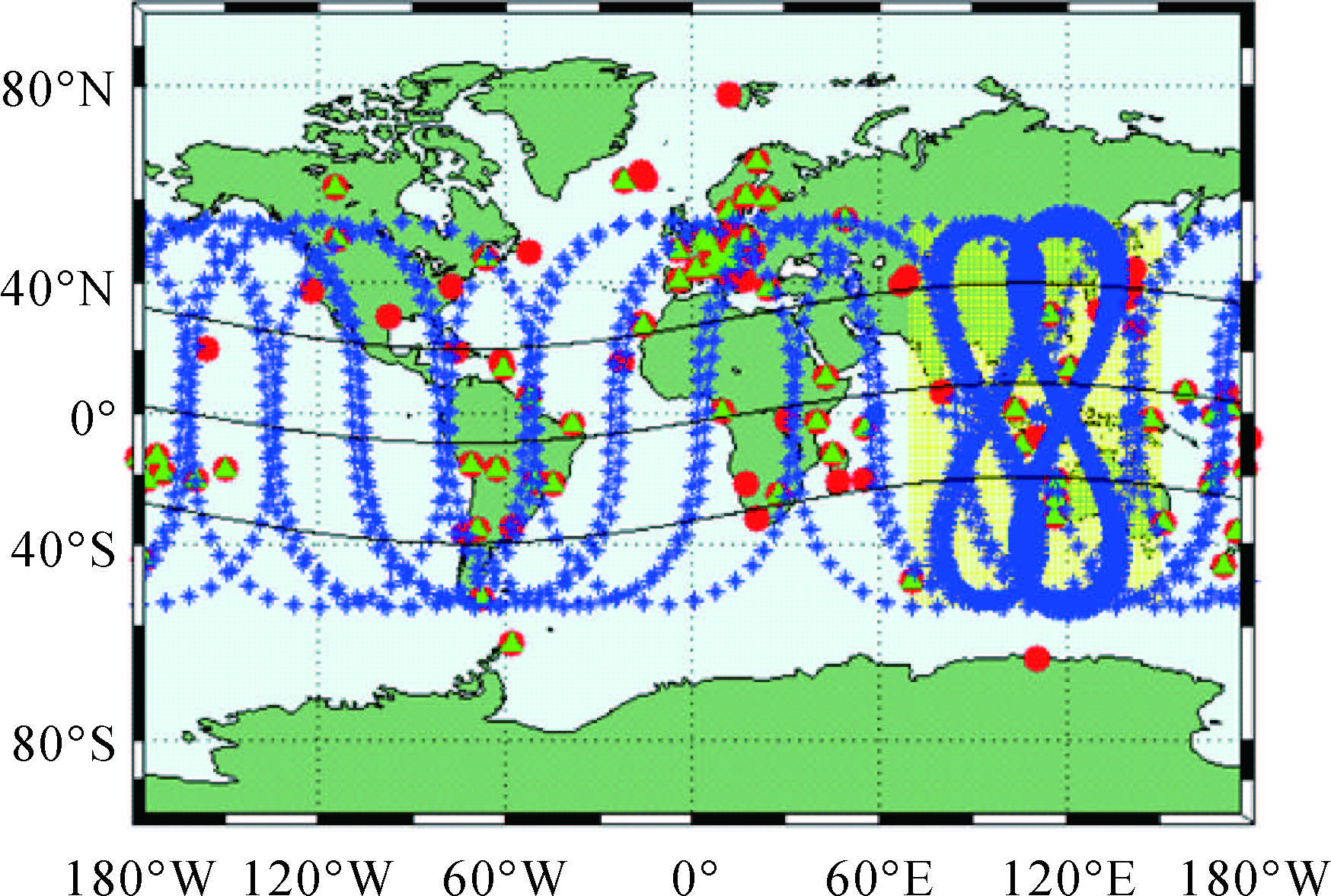
2 BDS卫星和接收机DCB结果分析选取2015年1月2日—3月31日(DOY002-090)MGEX的BDS三频观测数据(站点分布如图 1所示),采用两种不同的约束方案(所有BDS卫星约束称为约束1,IGSO和MEO卫星约束称为约束2),分别求解BDS的卫星和接收机DCB(DCBB1-B2=DCBC2I-C7I和DCBB1-B3=DCBC2I-C6I),并对其进行精度评估。这里需要说明3个问题:①由于BDS的MEO C13卫星自2014年初因故障不再提供服务,实际上只需对13颗卫星的DCB进行求解和分析。②目前BDS可提供B1、B2和B3共3个频点的导航信号,因此共有DCBB1-B2、DCBB1-B3和DCBB2-B3 3种差分码偏差,本文只需求解DCBB1-B2和DCBB1-B3,DCBB2-B3可通过DCBB1-B2和DCBB1-B3之间作差求得。③截至2015年,全球分布的MGEX站有100个左右,但并不是每个接收机都可以接收到BDS信号(能否接收到BDS信号与接收机类型有关),据统计目前全球大概有50~70个MGEX站可以接收BDS信号。
|
| 图 1 BDS卫星星下点轨迹(蓝色曲线)以及全球MGEX站分布(红色圆点) Fig. 1 BDS satellites sub-trajectories (blue curves) and the location of MGEX network (red dots) for one day in 2015 >注:绿色三角形代表能够接收北斗数据的MGEX跟踪站;黄色矩形阴影部分代表现阶段北斗系统公开服务区(55°S~55°N,70°E~150°E);3条黑色曲线分别代表磁赤道和±30°地磁纬度线 |
2.1 BDS卫星DCB(C2I-C7I/C2I-C6I)分析
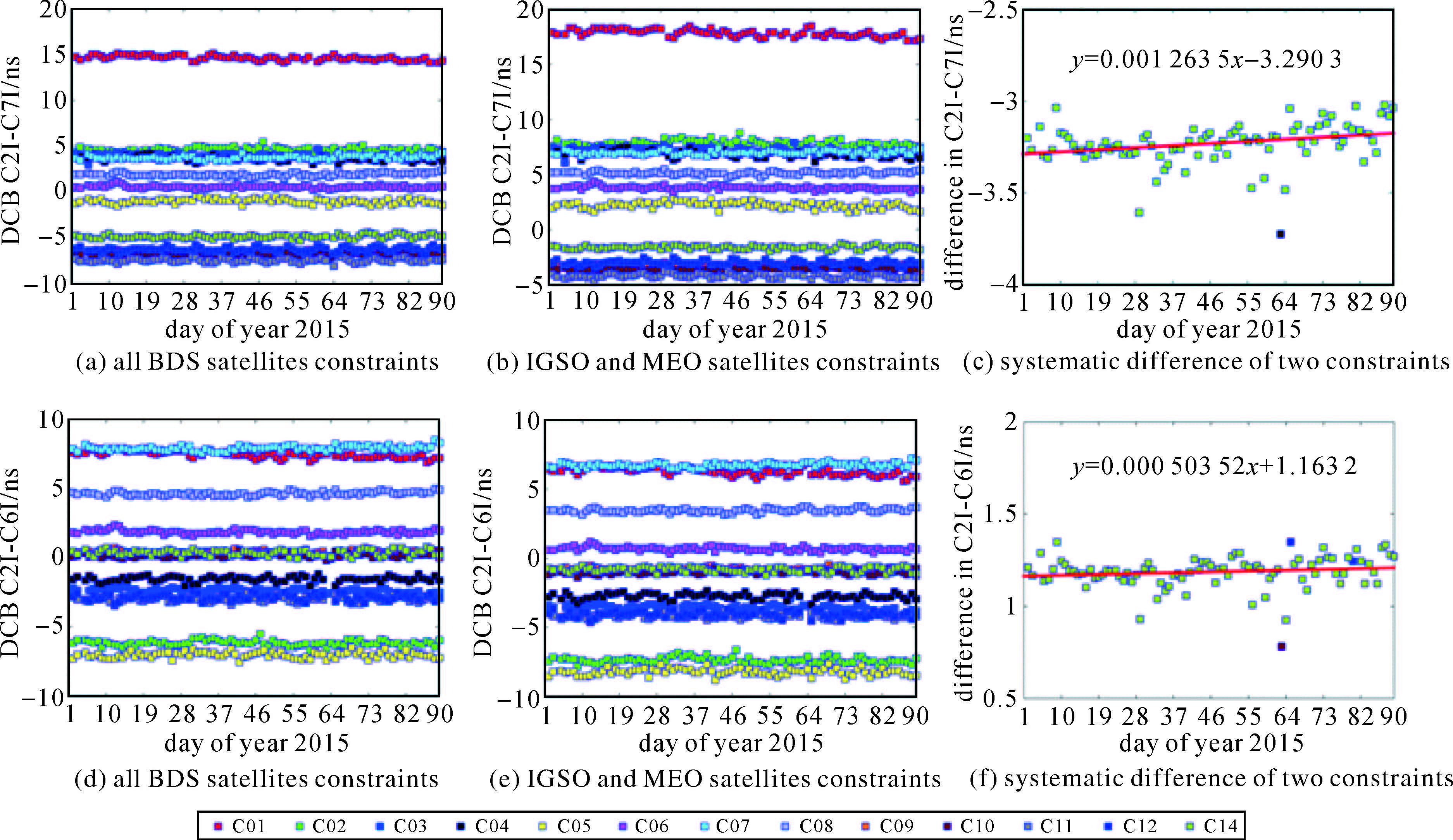
图 2为2015年(DOY002-090)在两种约束方案下3种类型BDS(IGSO、MEO和GEO)卫星DCB的时间序列,从整体上看,卫星DCB在长时段内较为稳定,大多分布在±8 ns之内,C01的DCBC2I-C7I除外(在约束1下C01 DCBC2I-C7I约为15 ns,在约束2下C01 DCBC2I-C7I约为18 ns)。同时可看出,在两种约束方案下,各卫星DCB差值整体趋势一致,存在系统性的偏差,DCBC2I-C7I间的系统性偏差约为-3.3 ns,DCBC2I-C6I间的系统性偏差约为1.2 ns。
|
| 图 2 2015年(DOY002-090)两种约束方案下BDS卫星DCB(C2I-C7I、C2I-C6I)的时间序列以及系统性偏差 Fig. 2 Time series and systematic difference of BDS satellites DCB under two constraints in year 2015 (DOY002-090) |
卫星的DCB在一段时间内通常被认为是稳定不变的,因此笔者统计了卫星DCB在一个月内的标准差,并把它作为反映卫星DCB估值精度和稳定性的指标[2, 24]。公式如下
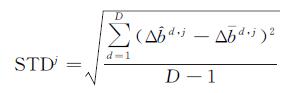 (7)
(7)
式中,STDj表示第j颗卫星DCB估值的稳定性;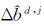
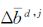
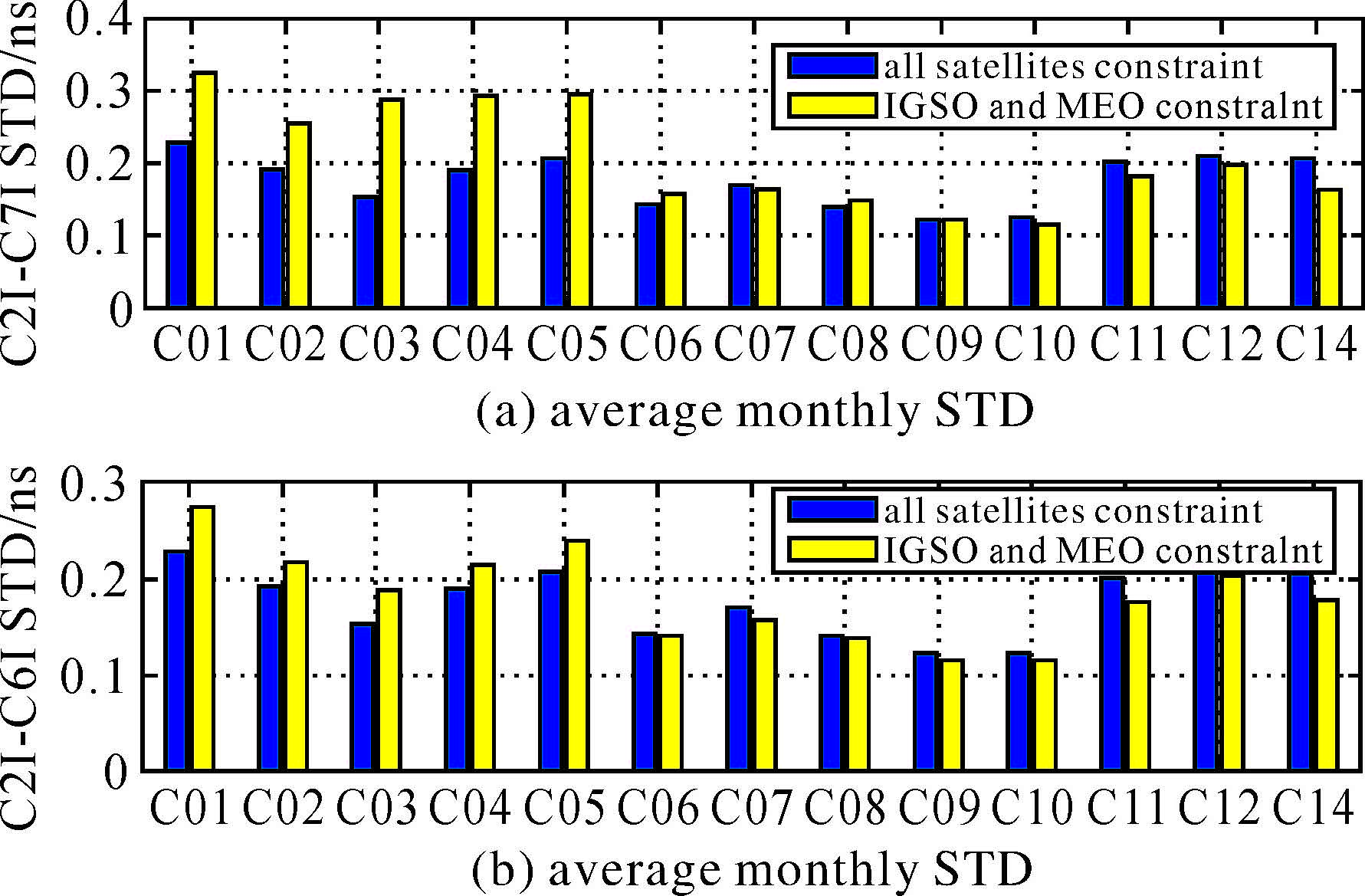
在将两种约束转换到统一的卫星参考基准后,对卫星DCB的月平均稳定性进行了统计(如图 3所示),总体上看,BDS卫星的稳定性优于0.2 ns(最大为0.32 ns)。3种类型卫星中,IGSO卫星DCB的STD指标最好(0.1 ns左右),其次是MEO卫星DCB的STD(0.2 ns左右),GEO卫星DCB的STD稍差(0.15~0.32 ns),IGSO和MEO卫星的稳定性普遍优于GEO卫星。GEO卫星DCB STD较差的原因,一方面在于BDS GEO卫星属于静止轨道卫星,始终位于亚太地区赤道上空,使得电离层观测值质量较差(多路径效应严重),并且亚太地区BDS跟踪站数量少;另一方面,亚太地区参与GIM建模的IGS跟踪站数量少,且受赤道异常影响,GIM在该区域的精度有限。
|
| 图 3 2015年(DOY002-090)两种约束方案下BDS卫星DCB(C2I-C7I/C2I-C6I)稳定性 Fig. 3 Stability for BDS satellites DCB under two constraints in year 2015 (DOY002-090) |
相对于约束1,施加约束2后,除了C06外,IGSO和MEO卫星DCB估值更加稳定(DCBC2I-C7I STD最大改善21%,DCBC2I-C6I STD最大改善13%),同时可看到GEO卫星DCB的STD会变差(DCBC2I-C7I STD的降低幅度普遍在50%以上,DCBC2I-C6I STD的降低幅度最大达23%),说明去除GEO卫星约束后,可提高IGSO/MEO卫星DCB估计的稳定性,这一方面与GEO卫星的星座分布、观测值质量较差以及亚太地区BDS地面跟踪站较少有关,另一方面可能与GEO卫星的内部稳定性有关,因此施加约束1最终会将GEO卫星的误差通过“零均值”基准污染其他卫星DCB参数的估值和稳定性,而约束2未将稳定性较差的GEO卫星纳入“零均值”基准,仅把“零均值”约束施加至稳定性较高的IGSO和MEO卫星上,可有效避免稳定性较差的GEO卫星对IGSO/MEO卫星DCB估值的影响,理论上更加严密可靠。
通过比较DCBC2I-C7I和DCBC2I-C6I的STD发现,DCBC2I-C6I更为稳定,这与ionki,j有关[3],电离层TEC变化引起的DCB估计误差会通过系数ionki,j进行调节,由于ionkC2I-C6I=-0.085 m/TECU,ionkC2I-C7I=-0.112 m/TECU,因此使得DCBC2I-C6I的STD更小。
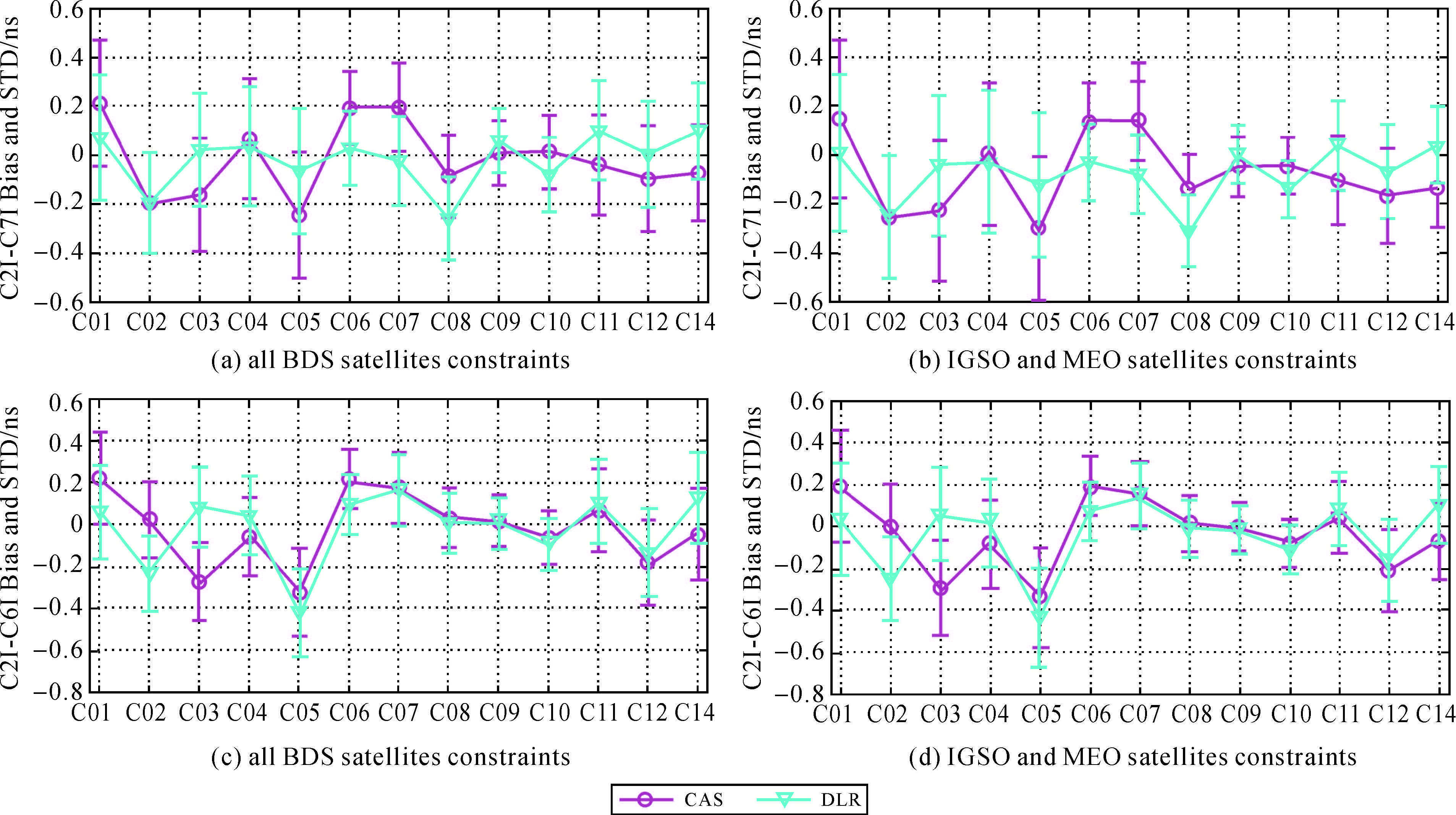
目前IGS提供以中国科学院(CAS)和德国宇航中心(DLR)为代表的多系统DCB产品,本文以CAS/DLR发布的BDS DCB产品为参考,给出了两种约束方案下BDS卫星DCB与CAS/DLR产品之间的平均偏差(Bias)以及标准差(STD)。如图 4所示,两种约束方案确定的BDS卫星DCB与CAS/DLR产品的Bias为-0.3~0.2 ns(C2I-C7I),-0.4~0.2 ns(C2I-C6I),同时IGSO(C06-C10)和MEO(C11-C13)的STD比GEO(C01-C05)的STD小。对比看来,约束2的DCB估值效果不仅与CAS/DLR产品有较好的一致性,而且考虑到了BDS卫星DCB间的稳定性差异。
|
| 图 4 两种约束方案下BDS卫星DCB(C2I-C7I、C2I-C6I)与CAS/DLR产品的平均偏差(Bias)以及标准差(STD) Fig. 4 The Bias and STD of two different constraints with respect to CAS/DLR BDS DCB |
2.2 BDS接收机DCB(C2I-C7I/C2I-C6I)分析
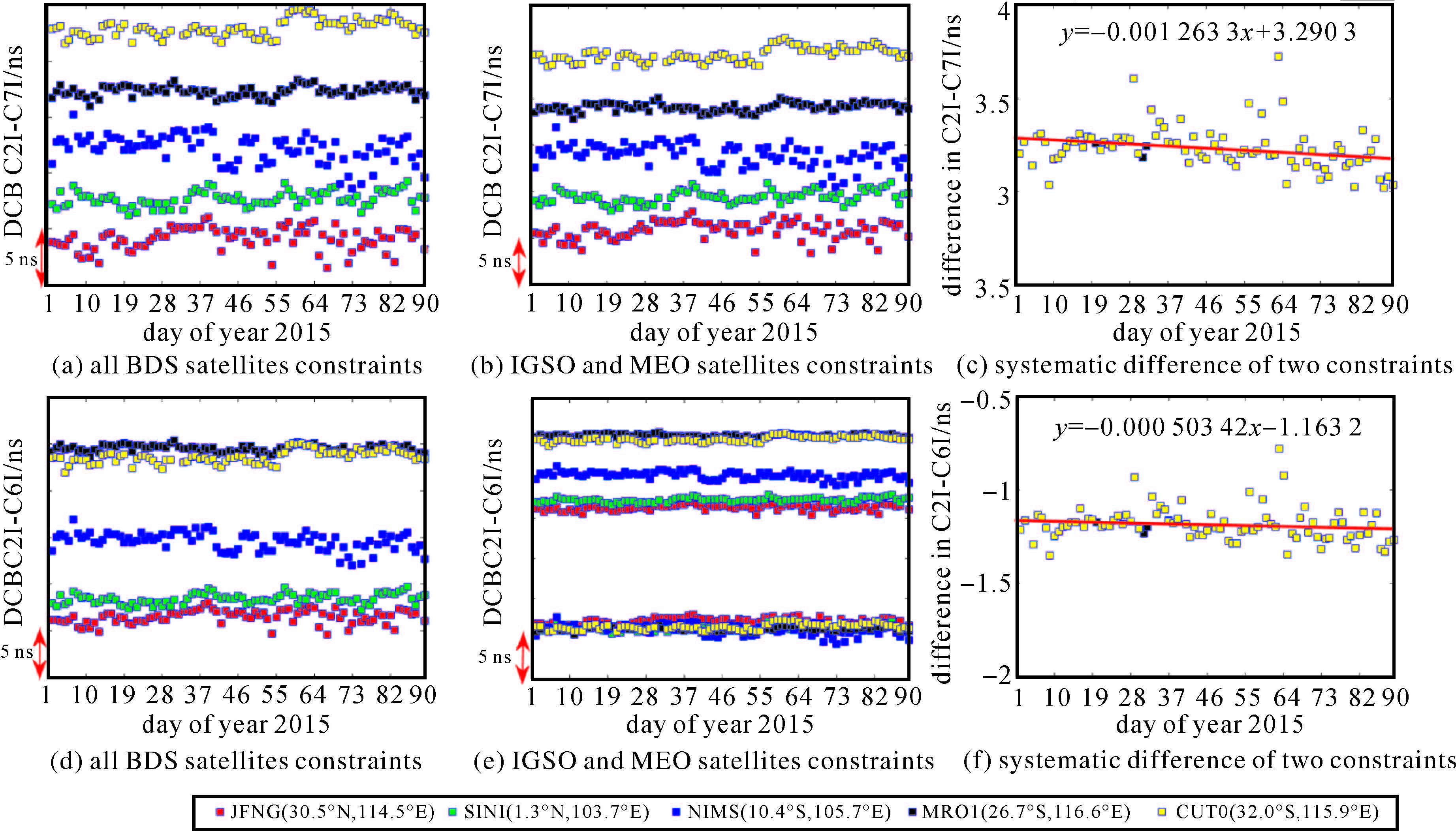
现阶段BDS已实现亚太大部分地区的服务能力,本文按纬度带选取2015年(DOY002-090)该地区数据连续性较好的5个BDS跟踪站,对其接收机DCB的时间序列进行分析(图 5)。在两种约束方案下,各接收机DCB差值整体趋势一致,存在系统性的偏差,该偏差与卫星DCB的系统性偏差大小相同,符号相反,卫星和接收机的组合DCB不会发生变化,不会影响TEC的使用。
|
| 图 5 2015年(DOY002-090)亚太地区5个BDS接收机在两种约束方案下的DCB(C2I-C7I,C2I-C6I)的时间序列以及系统性偏差 Fig. 5 Time series and systematic difference of 5 BDS receivers DCB under two constraints in the Asia-Pacific region of year 2015 (DOY002-090) |
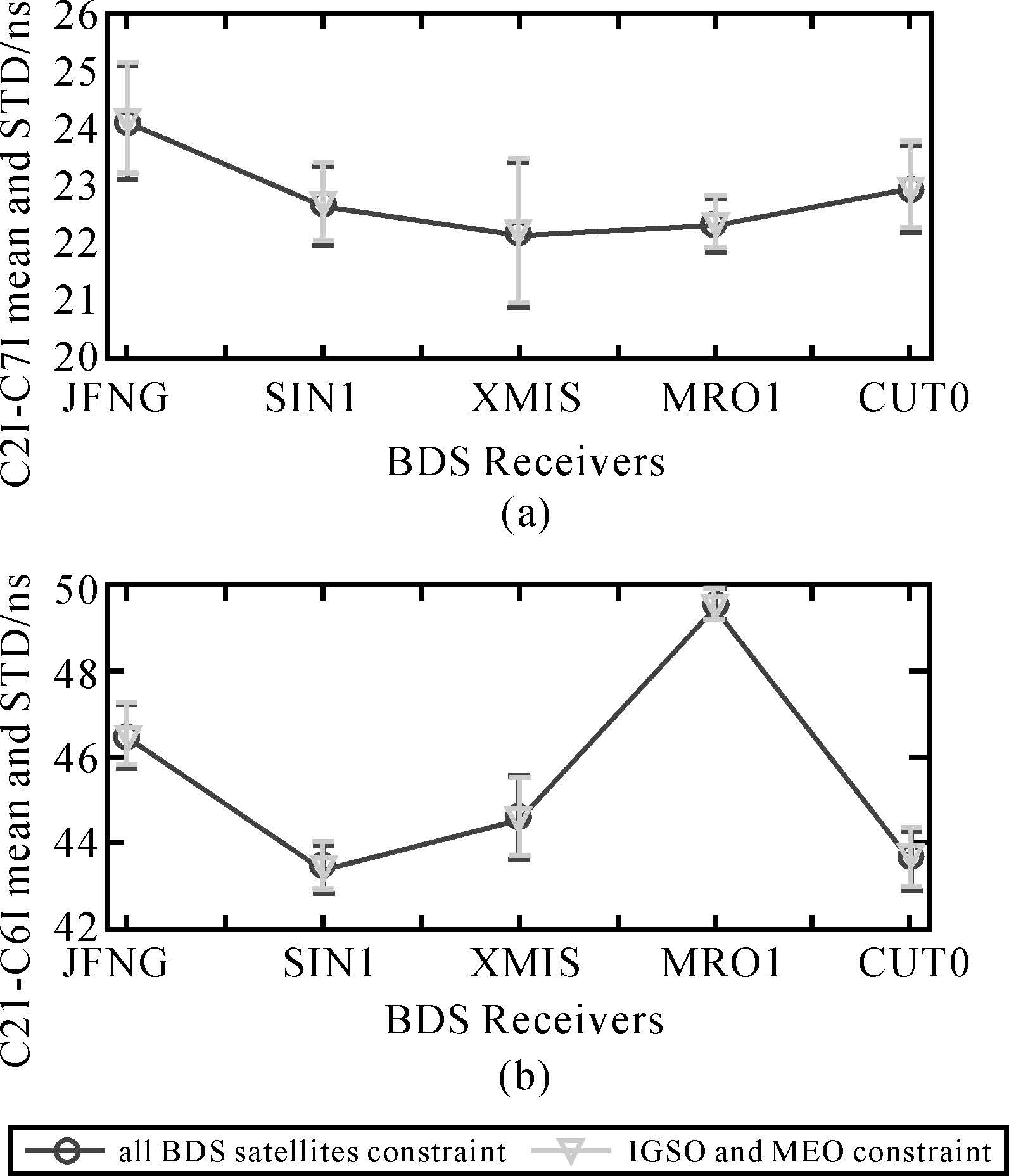
将约束1和约束2转换到统一基准后,统计了上述5个接收机在DOY002-090的均值(Mean)和标准差(STD),如图 6所示,可以看出,对于约束1,DCBC2I-C7I平均STD为0.838 ns,DCBC2I-C6I平均STD为0.655 ns;对于约束2,DCBC2I-C7I平均STD为0.817 ns,DCBC2I-C6I平均STD为0.636 ns。两种约束方案下,接收机DCB的Mean与STD基本重合,且STD在长时段内变化较为稳定(STD<1 ns),说明约束的选择不会影响接收机DCB的稳定性。
|
| 图 6 2015年(DOY002-090)亚太地区5个BDS接收机在两种约束方案下的DCB(C2I-C7I,C2I-C6I)的均值(Mean)和标准差(STD) Fig. 6 The Mean and STD of 5 BDS receivers DCB under two constraints in the Asia-Pacific region of year 2015 (DOY002-090) |
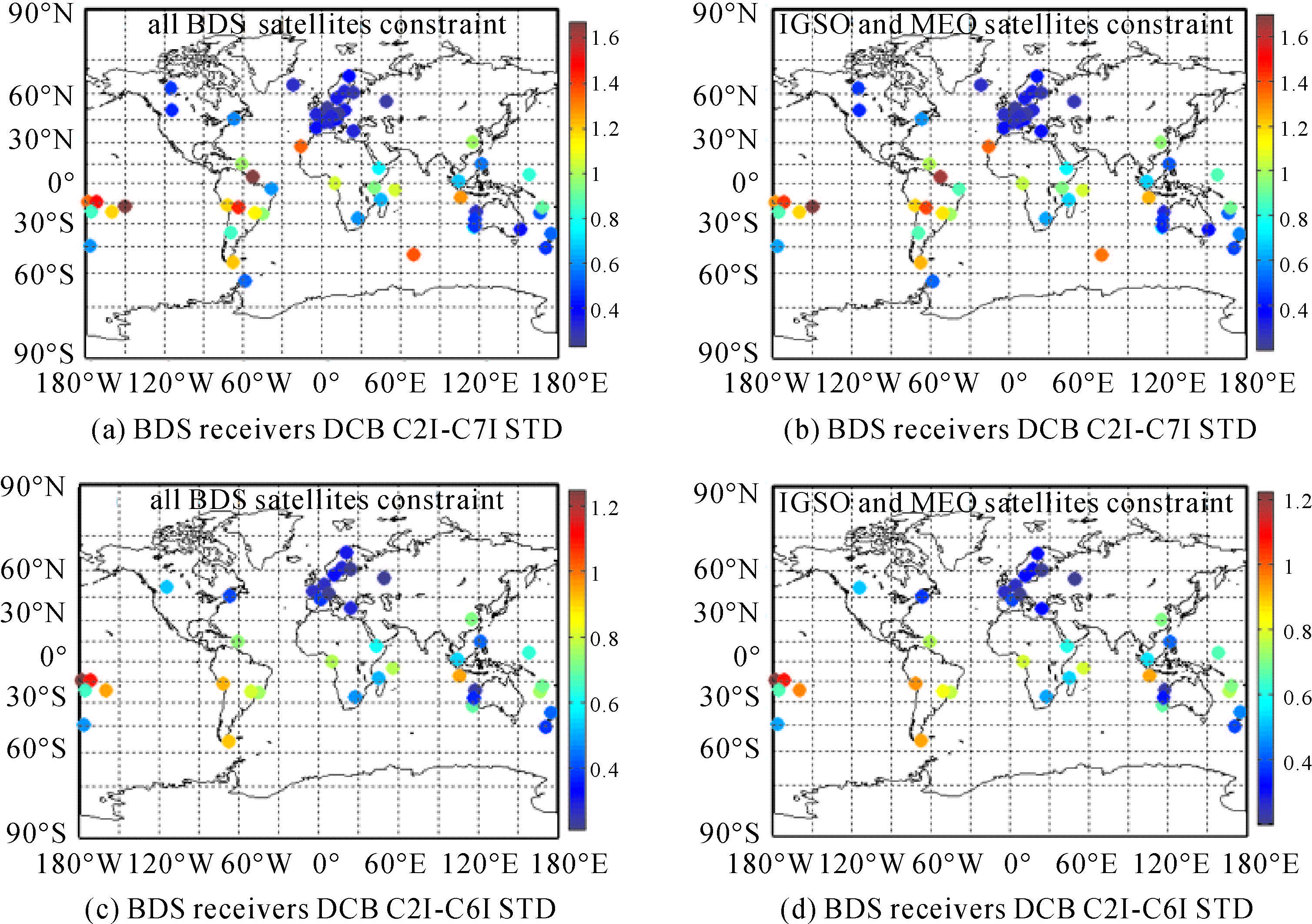
在此基础上,本文进一步对全球BDS接收机DCB稳定性进行了统计分析,如图 7所示。从整体上可看出,BDS接收机DCB稳定性整体上优于1 ns,STD大小与接收机所在位置有关,中高纬度区域较好(STD在0.4 ns左右),低纬度区域稍差(STD在0.8~1 ns),这可能是受赤道异常影响,GIM在低纬区域精度较差,说明电离层活动引起的GIM VTEC误差是影响BDS接收机DCB的变化的重要误差源。比较图 7(a)和7(b),或7(c)和7(d)可发现,施加两种约束后,BDS接收机DCB的STD无明显变化,说明约束的选择对BDS接收机DCB的稳定性不会产生明显影响;比较图 7(a)、7(b)与7(c)、7(d)可发现,与BDS卫星DCB类似,BDS接收机DCBC2I-C6I的稳定性优于DCBC2I-C7I,两者之间的稳定性差异受到系数ionki,j的调制作用;与BDS卫星DCB相比,接收机DCB的稳定性要低于卫星DCB。
3 结 论差分码偏差(DCB)是影响电离层建模和用户导航定位授时服务的重要误差源,在高精度GNSS应用中需要被准确估计。现阶段BDS卫星和地面跟踪站数量较少,利用BDS单系统获取的DCB精度有限,针对此,本文基于CODE GIM,对BDS卫星分别采用两种不同的“零均值”基准约束方案(约束1和约束2),求解BDS的DCB并对其进行精度评估。
|
| 图 7 2015年(DOY002-090)两种约束方案下BDS接收机DCB(C2I-C7I/C2I-C6I)稳定性统计 Fig. 7 Stability for BDS receivers DCB under two constraints in year 2015 (DOY002-090) |
结果表明,两种约束方案下,各卫星DCB差值整体趋势一致,存在系统性的偏差,各接收机DCB的系统性偏差与卫星DCB的系统性偏差大小相同,符号相反,卫星和接收机组合DCB不发生变化。相对于约束1,施加约束2后IGSO和MEO卫星DCB估值更加稳定(DCBC2I-C7I STD最大改善21%,DCBC2I-C6I STD最大改善13%),说明去除GEO卫星约束,可有效避免稳定性较差的GEO卫星对其他卫星DCB的影响,提高IGSO/MEO卫星DCB估计的稳定性,且其DCB估值效果与CAS/DLR产品有较好的一致性,理论上更加严密可靠。IGSO卫星DCB的STD指标最好(0.1 ns左右),其次是MEO卫星(0.2 ns左右),GEO卫星稍差(0.15~0.32 ns),IGSO和MEO卫星的稳定性普遍优于GEO卫星。通过比较DCBC2I-C7I和DCBC2I-C6I的STD发现,DCBC2I-C6I更为稳定,这是因为由电离层TEC变化引起的DCB估计误差会通过系数ionki,j进行调节,因此使得DCBC2I-C6I的STD更小。
两种约束方案下,BDS接收机DCB的STD无明显变化,说明约束的选择对BDS接收机DCB的稳定性不会产生明显影响。BDS接收机DCB稳定性整体上优于1 ns,STD与接收机所在位置有关,中高纬度区域较好(STD在0.4 ns左右),低纬度区域稍差(STD在0.8~1 ns),这可能是受赤道异常影响(GIM在低纬区域精度较差),说明电离层活动引起的GIM VTEC误差是影响BDS接收机DCB的变化的重要误差源。
随着BDS星座和地面跟踪站的不断完善,以及GIM时空分辨率和精度的提高,将来有望得到更为稳定、可靠的BDS卫星和接收机DCB。
| [1] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P. Differential Code Bias Estimation Using Multi-GNSS Observations and Global Ionosphere Maps[J]. Navigation, 2014, 61(3): 191–201. DOI:10.1002/navi.v61.3 |
| [2] | WANG Ningbo, YUAN Yunbin, LI Zishen, et al. Determination of Differential Code Biases with Multi-GNSS Observations[J]. Journal of Geodesy, 2016, 90(3): 209–228. DOI:10.1007/s00190-015-0867-4 |
| [3] | JIN S G, JIN R, LI D. Assessment of BeiDou Differential Code Bias Variations from Multi-GNSS Network Observations[J]. Annales Geophysicae, 2016, 34(2): 259–269. DOI:10.5194/angeo-34-259-2016 |
| [4] | China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document:Open Service Signal (Version 2.0)[Z]. Beijing, China:China Satellite Navigation Office, 2013. |
| [5] | WILSON B D, YINGER C H, FEESS W A, et al. New and Improved:The Broadcast Interfrequency Biases[J]. GPS World, 1999, 10(9): 56–66. |
| [6] | 章红平, 韩文慧, 黄玲, 等. 地基GNSS全球电离层延迟建模[J]. 武汉大学学报(信息科学版), 2012, 37(10): 1186–1189. ZHANG Hongping, HAN Wenhui, HUANG Ling, et al. Modeling Global Ionospheric Delay with IGS Ground-Based GNSS Observations[J]. Geomatics and Information Science of Wuhan University, 2012, 37(10): 1186–1189. |
| [7] | 李子申. GNSS/Compass电离层时延修正及TEC监测理论与方法研究[D]. 北京:中国科学院大学, 2012. LI Zishen. Study on the Mitigation of Ionospheric Delay and the Monitoring of Global Ionospheric TEC Based on GNSS/Compass[D]. Beijing:University of Chinese Academy of Science, 2012. http://d.wanfangdata.com.cn/Thesis/Y2430991 |
| [8] | SARDÓN E, ZARRAOA N. Estimation of Total Electron Content Using GPS Data:How Stable are the Differential Satellite and Receiver Instrumental Biases?[J]. Radio Science, 1997, 32(5): 1899–1910. DOI:10.1029/97RS01457 |
| [9] | 常青, 张东和, 萧佐, 等. GPS系统硬件延迟估计方法及其在TEC计算中的应用[J]. 地球物理学报, 2001, 44(5): 596–601. CHANG Qing, ZHANG Donghe, XIAO Zuo, et al. A Method for Estimating GPS Instrumental Biases and its Application in TEC Calculation[J]. Chinese Journal of Geophysics, 2001, 44(5): 596–601. |
| [10] | HERNÁNDEZ-PAJARES M, JUAN J M, SANZ J, et al. The Ionosphere:Effects, GPS Modeling and the Benefits for Space Geodetic Techniques[J]. Journal of Geodesy, 2011, 85(12): 887–907. DOI:10.1007/s00190-011-0508-5 |
| [11] | 王宁波, 袁运斌, 张宝成, 等. GPS民用广播星历中ISC参数精度分析及其对导航定位的影响[J]. 测绘学报, 2016, 45(8): 919–928. WANG Ningbo, YUAN Yunbin, ZHANG Baocheng, et al. Accuracy Evaluation of GPS Broadcast Inter-Signal Correction (ISC) Parameters and Their Impacts on GPS Standard Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 919–928. DOI:10.11947/j.AGCS.2016.20150554 |
| [12] | GUO Fei, ZHANG Xiaohong, WANG Jinling. Timing Group Delay and Differential Code Bias Corrections for BeiDou Positioning[J]. Journal of Geodesy, 2015, 89(5): 427–445. DOI:10.1007/s00190-015-0788-2 |
| [13] | SARDÓN E, RIUS A, ZARRAOA N. Estimation of the Transmitter and Receiver Differential Biases and the Ionospheric Total Electron Content from Global Positioning System Observations[J]. Radio Science, 1994, 29(3): 577–586. DOI:10.1029/94RS00449 |
| [14] | COCO D S, COKER C, DAHLKE S R, et al. Variability of GPS Satellite Differential Group Delay Biases[J]. IEEE Transactions on Aerospace and Electronic systems, 1991, 27(6): 931–938. DOI:10.1109/7.104264 |
| [15] | MANNUCCI A J, WILSON B D, YUAN D N, et al. A Global Mapping Technique for GPS-Derived Ionospheric Total Electron Content Measurements[J]. Radio Science, 1998, 33(3): 565–582. DOI:10.1029/97RS02707 |
| [16] | MA G, MARUYAMA T. Derivation of TEC and Estimation of Instrumental Biases from GEONET in Japan[J]. Annales Geophysicae, 2003, 21(10): 2083–2093. DOI:10.5194/angeo-21-2083-2003 |
| [17] | JIN Rui, JIN Shuanggen, FENG Guiping. M_DCB:Matlab Code for Estimating GNSS Satellite and Receiver Differential Code Biases[J]. GPS Solutions, 2012, 16(4): 541–548. DOI:10.1007/s10291-012-0279-3 |
| [18] | LI Zishen, YUAN Yunbin, LI Hui, et al. Two-step Method for the Determination of the Differential Code Biases of COMPASS Satellites[J]. Journal of Geodesy, 2012, 86(11): 1059–1076. DOI:10.1007/s00190-012-0565-4 |
| [19] | SCHAER S. Mapping and Predicting the Earth's Ionosphere Using the Global Positioning System[D]. Bern, Swiss:The University of Bern, 1999. http://www.oalib.com/references/17314439 |
| [20] | XUE Junchen, SONG Shuli, ZHU Wenyao. Estimation of Differential Code Biases for Beidou Navigation System Using Multi-GNSS Observations:How Stable are the Differential Satellite and Receiver Code Biases?[J]. Journal of Geodesy, 2016, 90(4): 309–321. DOI:10.1007/s00190-015-0874-5 |
| [21] | JIAO Wenhai, GENG Changjiang, MA Yinhu, et al. A Method to Estimate DCB of COMPASS satellites Based on Global Ionosphere Map[M]//SUN Jiadong, LIU Jingnan, YANG Yuanxi, et al. China Satellite Navigation Conference (CSNC) 2012 Proceedings. Berlin Heidelberg:Springer, 2012:347-353. |
| [22] | 薛军琛, 宋淑丽, 朱文耀. 基于BDS/GPS双系统的全球电离层建模[J]. 中国科学:物理学力学天文学, 2015, 47(7): 079505. XUE Junchen, SONG Shuli, ZHU Wenyao. Global Ionosphere Model Based on BDS/GPS Dual-system Observations[J]. Scientia Sinica:Physica, Mechanica & Astronomica, 2015, 47(7): 079505. |
| [23] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. A COMPASS for Asia:First Experience with the BeiDou-2 Regional Navigation System[R]. Notes, 2010. |
| [24] | WILSON B D, MANNUCCI A J. Instrumental Biases in Ionospheric Measurements Derived from GPS Data[C]//Proceedings of the 6th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1993). Salt Lake City, UT:Salt Palace Convention Center, 1993:1343-1351. |

