2. 北京大学遥感与地理信息系统研究所, 北京 100871;
3. 国土资源部城市土地资源监测与仿真重点实验室, 广东 深圳 518034;
4. 地理国情监测国家测绘地理信息局重点实验室, 湖北 武汉 430072;
5. 西安测绘研究所, 陕西 西安 710054
2. Institute of Remote Sensing & Geographical Information System, Peking University, Beijing 100871, China;
3. Key Laboratory of Urban Land Resources Monitoring and Simulation, Ministry of Land and Resources, Shenzhen 518034, China;
4. Key Laboratory for National Geographic Census and Monitoring, National Administration of Surveying, Mapping and Geoinformation, Wuhan 430072, China;
5. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
轨迹线通常由一系列按时间序列组织的位置坐标点组成,用以描述物体或地理现象的时空移动轨迹。随着位置感知设备的普及,各种类型的轨迹监测数据成为当前众源大数据的重要组成部分[1],它们对于城市群体\个体行为模式分析[1-2]、交通信息实时监测表达[3]、地理数据库更新[4]等具有重要意义。然而,具备空间/时间高分辨率特点的轨迹数据通常规模巨大。例如车载GPS设备若每10 s记录一次,一个中等规模城市的出租车单个工作日产生的数据量将达到GB级别。一方面,这对存储设备空间、网络传输带宽以及后期分析的计算资源造成巨大压力[5];另一方面,轨迹数据本身包含大量冗余信息,浪费存储计算资源的同时也对分析处理及可视化表达造成负面干扰。解决上述问题的途径之一是研究高效的轨迹数据化简方法,即在满足一定几何精度条件下简化数据构成,压缩数据规模。
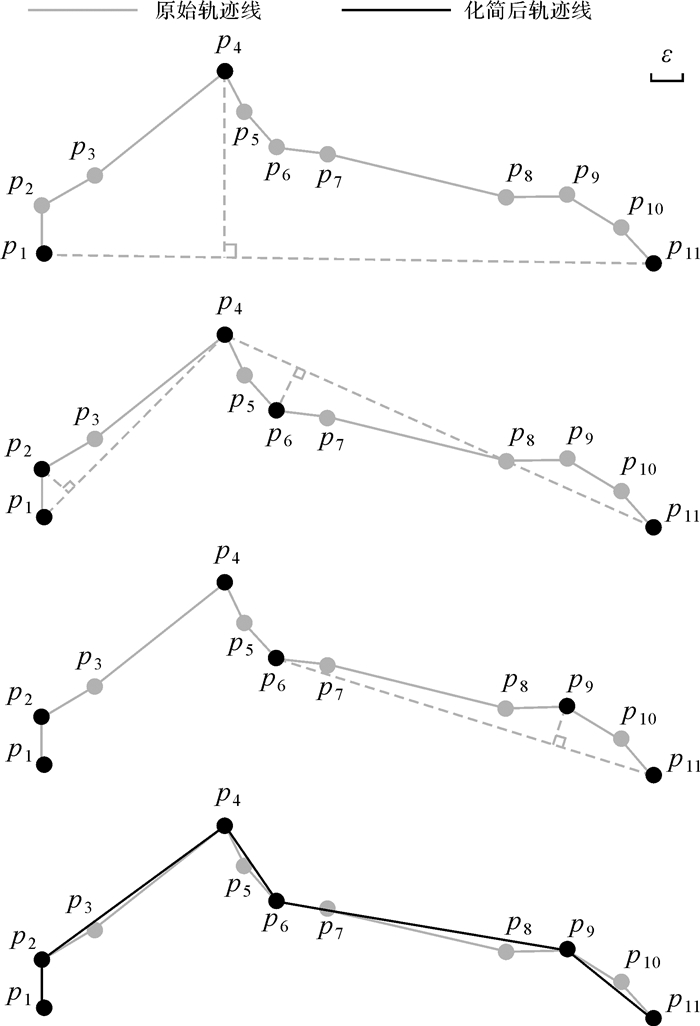
空间数据的综合化简在地图制图以及计算机视觉领域受到广泛关注。具体到线状目标的化简问题,国内外相关学者提出了一系列的算法模型[6-11]。这些方法主要面向快照式静态地理数据(如描述某一时刻道路、河流、境界等地理实体的线状目标),依据几何特征上的距离、角度、面积以及这些参量背后的地理意义来分析并保留重要的特征点,包括端点、极值点(局部极大极小点)、拐点等。它们虽然能够较好地保持原始线状目标的空间形态结构,但是缺乏对时间维信息的考虑,直接应用到时空轨迹线化简中容易丢失速度、加速度等移动变化特征。以应用最为广泛的Douglas-Peucker算法为例[9](如图 1所示),通过中间点相对当前基准线(首尾点连线)的偏移距离对原始轨迹线进行递归分段。某一轨迹点距基准线的偏移距离定义为该点到基准线的最短欧氏距离。当某一段轨迹线片段对应的最大偏移距离小于设定的几何误差ε,则该轨迹线片段化简拟合为对应的基准线。该过程中部分偏移距离较小但是对物体运动模式变化描述具有重要意义的轨迹点(如p3,p7,p8)将被舍弃。
|
| 图 1 Douglas-Peucker算法 Fig. 1 The principle Douglas-Peucker algorithm |
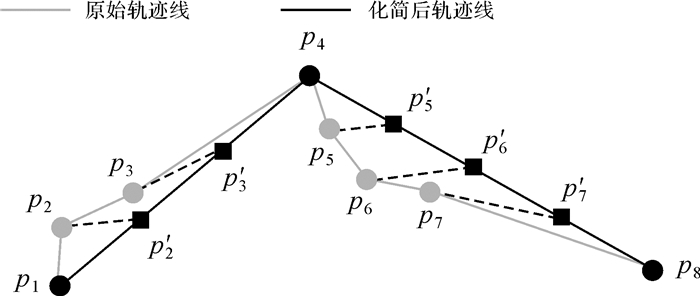
针对传统化简方法的不足之处,相关学者进行了深入研究。DP算法中某一舍弃轨迹点pi距对应拟合基准线间的最小欧氏距离定义为轨迹线在pi处的空间误差,没有考虑轨迹线蕴含的时间维信息。针对这一问题,文献[12]提出将时间同步欧氏距离(synchronized Euclidean distance)作为轨迹线化简后空间误差评价依据,并依此对DP算法进行改进,提出top-down time ratio(TD-TR)方法。如图 2所示,原始轨迹线包含轨迹点p1、p2、…、p8,化简后保留轨迹点p1、p4、p8,舍弃的轨迹点如p2处产生的空间误差定义为p2与p′2间的距离(即时间同步欧氏距离),其中p′2称为p2的时间同步拟合点,可在基准线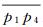
|
| 图 2 时间同步欧氏偏移距离定义 Fig. 2 The definition of synchronized euclidean distance |
在上述研究成果的基础上,本研究提出一种保持移动速度特征的轨迹线化简方法。速度特征是反映移动物体运动状态的重要指标,化简过程尽量保持原有轨迹线隐含的速度变化信息对于后期移动模式的分析、挖掘和预测有积极的作用。例如车辆交通事故领域,车辆轨迹线速度变化上的关键轨迹点是事故分析及理赔的重要依据。本文方法采用的基本思想是基于移动速度相似性原则对原始轨迹线进行层次化剖分,然后将剖分关系作为约束条件结合化简精度要求对原始轨迹线实施分区化简,使得距离误差控制下的轨迹点取舍行为尽量发生在移动速度均一的轨迹线片段内,而速度变化上的重要轨迹点由于处于分区临界位置而被保留,从而缓解化简操作对原始轨迹线隐含速度特征的破坏。下文首先介绍本文提出的方法,然后利用真实的车辆轨迹数据进行试验,并与其他已有方法的化简结果进行对比式分析,最后给出相关结论。
1 方法给定一条原始轨迹线T={p1,p2,…,pn},每个轨迹点pi表示为三元组信息〈xi,yi,ti〉,n是轨迹线包含的轨迹点数量。其中,xi和yi为轨迹点pi的空间位置坐标,ti表示pi产生的时间信息,由时间相邻轨迹点构成的直线段分别表示为e1、e2、…、en-1。高精度测量设备产生的轨迹点还包括定位点的高程信息以及移动物体的瞬时速度和方向信息,本研究暂不考虑这一情况。本文提出的化简方法主要包括轨迹直线段层次化聚类与轨迹线分区化简两个基本步骤。具体如下:
1.1 轨迹直线段层次化聚类轨迹线直线段层次化聚类是指在拓扑连接关系的约束下,依据移动速度相似性原则对所有轨迹直线段单元进行层次化组织。首先,分别计算每条轨迹直线段对应的物体移动速度值。考虑到轨迹线是对物体运动位置状态的离散化描述模型,本文方法的一个前置条件是假设同一轨迹直线段区域内物体的移动速度保持均匀。因此,对于由相邻轨迹点pi、pi+1组成直线段ei,对应的物体移动速度vi可由式(1)计算得到
 (1)
(1)
式中,d(pi,pi+1)表示轨迹点pi和pi+1间的欧氏距离,ti和ti+1则分别是轨迹点pi和pi+1的定位时间。
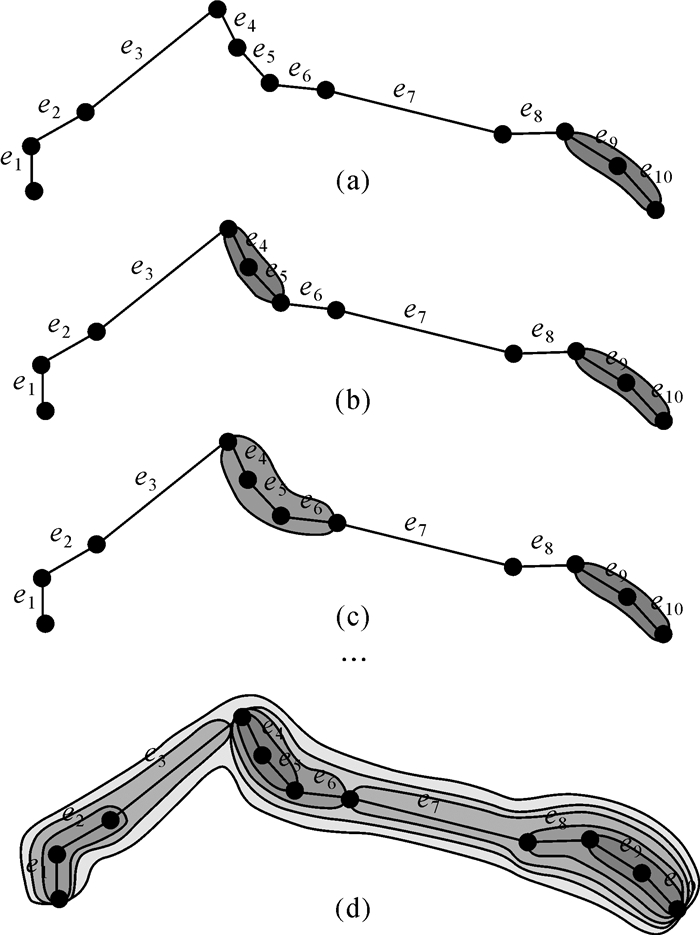
然后,以轨迹直线段为基本单元实施图 3所示的层次化聚类过程(注:图 3中轨迹线相邻轨迹点间时间间隔相同)。层次化聚类是指在空间邻近关系约束条件下,依据单个或多个属性特征对空间目标进行不同空间粒度的分组分区[18]。该过程的核心问题包括:①如何定义相邻聚类单元之间基于属性特征的差异性;②聚类过程中采用何种邻近约束策略。针对上述两个问题,文献[19]提出了single linkage、complete linkage、average linkage 3种属性特征差异性计算模型以及first-order和full-order两种聚类约束策略(限于论文篇幅,本文不再对上述模型和策略的具体细节展开描述)。基于文献[19]提供的建议以及轨迹直线段依据速度特征实施层次化聚类的具体特点,笔者采用average linkage和full-order构建针对轨迹直线段基于速度属性特征的层次化分类模型。
|
| 图 3 轨迹线直线段的层次化聚类过程示意图 Fig. 3 Hierarchical clustering procedure for line segments in a trajectory |
初始条件下每条轨迹直线段各自对应于一个独立的聚类单元,即G(e1)、G(e2)、…、G(en-1),然后依据拓扑连接边的长度由小到大依次合并相邻聚类单元,直至所有轨迹直线段形成一个完整的聚类单元。其中,连接边的长度对应于两个聚类单元间的移动速度差异,由各自包含的直线段的速度信息决定。假设两个聚类单元Gi和Gj拓扑相邻,Gi包含的m条轨迹直线段,对应的移动速度分别为ν0i,ν1i,…,νm-1i,Gj包含的n条轨迹直线段,对应的移动速度分别为ν0j,ν1j,…,νn-1j。Gi和Gj间的连接边长度L(Gi,Gj)可由式(2)计算得到
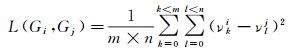 (2)
(2)
式中,将相邻的两个聚类单元间的连接边长度定义为各自包含轨迹直线段间的速度差异平方的均值。L(Gi,Gj)值越小,表明则两个聚类单元对应的轨迹线片段区域间物体移动速度越接近,组成更高级别聚类单元的优先级越高。每次相邻聚类单元发生合并操作后,新组成的聚类单元需要重新计算并更新与周围相邻聚类单元间的连接边长度,并调整连接边排序。如图 3(b)中,当G(e4)和G(e5)合并为G(e4,e5)后,L(G(e3),G(e4))需要更新为L(G(e3),G(e4,e5)),L(G(e5),G(e6))需要更新为L(G(e4,e5),G(e6))。
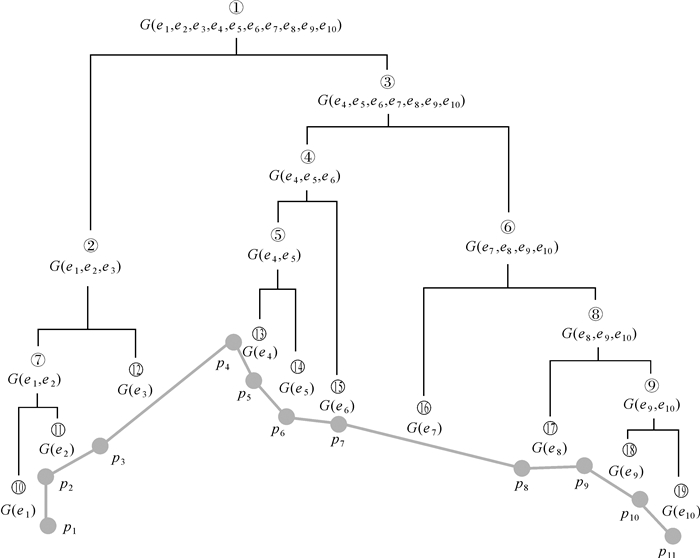
1.2 轨迹线分区化简按1.1节方法对原始轨迹线包含的直线段实施层次化聚类后,聚类结果可进一步组织为树结构模型。如图 4所示,树结构的根节点(编号为①)则对应于由所有轨迹直线段组成的最大聚类单元G(e1,e2,…,e10),而叶子节点(如编号为⑩)对应于由单条轨迹直线段构成的聚类单元(如G(e10))。从根节点到叶子节点,对应的轨迹线片段区域物体移动速度差异越来越小,形成一种层次化的剖分关系。
|
| 图 4 层次化聚类结果树结构组织 Fig. 4 Organization of hierarchical clusters using structure tree |
进一步,将建立的原始轨迹线剖分结构作为约束条件,结合设置的化简几何误差ε对原始轨迹线进行分区处理。该过程表现为从根节点开始,由上而下依次遍历如图 4所示的树结构。每遍历一个树节点:
(1) 提取该树节点对应聚类单元包含的所有轨迹线直线段,并连接组织为轨迹线片段。
(2) 以该轨迹线片段的首尾点构成的直线段为基准线,计算每一个中间轨迹点距基准线的时间同步欧氏距离,并将其中的最大值记录为dmax。
(3) 比较dmax与ε间的大小关系,如果dmax≤ε,将该部分轨迹线片段划分为同一个区域,同时跳过该树节点的孩子节点;如果dmax>ε,则后续进一步考察该节点包含的孩子节点。
按上述步骤完成对树结构的遍历后,原始轨迹线被分为不同的区域,同一区域内的轨迹线片段化简为由首尾轨迹点连接的直线段,依次连接每一区域内轨迹线片段的化简结果即可得到完整的化简结果。
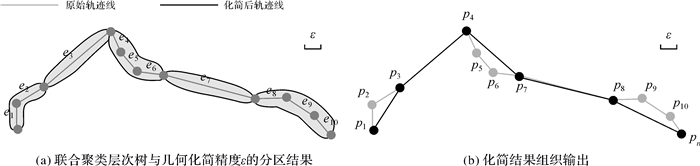
图 5(a)是在图 4层次化树结构基础上结合化简距离误差阈值ε获得的原始轨迹线分区结果,图 5(b)是依据分区信息导出的最终化简结果。对比图 5(b)和图 1(d)可以发现,DP算法依据几何偏移量对轨迹线进行分段化简,在移动速度上对所有轨迹点一视同仁,导致部分在移动速度变化上具有重要意义但是几何偏移特征不够明显的轨迹点被舍弃。而本文方法通过层次化聚类手段建立原始轨迹线在速度变化上的层次化剖分结构,并以此作为距离误差控制下轨迹线分区化简的约束条件,从而使得移动速度变化上具有重要意义的轨迹点如p3、p7、p8由于处在分区临界点而得以保留,最终缓解化简过程对原始轨迹线速度变化特征的破坏。
|
| 图 5 轨迹线分区及化简结果输出 Fig. 5 Original trajectory regionalization and simplified result output |
2 试验分析与评价
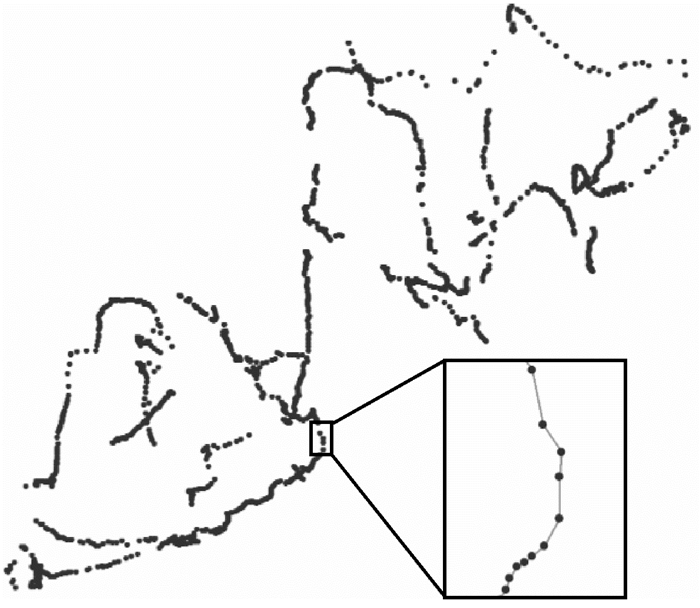
为了验证方法的有效性,本研究采用了真实数据进行试验测试。试验数据如图 6所示,包括由超过3000个轨迹点组成的25条独立轨迹线。这些轨迹数据来自车载GPS设备记录的某城区车辆运行轨迹,车辆类型包括公交车和出租车两种,相邻轨迹点采集的时间间隔为1 s。由于车辆运行过程中存在临时停车现象,表现为一定时间间隔内轨迹点坐标重合,通过预处理的方式探测得到并打断,直接将该部分轨迹线片段首尾点连接作为化简结果。
|
| 图 6 试验数据示例 Fig. 6 Experimental data |
采用对比式策略进行化简结果分析与评价,参考算法包括DP方法、TD-TR方法和OW-TR方法。考虑到试验数据各轨迹点处未记录车辆的瞬时速度和方向,因此没有将DR方法作为比较对象。由于不同方法采用不同的化简控制参数,如DP方法采用最短欧氏偏移距离,而TD-TR、OW-TR以及本文方法采用同步时间欧氏偏移距离,无法直接将化简结果进行比较。因此,采用调整控制参数进行多次化简的策略,使得不同方法获得的化简结果处于相同(非常接近)的压缩比率,然后实施分析评价。压缩比率ρ定义为化简后减少的轨迹点数量与原始轨迹点数量的比值,ρ越大则表明化简程度越大。试验中ρ取值由最小10%至最高80%。为了使结果评价更为准确,定义如下定量化指标:
(1) 时间同步距离误差。时间同步距离误差值定义如图 2所示,即原始轨迹线的每个轨迹点与化简后轨迹线上对应的时间同步拟合点间的距离。试验中统计原始轨迹线所有轨迹点化简后的时间同步距离误差,将其中的最大值(即最大时间同步距离误差)和平均值(即平均时间同步距离误差)作为评价指标。
(2) 速度误差。对于相邻轨迹点pi、pi+1组成的一条原始轨迹线直线段ei,化简前后的速度误差speed_error(ei)定义为
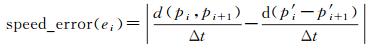 (3)
(3)
式中,Δt是两个轨迹点间的时间间隔,p′i、p′ i+1分别是轨迹点pi、pi+1在化简结果轨迹线上的同步时间拟合点。同样地,分别统计所有轨迹直线段处速度误差值中的最大值(称为最大速度误差)和平均值(称为平均速度误差)作为分析评价指标。
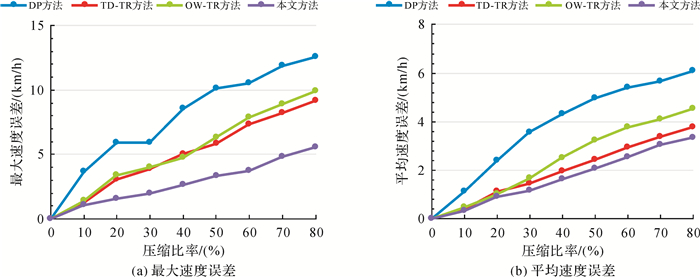
图 7对比了4种方法在不同压缩比率条件下产生的时间同步距离误差。可以发现,不管是最大时间同步距离误差,还是平均时间同步距离误差,TD-TR方法、OW-TR方法以及本文提出的方法表现较为接近,且明显优于DP方法。原因是前面3种方法均采用了时间同步距离作为轨迹点取舍的控制指标。其中,TD-TR方法采用全局性由上而下的比较策略,时间同步距离误差控制上好于采用局部启发式策略的OW-TR方法。而本文方法虽然也是一种全局性方法,由于增加了原始轨迹线在速度变化上的层次化剖分关系作为约束条件,使得部分速度变化大但是在时间同步距离指标上不是最优的轨迹点优先保留,导致同一压缩率水平下时间同步距离误差高于TD-TR方法,部分压缩比率区间甚至略高于OW-TR方法。也正是由于上述原因,使得本文方法在速度保持上优于其他几种方法。图 8(a)和图 8(b)分别是4种方法在不同压缩比率水平下的最大速度误差对比图和平均速度误差对比图。由于时间同步距离考虑了时间维信息,使得TD-TR和OW-TR两种方法在速度保持上优于采用最短欧氏距离作为控制参数的DP算法;而本文方法在TD-TR方法基础上,通过约束条件的形式加强速度变化在轨迹点取舍决策上的影响,使得化简结果在速度保持上更优。图 9展示了轨迹线局部片段利用4种不同方法化简后的结果实例。通过视觉分析可以看到,DP方法化简后丢失大量在速度变化上的重要轨迹点如pi、pj、pk、pl、pm、pn、po,这一情况在TD-TR方法化简结果(丢失pk、pl、pm、pn)以及OW-TR方法化简结果(丢失pk、pl、pm、pn)中有所缓解,而本文方法则能够比较好地保持上述重要轨迹点。

|
| 图 7 时间同步距离误差比较 Fig. 7 Comparison of synchronized Euclidean distance |
|
| 图 8 速度误差比较 Fig. 8 Comparison of speed error |

|
| 图 9 不同方法化简结果实例 Fig. 9 Sample of simplified results using different methods 注:压缩比率为70%,相邻轨迹点间时间间隔为1 s。 |
3 结论
以轨迹数据为代表的时空大数据给数据存储、传输以及计算分析等技术环节带来了挑战。解决上述问题的重要途径之一是使“大数据”变小,通过数据综合及压缩方法剔除冗余以及细节信息,保留轨迹数据隐含的主体特征。传统的地图综合方法主要面向静态的地理现象描述数据,关注地理数据的空间几何分布特征,对于带时间维信息蕴含移动特征的时空轨迹数据缺乏有效措施。本研究以轨迹线数据化简这一具体问题为例,在传统DP方法采用的迭代分区的思想的基础上,增加基于移动速度相似性原则的轨迹线层次化剖分措施,并以此作为约束条件使得距离误差控制下的轨迹点取舍行为尽量发生在移动速度均一的轨迹线片段内,从而达到更好地保持原始轨迹线移动模式特征这一目的。试验表明,在相同的压缩比率水平下,本文方法相对于其他已有方法在移动速度变化特征保持上具有优势。下一步工作包括:①进一步完善并验证提出的轨迹线层次化聚类分区方法。本文主要参考文献[18-19]构建式(2)所示的速度差异统计参量,是否最佳还需要更加全面的试验分析与评价工作。②提高算法执行效率,包括降低算法的复杂度以及构建并行化的计算构架,以应对海量位置感知器持续不断产生的轨迹数据对化简操作的需求。③提高轨迹线隐含模式特征的识别与分区能力。运动物体在不同时刻以及不同地理环境下存在不同的移动模式,如何分析挖掘这些特征差异并实施合理的分区分段处理具有重要意义。④进一步考虑轨迹点包含的高程信息,建立空间三维轨迹线化简模型。
| [1] | ZHENG Yu, XIE Xing, MA Weiying. GeoLife:A Collaborative Social Networking Service among User, Location and Trajectory[J]. IEEE Data(Base)Engineering Bulletin, 2010, 33(2): 32–39. |
| [2] |
刘瑜, 肖昱, 高松, 等.
基于位置感知设备的人类移动研究综述[J]. 地理与地理信息科学, 2011, 27(4): 8–13.
LIU Yu, XIAO Yu, GAO Song, et al. A Review of Human Mobility Research Based on Location Aware Devices[J]. Geography and Geo-Information Science, 2011, 27(4): 8–13. |
| [3] |
李清泉, 黄练.
基于GPS轨迹数据的地图匹配算法[J]. 测绘学报, 2010, 39(2): 207–212.
LI Qingquan, HUANG Lian. A Map Matching Algorithm for GPS Tracking Data[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 207–212. |
| [4] |
唐炉亮, 刘章, 杨雪, 等.
符合认知规律的时空轨迹融合与路网生成方法[J]. 测绘学报, 2015, 44(11): 1271–1276, 1284.
TANG Luliang, LIU Zhang, YANG Xue, et al. A Method of Spatio-temporal Trajectory Fusion and Road Network Generation Based on Cognitive Law[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1271–1276, 1284. DOI:10.11947/j.AGCS.2015.20140591 |
| [5] | MUCKELL J, OLSEN Jr P W, HWANG J H, et al. Compression of Trajectory Data:A Comprehensive Evaluation and New Approach[J]. GeoInformatica, 2014, 18(3): 435–460. DOI:10.1007/s10707-013-0184-0 |
| [6] |
武芳, 邓红艳.
基于遗传算法的线要素自动化简模型[J]. 测绘学报, 2003, 32(4): 349–355.
WU Fang, DENG Hongyan. Using Genetic Algorithms for Solving Problems in Automated Line Simplification[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4): 349–355. DOI:10.3321/j.issn:1001-1595.2003.04.013 |
| [7] |
钱海忠, 武芳, 陈波, 等.
采用斜拉式弯曲划分的曲线化简方法[J]. 测绘学报, 2007, 36(4): 443–449, 456.
QIAN Haizhong, WU Fang, CHEN Bo, et al. Simplifying Line with Oblique Dividing Curve Method[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 443–449, 456. DOI:10.3321/j.issn:1001-1595.2007.04.014 |
| [8] |
艾廷华, 郭仁忠, 刘耀林.
曲线弯曲深度层次结构的二叉树表达[J]. 测绘学报, 2001, 30(4): 343–348.
AI Tinghua, GUO Renzhong, LIU Yaolin. A Binary Tree Representation of Curve Hierarchical Structure in Depth[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 343–348. DOI:10.3321/j.issn:1001-1595.2001.04.013 |
| [9] | DOUGLAS D H, PEUCKER T K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J]. Cartographica:The International Journal for Geographic Information and Geovisualization, 1973, 10(2): 112–122. DOI:10.3138/FM57-6770-U75U-7727 |
| [10] | LI Zhilin, OPENSHAW S. Algorithms for Automated Line Generalization1 Based on a Natural Principle of Objective Generalization[J]. International Journal of Geographical Information Systems, 1992, 6(5): 373–389. DOI:10.1080/02693799208901921 |
| [11] | VISVALINGAM M, WHYATT J D. Line generalisation by repeated elimination of points[J]. The Cartographic Journal, 1993, 30(1): 46–51. DOI:10.1179/caj.1993.30.1.46 |
| [12] | KEOGH E, CHU S, HART D, et al.An online algorithm for segmenting time series[C]//Proceedings of 2001 IEEE International Conference on Data Mining (ICDM).San Jose, CA:IEEE, 2001:289-296. |
| [13] | POTAMIAS M, PATROUMPAS K, SELLIS T.Sampling Trajectory Streams with Spatiotemporal Criteria[C]//Proceedings of the 18th International Conference on Scientific and Statistical Database Management (SSDBM).Vienna, Austria:IEEE, 2006:275-284. |
| [14] | TRAJCEVSKI G, CAO Hu, SCHEUERMANN P, et al.On-line Data Reduction and The Quality of History in Moving Objects Databases[C]//Proceedings of the 5th ACM International Workshop on Data Engineering for Wireless and Mobile Access(MobiDE).Chicago, Illinois:ACM, 2006:19-26. |
| [15] | CHEN Yukun, JIANG Kai, ZHENG Yu, et al.Trajectory Simplification Method for Location-Based Social Networking Services[C]//Proceedings of the 2009 International Workshop on Location Based Social Networks.Seattle, Washington:ACM, 2009:33-40. |
| [16] | LONG Cheng, WONG R C W, JAGADISH H V. Trajectory Simplification:on Minimizing the Direction-Based Error[J]. Proceedings of the VLDB Endowment, 2014, 8(1): 49–60. DOI:10.14778/2735461 |
| [17] |
唐炉亮, 杨雪, 牛乐, 等.
一种众源车载GPS轨迹大数据自适应滤选方法[J]. 测绘学报, 2016, 45(12): 1455–1463.
TANG Luliang, YANG Xue, NIU Le, et al. An Adaptive Filtering Method Based on Crowdsourced Big Trace Data[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1455–1463. DOI:10.11947/j.AGCS.2016.20160117 |
| [18] | ASSUNÇÃO R M, NEVES M C, CÂMARA G, et al. Efficient Regionalization Techniques for Socio-Economic Geographical Units Using Minimum Spanning Trees[J]. International Journal of Geographical Information Science, 2006, 20(7): 797–811. DOI:10.1080/13658810600665111 |
| [19] | GUO D. Regionalization with Dynamically Constrained Agglomerative Clustering and Partitioning (REDCAP)[J]. International Journal of Geographical Information Science, 2008, 22(7): 801–823. DOI:10.1080/13658810701674970 |



