干涉合成孔径雷达(interferometric synthetic aperture radar, InSAR)可以高精度、高可靠性地获取地表三维信息和高程变化信息,被广泛应用于大地测绘、海洋监测、火山监测和地震检测等领域。干涉相位展开是lnSAR技术应用中尤为关键的环节,其相位展开精度直接影响着InSAR系统高程测量的精度,故干涉图展开算法的研究至关重要。
干涉图展开算法研究至今大致可分为路径跟踪法[1-11]、最小范数法[12-13]、最优估计法[14-23]三大类。其中经典相位展开算法,包括枝切法[1]、质量图引导法[3-5]、网络流法[7-9]、最小二乘法[12]等。为了得到较为理想的展开结果,通常要在相位展开之前使用前置预滤波器抑制干涉图中的相位噪声,即使用滤波器,如均值滤波器、Goldstein滤波器等,对干涉图展开前滤波,但在尽可能地抑制相位噪声的同时不免会模糊掉干涉条纹的边缘特性。基于数据融合的最优估计相位展开算法,包括扩展卡尔曼滤波相位展开算法(EKFPU)[14-15]、不敏卡尔曼滤波相位展开算法(UKFPU)[16-20]、粒子滤波相位展开算法[21-22]等,利用非线性滤波器自身具有的噪声抑制能力,可以在展开缠绕像元的同时抑制相位噪声,在一定程度上弥补了经典相位展开算法的不足,拓展了InSAR技术应用的范围。
为进一步促进基于数据融合的相位展开技术发展,本文将经Levenberg-Marquardt方法[24-25]修正后的嵌入式容积卡尔曼滤波器[26-27](MECKF)、基于修正矩阵束模型(AMPM)的局部相位梯度估计算法[20]以及量化跟踪策略[28]结合起来,提出一种新的基于数据融合的最优估计相位展开算法——修正嵌入式容积卡尔曼滤波的相位展开(modified embedded cubature Kalman filter phase unwrapping, MECKFPU)。MECKFPU算法利用MECKF同时执行相位展开和噪声抑制,利用AMPM局部相位梯度估计算法快速和精确地从复干涉图中获取相位梯度信息,以及利用量化跟踪策略从高质量像元到低质量像元的路径快速地搜索最佳待展开像元,从而保证了MECKFPU精确和快速地展开缠绕像元,具有比经典相位展开算法更稳健的相位展开能力,且相比于同类型的EKFPU、UKFPU等算法,MECKFPU拥有更佳的相位展开效率和精度,能够较好地解决干涉图展开问题。
1 MECKFPU算法 1.1 MECKF相位展开算法原理利用干涉图中相邻干涉相位之间的关系,将归一化复干涉的同向分量和正交分量分别作为干涉相位的两个观测值,在沿某一确定路径下,相位展开系统模型如下[20]
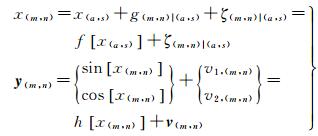 (1)
(1)
式中,x(m, n)和x(a, s)分别表示(m, n)像元和(a, s)像元的真实干涉相位;g(m, n)|(a, s)表示干涉图中(m, n)像元与(a, s)像元之间的相位梯度估计值,本文通过AMPM局部相位梯度估计算法[20]获得;ζ(m, n)|(a, s)表示干涉图中(m, n)像元与(a, s)像元之间的相位梯度估计误差;v1, (m, n)和v2, (m, n)分别表示附加在复干涉正交分量和同向分量上的噪声。
MECKF相位展开算法是在质量图引导策略指导下,同时利用待展开像元相邻8个像元中已展开像元信息,沿高质量区域到低质量区域的路径完成对缠绕像元递推估计。
嵌入式容积卡尔曼滤波器采用三阶嵌入式容积准则,利用附有权值的积分点实现对非线性系统后验均值和方差的逼近,具有良好的状态估计精度和数值稳定性。相应积分点和权值计算如下
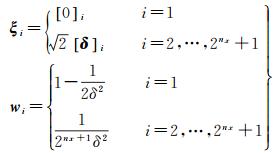 (2)
(2)
式中,nx表示状态变量维数,本文nx为1;[δ] i表示[δ]的第i列,其δ及[δ]的详细取值请参见文献[26-27],本文δ由经验取值为0.5。
根据相位展开系统模型,MECKF相位展开算法预测过程如下
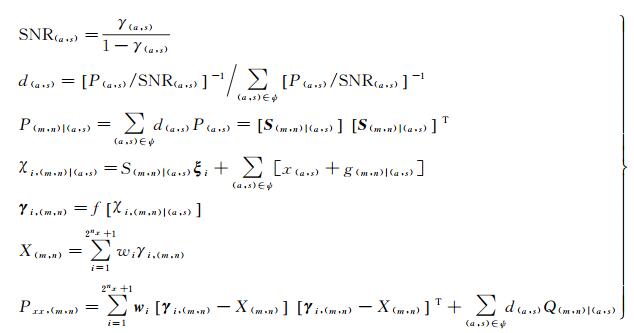 (3)
(3)
式中,(m, n)和(a, s)分别表示待展开像元以及待展开像元相邻8个像元中的已展开像元;γ(a, s)表示干涉图(a, s)像元的相干系数(或伪相干系数);ψ表示(m, n)像元相邻8个像元的集合;P(m, n)|(a, s)表示由(a, s)像元的估计误差方差P(a, s)通过权系数d(a, s)加权得到的(m, n)像元的预测估计误差方差的预测值;γi, (m, n)表示(m, n)像元积分点的预测值;Pxx, (m, n)表示状态预测值X(m, n)的预测估计误差方差;Q(m, n)|(a, s)表示g(m, n)|(a, s)的相位梯度估计误差方差[20]。
MECKF相位展开算法利用Levenberg-Marquardt方法优化预测过程中的预测估计误差方差,以提高算法收敛性,减小待展开像元的展开误差
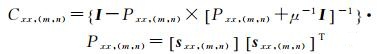 (4)
(4)
式中,μ表示优化Pxx, (m, n)的调节参数[24-25],本文由经验取值为0.3;I表示nx维单位矩阵。
MECKF相位展开算法更新过程如下
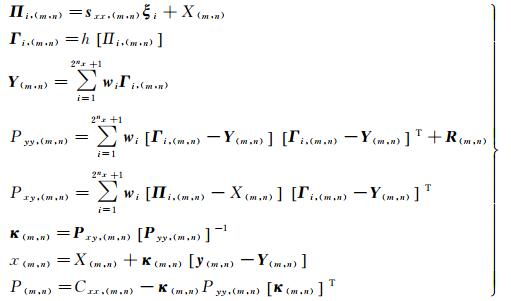 (5)
(5)
式中,y(m, n)和Y(m, n)分别表示(m, n)像元的观测值和观测预测值;R(m, n)表示(m, n)像元的观测预测协方差[20];κ(m, n)表示(m, n)像元的增益矩阵;x(m, n)和P(m, n)分别表示(m, n)像元的状态估计和状态估计误差方差。
1.2 结合量化跟踪策略的二维MECKF相位展开算法(MECKFPU)为减少MECKF相位展开算法搜索最佳待展开像元的时间消耗,引入文献[28]提出的量化跟踪策略来指导相位展开路径。量化跟踪策略通过归一化和量化路径引导图,利用附有链表的优先队列快速排序算法实现最佳待展开像元的快速搜索工作。利用干涉图伪相干系数图和微分偏差图构造指导MECKF相位展开算法展开路径的路径引导图[19], 如下
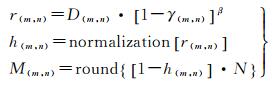 (6)
(6)
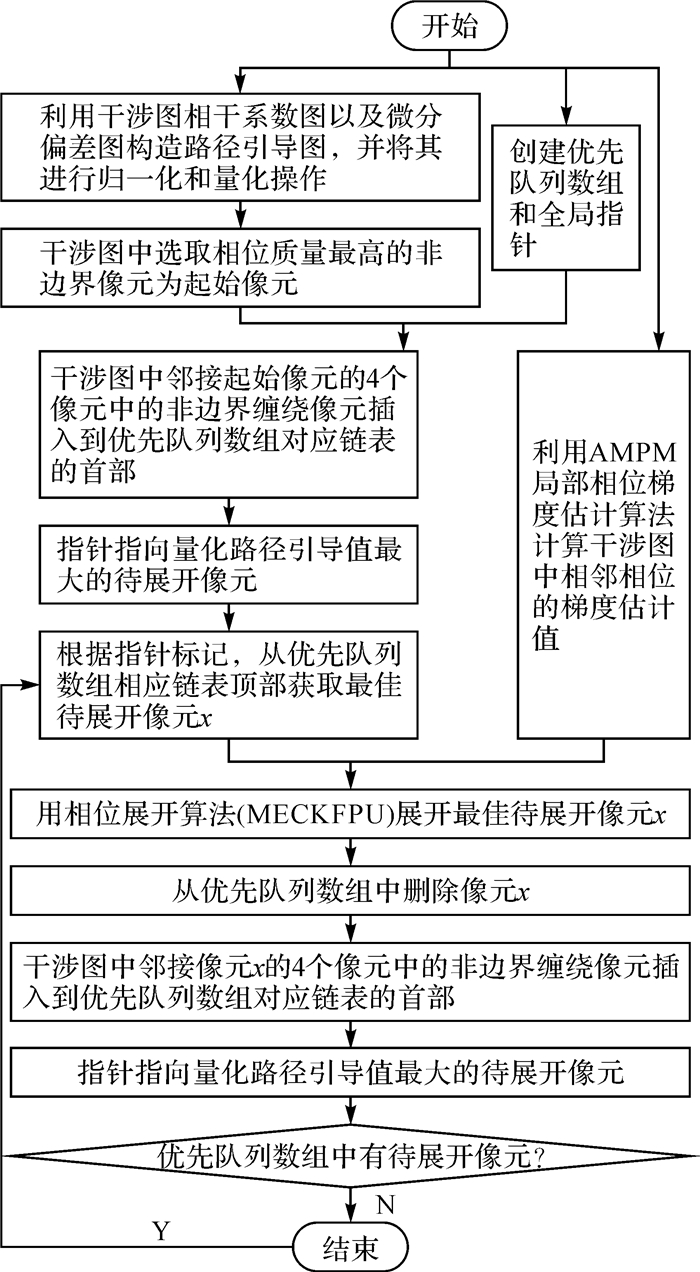
式中,D(m, n)表示像元(m, n)的微分偏差;β表示调整参数,详细请参见文献[19],本文由经验取值为0.2;normalization[·]表示归一化处理;round {·}表示四舍五入取整操作;M(m, n)表示(m, n)像元经归一化和量化处理后的量化路径引导值;N表示量化等级,本文取500。MECKFPU算法流程如图 1。
|
| 图 1 MECKFPU算法流程 Fig. 1 Flow chart of MECKFPU |
2 试验结果与分析 2.1 模拟数据试验 2.1.1 结合预滤波处理的金字塔地形干涉图展开试验
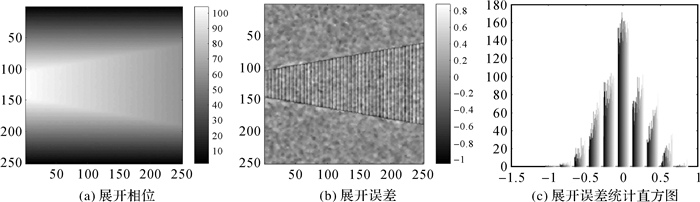
模拟干涉图主要参数:轨道高度为590 km,基线长度为610 m,下视角为45°,波长为0.04 m,基线倾角为10°,地面分辨率为6×6 m,场景为380 m的金字塔地形(256×256),干涉图见图 2。图 3为MECKFPU展开经均值滤波器(3×3)处理信噪比为3.01 dB图 2(c)后的结果。可以看出,MECKFPU的展开误差绝大分集中在[-0.5, 0.5]。表 1列出了枝切法、质量图引导法、迭代最小二乘法、网络流法、EKFPU、UKFPU和MECKFPU处理不同信噪比干涉图时的均方根误差(MSRE)。可以直观地看出,MECKFPU的展开精度最高。表 2列出了相同运算环境条件下上述各算法展开图 2(c)的运行时间,显然,MECKFPU时间消耗远远小于质量图引导法、EKFPU以及UKFPU算法,即使与枝切法、迭代最小二乘法以及网络流法等算法相比,MECKFPU时间消耗也是可以接受的。

|
| 图 2 金字塔地形干涉图 Fig. 2 Synthetic interferogram over pyramid |
|
| 图 3 MECKFPU处理经预滤波的金字塔地形干涉图结果 Fig. 3 The MECKFPU solution of pre-filtered interferogram over pyramid |
| rad | |||||||
| SNR/dB | 枝切法 | 质量图引导法 | 迭代最小二乘法 | 网络流法 | EKFPU | UKFPU | MECKFPU |
| 3.01 | 0.187 3 | 0.187 4 | 2.127 8 | 0.739 4 | 0.308 3 | 0.168 3 | 0.135 7 |
| 2.18 | 0.208 2 | 0.208 3 | 1.983 1 | 1.048 7 | 0.434 4 | 0.216 2 | 0.146 2 |
| 1.42 | 0.229 7 | 0.230 1 | 1.731 7 | 3.342 1 | 0.697 6 | 0.224 3 | 0.156 6 |
| 0 | 0.275 7 | 0.276 9 | 0.900 3 | 6.584 7 | 0.763 2 | 0.245 9 | 0.177 4 |
| -1.07 | 0.328 2 | 0.329 1 | 1.459 4 | 5.079 1 | 1.693 3 | 0.256 5 | 0.201 5 |
| s | ||||||
| 枝切法 | 质量图引导法 | 迭代最小二乘法 | 网络流法 | EKFPU | UKFPU | MECKFPU |
| 4.282 1 | 37.057 5 | 3.661 7 | 6.255 9 | 24.062 3 | 41.772 9 | 12.375 2 |
2.1.2 无预滤波处理的金字塔地形干涉图展开试验
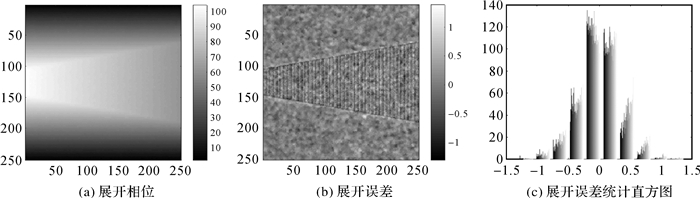
为了进一步分析MECKFPU的性能,直接用MECKFPU展开图 2(b),结果见图 4。可见MECKFPU对于不经预滤波处理的干涉图也可以得到理想的展开结果。表 3列出了质量图引导法、迭代最小二乘法、网络流法、EKFPU、UKFPU和MECKFPU处理不同信噪比(无预滤波处理的)干涉图时的MSRE。可见,相比于表 1,质量图引导法和EKFPU的展开精度明显降低,且干涉图信噪比越低其展开精度越低;迭代最小二乘法和网络流法不仅展开精度下降明显,而且算法较不稳定;UKFPU和MECKFPU的展开精度稍有变化,但无明显下降,且在干涉图信噪比较低的情况下,仍有较为理想的展开精度,远远高于其他算法的展开精度,其中MECKFPU的展开精度更高。由此可得,即使对于较低信噪比金字塔地形干涉图,MECKFPU仍有较高的展开精度。
|
| 图 4 MECKFPU处理无预滤波的金字塔地形干涉图结果 Fig. 4 The MECKFPU solution of without-filtered interferogram over pyramid |
| rad | ||||||
| SNR/dB | 质量图引导法 | 迭代最小二乘法 | 网络流法 | EKFPU | UKFPU | MECKFPU |
| 3.01 | 0.462 6 | 1.532 9 | 3.035 4 | 2.183 8 | 0.254 9 | 0.163 1 |
| 2.18 | 0.619 1 | 2.294 6 | 12.908 8 | 2.252 2 | 0.270 2 | 0.176 7 |
| 1.42 | 0.927 5 | 3.299 4 | 30.837 4 | 4.567 2 | 0.286 4 | 0.191 7 |
| 0 | 3.188 9 | 5.434 5 | 25.961 4 | 7.468 5 | 0.314 6 | 0.224 5 |
| -1.07 | 5.471 9 | 7.573 7 | 38.857 4 | 10.442 1 | 0.348 5 | 0.267 4 |
2.1.3 复杂多山地形干涉图展开试验
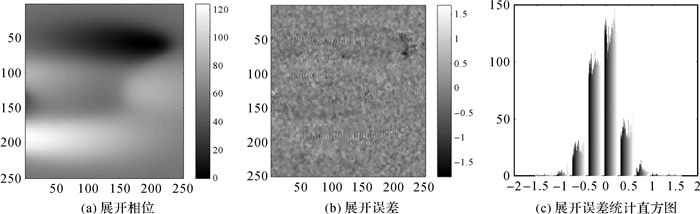
用多山地形场景取代上一节的金字塔地形场景,即可得复杂多山地形干涉图,见图 5。图 6为MECKFPU对信噪比为1.42 dB图 5(b)的处理结果。可见,MECKFPU的展开误差大部分集中在0附近。选取金字塔地形干涉图展开试验中表现出较好能力的UKFPU和MECKFPU做进一步比较,直接展开不经预滤波处理的不同信噪比复杂多山地形干涉图,其MSRE在表 4中列出,可看出,MECKFPU展开精度更高。综上可得,MECKFPU处理低信噪比复杂多山地形干涉图仍有较高的展开精度。

|
| 图 5 复杂多山地形干涉图 Fig. 5 Synthetic interferogram over peaks |
|
| 图 6 MECKFPU处理多山地形干涉图结果 Fig. 6 The MECKFPU solution of interferogram over peaks |
| rad | |||||
| SNR/dB | 3.01 | 2.18 | 1.42 | 0 | -1.07 |
| UKFPU | 0.233 7 | 0.243 7 | 0.279 1 | 0.327 7 | 0.519 9 |
| MECKFPU | 0.204 5 | 0.217 6 | 0.232 2 | 0.293 3 | 0.366 9 |
2.2 实测数据试验
在实测数据试验中,用MECKFPU算法展开经均值滤波器(3×3)处理后的局部Etna火山干涉图(256×256),见图 7。可见,展开相位平滑连续,重缠绕相位图干涉条纹与图 7(a)中干涉条纹保持一致,且干涉条纹清晰,几乎不存在相位噪声。这表明MECKFPU算法有效地抑制干涉图中的相位噪声,并获得了较好展开结果。综上所述,对于实际地形干涉图,MECKFPU仍有理想的展开效果和展开效率,具有良好的鲁棒性。

|
| 图 7 MECKFPU展开结果 Fig. 7 The MECKFPU solution |
3 结论
本文提出的MECKFPU是将经Levenberg-Marquardt方法修正后的嵌入式容积卡尔曼滤波器、AMPM局部相位梯度估计算法以及量化跟踪策略相结合的结果,并在模拟与实测数据处理试验中验证其有效性。本文算法与部分常用经典算法包括枝切法、质量图引导法、迭代最小二乘法、网络流法、EKFPU和UKFPU等算法在相关数据处理试验中进行了比较。结果表明,MECKFPU可以在快速和精确地展开干涉图的同时抑制相位噪声,具有较高的效率和良好的稳健性,能够有效地解决干涉图展开问题。
| [1] | GOLDSTEIN R M, ZEBKER H A, WERNER C L. Satellite Radar Interferometry:Two-dimensional Phase Unwrapping[J]. Radio Science, 1988, 23(4): 713–720. DOI:10.1029/RS023i004p00713 |
| [2] | ASUNDI A, ZHOU Wensen. Fast Phase-unwrapping Algorithm Based on a Gray-scale Mask and Flood Fill[J]. Applied Optics, 1998, 37(23): 5416–5420. DOI:10.1364/AO.37.005416 |
| [3] | ZHAO Ming, HUANG Lei, ZHANG Qican, et al. Quality-guided Phase Unwrapping Technique:Comparison of Quality Maps and Guiding Strategies[J]. Applied Optics, 2011, 50(33): 6214–6224. DOI:10.1364/AO.50.006214 |
| [4] | FANG Suping, MENG Lei, WANG Leijie, et al. Quality-guided Phase Unwrapping Algorithm Based on Reliability Evaluation[J]. Applied Optics, 2011, 50(28): 5446–5452. DOI:10.1364/AO.50.005446 |
| [5] | ZHONG Heping, TANG Jinsong, ZHANG Sen, et al. An Improved Quality-guided Phase-unwrapping Algorithm Based on Priority Queue[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(2): 364–368. DOI:10.1109/LGRS.2010.2076362 |
| [6] | GHIGLIA D C, PRITT M D. Two-dimensional Phase Unwrapping:Theory, Algorithms, and Software[M]. New York: John Wiley and Sons Inc, 1998. |
| [7] | CHEN C W.Statistical-cost Network-flow Approaches to Two-dimensional Phase Unwrapping for Radar Interferometry[D].Stanford, California:Stanford University, 2001. |
| [8] | COSTANTINI M. A Novel Phase Unwrapping Method Based on Network Programming[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 813–821. DOI:10.1109/36.673674 |
| [9] | CHEN C W, ZEBKER H A. Network Approaches to Two-dimensional Phase Unwrapping:Intractability and Two New Algorithms[J]. Journal of the Optical Society of America A, 2000, 17(3): 401–414. DOI:10.1364/JOSAA.17.000401 |
| [10] | GAO Dapeng, YIN Fuliang. Mask Cut Optimization in Two-dimensional Phase Unwrapping[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(3): 338–342. DOI:10.1109/LGRS.2011.2168940 |
| [11] | FLYNN T J. Two-dimensional Phase Unwrapping with Minimum Weighted Discontinuity[J]. Journal of the Optical Society of America A, 1997, 14(10): 2692–2701. DOI:10.1364/JOSAA.14.002692 |
| [12] | GHIGLIA D C, ROMERO L A. Robust Two-dimensional Weighted and Unweighted Phase Unwrapping that Uses Fast Transforms and Iterative Methods[J]. Journal of the Optical Society of America A, 1994, 11(1): 107–117. DOI:10.1364/JOSAA.11.000107 |
| [13] |
陈强, 杨莹辉, 刘国祥, 等.
基于边界探测的InSAR最小二乘整周相位解缠方法[J]. 测绘学报, 2012, 41(3): 441–448.
CHEN Qiang, YANG Yinghui, LIU Guoxiang, et al. InSAR Phase Unwrapping Using Least Squares Method with Integer Ambiguity Resolution and Edge Detection[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 441–448. |
| [14] | LOFFELD O, NIES H, KNEDLIK S, et al. Phase Unwrapping for SAR Interferometry:A Data Fusion Approach by Kalman Filtering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 47–58. DOI:10.1109/TGRS.2007.909081 |
| [15] | NIES H, LOFFELD O, WANG R.Phase Unwrapping Using 2D-Kalman Filter:Potential and Limitations[C]//Proceedings of 2008 IEEE International Geoscience and Remote Sensing Symposium.Boston, MA:IEEE, 2008:IV-1213-IV-1216. |
| [16] | WAGHMARE R G, MISHRA D, SAI SUBRAHMANYAM G R, et al. Signal Tracking Approach for Phase Estimation in Digital Holographic Interferometry[J]. Applied Optics, 2014, 53(19): 4150–4157. DOI:10.1364/AO.53.004150 |
| [17] |
谢先明.
结合滤波算法的不敏卡尔曼滤波器相位解缠方法[J]. 测绘学报, 2014, 43(7): 739–745.
XIE Xianming. An UKF Phase Unwrapping Algorithm with a Pre-filtering Procedure[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 739–745. DOI:10.13485/j.cnki.11-2089.2014.0102 |
| [18] | CHENG Zhongtao, LIU Dong, YANG Yongying, et al. Practical Phase Unwrapping of Interferometric Fringes Based on Unscented Kalman Filter Technique[J]. Optics Express, 2015, 23(25): 32337–32349. DOI:10.1364/OE.23.032337 |
| [19] | XIE Xianming, ZENG Qingning. Efficient and Robust Phase Unwrapping Algorithm Based on Unscented Kalman Filter, the Strategy of Quantizing Paths-guided Map, and Pixel Classification Strategy[J]. Applied Optics, 2015, 54(31): 9294–9307. DOI:10.1364/AO.54.009294 |
| [20] | XIE Xianming, LI Yinghui. Enhanced Phase Unwrapping Algorithm Based on Unscented Kalman Filter, Enhanced Phase Gradient Estimator, and Path-Following Strategy[J]. Applied Optics, 2014, 53(18): 4049–4060. DOI:10.1364/AO.53.004049 |
| [21] | MARTINEZ-ESPLA J J, MARTINEZ-MARIN T, LOPEZ-SANCHEZ J M. A Particle Filter Approach for InSAR Phase Filtering and Unwrapping[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(4): 1197–1211. DOI:10.1109/TGRS.2008.2008095 |
| [22] | WAGHMARE R G, SUKUMAR P R, SUBRAHMANYAM G R K S, et al. Particle-filter-based Phase Estimation in Digital Holographic Interferometry[J]. Journal of the Optical Society of America A, 2016, 33(3): 326–332. DOI:10.1364/JOSAA.33.000326 |
| [23] | KULKARNI R, RASTOGI P. Simultaneous Estimation of Phase Derivative and Phase Using Parallel Kalman Filter Implementation[J]. Measurement Science and Technology, 2016, 27(6): 065203. DOI:10.1088/0957-0233/27/6/065203 |
| [24] | MORÉ J J.The Levenberg-Marquardt Algorithm:Implementation and Theory[M]//WATSON G A.Numerical Analysis.Berlin:Springer, 1978:105-116. |
| [25] |
侯代文, 殷福亮.
基于迭代中心差分卡尔曼滤波的说话人跟踪方法[J]. 电子与信息学报, 2008, 30(7): 1684–1689.
HOU Daiwen, YIN Fuliang. Iterated Central Difference Kalman Filter Based Speaker Tracking[J]. Journal of Electronics & Information Technology, 2008, 30(7): 1684–1689. |
| [26] |
张鑫春, 郭承军.
均方根嵌入式容积卡尔曼滤波[J]. 控制理论与应用, 2013, 30(9): 1116–1121.
ZHANG Xinchun, GUO Chengjun. Square-root Imbedded Cubature Kalman Filtering[J]. Control Theory & Applications, 2013, 30(9): 1116–1121. |
| [27] |
张鑫春. INS/GNSS深组合导航系统的非线性研究[D]. 成都: 电子科技大学, 2014. ZHANG Xinchun.Research on the Nonlinearity of INS/GNSS Deeply Integration[D].Chengdu:University of Electronic Science and Technology of China, 2014. |
| [28] |
钟何平, 唐劲松, 张森, 等.
利用量化质量图和优先队列的快速相位解缠算法[J]. 武汉大学学报(信息科学版), 2011, 36(3): 342–354.
ZHONG Heping, TANG Jinsong, ZHANG Sen, et al. A Fast Phase Unwrapping Algorithm Based on Quantized Quality Map and Priority Queue[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 342–354. |



