2. 中国测绘科学研究院, 北京 100830;
3. 甘肃省地理国情监测工程实验室, 甘肃 兰州 730070
2. Chinese Academy of Surving and Mapping, Beijing 100830, China;
3. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China
正射影像作为卫星影像最为重要的成果资料之一,在测绘、国土资源管理、地理国情监测中发挥着极为重要的作用。大范围的正射影像往往由多张卫星影像镶嵌合成,受季节、光照、大气条件等影响,同一测区卫星影像镶嵌后在视觉上连续性较差,表现为一张“大花布”,严重影响了影像的使用。针对测绘的卫星影像色彩一致性处理,其目的是在不损坏影像纹理信息、不影响影像地物判读的前提下使测区影像的色调过渡平滑,美观自然。目前,卫星影像色彩一致性处理方法主要有选取参考影像、基于影像重叠区域和建立色彩参考数据库的方法等。
基于参考影像的方法通过在测区选取成像条件良好的影像作为基准,其他影像与该基准影像相匹配以达到改变其色调的目的。文献[1-3]利用Wallis滤波的方法使影像不同区域有相似的均值和方差,匀光软件GeoDodging使用该策略使不同影像的色彩、亮度趋于一致。文献[4-5]采用直方图匹配的方法,通过改变影像直方图的形状使其色调与基准影像一致,这是典型的非线性色彩校正方法。上述方法对于景物内容相似的影像可以取得一定效果,但由于卫星影像覆盖范围广、场景内容差异大,使用上述方法容易造成整体或局部性色偏;基于重叠区域的方法是目前最为主流的处理方式,这类方法根据卫星影像重叠区域建立影像间亮度、色彩的对应关系,对相邻影像进行校正。文献[6]采用重叠区域直方图匹配的方法改变相邻影像的色调。文献[7-8]通过统计相邻影像重叠区域的均值和方差,建立影像间线性关系。文献[9-12]则通过在影像重叠区域提取伪不变特征点(pseudo invariant features,PIF),对相邻影像进行相对辐射校正,但辐射校正的效果与PIF点的质量关系较大,效果不稳定。文献[13]提出使用重叠区域全部像素参与计算,通过寻找“脊”的方式构建影像间的辐射校正关系,该方法对于时相差异较小的影像可以取得一定效果。文献[14-15]则通过对影像自动分割,构建不同地物对应的线性关系,但该方法复杂度较高,并且没有考虑地物变化带来的分割误差。文献[16]采用伽马校正的思路进行色彩校正,通过影像的重叠区域内插出非重叠区域的校正参数对测区影像进行色彩均衡处理,该方法应用于ArcGIS软件的色彩校正模块。文献[17]提出最小二乘区域网平差的匀色方法应用于数字摄影测量软件DPGrid中,但该方法存在计算量大的缺陷。一般经上述方法处理后仍需对影像的接边处平滑过渡处理[18-19],另外,这类方法需要考虑影像间色彩传递顺序[20],计算较为复杂,且色彩传递过程极有可能带来误差累积,导致远离基准位置的影像出现色差,因此上述方法并不适用于大范围卫星影像的色彩一致性处理;建立参考数据库的方法是近年来提出的一种卫星影像色彩一致性处理思路。文献[21-22]通过对不同分辨率、不同季节的卫星影像分割处理,统计各区域均值、方差,建立参考数据库,以此为基础对待处理影像进行色彩平衡,但该方法没有考虑影像中地物的变化,并且收集不同分辨率、不同季节且色彩一致性较好的大范围卫星影像是较为困难的,因此实用性不强。
随着测区范围的增大,覆盖同一测区的影像可能是多源的,由于不同卫星成像机理的差异,影像会呈现出不同的色调。即使卫星种类相同,由于季节、光照和大气条件的不同,影像也会存在明显的色调差异。另外,由于成像系统的不稳定性,某些影像甚至会出现严重的色彩畸变。在实际的测绘生产中,经上述算法处理后通常仍需使用图像处理软件进行大量的人工调色,这种作业模式工作效率低下,且处理效果受作业员主观因素的影响较大,无法适应大范围卫星影像色彩一致性处理要求。本文提出一种以现有或网络公开低分辨率卫星影像为色调基准,对测区内影像进行自动色彩校正的算法,以减小大范围、大时间跨度卫星影像间的色彩差异。
1 利用基准色调底图对卫星影像色彩校正引起卫星影像色调差异的原因可概括为以下几类
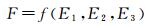 (1)
(1)
式中,E1表示不同季节下由于植被生长状况不同造成影像间色彩分布存在差异[13];E2表示由于光照条件不同或成像系统畸变等原因造成的色调差异;E3表示云雾干扰对影像清晰度和色调的改变。
E1是色彩一致性处理中最复杂的问题,不同季节下植被覆盖区域呈现不同的色调,理论上需要对植被做特殊处理,但是由于植被分布的离散性和随机性,往往无法全自动地对植被准确定位,因此处理较为困难;对于E2,当影像间亮度差异或色彩畸变是整体性发生时,可以通用构建线性模型对其亮度、色彩进行校正,但当这类畸变分布不均匀时,整体构建的线性模型对影像局部并不完全适用;对于E3,云雾干扰会造成影像信息的损失,不同浓度云雾对影像色彩的干扰程度不同,需要针对性处理。实际生产中卫星影像可能受上述多重因素交叉干扰,因此,想要用常规方法解决卫星影像的色彩一致性问题是较为困难的。
在大数据时代,往往可以找到覆盖测区的历史成果数据,这里称这些色彩一致性较好的影像为基准色调底图。本文充分利用基准色调底图与源影像色彩分布的空间相关性,对测区内影像进行自动的色彩校正,使其色调与底图一致,进而消除影像间的色调差异。
1.1 基准色调底图的选取基准色调数据源的选取需要考虑两方面因素:第一,基准色调底图本身的色彩一致性较好,且没有厚云层等非地面物体干扰;第二,基准色调底图分辨率不能过高,低分辨率基准色调底图覆盖同等区域数据量较小,基本可以保证一张影像覆盖测区,不需要分块存储,可用图像处理软件对其进行整体色彩调整,模拟各种季节下的色调。
生产单位往往保存有同一测区的历史影像数据,这些影像入库之前都经过了色彩一致性处理,可作为基准色调底图,如果是高分辨率的影像数据,对其降采样处理即可。另外,互联网上有很多卫星影像数据,如天地图、百度地图、GoogleEarth等都有卫星影像浏览的功能,通过数据流截取的方式可以获得特定区域、特定分辨率的卫星影像数据。GoogleEarth卫星影像以Landsat、Digital Global和NOAA为主要数据源,80m以下低分辨率的影像已经过色彩一致性处理且现势性较好,是理想的基准色调数据。由于本文算法通过滤波的方式提取基准色调影像的低频信息,对于同样的滤波效果,基准色调影像的分辨率越低所需滤波半径成比例减小,相应的计算效率呈几何倍数提升,但如果分辨率过低又会造成对影像色彩变化趋势模拟效果不精细,因此分辨率的选择需要兼顾二者需求。综上,本文推荐使用300m分辨率影像作为基准色调底图。
1.2 影像色彩分布的空间相关性测区内经过几何纠正的卫星影像和覆盖测区的基准色调底图均带有地理坐标,可以实现精确的位置对应。卫星影像都是在较高的轨道获取的,对地观测过程基本是正射向下,因此影像中地物的表现形式基本一致。
在不同的观测尺度下地物表现出不同的观测特性,从小尺度来看地物在迅速变化,如房屋的建设与拆迁、植被的增加与减少等。但在大的观测尺度下,地物的空间分布变化较小,如山体、城市等的空间位置、体积大小等几乎不变。如图 1(a)和图 1(b)分别为降采样源影像和对应区域基准色调底图,前者拍摄于植被枯萎的冬季,山体没有绿色覆盖,后者拍摄于植被覆盖较为丰富的夏季。将二者相减得到图 1(c),其中绿色、黄色和黑色分别是植被、裸露山体和城市在不同季节下的色彩差值,蓝色、红色的噪点是由于地物的变迁引起的色彩差异。这说明不同种类地物的色彩差异有其特定的对应关系,从整体上看图 1(c)的空间分布与图 1(a)和图 1(b)高度相似,表明待处理影像与其对应基准色调底图的色彩分布存在较高的空间相关性。

|
| 图 1 源影像与基准色调底图空间相关性 Fig. 1 The spatical correlation between source image and color reference map |
从频谱角度分析,影像可分解为高频和低频,高频信息是由灰度的尖锐过度造成的,包括影像的粗糙纹理和边缘等,低频信息与影像缓慢变化的灰度分量有关,如影像的色调、背景等[23],即影像的低频信息反映了其色彩的变化趋势。如图 1(d)和图 1(e)为经过低通滤波处理后的影像,排除噪点的干扰后,二者有更好的相关性。图 1(g)和图 1(h)表示低频信息对应梯度方向图,二者空间相似度较高,表明影像低频信息的梯度方向几乎不变,由于影像低频部分较为平滑,局部区域近似一个平面,因此对其整体性的替换不会对影像的高频信息产生干扰。
基于此,本文提出用覆盖测区基准色调底图的低频信息作为色彩控制,将测区内源影像的低频信息用对应区域基准色调底图的低频信息替换,使其呈现与基准色调底图一致的色调,同时可保证相邻影像重叠区域低频信息完全拟合,使相邻影像接边处的色调趋于一致。
2 算法具体流程算法主要包括3部分内容:第一,对影像低通滤波处理,分离影像低频信息;第二,将基准色调底图的低频信息与源影像高频信息合成调色后的影像;第三,计算影像各区域独立的增益系数,对源影像高频信息拉伸处理。
算法主要步骤为:首先,对源影像Isrc降采样处理,使其与低分辨率基准色调底图Iref有相同的分辨率,定义降采样后源影像为Isrcdown;其次,对降采样影像和对应区域的基准色调底图进行高斯滤波处理分离二者的高频和低频信息,用Iref的低频信息Lref替换Isrcdown的低频信息Lsrcdown,重构合成调色后的影像Idstdown,该影像在具有Iref色调的同时具有Isrcdown的纹理信息;再次,提取Iref和Isrcdown的亮度分量,计算得各像素对应的增益系数得到增益系数图a;最后,将Isrcdown、Idstdown和a通过双线性插值的方式分别升采样为Lsrc、Ldst和A,使用图 2中公式计算得到色彩校正后的影像Idst。算法流程如图 2。

|
| 图 2 算法流程 Fig. 2 Algorithm flow chart |
2.1 分离影像低频信息
对影像低通滤波处理可分离影像的低频信息,模拟影像的色彩变化。常用的低通滤波器有均值滤波器、中值滤波器和高斯滤波器等。图 3为示例影像经相同半径的3种滤波器处理后的效果图。经观察,均值滤波器处理后影像的亮部、暗部被强制“压平”,影像的色彩空间分布与源影像的拟合度较低;中值滤波器处理后影像亮度分布会有偏向性,且不同地物交界处梯度较大;高斯滤波处理后影像色调的整体空间分布与源影像一致性较好,且影像色彩过渡较为平滑。相对其他滤波器高斯滤波有其独特的优势:第一,高斯滤波具有旋转不变性;第二,高斯卷积核是线性核,并且是尺度变换唯一的变换核[24];第三,高斯滤波对于去除服从正态分布的噪声效果较好,而自然界的绝大部分噪声符合正态分布。综上,本文选择高斯滤波器分离影像的低频信息。

|
| 图 3 不同滤波器处理效果 Fig. 3 Effect of different filter |
关于高斯滤波器卷积核尺寸的选择也是需要讨论的问题,图 3(a)示例影像大小为107×131像素,图 4为该影像经过不同半径高斯滤波处理后的结果,随着滤波半径的增大影像的模糊度在提高,但同时会造成影像色彩分布与源影像的拟合度降低,因此需要寻求一个使二者综合达到最优的滤波半径。经试验,本文建议使用影像对角线长度的4%左右作为高斯滤波半径,算法实现中也可将此参数作为可调参数允许人工干预,对于图 3(a),滤波半径取5时滤波效果较好。

|
| 图 4 不同滤波半径效果比较 Fig. 4 Effect of different filtering radius |
2.2 对降采样影像色彩校正
源影像的分辨率较高,基准色调底图的分辨率较低,因此需要对源影像进行降采样处理。这里对影像进行大间隔分块,以计算每块均值的方式对其降采样,分块间隔以使降采样后影像的分辨率与基准色调底图分辨率一致为准。
影像的高频和低频信息可用数学模型描述如下
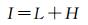 (2)
(2)
式中,I表示影像;L和H分别表示该影像的低频信息和高频信息,则降采样后源影像和对应区域的基准色彩底图可分别表示如式(3)和式
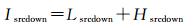 (3)
(3)
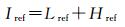 (4)
(4)
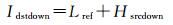 (5)
(5)
分别提取Isrcdown的高频信息和Iref的低频信息,二者相加得到调色后的影像Idstdown,如图 5(c),该影像在具有Isrcdown高频信息的同时其低频信息与Iref完全拟合。

|
| 图 5 对降采样影像色彩校正 Fig. 5 Correct the sample image color |
2.3 构建独立线性模型对源影像色彩恢复
将Isrcdown和Idstdown通过双线性插值的方式升采样到原始影像大小,由于2.2节采用大间隔分块取均值的方式降采样,因此插值得到的影像较为平滑,并且与源影像的拟合度较好,局部可近似代表该区域的均值,可认为二者分别代表源影像和目标影像的低频信息,分别记为Lsrc和Ldst。
相对辐射校正中,认为不同时相的影像之间像素亮度整体满足线性关系
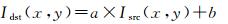 (6)
(6)
式中,Idst(x, y)和Isrc(x, y)分别表示目标影像和源影像在(x, y)处的像素值;a、b作为线性模型中的参数分别表示增益和偏移量。通常a、b是由对应样本点的DN值(eigital number)确定。但由于影像各部分亮度值存在较大差别,整体构建的线性模型影像与各局部并不完全符合,会造成影像间接边处清晰度不同。基于此,本文提出构建影像局部独立线性模型的方案。对于影像的局部范围R,认为该区域所有的像素都满足线性模型,则有式(7),两边同时除以R区域像素个数得式(8)
 (7)
(7)
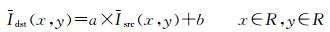 (8)
(8)
式中,Idst(x, y)和Isrc(x, y)分别表示目标影像和待处理影像在对应区域R的亮度均值。另外,假设该局部范围存在的暗色调地物,如山体、房屋的阴影等,这些区域的光线来自于周围地物的漫反射,理论上对这些区域进行颜色校正后其亮度变化不大。即当Isrc(x, y)→0时,有Idst(x, y)→0,代入式(7)得b→0,因此对于该局部区域有
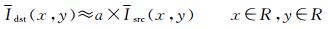 (9)
(9)
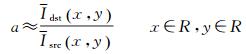 (10)
(10)
以对源影像降采样的分块间隔代表区域R,则增益系数a可根据Isrcdown和Idstdown对应像素的亮度值计算得到。同时为防止对雪地、冰面、云朵等高亮物体拉伸造成灰度值越界产生亮度爆点,规定这些区域增益系数为1,高亮地物的分割阈值通过统计的方式确定,计算影像的亮度平均值,认为大于该平均值3倍的地物为高亮地物。如图 6(a)、(b)分别表示Isrcdown和Idstdown的亮度分布,图 6(c)表示计算得到的增益系数a乘以50得到的分布图,对该影像同样用双线性插值的方式升采样,即可得到与源影像像素对应的增益系数图A。

|
| 图 6 增益系数 Fig. 6 Gain coefficient map |
对式(6)变形可得式
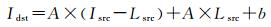 (11)
(11)
由于b相对于A×Lsrc是个微小量,将式(10)代入式(11)可得
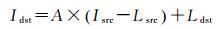 (12)
(12)
根据式(12)计算可得到色彩校正后的影像,即目标影像为高频、低频两部分的组合,其高频信息为经过拉伸的源影像高频信息,其低频信息为色彩校正后的低频信息。如图 7为一组模拟图像信号的示意图,图 7(a)表示源影像模拟信号,其中曲线Lsrc表示源图像低频信息,折线表示其高频信息,图 7(b)表示色彩映射后的影像,其低频信息替换为Ldst,高频信息得到相应拉伸。
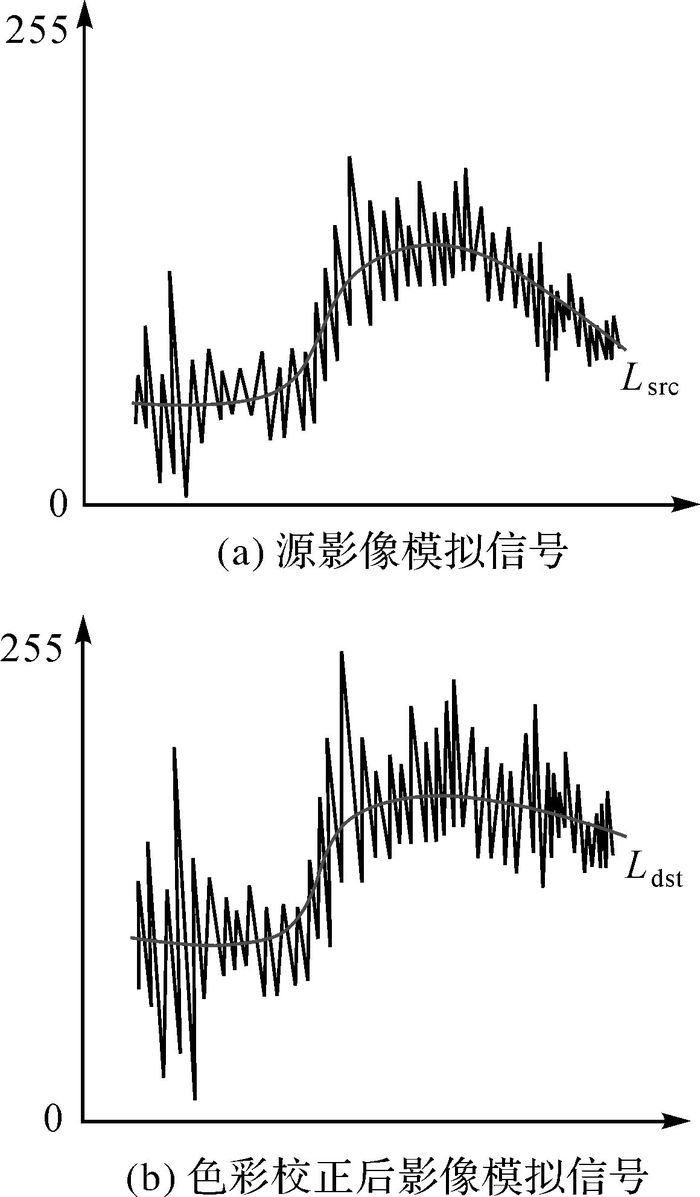
|
| 图 7 模拟影像信号 Fig. 7 Analog image signal |
3 试验分析
本文使用Visual Studio 2010 C++编写程序,对240景高分一号多光谱影像进行色彩一致性处理,计算机CPU型号为Intel(R)Xeon(R) X5650 2.6GHz,内存16GB,耗时34min。试验中对影像的正射纠正和镶嵌处理均使用PixelGrid软件完成。为进行对比试验,本文采用经典的图像回归法(IR,image regression)[26-27],根据源影像与基准色调底图均值、方差构建影像间的线性模型对源影像进行色彩校正。
3.1 试验数据本文选取240景高分一号多光谱影像作为试验数据,覆盖范围包括北京、天津以及河北、山西大部,内蒙古、山东局部近20万km2,分布年份为2013年和2014年,时相分布为5月到次年2月,完整覆盖夏、秋、冬3个季节,如图 8所示。
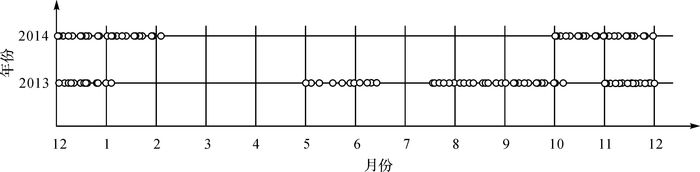
|
| 图 8 影像时相分布 Fig. 8 The time and phase distribution of images |
该测区同时包括植被茂盛和植被稀少的区域,影像质量参差不齐,部分影像存在云雾干扰,个别影像是非常有代表性的大范围、大时间跨度卫星影像色彩一致性测试数据。图 9(a)为覆盖该区域的300m分辨率GoogleEarth影像,仅占用内存29MB,该影像整体色彩分布均衡,绿色的分布范围整体符合该区域植被夏季的空间分布,是理想的基准色调数据。卫星影像和基准色调底图均为WGS-84坐标系统,图 9(b)表示源影像与基准色调底图的叠加示意图。

|
| 图 9 试验数据 Fig. 9 Experimental data |
3.2 试验结果评价与分析 3.2.1 主观评价
图 10(a)为未经处理的原始影像镶嵌结果,相邻影像之间色调差异巨大,影像拼接处存在明显色调差异,部分影像呈现紫色、蓝色、粉红等与实际情况不符的色调,影像间的亮度差异较大。图 10(b)表示IR法处理后的结果,可以发现影像色彩校正结果与对应基准色调底图“贴合度”不高,这是由于不同种类地物对应不同的线性关系,导致影像整体构建的线性模型不准确造成的。图 10(c)表示经本文算法处理后的镶嵌结果。测区内影像的色调得到校正,与对应区域基准色彩底图相一致,整个测区影像的色彩一致性较好,影像接边处不存在明显色调差异,整体符合该测区夏季色彩的空间分布。细节1中个别影像被厚度不均匀的云雾干扰,本文算法处理后,视觉上已不存在明显云雾痕迹,对于受大范围云雾干扰的影像,本文算法可以将其色彩校正为基准色调底图对应的色调,并且可在一定程度上提高其清晰度。细节2展示了在水体拼接处的处理效果,本文算法处理后水体接边处已不存在明显视觉差异。细节3展示了对于亮度差异较大影像的处理效果,影像中存在城区,由于本文算法使用源影像高频信息,因此对源影像的纹理保护较好,即使对于城区边界变化较快的影像,由于本文算法采用较大半径的低通滤波提取影像低频信息,对高频信息变化并不“敏感”,可保证影像城区与非城区的色调平滑过渡。

|
| 图 10 试验结果镶嵌图 Fig. 10 The mosaic result of experiment result |
3.2.2 定量评价
为对处理效果进行定量评价,本文选取几组典型的色彩差异影像对其重叠区域进行统计分析,如表 1。试验1是由于季节原因造成的色调差异,如图 11(a),左半部分影像拍摄于植被较为茂盛的8月并且影像整体偏蓝色,右半部分影像拍摄于农作物收割后的11月整体偏棕色,二者地物类型差别明显,经处理后影像整体色调趋于一致,右侧影像由原来的棕色转变为轻微偏绿,但地物的可辨识度并没有降低,房屋、农田等地物可清晰区分;试验2是由于光照条件的不同造成的色调差异,如图 11(d),上半部分整体偏暗,从表 2中也可看出二者均值差别较大,经处理后上半部分影像亮度有较大提升,整体已不存在亮度差别;试验3是由云雾干扰造成影像之间的色彩差异,如图 11(g),左半部分成像清晰,右半部分影像存在云雾干扰,信息损失严重,经处理后影像清晰度明显提高,色彩得到恢复;试验4是由多种原因综合造成的色调差异,如图 11(j),左半部分影像偏紫色右半部分影像偏棕色,经处理后二者整体色调趋于一致,已不存在明显色调差异。

|
| 图 11 镶嵌效果对比 Fig. 11 Comparison of image mosaic |
| 影像信息 | 影像 | 日期 | 色差原因 |
| 试验1(季节) | 影像1 | 2013-08-14 | 季节不同 |
| 影像2 | 2013-11-23 | ||
| 试验2(光照) | 影像1 | 2013-08-10 | 光照条件差异 |
| 影像2 | 2013-08-10 | ||
| 试验3(云雾) | 影像1 | 2013-11-07 | 云雾干扰 |
| 影像2 | 2014-01-27 | ||
| 试验4(综合) | 影像1 | 2013-09-15 | 成像系统畸变等原因 |
| 影像2 | 2013-09-03 |
试验中分别统计了上述影像重叠区域R、G、B 3个波段的均值、标准差、均方根误差和直方图相似度等参数。均值可以反映影像的整体色调,标准差反映了影像纹理特征的清晰度,二者均是越接近越好;均方根误差可反映影像间纹理的贴合度,按式(13)计算,该参数越小表明二者贴合度越好;直方图相似度可反映影像色彩的整体分布规律,按式(14)计算,该参数越大表示影像重叠区色调越接近。由表 2可看出本文算法处理后重叠区域各项统计指标明显偏好,表明影像的重叠区域色彩分布相似度显著提高。
| 试验结果统计 | 统计指标 | 通道 | 影像1 | 影像2 | IR法处理后 影像1 | IR法处理后 影像2 | 本文方法处理 后影像1 | 本文方法处理 后影像2 |
| 试验1 | 均值 | R | 57.23 | 32.96 | 100.45 | 90.57 | 75.23 | 74.07 |
| G | 45.94 | 35.57 | 107.13 | 94.55 | 80.58 | 79.81 | ||
| B | 45.03 | 55.13 | 82.85 | 72.81 | 62.88 | 62.19 | ||
| 标准差 | R | 14.65 | 20.29 | 25.71 | 44.77 | 21.09 | 28.33 | |
| G | 15.04 | 17.42 | 30.32 | 38.55 | 21.17 | 23.35 | ||
| B | 15.69 | 15.81 | 28.90 | 21.65 | 21.76 | 20.61 | ||
| 均方根误差 | R | 30.64 | 42.31 | 24.04 | ||||
| G | 18.37 | 36.19 | 19.07 | |||||
| B | 16.05 | 22.51 | 15.04 | |||||
| 直方图相似度 | R | 0.27 | 0.81 | 0.72 | ||||
| G | 0.65 | 0.71 | 0.90 | |||||
| B | 0.79 | 0.43 | 0.85 | |||||
| 试验2 | 均值 | R | 12.38 | 36.67 | 55.81 | 63.44 | 48.43 | 47.20 |
| G | 14.96 | 46.02 | 75.13 | 79.27 | 64.42 | 63.53 | ||
| B | 19.97 | 55.56 | 53.31 | 58.97 | 47.32 | 46.59 | ||
| 标准差 | R | 7.51 | 17.18 | 23.16 | 29.93 | 21.18 | 22.92 | |
| G | 6.97 | 17.59 | 24.31 | 30.44 | 18.58 | 21.42 | ||
| B | 4.55 | 11.88 | 10.68 | 12.78 | 13.12 | 15.58 | ||
| 均方根误差 | R | 26.29 | 14.87 | 7.30 | ||||
| G | 32.92 | 14.09 | 7.30 | |||||
| B | 36.41 | 4.66 | 5.59 | |||||
| 直方图相似度 | R | 0.11 | 0.96 | 0.95 | ||||
| G | 0.02 | 0.93 | 0.94 | |||||
| B | 0.08 | 0.93 | 0.93 | |||||
| 试验3 | 均值 | R | 73.42 | 57.19 | 89.07 | 95.36 | 74.86 | 74.54 |
| G | 76.57 | 53.36 | 94.75 | 111.25 | 82.26 | 81.88 | ||
| B | 94.26 | 52.33 | 74.06 | 83.74 | 63.24 | 63.14 | ||
| 标准差 | R | 14.69 | 14.92 | 17.95 | 24.98 | 17.96 | 20.97 | |
| G | 14.22 | 14.32 | 17.74 | 28.26 | 14.15 | 19.56 | ||
| B | 11.46 | 13.57 | 9.13 | 21.83 | 10.79 | 17.03 | ||
| 均方根误差 | R | 18.76 | 16.33 | 10.95 | ||||
| G | 24.94 | 24.13 | 9.95 | |||||
| B | 42.94 | 18.96 | 10.43 | |||||
| 直方图相似度 | R | 0.36 | 0.79 | 0.91 | ||||
| G | 0.12 | 0.72 | 0.97 | |||||
| B | 0.09 | 0.86 | 0.97 | |||||
| 试验4 | 均值 | R | 25.04 | 47.08 | 56.60 | 63.48 | 43.43 | 44.91 |
| G | 21.32 | 46.22 | 58.43 | 75.58 | 58.36 | 60.37 | ||
| B | 27.97 | 70.69 | 55.22 | 63.39 | 44.01 | 46.08 | ||
| 标准差 | R | 19.26 | 23.82 | 39.22 | 32.41 | 34.53 | 31.59 | |
| G | 15.59 | 21.48 | 33.07 | 35.24 | 27.18 | 27.10 | ||
| B | 13.35 | 15.93 | 26.48 | 14.44 | 23.16 | 18.85 | ||
| 均方根误差 | R | 24.33 | 17.90 | 14.76 | ||||
| G | 26.96 | 23.02 | 12.78 | |||||
| B | 43.55 | 18.11 | 11.59 | |||||
| 直方图相似度 | R | 0.13 | 0.49 | 0.85 | ||||
| G | 0.39 | 0.69 | 0.95 | |||||
| B | 0.43 | 0.69 | 0.95 | |||||
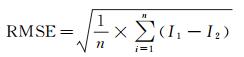 (13)
(13)
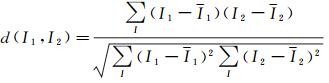 (14)
(14)
针对测绘生产中卫星影像间存在色彩差异的问题,本文提出以色彩一致性较好的现有或网络公开卫星影像作为基准色调底图,对测区影像全自动色彩校正的算法。以对应区域基准色调底图的低频信息替换降采样源影像的低频信息,并且构建影像独立的线性模型对源影像进行色彩恢复处理。选取240景高分一号多光谱影像进行试验,本文算法处理后影像的整体色彩一致性较好,影像接边处不存在明显色调差异。另外该算法不需考虑影像间的位置关系,且不存在色彩传递造成的误差累积问题,适用于大范围、大时相跨度卫星色彩一致性处理。
| [1] |
张力, 张祖勋, 张剑清.
Wallis滤波在影像匹配中的应用[J]. 武汉测绘科技大学学报, 1999, 24(1): 24–27, 35.
ZHANG Li, ZHANG Zuxun, ZHANG Jianqing. The Image Matching Based on Wallis Filtering[J]. Journal of Wuhan Technical University of Surveying and Mapping (Wtusm), 1999, 24(1): 24–27, 35. |
| [2] |
李德仁, 王密, 潘俊.
光学遥感影像的自动匀光处理及应用[J]. 武汉大学学报(信息科学版), 2006, 31(9): 753–756.
LI Deren, WANG Mi, PAN Jun. Auto-Dodging Processing and Its Application for Optical Rs Images[J]. Geomatics and Information Science of Wuhan University, 2006, 31(9): 753–756. |
| [3] | SUN M W, ZHANG J Q. Dodging Research for Digital Aerial Images[J]. International Archives of the Photogrammetry, 2008(37): 349–353. |
| [4] | HORN B K P, WOODHAM R J. Destriping LANDSAT MSS Images by Histogram Modification[J]. Computer Graphics and Image Processing, 1979, 10(1): 69–83. DOI:10.1016/0146-664X(79)90035-2 |
| [5] | WEINREB M P, XIE R, LIENESCH J H, et al. Destriping GOES Images by Matching Empirical Distribution Functions[J]. Remote Sensing of Environment, 1989, 29(2): 185–195. DOI:10.1016/0034-4257(89)90026-6 |
| [6] | HELMER E H, RUEFENACHT B. Cloud-Free Satellite Image Mosaics with Regression Trees and Histogram Matching[J]. Photogrammetric Engineering and Remote Sensing, 2005, 71(9): 1079–1089. DOI:10.14358/PERS.71.9.1079 |
| [7] | CRESSON R, SAINT-GEOURS N. Natural Color Satellite Image Mosaicking Using Quadratic Programming in Decorrelated Color Space[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(8): 4151–4162. DOI:10.1109/JSTARS.2015.2449233 |
| [8] |
肖甫, 吴慧中, 肖亮, 等.
一种光照鲁棒的图像拼接融合算法[J]. 中国图象图形学报, 2007, 12(9): 1671–1675.
XIAO Fu, WU Huizhong, XIAO Liang, et al. An Ambient Light Independent Image Mosaic Algorithm[J]. Journal of Image and Graphics, 2007, 12(9): 1671–1675. DOI:10.11834/jig.20070929 |
| [9] | DE CARVALHO O A, GUIMARÃES R F, SILVA N C, et al. Radiometric Normalization of Temporal Images Combining Automatic Detection of Pseudo-Invariant Features from the Distance and Similarity Spectral Measures, Density Scatterplot Analysis, and Robust Regression[J]. Remote Sensing, 2013, 5(6): 2763–2794. DOI:10.3390/rs5062763 |
| [10] | CANTY M J, NIELSEN A A, SCHMIDT M. Automatic Radiometric Normalization of Multitemporal Satellite Imagery[J]. Remote Sensing of Environment, 2004, 91(3-4): 441–451. DOI:10.1016/j.rse.2003.10.024 |
| [11] | CANTY M J, NIELSEN A A. Automatic Radiometric Normalization of Multitemporal Satellite Imagery with the Iteratively Re-Weighted MAD Transformation[J]. Remote Sensing of Environment, 2008, 112(3): 1025–1036. DOI:10.1016/j.rse.2007.07.013 |
| [12] | YANG Xiaojun, LO C P. Relative Radiometric Normalization Performance for Change Detection from Multi-Date Satellite Images[J]. Photogrammetric Engineering and Remote Sensing, 2000, 66(8): 967–980. |
| [13] |
吴炜, 沈占锋, 李均力, 等.
联合概率密度脊提取的影像镶嵌色彩一致性处理方法[J]. 测绘学报, 2013, 42(2): 247–252.
WU Wei, SHEN Zhanfeng, LI Junli, et al. Ridge of Joint Probability Density Based Color Normalization Method for Image Mosaic[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 247–252. |
| [14] | ZHANG Liangpei, WU Chen, DU Bo. Automatic Radiometric Normalization for Multitemporal Remote Sensing Imagery With Iterative Slow Feature Analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(10): 6141–6155. DOI:10.1109/TGRS.2013.2295263 |
| [15] |
陈旭, 林宏, 强振平.
基于自分类和颜色空间变换的遥感图像色彩校正方法[J]. 遥感学报, 2009, 13(5): 816–826.
CHEN Xu, LIN Hong, QIANG Zhenping. Color Calibration of Remote Sensing Imagery based on Automatic Classification and Color Space Transformation[J]. Journal of Remote Sensing, 2009, 13(5): 816–826. |
| [16] | ZHOU Xiuguang. Multiple Auto-Adapting Color Balancing for Large Number of Images[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2015(XL-7/W3): 735–742. |
| [17] |
孙明伟, 张祖勋, 张剑清. 一种航空遥感影像的最小二乘区域网匀色方法: CN, CN201110044025. 8[P]. 2011-07-20. SUN Mingwei, ZHANG Zuxun, ZHANG Jianqing.Least Square Area Network Color-Homogenizing Method of Aerial Remote Sensing Image:CN, CN201110044025.8[P].2011-07-20. |
| [18] |
王建忠, 肖绍良, 杨云夏.
图像镶嵌及其边界处理[J]. 模式识别与人工智能, 1993, 6(3): 189–195.
WANG Jianzhong, XIAO Shaoliang, YANG Yunxia. Image Mosaic and Its Boundary Problems[J]. Pattern Recognition and Artificial Intelligence, 1993, 6(3): 189–195. |
| [19] |
朱述龙, 钱曾波.
遥感影像镶嵌时拼接缝的消除方法[J]. 遥感学报, 2002, 6(3): 183–187.
ZHU Shulong, QIAN Zengbo. The Seam-line Removal under Mosaicking of Remotely Sensed Images[J]. Journal of Remote Sensing, 2002, 6(3): 183–187. DOI:10.11834/jrs.20020305 |
| [20] | CHEN Chong, CHEN Zhenjie, LI Manchun, et al. Parallel Relative Radiometric Normalisation for Remote Sensing Image Mosaics[J]. Computers & Geosciences, 2014(73): 28–36. |
| [21] | YU Lei, ZHANG Yongjun, SUN Mingwei, et al. Colour Balancing of Satellite Imagery based on A Colour Reference Library[J]. International Journal of Remote Sensing, 2016, 37(24): 5763–5785. DOI:10.1080/01431161.2016.1249306 |
| [22] | ZHANG Yongjun, YU Lei, SUN Mingwei, et al. A Mixed Radiometric Normalization Method for Mosaicking of High-Resolution Satellite Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(5): 2972–2984. DOI:10.1109/TGRS.2017.2657582 |
| [23] | GONZALEZ R C, RAFAEL C, WOODS R E, et al. Digital Image Processing[J]. Prentice Hall International, 1977, 28(4): 484–486. |
| [24] | BURT P J, ADELSON E H. The Laplacian Pyramid as A Compact Image Code[M]. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc, 1987. |
| [25] | LINDEBERG T. Scale-Space Theory:A Basic Tool for Analyzing Structures at Different Scales[J]. Journal of Applied Statistics, 1994, 21(1-2): 225–270. |
| [26] |
丁丽霞, 周斌, 王人潮.
遥感监测中5种相对辐射校正方法研究[J]. 浙江大学学报(农业与生命科学版), 2005, 31(3): 269–276.
DING Lixia, ZHOU Bin, WANG Renchao. Comparison of Five Relative Radiometric Normalization Techniques for Remote Sensing Monitoring[J]. Journal of Zhejiang University (Agriculture & Life Sciences), 2005, 31(3): 269–276. |
| [27] | YANG Xiaojun, LO C P. Relative Radiometric Normalization Performance for Change Detection from Multi-Date Satellite Images[J]. Photogrammetric Engineering and Remote Sensing, 2000, 66(8): 967–980. |
| [28] |
张鹏强, 余旭初, 刘智, 等.
多时相遥感图像相对辐射校正[J]. 遥感学报, 2006, 10(3): 339–344.
ZHANG Pengqiang, YU Xuchu, LIU Zhi, et al. A Study on Relative Radiometric Correction of Multitemporal Remote Sensing Images[J]. Journal of Remote Sensing, 2006, 10(3): 339–344. DOI:10.11947/j.AGCS.2016.20160248 |
| [29] |
韩杰, 谢勇.
GF-1卫星WFV影像间匀色方法[J]. 测绘学报, 2016, 45(12): 1423–1433.
HAN Jie, XIE Yong. Image Dodging Algorithm for GF-1 Satellite WFV Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1423–1433. DOI:10.11947/j.AGCS.2016.20160248 |
| [30] |
张友水, 冯学智, 周成虎.
多时相TM影像相对辐射校正研究[J]. 测绘学报, 2006, 35(2): 122–127.
ZHANG Youshui, FENG Xuezhi, ZHOU Chenghu. Relative Radiometric Correction for Multitemporal TM Images[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 122–127. DOI:10.3321/j.issn:1001-1595.2006.02.006 |



