2. 地理空间信息技术协同创新中心, 湖北 武汉 430079;
3. 数字云冈联合实验室, 山西 大同 037000
2. Collaborative Innovation Center of Geospatial Technology, Wuhan University, Wuhan 430079, China;
3. Laboratory of Digital Yungang; Datong 037000, China
激光扫描技术是高精度三维重建[1-3]的重要手段,能够获取精度优于2 mm的对象表面密集点云,在精密测量[4]、虚拟地理环境[5]、文物保护[6]及虚拟现实[7]等方面应用广泛。扫描对象的完整性是高精度三维重建的基本要求,为了保证对象数据尽可能完整,目前常用方法是:多站扫描和多种扫描仪联合扫描。然而对结构复杂且不可移动的对象如石窟寺、古建筑、雕塑等进行扫描时,往往因为作业空间受限、遮挡严重等问题造成扫描死角,在扫描对象非直视区域出现点云数据缺失和空洞[8],如图 1所示,图(a)中由于佛像不可移动,无法获取佛像背面结构数据,图(b)中由于结构复杂且遮挡严重,无法获取佛像手臂下方结构数据。

|
| 图 1 扫描盲区 Fig. 1 Scanning blind spot |
针对扫描对象的缺失和空洞的问题,研究者提出了基于顶点[9]、基于体素[10]和基于三角网[11]的3大类空洞自动修补方法,主要思路是依据对象表面已有数据的形状走势或结构模式,用曲面逼近的方式等进行空洞填补。这些方法均建立在对象表面连续规律变化的理论基础上,若空洞区域缺失数据过多或者形状不规则,则无法保证填补结果的正确性。文献[12]提出了利用CCD相机和单层反射平面镜辅助激光扫描方法,该方法需要制作带感光标靶的单层平面镜,对镀层平整度和反射率要求极高,制作成本高昂,试验灵活性较小。
本文利用普通平面镜辅助地面三维激光扫描仪的方法对非直视区域进行扫描研究,文章的第1节将重点介绍普通平面镜辅助激光扫描原理,镜面反射系统及物点坐标解算;第2节重点分析球标靶球心坐标拟合试验和多镜面辅助扫描试验,并进行结果精度分析;最后总结试验结果及进一步改进试验。
1 原理与方法普通平面镜辅助相位式或脉冲式激光扫描仪扫描过程中,激光直接到达扫描对象表面形成直视区域激光点云,激光经普通平面镜反射到达扫描对象表面形成非直视区域的反射成像点云,配准[13]融合直视区域激光点云和非直视区域反射成像点云获得扫描对象完整点云。
本文技术路线如图 2所示,首先利用扫描仪对镜面反射系统进行检校,获得镜面与标靶球的相对空间位置关系;然后利用检校数据确定镜面位置,结合球标靶球心坐标,获得反射区域成像点云;再解算反射区域成像点云对应物点坐标,与直射区域激光点云联合获得完整点云。本节将详细分析和研究普通平面镜的反射、折射、玻璃传播对激光光束方向及测距影响的机理,阐述镜面反射系统的设计与检校方法,推导激光扫描经普通平面镜反射像点对应的物点坐标解算方程。
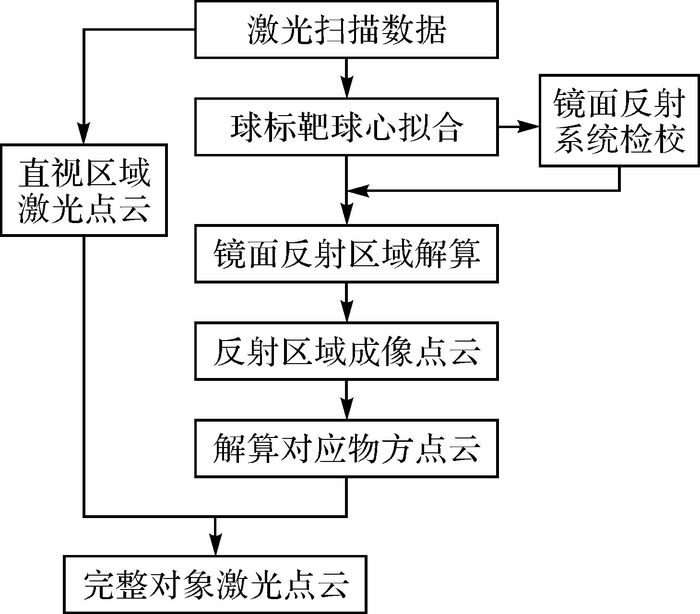
|
| 图 2 技术路线 Fig. 2 Technology of experiment diagram |
1.1 普通平面镜辅助激光扫描原理
理想单层镜面反射激光原理如图 3(a)所示,物点A与点云像点B关于镜面对称,根据单层镜面方程和点云像点B坐标,很容易解算物点A坐标。然而,普通平面镜对光线的影响复杂得多,其原理示意如图 3(b)所示,普通平面镜具有一定厚度的玻璃,激光在传播过程中既有反射也有折射,而且在玻璃媒介中传播速度小于光速,导致扫描仪测得时间变长,根据激光测距原理,点云位置B较像点位置A′更远。
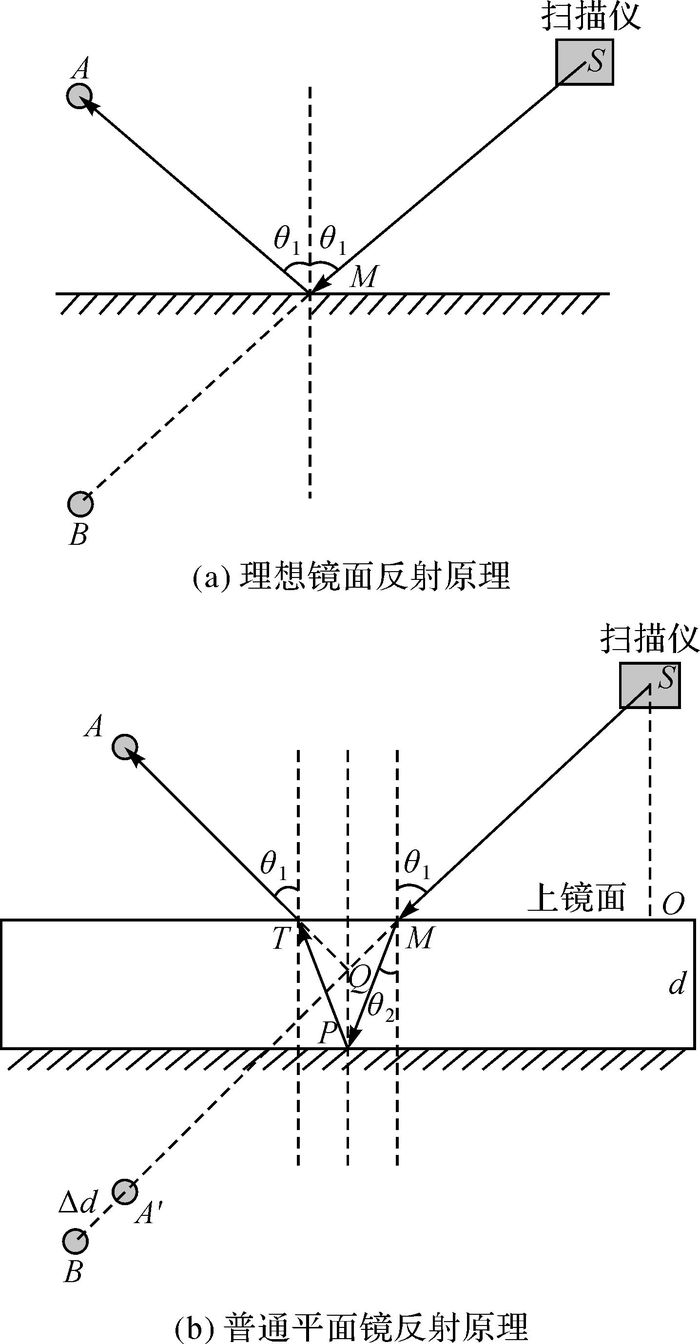
|
| 图 3 理想镜面和普通平面镜反射原理 Fig. 3 Schematicdiagram for ideal and ordinary mirror reflection |
在普通平面镜反射原理图中,本文将上镜面和反射层近似为理想平面,记S为激光发射中心, O为S在上镜面内的投影点, M为激光在上镜面的入射点, P为激光在反射层的反射点, T为激光在上镜面的出射点, A为物点, B为物点A所对应的激光点云,为了便于分析,本文定义入射方向SM与反射方向TA的交点Q为等效反射点。根据原理图中几何关系,解算激光点云B与像点A′之间的距离Δd
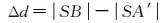 (1)
(1)
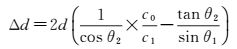 (2)
(2)
式中,θ1为入射角;θ2为折射角;d为普通平面镜厚度;c0为激光在空气中的传播速度;c1为激光在镜子中的传播速度。
1.2 镜面反射系统本文基于普通平面镜和球标靶设计了一套镜面反射系统,如图 4所示,普通平面镜和4个球形标靶通过设计的平板实现刚性连接,镜子设计为圆形,平板外框为方形,为避免镜子中反射的标靶球对扫描产生影响,标靶球固定在平板的四角。普通平面镜具有良好的反射性,其主体材料为玻璃,在工艺上可以较好保证上下镜面的平整度,且造价低廉。球标靶[14-15]广泛应用于脉冲式或相位式地面激光扫描点云数据配准[16-18],其优势在于扫描仪从不同方向均可以获得半球面点云,拟合球面点云获得高精度球心坐标[19]。

|
| 图 4 镜面反射系统 Fig. 4 Mirror reflecting system |
镜面辅助非直视区域研究中,拟合高精度球心坐标是基础,直接影响试验结果精度。为了保证拟合精度,一方面选择高强度PVC材质的球标靶,对激光具有很好的反射性,保证球面点云数量和曲度;另一方面改进拟合算法,利用RANSAC方法[20]初步获取球心坐标与半径,设置半径阈值,剔除较大噪声点,最后利用整体最小二乘法[21-24]拟合球面点云获取球心坐标。
激光束经平面镜反射到达非直视区域,解算非直视区域点云在扫描仪坐标系下坐标,需要确定平面镜的空间几何位置。因此,在激光扫描作业前需检校镜面反射系统参数,建立球标靶和平面镜的相对位置关系,以便在扫描作业中,通过球标靶位置解算得到平面镜位置。
1.2.1 镜面反射系统坐标系镜面反射系统中球标靶和平面镜刚性连接,4个球标靶按照顺时针顺序依次编号,记球标靶球心分别为P1、P2、P3和P4。P1、P3和P4所在平面为球心平面,球心平面与上镜面的相对空间位置保持不变,两平面之间存在确定的旋转矩阵[25-26]和平移距离,为了准确地描述两平面相对位置,本文建立了如图 5所示的镜面反射系统坐标系。
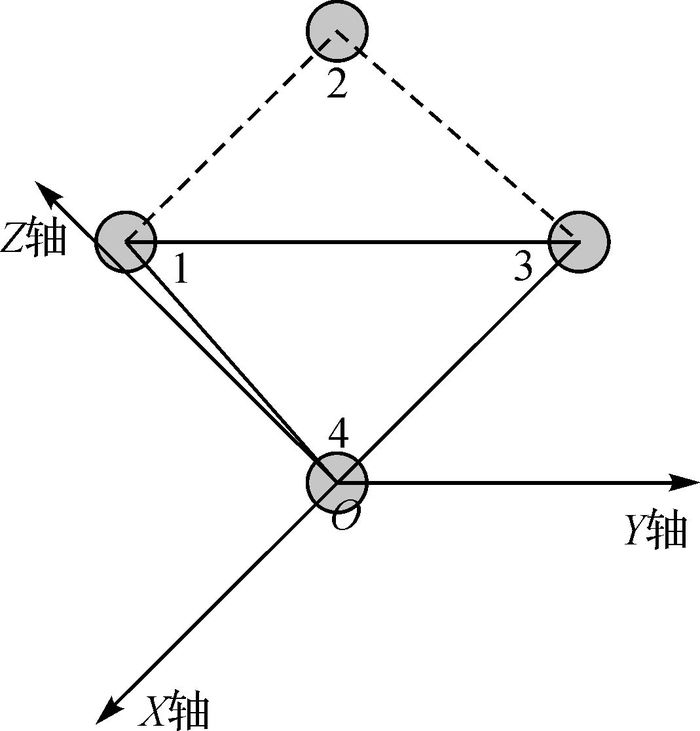
|
| 图 5 镜面反射系统坐标系 Fig. 5 Coordinate system of mirror reflection system |
坐标系以P4为原点,以P3、P4所在方向为X轴方向,计算P1、P3和P4所在平面法向量,取与扫描仪坐标系Z轴方向夹角为锐角的法向量为Y轴,根据左手坐标系原则,在P1、P3和P4平面内计算过原点P4的Z轴,得到Z=X×Y,单位化X、Y、Z轴方向,得到扫描仪坐标系与镜面反射系统坐标系之间的旋转矩阵R
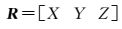 (3)
(3)
镜面反射系统参数包括球心平面与上镜面之间的罗德里格斯[27]旋转矩阵R0和平移距离D,本文借助规格一样且表面反射率很好的球标靶,设计了如图 6所示检校试验。检校步骤:①调节平面镜倾斜角度,将球标靶放置于镜面上,球标靶与上镜面相切;②提取镜面上球标靶点云数据,拟合球心坐标与半径,任意选取3个球心坐标拟合平面,取垂直平面向上的向量为平面法向量,结合球标靶半径解算上镜面方程;③拟合P1、P3和P4所在平面方程,取法向量向上平面方程为球心平面方程;④规定P4为旋转中心,两平面交线为旋转轴,解算旋转矩阵R0, D为旋转中心到上镜面的距离。

|
| 图 6 检校系统参数试验 Fig. 6 Experiment of calibrating system parameter |
根据球心平面法向量V1,上镜面法向量V2,得到交线向量K和向量夹角θ
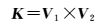 (4)
(4)
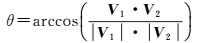 (5)
(5)
以K为旋转轴,θ为旋转角,解算球心平面到上镜面的旋转矩阵R0
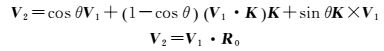
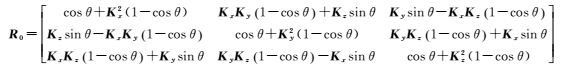
若上镜面方程为A2x+B2y+c2z+D2=0, 则平移距离为
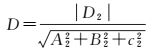 (8)
(8)
根据普通平面镜反射激光原理,如图 3(b),联立上镜面方程与激光束SB,得到入射点M和入射角θ1。|MQ|在上镜面法向量方向上的分量f(θ1)与入射角θ1存在关系
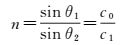 (9)
(9)
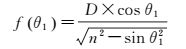 (10)
(10)
随着入射角θ1的变化,f(θ1)的变化梯度为f′(θ1)
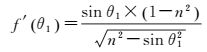 (11)
(11)
式中, n为平面镜折射率;θ1为入射角;θ2为折射角;c0为激光在空气中的传播速度;c1为激光在镜子中的传播速度。镜子的折射率n>1,入射角0≤θ1≤π/2,易得f′(θ1)<0且不为常数,f(θ1)呈非线性减小趋势,故等效反射点Q分布于曲面上,不存在固定的反射平面。
本文采用逐点分析解算激光点云对应物点坐标。解算步骤:①根据普通平面镜折射几何关系,结合折射率n、入射点M及平面镜厚度d,计算等效反射点Q(XQ, YQ, ZQ)及Δd;②确定扫描中心点S在上镜面内的投影点O,理论上,SOMQBA处于同于一个平面,计算SOMQBA平面法向量τ=BS×OS,并单位化τ;③以τ为旋转轴,2θ1为旋转角,旋转QS得到反射方向QA;④将激光点云B校正Δd得到像点A′,满足|QA|=|QA′|,结合反射方向QA,解算物点A坐标
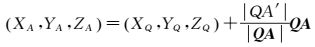 (12)
(12)
本文主要试验器材包括平面镜、球标靶及扫描仪,两块平面镜厚度分别为4.3 mm和4.7 mm,折射率为1.567;扫描仪为FARO Focus 3D X330,距离精度为2 mm,测距噪声为0.5 mm,扫描仪模式设为室内10 m,扫描角度分辨率为0.04°,实际扫描距离为5 m左右。
2.1 球标靶拟合与精度分析精确的标靶球拟合是本方法解算非直视区域激光点精确坐标的保障,本试验对激光扫描标靶球拟合精度进行了评定。如图 7所示为球标靶拟合结果,图 7(a)为球标靶球面点云,良好的球面点云结果是球面准确拟合的基础,图 7(b)为球面拟合结果,拟合球面与球面点云准确重合。本文试验采用两个参数评定球心拟合精度,一是对同一个球标靶点云数据独立拟合n次,计算n个球心坐标的离散中误差,根据离散中误差值评定球心坐标拟合的稳定性;二是保持两个球标靶的位置不变,从不同两个方向扫描球标靶,拟合球心坐标,获得两次扫描下的球心距离差值,独立计算n次球心距离差值,并求取距离差值的均值和中误差,根据均值和中误差评定球心拟合精度。
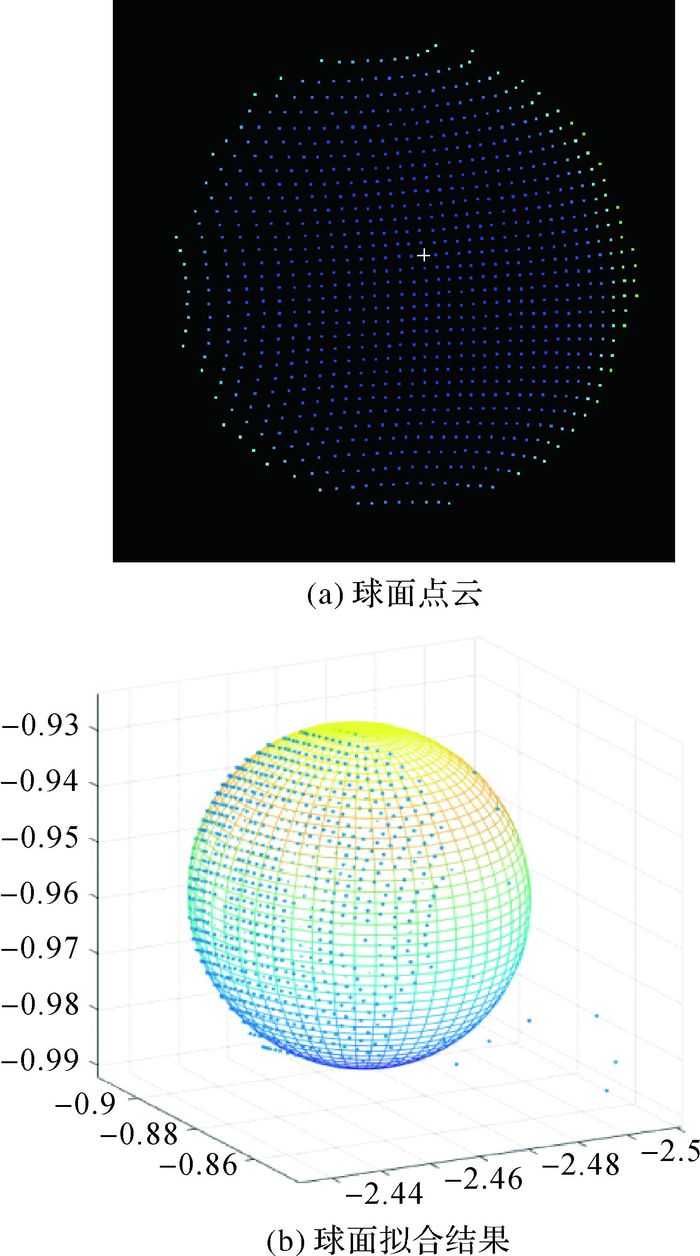
|
| 图 7 球标靶拟合 Fig. 7 Fitting ball target |
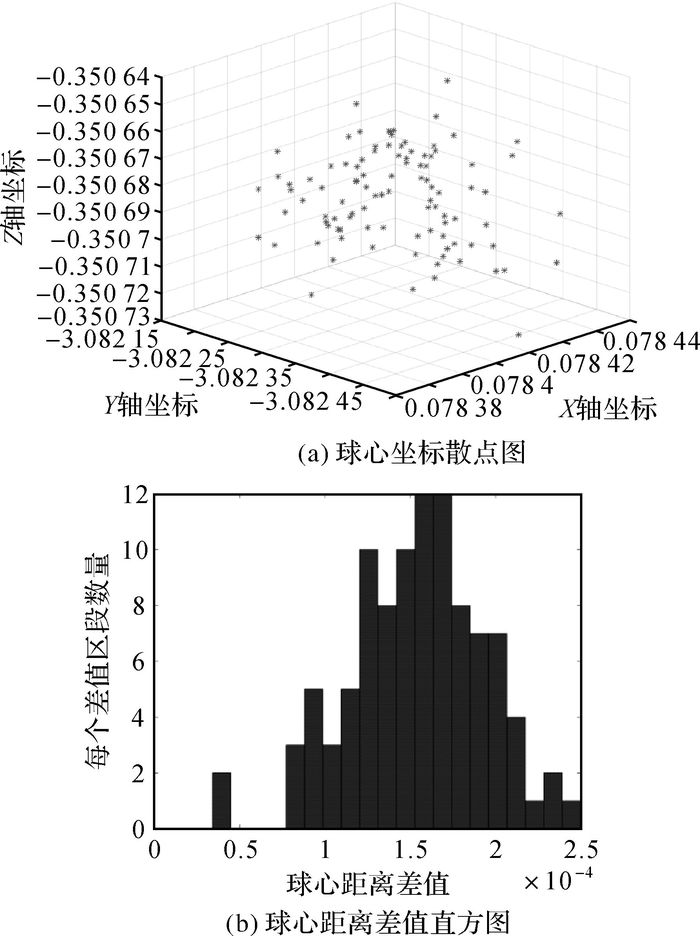
图 8(a)为n次球心坐标散点图,其离散中误差为0.05 mm,说明球心拟合结果足够稳定;图 8(b)为n次球心距离差值直方图,距离差值均值为0.15 mm,说明两站扫描数据中,对同一个球标靶拟合的结果与球心真值差距很小;距离差值中误差为0.04 mm,进一步说明球心坐标拟合结果的稳定性。
|
| 图 8 球标靶球心拟合精度 Fig. 8 Accuracy of fitting the center of ball target |
2.2 镜面系统检校参数分析
镜面系统参数见表 1所示,旋转矩阵与单位矩阵非常接近,说明球心平面和上镜面之间存在很小的夹角,并且平移量与球半径差别在1 mm以内。检校镜面系统参数的关键在于获取准确的上镜面位置,在2.1节中高精度拟合球标靶的保证下,为了验证3个球心所在平面与上镜面平行,检校试验选择4个球标靶放置于镜面上,如图 6所示,依次计算一个球心到另外3个球心所在平面的距离值,结果见表 2所示,4个球心半径差别小于0.3 mm,且距离值均在0.3 mm左右,说明3个球心所在平面与上镜面保持平行,平移平均半径距离获取的上镜面是准确的,验证了镜面系统检校参数的准确性。
| 旋转矩阵 | 平移量/mm | ||
| 0.999 99 | 0.002 28 | 1.76×10-6 | 30.543 |
| -0.002 28 | 0.999 99 | 0.001 55 | |
| 1.76×10-6 | -0.001 55 | 0.999 99 | |
| 1号球 | 2号球 | 3号球 | 4号球 | |
| 半径/mm | 29.6 | 29.6 | 29.8 | 29.9 |
| 距离/mm | 0.28 | 0.34 | 0.21 | 0.24 |
2.3 平面镜辅助激光扫描
为验证平面镜辅助激光扫描方法,本文利用一尊长宽高尺寸为14×18×31 cm的佛像头部塑像为对象设计了两组试验,分别验证平面镜辅助扫描获取被遮挡细节部位的空洞区域几何数据(试验1)和在平面镜辅助下获取完整佛像头部完整三维几何数据(试验2)。
试验1如图 9(a)所示,调整平面镜系统俯仰角,使扫描仪与佛头鼻孔部位形成通视。利用一站数据同时获取佛像头部主体部分几何数据与用平面镜反射辅助获取佛像头部细节几何数据。

|
| 图 9 佛头扫描试验图 Fig. 9 Scanning data of Buddha head |
针对试验2,传统办法是至少设置3站以上扫描站,然后配准融合扫描数据,得到完整佛头数据,本试验采用本文提出的镜面辅助激光扫描方法,通过一站扫描获取佛像头部完整数据。试验2如图 9(b)所示,平面镜分别置于佛头左后侧和右后侧,调整镜面位置及俯仰角,使扫描仪通过镜面与佛头背部形成通视,保证3个方向获得的点云数据具有一定的重叠度。
图 10为试验2点云数据,蓝色点云为1号镜面反射激光点云,黄色点云为2号镜面反射激光点云,红色点云为解算蓝色点云对应物点坐标,绿色点云为解算黄色点云对应物点坐标。图 11分别为佛头点云数据和对应模型数据。

|
| 图 10 佛头扫描点云及解算镜面反射点云 Fig. 10 Point clouds of Buddha head and result of solving reflected point clouds |

|
| 图 11 佛头数据 Fig. 11 Data of Buddha head |
2.4 平面镜辅助扫描结果分析
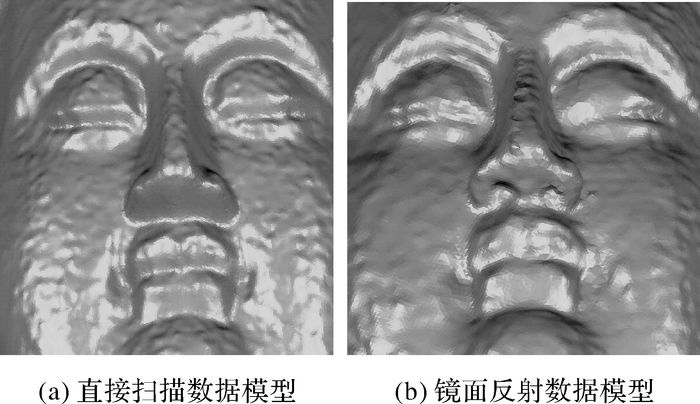
扫描试验1结果如图 12所示,图(a)为扫描仪直接获取面部三维模型,由于扫描空间限制,无法获取佛头鼻孔部位准确的三维模型;图(b)为采用平面镜辅助扫描方法获取的佛头鼻孔部位准确的三维模型。
|
| 图 12 佛头鼻子结构对比 Fig. 12 Comparison of Buddha nose structure |
针对试验2中,扫描仪直接获取的数据是佛头正脸部分,解算反射区域数据获取的是佛头背面两侧部分,本文从如下3个方面评定实验结果精度。
(1) 比较反射区域数据与直接获取数据在对象表面结构的差异。试验中以扫描仪直接获取数据为准。激光扫描的目的在于准确获取对象表面结构数据,图 13为佛头额头右侧模型,图(a)为扫描仪直接获取数据模型,图(b)为解算镜面反射数据生成的模型,比较两种方式下的佛头右侧表面结构,模型细节差异较小,因此镜面辅助扫描可以很好地保留对象表面的复杂结构。

|
| 图 13 佛头表面结构对比 Fig. 13 Comparison of Buddha head structure |
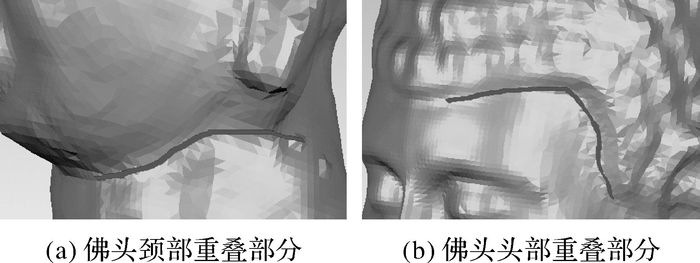
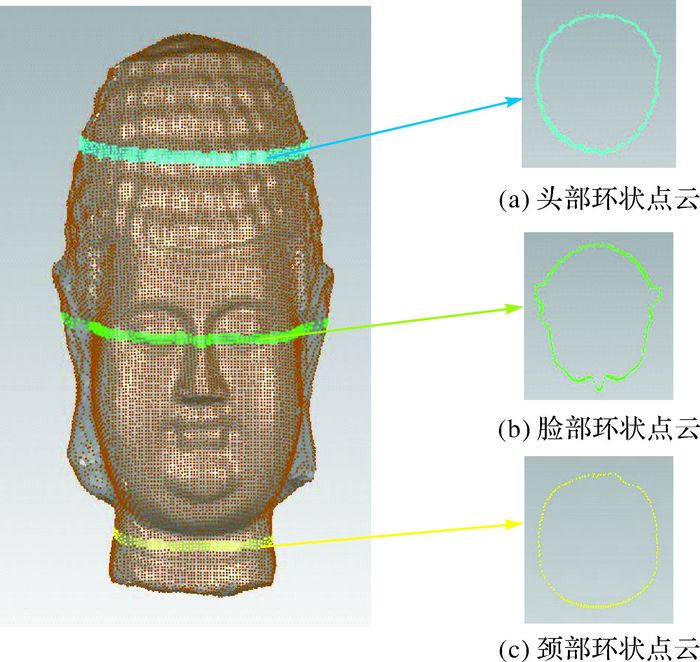
(2) 直观分析反射区域与直接获取区域在公共部分的重合情况。理论上,两种方式获得的数据在公共部分完全重合。如图 14所示,佛头在颈部和额头处的几何走势一致;本试验也选取佛头模型头部、脸部和颈部点云数据,分析公共部分的点云重合情况,结果如图 15所示,直接获取区域点云与反射区域点云在公共部分重叠情况良好。
|
| 图 14 佛头模型公共部分重叠情况 Fig. 14 Common part of Buddha head mode overlap |
|
| 图 15 佛头点云切面比较 Fig. 15 Comparison of Buddha head section points |
(3) 定量分析试验结果几何精度。在保证球标靶球心拟合精度的前提下,本文采用如图 16(a)所示的球标靶设计,解算结果如图 16(b)所示,拟合镜面反射球心坐标为(-0.007 1,-1.007 3,-0.287 6),直接扫描球面球心坐标为(-0.007 3,-1.007 2,-0.287 8),球心距离误差为0.3 mm,相对于激光扫描仪测距精度2 mm和噪声误差0.5 mm的精度水平,本文方法解算结果已达到足够精度。

|
| 图 16 验证解算结果精度试验 Fig. 16 Experiment for verifying the accuracy of result |
3 结论与展望
本文提出了一种普通平面镜辅助的地面三维激光扫描方法,通过镜面辅助扫描可以很好的解决地面三维激光扫描存在的死角和空洞,特别对表面存在不规则变化的非直视区域具有明显优势。研究了普通平面镜反射激光扫描测量原理,设计了镜面反射系统,提出了镜面系统检校方法,推导了激光镜面成像点的对象物点坐标解算方法,并进行了试验验证。笔者将从以下几个方向展开进一步研究:基于光学反射镜面设计镜面反射系统,表面更加平整,激光反射中散射、能量损失更小,有望获得更高精度;基于不同曲率的镜面进行研究,扩展镜面辅助激光扫描的应用范围。
| [1] |
谷晓英. 三维重建中点云数据处理关键技术研究[D]. 秦皇岛: 燕山大学, 2015. GU Xiaoying.Research on the Key Technologies of Point Clouds Processing in 3D Reconstruction[D].Qinhuangdao:Yanshan University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10216-1015901965.htm |
| [2] |
杨宇, 阚凌雁, 于佳, 等.
基于激光扫描的人脸三维重建方法[J]. 红外与激光工程, 2014, 43(12): 3946–3950.
YANG Yu, KAN Lingyan, YU Jia, et al. Face 3D Reconstru-ction Based on Laser Scanning System[J]. Infrared and Laser Engineering, 2014, 43(12): 3946–3950. DOI:10.3969/j.issn.1007-2276.2014.12.018 |
| [3] |
潘建刚. 基于激光扫描数据的三维重建关键技术研究[D]. 北京: 首都师范大学, 2005: 33-34. PAN Jiangang.The Research of The Key Problems of 3D Reconstruction from Laser Scan Data[D].Beijing:Capital Normal University, 2005:33-34. http://d.wanfangdata.com.cn/Thesis/W026198 |
| [4] |
李珵, 卢小平, 朱宁宁.
三维激光扫描隧道断面形变监测精度验证[J]. 测绘通报, 2013(S1): 69–72.
LI Cheng, LU Xiaoping, ZHU Ningning. Verification of Accuracy of Tunnel Section Deformation Monitoring by 3D Laser Scanning[J]. Bulletin of Surveying and Mapping, 2013(S1): 69–72. |
| [5] | DU Jie, CHEN Xiaoyong, FUMIO Y. Generation of 3D Virtual Geographic Environment Based on Laser Scanning Technique[J]. Geo-Spatial Information Science, 2003, 6(3): 37–42. DOI:10.1007/BF02826891 |
| [6] |
周俊召, 郑书民, 胡松, 等.
地面三维激光扫描在石窟石刻文物保护测绘中的应用[J]. 测绘通报, 2008(12): 68–69.
ZHOU Junzhao, ZHENG Shumin, HU Song, et al. Application of Ground 3D Laser Scanning in The Inspections of Stone Carvings[J]. Bulletin of Surveying and Mapping, 2008(12): 68–69. |
| [7] |
李晖, 吴禄慎.
三维激光扫描技术在虚拟现实中的应用[J]. 南昌大学学报(工科版), 2007, 29(3): 239–242.
LI Hui, WU Lushen. Application of 3D Laser Scan Technology in Virtual Reality[J]. Journal of Nanchang University(Engineering & Technology), 2007, 29(3): 239–242. |
| [8] |
陆旻丰, 吴杭彬, 刘春, 等.
地面三维激光扫描数据缺失分类及成因分析[J]. 遥感信息, 2013, 28(6): 82–86.
LU Minfeng, WU Hangbin, LIU Chun, et al. Classification and Cause Analysis of Terrestrial 3D Laser Scanning Missing Data[J]. Remote Sensing Information, 2013, 28(6): 82–86. |
| [9] |
陈志杨, 张三元, 叶修梓.
点云数据中空洞区域的自动补测算法[J]. 计算机辅助设计与图形学学报, 2005, 17(8): 1793–1797.
CHEN Zhiyang, ZHANG Sanyuan, YE Xiuzi. An Algorithm for Automatic Filling of Holes of Point Cloud in Reverse Engineering[J]. Journal of Computer-Aided Design & Computer Graphics, 2005, 17(8): 1793–1797. |
| [10] | JU Tao. Robust Repair of Polygonal Models[J]. ACM Transactions on Graphics (TOG), 2004, 23(3): 888–895. DOI:10.1145/1015706 |
| [11] | ZHAO Wei, GAO Shuming, LIN Hongwei. A Robust Hole-Filling Algorithm for Triangular Mesh[J]. The Visual Computer, 2007, 23(12): 987–997. DOI:10.1007/s00371-007-0167-y |
| [12] | FASANO A, CALLIERI M, CIGNONI P, et al.Exploiting Mirrors for Laser Stripe 3D Scanning[C]//Proceedings of the 4th International Conference on 3-D Digital Imaging and Modeling.Banff, Alta., Canada:IEEE, 2003:243-250. |
| [13] |
陈阳. 三维点云数据配准方法研究[D]. 天津: 天津大学, 2013. CHEN Yang.Research on Registration of 3D Point Cloud[D].Tianjin:Tianjin University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10056-1015017588.htm |
| [14] |
贾东峰, 程效军, 刘燕萍.
球标靶在点云数据配准中的应用分析[J]. 工程勘察, 2011, 39(9): 64–68.
JIA Dongfeng, CHENG Xiaojun, LIU Yanping. Research on The Application of Target Balls in Registration of Point Clouds[J]. Geotechnical Investigation & Surveying, 2011, 39(9): 64–68. |
| [15] |
姚吉利, 马宁, 贾象阳, 等.
球形标靶的固定式扫描大点云自动定向方法[J]. 测绘学报, 2015, 44(4): 431–437.
YAO Jili, MA Ning, JIA Xiangyang, et al. An Approach for Automatic Orientation of Big Point Clouds from the Stationary Scanners Based on the Spherical Targets[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 431–437. DOI:10.11947/j.AGCS.2015.20130357 |
| [16] |
肖博文. 基于平面提取的三维点云点配准算法研究[D]. 北京: 中国科学院大学(工程管理与信息技术学院), 2016. XIAO Bowen.3D Point Cloud Registration Algorithm Based on Plane Extraction[D].Beijing:University of Chinese Academy of Sciences (School of Engineering Management and Information Technology), 2016. |
| [17] |
常江. 基于特征匹配的三维点云配准算法研究[D]. 太原: 中北大学, 2015. CHANG Jiang.Algorithm Research of Third Point Cloud Registration Based on Feature Matching[D].Taiyuan:North University of China, 2015. http://d.wanfangdata.com.cn/Thesis/D640784 |
| [18] |
周朗明, 郑顺义, 黄荣永.
旋转平台点云数据的配准方法[J]. 测绘学报, 2013, 42(1): 73–79.
ZHOU Langming, ZHENG Shunyi, HUANG Rongyong. A Registration Algorithm for Point Clouds Obtained by Scanning Objects on Turntable[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 73–79. |
| [19] |
张毅, 闫利, 杨红, 等.
地面激光扫描球形标靶的球心误差研究[J]. 武汉大学学报(信息科学版), 2012, 37(5): 598–601.
ZHANG Yi, YAN Li, YANG Hong, et al. Spherical Center Error of Sphere Target in TLS[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5): 598–601. |
| [20] | SCHNABEL R, WAHL R, KLEIN R. Efficient RANSAC for Point-Cloud Shape Detection[J]. Computer Graphics Forum, 2007, 26(2): 214–226. DOI:10.1111/cgf.2007.26.issue-2 |
| [21] |
龚循强, 李志林.
稳健加权总体最小二乘法[J]. 测绘学报, 2014, 43(9): 888–894, 901.
GONG Xunqiang, LI Zhilin. A Robust Weighted Total Least Squares Method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9): 888–894, 901. DOI:10.13485/j.cnki.11-2089.2014.0140 |
| [22] |
袁豹, 岳东杰, 赵元忆, 等.
基于稳健加权总体最小二乘法的地面三维激光扫描球型标靶定位[J]. 勘察科学技术, 2013(1): 19–22.
YUAN Bao, YUE Dongjie, ZHAO Yuanyi, et al. Spherical Target Positioning of Terrestrial 3D Laser Scanning Based on Robust Weighted Total Least Squares Method[J]. Investigation Science and Technology, 2013(1): 19–22. |
| [23] |
鲁铁定, 周世健, 张立亭, 等.
基于整体最小二乘的地面激光扫描标靶球定位方法[J]. 大地测量与地球动力学, 2009, 29(4): 102–105.
LU Tieding, ZHOU Shijian, ZHANG Liting, et al. Sphere Target Fixing of Point Cloud Data Based on TLS[J]. Journal of Geodesy and Geodynamics, 2009, 29(4): 102–105. |
| [24] |
官云兰, 詹新武, 程效军, 等.
一种稳健的地面激光扫描标靶球定位方法[J]. 工程勘察, 2008, 36(10): 42–45, 49.
GUAN Yunlan, ZHAN Xinwu, CHENG Xiaojun, et al. A Robust Method for Determination of Registration Sphere in Terrestrial Laser Scanner[J]. Geotechnical Investigation & Surveying, 2008, 36(10): 42–45, 49. |
| [25] |
谭燕, 邹峥嵘.
近景摄影测量中不测定初始值的旋转矩阵构成方法研究[J]. 测绘科学, 2009, 34(5): 28–31.
TAN Yan, ZOU Zhengrong. A Research of the Consruction of Rotation Matrix Without Approximate Values in Close-Rang photogrammetry[J]. Science of Surveying and Mapping, 2009, 34(5): 28–31. |
| [26] |
江刚武, 姜挺, 丁静, 等.
直接利用旋转矩阵进行空间后方交会的原理和方法[J]. 测绘科学技术学报, 2009, 26(1): 15–19, 23.
JIANG Gangwu, JIANG Ting, DING Jing, et al. Principle and Method of Space Resection Using Orientation Matrix[J]. Journal of Geomatics Science and Technology, 2009, 26(1): 15–19, 23. |
| [27] |
姚吉利, 韩保民, 杨元喜.
罗德里格矩阵在三维坐标转换严密解算中的应用[J]. 武汉大学学报(信息科学版), 2006, 31(12): 1094–1096, 1119.
YAO Jili, HAN Baomin, YANG Yuanxi. Applications of Lodrigues Matrix in 3D Coordinate Transformation[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1094–1096, 1119. |



