2. 大地测量与地球动力学国家重点实验室, 湖北 武汉 430077
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China
精密单点定位(PPP)是一种无需基准站、作业模式灵活、成本低、精度高的定位技术[1-2]。PPP技术利用高精度的卫星轨道和钟差及相关信息,通过精确的误差改正模型和合理的参数估计方法,为全球导航卫星系统用户提供厘米级的定位服务[3-4]。近年来,BDS系统已在亚太地区全面提供定位、导航和授时(PNT)服务,并计划于2020年完成全球覆盖的星座组建。同时,GPS系统也加快了现代化进程,使系统面向多频化、多样化应用等方面发展。随着GNSS高速发展,其应用也逐步向多系统、多频率兼容互操作的方向转变,而多系统融合的PPP能更好地发挥多系统联合定位的优势,提高定位服务的可用性和可靠性[5-8]。因此,深入研究不同的PPP函数模型有助于掌握提高PPP精度和缩短收敛时间的关键因素,也是拓展新的应用领域的重要基础。
按照电离层处理方式不同,PPP函数模型主要包括无电离层组合模型、估计电离层的非组合模型(UC)和电离层加权模型(ionosphere-weighted,IW)。无电离层组合模型包括传统的相位与伪距频率间的组合(ionosphere-free,IF)[4, 9-10]和Uofc模型。Uofc模型保留IF模型中相位组合并引入两个同频率伪距与相位的无电离层组合[11-13]。相比于IF模型,Uofc模型具有观测噪声小,且保留各频率上模糊度信息等优势。但是Uofc组合导致观测值之间存在相关性,且未知参数增多。研究表明,Uofc模型与非组合模型可利用能消除电离层的满秩转换矩阵进行等价变换[10, 14-15]。另外,也有学者指出采用原始观测值并将电离层延迟参数化的UC模型,除了具有保留原始观测信息和具有更小的观测噪声等优势之外,还可以充分考虑电离层的时空相关信息构建约束函数模型[16-18]。随着对电离层特性的深入研究和电离层建模精度的不断提高,顾及电离层约束的IW模型能有效且合理地增强函数模型强度、缩短收敛时间并改善定位精度[19]。
近年来,大量研究都是针对某一特定的函数模型来分析PPP的效果,鲜有文献从函数模型参数之间相关特性的角度进行深入探讨,系统性地比较3种PPP函数模型。本文从理论上详细地研究每种函数模型各类参数之间相关特性,给出3种PPP函数模型(IF模型、UC模型及IW模型)的独立参数化方式,系统性地分析3种模型相互关系,最后给出双系统定位的参数化处理方案。本文利用GPS单系统和GPS+BDS组合PPP算例分析验证理论的正确性。
1 3种PPP函数模型 1.1 非组合(UC)模型观测s颗卫星的双频单历元UC观测方程和随机模型为
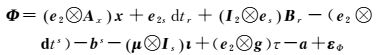 (1a)
(1a)
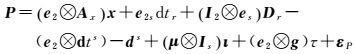 (1b)
(1b)
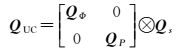 (1c)
(1c)
式中,Φ和P表示扣除测站海潮、固体潮、相对论效应、相位缠绕等误差改正的相位和伪距观测值;x为测站坐标改正数,对应的系数阵为Ax;dtr、Br=[B1,B2]T和Dr=[D1,D2]T分别表示接收机钟差、相位和伪距接收机硬件延迟,Bi、Di分别表示频率fi的相位和伪距接收机硬件延迟;dts=[dt1,dt2,…,dts]T、bs=[b1T,b2T]T和ds=[d1T,d2T]T分别表示s颗卫星钟差、相位和伪距卫星硬件延迟,其中,bi=[bi1,bi2,…,bis]T、di=[di1,di2,…,dis]T,bij和dij表示频率fi的第j颗卫星的相位和伪距硬件延迟;ι=[ι1,ι2,…,ιs]T和τ分别表示s颗卫星的电离层延迟和天顶对流层延迟,对应的系数阵分别为μ=[1,f12/f22]T和g=[g1,g2,…,gs]T;aT=[a1T,a2T]是双频的模糊度,ai=[ai1,ai2,…,ais]T,aij表示频率fi的第j颗卫星的模糊度;εΦ和εP为相位和伪距观测噪声,对应的方差因子阵为QΦ=diag(σΦ12,σΦ22)和QP=diag(σP12,σP22);Qs是不同卫星的观测信息的协因数阵;es为全部元素为1的s维列向量;Is是s维单位矩阵;运算符号⊗表示克罗内克积。
1.2 无电离层组合模型(IF)无电离层组合模型的观测方程是对式(1a)和(1b)两边左乘一个组合转换矩阵
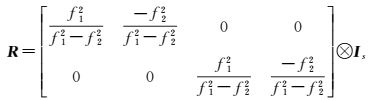
设无电离层组合系数阵为
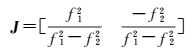
则IF组合观测方程为
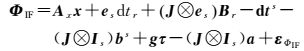 (2a)
(2a)
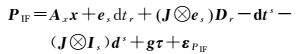 (2b)
(2b)
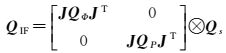 (2c)
(2c)
式中,ΦIF和PIF分别表示IF相位和伪距观测量;εΦIF和εPIF分别为对应的观测噪声;QIF为对应的方差-协方差矩阵。
1.3 顾及电离层信息的加权模型(IW)UC模型与IF模型对电离层延迟误差的处理方式不同,UC模型将电离层延迟作为参数估计,而IF模型将它们通过观测值组合消除。随着对电离层特性的深入研究,通过引入外部的电离层信息或通过电离层建模形式对电离层延迟参数进行约束,能有效地增强UC模型的强度,进而改善模糊度的固定效率和提高定位精度[20]。
一般说来,电离层延迟误差引起的信号群延迟、多普勒频移等问题是影响GNSS精密定位的主要因素之一[21-22]。对于单频GNSS用户可以采用电离层模型消除电离层延迟,如Kloubuchar全球经验模型[21-22]。该模型的参数可从广播星历中获取,实时改正,操作方便。但由于电离层变化复杂,在不同的纬度特别是赤道和高纬度地区,影响十分显著,所以修正精度较差。相关研究指出,Kloubuchar模型的改正程度仅约为55%[23]。另外,IGS组织利用长期的全球跟踪站反演电离层信息,为用户提供二维或三维的全球格网电离层改正信息,构建全球电离层改正模型[24]。目前,IGS提供的最终电离层产品精度可以达到2~8 TECU,即为用户提供分米级的电离层改正[25]。因此,不同的电离层模型提供不同精度的电离层误差改正,对定位的收敛时间有显著的影响。
IW模型以UC模型(1)为基础,在此基础上对电离层延迟参数附加伪观测方程
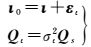 (3)
(3)
式中,ι0=[ι01,ι02,…,ι0s]为电离层延迟伪观测值,可用采用经验电离层模型计算或者直接采用IGS提供的全球格网产品的内插结果;ει表示伪观测值噪声;Qι为对应的方差-协方差矩阵;σι为电离层延迟伪观测信息对应的精度,对应采用电离层模型或者产品的精度。
2 PPP模型的独立参数化从式(1)可以看出,UC模型的钟差、硬件延迟、电离层延迟及模糊度等参数之间存在明显的相关性,从而导致观测方程设计矩阵秩亏。而式(2)给出的IF模型同样由于参数相关而引起设计矩阵秩亏。通常有两种解决设计矩阵秩亏问题的方法,第1种方法是引入适当的外部基准,进而独立求解各类参数;第2种方法是采用合理的独立参数化方法,构造相互独立的参数进行求解。下面详细分析每个模型的参数相关性,并给出每个函数模型的独立参数化方式。
2.1 3种模型的独立参数化由于IW模型只是在UC模型基础上增加了电离层约束信息,其独立参数化方式与UC模型相同,因此这里只讨论UC模型和IF模型的独立参数化方式。
2.1.1 UC模型的独立参数化式(1)给出了具体参数化的UC模型,下面讨论各类参数的处理方式。首先讨论卫星钟差与卫星硬件延迟的处理方式。PPP采用的IGS发布的精密卫星钟差dtIFs中包含IF卫星伪距硬件延迟[9],即
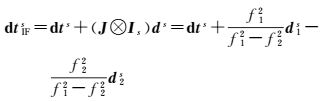 (4)
(4)
引入d12s=d2s-d1s表示两个频率间的卫星伪距硬件延迟偏差,则不同频率卫星钟差与dtIFs和d12s的关系为
 (5a)
(5a)
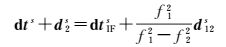 (5b)
(5b)
式中,卫星DCB和精密卫星钟差可从IGS发布的相应产品获取改正[26]。
下面讨论接收机钟差、接收机硬件延迟及电离层延迟的相关性及相应的处理方式。显然,Dr与dtr完全线性相关,所以只能合并估计,即新的接收机钟差为dtr=e2dtr+Dr。同时考虑到新的接收机钟差dtr与电离层延迟ι系数阵的相关关系
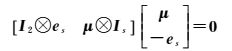
即dt′r与ι的系数阵之间秩亏且秩亏数为1,故需要减少1个接收机钟差或电离层延迟以保证待估参数相互独立。经公式推导且方便程序实现,本文通过减少1个接收机钟差来消除秩亏,用IF钟差dtrIF代替两个频率的接收机钟差,相应地电离层参数变为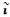
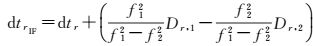 (6a)
(6a)
 (6b)
(6b)
式中,D12=Dr,2-Dr,1表示两个频率间接收机伪距硬件延迟偏差。
最后讨论模糊度与硬件延迟的独立参数化方式。经过上述参数处理后,考虑到a与bs、ds完全线性相关,且顾及Br、Dr与a系数阵的相关关系

需要将硬件延迟与模糊度合并估计。整理合并后,构造新的模糊度aUC形式如下
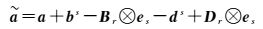 (7)
(7)
所以,经上述各项参数之间相关性探讨,构造了相互独立的待估参数,将式(5a)、式(5b)、式(6)和式(7)代入式(1),整理后得独立参数化后的UC模型
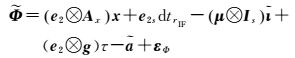 (8a)
(8a)
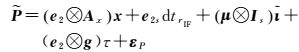 (8b)
(8b)
式中,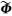
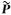
式(2)中,卫星钟差及卫星硬件延迟的形式与式(4)相同,可以通过直接引入精密卫星钟差改正。IF模型构造的接收机钟差与UC模型相同,即式(6a)。令无电离层组合模糊度aIF为
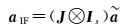 (9)
(9)
将式(6a)和式(9)代入式(2)整理后,得到独立参数化后的IF模型如下
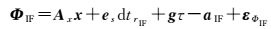 (10a)
(10a)
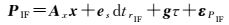 (10b)
(10b)
显然,式(10)中IF组合无法估计各频率上独立的模糊度。
2.2 3种模型的关系为方便阐述函数模型之间的关系,将独立参数化后的UC模型式(8)表示为
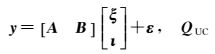 (11)
(11)
式中,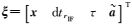
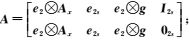
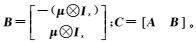
根据等价性原理[10, 27],IF模型与UC模型的转换矩阵R不能同时满足条件RTC=0且rank(R)=n-t,所以IF模型与UC模型不等价。IF模型无法独立求解两个频率模糊度,从模糊度解算的角度二者也不等价[10]。事实上,4个双频伪距和相位观测方程经无电离层组合后消除了一个电离层参数,应该得到3个等价的无电离层组合方程,而传统的IF模型只保留了两个方程,舍弃了伪距与相位之间的组合方程,但是该组合观测信息对定位贡献较弱,且与伪距、相位的无电离层组合信息相关,所以二者定位精度相当。此外,由于UC模型包含的待估参数较多,导致计算效率低,同时UC模型大量参数之间的相互关系往往会导致方程性态变差,导致待估参数的数值稳定性可能较IF模型差。
2.2.2 UC模型与IW模型的关系IW模型在UC模型式(8)的基础上增加电离层延迟的伪观测方程,增强了UC模型的强度。IW模型电离层延迟参数解算精度高于UC模型的解算精度,而电离层延迟参数解算精度直接影响其他待估参数的解算质量,从而改善定位效果。通过讨论UC模型与IW模型的电离层估计效果来分析二者之间的关系。
为了描述简单,令法方程元素N11=ATQUC-1A、N12=ATQUC-1B、N22=BTQUC-1B、W1=ATQUC-1y和W2=BTQUC-1y,则UC模型的位置参数最小二乘解为
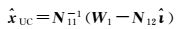 (12)
(12)
式中,UC模型的电离层参数估值及其协方差阵为
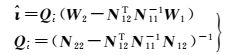 (13)
(13)
IW模型的位置参数最小二乘解为
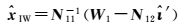 (14)
(14)
式中,IW模型的电离层参数估值及其协方差阵为
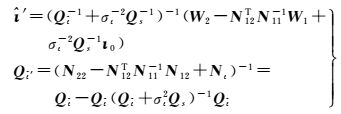 (15)
(15)
式(12)和式(14)分别是UC模型和IW模型的位置参数解,二者的区别在于电离层延迟参数的估值,即电离层延迟参数估值的精度直接反映了两个模型定位参数解的精度。从式(13)和式(15)得出,IW模型的电离层延迟参数的协方差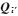
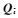
随着我国BDS的迅速发展,GPS和BDS组合PPP不仅缩短了GPS单系统的收敛时间,而且增加GPS单系统PPP的可靠性和可用性。所以基于上文讨论的独立参数化的UC模型和IF模型,下面直接给出双系统组合的PPP模型。
3.1 GPS和BDS组合的UC模型以上下标G和C区分GPS和BDS系统,则根据式(8)给出GPS和BDS组合的UC模型为
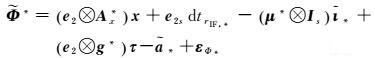 (16a)
(16a)
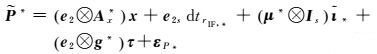 (16b)
(16b)
式中,*=“G”或“C”;其余符号含义与式(8)相同。
3.2 GPS和BDS组合的IF模型根据式(10),GPS和BDS组合的IF模型为
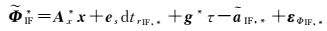 (17a)
(17a)
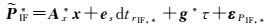 (17b)
(17b)
式中,*=“G”或“C”;其余符号含义与式(10)相同。
3.3 GPS和BDS双系统组合的时空统一多系统融合的关键性问题是需要采用统一的时间系统和坐标系统。由于GPS和BDS系统的时间基准及时延偏差存在差异,一般将BDS的时间基准统一到GPST。系统间的时延偏差,可用两种方法进行处理。一种方法是引入系统的频间偏差(ISB)参数,考虑到ISB的稳定性,一般作为常数或者分段常数进行估计[28]
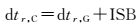 (18)
(18)
另一种方法是独立估计各系统的接收机钟差,不考虑ISB[28],本文采用该方法处理。该方法处理简单且能确保估值消除时间偏差的影响,与第1种方法相比,由于每个历元都引入了两个钟差参数,导致模型强度略微偏低。另外,由于PPP采用了IGS精密轨道产品,所有轨道产品已经统一在相同的ITRF坐标参考框架,故不存在坐标转换问题。
3.4 GPS和BDS双系统随机模型GPS和BDS观测值都采用高度角定权,同时考虑到GPS、BDS观测噪声及卫星轨道产品的精度差异,根据大量计算统计得出GPS和BDS权比为1:0.8。此外,由于BDS的GEO卫星的静止特性,导致其与地面监测站的几何构型较差,所以GEO卫星的轨道精度比IGSO和MEO卫星低。因此,在实际应用中对GEO卫星观测值进行了适当地降权处理[29]。
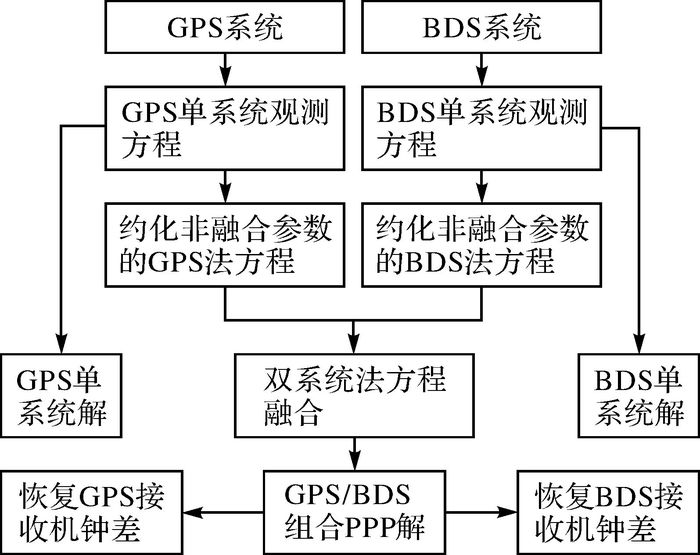
图 1给出的是GPS/BDS组合的PPP解算流程,采用自主开发的Multi-PPP软件,软件不仅可实现单系统PPP,还可在单系统法方程层面实现多系统融合解。
|
| 图 1 GPS/BDS组合PPP数据处理流程 Fig. 1 The data processing flow of GPS/BDS combined PPP |
4 试验分析
MGEX是IGS建立的GNSS多频多模跟踪站的试验网,本文算例选取MGEX网中同时跟踪GPS和BDS卫星较多的5个测站,分别为中国的JFNG、澳大利亚的CUT0、GMSD、KARR和MRO1。选择2015年DOY137—150数据,且采样间隔为30 s。以静态单天解作为各测站的参考坐标。轨道产品采用德国地学中心(GFZ)提供的15 min间隔的精密星历和30 s的精密钟差。电离层约束采用IGS提供的最终全球格网产品(GIMs)通过内插方式获取的电离层改正。根据GIMs产品的精度,本文取电离层伪观测值的方差为0.09 m2。试验采用静态PPP和静态数据动态PPP解算两种模式,动态解算采用卡尔曼滤波方法,状态系统的动态噪声设为白噪声[30]。统计分析北(N)、东(E)和高程(U)3个方向的定位误差和以及3个方向收敛至1 dm的时间。
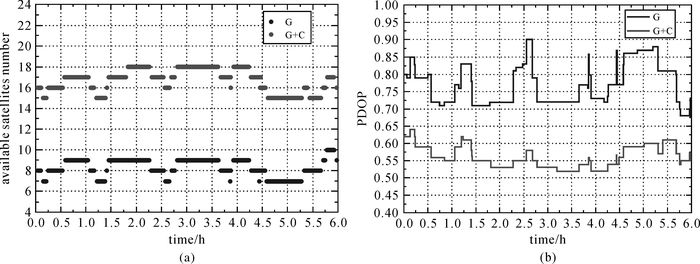
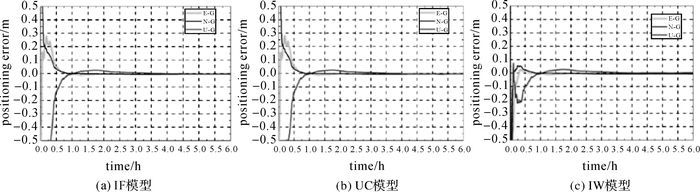
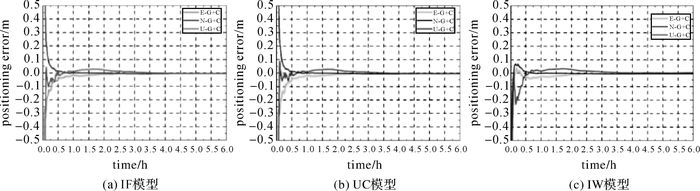
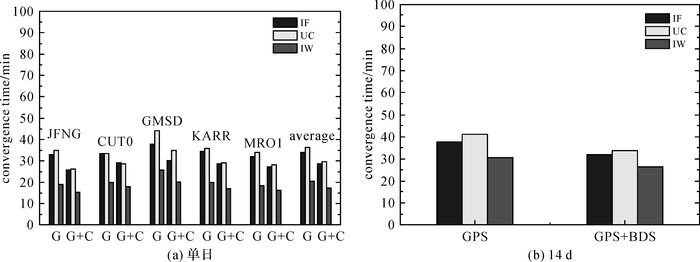
4.1 静态PPP试验算例给出3种PPP模型GPS单系统和GPS+BDS组合的静态PPP定位情况。图 2为可视卫星数以及PDOP值,图 3、图 4分别为GPS单系统和GPS/BDS组合的IF模型(a)、UC模型(b)和IW模型(c)的静态PPP E、N、U方向的定位误差。从图中可以看出,GPS/BDS组合PPP的收敛时间相比于GPS单系统有所改善。图 5为5个测站1 d平均收敛时间统计及所有测站平均收敛时间统计(a)和14 d平均收敛时间(b)。表 1为3种PPP模型的平均定位精度统计结果。从图 5和表 1可以看出,对于静态PPP,UC模型比IF模型的收敛时间长,IW模型的收敛时间相比于IF模型和UC模型明显缩短。在定位精度方面,3种PPP模型定位精度相当,3种PPP模型的3个方向静态定位精度均优于2 cm,平面定位精度甚至优于厘米级。
|
| 图 2 JFNG站可视卫星数与PDOP值变化 Fig. 2 The number of available satellites and PDOP at JFNG station |
|
| 图 3 3种模型GPS单系统静态PPP误差 Fig. 3 Static PPP positioning errors of the three models with GPS-only combinations |
|
| 图 4 3种模型GPS/BDS组合静态PPP误差 Fig. 4 Static PPP positioning errors of the three models with GPS/BDS combinations |
|
| 图 5 GPS和GPS/BDS组合3种模型单日静态PPP收敛时间和14 d平均收敛时间 Fig. 5 Convergence time of 3 static PPP models with GPS-only and GPS/BDS combination for 5 stations and the average convergence time of 14 days |
| cm | |||||||||||
| 系统 | IF模型 | UC模型 | IW模型 | ||||||||
| E | N | U | E | N | U | E | N | U | |||
| GPS | 1.4 | 0.6 | 1.3 | 1.5 | 0.8 | 1.8 | 1.3 | 0.8 | 1.3 | ||
| GPS+BDS | 0.9 | 0.8 | 1.2 | 1.2 | 0.8 | 1.6 | 0.7 | 0.8 | 0.9 | ||
4.2 模拟动态PPP试验
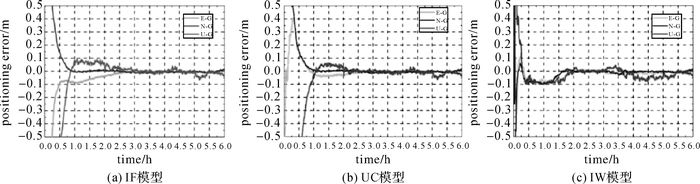
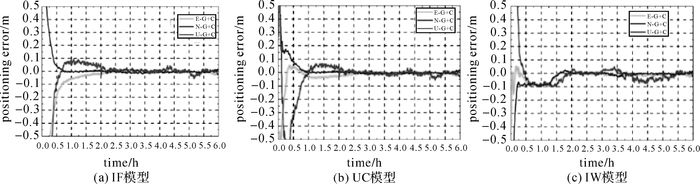
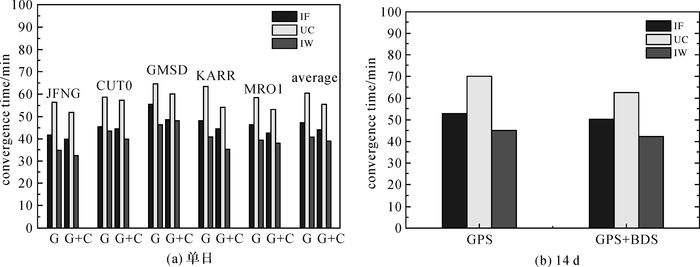
算例给出3种PPP模型GPS单系统和GPS+BDS组合的动态PPP定位情况。图 6、图 7分别为GPS单系统和GPS/BDS组合的IF模型(a)、UC模型(b)和IW模型(c)的动态PPP ENU方向的定位误差。从图中可以看出,GPS/BDS组合PPP的平面方向的收敛时间相比于GPS单系统有所改善。图 8为5个测站1 d平均收敛时间统计及所有测站平均收敛时间统计(a)和14 d平均收敛时间(b)。表 2为3种PPP模型的平均定位精度统计结果。从图 8和表 2可以看出,动态PPP的收敛时间方面,UC模型比IF模型的收敛时间更长,IW模型的收敛时间相比于IF模型和UC模型明显缩短;定位精度方面,3种模型动态PPP平面均优于3 cm,高程方向优于5 cm。
|
| 图 6 3种模型GPS单系统的动态PPP定位误差 Fig. 6 Kinematic PPP positioning errors of the three models with GPS-only combinations |
|
| 图 7 3种模型GPS/BDS组合动态PPP定位误差 Fig. 7 Kinematic PPP positioning errors of the three models with GPS/BDS combinations |
|
| 图 8 GPS和GPS/BDS组合3种模型单日动态PPP收敛时间和14 d平均收敛时间 Fig. 8 Convergence time of 3 kinematic PPP models with GPS-only and GPS/BDS combination for 5 stations and the average convergence time of 14 days |
| cm | |||||||||||
| 系统 | IF模型 | UC模型 | IW模型 | ||||||||
| E | N | U | E | N | U | E | N | U | |||
| GPS | 2.3 | 1.9 | 4.6 | 3.6 | 2.6 | 5.3 | 3.0 | 3.3 | 4.3 | ||
| GPS+BDS | 2.8 | 2.1 | 5.0 | 2.9 | 2.2 | 4.8 | 2.6 | 2.1 | 4.7 | ||
5 结论
本文从公式推导角度,详细讨论了无电离层组合模型和非组合PPP模型的独立参数化方法,并从参数估计角度,论述无电离层组合模型(IF)、非组合模型(UC)和附加电离层约束模型(IW)的相互关系。试验分析了3种模型的静态和动态解算精度以及收敛时间,得出以下结论:
(1) UC模型和IF模型的钟差、时延偏差、电离层和模糊度参数之间存在相关性,需通过独立参数化方法确定可估参数。
(2) 从参数估计角度分析,IW模型在UC模型的基础上对电离层参数进行约束,增强了模型强度,提高参数估计精度,进而缩短定位收敛时间。
(3) GPS和BDS双系统组合相比于GPS单系统有效地改善了卫星的几何构型强度,组合PPP的收敛时间明显比单系统的短。
| [1] |
屈利忠, 赵齐乐, 郭靖, 等.
GNSS融合动态精密单点定位性能分析[J]. 大地测量与地球动力学, 2016, 36(4): 298–302.
QU Lizhong, ZHAO Qile, GUO Jing, et al. Performance Analysis on Multi-GNSS Kinematic Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2016, 36(4): 298–302. |
| [2] | COLOMBO O L, SUTTER A W, EVANS A G.Evaluation of Precise, Kinematic GPS Point Positioning[C]//Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2004), Long Beach, CA, USA:Long Beach Convention Center, 2004:1423-1430. |
| [3] | ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005–5017. DOI:10.1029/96JB03860 |
| [4] | KOUBA J, HéROUS P. Precise Point Positioning Using IGS Orbit and Clock Products[J]. GPS Solutions, 2001, 5(2): 12–28. DOI:10.1007/PL00012883 |
| [5] |
李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D]. 武汉: 武汉大学, 2013. LI Xingxing.Rapid Ambiguity Resolution in GNSS Precise Point Positioning[D].Wuhan:Wuhan University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10486-1014135460.htm |
| [6] |
辜声峰. 多频GNSS非差非组合精密数据处理理论及其应用[D]. 武汉: 武汉大学, 2013. GU Shengfeng.Research on the Zero-difference Un-combined Data Processing Model for Multi-frequency GNSS and Its Applications[D].Wuhan:Wuhan University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10486-1014135106.htm |
| [7] |
李敏. 多模GNSS融合精密定轨理论及其应用研究[D]. 武汉: 武汉大学, 2011. LI Min.Research on Multi-GNSS Precise Orbit Determination Theory and Application[D].Wuhan:Wuhan University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10486-1011404080.htm |
| [8] |
任晓东, 张柯柯, 李星星, 等.
BeiDou、Galileo、GLONASS、GPS多系统融合精密单点[J]. 测绘学报, 2015, 44(12): 1307–1313, 1339.
REN Xiaodong, ZHANG Keke, LI Xingxing, et al. Precise Point Positioning with Multi-constellation Satellite Systems:BeiDou、Galileo、GLONASS、GPS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1307–1313, 1339. DOI:10.11947/j.AGCS.2015.20140568 |
| [9] | KOUBA J.A Guide to Using International GNSS Service (IGS) Products[J].IGS Central Bureau, Pasadena, 2009.http://igscb.jpl.nasa.gov/components/usage.html. |
| [10] |
李博峰, 葛海波, 沈云中.
无电离层组合、Uofc和非组合精密单点定位观测模型比较[J]. 测绘学报, 2015, 44(7): 734–740.
LI Bofeng, GE Haibo, SHEN Yunzhong. Comparison of Ionosphere-free, Uofc and Uncombined PPP Observation Models[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 734–740. DOI:10.11947/j.AGCS.2015.20140161 |
| [11] | GAO Y, SHEN X.Improving Ambiguity Convergence in Carrier Phase-based Precise Point Positioning[C]//Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS-2001).Salt Lake City, USA:Salt Palace Convention Center, 2001:1532-1539. |
| [12] |
阮仁桂, 郝金明, 张勇.
基于UofC模型的精密单点定位精度分析[J]. 大地测量与地球动力学, 2009, 29(6): 104–108.
RUAN Rengui, HAO Jinming, ZHANG Yong. Evaluation of Precise Point Positioning with UofC Model[J]. Journal of Geodesy and Geodynamics, 2009, 29(6): 104–108. |
| [13] |
蔡昌盛, 戴吾蛟, 匡翠林, 等.
利用UofC消电离层组合的GPS/GLONASS精密单点定位研究[J]. 武汉大学学报(信息科学版), 2012, 37(7): 827–830.
CAI Changsheng, DAI Wujiao, KUANG Cuilin, et al. Study on GPS/GLONASS Precise Point Positioning Using UofC Ionosphere-free Combination[J]. Geomatics and Information Science of Wuhan University, 2012, 37(7): 827–830. |
| [14] | SCHAFFRIN B, GRAFAREND E. Generating Classes of Equivalent Linear Models by Nuisance Parameter Elimination[J]. Manuscripta Geodaetica, 1986(11): 262–271. |
| [15] | XU Guochang. GPS Data Processing with Equivalent Observation Equations[J]. GPS Solutions, 2002, 6(1-2): 28–33. DOI:10.1007/s10291-002-0009-3 |
| [16] |
张宝成. GNSS非差非组合精密单点定位的理论方法与应用研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2012. ZHANG Baocheng.Study on the Theoretical Methodology and Applications of Precise Point Positioning Using Un-differenced and Uncombined GNSS Data[D].Wuhan:Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2012. |
| [17] | LOU Yidong, ZHENG Fu, GU Shengfeng, et al. Multi-GNSS Precise Point Positioning with Raw Single-frequency and Dual-frequency Measurement Models[J]. GPS Solutions, 2016, 20(4): 849–862. DOI:10.1007/s10291-015-0495-8 |
| [18] | LI Xingxing, ZHANG Xiaohong, REN Xiaodong, et al. Precise Positioning with Current Multi-constellation Global Navigation Satellite Systems:GPS, GLONASS, Galileo and BeiDou[J]. Scientific Reports, 2015, 5: 8328. DOI:10.1038/srep08328 |
| [19] | LI Bofeng, LI Zhen, ZHANG Zhiteng, et al. ERTK:Extra-wide-lane RTK of Triple-frequency GNSS Signals[J]. Journal of Geodesy, 2017, 91(9): 1031–1047. DOI:10.1007/s00190-017-1006-1 |
| [20] | LI Bofeng, SHEN Yunzhong, FENG Yanming, et al. GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK[J]. Journal of Geodesy, 2014, 88(2): 99–112. DOI:10.1007/s00190-013-0670-z |
| [21] | KLOBUCHAR J A. Ionospheric Time-delay Algorithm for Single-frequency GPS Users[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, AES-23(3): 325–331. DOI:10.1109/TAES.1987.310829 |
| [22] | KLOBUCHAR J A.Ionospheric Effects on GPS[M]//SPILKER Jr J J, AXELRAD P, PARKINSON B W, et al.Global Positioning System:Theory and Applications.AIAA, 1996(1):485-515. |
| [23] |
袁运斌. 基于GPS的电离层监测及延迟改正理论与方法的研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2002. YUAN Yunbin.Study on Theories and Methods of Correcting Ionospheric Delay and Monitoring Ionosphere Based on GPS[D].Wuhan:Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2002. http://d.wanfangdata.com.cn/Thesis/Y568495 |
| [24] | FELTENS J, SCHAER S.IGS Products for the Ionosphere[C]//Proceedings of the 1998 IGS Analysis Center Workshop.Darmstadt, Germany, 1998. |
| [25] | IGS MGEX.http://mgex.igs.org/IGS_MGEX_Products.html. |
| [26] | MONTENBRUCK O, STEIGENBERGER P, KHACHIKYAN R, et al. IGS-MGEX:Preparing the Ground for Multi-Constellation GNSS Science[J]. Inside GNSS, 2014, 9(1): 42–49. |
| [27] | LI Bofeng, TEUNISSEN P J G. GNSS Antenna Array-aided CORS Ambiguity Resolution[J]. Journal of Geodesy, 2014, 88(4): 363–376. DOI:10.1007/s00190-013-0688-2 |
| [28] | TU Rui, GE Maorong, ZHANG Hongping, et al. The Realization and Convergence Analysis of Combined PPP Based on Raw Observation[J]. Advances in Space Research, 2013, 52(1): 211–221. DOI:10.1016/j.asr.2013.03.005 |
| [29] | LI Bofeng. Stochastic Modeling of Triple-frequency BeiDou Signals:Estimation, Assessment and Impact Analysis[J]. Journal of Geodesy, 2016, 90(7): 593–610. DOI:10.1007/s00190-016-0896-7 |
| [30] |
杨元喜.
自适应动态导航定位[M]. 北京: 测绘出版社, 2006.
YANG Yuanxi. Adaptive Navigation and Kinematic Positioning[M]. Beijing: Surveying and Mapping Press, 2006. |



