2. 中国科学院大学, 北京 100049;
3. 北京师范大学, 北京 100875
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Beijing Normal University, Beijing 100875, China
随着地理信息技术的不断发展及应用的深入,每天都有大量具有地理标记的信息资源产生,并借助于网络传播到全球各地供不同用户检索使用[1]。为快速获取网络中的地理信息资源,地名信息检索技术正日益受到重视[2-7]。地名信息检索一般依据检索词中的主题、地名和空间关系[2],与网络中具有地理标记的各类资源描述进行相似性匹配,进而获取满足条件的资源。地名作为地名信息检索中的重要组成部分,通常利用地名词典或地名库将地名解析为空间坐标形式,然后计算空间相似性。对于具有实际边界的面状地名,最小外包矩形为空间范围计算中的常见方式,且通常利用二者间的重叠面积或者Hausdorff距离[8]计算空间相似性。然而多数地名仅以中心点坐标形式表达其空间位置,难以具体描述空间范围,进而发现潜在的地理信息资源,造成检索中的片面性和局限性。
在地名信息检索研究中,地名本体[9-10]或地名词典[11-12]的构建通常是地理信息资源描述中地名识别、消歧及空间关系表达的基础[2, 4]:地名本体是依据专家知识将地名、地名所表达的地理实体类型及空间关系等数据组织成统一的地名描述体系,然而本体构建过程较为繁琐,需要大量领域专家的参与,且不同组织机构间难以形成统一的标准体系,不易于进行大规模实施[5];地名词典是存储具有地理坐标属性的地名目录[12],一般包括3个基本要素,即地名、要素类型及空间范围(位置),通常利用地理要素中心点表达其空间位置[13]。基于较为成熟的地名词典GeoNames(http://www.geonames.org/),Getty Thesaurus of Geographic Names(http://www.getty.edu/research/tools/vocabularies/tgn/),以及Alexandria Digital Library(http://legacy.alexandria.ucsb.edu/)等,当前在地名信息集成[14-15]、地名语义增强[16],以及空间相似性匹配[17-18]等方面取得众多成就。然而在地名本体或地名词典中,多数地名同样存在空间范围描述的缺失,仅以地名中心点坐标形式表达其空间位置,限制了地理信息资源检索的准确性。
当前主要存在两种类型的地名点,即感兴趣点和城市(村镇)点:前者可用于城市边界的近似表达,而后者可用于更大行政边界的近似表达[19]。地名点的信息检索一般简化为计算参考点与目标点对应的空间关系相似性[6, 20]。为了实现点状地名空间范围的近似表达,文献[1, 19]研究采用基于点集的方法构建地名的模糊边界,进而判断目标地名点与该范围的关系。文献[21-22]研究利用泰森多边形描述同类地名点间的模糊空间关系,但将地名点视为均一性质,忽略了地名点间的差异性,难以突出地名在检索中的不同重要程度。文献[23]研究基于密度表面方法描述地名点集的模糊边界范围,考虑了源地名点与目标地名点间距离因素对检索结果的影响,但通常难以准确描述地名间的空间关系。
为解决当前点状地名信息检索研究中的不足,本文在深入分析地名及其空间属性、空间关系的基础上,利用泰森多边形在空间关系表达与空间范围近似中的优势,且考虑同类型地名点性质上的差异对检索结果的影响,提出了针对点状地名信息的加权泰森多边形检索法。该方法选取同类型地名所具有的面积属性作为权重指标构建泰森多边形,以形成对地名边界的近似表达,进而判断各待匹配点与检索点间所对应的空间关系。在此基础上实现空间关系的相似性度量,并依据空间相似性对检索结果进行排序。
1 点状地名信息的加权泰森多边形检索法由于当前缺乏有效方法实现地名点空间范围的近似表达,因而难以准确描述地名点间的各类空间关系;且同类型地名点通常存在性质上的差异,会影响到地名信息检索结果的准确性。鉴于以地名中心点表达空间位置的方式在地名信息检索中的局限性,本文利用加权泰森多边形实现地名边界近似,由此建立地名间的近似空间关系,空间关系相似性度量也即转换为地名面间的相似性度量,从而提高地名信息检索效率。以下将详细论述该方法。
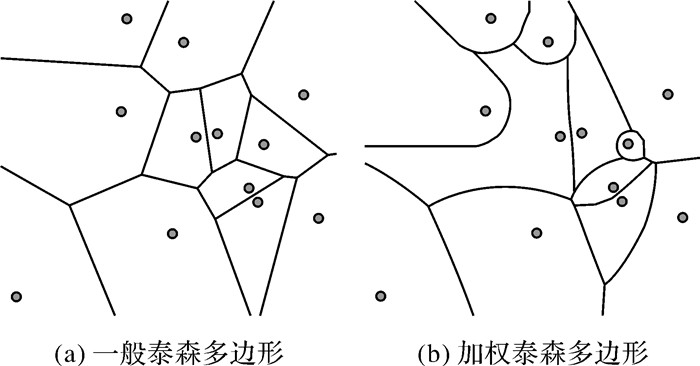
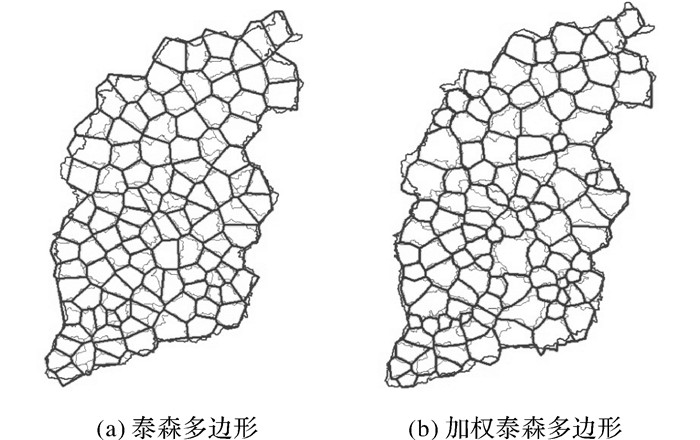
1.1 加权泰森多边形泰森多边形是对空间平面的一种剖分,其特点是多边形内的任何位置离该多边形的样点的距离最近,离相邻多边形内样点的距离远,且每个多边形内含且仅包含一个样点,可较好地解决空间邻接及最邻近问题(图 1(a)):如果泰森多边形中的任意两点拥有共同的边界,则此两点的空间关系可视为相邻关系,由此通过多边形的包含关系查询任意位置处的最邻近点[22]。而加权泰森多边形则是选取空间要素的某种属性特征赋予相应的权重,并依据权重因子实现空间区域的划分,划分的区域大小在一定程度上代表该区域中要素在所选属性特征上的重要性(图 1(b))[24]。鉴于同类型地名点间性质上的差异,一般难以采用统一标准近似表达地名边界,应选取适当的权重因子作为衡量地名重要性的指标,并参与到地名边界表达中[25],以提高地名边界近似的准确性。
|
| 图 1 泰森多边形示例 Fig. 1 Examples of Voronoi diagrams |
对于平面中的任意点集P={P1,P2,…,Pn}(n≥3),λi(i≥1)为各点所对应的属性因子,则区域
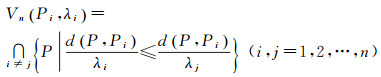 (1)
(1)
将平面分为n部分,由Vn(Pi,λi)(i ≥ 1)确定的平面分割方法称为点的加权泰森多边形,λi称为点Pi的权重,且各分割区域中的每个点到该区域中心的距离与该点到相邻区域中心的距离之比小于两中心点的权重之比[26]。泰森多边形可看作加权泰森多边形在权重值相等时的一个特例。
利用加权泰森多边形对地名边界的近似表达,可近似计算各地名点对应的空间区域面积,并判断两地名点对应的共同边界长度;依据地名边界的连续性表达,近似建立地名间的各类空间关系,以支持地名信息检索。其中,方位关系、距离关系和拓扑关系是空间关系的重要组成部分,是判断地名间相互关系的前提,也是地名信息检索的重要基础。地名信息检索一般可表达为地名+空间关系+属性的形式[5]。鉴于空间关系在检索中的重要作用,下文中将分别针对拓扑关系、方位关系和距离关系计算展开论述。
1.2 空间关系相似性计算在地名信息检索中,一般通过计算源地名与目标地名在拓扑关系、方位关系或距离关系中的相似性获取符合条件的地名信息,并依据相似度对计算结果进行排序。本文选取地名点的面积作为权重指标生成加权泰森多边形,实现对地名边界的近似表达,从而将离散地名点间的空间关系计算转换为连续的地名面间的空间关系计算。鉴于地名类型及其隶属层次关系间的差异影响地名边界的近似性[27],本文针对同类型且处于同一层次中的地名点实现地名边界的近似,以减少计算中的误差。地名间的空间关系可由拓扑关系、方位关系和距离关系中的一种或多种进行描述,因而空间关系的相似性计算可采用以下公式
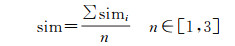 (2)
(2)
式中,sim是地名空间关系的总体相似度;simi是地名拓扑关系、方位关系或距离关系的相似度。依据此公式计算获取各地名点的相似性。
1.2.1 拓扑关系拓扑关系是空间中任意两地理对象在连续形变后还能保持不变的相互关系,而拓扑关系模型主要有区域连接演算模型与9交模型[19],可用于描述点、线、面要素间各种相互关系。本文利用加权泰森多边形实现地名边界的近似表达,因此地名点间拓扑关系的判断将转换为对地名面间拓扑关系的判断,而面要素的拓扑关系主要有包含、被包含、相等、相交、邻接和叠加6种。鉴于4交模型[28]在两个面要素内部交集、边界交集以及相互间差集的基础上建立拓扑关系描述,并利用拓扑距离描述拓扑关系间的关联性,因而可方便计算任意两地名点间的拓扑关系相似性。本文选取6种主要拓扑关系以评价其相似性,各拓扑关系间的拓扑距离度量如下表所示(表 1)。
基于拓扑距离度量,本文构建以下公式计算两个拓扑关系的相似性
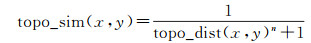 (3)
(3)
式中,topo_dist(x,y)是两个拓扑关系间的拓扑距离;n是调节因子(本文选取n=2),用于调节公式在拓扑距离变化中的收敛速度。拓扑关系相似性反比于拓扑距离:拓扑距离越大,其拓扑关系相似性越低。
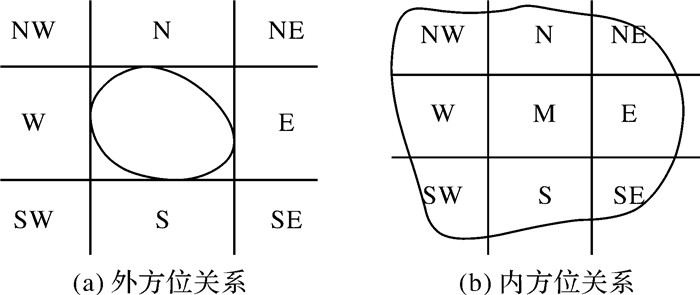
1.2.2 方位关系空间中任意两个地名点间相对方位关系表达一般采用锥形模型[29-30],即以源地名点为中心,8等分整个空间范围(东、南、西、北、东北、东南、西南和西北),判断目标地名点所处的空间区域,即为源地名点与目标地名点间的相对方位关系。本文方位关系判断针对于地名面,由于面要素可分为外部区域和内部区域,其方位关系也应分为外方位关系和内方位关系,但锥形模型通常难以直接用于面要素方位关系判断。为此当前研究改进锥形模型,利用面要素的最小外包矩形划分内外空间方位(图 2)[30-31],以分别计算地名间的方位相似性。
|
| 图 2 基于最小外包矩形的内外方位关系 Fig. 2 Minimum bounding rectangle-based outer and inner direction relationship |
面要素外方位相似性主要依据检索词中的方位条件,判断目标要素所对应的源要素8方位区域(图 2(a))。由于目标要素可能不完全位于源要素的一个方位区域中,存在与多个区域相交的情况,因此本文采用式(4)判断目标要素与源要素间方位关系
 (4)
(4)
式中,x和y分别表示检索中的目标要素与源要素;dir_region(y)表示依据检索词中方位关系判断的所需方位区域;intersection_area表示目标要素在所需方位区域的对应面积。面要素外方位关系的相似性计算就是计算目标要素在所需方位区域的对应面积与目标要素本身面积之比,比值越大意味着相似性程度越高。当目标要素完全位于所需方位区域时,其相似性为1。面要素内方位相似性计算则依据内方位锥形模型[32]进行相应判断:依据面要素的最小外包矩形9等分整个矩形区域(图 2(b)),进而获取9种内方位关系,由此判断目标要素与源要素的内方位关系相似性,其计算仍采用式(4)进行。
1.2.3 距离关系地名点间的距离关系一般包括定性关系和定量关系:定性关系是从认知角度衡量源地名与目标地名间的相对距离,其中最常见的定性关系为“周边(附近)”关系,但由于缺乏统一标准实现定性关系的定量化,并且地名关系的定性表达具有较大模糊性,因而通常难以准确计算二者定性关系的相似性;而定量关系主要依据源地名与目标地名所处的空间位置计算二者间的相对距离,主要分为点-点、点-面,以及面与面的距离,而距离计算通常采用欧拉公式进行(式(5))
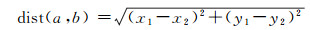 (5)
(5)
式中,a(x1,y1)和b(x2,y2)分别表示源地名与目标地名点的空间位置。定量距离关系的相似性可依据以下公式进行计算
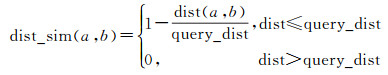 (6)
(6)
式中,a和b分别表示源地名与目标地名的空间位置;query_dist表示检索距离。定量距离关系的相似性计算就是计算两地名点间的相对距离与检索距离间的相近程度,目标地名与源地名间的距离越接近相似性程度越高,当两地名点间距离大于检索距离时,相似性程度减少为0。
定性距离关系的相似性计算,主要依据对距离远近的经验性认知,将定性距离描述转换为定量的距离数值表达,进而实现定性距离关系的定量化计算。对于空间区域内源地名点与各目标地名点间相邻关系判断,主要依据在生成的泰森多边形中两个相邻地名间有且仅有一个共同边界[22]。因此通过判断源地名点与目标地名点所在泰森多边形间的相邻关系,获取符合条件的相邻地名点。为进一步实现相邻地名距离关系相似性的排序,采用式(7),距离越近表明两点间的相似性越大
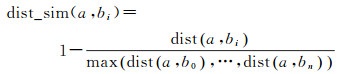 (7)
(7)
式中,a和bi分别表示源地名点与第i个目标地名点,而dist表示两地名点间的相对距离。
另外,对于其他定性距离关系,如近、中等、远和很远等距离描述词汇的度量,则从经验性认知的角度经多次试验评估设定,主要以目标地名点所在多边形与源地名点所在多边形间相隔的最少多边形个数为基础,形成两地名点间定性关系定量化计算标准,以实现相似性计算
 (8)
(8)
式中,VN表示两地名点间相隔最少多边形数目,最终定性距离的相似性计算公式如下
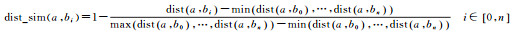 (9)
(9)
式中,max(dist)和min(dist)分别表示源地名点与目标地名点间的最大、最小距离,距离越近意味着相似性越大。由于对距离远近的经验性认知依据用户的不同而有所差异,本文制定的定量化指标难以满足所有人的检索需求,但为定性关系的定量化表达提供一种解决方案。未来考虑利用专家打分法、层次分析法等确定取值范围,以提高本文方法的有效性与准确性。
2 试验为了验证本文所述方法,试验以全国行政区划边界近似与检索为例,验证加权泰森多边形在地名边界近似与检索中的可行性与有效性。由于行政区划地名间存在较强的隶属层次关系,而且地名边界近似表达的准确性与地名点分布情况密切相关,一般地名点密度越大则由此生成的泰森多边形对地名边界近似的精度越高。为获取较高精度的地名边界近似结果,本文以处于底层的地名点为基础,将地名点的面积属性作为权重指标生成泰森多边形,进而计算处于其他各层地名所对应的底层多边形集合,并以此作为该层地名所对应的空间范围,最终实现各层次地名边界的近似表达。
试验选取了全国2408个县级的行政区划面矢量数据为基础数据,同时选取了全国344个市级的行政区划面矢量数据及31个省级面矢量数据。为生成各层次地名的矢量点,试验以县级地名行政区中心点为地名坐标点对各图层进行处理,并将各地名所对应的行政区面积作为字段值记录到地名点中,利用ArcGIS中的相应工具分别生成山西省地名点的泰森多边形(图 3(a))与加权泰森多边形[25](图 3(b))。在图 3(a)中,每个地名点间权重指标均为1,因此对于面积较小的地名点其边界近似的误差较大;在图 3(b)中,多边形的生成依赖于地名点所对应的面积权重指标,其边界近似效果要优于前者。
|
| 图 3 地名边界近似 Fig. 3 Approximation of place boundary |
为验证加权泰森多边形在地名边界近似中的准确性,试验任意选取内陆中的6省作为目标区域,分别统计泰森多边形与加权泰森多边形在省级单位面积近似中的准确性,主要利用以下公式计算
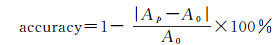 (10)
(10)
式中,A0表示原始地名面积;Ap表示近似地名面积,二者越接近意味着面积近似的准确性越高。
从表 2中可以看出,加权泰森多边形与普通泰森多边形在地名面积近似准确性上均高于98%,且二者各项地名面积的近似程度接近,但加权泰森多边形考虑地名点面积属性在地名边界近似中的影响,因而对于具有不同面积属性的地名点,采用加权泰森多边形更能表达其边界范围,进而提高地名信息检索的效率。
| 省名称 | 原面积 /万km2 | 泰森多 边形近 似面积 /万km2 | 准确率 /(%) | 加权泰森 多边形近 似面积 /万km2 | 准确率 /(%) |
| 山西 | 24.86 | 25.33 | 98.1 | 24.35 | 97.9 |
| 河南 | 23.98 | 24.40 | 98.2 | 23.58 | 98.3 |
| 湖北 | 25.27 | 25.38 | 99.6 | 25.36 | 99.6 |
| 湖南 | 26.99 | 26.82 | 99.4 | 27.07 | 99.7 |
| 江西 | 21.25 | 21.54 | 98.6 | 20.94 | 98.5 |
| 安徽 | 19.41 | 19.18 | 98.8 | 19.49 | 99.6 |
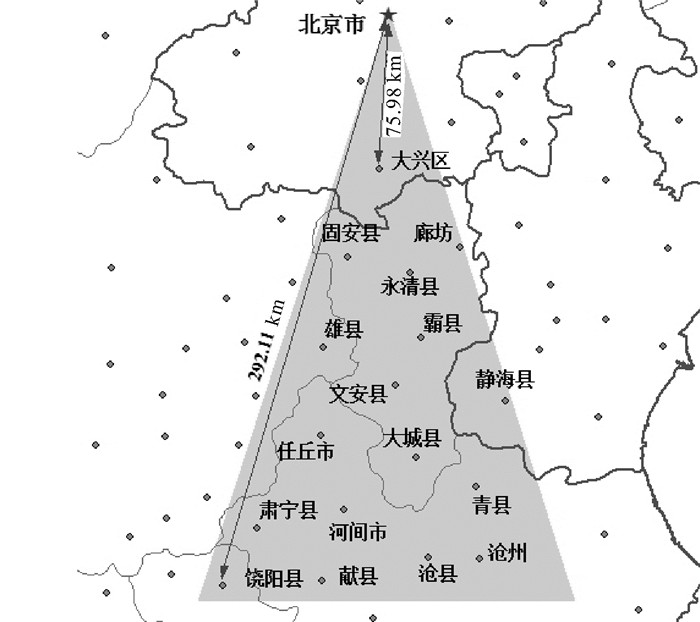
为验证该方法在地名信息检索中的有效性,本文以全国县级点矢量数据为基础构建试验原型系统,并与传统以地名点为核心的检索方法进行比较。当检索词为“北京以南300 km内的城镇”时,传统方法是以北京中心点为核心采用基于锥形模型的方位判别方法,并以距离为限制条件对周边地名进行检索,以返回各地名的相似性检索结果(表 3、图 4)。
| 序号 | 名称 | 相似度 | 距离/km |
| 1 | 大兴区 | 0.873 3 | 75.98 |
| 2 | 廊坊 | 0.800 9 | 119.47 |
| 3 | 固安县 | 0.798 5 | 120.91 |
| 4 | 永清县 | 0.788 2 | 127.10 |
| 5 | 霸县 | 0.733 9 | 159.67 |
| 6 | 雄县 | 0.722 0 | 166.79 |
| 7 | 文安县 | 0.696 1 | 182.35 |
| 8 | 静海县 | 0.669 4 | 198.33 |
| 9 | 任丘市 | 0.651 2 | 209.26 |
| 10 | 大城县 | 0.636 9 | 217.84 |
|
| 图 4 传统检索结果 Fig. 4 Traditional retrieval result |
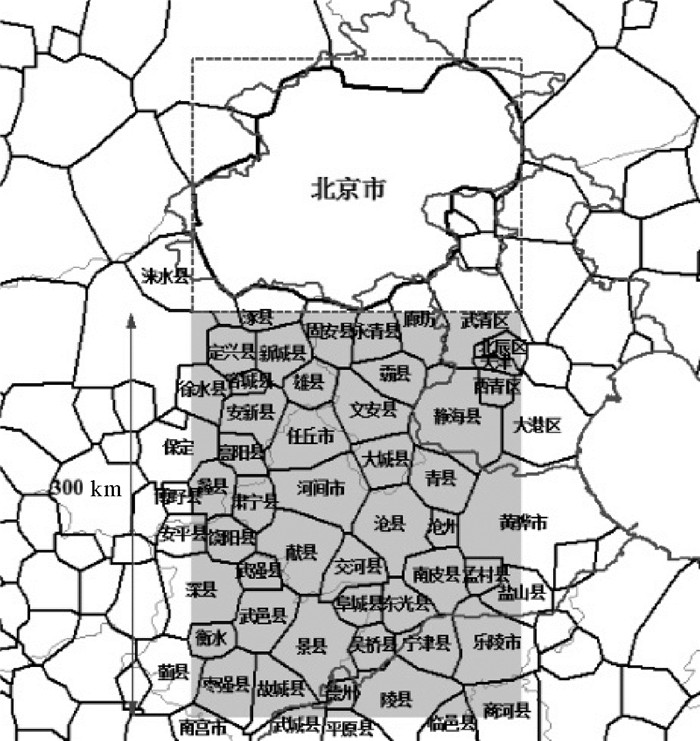
而本文方法则主要考虑地名边界的近似表达,通过建立北京与周边地名间的外方位关系,计算北京与周边地名空间关系的相似性(表 4,图 5)。
| 序号 | 名称 | 相似度 | 距离/km |
| 1 | 新城县 | 0.992 3 | 4.64 |
| 2 | 定兴县 | 0.984 3 | 9.36 |
| 3 | 霸县 | 0.953 0 | 28.23 |
| 4 | 雄县 | 0.945 1 | 32.94 |
| 5 | 天津 | 0.944 6 | 33.24 |
| 6 | 永清县 | 0.942 8 | 0 |
| 7 | 静海县 | 0.937 2 | 37.64 |
| 8 | 西青区 | 0.929 4 | 42.36 |
| 9 | 文安县 | 0.929 4 | 42.36 |
| 10 | 容城县 | 0.929 4 | 42.36 |
|
| 图 5 本文检索结果 Fig. 5 Proposed retrieval result |
从试验结果中可以看出,由于地名起算点的不同(后者利用地名边界对应最小外包矩形间的最短距离计算),两种方法所计算出的地名距离及其空间相似性结果显示出较大差异。由于本文充分考虑了地名点的面积因素在地名边界近似中的重要作用,利用加权泰森多边形形成地名边界的近似表达,从而建立地名点间更丰富的空间关系,可更好满足于点状地名信息检索的需求。
3 讨论本文所提出的基于加权泰森多边形的地名边界近似方法针对同类型地名点集,选取地名的面积属性作为权重因子形成地名边界的近似表达,进而建立地名间的相对空间关系。地名边界的近似精度与地名点分布情况密切相关,一般地名点分布越集中,地名边界近似表达精度越高。另外同类型地名所代表的地理对象间存在隶属层次关系,主要体现在两者空间范围表达上的包含性[23]。相对处于较高层次上的地名点,处于底层的地名点具有较细的空间粒度,因此可由处于底层的地名点近似表达处于其他层次的地名边界,进而支持地名间空间关系的建立。
由于泰森多边形在解决空间邻接及最邻近问题上具有巨大优势,因此针对空间上连续的同类型地名点,可较为准确的表达各地名点间的邻接性,进而建立各地名点间的空间关系。同样针对空间上离散的同类型地名点,通过选取恰当的权重指形成各地名点间影响范围的模拟,将离散的地名点转化为连续地名空间范围,可近似表达各地名点间的邻接性。另外针对与山峰、山谷等地形特征相关联的地名点,仍可利用同类型地名点所具有的高程值作为权重指标近似表达空间范围,以支持空间相似性计算。
在处理空间关系相似性时,由于地名边界近似表达中存在模糊性,因而在空间关系相似性计算中也存在模糊性。本文所采用的计算方法未考虑空间范围及关系的不确定性,仅依据地名边界的近似表达计算二者间的空间关系,从而影响了检索结果的准确性。未来考虑引入不确定场模型描述空间范围及关系的不确定性,以表达地名周边不同位置处的概率分布情况。依据地理学第一定律“任何事物都相关,只是相近的事物关联更紧密”[33],地名周边概率分布应与地名点距离成反比关系。针对空间范围及关系的不确定场的定量化表达,实现地名信息检索的不确定性计算,在一定程度上提高了检索效率。
4 结论鉴于以中心点记录地名空间位置的方式难以表达地名的空间范围,造成地名信息检索的局限性,针对点状地名的边界近似及检索问题,本文考虑同类型地名的不同性质在检索中的重要作用,提出了针对点状地名信息的加权泰森多边形检索法,依据同类型地名的面积属性作为权重指标构建泰森多边形,以近似表达地名的空间范围,进而建立地名间的各类空间关系,并从拓扑关系、方位关系与距离关系3个方面给出具体公式以计算其空间相似性。最后利用全国行政区划数据进行试验,相比普通泰森多边形的地名边界近似效果,该方法更能体现面积属性差异所造成的边界近似的差异,且其面积近似精度可达98%;另外相比通常的点状地名信息检索方法,该方法在地名边界近似的基础上实现地名信息检索,更有利于空间关系表达以提高空间相似性计算效率,从而证明了该方法的有效性。未来可依据地名信息检索的侧重点,选择多种要素(如地名热度、经济实力及道路通达性)作为权重指标生成加权泰森多边形,以综合评估各地名间的不同影响力,进而满足不同用户对地名信息的检索需求。
| [1] | GAO Yong, JIANG Dan, ZHONG Xiang, et al. A Point-set-based Footprint Model and Spatial Ranking Method for Geographic Information Retrieval[J]. ISPRS International Journal of Geo-Information, 2016, 5(7): 122. DOI:10.3390/ijgi5070122 |
| [2] | JONES C B, PURVES R S. Geographical Information Retrieval[J]. International Journal of Geographical Information Science, 2008, 22(3): 219–228. DOI:10.1080/13658810701626343 |
| [3] | KIM J, VASARDANI M, WINTER S. Similarity Matching for Integrating Spatial Information Extracted from Place Descriptions[J]. International Journal of Geographical Information Science, 2017, 31(1): 56–80. DOI:10.1080/13658816.2016.1188930 |
| [4] | VASARDANI M, WINTER S, RICHTER K F. Locating Place Names from Place Descriptions[J]. International Journal of Geographical Information Science, 2013, 27(12): 2509–2532. DOI:10.1080/13658816.2013.785550 |
| [5] |
周静, 张书亮, 张小波.
顾及地理实体的地名信息检索方法研究[J]. 地球信息科学学报, 2015, 17(11): 1362–1369.
ZHOU Jing, ZHANG Shuliang, ZHANG Xiaobo. A Place Name Information Retrieval Method Considering Geographic Entity[J]. Journal of Geo-information Science, 2015, 17(11): 1362–1369. |
| [6] |
刘家骏, 李浩然, 钟翔, 等.
地理信息检索中空间相似性度量的一种模糊方法[J]. 地理与地理信息科学, 2015, 31(4): 38–42.
LIU Jiajun, LI Haoran, ZHONG Xiang, et al. A Fuzzy Method to Measure Spatial Similarity in Geographic Information Retrieval[J]. Geography and Geo-information Science, 2015, 31(4): 38–42. |
| [7] |
程钢, 卢小平.
顾及通名语义的汉语地名相似度匹配算法[J]. 测绘学报, 2014, 43(4): 404–410, 418.
CHENG Gang, LU Xiaoping. Matching Algorithm for Chinese Place Names by Similarity in Consideration of Semantics of General Names for Places[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 404–410, 418. DOI:10.13485/j.cnki.11-2089.2014.0060 |
| [8] | ATALLAH M J. A Linear Time Algorithm for the Hausdorff Distance between Convex Polygons[J]. Information Processing Letters, 1983, 17(4): 207–209. DOI:10.1016/0020-0190(83)90042-X |
| [9] |
梁汝鹏, 李淑霞, 李文娟.
基于地名本体的空间数据组织与服务研究[J]. 信息工程大学学报, 2010, 11(2): 175–179.
LIANG Rupeng, LI Shuxia, LI Wenjuan. Research on Data Management and Retrieval Service Based on Toponym Ontology[J]. Journal of Information Engineering University, 2010, 11(2): 175–179. |
| [10] |
王东旭, 诸云强, 潘鹏, 等.
地理数据空间本体构建及其在数据检索中的应用[J]. 地球信息科学学报, 2016, 18(4): 443–452.
WANG Dongxu, ZHU Yunqiang, PAN Peng, et al. Construction of Geodata Spatial Ontology and Its Application in Data Retrieval[J]. Journal of Geo-Information Science, 2016, 18(4): 443–452. |
| [11] | LAURINI R. Geographic Ontologies, Gazetteers and Multilingualism[J]. Future Internet, 2015, 7(1): 1–23. DOI:10.3390/fi7010001 |
| [12] | CARDOSO S D, AMANQUI F K, SERIQUE K J A, et al. SWI:A Semantic Web Interactive Gazetteer to Support Linked Open Data[J]. Future Generation Computer Systems, 2016, 54(2): 389–398. |
| [13] | GAO Song, LI Linna, LI Wenwen, et al. Constructing Gazetteers from Volunteered Big Geo-data Based on Hadoop[J]. Computers, Environment and Urban Systems, 2017, 61(1): 172–186. |
| [14] | MOURA T H V M, DAVIS JR C A, FONSECA F T. Reference Data Enhancement for Geographic Information Retrieval Using Linked Data[J]. Transactions in GIS, 2016, 21(4): 683–700. |
| [15] | GRVTTER R, PURVES R S, WOTRUBA L. Evaluating Topological Queries in Linked Data Using DBpedia and GeoNames in Switzerland and Scotland[J]. Transactions in GIS, 2017, 21(1): 114–133. DOI:10.1111/tgis.2017.21.issue-1 |
| [16] | JANOWICZ K, KEBLER C. The Role of Ontology in Improving Gazetteer Interaction[J]. International Journal of Geographical Information Science, 2008, 22(10): 1129–1157. DOI:10.1080/13658810701851461 |
| [17] | PURVES R S, CLOUGH P, JONES C B, et al. The Design and Implementation of SPIRIT:A Spatially Aware Search Engine for Information Retrieval on the Internet[J]. International Journal of Geographical Information Science, 2007, 21(7): 717–745. DOI:10.1080/13658810601169840 |
| [18] | FRONTIERA P, LARSON R, RADKE J. A Comparison of Geometric Approaches to Assessing Spatial Similarity for GIR[J]. International Journal of Geographical Information Science, 2008, 22(3): 337–360. DOI:10.1080/13658810701626293 |
| [19] | LIU Yu, YUAN Yihong, XIAO Danqing, et al. A Point-set-based Approximation for Areal Objects:A Case Study of Representing Localities[J]. Computers, Environment and Urban Systems, 2010, 34(1): 28–39. DOI:10.1016/j.compenvurbsys.2009.05.001 |
| [20] |
张毅, 邬阳, 高勇, 等.
基于空间陈述的定位及不确定性研究[J]. 地球信息科学学报, 2013, 15(1): 38–45.
ZHANG Yi, WU Yang, GAO Yong, et al. On the Description-based Spatial Positioning and the Associated Uncertainty[J]. Journal of Geo-Information Science, 2013, 15(1): 38–45. |
| [21] | GONG Yongxi, WU Lun, LIN Yaoyu, et al. Probability Issues in Locality Descriptions Based on Voronoi Neighbor Relationship[J]. Journal of Visual Languages & Computing, 2012, 23(4): 213–222. |
| [22] | ALANI H, JONES C B, TUDHOPE D. Voronoi-based Region Approximation for Geographical Information Retrieval with Gazetteers[J]. International Journal of Geographical Information Science, 2001, 15(4): 287–306. DOI:10.1080/13658810110038942 |
| [23] | JONES C B, PURVES R S, CLOUGH P D, et al. Modelling Vague Places with Knowledge from the Web[J]. International Journal of Geographical Information Science, 2008, 22(10): 1045–1065. DOI:10.1080/13658810701850547 |
| [24] | CHAKROUN H, BENIE G B, O'NEILL N T, et al. Spatial Analysis Weighting Algorithm Using Voronoi Diagrams[J]. International Journal of Geographical Information Science, 2000, 14(4): 319–336. DOI:10.1080/13658810050024269 |
| [25] | DONG Pinliang. Generating and Updating Multiplicatively Weighted Voronoi Diagrams for Point, Line and Polygon Features in GIS[J]. Computers & Geosciences, 2008, 34(4): 411–421. |
| [26] |
郭丽敏, 周廷刚, 苏迎春.
基于加权Voronoi图的城市腹地界定方法研究——以成渝经济圈为例[J]. 地球信息科学学报, 2014, 16(3): 411–417.
GUO Limin, ZHOU Tinggang, SU Yingchun. Definition of Urban Hinterlands of Chengdu-Chongqing Economic Circle Based on Weighted Voronoi Diagram[J]. Journal of Geo-Information Science, 2014, 16(3): 411–417. |
| [27] | HWANG S, THILL J C.Modeling Localities with Fuzzy Sets and GIS[M]//PETRY F E, ROBINSON V B, COBB M A.Fuzzy Modeling with Spatial Information for Geographic Problems.Berlin:Springer, 2005:480-492. |
| [28] |
邓敏, 刘文宝, 冯学智.
GIS面目标间拓扑关系的形式化模型[J]. 测绘学报, 2005, 34(1): 85–90.
DENG Min, LIU Wenbao, FENG Xuezhi. A Generic Model Describing Topological Relations among Area Objects in GIS[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(1): 85–90. |
| [29] | DU Shihong, WANG Qiao, YANG Yipeng.Fuzzy Description of Fuzzy Direction Relations and Their Similarities[C]//Proceedings of the 12th International Conference on Geoinformatics:Geospatial Information Research:Bridging the Pacific and Atlantic.Berlin:Springer, 2004:496-502. |
| [30] | LIU Y, GUO Q H, WIECZOREK J, et al. Positioning Localities Based on Spatial Assertions[J]. International Journal of Geographical Information Science, 2009, 23(11): 1471–1501. DOI:10.1080/13658810802247114 |
| [31] | SKIADOPOULOS S, GIANNOUKOS C, VASSILIADIS P, et al.Computing and Handling Cardinal Direction Information[C]//BERTINO E, CHRISTODOULAKIS S, PLEXOUSAKIS D, et al.Proceedings of the 9th International Conference on Extending Database Technology.Heraklion, Crete, Greece:Springer, 2004:329-347. |
| [32] | LIU Yu, WANG Xiaoming, JIN Xin, et al.On Internal Cardinal Direction Relations[C]//COHN A G, MARK D M.Proceedings of International Conference COSIT.Ellicottville:Springer, 2005:283-299. |
| [33] | TOBLER W R. A Computer Movie Simulating Urban Growth in the Detroit Region[J]. Economic Geography, 1970, 46(S1): 234–240. |


