2. 31009部队, 北京 100088
2. 31009 Troop, Beijing 100088, China
居民地是地形图的重要要素之一[1],其数量和分布有助于判断地区的自然条件、土地利用、政治经济和文化发展等状况。而面状居民地又是中小比例尺地形图上居民地的一种重要的表达形式[2]。随着比例尺的减小,受地图表达的限制,需要对居民地进行选取操作。可以说,居民地选取质量的好坏直接影响着地图的科学性和使用价值[3]。
目前居民地选取方法主要分为两类:一是纯粹的数学和模型算法,如基于遗传算法的选取方法[4]、基于Circle原理的选取方法[5]、基于Kohonen的选取方法[6]、基于Voronoi图的选取方法[7]、基于属性权重模型的选取方法[8-9]等;二是智能化的方法,即基于知识的方法,如专家系统[10]、基于规则推理[11]等。居民地的选取主观性较强,选取的思维过程是模糊的、不确定的,难以形式化表达为精确的自动选取模型[12],尤其是对面状居民地的选取。因此,第1类建立精确模型的方法对于单一分布的点群选取效果较好,但对于环境稍复杂的面状居民地选取适用性较弱。从理论上讲要解决居民地自动选取的问题,应该从智能化方法上寻找突破口。第2类方法中,传统的制图综合专家系统和基于规则推理的方法,受到知识获取瓶颈的制约,一直难以有效地应用[13-14]。但也有一些实质性成果面世,文献[15—16]提出了基于案例类比推理和基于决策树的道路网智能选取方法,计算机通过对专家选取案例的学习进行相似道路网的自动选取,该方法某种程度上突破了知识获取与形式化表达的瓶颈。
上述研究极大地推动了居民地选取的发展,但进一步研究发现,居民地选取方法还存在以下几个问题:①基于算法和模型的方法暂时无法形式化反映专家在居民地选取过程中复杂的思维过程;②文献[15]中基于案例类比的方法中案例匹配机制研究得还不够深入,且在灵活性等方面还有较大提升空间;③文献[16]中方法在案例较少时难以构建决策树,易受噪声影响。
针对以上不足,本文沿用案例类比的思想,结合KNN算法进行居民地的案例类比选取。首先把制图专家对居民地交互选取结果作为案例对象,采用三元法对其进行描述、属性赋值以及归一化处理后构建源案例库;然后采用逐步消元法对居民地最佳属性组合进行选择判定,并训练数据确定KNN算法的最佳K值;最后,基于案例推理方法,结合KNN算法,将新案例与源案例库检索匹配,得出决策结果,进而指导居民地的自动选取,达到学习专家综合知识并模仿专家综合结果的目的,同时在一定程度上使得选取结果更加符合人类的认知习惯,增强地图的可读性。
1 案例推理和KNN算法原理 1.1 案例推理基本原理长期以来,制图专家知识的表达一直是制约制图综合发展的瓶颈[17]。这是因为专家在进行交互式综合时,除了有显性的制图综合规则外,还隐性包含了制图专家自身的制图经验,难以形式化表达。基于案例推理CBR(case-based reasoning)符合制图者的心理认知过程,如图 1所示。具体是指在进行问题求解时,使用以前求解类似问题的经验和获取的知识来推理,并且将新获取的知识形成新的案例加入到案例库中去,从而通过不断充实案例库来丰富系统的经验[18]。
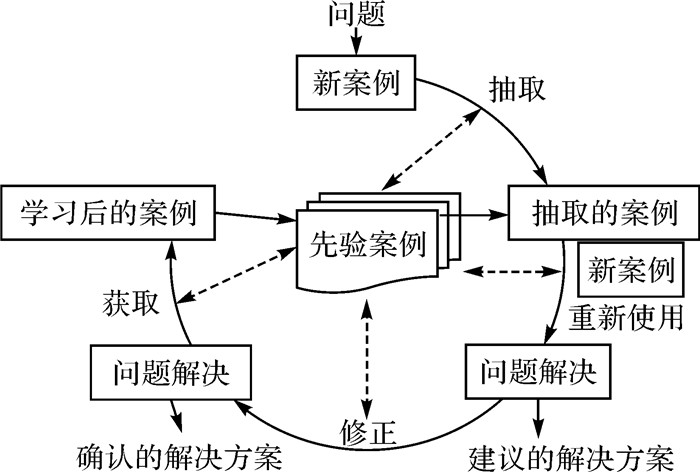
|
| 图 1 一般的CBR模型 Fig. 1 General CBR model |
CBR基于以下两条原则:①相似的问题有相似的解决方法;②同类的问题会再次发生[17]。这与制图综合的情况相符合。与基于模型推理和基于规则推理相比,案例推理降低了知识的获取难度,简化了问题的求解途径,提高了推理的制图效率,不需要得出像规则那样准确和抽象的知识,而是直接使用隐含的难以提取规则的专家案例,且以获取新案例的方式实现自学习,系统维护简单。
1.2 KNN算法基本思想KNN是基于统计模式的有监督学习的类比算法[19],其核心思想是:首先对整个案例库检索,逐个进行计算,算出待求解的目标案例与案例库中的源案例之间的相似度,然后选择K个相似度高的源案例,依次统计出这K个案例对象的所属类别,找出包含最多个数的类别作为案例分类决策的结果[20]。
KNN在居民地案例推理中具体定义如下:
定义1:专家选取居民地案例集合X:X={X1, X2, …, Xn},其中Xi是集合X中第i个居民地案例,n为居民地案例的总个数。
定义2:待决策居民地案例集合Y:Y={Y1, Y2, …, Yn},其中Yi是集合Y中第i个居民地案例,n为居民地案例的总个数。
定义3:专家选取居民地案例Xi={ai1, ai2, …air, …, aim}, 其中air为专家选取居民地案例Xi的第r个属性,m为每个案例的属性总个数。
定义4:待决策居民地案例Yj={bj1, bj2, …bir, …, bjm}, 其中bjr为待决策案例Yi的第r个属性,m为每个案例的属性个数。
定义5:待决策居民地案例Yj与专家选取居民地案例Xi之间的相似值的计算采用欧氏距离表达,即公式
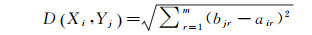 (1)
(1)
定义6:待决策居民地案例Yj的K个最近邻对象集合
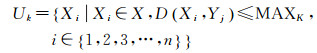
式中,MAXk表示待决策居民地案例Yj与所有专家选取居民地案例相似度按从小到大排序的第K个距离值。
KNN算法直观,易于实现,且在案例较少时也能做出决策。与泛化案例构建案例库的简单类比推理和采用决策树提取隐含规则方法相比,KNN算法不需要产生额外的数据来描述规则,它的规则就是案例本身。它并不严格要求数据的一致性,在一定程度上允许存在噪声。噪声数据是指制图专家由于疲劳、注意力不集中等原因导致的居民地选取的错误结果。这些噪声数据加入案例库后,若采用简单类比推理和归纳推理等方法的学习机制会直接影响案例推理的效果。KNN根据待分类样本的K个近邻样本来预测待分类案例的类别,在一定程度上能有效避免噪声的影响,从而使案例分类决策更准确。
2 居民地案例的设计与构建 2.1 居民地案例的描述在进行基于案例推理时,首先需要将专家选取结果转化为专家选取案例。本文采用三元表示法,由制图综合案例对象(Object-O)、特征(Feature-F)以及综合标记(Label-L)组成的一条记录表示制图综合案例。其形式化的表示为
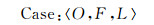 (2)
(2)
式中,案例对象(O)是指具体操作的居民地对象,如FID_068、FID_066;特征(F)也称为描述性项或属性,包含居民地自身信息的描述以及通过空间分析获得的居民地所处的制图环境的描述,现总结6个居民地属性指标[21-22],如居民地行政等级(grade)、居民地面积(area)、邻近道路等级(neighbor roads grade,NRG)、最近居民地距离(nearest habitation distance,NHD)、邻近居民地等级差(nearest habitation grade difference,NHG)、居民地密度(density)等来反映居民地自身属性,居民地与居民地之间的关系以及居民地与其他要素之间的关系;综合标记(L)是指居民地所处的综合操作,例如选取(S)、删除(D),合并(H)等,其中删除(D)在案例显示时应表示为面要素降维到点要素,为方便表示,文中将降维标记为删除,如表 1所示。
| 案例对象(O) | 特征(F) | 综合 标记 (L) | |||||
| 行政等级 (grade) | 面积(Area) /m2 | 邻近道路等级 (NRG) | 最近居民地距离 (NHD)/m | 邻近居民地等 级差(NHG) | 居民地密度 (density) | ||
| FID_01 | 一级 | 554 648.1 | 1.3 | 3 775.671 288 | 0 | 0.079 7 | S |
| FID_02 | 三级 | 1 540 231 | 3.6 | 1 989.575 15 | 0 | 0.023 3 | S |
| FID_03 | 二级 | 906 271.4 | 1.5 | 865.077 997 | 0 | 0.035 5 | S |
| FID_04 | 四级 | 457 897.8 | 0 | 1 989.575 15 | 0 | 0.064 5 | D |
| FID_05 | 一级 | 835 933.5 | 1.6 | 261.653 21 | 0.571 429 | 0.047 1 | H |
| ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ |
采用三元描述法,对专家选取居民地数据进行统一,确保在进行案例匹配时新的目标案例能够在源案例库中匹配到综合结果,方便数据的检索、存储和管理。
2.2 居民地属性的赋值、归一化处理不同变量的量纲不同,为了消除量纲的影响,便于KNN相似度的计算,需对居民地属性赋值并进行归一化处理。居民地属性类型主要包括两种:数值型和字符型。
首先考虑字符型属性的处理,其中为方便计算将居民地行政等级数值化为4个等级,从1到4分别对应市(一级)、区(二级)、镇(三级)、村庄(四级)。居民地行政等级赋值并进行归一化处理,如表 2所示:
| 居民地 名称 | 居民地行政 等级(G) | 归一化处理过程 | |
| 数值化表示 (赋值) | 归一化处理 后值 | ||
| 霸州市 | 一级 | 4 | 1 |
| 房山区 | 二级 | 3 | 0.75 |
| 胜芳镇 | 三级 | 2 | 0.5 |
| 大辛庄 | 四级 | 1 | 0.25 |
对于数值型属性,采用min-max标准化(min-max normalization)使结果值映射到[0-1]之间。转换函数如下
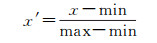 (3)
(3)
式中,max为样本属性数据的最大值;min为样本属性数据的最小值。
对area、NRG、NRD属性特征进行归一化处理后结果如表 3所示:
| 案例对象(O) | 特征(F) | 综合 标记(L) | |||||
| 行政等级 (grade) | 面积(area) | 邻近道路 等级 (NRG) | 最近居民地 距离 (NHD) | 邻近居民地 等级差 (NHG) | 居民地密度 (density) | ||
| 居民地_01 | 1 | 0.023 4 | 0.109 2 | 0.046 4 | 0 | 0.079 7 | S |
| 居民地_02 | 0.5 | 0.065 | 0.302 5 | 0.024 5 | 0 | 0.023 3 | S |
| 居民地_03 | 0.75 | 0.038 2 | 0.126 1 | 0.010 6 | 0 | 0.035 5 | S |
| 居民地_04 | 0.25 | 0.019 3 | 0 | 0.024 5 | 0 | 0.064 5 | D |
| 居民地_05 | 1 | 0.035 3 | 0.134 5 | 0.003 2 | 0.571 4 | 0.047 1 | H |
| ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ |
2.3 居民地属性的筛选
居民地选取本身顾及属性较多,属性选择的判定对于选取结果的好坏起到决定性作用,而属性的选择与数据类型、制图专家的主观判断密切相关。本文采用逐步消元法解决居民地属性选取多少和选取哪些的问题,并用十折交叉验证的方法得出分类正确百分比。十折交叉验证是将数据集分成10份,轮流将其中9份作为训练数据,1份作为测试数据,进行试验,得出相应的正确率,10次结果正确率的平均值最终试验结果[23]。逐步消元法的具体步骤是:首先从训练数据完整的属性集中移除单个属性,余下属性形成一个属性子集,对每个属性子集进行十折交叉验证,通过对比分类正确率确定最佳对象的属性子集,按照这种方式重复,即在逐步减少属性数量的同时进行十折交叉验证,记录分类正确的百分比,结果如表 4所示。
| 属性数量 | 最佳子集的属性 | 分类正确率 /(%) |
| 6 | area, grade, NRG, NHD, NHG, density | 81.28 |
| 5 | area, grade, NRG, NHG, density | 83.65 |
| 4 | area, grade, NRG, density | 87.08 |
| 3 | area, grade, density | 84.36 |
| 2 | grade, density | 81.686 |
| 1 | grade | 74.87 |
| 0 | 64.31 |
从试验结果可以看出,当属性个数为4且属性组成为area、grade、NRG、density时分类正确率最高。由此确定参与决策的属性,并依此整理专家选取结果数据,构建居民地源案例库。
3 基于KNN算法的居民地案例匹配基于KNN算法实现案例匹配的一般步骤为:
(1) 训练数据,确定最佳K值。
(2) 根据距离函数计算待分类居民地x与源案例库每个训练样本的距离,选择与案例样本距离最小的K个样本作为x的K个最近邻。
(3) 根据K个最近邻判断出x所属类别。
判断的依据是,设选取(S)个数为m,删除(D)个数为n,合并(H)个数为p,K=m+n+p,其中函数max(a, b)为a、b二者最大值:①若m>max(n, p),则待处理居民地综合操作结果为选取(S);②若n>max(m, p),则待处理居民地综合操作结果为删除(D);③若p>max(m, n),则待处理居民地综合操作结果为合并(H);④若m=n=p,则属于模糊结果,交由专家处理,进行人工交互判断,问题解决后与①、②、③决策案例一起存入源案例库作为更新案例,实现案例的自学习。
3.1 K值的选择KNN算法中K值决定了分类模型的好坏,K值太小会导致分类精度下降,K值过大会导致误差过大从而影响分类的效率[24]。本文采用控制变量法和十折交叉验证训练数据样本,通过查全率(recall)、查准率(precision)、F1测度值和分类正确率4个指标来判断最佳K的取值[23]。评价指标值越大,说明此时的K近邻模型的分类性能越好,案例匹配的精度越高。以选取操作为例公式如下
 (4)
(4)
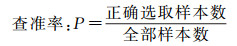 (5)
(5)
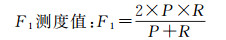 (6)
(6)
查全率度量分类器正确预测正例的比例,查全率越高,分类的误判率越低;查准率确定分类模型为正例的部分记录中实际为正例的记录所占的比例;F1测度值是查全率和查准率的调和均值,即在认为二者具有同等重要作用的前提下,将二者结合为一个指标。现将训练数据(206个案例)中不同K值试验结果如表 5所示:
| K值 大小 | 查全率 (R) | 查准率 (P) | F1测 度值 | 分类正确率 /(%) |
| K=1 | 0.899 | 0.899 | 0.899 | 89.90 |
| K=2 | 0.899 | 0.9 | 0.895 | 89.90 |
| K=3 | 0.909 | 0.908 | 0.908 | 90.88 |
| K=4 | 0.912 | 0.913 | 0.910 | 91.20 |
| K=5 | 0.902 | 0.901 | 0.902 | 90.23 |
| K=6 | 0.899 | 0.898 | 0.898 | 89.90 |
| K=7 | 0.906 | 0.905 | 0.905 | 90.55 |
| K=8 | 0.909 | 0.908 | 0.908 | 90.88 |
由推理结果可以看出,当训练样本个数为206,K=4时,采用KNN算法进行案例分类正确率最高。
3.2 最佳K值的确定文献[25]研究发现最佳K值一定程度上与案例的规模存在关联,即K取训练样本的2%时可以取得的分类效果最好。为了进一步探寻本文居民地选取案例类比推理最佳K值的选择与案例库规模的关系,本文采取不同的K值对其应用效果进行了大量的测试,并采用不同的案例个数进行验证,依据3.1节提供的方法,依次确定每组训练数据的最佳K值,试验结果如表 6所示。
| 试验 | A组 | B组 | C组 | D组 |
| 案例个数 | 100 | 206 | 306 | 486 |
| 最佳K值 | 2 | 4 | 6 | 9 |
分析试验结果发现,针对当前居民地数据,最佳K值与案例样本的总数确实存在一定的相关关系,验证了文献[24]的结论,即K取训练样本的2%时可以取得的分类效果最好。
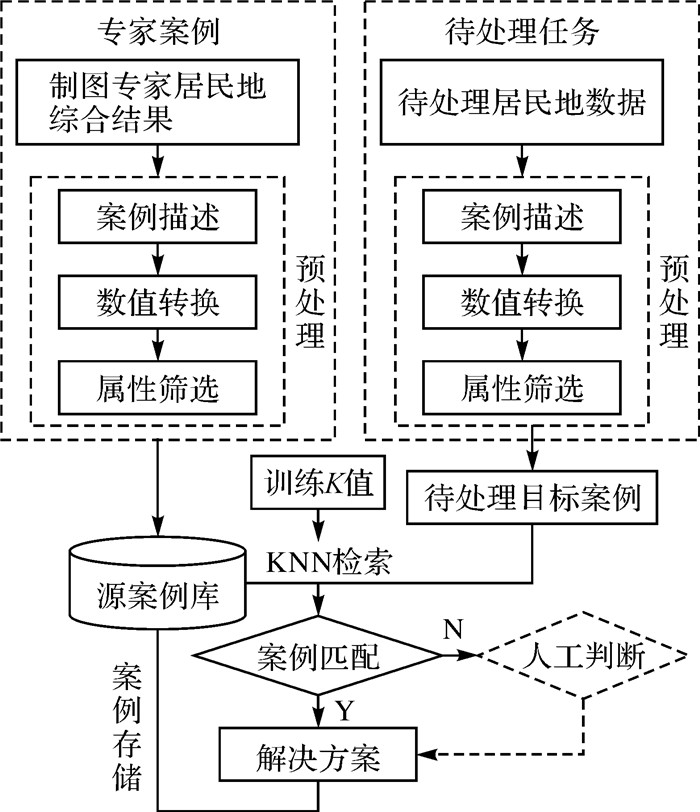
4 试验与分析 4.1 试验流程因大比例尺地图中居民地综合面临的算子较多,如选取、合并、典型化、融合、位移等,本文暂不予以考虑。本文主要针对中小比例尺面状居民地数据,采用基于KNN算法和案例推理进行居民地选取,其基本步骤与流程如图 2所示。
|
| 图 2 基于KNN与案例推理的居民地选取技术路线 Fig. 2 The technology route of habitation selection based on KNN and CBR |
图 2所示技术路线图中主要包括以下5个步骤:
(1) 专家案例描述。对制图专家的居民地选取结果通过三元法进行结构化描述,构建专家选取居民地案例。
(2) 数值转换。将居民地案例输入,对案例进行属性赋值、归一化等数值转换处理。
(3) 案例属性筛选。采用逐步消元法,确定参与决策的最佳属性组合。构建格式统一的源案例库。
(4) 案例匹配。训练数据,确定最佳K值,启动类比推理和KNN检索机制,将每个待处理居民地案例与源案例库中的案例进行匹配,根据匹配结果得出解决方案,并依据解决方案指导居民地的选取。
(5) 人工处理。若KNN检索中判断案例类别个数相等,此时机器无法做出判决,需进行人工处理。将人工处理后的居民地数据源与成功匹配的居民地数据一起作为新案例加入到源案例库中。
4.2 试验与分析为了验证本文提出的居民地智能选取方法的有效性和优势性,利用居民地数据进行了相关试验。依据流程设计试验如下:以综合的比例尺为1:10万至1:20万,北京及其周边602个专家交互选取居民地作为源案例库,如图 3所示。

|
| 图 3 专家案例数据示例 Fig. 3 Example of expert cases data |
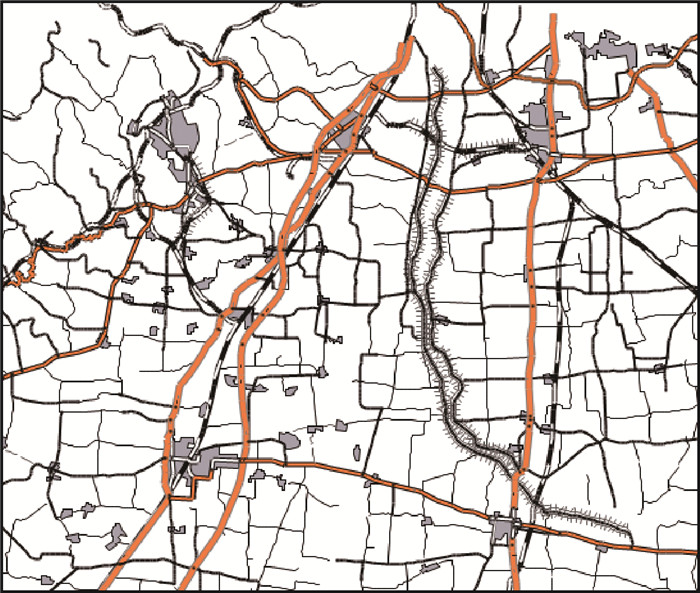
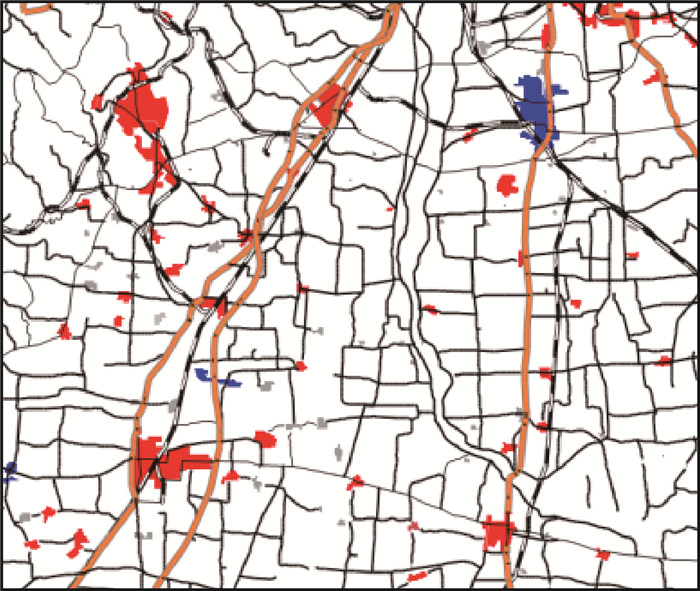
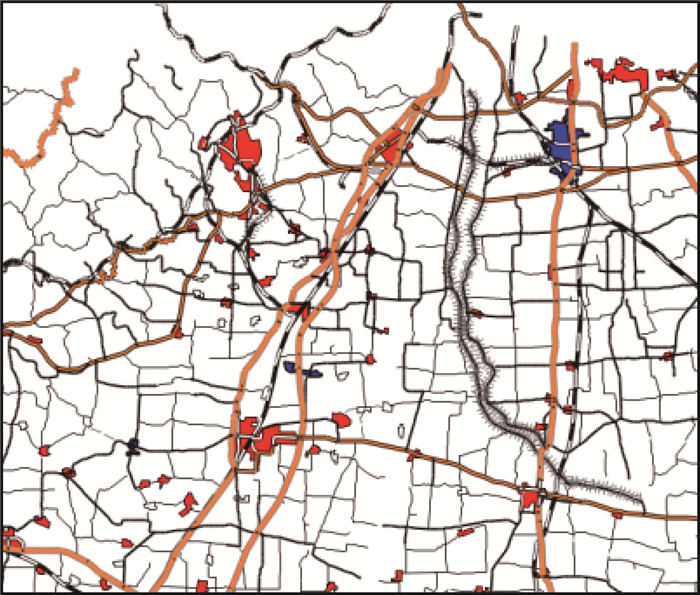
将制图环境相似的涿州市附近150个居民地作为试验案例,部分如图 4所示。数据预处理完成后,进行试验案例与源案例库的KNN检索匹配,依据3.2节的结论可知,此时最佳K值为12。图 5为KNN试验自动综合的结果,专家交互选取结果如图 6所示。图中居民地选取的对象标记为红色,删除居民地对象标记为灰白色,蓝色为合并居民地对象。从图中可以看出,图 5与图 6对应居民地颜色大部分一致,即综合结果总体相似度很高,只存在少量不一致的情况。
|
| 图 4 试验案例示例(部分) Fig. 4 Example of experiment data (part) |
|
| 图 5 KNN综合结果 Fig. 5 KNN generalization result |
|
| 图 6 专家综合结果 Fig. 6 Expert generalization result |
为检验KNN算法综合结果的科学性和准确性,对此方法结果与图 6专家交互选取结果进行详细对比与分析。为方便比较,仅显示居民地要素,如图 7、图 8所示,相关数据统计见表 7。
| 比较项目 | 专家交互选取 | KNN算法 |
| 选取个数/错误选取个数 | 103/0 | 93/10 |
| 删除个数/错误删除个数 | 40/0 | 37/3 |
| 合并个数/错误合并个数 | 7/0 | 4/3 |
| 选取查全率R1/(%) | 100 | 90.29 |
| 删除查全率R2/(%) | 100 | 92.5 |
| 合并查全率R3/(%) | 100 | 57.14 |
| 有效决策率/(%) | 100 | 100 |
| 决策正确率/(%) | 100 | 89.33 |
分析试验对比结果可知,与专家交互选取结果相比,采用基于KNN的案例推理方法综合后的居民地基本上保持了其分布特征,取得了较好的综合效果。在复杂的制图环境下,决策正确率达89.33%,且忠于专家经验,很大程度上还原了专家的制图水平。仅存在极少量与专家选取不一致的综合结果,部分如图 7、图 8箭头所示,进一步分析发现该部分居民地处在专家判断标准的边缘,存在不可避免的模糊性,导致错误的产生。
进一步研究发现,基于案例推理的居民地选取效果高度依赖源案例库数据的质量。制图专家对居民地交互选取过程中,由于疲劳、注意力不集中、视觉误差、操作失误等原因,会造成居民地选取的操作结果出现错误。这些被称作噪声的错误案例加入到源案例库后会直接影响学习效果,最终影响指导解决新任务的质量。本文提出的基于KNN的案例推理方法与依据案例归纳出规则的基于决策树方法相比,抗噪能力更强,在一定程度上能够允许噪声的存在,能有效弥补目前案例推理模型在制图综合应用中抗噪能力弱的缺点。
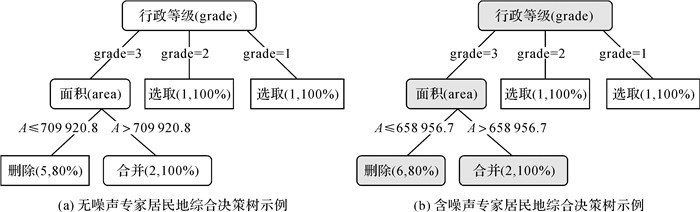
传统的决策树方法中每一个根节点到叶子节点的分枝都是一条由案例演绎归纳得到的规则,如图 9(a)所示,为无噪声专家居民地综合简单决策树示意图。若加入错误的案例即噪声,如:将行政等级grade为3,面积area为658 956.7 m2的居民地案例由选取错操作为合并,则会归纳出错误的规则,如图 9(b)灰色标志决策所示。而案例推理模型是已解决的新问题不断加入到案例库中,这种“滚雪球”式的发展会指导更多的案例进而造成更多错误决策。
|
| 图 9 两种情况决策树生成对比示例 Fig. 9 Comparison of two cases of decision tree generation |
而由1.2节KNN算法基本思想可知,KNN算法是K个案例参与决策待处理案例结果,故决策时个别噪声的存在对判断结果影响甚微,即基于KNN的案例推理模型在一定程度上受噪声案例影响较小。为证明本文算法在抗噪方面的优势性,设计试验在源案例库中分别添加不同比例随机噪声进行对比试验,二者决策正确率具体统计结果如表 8所示,对比趋势图如图 10所示。
| (%) | ||
| 加噪程度 | 决策树 | KNN/ |
| 0 | 88 | 89.33 |
| 2 | 86.67 | 88.57 |
| 4 | 85.33 | 86 |
| 6 | 82 | 85.33 |
| 8 | 80 | 85.33 |

|
| 图 10 加噪后决策树与KNN算法决策正确率结果趋势图 Fig. 10 The trend of decision tree and KNN after adding noise |
分析试验结果可知,KNN算法更稳定。随着噪声数据的加入,决策树方法正确率受影响较大,而使用KNN算法的决策正确率相对稳定,可见KNN算法在随机噪声干扰下鲁棒性更强,有效弥补了目前案例推理模型在制图综合应用中抗噪能力弱的缺点。
5 结论本文提出一种基于KNN案例推理的居民地选取方法,该方法直接以制图专家对居民地交互选取结果作为案例对象,利用案例类比推理和KNN算法完成了居民地选取从已有专家案例到未知结果决策的转化,达到了学习专家综合知识并模仿专家综合结果的目的。本文方法决策正确率高,受噪声影响相对较小,有效弥补了目前案例推理模型在制图综合应用中抗噪能力弱的缺点,且不需要提取规则;同时能有效利用专家经验,一定程度上降低制图综合的难度,为智能化自动综合提供了新思路。
本文案例之间相似度是根据案例的所有属性计算的,KNN计算时默认每个属性的作用都相同,即被赋予相同权重。如何进一步优化KNN算法,对案例属性合理赋权值,使得案例推理对居民地选取结果准确率更高,是本文进一步的研究方向。
| [1] |
王家耀.
地图制图学与地理信息工程学科进展与成就[M]. 北京: 测绘出版社, 2011.
WANG Jiayao. Advances in Cartography and Geographic Information Engineering[M]. Beijing: Surveying and Mapping Press, 2011. |
| [2] |
王家耀.
普通地图制图综合原理[M]. 北京: 测绘出版社, 1993.
WANG Jiayao. The Principles of General Cartographic Generalization[M]. Beijing: Surveying and Mapping Press, 1993. |
| [3] |
杜凤艳. ArcGIS环境下居民地属性综合的研究[D]. 太原: 太原理工大学, 2007. DU Fengyan.Study on the Attribute Generalization of City Settlements in ArcGIS[D].Taiyuan:Taiyuan University of Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10112-2008017470.htm |
| [4] |
邓红艳, 武芳, 钱海忠.
基于遗传算法的点群目标选取模型[J]. 中国图象图形学报, 2003, 8(8): 970–976.
DENG Hongyan, WU Fang, QIAN Haizhong. A Model of Point Cluster Selection Based on Genetic Algorithms[J]. Journal of Image and Graphics, 2003, 8(8): 970–976. DOI:10.11834/jig.200308346 |
| [5] |
钱海忠, 武芳, 邓红艳.
基于CIRCLE特征变换的点群选取算法[J]. 测绘科学, 2005, 30(3): 83–85.
QIAN Haizhong, WU Fang, DENG Hongyan. A Model of Point Cluster Selection with CIRCLE Characters[J]. Science of Surveying and Mapping, 2005, 30(3): 83–85. |
| [6] |
蔡永香, 郭庆胜.
基于Kohonen网络的点群综合研究[J]. 武汉大学学报(信息科学版), 2007, 32(7): 626–629.
CAI Yongxiang, GUO Qingsheng. Points Group Generalization Based on Konhonen Net[J]. Geomatics and Information Science of Wuhan University, 2007, 32(7): 626–629. |
| [7] |
艾廷华, 刘耀林.
保持空间分布特征的群点化简方法[J]. 测绘学报, 2002, 31(2): 175–181.
AI Tinghua, LIU Yaolin. A Method of Point Cluster Simplification with Spatial Distribution Properties Preserved[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 175–181. |
| [8] |
胡慧明, 钱海忠, 何海威, 等.
采用层次分析法的面状居民地自动选取[J]. 测绘学报, 2016, 45(6): 740–746.
HU Huiming, QIAN Haizhong, HE Haiwei, et al. Auto-selection of Areal Habitation Based on Analytic Hierarchy Process[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 740–746. DOI:10.11947/j.AGCS.2016.20150078 |
| [9] |
胡慧明, 钱海忠, 何海威, 等.
采用主成分分析法的面状居民地自动选取[J]. 测绘与空间地理信息, 2016, 39(4): 41–45, 49.
HU Huiming, QIAN Haizhong, HE Haiwei, et al. Auto-selection of Areal Habitation Based on Analytic Hierarchy Process[J]. Geomatics & Spatial Information Technology, 2016, 39(4): 41–45, 49. |
| [10] |
王光霞.
用专家系统技术实施居民地自动综合[J]. 解放军测绘学院学报, 1996, 13(1): 55–59.
WANG Guangxia. The Expert System Method for Inhabited Place Automatic Generalization[J]. Journal of Geomatics Science and Technology, 1996, 13(1): 55–59. |
| [11] |
温婉丽. 基于知识的居民地地图自动综合的研究[D]. 西安: 长安大学, 2006. WEN Wanli.Map of Residents to Automatic Comprehensive Research Based on the Knowledge[D].Xi'an:Chang'an University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-11941-2009257284.htm |
| [12] |
钱海忠, 武芳, 王家耀.
自动制图综合及其过程控制的智能化研究[M]. 北京: 测绘出版社, 2012.
QIAN Haizhong, WU Fang, WANG Jiayao. Study of Automated Cartographic Generalization and Intelligentized Generalization Process Control[M]. Beijing: Surveying and Mapping Press, 2012. |
| [13] |
武芳, 钱海忠, 邓红艳, 等.
面向地图自动综合的空间信息智能处理[M]. 北京: 科学出版社, 2008.
WU Fang, QIAN Haizhong, DENG Hongyan, et al. Intelligent Processing of Spatial Information for Automatic Map Generalization[M]. Beijing: Science Press, 2008. |
| [14] | RUAS A.Automating the Generalisation of Geographical Data:the Age of Maturity[C]//Proceedings of the 20th International Cartographic Conference.Beijing:[s.n.], 2001. |
| [15] |
郭敏, 钱海忠, 黄智深.
道路网智能选取的案例类比推理法[J]. 测绘学报, 2014, 43(7): 761–770.
GUO Min, QIAN Haizhong, HUANG Zhishen. Intelligent Road-network Selection Using Cases Based Reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 761–770. DOI:10.13485/j.cnki.11-2089.2014.0120 |
| [16] |
郭敏, 钱海忠, 黄智深, 等.
ID3决策树推理模型及其在道路网选取中的应用[J]. 测绘科学技术学报, 2012, 29(4): 308–312.
GUO Min, QIAN Haizhong, HUANG Zhishen, et al. ID3 Decision Tree Oriented Knowledge Reasoning Model and Its Application in Road Network Selection[J]. Journal of Geomatics Science and Technology, 2012, 29(4): 308–312. |
| [17] | HOLT A. Applying Case-based Reasoning Techniques in GIS[J]. International Journal of Geographical Information Science, 1999, 13(1): 9–25. DOI:10.1080/136588199241436 |
| [18] | AAMODT A, PLAZA E. Case-based Reasoning:Foundational Issues, Methodological Variations, and System Approaches[J]. Ai Communications, 1994, 7(1): 39–59. |
| [19] |
冯锐.
基于案例推理的经验学习[M]. 上海: 华东师范大学出版社, 2012.
FENG Rui. Experiential Learning on Case-based Reasoning[M]. Shanghai: East China Normal University Press, 2012. |
| [20] |
周伟达. 核机器学习方法研究[D]. 西安: 西安电子科技大学, 2003. ZHOU Weida.Kernel Based Learning Machines[D].Xi'an:Xidian University, 2003. http://doi.wanfangdata.com.cn/10.7666/d.y579396 |
| [21] |
王家耀, 姚杰.
模糊综合评判在制图综合中的应用(以居民地选取为例)[J]. 测绘学院学报, 1985(2): 47–54.
WANG Jiayao, YAO Jie. An Application of Fuzzy Comprehensive Estimation in Cartographic Generalization[J]. Journal of the Institute of Surveying and Mapping, 1985(2): 47–54. |
| [22] |
胡慧明. 基于层次结构模型的居民地自动选取方法研究[D]. 郑州: 信息工程大学, 2016. HUI Huiming.Research on Automatic Habitation Selection Method Based on Hierarchical Structure Model[D].Zhengzhou:Information Engineering University, 2016. http://www.cnki.com.cn/Article/CJFDTOTAL-MOTO201409008.htm |
| [23] |
袁梅宇.
数据挖掘与机器学习——WEKA应用技术与实践[M]. 北京: 清华大学出版社, 2014.
YUAN Meiyu. Data Mining and Machine Learning:WEKA Application Technology and Practice[M]. Beijing: Tsinghua University Press, 2014. |
| [24] |
严爱军, 钱丽敏, 王普.
案例推理属性权重的分配模型比较研究[J]. 自动化学报, 2014, 40(9): 1896–1902.
YAN Aijun, QIAN Limin, WANG Pu. A Comparative Study of Attribute Weights Assignment for Case-based Reasoning[J]. Acta Automatica Sinica, 2014, 40(9): 1896–1902. |
| [25] |
于瑞萍. 中文文本分类相关算法的研究与实现[D]. 西安: 西北大学, 2007. YU Ruiping.Research and Implement on the Related Algorithms of Chinese Text Classification[D].Xi'an:Northwest University, 2007. http://d.wanfangdata.com.cn/Thesis/Y1090940 |





