2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘信息技术总站, 陕西 西安 710054
2. State key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. Xi'an Technical Division of Surveying and Mapping, Xi'an 710054, China
地理信息检索是一类极为重要的信息检索[1],传统GIS提供的检索模式具有很大局限性,主要体现在查询的输入条件仅基于语义信息或精确的地理范围,忽略了对象的几何信息及其空间关系信息。为解决这一问题,自然语言检索和结构化空间数据语言检索等新型检索模式成为研究的热点。但这些模式中输入的检索条件仍然难以描述、处理和理解较为复杂的、包含有空间关系的空间场景,尤其对于检索给定空间实体间粗略相对位置关系条件的实体集合更为困难。例如,要在网络地图上检索“东边与学校相邻接,且南边与街道相远离的医院”,无法在目前的空间数据库中表达和快速检索到满足这一约束条件的所有医院,另外,用户忘记关键字或提供的关键字不完全准确,也可能导致无法找到所需地理信息。
鉴于此,基于手绘地图(草图)的地理信息检索逐渐受到重视。手绘地图检索条件包含的内容比空间查询语言更接近于人们对地理空间场景的理解,而且能提供许多不能用空间查询语言完全表示的细节。文献[2]提出基于草图的空间数据检索,但主要侧重于基于拓扑关系相似的检索;文献[3]论述了草图处理、检索系统设计等问题,但对线要素与其他要素间的空间关系考虑不足;文献[4]研究了无线网络环境下的草图检索;文献[5-6]探讨了空间场景的相似性度量及其在检索中的应用;文献[7]提出基于支持向量机的手绘草图检索方法;文献[8]通过草图空间关系的定性描述和校准,将草图信息集成到GIS系统中;文献[9]提出了基于二元约束满足问题求解的草图检索方法。上述方法的不足之处在于检索中侧重于拓扑关系,对手绘对象间方向关系考虑不全面,且在检索结果的相似性度量和排序上研究不多。实际上,在手绘地图检索过程中,对象间的方向关系与拓扑关系一样属于强约束条件,仅次于属性信息,当对象间不相交时,方向关系的约束力强于拓扑关系。因此,本文重点基于开域空间方向关系对手绘地图检索展开研究,并提出检索结果的相似度计算与排序方法。
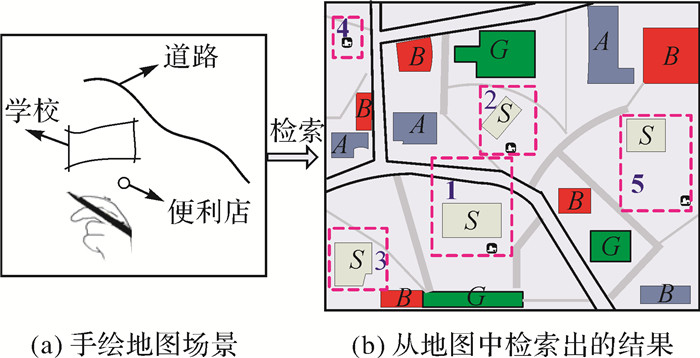
1 问题描述及相关研究手绘地图检索的基本过程是:用户将手绘地图场景提交给检索系统,类似于当前主流的搜索引擎,系统输出一系列与手绘地图相似的结果序列。图 1(b)(见文末)中虚线框内的结果是图 1(a)手绘地图检索结果,框内的数字代表排序值,共有5个结果,相似度越高排序越靠前。
|
| 图 1 手绘地图检索示例 Fig. 1 Hand-drawn map retrieval example |
由图 1可见,手绘地图检索有以下特点:
(1) 将需要检索的空间场景以手绘地图的形式表达出来,这一认知过程具有模糊性和不确定性,但绘制后的手绘地图中对象间方向关系确定且可以量化。
(2) 因为(1)的原因,手绘地图检索输出的是一系列经过排序的结果序列,而非单一的最精确的结果[6]。图 1(b)中5个结果中并非都与输入的手绘地图高度一致。
(3) 因人对方向关系的认知受到对象间距离的影响,距离越小,认知越准确,距离越大,认知越模糊,当对象间距离较大时,需要放宽方向关系约束条件,图 1(b)中结果“5”能被选中就是基于这一因素。
(4) 要从大范围地理信息中检索出一系列相似场景,需建立空间索引以提高检索效率。
根据以上特点,要求面向手绘地图检索的空间方向关系描述具备以下特征:①与基于语义或自然语言的检索不同,描述方法不需要与“东”或“西南”等方位术语相关联,但需根据手绘对象间位置关系进行自适应描述;②既要能精确定量化描述对象间方向关系,又要具备模糊化描述能力,以便扩大检索范围,在尽可能多的检索结果序列中将相似度高的场景排在前面;③方向关系描述方法要便于与空间索引相关联。
经过几十年的发展,方向关系描述模型已取得了较大进展,常见的有方向矩阵模型、MBR模型、锥形模型、投影模型、统计模型、Voronoi模型及这些模型的各种改进。文献[10-17]从定性与定量、精确与模糊、详细与概略等多方面对上述模型进行了研究,取得了很好的效果,但这些模型并不能完全适用于手绘地图检索,主要原因是:①将空间区域固定地划分为几个方向区域以便将方位术语与模型关联起来,不能根据手绘输入对象间位置关系自适应划分空间区域;②上述模型在划分的固定区域内难以区分对象间的方向关系,图 1(b)结果“1”和“2”如果采用方向关系矩阵描述,则不能区分“学校”与“便利店”间的方向关系哪个更能接近手绘地图;③目前方向关系的模糊描述方法大多都与方位术语相关联,而手绘地图检索中方向关系的描述一般不与术语关联;④现有模型中除MBR模型和方向关系矩阵模型外,大多数在空间数据库中与空间索引建立关联关系比较复杂。
针对上述问题,本文借鉴和组合现有空间方向关系描述方法,提出一种适用于手绘地图检索的,基于开域的空间方向关系描述模型,将开域方向关系转化为拓扑关系进行计算。利用该模型对检索的约束条件进行松弛化处理,设计检索流程和基于开域空间方向关系相似度的结果排序策略,建立基于R树的空间索引,以提高查询检索效率,最后以实际数据验证了本文方法的有效性。
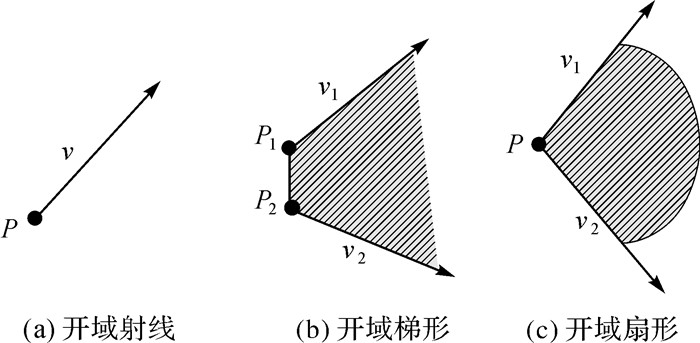
2 面向手绘地图检索的开域空间方向关系描述与计算 2.1 开域空间方向关系描述与约束条件的松弛化开域是指只有部分边界被定义或部分区域无限向外延伸情况下的几何区域[18]。为便于描述方向关系,将其划分为最基本的开域射线、梯形和扇形,如图 2。复杂开域可由这3种组合推导得出。
|
| 图 2 开域 Fig. 2 Open areas |
图 2所示的3类开域可抽象为OpenLine〈P, v〉、OpenTrap〈P1, P2, v1, v2〉和OpenSect〈P, v1, v2〉,P、P1、P2是点的坐标,v、v1、v2是射线方向。
约束条件松弛化是指对手绘输入对象间方向关系这一约束条件进行“放宽”处理,以便适当扩大检索范围,检索到尽可能多的结果,防止条件太过“苛刻”而遗漏结果。
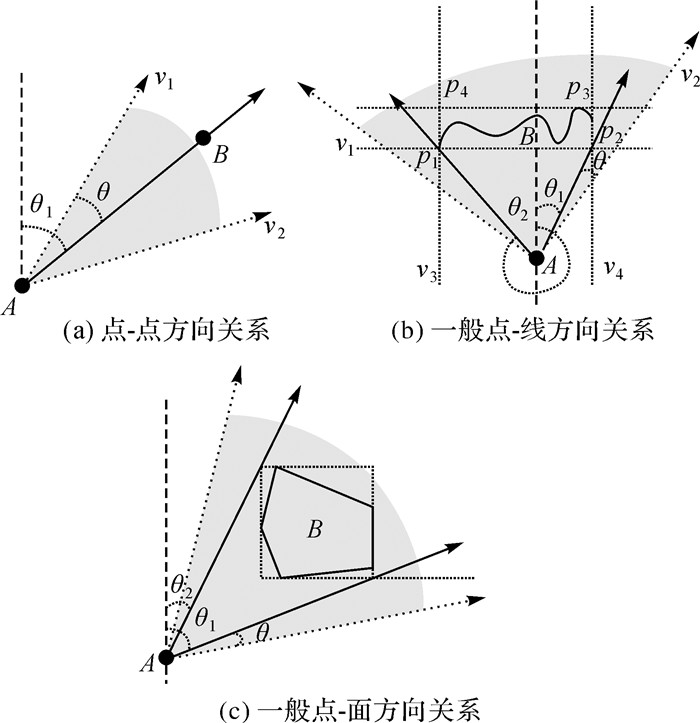
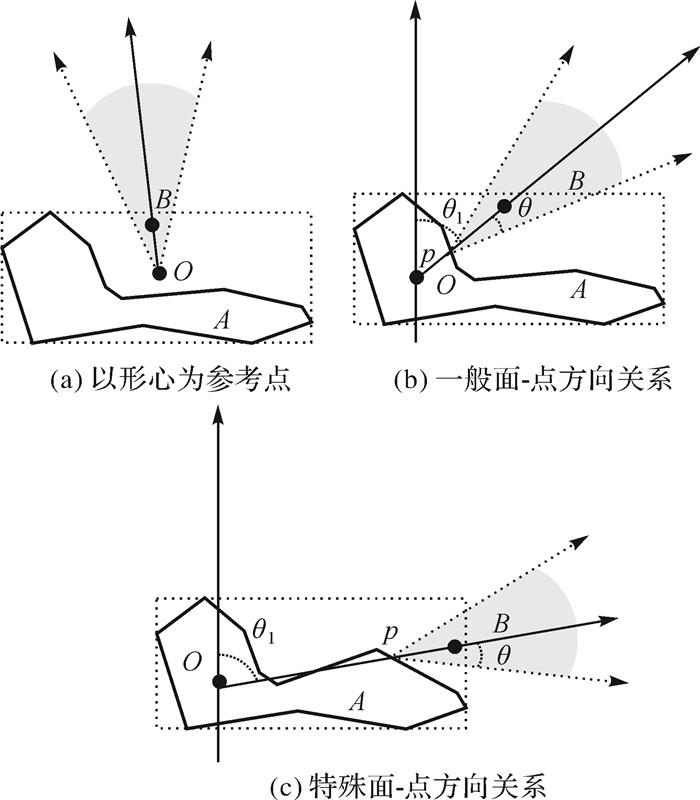
2.1.1 参考对象为点参考对象A为点,目标对象B分别为点、线和面时开域方向关系及松弛化,如图 3所示。图 3(a)中,A与B间方向关系以方位角θ1(规定方位角θ1∈[0, 2π])描述,θ1以参考点A的子午线北方向为基准(下同)。以射线AB为基准边,向两边各扩展θ,构成开域扇形,θ为松弛化角度,扇形区域为松弛化区域。图 3(b)、(c)中A处于线/面对象外接矩形外部时,定义为一般点-线和点-面方向关系,图 3(b)A落入开域梯形OpenTrap〈P1, P2, v3, v4〉内,可通过开域扇形OpenSect〈A, θ1, 2π-θ2〉描述方向关系,其松弛化策略是以射线Ap1和Ap2为基准边,向两边各扩展θ角度范围。图 3(c)点-面关系的描述与图 3(b)类似。
|
| 图 3 一般情况下点对象与单个对象间的开域方向关系及其松弛化 Fig. 3 Directional relations and relaxation between general point and single object |
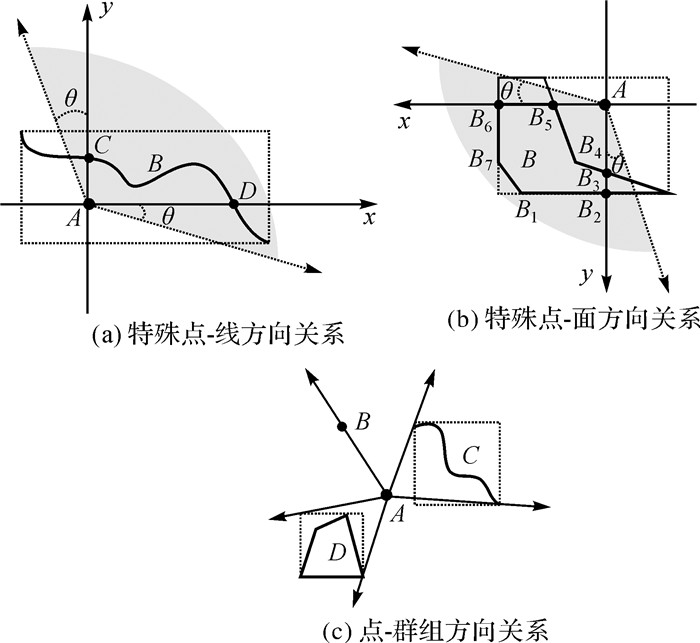
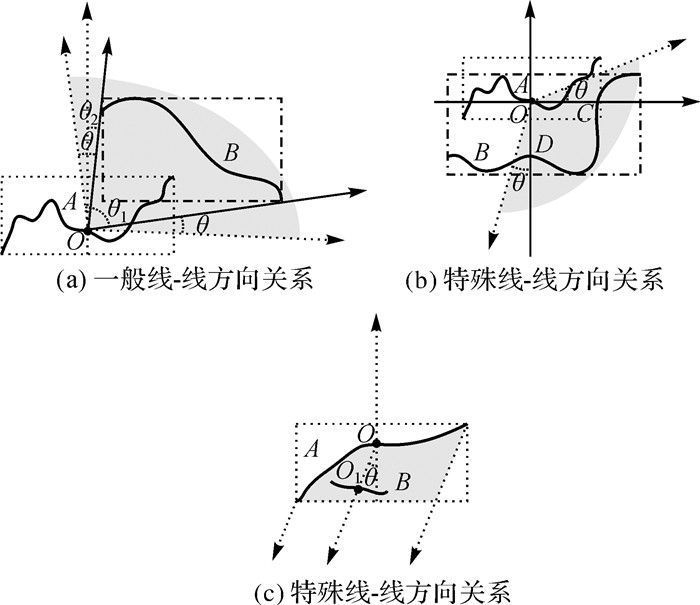
当点处于线/面对象最小外接矩形内部时定义其为特殊情况。图 4(a)中,以A为中心做两条相互垂直的直线x和y,将区域划分为4个象限,求取落入4个象限中长度最长的部分C、D,转化为A与C、D的方向关系,其通过开域扇形OpenSect〈A, 0, π/4〉描述,松弛化策略是以Ax和Ay为基准边向两边各扩展θ角度范围。类似的,图 4(b)中A与B方向关系近似为B落入4个象限中面积最大部分B1B2B3B4B5B6B7与A的方向关系。图 4(c)是A与群组对象B、C和D间的方向关系,其描述方法是先分解为单个对象间的方向关系进行描述,最后进行组合。
|
| 图 4 特殊情况下以点对象为参考对象的开域方向关系及其松弛化 Fig. 4 The special case point objects is the direction relation of the reference object and its relaxation |
综上,参考对象为点时,上述各类方向关系及其松弛化描述如表 1所示(并未穷举所有情况)。
2.1.2 参考对象为线图 5(a)中,若目标对象B位于A的最小外接矩形东、南、西或北方向,以A的中点O为起始点,通过开域射线OB描述AB方向关系;若B位于A的最小外接矩形东北、西北、西南或东南方向,以OB与外接矩形的延长线交点p为起始点,通过开域射线pB描述AB方向关系。图 5(b)中,目标对象B位于A的最小外接矩形内部,以A的中点O为起始点,通过开域射线OB描述AB方向关系。
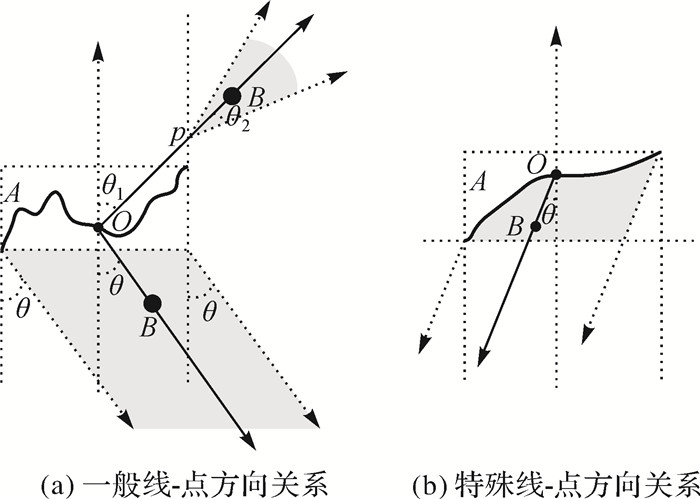
|
| 图 5 线-点对象开域方向关系及其松弛化 Fig. 5 Directional relations and relaxation between line and point |
图 6(a)中,若B未完全落入A的最小矩形内,且A的中点O未落入B的最小外接矩形内,可依据图 3(b)描述;图 6(b)中,B未完全落入A的最小矩形内部,但A的中点O落入B的最小外接矩形内,可依据图 4(a)描述;图 6(c)中,若B完全落入A的最小矩形内部,求对象B的中心O1,问题转化为线A与点O1的方向关系,可依据图 5(b)描述。
|
| 图 6 线-线对象间开域方向关系及其松弛化 Fig. 6 Directional relations and relaxation between line and line |
线-面开域方向关系及其松弛化与线-线方向关系思路基本一致,如图 7所示。
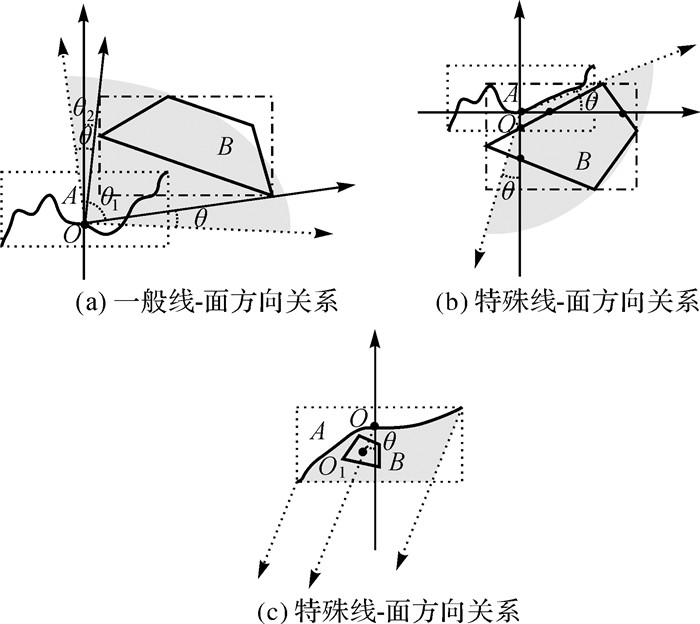
|
| 图 7 线-面对象间开域方向关系及其松弛化 Fig. 7 Directional relations and relaxation between line and polygon |
以线为参考对象时各类开域方向关系及其松弛化描述如表 2所示(部分)。
| 类型 | 方向关系描述 | 松弛化描述 | 示例 |
| 一般线-点 | OpenLine〈O, π-θ 〉 | OpenTrap〈p1, p2, v1, v2〉 | 图 5(a) |
| 一般线-点 | OpenLine〈p, θ1〉 | OpenSect〈p, θ1+θ2, θ1-θ2〉 | 图 5(a) |
| 特殊线-点 | OpenLine〈O, π+θ〉 | OpenTrap〈p1, p3, v3, v2〉∩p1p2 | 图 5(b) |
| 一般线-线 | OpenSect〈O, θ1, θ2〉 | OpenSect〈A, θ1+θ, 2π+θ2-θ〉 | 图 6(a) |
| 特殊线-线 | OpenSect〈O, π/2, π〉 | OpenSect〈O, π/2-θ, π+θ〉 | 图 6(b) |
| 特殊线-线 | OpenLine〈O, π+θ〉 | OpenTrap〈p1, p3, v3, v2〉∩p1p2 | 图 6(c) |
| 一般线-面 | OpenSect〈O, θ1, θ2〉 | OpenSect〈A, θ1+θ, 2π+θ2-θ〉 | 图 7(a) |
| 特殊线-面 | OpenSect〈O, π/2, π〉 | OpenSect〈O, π/2-θ, π+θ〉 | 图 7(b) |
| 特殊线-面 | OpenLine〈O, π+θ〉 | OpenTrap〈p1, p3, v3, v2〉∩p1p2 | 图 7(c) |
2.1.3 参考对象为面
若面为凸多边形,以面的形心为参考点,问题转化为点与目标对象方向关系,但当面为凹多边形时,面的形心可能在外部,此时采用形心作为参考点描述方向关系将与人的认知不符。以图 8(a)为例,B处于A的北部偏西,与人的认知不符,本文参考文献[15]和[19]计算面目标内心,使其始终处于面的内部且能反映面目标的面积及形状分布。图 8(b)以A的内心O为起始点,OB与A的边只有一个交点p,以p为起始点,通过开域射线pB描述AB方向关系;图 8(c)中,若OB与A的边超过一个交点,以距离B最近的交点p为起始点描述AB方向关系。
|
| 图 8 面-点对象间开域方向关系及其松弛化 Fig. 8 Directional relations and relaxation between polygon and point |
图 9中,求A的内心O,问题转化为点-线开域方向关系,可借鉴图 3(b)和图 4(a)描述方向关系并松弛化。图 10中,求A的内心O,问题转化为点-面方向关系,可借鉴图 3(c)和图 4(b)描述。
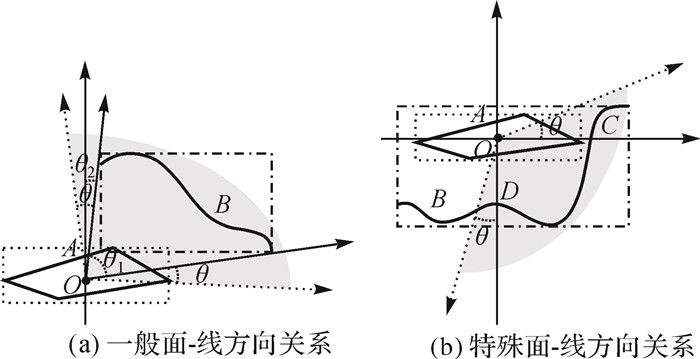
|
| 图 9 面-线对象间开域方向关系及其松弛化 Fig. 9 Directional relations and relaxation between polygon and line |
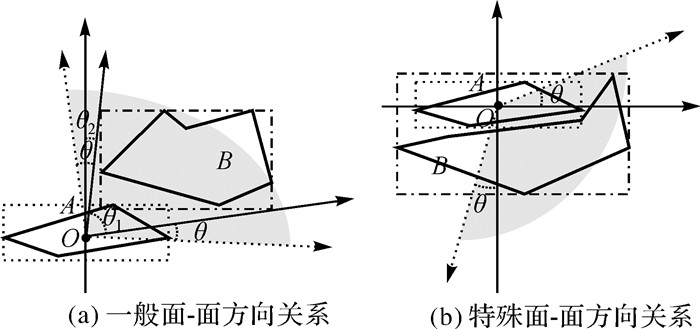
|
| 图 10 面-面对象间开域方向关系及其松弛化 Fig. 10 Directional relations and relaxation between polygon and polygon |
综上,以面为参考对象时开域方向关系及其松弛化描述如表 3所示(部分)。
| 类型 | 方向关系描述 | 松弛化描述 | 示例 |
| 一般面-点 | OpenLine〈p, θ1〉 | OpenSect〈p, θ1-θ, θ1+θ〉 | 图 8(b) |
| 特殊面-点 | OpenLine〈p, θ1〉 | OpenSect〈p, θ1-θ, θ1+θ〉 | 图 8(c) |
| 一般面-线 | OpenSect〈O, θ1, θ2〉 | OpenSect〈A, θ1+θ, 2π+θ2-θ〉 | 图 9(a) |
| 特殊面-线 | OpenSect〈O, π/2, π〉 | OpenSect〈O, π/2-θ, π+θ〉 | 图 9(b) |
| 一般面-面 | OpenSect〈O, θ1, θ2〉 | OpenSect〈 A, θ1+θ, 2π+θ2-θ〉 | 图 10(a) |
| 特殊面-面 | OpenSect〈O, π/2, π〉 | OpenSect〈O, π/2-θ, π+θ〉 | 图 10(b) |
2.2 基于拓扑关系的开域空间方向关系计算
开域方向关系可通过开域拓扑关系计算。开域拓扑关系包括穿越、包含及相交关系。
2.2.1 穿越关系图 11(a)中开域射线是否穿越点B,判断v与θ是否相同即可;图 11(b)中射线pv是否穿越线段p1p2,判断v是否在pp1和pp2之间;图 11(c)中射线pv是否穿越MBR,分3种情况,p在MBR内,则穿越,p在MBR外,若射线pv穿越MBR一条边或穿越MBR两不相邻顶点,则穿越,p在MBR上,若射线pv穿越与p不相邻的MBR一边或顶点时,则穿越。

|
| 图 11 穿越关系 Fig. 11 Crossing |
2.2.2 包含关系
包含关系是指开域梯形或扇形与封闭二维几何图形间的拓扑关系。图 12(a)是否包含点(规定点和线段在边界上不属于包含),只需判断P1O在v1和P1P2之间,且P2O在P2P1和v2之间即可;图 12(b),判断PO在v1和v2之间即可;图 12(c)、(d)、(e)、(f)、(g)、(h)和(i)是开域扇形和梯形包含线段,可分别利用是否穿越点和包含点的方法组合判定;图 12(j)和(k)是包含多边形,只需判断是否包含点或点在边界上即可。
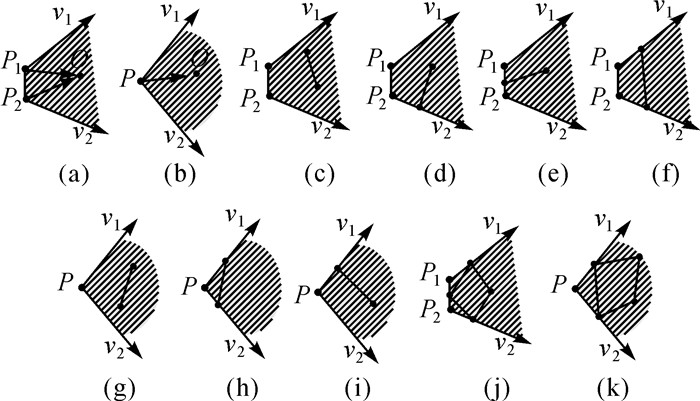
|
| 图 12 包含关系 Fig. 12 Contain |
2.2.3 相交关系
相交关系是指开域梯形和扇形与MBR相交关系,图 13(a)-(d)指开域梯形与MBR的相交关系,图 13(e)-(f)是开域扇形与MBR相交关系,均可通过上述穿越与包含关系计算出。
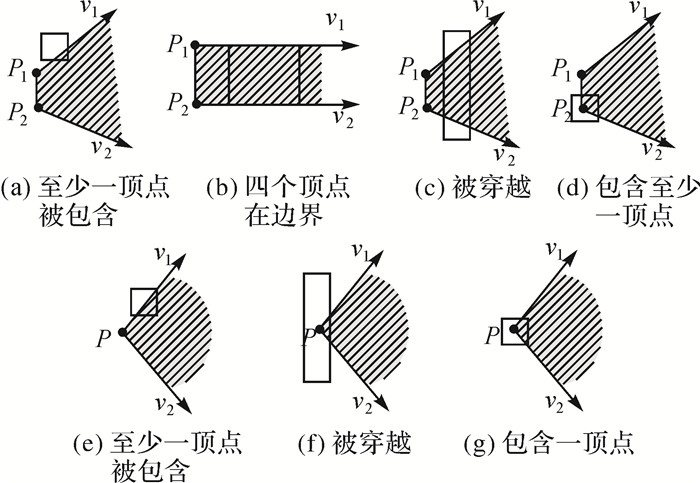
|
| 图 13 相交关系 Fig. 13 Intersect |
3 检索方法 3.1 检索流程
手绘地图检索流程如图 14所示,包括以下步骤:
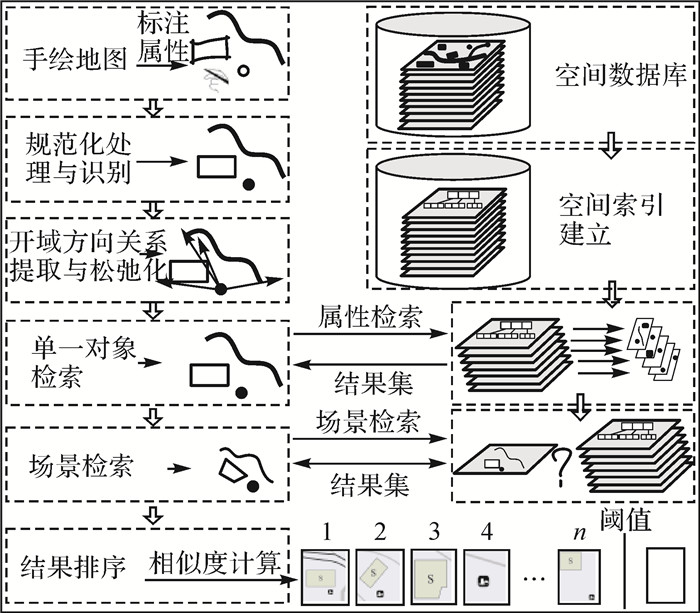
|
| 图 14 检索流程 Fig. 14 Retrieval process |
(1) 对某一幅被检索地图数据构建R树索引。R树由中间节点和叶节点组成,叶节点存储实际空间对象的最小外接矩形MBR和指向实际对象的指针,中间节点存储所有子节点MBR的最小外接矩形和指向子节点的指针。依参考文献[20],R树的建立从空树开始,利用传统的插入算法逐个插入记录,直至生成整个R树。
(2) 手绘地图的规范化处理与识别。手绘输入需查询的地图场景q。因手绘输入的地图具有一定的随意性,尤其是绘制的线对象会存在断裂,面对象存在首末结点不重合等问题,本文采用文献[3]提出的方法对其进行规范化处理,对断裂的线对象进行连接处理,对面对象进行首末结点重合处理或直角化处理,并识别提取通过人工赋值的属性信息和几何位置信息。
(3) 开域方向关系提取与松弛化处理。依据第2节所述方法,提取并计算输入手绘地图的开域空间方向关系,并进行松弛化处理。依据输入顺序,一般以最先输入对象A为参考对象,后续输入对象B1、B2、…、Bi为目标对象集合B。因线对象的特殊性,手绘输入的线一般不完整,故尽可能以线-线交叉点或后续输入的点/面为参考对象。依据2.1节和2.2节,计算A与B间的开域方向关系DR(A, B1)、DR(A, B2)、…、DR(A, Bi)、松弛化区域和距离。
(4) 基于属性的单一对象检索。在空间数据库中检索所有与A属性类别一致的对象序列为d1、d2、…、dj,依据A、B间的开域方向关系DR(A, Bi),给定的松弛化角度θi,先以d1为参考对象和圆心,在给定区域内(因用户关注一定区域内的查询结果,故缩小查询范围)构造松弛化后的开域Oi。
(5) 场景检索。基于所建的R树索引,对于非叶子节点,判断开域O1是否与非叶子节点的最小外接矩形有交集。若有,则保留该节点为根的子树,若无,则剪除该节点为根的子树。对于叶子节点,若O1与该结点最小外接矩形有交集,则将结点内空间对象放入结果集。通过递归调用,检索到O1中包含的对象序列b11、b12、…、d1m,分别计算(A, B1)与(d1, b11)、(A, B1)与(d1, b12)、…、(A, B1)与(d1, b1m)间的开域方向关系相似度,依据相似度对b11、b12、…、d1m进行排序,依次类推,对所有开域Oi进行结果检索和排序。
(6) 结果排序。重新执行步骤(4)-(5),直至完全遍历d1、d2、…、dj,形成最终的结果集合。对结果集合进行组合,计算群组对象间的方向关系相似度,将最终检索结果进行排序输出。
3.2 面向手绘地图检索的开域空间方向关系相似度计算设A和A′为参考对象,B和B′为目标对象,两组开域方向关系相似度记为sim((A, B), (A′, B′))∈[0, 1]。
对开域射线描述的方向关系,记A与B间方向关系为OpenLine〈A, θ〉,A′与B′间的方向关系为OpenLine〈A′, θ′〉,二者相似度通过式(1)计算,θ′-θ是两条射线间的夹角。
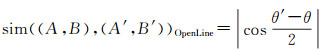 (1)
(1)
对通过开域扇形描述的方向关系,记A与B间方向关系为OpenSect〈A, θ1,θ2〉,A′与B′间的方向关系为OpenSect〈A′, θ′1, θ′2〉,相似度可通过式(2)来计算,θ′1-θ1+θ′2-θ2是4条射线夹角之和。
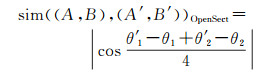 (2)
(2)
对图 4(c)群组目标间开域方向关系相似度,设群组P中除参考对象外的对象数为M,群组Q中除参考对象外的对象数为N,则两个群组间的方向关系相似度sim (P, Q)G为
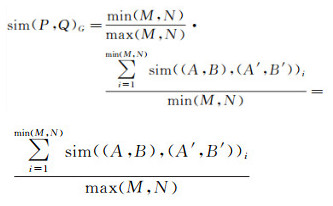 (3)
(3)
式中,sim((A, B), (A′, B′))i是单个开域方向关系间的相似度。
3.3 检索结果评价 3.3.1 查全率和查准率查全率Rn=n/N,查准率Pn=n/T,N为人工主观从地图数据库中找到的与输入手绘地图相关的结果数目,n为计算机利用本文方法自动检索出的存在于T中正确的结果数目,T为计算机自动检索出结果总数。
3.3.2 平均准确率设g1、g2、…、gT为利用算法检索输出的结果场景,rank(g1)、rank(g2)、…、rank(gT)为检索结果序列对应从小到大的排序值(该排序值是由人工确定),平均准确率AP可通过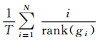
试验空间范围为西安市三环以内城区,108°46′E-109°09′E,34°06′N-34°23′N,面积约900 km2,南北宽30余km,矢量数据来源于OpenStreetMap,数据比例尺经分析在城市区域大于1:5万,主要包括居民地、道路、水系等。因OpenStreetMap数据中地名与点类数据较少,故增加POI数据。POI数据来源于国内某网络地图公司,通过开放的API接口获取,共计7109个,在ArcGIS平台下对数据进行符号化显示,并采用C#语言实现本文提出的方法。
以表 4中通过鼠标手工绘制的5类手绘地图场景为输入条件,通过规范化处理和识别后,在上述地图数据中检索对应的空间场景。
| 序号 | 1 | 2 | 3 | 4 | 5 |
| 手绘场景 | 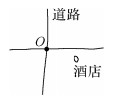 | 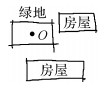 | 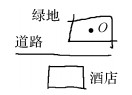 | 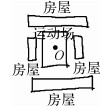 | 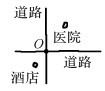 |
| 语义 | 十字路口东南方向(偏北)200 m内的酒店 | 绿地以东(偏北)和南(偏东)200 m内均为房屋的场景 | 道路400 m内以北(偏东)为绿地,以南(偏西)为酒店的场景 | 以运动场为中心,200 m范围东南西北为房屋的场景 | 交叉路口东北方向(偏西),西南方向(偏东)500 m内的酒店 |
| 参数 | 松弛化角度θ=15°; | 松弛化角度θ=20° | 松弛化角度θ=30° | 松弛化角度θ=30° | 松弛化角度θ=40° |
图 15是表 4中第2类场景在全图范围内检索到的部分结果,扇形区域为松弛化区域,凡是与松弛化区域有交集的房屋均标记为检索结果。图 16是5类场景检索排名前5的检索结果。
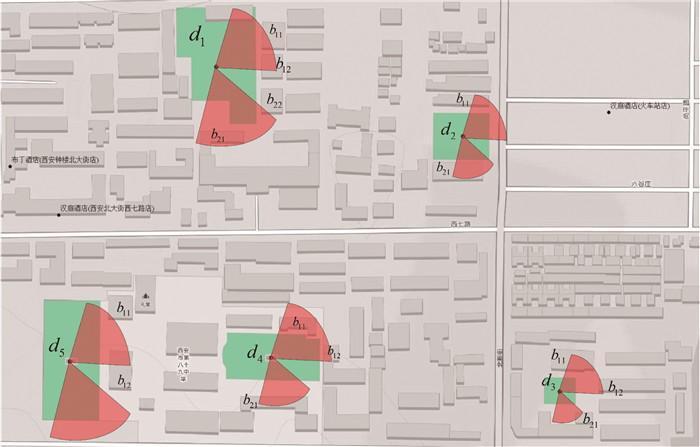
|
| 图 15 第2类场景的部分检索结果 Fig. 15 Part of the second type of scene retrieval results |
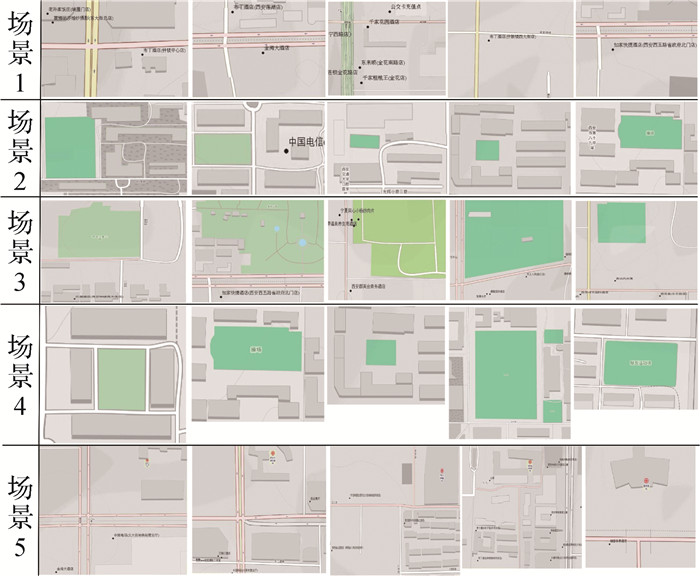
|
| 图 16 排名前5的结果 Fig. 16 Top 5 results |
表 5是表 4中5类场景检索的平均相似度、查全率、查准率和平均准确率。
| 评价指标 | 场景1 | 场景2 | 场景3 | 场景4 | 场景5 |
| 平均相似度 | 0.92 | 0.83 | 0.86 | 0.75 | 0.72 |
| 查全率 | 1 | 0.88 | 0.89 | 0.91 | 1 |
| 查准率 | 1 | 0.90 | 0.83 | 0.96 | 0.97 |
| 平均准确率 | 1 | 0.78 | 0.79 | 0.87 | 0.96 |
4.2 结果分析
为分析松弛化角度θ大小对检索结果的影响,将表 4中5类场景检索过程中查全率、查准率和平均准确率随θ取值的变化曲线绘制为图 17,θ从0开始,每隔5°递增,一直到60°。
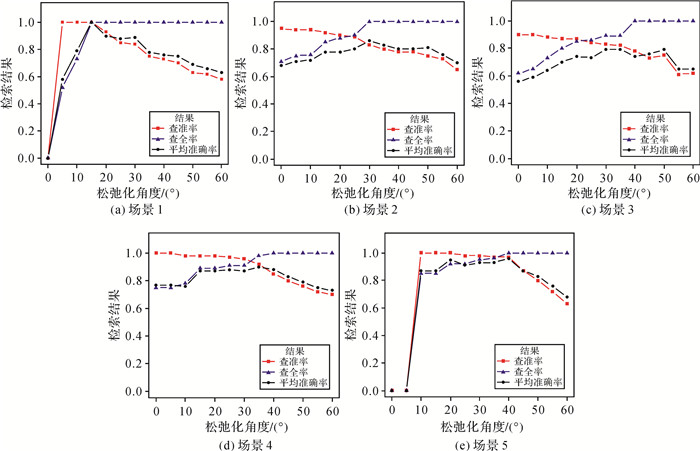
|
| 图 17 检索结果随松弛化角度变化的曲线 Fig. 17 The change curves of the retrieval results with the relaxation angle |
利用文献[3]手绘地图检索方法和文献[5]提出的详细深度方向关系矩阵检索表 4中比较典型的手绘地图场景2和场景5并与本文方法进行比较,则查全率、查准率、平均准确率和耗时结果对比如图 18所示。
4.3 试验结论
(1) 分析图 15、图 16和表 5,采用本文方法可在较大范围地图场景中,在确定的松弛化区域内有效检索到排名靠前的结果,其中类似于场景1和场景5这样的点状手绘地图场景检索效果更佳。
(2) 分析图 17,当松弛化角度不为0,且逐渐增大时,5种手绘地图场景的查准率逐渐减小,而查全率逐渐增大,且到一定程度时趋于1,平均准确率呈现逐渐增大又减小的趋势。希望在尽可能大的查全率和平均准确率前提下查准率能够提高,通过分析检索结果随松弛化角度的变化曲线图,可以为大规模检索时松弛化角度的确定提供先验知识。
(3) 分析图 18,仅场景2中本文方法的查准率与文献[3]相当,但高于文献[5],其余查准率、查全率和平均准确率均高于文献[3, 5]方法,类似于场景2这样的面状要素手绘地图场景检索耗时更低,主要是本文采用了松弛化策略和空间索引,缩小了检索范围。
(4) 由以上结果可以看出基于开域的空间方向关系描述应用于手绘地图检索时具有以下优势:能根据手绘输入对象间位置关系自适应划分空间区域,并以相对精确程度定量化描述对象间方向关系;不与方位术语相关联,且便于采用松弛化策略模糊化描述方向关系,从而可扩大检索范围,获取检索结果序列;更易与R树空间索引紧密关联,从而可提高检索效率。这一方向关系描述方法还可应用于其他定量空间方向查询中,但该方法不能替代其他方向关系模型对空间方向的认知效果。
5 结束语本文提出一种基于开域空间方向关系的手绘地图检索方法。该方法的主要特点和优势是:①本文提出的开域空间方向关系描述方法可根据输入对象的相对位置关系,既能自适应定量化描述点线面对象间方向关系,又便于采用松弛化策略扩大检索范围;②设计的手绘地图检索流程和方向关系相似度计算方法,能较为全面地检索到符合条件的结果序列,并将相似度高的场景排在序列前面;③将R树空间索引引入手绘地图检索并与开域空间方向关系紧密结合,提高了检索效率;④采用实际数据进行试验后结果表明,该方法可在较大范围地图场景中有效检索到排名靠前的结果,与已有方法相比,准确率和效率更高。下一步将联合空间拓扑关系、距离关系和实体几何形状进一步提升检索方法的普适性和准确率,采用深度学习和用户相关反馈技术自适应确定范围参数和松弛化参数,提高检索效率。
| [1] | JONES C B, PURVES R S. Geographical Information Retrieval[J]. International Journal of Geographical Information Science, 2008, 22(3): 219–228. DOI:10.1080/13658810701626343 |
| [2] | EGENHOFER M J. Query Processing in Spatial-query-by-sketch[J]. Journal of Visual Languages & Computing, 1997, 8(4): 403–424. |
| [3] | BLASER A D.Sketching Spatial Queries[D].Maine:University of Maine, 2000. https://www.semanticscholar.org/paper/Multimodal-spatial-querying-what-people-sketch-and-Schlaisich-Egenhofer/13611f2f92c5e3de36d71fa02afbb3ab1bd5eb5e |
| [4] | CADUFF D, EGENHOFER M J. Geo-mobile Query-by-sketch[J]. International Journal of Web Engineering and Technology, 2007, 3(2): 157–175. DOI:10.1504/IJWET.2007.012052 |
| [5] | GOYAL R.Similarity Assessment for Cardinal Directions between Extended Spatial Objects[D].Maine:University of Maine, 2000. http://portal.acm.org/citation.cfm?id=931304 |
| [6] | NEDAS K A, EGENHOFER M J. Spatial-scene Similarity Queries[J]. Transactions in GIS, 2008, 12(6): 661–681. DOI:10.1111/tgis.2008.12.issue-6 |
| [7] |
袁贞明, 吴飞, 庄越挺.
基于草图内容的空间拓扑数据检索方法[J]. 浙江大学学报(工学版), 2006, 40(10): 1663–1668.
YUAN Zhenming, WU Fei, ZHUANG Yueting. Spatial Topological Data Retrieval Based on Sketch Content[J]. Journal of Zhejiang University (Engineering Science), 2006, 40(10): 1663–1668. DOI:10.3785/j.issn.1008-973X.2006.10.002 |
| [8] | JAN S, SCHWERING A, CHIPOFYA M, et al. Qualitative Representations of Extended Spatial Objects in Sketch Maps[M]. Cham: Springer, 2014: 37-54. |
| [9] |
申世群, 刘大有, 王生生, 等.
基于草图的空间数据检索研究[J]. 电子学报, 2010, 38(8): 1819–1824.
SHEN Shiqun, LIU Dayou, WANG Shengsheng, et al. Research on Spatial Data Retrieval Based on Sketch[J]. Acta Electronica Sinica, 2010, 38(8): 1819–1824. |
| [10] | YAN Haowen, CHU Yandong, LI Zhilin, et al. A Quantitative Description Model for Directional Relations Based on Direction Groups[J]. Geoinformatica, 2006, 10(2): 177–196. DOI:10.1007/s10707-006-7578-1 |
| [11] | CLEMENTINI E. Directional Relations and Frames of Reference[J]. Geoinformatica, 2013, 17(2): 235–255. DOI:10.1007/s10707-011-0147-2 |
| [12] | DU Shihong, GUO Luo. Modeling and Querying Approximate Direction Relations[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(4): 328–340. DOI:10.1016/j.isprsjprs.2010.03.001 |
| [13] | DU Shihong, FENG C C, WANG Qiao. Multi-scale Qualitative Location:A Direction-based Model[J]. Computers, Environment and Urban Systems, 2013, 41(1): 151–166. |
| [14] |
陈迪, 朱欣焰, 周春辉, 等.
基于自适应采样粒度模型的空间方向关系模糊描述方法[J]. 测绘学报, 2013, 42(3): 359–366.
CHEN Di, ZHU Xinyan, ZHOU Chunhui, et al. A Fuzzy Description Method for Directional Relationship Based on Adaptive Sampling Granularity Model[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 359–366. |
| [15] |
唐雪华, 秦昆, 孟令奎.
基于拓扑参考的定性方向关系矩阵描述模型[J]. 测绘学报, 2014, 43(4): 396–403.
TANG Xuehua, QIN Kun, MENG Lingkui. A Qualitative Matrix Model of Direction-relation Based on Topological Reference[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 396–403. DOI:10.13485/j.cnki.11-2089.2014.0059 |
| [16] | DENG Min, LI Zhilin. A Statistical Model for Directional Relations between Spatial Objects[J]. Geoinformatica, 2008, 12(2): 193–217. DOI:10.1007/s10707-007-0031-2 |
| [17] |
陈占龙, 周林, 龚希, 等.
基于方向关系矩阵的空间方向相似性定量计算方法[J]. 测绘学报, 2015, 44(7): 813–821.
CHEN Zhanlong, ZHOU Lin, GONG Xi, et al. A Quantitative Calculation Method of Spatial Direction Similarity Based on Direction Relation Matrix[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 813–821. DOI:10.11947/j.AGCS.2015.20140198 |
| [18] | LIU X, SHEKHAR S, CHAWLA S. Object-based Directional Query Processing in Spatial Databases[J]. IEEE Transactions on Knowledge and Data Engineering, 2003, 15(2): 295–304. DOI:10.1109/TKDE.2003.1185835 |
| [19] |
陈涛, 艾延华.
多边形骨架线与形心自动搜寻算法研究[J]. 武汉大学学报(信息科学版), 2004, 29(5): 443–446, 455.
CHEN Tao, AI Tinghua. Automatic Extraction of Skeleton and Center of Area Feature[J]. Geomatics and Information Science of Wuhan University, 2004, 29(5): 443–446, 455. |
| [20] |
张明波. 空间数据库R树索引算法研究[D]. 北京: 中国科学院研究生院, 2005. ZHANG Mingbo.Research on R-tree Indexing Algorithm of Spatial Database[D].Beijing:Graduate School of Chinese academy of Sciences, 2005. http://www.irgrid.ac.cn/handle/1471x/144843 |



