2. 中南大学有色金属成矿预测教育部重点实验室, 湖南 长沙 410083
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring(Central South University), Ministry of Education, Changsha 410083, China
森林参数(树高、生物量等)不仅可用来估计地表生物量和蓄积量,也对全球碳循环研究和全球气候变化分析具有重要意义。近些年来随着我国地理国情监测进程不断推进,在植被覆盖区域下的不包括植被高度的准确数字高程模型(DEM)数据对于林业科学、测绘科学等也是必不可少的基础数据。目前传统实地勘测无法快速、大范围地获取植被高度,光学遥感或者摄影测量手段虽然可以进行大范围地形测绘但是无法获取林下地形[1]。而极化干涉SAR技术(polarimetric synthetic aperture radar interferometry,PolInSAR),将极化技术与干涉技术有效结合起来,充分利用了干涉SAR对植被的空间分布和高度敏感的特性以及极化SAR对植被散射体的形状和方向敏感的特性,从而具有植被高度估计和林下地形测绘的潜力[2-4]。
目前,极化干涉SAR植被参数反演方法主要分为两大类:①基于干涉相位差分法的几何方法,包括DEM差分法[3]、ESPRIT法[5-6];②基于极化相干散射模型的物理方法,包括六维非线性迭代[7]、三阶段算法[8-9]、固定消光系数法[10]、复数域最小二乘算法[11-13]。经过大量试验分析表明[12, 14-15],基于极化相干散射模型的物理方法相比来说具有更高的植被高度和林下地形反演精度,其中最常用的极化相干散射模型是随机地体两层模型(random volume over ground,RVoG)[16]。针对该模型的不足之处,文献[2]利用冠层填充因子来对三层植被散射模型(冠层、枝干层、地表层)进行描述,并用真实数据验证了该模型的有效性;文献[17]考虑了时间去相干的影响,建立了一个简单的时间去相干模型,而文献[18]假设散射体服从布朗运动,分析不同高度受到不同水平的时间去相干影响,从而提出了更完善的时间去相干模型;文献[19]提出了一种考虑地形坡度的S-RVoG(slope-RVoG),较好地纠正了距离向地形坡度对树高反演的失真。本文选取的BioSAR2008项目试验区域整体地势平坦,森林资源丰富,主要是具有明显三层植被结构的自然针叶林(松树、云杉等)。因此根据试验区特点,为了有效降低经典两层RVoG反演的误差,选取三层植被RVoG模型来进行植被高度反演。此外,目前所进行的极化干涉SAR植被参数反演的试验数据基本上是机载数据,由于机载SAR系统的近距远距入射角差异大,致使相高转换系数--垂直向波数在近距远距大小差异较大,即树高反演敏感程度不同,最终导致试验结果存在其引起的整体系统误差。
针对上述两个方面问题,本文提出了融合升降轨的极化干涉SAR三层植被高度反演算法。该方法以三层植被RVoG模型作为反演模型,来修正微波在穿透植被时的散射过程;同时根据机载SAR系统有效垂直波数在近距远距上差异较大引起的趋势项系统误差,采用了融合升降轨道数据联合反演的方式来削弱该部分系统误差;之后,采用相干性加权非线性迭代平差算法来进行植被高度反演;最后,利用德国宇航局DLR提供的BioSAR2008项目中的两景升轨及两景降轨E-SAR P波段全极化数据进行试验验证。
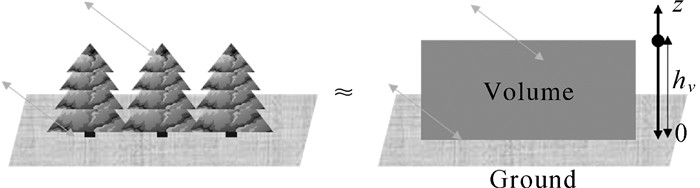
1 极化干涉SAR植被参数反演 1.1 RVoG模型及其扩展PolInSAR植被高度反演中使用频率最高和最具代表性的植被散射模型是随机地体二层散射模型(random volume over ground,RVoG)。该模型是由文献[13]根据复相干系数分析提出的,见图 1,描述了植被覆盖区域是由不可穿透的地表层和随机取向随机分布散射粒子组成的植被冠层构成。在高精度配准、距离向带通滤波和信噪比补偿之后复相干系数可表示为如下[7]
 (1)
(1)
|
| 图 1 RVoG模型示意图 Fig. 1 Illustration of RVoG model |
式中,ω为单位复数矢量,代表极化通道;γ(ω)表示某一极化通道对应的复干涉相干系数;μ(ω)表示某一极化通道对应的地体幅度比;φ0表示植被下的地表相位;γv表示由植被冠层产生的纯体去相干系数(volume-only coherence);f(z)是电磁波在植被冠层的相对反射率函数;σ表示电磁波在植被冠层传播中的平均消光系数;hv表示植被高度;θ表示雷达卫星入射角;kz表示垂直向波数。
尽管两层RVoG模型在PolInSAR植被高度反演中已得到了广泛的应用,但是在实际中由于树种和树龄等不同因素的影响,RVoG模型并不适用。例如,有些树木(如苏格兰松树等)的冠层深度较小且中间夹杂着枝干,具有典型的三层植被结构(植被冠层、树干层和地表层)特点,这种情况下利用两层RVoG模型反演树高的精度往往会变差。因此为了描述三层植被模型,文献[2]定义了冠层填充因子(canopy-fill-factor),即引起体散射的植被冠层厚度与植被总树高之比rh,见图 2。当植被垂直结构为三层模型时,三层RVoG模型相比两层RVoG模型主要有两方面的变化:一方面,体散射积分区间发生变化,由于冠层填充因子rh的作用,引起体散射的有效植被冠层高度则变为rhhv;另一方面,枝干层相位偏移项的增加,由于枝干层的存在,植被冠层被抬高了(1-rh)hv,因而纯体去相干系数增加了一相位偏移项eikz(1-rh)hv。因此考虑用冠层填充因子rh来描述植被三层垂直结构后,对应的体去相干系数γv变化为如下形式
 (2)
(2)

|
| 图 2 三层RVoG模型示意图 Fig. 2 Illustration of three-layer RVoG model |
1.2 垂直向波数
垂直向波数kz主要依赖于成像几何(垂直基线B⊥,斜距R和入射角θ)和雷达波长λ,其表达式为[20]
 (3)
(3)
式中,θ为雷达卫星入射角;λ为雷达波长;Δθ为入射角的差异值;B⊥为垂直基线;R为斜距。影响因素m取决于雷达观测模式:对于单站观测模式,m=2;对于双站观测模型,m=1。
在传统干涉SAR应用中,垂直向波数kz代表着干涉相位到高度变化的敏感程度。而在极化干涉SAR反演植被参数应用中,垂直向波数kz则是将相对反射率函数f(z)映射到体去相干系数,决定着干涉相位映射到相对反射率函数f(z)的敏感程度,尤指植被高度hv。干涉SAR高程精度Haccuracy可以由干涉相位的标准差ϕInt[21]和垂直向波数kz,其公式如下
 (4)
(4)
式中,γ是复相干系数;LInt是参与相干性估计的样本总个数。因此干涉SAR高程精度Haccuracy越高则树高反演结果越可靠。
但是目前所进行的极化干涉SAR植被高度反演所用的数据基本上是机载数据,在其树高反演结果中普遍存在着由垂直向波数导致的整体系统误差。本文根据雷达成像几何(如图 3)和树高反演结果分析这部分系统误差。假设整景SAR数据的复相干系数水平大致相同,此时高程精度Haccuracy主要取决于垂直向波数kz的大小,一般机载数据是在0.01~0.2之间。而在近距,由于入射角差异值Δθnear大且斜距Snear小,垂直向波数kz较大,则高程反演精度高,因此干涉相位转为树高的敏感度高;在远距,进行相应分析可知其高程反演精度低,干涉相位转为树高的敏感度低。因此对于机载数据,由于近距与远距有效垂直波数kz差异较大,对最终的树高反演结果会引入一个趋势项系统误差。针对这一问题,本文将采用融合升降轨数据来削弱该误差。

|
| 图 3 机载SAR的成像几何 Fig. 3 Imaging geometry of airborne SAR |
2 反演算法 2.1 平差准则与随机模型建立
根据文献[11-13]所阐述的复数域最小二乘平差方法,采用以复数观测值残差的模的平方和最小作为平差准则,同时考虑了其实部和虚部的误差,整体求得复数最小二乘解。该平差准则实质上是复数的实部、虚部联合平差,公式如下
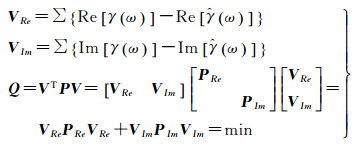 (5)
(5)
式中,VRe、VIm分别表示复相干系数实部误差、虚部误差;Re()、Im()分别表示取复数的实部、虚部;γ(ω)是代表某一极化通道对应的复相干系数,则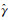
而对于随机模型,由于不同极化通道对应的复相干系数受到的噪声水平是不一样的,故本文采用相干幅度标准差(Cramer-Rao边界)[21-22]对复相干系数进行定权,并假设实部和虚部是同等精度观测。根据Cramer-Rao边界,复相干系数幅度的标准差可以表示为如下
 (6)
(6)
式中,L是参与相干性估计的样本总个数。选取不同极化通道对应的最小方差作为单位权中误差,则任一极化通道对应的复相干系数可按照如下进行定权
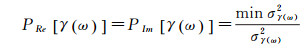 (7)
(7)
针对式(1)和式(2)中所描述的三层植被非线性数学模型以及由垂直向波数引起的系统误差问题,提出了融合升降轨的非线性迭代平差三层植被参数反演算法。该算法假设了植被是完全发育的、各向同性的,因而升轨两次观测的植被高度、冠层填充因子、消光系数是不变的,但是因为升降轨道数据获取时间不同,一般认为其地体幅度比发生了变化。在该算法中本文选取了升轨基线的5个极化通道γ1i(HH、HV、VV、HH+VV、HH-VV)和降轨基线的5个极化通道γ2i(HH、HV、VV、HH+VV、HH-VV)进行植被参数反演,因此可以得到20个观测量(每个极化通道对应的复相干系数有实部Re和虚部Im),15个待估参数(地表相位φ1和φ2、树高hv、冠层填充因子rh、消光系数σ、10个地体幅度比μ1i, μ2i),多余观测数为5,因此该算法可以归结为如下的有约束的复数最小二乘非线性迭代平差问题,如下
 (8)
(8)
式中,hv是树高;rh是冠层填充因子;σ是植被冠层的平均消光系数;φ1、φ2分别是升轨基线、降轨基线的地表相位;μ1i、μ2i分别代表升轨基线5个极化通道、降轨基线5个极化通道对应的地体幅度比;P1i、P2i分别代表升轨基线5个极化通道、降轨基线5个极化通道对应复相干系数的权值。
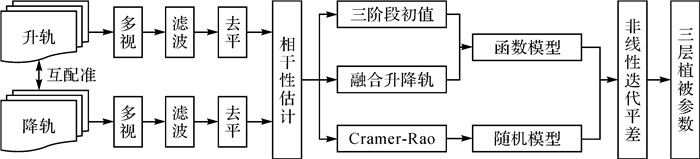
结合上述情况,本文融合升降轨非线性迭代平差算法的主要反演流程可由以下4步骤完成(见图 4):
|
| 图 4 本文算法流程 Fig. 4 Flow chart of the algorithm |
(1) 把降轨基线数据配准到升轨基线数据的SAR坐标系下,再分别进行升轨、降轨基线数据的配准、距离向频谱滤波、去平、多视等极化干涉SAR数据预处理。
(2) 升轨、降轨基线数据分别进行HH、VV、HV、HH+VV、HH-VV这5个极化通道的复相干系数估计,可引入PD相干最优算法[23, 24]并在复单位圆平面内进行整体最小二乘直线拟合接着地表相位判断确定地表相位初始值φ10、φ20[8-9]。
(3) 根据试验区先验信息(本文选取的BioSAR2008试验区主要是自然针叶林,其冠层填充因子的初始值rh0可设为0.6[14])确定冠层填充因子初始值rh0,升轨、降轨基线数据分别进行基于三层植被RVoG模型的体去相干系数计算(假设某一极化通道对应的地体幅度比为0),并进行二维查找表方法计算出其树高初始值hv10、hv20,消光系数初始值σ10、σ20,然后反算出其他极化通道的地体幅度比初始值μ1i0、μ2i0。
(4) 将步骤(3)中得到的hv10、hv20和σ10、σ20分别取平均值作为树高初始值hv0和消光系数初始值σ0,因而将hv0、σ0、rh0、φ10、φ20、μ1i0、μ2i0作为融合升降轨反演的初始值,接着联合升轨、降轨基线数据进行非线性迭代平差联合反演三层植被参数(hv、σ、rh、φ1、φ2、μ1i、μ2i)。
3 试验结果与分析 3.1 BioSAR2008项目试验区数据分析为了验证三层植被模型的正确性和融合升降轨道算法的可行性,本文采用BioSAR2008项目瑞典北部温德恩直辖市林区E-SAR P波段全极化数据进行试验。BioSAR2008项目主要目的是研究极化数据提取北半球寒温带植被的生物量,该区域整体地势平坦,森林资源丰富,主要为74%的自然针叶林(松树、云杉等)和26%的自然阔叶林(桦木等),其中林分1、2、4、5以松树、云杉居多,林分3、8、10以云杉居多,林分7、9、12以松树居多,林分6以云杉、桦木居多,林分11以松树、桦木居多。本次试验采用P波段全极化数据,该波段具有强穿透能力的,能够准确获取该区域植被的垂直结构,但是该E-SAR传感器的入射角变化较大达到了28.5°,见表 1,这也表示了该区域数据近距远距的垂直向波数差异较大,会导致树高反演会存在较严重的由垂直向波数引起的系统误差。
| 传感器 | 影像编号 | 影像属性 | 时间基线/min | 垂直基线/m | 入射角范围 | 垂直向有效波数范围 |
| E-SAR P波段 全极化 | 0103 | 升轨/Master | 32 | 1.324 | 约25.0°~53.5° | 0.024~0.135 |
| 0107 | 升轨/Slave | |||||
| 0104 | 降轨/Master | 53 | 0.219 | 0.024~0.195 | ||
| 0110 | 降轨/Slave |
本文选取2景升轨、2景降轨P波段E-SAR全极化数据,组成两组干涉对,见表 1。按照极化干涉SAR数据处理流程,分别得到了两组干涉对的复相干系数,见图 5,其相干性整体都较高。由表 2中参数可知数据获取的时间基线均较短,说明该升降轨数据受到的时间去相干[17-18, 31]的影响较小。另外,本试验区域有实测激光雷达(LiDAR)数据,该数据是于2008年8月搭载在直升机上的TopEye激光雷达获取的,为试验结果的精度评定提供了有力依据。

|
| 图 5 相干性统计图 Fig. 5 The histograms of coherence |
| 反演策略 | 干涉对 | ||
| 升轨 0103-0107 | 降轨 0104-0110 | 反演方式 | |
| ①两层模型单基线反演 | 两层 | 两层 | 单独反演 |
| ②三层模型单基线反演 | 三层 | 三层 | 单独反演 |
| ③三层模型升降轨联合反演 | 三层 | 三层 | 联合反演 |
该项目的研究数据为欧空局ESA提供的开放获取数据,已有较多相关成果:文献[25]对该试验区的L波段、P波段数据均展开了极化TomoSAR试验,有效恢复了植被顶层高度;文献[26]运用了多元线性回归、支持向量机和随机森林等3个方法试验证明森林极化信息和垂直结构信息的联合可以提高生物量估计;文献[27]考虑L波段时间去相干影响,采用RMoG(rand-motion-over-ground)模型来进行多基线极化干涉SAR植被高度反演;文献[28]基于RVoG模型采用复数最小二乘平差算法进行了单基线极化干涉SAR植被高度反演,随后文献[29]提出了一种基于高斯垂直后向散射模型(gaussian vertical backscatter, GVB)的多基线极化干涉SAR提取松树林高度和林下地形的新方法;文献[30]利用模拟数据和真实数据研究了森林密度对于树高反演模型的影响[30]。之前算法反演的该试验区域树高结果都存在着一部分有由垂直向波数引起的趋势项系统误差,特别是用P波段全极化干涉数据反演时结果更加明显[25, 29]。
3.2 植被高度反演策略为了清晰地验证三层植被模型的正确性和融合升降轨算法的有效性,本文拟采用了3组植被高度反演策略开展试验,见表 2。
(1) 两层RVoG模型+单基线复数最小二乘非线性迭代平差算法,分别用于0103-0107基线、0104-0110基线单独反演。
(2) 三层RVoG模型+单基线复数最小二乘非线性迭代平差算法,分别用于0103-0107基线、0104-0110基线单独反演。该试验用于与试验(1)对比验证三层RVoG模型的正确性。
(3) 三层RVoG模型+融合升降轨复数最小二乘非线性迭代平差算法(本文方法),用于0103-0107基线和0104-0110基线联合反演。该试验用于与试验(2)对比验证融合升降轨数据削弱垂直向波数引起的系统误差的有效性。
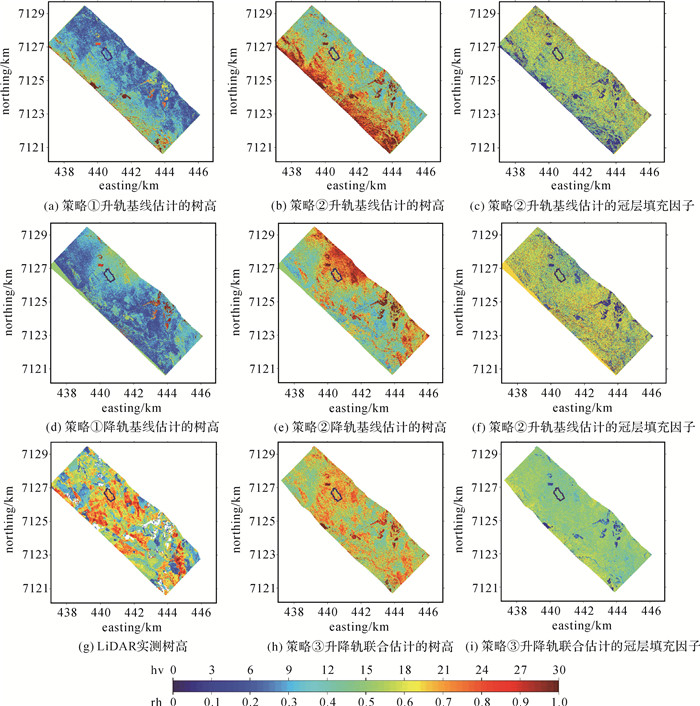
3.3 试验结果与分析3组策略反演结果均是采用复数最小二乘非线性迭代平差算法来反演得到的,之后投影在WGS-84下的UTM 34°N坐标系下展示的(见图 6)。为了能够更加清晰显示3组反演策略结果的差异,特地对林分2区域进行了局部放大对比显示(见图 7)。选取了BioSAR2008项目试验区的12个林分区域作为统计验证,以LiDAR实测树高为准,与3组策略下各个林分区域反演树高结果进行比较(见表 3、图 8),且将3组策略下12个林分平均树高与LiDAR实测林分平均树高进行可行性分析,计算其互相关系数R2和均方根误差RMSE(见图 9)。为了比较算法的时间效率,本文3组树高反演策略均在双路CPU(intel-E5-2640 V3)、2.6 GHz主频、16核32线程配置的工作站上处理完成。对于本次试验采用的升降轨数据,配准后的升降轨全极化数据均是6472行、1501列,采用策略①和策略②平均用时约11 h,而采用策略③平均用时约12 h,这表明3组反演策略的计算时间基本相当。
|
| 图 6 3组反演策略下结果 Fig. 6 The results using three inversion strategies |

|
| 图 8 3组反演策略与实测LiDAR在12个林分上树高结果对比图 Fig. 8 Comparison of forest height results based 3 inversion strategies and measured by LiDAR in 12 forest stands |

|
| 图 9 3组反演策略下12个林分平均树高的可行性验证 Fig. 9 Validation plot for mean forest height based three inversion strategies in 12 forest stands |
| 林分 | 升轨0103-0107 | 降轨0104-0110 | 融合升降轨 | ||||||||||||
| 两层RVoG | 三层RVoG | 两层RVoG | 三层RVoG | 三层RVoG | |||||||||||
| mean | mean | RMSE | mean | RMSE | mean | RMSE | mean | RMSE | mean | RMSE | |||||
| 1 | 16.77 | 8.84 | 8.39 | 16.8 | 4.15 | 7.60 | 9.49 | 15.07 | 3.39 | 17.02 | 2.26 | ||||
| 2 | 20.94 | 9.8 | 11.47 | 18.39 | 4.66 | 11.17 | 10.24 | 20.84 | 3.68 | 20.43 | 2.55 | ||||
| 3 | 22.46 | 13.16 | 10 | 23.52 | 4.19 | 9.95 | 13.12 | 18.33 | 5.8 | 20.54 | 3.06 | ||||
| 4 | 18.31 | 8.62 | 9.99 | 16.5 | 3.98 | 7.84 | 10.72 | 15.57 | 4.34 | 17.18 | 2.66 | ||||
| 5 | 16.49 | 11.43 | 5.93 | 20.97 | 6.21 | 7.44 | 9.39 | 14.51 | 3.32 | 17.93 | 2.42 | ||||
| 6 | 14.94 | 7.72 | 7.93 | 14.77 | 3.95 | 6.68 | 8.81 | 13.39 | 3.89 | 14.15 | 2.48 | ||||
| 7 | 19.64 | 12.52 | 7.92 | 22.4 | 5.03 | 11.02 | 9.29 | 20.43 | 3.87 | 21.64 | 3.13 | ||||
| 8 | 17.65 | 6.94 | 10.97 | 13.73 | 4.94 | 7.40 | 10.52 | 14.6 | 4.33 | 15.34 | 2.93 | ||||
| 9 | 20.09 | 9.05 | 11.41 | 17.15 | 4.98 | 10.63 | 9.98 | 19.92 | 4.04 | 19.9 | 2.79 | ||||
| 10 | 22.66 | 11.75 | 11.3 | 21.43 | 3.92 | 10.78 | 12.27 | 20.24 | 4.36 | 21.2 | 2.51 | ||||
| 11 | 18.5 | 12.56 | 7.6 | 21.75 | 6.23 | 7.36 | 11.67 | 14.18 | 5.59 | 17.88 | 2.79 | ||||
| 12 | 20.72 | 13.54 | 8.06 | 23.58 | 5.04 | 9.66 | 11.88 | 16.8 | 5.11 | 19.27 | 2.62 | ||||
| 平均RMSE | 9.25 | 4.77 | 10.62 | 4.31 | 2.68 | ||||||||||
另外,本文分别从反演模型和反演手段两个角度分析本文算法的有效性:
(1) 从反演模型角度分析。当采用策略①(两层RVoG+单基线)时,其植被高度反演结果整体出现低估现象(见图 6(a)、(d)、(g)),其树高反演平均精度约为9.94 m(升轨9.25 m,降轨10.62 m)(见表 3)。当采用策略②(三层RVoG+单基线)时,该三层植被模型利用冠层填充因子来修正微波在植被覆盖区域的衰减过程,因而整体树高低估现象明显得到了明显改善(见图 6(b)、(e)、(g)),其树高反演平均精度达到了4.54 m(升轨4.77 m,降轨4.31 m),提高了54.3%(见表 3)。另外,三层植被模型反演的林分平均冠层填充因子主要集中在0.53左右(升轨0.51,降轨0.55)(见图 6(c)、(f)),这与自然针叶林(松树、杉树等)的形态特征较为吻合。
将图 7中蓝色多边形标记的林分2局部放大对比显示,可见三层植被模型反演树高结果得到了较好的补偿,更加接近LiDAR实测树高,特别是降轨单基线三层植被模型反演时精度达到了3.68 m。但是不管是升轨还是降轨,策略②反演得到的植被高度结果仍存在较多异常点,其原因为非线性迭代初始值计算不准导致的。在林分平均树高反演精度方面,与LiDAR实测林分平均树高做可行性分析(见图 9(a)-(d)),策略②中升轨反演的林分平均树高精度(2.63 m)明显比策略①中升轨的(8.84 m)提高了6.21 m,而且其互相关系数也提升了0.026;而策略②中升轨反演的林分平均树高精度(2.64 m)明显比策略①中升轨的(10.21 m)提高了7.54 m,而其互相关系数并没有提高。
(2) 从反演手段角度分析。本试验所使用升降轨数据的垂直向波数从近距到远距的变化很大(见表 2),因而其树高反演结果必然存在着一部分由垂直向波数引起的系统误差。无论是策略①,还是策略②,都验证了这一结论的正确性,其树高反演结果中都存在着近距低估、远距高估的现象,整体上存在着由垂直向波数引起的趋势项系统误差。当采用策略③(三层RVoG+融合升降轨)时,其植被高度反演结果已较明显削弱了其整体趋势项误差(见图 6(h)),其树高反演平均精度约为2.68 m,比策略②平均树高反演精度(4.54 m)提高了41.0%(见表 3)。说明融合升降轨数据能有效降低由垂直向波数引起的系统误差,从而提高了树高反演精度。另外,融合升降轨的三层植被模型反演的冠层填充因子主要集中在0.50左右,这与自然针叶林(松树、杉树等)的形态特征较吻合。
在策略②反演下,林分2树高结果(见图 7(b)、(e))同样存在相同的趋势项误差,特别是策略②升轨反演下的树高结果较为明显。策略③联合升降轨数据得到的林分2树高结果(见图 7(h))不仅有效降低了其垂直向波数引起的趋势项误差,而且减少了较多异常点,得到反演结果精度较高。另外策略③也证明了融合升降轨数据反演林分平均树高的可行性,林分平均树高反演精度提高到1.35 m,与LiDAR对应的互相关系数提高到0.854。
4 结论本文提出了融合升降轨的极化干涉SAR三层模型植被高度反演方法,通过BioSAR2008项目的机载E-SAR P波段全极化数据进行了试验,采用了3组反演策略来验证新方法在机载极化干涉SAR植被高度反演的有效性,试验结果表明:
(1) 相对于经典两层RVoG模型,本文利用冠层填充因子描述的三层植被模型修正了微波在植被覆盖区域的衰减过程,相对于经典两层RVoG模型树高反演精度提高了54.3%。另外其反演出的林分区域冠层填充因子主要集中在0.53左右,这与试验区自然针叶林(松树、杉树等)的形态特征较为吻合,证明了三层植被模型的有效性。
(2) 针对现有机载SAR系统反演树高存在的近距远距垂直向波数差异较大的问题,提出了一种行之有效而又简单的手段--融合升降轨数据联合反演,有效地补偿由垂直向波数引起的系统误差,使得树高反演精度相对于单基线三层RVoG模型反演结果提高了41.0%。
| [1] | LOPEZ-MARTINEZ C, PAPATHANASSIOU K P. Cancellation of Scattering Mechanisms in PolInSAR:Application to Underlying Topography Estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(2): 953–965. DOI:10.1109/TGRS.2012.2205157 |
| [2] | NEUMANN M, FERRO-FAMIL L, REIGBER A. Estimation of Forest Structure, Ground, and Canopy Layer Characteristics from Multibaseline Polarimetric Interferometric SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3): 1086–1104. DOI:10.1109/TGRS.2009.2031101 |
| [3] | CLOUDE S R, PAPATHANASSIOU K P. Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1551–1565. DOI:10.1109/36.718859 |
| [4] | GARESTIER F, DUBOIS-FERNANDEZ P C, PAPATHANASSIOU K P. Pine Forest Height Inversion Using Single-pass X-band PolInSAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 59–68. DOI:10.1109/TGRS.2007.907602 |
| [5] | YAMADA H, YAMAGUCHI Y, KIM Y, et al. Polarimetric SAR Interferometry for Forest Analysis Based on the ESPRIT Algorithm (Special Issue on New Technologies in Signal Processing for Electromagnetic-wave Sensing and Imaging)[J]. IEICE Transactions on Electronics, 2001, E84-C(12): 1917–1924. |
| [6] |
谈璐璐, 杨立波, 杨汝良.
基于ESPRIT算法的极化干涉SAR植被高度反演研究[J]. 测绘学报, 2011, 40(3): 296–300.
TAN Lulu, YANG Libo, YANG Ruliang. Investigation of Tree Height Retrieval with Polarimetric SAR Interferometry Based on ESPRIT Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 296–300. |
| [7] | PAPATHANASSIOU K P, CLOUDE S R. Single-baseline Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(11): 2352–2363. DOI:10.1109/36.964971 |
| [8] | CLOUDE S R, PAPATHANASSIOU K P. Three-stage Inversion Process for Polarimetric SAR Interferometry[J]. IEE Proceedings:Radar, Sonar and Navigation, 2003, 150(3): 125–134. DOI:10.1049/ip-rsn:20030449 |
| [9] |
谈璐璐, 陈兵, 杨汝良.
利用PolInSAR数据反演植被高度的改进三阶段算法[J]. 系统仿真学报, 2010, 22(4): 996–999.
TAN Lulu, CHEN Bing, YANG Ruliang. Improved Three-stage Algorithm of Tree Height Retrieval with PolInSAR Data[J]. Journal of System Simulation, 2010, 22(4): 996–999. |
| [10] |
李新武, 郭华东, 廖静娟, 等.
航天飞机极化干涉雷达数据反演地表植被参数[J]. 遥感学报, 2002, 6(6): 424–429.
LI Xinwu, GUO Huadong, LIAO Jingjuan, et al. Inversion of Vegetation Parameters Using Spaceborne Polarimetric SAR Interferometry[J]. Journal of Remote Sensing, 2002, 6(6): 424–429. DOI:10.11834/jrs.20020605 |
| [11] | LOPEZ-SANCHEZ J M, BALLESTER-BERMAN J D, MARQUEZ-MORENO Y. Model Limitations and Parameter-estimation Methods for Agricultural Applications of Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3481–3493. DOI:10.1109/TGRS.2007.900690 |
| [12] |
朱建军, 解清华, 左廷英, 等.
复数域最小二乘平差及其在PolInSAR植被高反演中的应用[J]. 测绘学报, 2014, 43(1): 45–51.
ZHU Jianjun, XIE Qinghua, ZUO Tingying, et al. Criterion of Complex Least Squares Adjustment and Its Application in Tree Height Inversion with PolInSAR Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 45–51. DOI:10.13485/j.cnki.11-2089.2014.0007 |
| [13] |
付海强, 朱建军, 汪长城, 等.
极化干涉SAR植被高反演复数最小二乘平差法[J]. 测绘学报, 2014, 43(10): 1061–1067.
FU Haiqiang, ZHU Jianjun, WANG Changcheng, et al. Polarimetric SAR Interferometry Vegetation Height Inversion Method of Complex Least Squares Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1061–1067. DOI:10.13485/j.cnki.11-2089.2014.0170 |
| [14] |
付海强. 基于测量平差理论的PolInSAR植被垂直结构提取模型与方法[D]. 长沙: 中南大学, 2014. FU Haiqiang.Theory and Method of Extracting Vegetation Vertical Structure with PolInSAR Based on Surveying Adjustment[D].Changsha:Central South University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10533-1014407783.htm |
| [15] |
罗环敏. 基于极化干涉SAR的森林结构信息提取模型与方法[D]. 成都: 电子科技大学, 2011. LUO Huanmin.Models and Methods of Extracting Forest Structure Information by Polarimetric SAR Interferometry[D].Chengdu:University of Electronic Science and Technology of China, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10614-1011191830.htm |
| [16] | TREUHAFT R N, MADSEN S N, MOGHADDAM M, et al. Vegetation Characteristics and Underlying Topography from Interferometric Radar[J]. Radio Science, 1996, 31(6): 1449–1485. DOI:10.1029/96RS01763 |
| [17] | PAPATHANASSIOU K P, CLOUDE S R.The Effect of Temporal Decorrelation on the Inversion of Forest Parameters from PolInSAR Data[C]//Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium.Toulouse, France:IEEE, 2003:1429-1431. |
| [18] | LAVALLE M, SIMARD M, HENSLEY S. A Temporal Decorrelation Model for Polarimetric Radar Interferometers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(7): 2880–2888. DOI:10.1109/TGRS.2011.2174367 |
| [19] | LU Hongxi, SUO Zhiyong, GUO Rui, et al. S-RVoG Model for Forest Parameters Inversion over Underlying Topography[J]. Electronics Letters, 2013, 49(9): 618–620. DOI:10.1049/el.2012.4467 |
| [20] | BAMLER R, HARTL P. Synthetic Aperture Radar Interferometry[J]. Inverse Problems, 1998, 14(4): R1–R54. DOI:10.1088/0266-5611/14/4/001 |
| [21] | SEYMOUR M S, CUMMING I G.Maximum Likelihood Estimation for SAR Interferometry[C]//Surface and Atmospheric Remote Sensing:Technologies, Data Analysis and Interpretation, International Geoscience and Remote Sensing Symposium, 1994.Pasadena, CA:IEEE, 1994, 4:2272-2275. |
| [22] | ROUEFF A, ARNAUBEC A, DUBOIS-FERNANDEZ P C, et al. Cramer-Rao Lower Bound Analysis of Vegetation Height Estimation with Random Volume over Ground Model and Polarimetric SAR Interferometry[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(6): 1115–1119. DOI:10.1109/LGRS.2011.2157891 |
| [23] | TABB M, ORREY J, FLYNN T, et al.Phase Diversity:A Decomposition for Vegetation Parameter Estimation Using Polarimetrie SAR Interferometry[C]//Proceedings of 4th European Synthetic Aperture Radar Conference.Cologne:EUSAR, 2002:721-724. |
| [24] |
解清华, 汪长城, 朱建军, 等.
顾及地形因素的S-RVOG模型和PD相干最优算法联合反演植被高度[J]. 测绘学报, 2015, 44(6): 686–693.
XIE Qinghua, WANG Changcheng, ZHU Jianjun, et al. Forest Height Inversion by Combining S-RVOG Model with Terrain Factor and PD Coherence Optimization[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 686–693. DOI:10.11947/j.AGCS.2015.20130731 |
| [25] | TEBALDINI S, ROCCA F. Multibaseline Polarimetric SAR Tomography of a Boreal Forest at P-and L-bands[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 232–246. DOI:10.1109/TGRS.2011.2159614 |
| [26] | NEUMANN M, SAATCHI S S, ULANDER L M H, et al. Assessing Performance of L-and P-band Polarimetric Interferometric SAR Data in Estimating Boreal Forest Above-ground Biomass[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(3): 714–726. DOI:10.1109/TGRS.2011.2176133 |
| [27] | LAVALLE M, KHUN K. Three-baseline InSAR Estimation of Forest Height[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(10): 1737–1741. DOI:10.1109/LGRS.2014.2307583 |
| [28] | FU Haiqiang, WANG Changcheng, ZHU Jianjun, et al. Inversion of Vegetation Height from PolInSAR Using Complex Least Squares Adjustment Method[J]. Science China Earth Sciences, 2015, 58(6): 1018–1031. DOI:10.1007/s11430-015-5070-1 |
| [29] | FU Haiqiang, WANG Changcheng, ZHU Jianjun, et al. Estimation of Pine Forest Height and Underlying DEM Using Multi-baseline P-band PolInSAR Data[J]. Remote Sensing, 2016, 8(10): 820. DOI:10.3390/rs8100820 |
| [30] | WANG Changcheng, WANG Lei, FU Haiqiang, et al. The Impact of Forest Density on Forest Height Inversion Modeling from Polarimetric InSAR Data[J]. Remote Sensing, 2016, 8(4): 291. DOI:10.3390/rs8040291 |
| [31] | LEE S K, KUGLER F, PAPATHANASSIOU K P, et al.Quantifying Temporal Decorrelation over Boreal Forest at L-and P-band[C]//Proceedings of the 7th European Conference on Synthetic Aperture Radar (EUSAR).Friedrichshafen, Germany:IEEE, 2008:1-4. |




