2. 中国科学院武汉物理与数学研究所波谱与原子分子物理国家重点实验室, 湖北 武汉 430071
2. State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, Wuhan 430071, China
机载激光雷达(light detection and ranging, LiDAR)集全球定位系统、惯性导航系统和激光扫描系统于一体,是一种快速获取地表三维信息的主动式探测技术[1]。早期的机载激光雷达能够记录有限个离散的返回信号,通过发射脉冲和回波脉冲之间的时间间隔获取距离。随着数据存储能力和处理速度的提高,新一代的三维激光扫描系统逐渐具备全波形采集和分析技术。近十多年来,全波形激光雷达系统发展迅速,被广泛应用于地基、机载、车载和星载等平台。1999年,NASA设计了机载激光植被成像传感器[2](laser vegetation imaging sensor, LVIS);2003年,NASA发射了搭载激光测高系统[2](geoscience laser altimeter system, GLAS)的ICESAT(ice, cloud and land elevation satellite)卫星;国内外对机载小光斑全波形激光雷达数据处理的相关研究起始较晚。2004年,RIEGL公司首次在商业LiDAR系统中提供了具备全波形数字化能力的小光斑激光雷达扫描仪[3]。目前,全球主要的商业全波形激光雷达系统主要有瑞士的TopEye MarkⅡ、奥地利的Rigel LMS-Q560、LMS-Q680和加拿大的Optech Inc ALTM3100[4]。全波形激光雷达能够以很小的采样间隔记录散射体的整个后向散射回波波形,其中所蕴含的丰富信息量很快引起了本研究领域学者的极大兴趣,开启了全波形激光雷达数据处理与应用研究时代。
相对于离散激光雷达系统,全波形激光雷达系统能够提供更多的目标信息[5],单次激光脉冲可获取一个激光脚印内复杂地物目标的回波形态,可充分分析脉冲时间、幅度、脉宽及多回波分布等综合信息[6]。波形分解算法对地物目标的垂直结构,尤其是植被冠层的精细结构分析[7]有很大的帮助。因此,全波形数据的处理在大气监测、三维城市建模、地形测绘与可视化、机器人导航和电力线检测等民用领域和战场侦察、精确制导等军事领域都得到了广泛应用。目前,已有很多算法应用到波形处理研究中,通常将其分为3类[3]:阈值法、反卷积法和波形分解法。阈值法对脉冲个数较少的波形处理效果好,回波脉冲的探测能力有限。反卷积法[8]通过将已知的发射脉冲和回波信号作反卷积处理来获取地物的后向散射回波信息。与阈值法相比,这种方法虽然提高了回波检测能力,却仍然没有分解出波形参数[9]。波形分解法认为回波信号是激光路径内各个地物对激光脉冲响应的总和。文献[10]提出了波形数据可以用一系列高斯函数拟合。文献[11]考虑到回波分量波形的多样性,进一步提出了广义高斯模型,并使用Levenberg Marquardt(LM)算法[12]进行参数优化。文献[13]提出了用于探测和定位全波形数据中回波分量的均方差方法。文献[14]将期望最大化算法(expectation maximation, EM)用于波形拟合。文献[15]考虑波形分解的物理意义和数学意义,提出用改进的EM算法优化模型参数。文献[16]提出逐级递进分解策略解决高斯函数个数的确定问题。文献[17]针对微弱回波分解能力不足的缺点,提出一种迭代的波形分解方法。
传统LM算法[18-19]在一定程度上依赖初值,而激光雷达数据处理一般采用固定数的波形分解方法[20],容易遗漏部分重叠的返回波。针对波形分解的研究现状,本文提出一种全波形激光雷达的优化分解算法(optimization decomposition method, ODM),该算法通过改进回波分量初值设定来获取回波脉冲的位置、宽度和强度[21-22],在依次输入初始回波分量的同时,利用LM算法优化模型参数,剔除小于误差阈值的分量。针对一套全波形激光雷达演示系统获得的大量全波形数据进行了波形分解试验,定量分析结果验证了该方法对于分解相近回波分量的有效性、可靠性和准确性。
1 全波形记录原理全波形激光雷达的波形,是指激光发射脉冲或接收脉冲的能量随着时间变化的函数。全波形激光雷达系统可对同目标接触和相互作用后反射回来的后向散射回波脉冲进行小时间间隔的强度采样,对强度进行数字量化,并记录下后向散射脉冲的强度值。后向散射回波波形是激光脉冲所照射的激光足印中所有目标与激光脉冲接触、相互作用并后向散射后的能量与系统噪声的叠加效果[4]。全波形激光雷达对发射脉冲和后向散射回波脉冲都进行小间隔采样,获取的原始数据如图 1所示,几乎能记录整个后向散射回波波形。

|
| 图 1 全波形原始信号 Fig. 1 Raw waveform |
与传统激光雷达系统记录点云数据不同,全波形激光雷达系统能够以波形的形式记录一定高程范围内不同高程点上的后向散射能量[23-24]。理论上回波波形可以看作是若干个高斯函数的叠加,如图 1(b)所示,高斯函数的振幅、峰值位置、波形宽度、峰值与峰值之间的间距等都是波形分析中的重要参数[25-27]。
设理想波形模型为高斯混合模型,表达为k个高斯函数分量的叠加
 (1)
(1)
式中,Ai、μi、Fi分别表示第i个高斯分量的脉冲振幅、中心位置和半高宽;noise是原始波形的背景噪声。波形拟合实质是通过n个采样点,逐步迭代计算得到3×k个高斯参数和一个背景噪声参数的最优解,使得拟合波形与原始波形相差尽可能小。
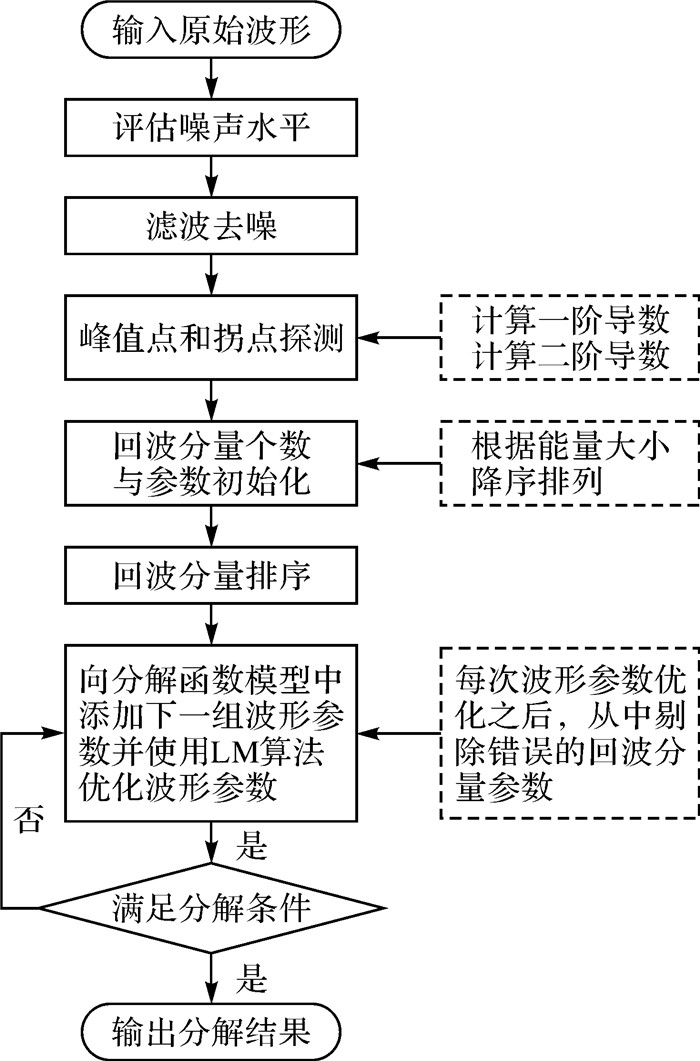
2 全波形优化分解算法针对易遗漏的重叠的回波分量,本文提出了改进的预估回波分量个数和回波分量初值的算法。图 2所示为该算法总体流程,其中,实线框为主要分解步骤,虚线框为相应步骤的补充说明。为了详细描述波形分解算法的处理过程,选取图 1(b)作为实例。这段波形基于Matlab生成,含有5个高斯分量,544个采样点。高斯分量的振幅、中心位置和半高宽参数见表 1。
|
| 图 2 全波形分解流程 Fig. 2 Flow chart of waveform decomposition |
| 排序 | 振幅/mV | 中心位置(采样点) | 半高宽(采样点) |
| 1 | 450 | 475 | 20 |
| 2 | 150 | 250 | 40 |
| 3 | 175 | 460 | 30 |
| 4 | 250 | 375 | 18 |
| 5 | 150 | 400 | 20 |
2.1 全波形数据预处理
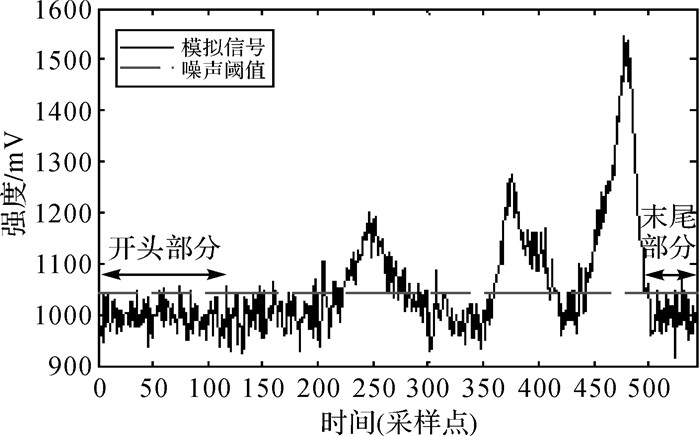
通常,为保证波形记录没有遗漏,所记录的波形范围会超过要求的范围。于是,回波数据的开头部分或者末尾部分会用来估算噪声水平。开头部分或结尾部分的范围依试验数据的特点而定,尽量取不存在回波分量的背景噪声。μn和σn分别表示噪声均值和标准差。探测目标的距离范围不定可能造成开头部分或末尾部分有回波分量的存在,于是噪声水平可能被高估。考虑到开头和结尾同时存在回波分量的可能性很低,选择其中一个部分,如图 3所示,来进行噪声水平的估算。首先,μf、μr、σf、σr分别表示前后部分的噪声均值和前后部分的标准差。如果μf < μr,则μn=μf,σn=σf;否则,μn=μr,σn=σr,噪声阈值thn计算公式为
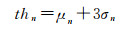 (2)
(2)
|
| 图 3 噪声水平的评估 Fig. 3 Evaluating noise level |
波形在采集的过程中由于多方面的原因会产生背景噪声,这些噪声一般呈现小振幅抖动。原始波形中的噪声可以被看作是高斯白噪声,回波分量采用高斯函数混合模型拟合,高斯平滑滤波器可以实现原始波形的最优匹配滤波[28]。滤波器的带宽设为发射波的半高宽。
2.2 全波形参数初始化估计原始波形数据经过高斯平滑滤波器预处理之后,大部分随机噪声被消除,处理后的波形更接近真实回波信号,有利于下一步的波形分解。为了不遗漏回波分量,本文除了采用一般的波形分解方法即利用局部峰值点确定回波分量之外,还进行了二次峰值点探测,确定重叠的回波分量。
2.2.1 全波形分量初判断计算每个采样点的一阶导数,即一阶差分,卷积核为[-1, 0, 1],将零交叉值(由正变负)的点视为波峰位置;计算每个采样点的二阶导数,即二阶差分,卷积核为[1, -2, 1],将零交叉值的点视为拐点位置,剔除小于噪声阈值thn的峰值点和拐点。
对于每一个峰值点,估算它所在回波分量的初值。对于峰值点Pi,若其左右单调区间内均无拐点,则认为Pi不属于任何回波分量。否则,分别计算其左右单调区间内拐点位置的均值,记为μiL、μiR。分别计算μiL、μiR与Pi的距离,记为diL、diR。若diL、diR均小于发射波半高宽dFWHM/2,则认为Pi不属于任何回波分量。否则,Pi可能属于某一回波分量,估算其初值。将Pi的振幅作为脉冲振幅初始值Ai0,Pi的位置作为中心位置初始值μi0,半高宽初始值Fi0计算公式为
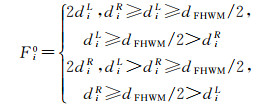 (3)
(3)
式中,半高宽阈值为dFWHM。当左右区间内拐点平均位置到峰值点距离diR、diL均不小于dFWHM/2时,取diR、diL较小值的2倍作为Fi的初始值。当diR、diL中的一个不小于dFWHM/2,另一个小于dFWHM/2时,取diR、diL较大值的2倍作为Fi的初始值。
初判断出来的回波分量的峰值点如图 4所示,图中找出了8个可能存在的回波分量所对应的峰值点。
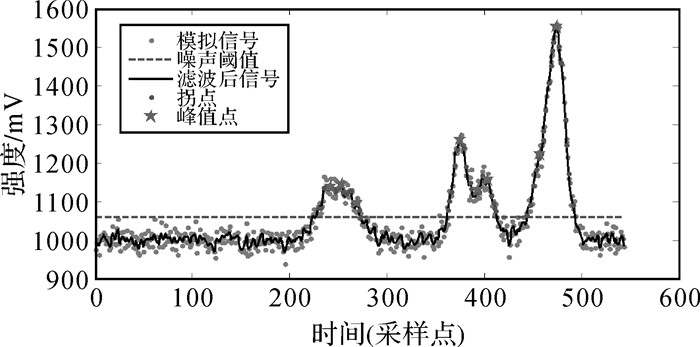
|
| 图 4 回波分量初判断 Fig. 4 First evaluating of components |
2.2.2 全波形分量二次判断
根据峰值点检测回波分量,大部分距离较远或重叠度不高的回波分量被探测了出来。然而,这种方法很容易遗漏重叠的回波分量[29]。针对这个问题,进行二次探测回波分量。
对于初判断中的每个回波分量,搜索其峰值点左右区间内的拐点,若存在不属于区间[μ-Fi/2, μ+Fi/2]的连续拐点,且这组拐点间的最大距离大于dFWHM/2,则说明附近可能存在其他的回波分量。将这组连续拐点中的振幅较大值作为新的回波分量的脉冲振幅初始值Aj0,将具有较大振幅的拐点的位置作为新的回波分量的中心位置初始值μj0,将这组拐点间的最大距离的2倍作为新的回波分量的半高宽初始值Fj0。如图 5所示,经过二次判断,又找出了1个可能存在的回波分量所对应的峰值点。

|
| 图 5 回波分量二次判断 Fig. 5 Second evaluating of components |
2.3 参数最优化估计
将初始化估计的回波分量按能量大小降序排列,回波能量用振幅与半高宽的乘积(Ai0×Fi0)表示。采用LM算法,按顺序向波形分解函数模型中输入初始波形参数,迭代计算最优解。每次添加一组波形参数,就更新一次波形分解模型参数,剔除其中幅值小于噪声阈值或者半高宽小于发射波半高宽dFWHM的回波分量,并合并相对距离小于dFWHM/2的两个初始回波分量。直到原始波形与拟合波形之间的残差小于噪声的标准差σn或者波形分解参数达到上限Nmax,停止输入初始波形参数。
3 波形分解实测及模拟验证 3.1 实测验证与分析本文使用的数据来自一套全波形激光雷达演示系统,该系统各项参数见表 2。试验时,激光垂直照射到两块白板上,两块白板平分一块光斑。两块白板相距10、20、30、40、50、60、70、80、90、100 cm。每种间隔选取1000个回波信号进行波形分解,提取各项波形参数。每段回波信号的采样点个数为30~40个。对于实测回波信号,取开头10个采样点和结尾10个采样点用作噪声评估。
| 工作高 度/m | 激光波 长/nm | 发射脉冲 宽度/ns | 脉冲频 率/kHz | 扫描角 /(°) | 采样率 /Gsps | 光斑大小 /mm |
| 1 | 450~2400 | <2 | 1~20 | 0 | 1.8 | 2 |
由于实际测量时波形参数的真实值未知,于是通过决定系数R2来评价波形拟合的精度
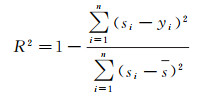 (4)
(4)
式中,si表示原始波形中第i个采样点的强度值;yi表示波形分解模型中第i个点的强度值。决定系数R2是衡量两个随机变量之间线性相关程度的指标,决定系数越接近1,说明拟合数据与原始数据相关性越强,波形拟合的精度越高。虽然决定系数R2可以评价拟合波形整体与原始波形的近似程度,但不能说明分解相近回波分量的能力。于是计算分解得到的波形分量总数与真实波形分量总数的比值Rt。比值Rt越接近1,说明分解的波形分量个数越接近真实的目标个数,分解相近回波分量的能力越高。
本文对相对距离分别为10、20、30、40、50 cm的5组原始数据采用ODM方法和传统LM算法进行了对比分析,如图 6所示。当两回波分量的相对距离是10 cm时,如图 6(a)所示,采用两种方法的分解效果相近,都从原始数据中分解出一个回波分量,并且有较高的拟合决定系数R2值(大于0.98)和较小的拟合残差RMSE值(2左右)。当两回波分量的相对距离是20、30、40 cm时,如图 6(b)-(d)所示,虽然采用两种方法进行波形分解都有较高的拟合决定系数R2值和较小的拟合残差RMSE值,即拟合的波形都能很好地近似原始波形,但是使用ODM方法可以分解出两个回波分量,而传统的LM算法只能分解出一个回波分量,这说明ODM方法分解相近回波分量的效果更好,能够更好地从原始数据中提取出更多的目标信息。当两回波分量的相对距离是50 cm时,如图 6(e)所示,采用两种方法的分解效果相近,都从原始数据中分解出两个回波分量,并且有较高的拟合决定系数R2值(大于0.99)和较小的拟合残差RMSE值(小于2),这说明对于相对距离超出某个范围的两个回波分量,采用两种方法得到的分解效果相近。
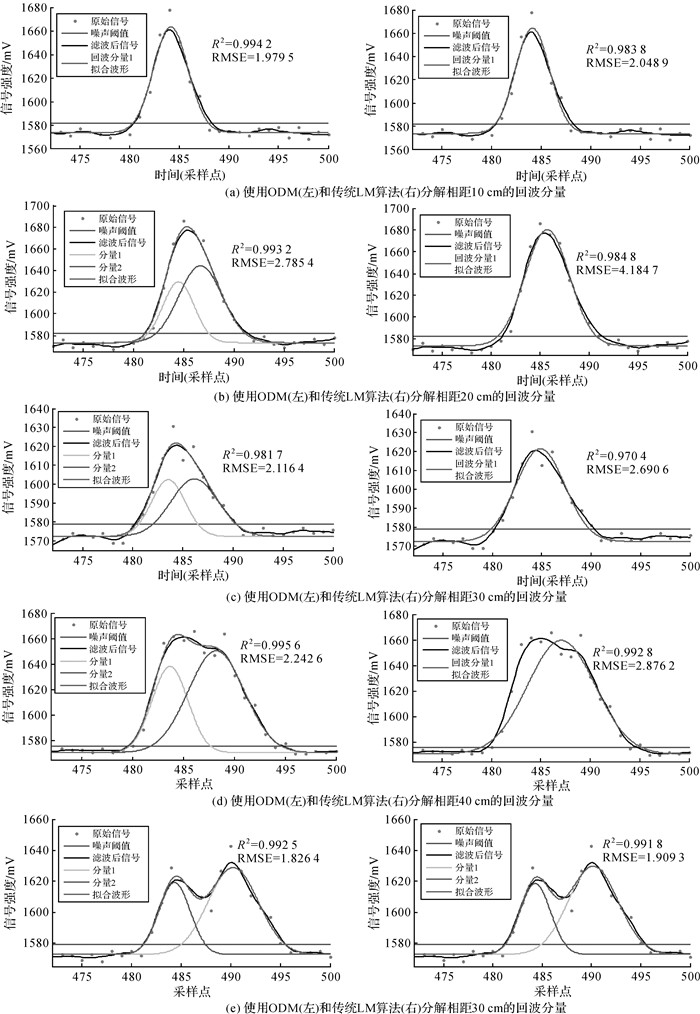
|
| 图 6 实测数据分解结果对比图 Fig. 6 Final decomposition result of measured data |
对选取的10 000个回波信号的分解结果进行统计分析,分解得到的波形分量总数与真实波形分量总数的比值Rt以及决定系数R2的平均值和标准差见表 3。由表 3可知,ODM算法成功分解出85.75%的回波分量,远高于采用传统LM算法分解出的波形分量数60.08%,这说明ODM分解相近回波分量的效果更好,能够更好地从原始数据中提取出更多的目标信息。采用ODM算法分解结果的拟合决定系数均值和标准差分别是0.962 2和0.107 6,采用传统LM算法分解结果的拟合决定系数均值和标准差分别是0.870 3和0.301 5,这说明采用ODM算法拟合的波形更接近原始波形,拟合精度更高。
| 方法 | Rt/(%) | μR2 | σR2 |
| 传统LM方法 | 60.08 | 0.870 3 | 0.301 5 |
| ODM | 85.75 | 0.962 2 | 0.107 6 |
3.2 模拟测试与分析
为进一步验证回波分量的相对距离对波形分解可行性的影响,利用Matlab模拟了只含两个回波分量的波形数据。模拟数据的波形参数(振幅、中心位置、半高宽)是一系列随机整数,其范围见表 4。模拟回波信号开头50个采样点和末尾50个采样点被用作评估噪声水平。模拟输入的各项波形参数作为真实值,可与分解结果对比来定量评估波形参数的精确性。以振幅参数为例,AT表示振幅的真实值,AC表示振幅的优化结果,则振幅的偏差EA
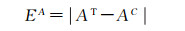 (5)
(5)
| 振幅 /mV | 中心位置 (采样点) | 半高宽 (采样点) | 信噪比 | 数据长度 (采样点) |
| 30~300 | 80~92 | 3~20 | 10~40 | 181 |
分别计算EA的均值μeA和标准差σeA,这两个误差评估参数是评价振幅的可靠性和准确性的重要指标。同样,中心位置和半高宽两项波形参数的误差评估参数记为μeL、σeL、μeF、σeF。对5000个模拟信号的分解结果进行统计分析,其分解得到的波形分量总数与真实波形分量总数的比值Rt及各项误差评估参数的平均值和标准差如表 5所示。由表 5可知,虽然采用两种方法分解得到各项波形参数的误差水平相近,但是ODM算法成功分解出83.75%的回波分量,远高于采用传统LM算法分解出的波形分量数55.73%,这说明ODM分解相近回波分量的效果更好,能够更好地从原始数据中提取出更多的目标信息。
| 方法 | Rt/(%) | μeA | σeA | μeL | σeL | μeF | σeF |
| 传统LM方法 | 55.73 | 6.89 | 33.81 | 0.301 3 | 0.102 2 | 0.867 7 | 1.376 4 |
| ODM | 83.75 | 7.73 | 25.73 | 0.237 6 | 0.132 7 | 0.603 2 | 1.276 1 |
4 结论
相对于离散激光雷达系统,全波形激光雷达系统能够提供更多的目标信息。发射单次激光脉冲可获取一个激光脚印内复杂地物目标的回波形态,可充分分析包括脉冲时间、幅度、脉宽以及多回波分布等全波形综合信息。传统LM算法在一定程度上依赖初值,而激光雷达数据处理一般采用固定数的波形分解方法,容易遗漏部分重叠的返回波。针对波形分解的研究现状,本文提出ODM方法,该算法通过改进回波分量初值设定来获取回波脉冲的位置、宽度和强度,在依次输入初始回波分量的同时,利用LM算法优化模型参数,剔除小于误差阈值的分量。利用ODM方法对实测试验数据和模拟试验数据进行了波形分解试验,定性和定量地验证了该方法的有效性、可靠性和准确性。ODM方法不仅能很好地拟合原始波形,还能有效地分解相近的回波分量,能够更好地从原始数据中提取出更多的信息。对于一些非对称或拖尾的波形,该方法还不能非常准确地拟合。在未来的工作中,将探索如何提高波形参数的精度,提高分解相近回波分量的能力,使算法更普遍地适用于各种形状的波形。例如,可以考虑用其他随机模型代替高斯模型来拟合波形分量,从而提高波形拟合的精度。
| [1] | ACKERMANN F. Airborne Laser Scanning-Present Status and Future Expectations[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(2-3): 64–67. DOI:10.1016/S0924-2716(99)00009-X |
| [2] |
蓝晓萍, 黄庚华, 王海伟, 等.
激光大足印多目标距离信息提取与验证技术[J]. 光学学报, 2015, 35(7): 9–16.
LAN Xiaoping, HUANG Genghua, WANG Haiwei, et al. Technology of Laser Large-footprint Multi-Objective Relative Distance Information Extraction and Verification[J]. Acta Optica Sinica, 2015, 35(7): 9–16. |
| [3] |
王素元, 马洪超, 王杰栋, 等.
基于分组LM算法的全波形LiDAR高斯分解[J]. 测绘与空间地理信息, 2016, 39(7): 144–147.
WANG Suyuan, MA Hongchao, WANG Jiedong, et al. Gaussian Decomposition of Full-waveform LiDAR Based on Grouping LM Algorithm[J]. Geomatics & Spatial Information Technology, 2016, 39(7): 144–147. |
| [4] |
王金虎, 李传荣, 周梅.
机载全波形激光雷达数据处理及其应用[J]. 国外电子测量技术, 2012, 31(6): 71–75, 79.
WANG Jinhu, LI Chuanrong, ZHOU Mei. Airborne Full-waveform LiDAR Data Processing and Application[J]. Foreign Electronic Measurement Technology, 2012, 31(6): 71–75, 79. |
| [5] |
王海伟, 程鹏飞, 蓝晓萍, 等. 多通道全波形激光雷达遥感技术综述[C]//第九届成像光谱技术与应用研讨会暨交叉学科论坛论文集. 文昌: 中国空间科学学会空间遥感专业委员会, 2014: 7. WANG Haiwei, CHENG Pengfei, LAN Xiaoping, et al.Multi-channel Full Waveform LiDAR Remote Sensing Technology Review[C]//Proceedings of the Symposium on Imaging Spectroscopy Technology and Applications.Wenchang:Space Remote Sensing Specialized Committee of Chinese Space Science Society, 2014:7. |
| [6] |
王金虎. 全波形激光雷达数据处理与应用技术研究[D]. 北京: 中国科学院研究生院, 2012. WANG Jinhu.Full-waveform LiDAR Data Processing and Application Technology Research[D].Beijing:Graduate University of Chinese Academy of Sciences, 2012. http://d.wanfangdata.com.cn/Thesis/Y2249078 |
| [7] | ZLINSZKY A, SCHROIFF A, KANIA A, et al. Categorizing Grassland Vegetation with Full-waveform Airborne Laser Scanning:A Feasibility Study for Detecting Natura 2000 Habitat Types[J]. Remote Sensing, 2014, 6(9): 8056–8087. DOI:10.3390/rs6098056 |
| [8] | SHAN J, TOTH C K. Topographic Laser Ranging and Scanning:Principles and Processing[J]. International Journal of Remote Sensing, 2010, 31(12): 3333–3334. DOI:10.1080/01431160903112612 |
| [9] | JUTZI B, STILLA U. Range Determination with Waveform Recording Laser Systems Using a Wiener Filter[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 61(2): 95–107. DOI:10.1016/j.isprsjprs.2006.09.001 |
| [10] | HOFTON M A, MINSTER J B, BLAIR J B. Decomposition of Laser Altimeter Waveforms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(4): 1989–1996. DOI:10.1109/36.851780 |
| [11] | CHAUVE A, MALLET C, BRETAR F, et al.Processing Full-waveform LiDAR Data:Modelling Raw Signals[C]//Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences.Espoo, Finland:[s.n.], 2007, 36(1):102-107. |
| [12] | MARQUARDT D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431–441. DOI:10.1137/0111030 |
| [13] | RONCAT A, WAGNER W, MELZER T, et al. Echo Detection and Localization in Full-waveform Airborne Laser Scanner Data Using the Averaged Square Difference Function Estimator[J]. The Photogrammetric Journal of Finland, 2008, 21(1): 62–75. |
| [14] | SOEDERMAN U, PERSSON A, TOEPEL J, et al.On Analysis and Visualization of Full-waveform Airborne Laser Scanner Data[C]//Proceedings Volume 5791, Laser Radar Technology and Applications X.Orlando, Florida:SPIE, 2005:184-192. |
| [15] | MA Hongchao, LI Qi. Modified EM Algorithm and Its Application to the Decomposition of Laser Scanning Waveform Data[J]. Journal of Remote Sensing, 2009, 13(1): 35–41. |
| [16] |
覃驭楚, 李斌, 牛铮, 等.
小光斑激光雷达全波形数据递进分解与相对辐射校正[J]. 中国科学:地球科学, 2011, 54(4): 625–630.
QIN Yuchu, LI Bin, NIU Zheng, et al. Stepwise Decomposition and Relative Radiometric Normalization for Small Footprint LiDAR Waveform[J]. Science China Earth Science, 2011, 54(4): 625–630. |
| [17] |
赖旭东, 秦楠楠, 韩晓爽, 等.
一种迭代的小光斑LiDAR波形分解方法[J]. 红外与毫米波学报, 2013, 32(4): 319–324.
LAI Xudong, QIN Nannan, HAN Xiaoshuang, et al. Iterative Decomposition Method for Small Foot-print LiDAR Waveform[J]. Journal of Infrared and Millimeter Waves, 2013, 32(4): 319–324. |
| [18] |
李鹏程, 徐青, 邢帅, 等.
全局收敛LM的激光雷达波形数据分解方法[J]. 红外与激光工程, 2015, 44(8): 2262–2267.
LI Pengcheng, XU Qing, XING Shuai, et al. Full-waveform LiDAR Data Decomposition Method Based on Global Convergent LM[J]. Infrared and Laser Engineering, 2015, 44(8): 2262–2267. |
| [19] |
梁敏, 王仁礼, 李国新.
基于全波形激光雷达数据分解方法的研究[J]. 地理信息世界, 2016, 23(5): 51–54.
LIANG Min, WANG Renli, LI Guoxin. Study of Decomposition Based on Full-waveform LiDAR Data[J]. Geomatics World, 2016, 23(5): 51–54. |
| [20] |
赵泉华, 李红莹, 李玉.
全波形LiDAR数据分解的可变分量高斯混合模型及RJMCMC算法[J]. 测绘学报, 2015, 44(12): 1367–1377.
ZHAO Quanhua, LI Hongying, LI Yu. Gaussian Mixture Model with Variable Components for Full Waveform LiDAR Data Decomposition and RJMCMC Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1367–1377. DOI:10.11947/j.AGCS.2015.20140501 |
| [21] | HEINZEL J, KOCH B. Exploring Full-waveform LiDAR Parameters for Tree Species Classification[J]. International Journal of Applied Earth Observation and Geoinformation, 2011, 13(1): 152–160. DOI:10.1016/j.jag.2010.09.010 |
| [22] | GUO Li, CHEHATA N, MALLET C, et al. Relevance of Airborne LiDAR and Multispectral Image Data for Urban Scene Classification Using Random Forests[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(1): 56–66. DOI:10.1016/j.isprsjprs.2010.08.007 |
| [23] |
左志权, 张祖勋, 张剑清.
知识引导下的城区LiDAR点云高精度三角网渐进滤波方法[J]. 测绘学报, 2012, 41(2): 246–251.
ZUO Zhiquan, ZHANG Zuxun, ZHANG Jianqing. A High-quality Filtering Method with Adaptive TIN Models Tor Urban LiDAR Points Based on Priori-knowledge[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 246–251. |
| [24] |
隋立春, 张熠斌, 柳艳, 等.
基于改进的数学形态学算法的LiDAR点云数据滤波[J]. 测绘学报, 2010, 39(4): 390–396.
SUI Lichun, ZHANG Yibin, LIU Yan, et al. Filtering of Airborn LiDAR Point Cloud Data Based on the Adaptive Mathematical Morphology[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 390–396. |
| [25] |
刘梦华, 周梅.
顾及入射角的全波形激光雷达数据校正方法[J]. 遥感技术与应用, 2014, 29(4): 675–680.
LIU Menghua, ZHOU Mei. Full-Waveform LiDAR Data Correction with Incidence Angle[J]. Remote Sensing Technology and Application, 2014, 29(4): 675–680. |
| [26] | ALLOUIS T, DURRIEU S, VÉGA C, et al. Stem Volume and Above-ground Biomass Estimation of Individual Pine Trees from LiDAR Data:Contribution of Full-waveform Signals[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(2): 924–934. DOI:10.1109/JSTARS.2012.2211863 |
| [27] | ZHOU M, LIU M H, ZHANG Z, et al.Enhanced Component Detection Algorithm of Full-waveform LIDAR Data[C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences.Hannover, Germany:ISPRS, 2013:393-397. |
| [28] |
李奇, 马洪超.
基于激光雷达波形数据的点云生产[J]. 测绘学报, 2008, 37(3): 349–354.
LI Qi, MA Hongchao. The Study of Point-cloud Production Method Based on Waveform Laser Scanner Data[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 349–354. |
| [29] | LIN Y C, MILLS J P, SMITH-VOYSEY S. Rigorous Pulse Detection From Full-waveform Airborne Laser Scanning Data[J]. International Journal of Remote Sensing, 2010, 31(5): 1303–1324. DOI:10.1080/01431160903380599 |



