2. 南京信息工程大学地理与遥感学院, 江苏 南京 210044
2. School of Geography and Remote Sensing, Nanjing University of Information Science & Technology, Nanjing 210044, China
大视场、宽覆盖、高分辨率是对地观测卫星光学传感器发展的重要方向。然而受单台高分辨率相机幅宽限制,卫星无法同时获取大范围高分辨率卫星影像。目前我国常采用多相机拼接成像技术,将多台高分辨率相机沿垂轨方向安置,实现高分辨率与宽覆盖的结合,例如ZY-1 02C卫星、HJ卫星、GF-1卫星、GF-2卫星等。在利用这些多相机拼接成像传感器数据进行大区域定量遥感研究时,往往需要对同轨相邻相机影像进行拼接处理,以获取大面积高分辨率卫星数据,这也是研制该类型传感器的一个重要目的[1]。
目前,常用的卫星传感器可见/近红外波段的在轨辐射定标方法主要包括场地定标[2-3]、星上定标[4-5]和交叉定标[6-7]3种方法。在国内,官方常采用场地定标方法获得传感器在轨绝对辐射定标系数,然而利用其对该类型传感器同轨各相机影像进行绝对辐射校正后,发现相邻相机影像重叠区域内辐射信息存在较大差异,部分波段相对差异达到32.44%[8],该差异会对大气状况评估[9]、精准农业[10]、矿物勘探[11]、影像判读[12]等研究产生负面影响。
对于该问题,研究人员通常采用影像间匀色方法[12-13]或辐射归一化处理方法(relative radiometric normalization,RRN)[14-15],在影像空间域或频率域中调整影像重叠区、接边区或整幅影像的辐射信息后,实现影像间辐射信息平滑过渡,使拼接后影像具有统一的辐射标准。但是上述方法破坏了影像原始辐射信息,且该信息的损失对于不同时相、不同区域的影像是不相同的,进而无法保障后续定量遥感专题产品精度的稳定性。同时,用户在利用多相机拼接成像传感器影像进行大区域遥感研究时,若每次都需要对其进行辐射归一化或匀色处理,则会降低数据处理效率,加之该过程并无统一的处理标准,不同用户的处理结果可能存在较大差异。
GF-1卫星搭载的WFV传感器采用四相机拼接成像技术,能够获取幅宽优于800 km、星下点分辨率优于16 m的4波段(蓝、绿、红和近红外)多光谱卫星影像,其中相邻相机重叠区域视场角约为0.44°,该数据已经在我国灾害监测、环境保护、资源调查等领域发挥重要作用[1]。同样,利用官方发布的定标结果对同轨四相机影像进行绝对辐射校正后,重叠区域辐射信息也存在较大差异[8]。因此,从星载多相机拼接成像传感器在轨辐射定标过程中遇到的实际问题出发,以GF-1卫星WFV传感器为例,本文提出一种基于改进型辐射区域网平差的在轨辐射定标方法,详细阐述了该方法的技术流程,实现了该类型传感器在轨绝对辐射定标和相机间相对辐射校正的一体化处理。在此基础上,利用一组WFV影像进行试验,验证了该方法的有效性和可行性。
1 方法介绍 1.1 辐射区域网平差辐射区域网平差(radiometric block adjustment, RBA)是将影像几何区域网平差的思想应用于影像的辐射处理之中。它是将影像中具有辐射测量数据的区域作为辐射控制点RCPs(radiometric control points),将影像重叠区域光谱均匀地物作为辐射连接点RTPs(radiometric tie points),构建辐射区域网平差模型,实现对影像辐射信息的处理[14]。目前,根据该模型中对RCPs和RTPs数据的使用情况,其应用领域主要分为以下两个方面:
(1) 仅利用RTPs信息实现影像辐射归一化处理,该过程与摄影测量中立体影像对相对定向的基本思想相似。例如,文献[14]采用该模型降低了航空雷达强度数据过校正的影响,解决了该数据的坏线问题,实现了单景影像内部辐射归一化处理。文献[16]采用基于多项式的辐射区域网平差方法,改进了SPOT5 HRS影像拼接过程中的辐射处理环节,分析了全局权重值对处理结果的影响,实现了SPOT5 HRS多时相影像间的辐射归一化处理。文献[17]针对航空数字影像条带间辐射不一致性问题,建立了RTPs提取模型,在考虑雾霾、时相、双向反射分布函数(bidirectional reflectance distribution function,BRDF)影响后,采用辐射区域网平差方法,实现了影像间辐射差异最小化的目的。文献[18]阐述了基于辐射区域网平差方法获取相对辐射校正模型参数的过程,实现了无人机影像数据辐射归一化处理,其处理结果可为精准农业研究提供可靠的数据支持。文献[19]在对不同传感器获得的大区域航空影像数据进行拼接时,结合重叠区域RTPs信息,采用辐射区域网平差技术实现影像间的相对辐射校正处理。
(2) 先利用RTPs实现影像的辐射归一化,然后利用RCPs完成绝对辐射定标,该处理过程与摄影测量中立体影像对分步定向的基本思想相近似,即先相对定向后绝对定向。例如,文献[20]基于辐射区域网平差方法,利用RTPs对AgCam (agricultural cameras)相机的渐晕效应、CCD的不一致响应和暗电流进行校正,降低了该相机正射拼接影像的辐射不一致性,进而利用RCPs实现影像的绝对辐射定标。文献[21]采用摄影测量模型对数字测图相机影像(digital mapping camera,DMC)进行几何处理后,利用辐射区域网平差模型,先将RTPs数据用于影像间BRDF校正模型参数求解,然后将RCPs数据用于大气校正处理,最终提高了航空影像间相对辐射一致性和影像的绝对辐射定标精度。文献[22]采用辐射区域网平差技术,在利用RTPs消除无人机影像间因光照和传感器性能变化导致的辐射差异后,利用RCPs实现影像的绝对辐射定标。文献[23]综合考虑了地表BRDF特性和大气辐射特性等多种因素的影响后,采用辐射区域网平差方法,实现了航空正射校正影像条带间的无色差拼接,同时利用四角点RCPs进行绝对辐射定标,并利用影像中心RCPs检验绝对校正精度。文献[24]在对多条机载波形雷达航带数据进行辐射处理时,详细阐述了重叠区域RTPs信息自动提取方法,以及利用RCPs获取绝对辐射定标系数的具体过程。文献[8]针对GF-1卫星WFV多相机拼接成像特征,以MODIS为辐射参考基准,采用基于时间序列多点法交叉定标方法获取敦煌辐射校正场处RCPs数据,通过目视解译方式提取光谱均匀地物作为RTPs,采用该技术依次完成相机间相对辐射校正和在轨绝对辐射定标,并与官方结果进行比对,验证了方法的可靠性和可行性。
然而,在对辐射区域网平差研究现状分析后可以发现,大多是国外研究人员针对航空遥感影像辐射处理开展的,或只进行相对辐射校正,或采用分步处理方式即先完成相对辐射校正,后实现绝对辐射定标,然而此过程并未充分考虑相对辐射校正与绝对辐射定标之间的耦合关系,即二者的处理过程及处理顺序均会对彼此产生影响。例如:①若先对各相机进行在轨绝对辐射定标,然后利用其进行绝对辐射校正,则会发现重叠区域辐射差异较大,各相机影像辐射信息不一致,从而无法对各相机影像进行整体定量化研究,因此需要进行相对辐射校正处理,而后者的处理方式并无统一规范,且处理后均会改变原有的绝对辐射校正精度。②若先进行相对辐射校正处理,使得原始图像DN值信息具有统一辐射标准,但该过程会导致原始信息发生改变,后续基于此信息获得的绝对辐射定标精度也会受到影响。因此,若直接采用现有的辐射区域网平差方法,实现星载多相机拼接成像传感器在轨辐射定标,则前期的相对辐射校正会破坏各影像原始辐射信息,进而影响绝对辐射定标精度。所以,本文将对现有的辐射区域网平差技术进行改进,在获取该类型传感器在轨绝对辐射定标系数的过程中,同时考虑相机间相对辐射校正问题,实现二者的一体化处理。
1.2 改进型辐射区域网平差本文所构建的改进型辐射区域网平差模型是在文献[8]的数据处理流程基础上进行优化后实现的。采用与文献[8]相同的方式获取RCPs和RTPs,改进后的定标模型不同之处在于其数据处理方式。文献[8]采用分步式处理方法依次完成相对辐射校正和绝对辐射定标,而改进后的定标模型则在求解绝对辐射定标系数的过程中,同时顾及相机间辐射约束条件,采用整体平差处理的方式,实现二者的一体化处理。
该定标模型构建的具体过程如下:
(1) 利用场地/交叉定标法在WFV1、WFV2、WFV3和WFV4影像中分别获取m、n、p和q个辐射控制点,对于任意一个辐射控制点,均可列立一个方程如式(1)所示
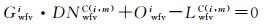 (1)
(1)
式中,Gwfvi和Owfvi分别代表某一台WFV相机绝对辐射定标系数中的增益和偏移量;DNwfvC(i, m)和LwfvC(i, m)分别代表该相机中第i波段第m个辐射控制点的影像DN值和该辐射控制点的表观辐亮度,下同。
(2) 在WFV1和WFV2、WFV2和WFV3、WFV3和WFV4影像重叠区域内,分别获取f、g和h对辐射连接点。为方便表述,以下以重叠区域表观辐亮度相关函数FL()为线性函数为例,对于任意一对辐射连接点,均可列立一个辐射约束条件方程如式(2)所示
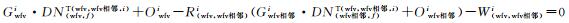 (2)
(2)
式中,Gwfv相邻i和Owfv相邻i分别代表相邻WFV相机绝对辐射定标系数中的增益和偏移量; DN(wfv, f)T(wfv, wfv相邻, i)和DN(wfv相邻, f)T(wfv, wfv相邻, i)代表影像重叠区域中第i波段第f个辐射连接点在相邻两台WFV相机中的影像DN值; R(wfv, wfv相邻)i和W(wfv, wfv相邻)i代表重叠区域表观辐亮度相关性函数FL()中的拟合参数,下同。
若FL()为非线性函数时,也可以利用该流程进行处理。
(3) 采用整体平差处理,构建第i波段的在轨辐射定标模型。令
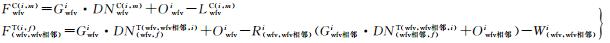 (3)
(3)
由于式(3)中待求解的定标系数(Gwfvi、Owfvi、Gwfv相邻i和Owfv相邻i)与待求解的辐射约束条件方程参数(R(wfv, wfv相邻)i和W(wfv, wfv相邻)i)成非线性形式即乘积关系,为同时求解上述未知参数,本文将FwfvC(i, m)和F(wfv, wfv相邻)T(i, f)按照泰勒公式进行线性化处理,得式(4)
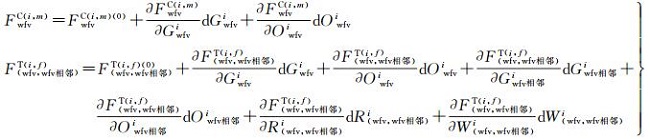 (4)
(4)
式中,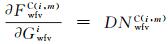
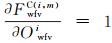
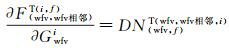

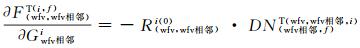
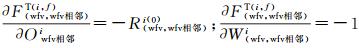
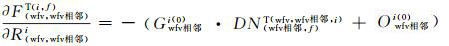
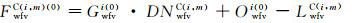

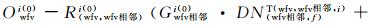
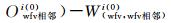
用dXCi表示各相机绝对辐射定标系数的改正参数,dXRi表示重叠区域影像表观辐亮度相关函数的系数改正参数,BCi代表辐射控制点方程的常数项,BRi代表辐射连接点方程的常数项,则
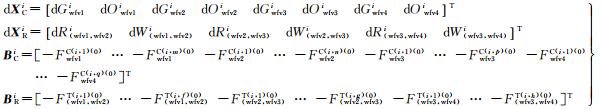
最终,本文构建的基于改进型辐射区域网平差的辐射定标模型可以表示为
 (5)
(5)
式中,系数矩阵A为(m+n+p+q+f+g+h)× 14的矩阵

常数项B =[BCiBRi]T为(m+n+p+q+f+g+h)×1的列向量,残差值V为(m+n+p+q+f+g+h)×1的列向量,改变量dX =[dXCi dXRi]T为14×1的列向量;dGwfv1i和dOwfv1i分别代表WFV1影像第i波段绝对定标系数的增益和偏移量的改正量;Gwfv1i(0)和Owfv1i(0)为相应的初始值;dR(wfv1, wfv2)i和dW(wfv1, wfv2)i代表经泰勒一次展开后WFV1和WFV2影像表观辐亮度相关系数的改变量;R(wfv1, wfv2)i(0)和W(wfv1, wfv2)i(0)为相应的初始值,其他参数具有相似的含义。
(4) 以残差值V的平方和最小为准则,即采用最小二乘方法求解改变量dX,如式(6)所示
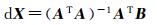 (6)
(6)
(5) 最后利用式(7)将改变量dX与相应的初始值X(0)进行叠加,得到各相机在轨绝对辐射定标系数及辐射约束条件方程参数
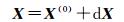 (7)
(7)
此过程为迭代计算,当改变量dX小于限差时计算终止,否则利用新的近似值重复第(3)至第(5)步,直到满足要求为止。
2 辐射信息提取 2.1 辐射控制点提取以辐射性能较高的MODIS影像为参考,将敦煌辐射校正场作为传递平台,收集同一天内在敦煌辐射校正场上空过境的MODIS和WFV有效影像对。通过数据检索获取自GF-1卫星发射后400天内的有效影像对(WFV1相机4对、WFV2相机3对、WFV3相机0对,WFV4相机7对),如表 1所示。
| 序号 | 发射后天数 | GF-1相机 | WFV成像时间 | MODIS成像时间 |
| 1 | 214 | WFV1 | 12:33 | 13:00 |
| 2 | 275 | WFV1 | 12:37 | 12:30 |
| 3 | 312 | WFV1 | 12:46 | 12:45 |
| 4 | 332 | WFV1 | 12:36 | 12:25 |
| 5 | 243 | WFV2 | 12:48 | 12:30 |
| 6 | 300 | WFV2 | 12:51 | 12:25 |
| 7 | 312 | WFV2 | 12:46 | 12:45 |
| 8 | 175 | WFV4 | 13:07 | 12:55 |
| 9 | 179 | WFV4 | 13:06 | 12:30 |
| 10 | 248 | WFV4 | 13:11 | 12:50 |
| 11 | 252 | WFV4 | 13:09 | 12:25 |
| 12 | 264 | WFV4 | 13:05 | 12:45 |
| 13 | 268 | WFV4 | 13:05 | 12:25 |
| 14 | 399 | WFV4 | 13:11 | 12:55 |
利用交叉辐射定标方法提取WFV传感器各相机影像辐射控制点信息,即敦煌辐射校正场中心区域MODIS影像上WFV相机等效表观辐亮度均值(5×5像素窗口)和相应区域WFV影像DN值均值(156×156像素窗口),如表 2所示。
| 序号 | 波段 | DNWFV | LWFV |
| 1 | 1 | 397.586 | 70.142 9 |
| 2 | 427.601 | 58.040 8 | |
| 3 | 438.625 | 49.777 3 | |
| 4 | 275.258 | 35.579 1 | |
| 2 | 1 | 416.335 | 75.091 6 |
| 2 | 450.744 | 65.442 2 | |
| 3 | 469.023 | 57.865 4 | |
| 4 | 301.809 | 42.749 6 | |
| 3 | 1 | 539.586 | 95.472 1 |
| 2 | 615.303 | 84.641 1 | |
| 3 | 662.306 | 75.788 5 | |
| 4 | 434.308 | 56.303 9 | |
| 4 | 1 | 652.280 | 115.944 1 |
| 2 | 745.295 | 109.841 0 | |
| 3 | 799.055 | 98.783 4 | |
| 4 | 510.842 | 73.185 2 | |
| 5 | 1 | 316.303 | 60.650 7 |
| 2 | 347.318 | 52.426 4 | |
| 3 | 368.453 | 45.443 3 | |
| 4 | 237.052 | 33.721 4 | |
| 6 | 1 | 452.944 | 88.582 1 |
| 2 | 529.220 | 83.291 4 | |
| 3 | 578.979 | 74.597 6 | |
| 4 | 372.398 | 55.635 2 | |
| 7 | 1 | 526.744 | 93.499 3 |
| 2 | 615.577 | 85.160 7 | |
| 3 | 668.195 | 76.538 9 | |
| 4 | 437.474 | 57.126 3 | |
| 8 | 1 | 474.859 | 84.741 9 |
| 2 | 491.402 | 77.374 7 | |
| 3 | 481.557 | 68.393 4 | |
| 4 | 337.427 | 48.533 7 | |
| 9 | 1 | 457.866 | 86.192 1 |
| 2 | 471.295 | 79.861 5 | |
| 3 | 467.803 | 71.184 3 | |
| 4 | 323.390 | 50.562 1 | |
| 10 | 1 | 360.305 | 61.736 3 |
| 2 | 345.958 | 52.131 3 | |
| 3 | 327.307 | 45.181 1 | |
| 4 | 232.008 | 31.865 9 | |
| 11 | 1 | 362.025 | 65.881 3 |
| 2 | 348.032 | 57.863 4 | |
| 3 | 329.807 | 50.099 7 | |
| 4 | 232.857 | 36.096 9 | |
| 12 | 1 | 349.273 | 64.525 4 |
| 2 | 341.829 | 55.451 1 | |
| 3 | 337.704 | 48.511 3 | |
| 4 | 237.508 | 34.882 9 | |
| 13 | 1 | 358.641 | 71.371 3 |
| 2 | 355.565 | 63.919 0 | |
| 3 | 352.781 | 56.766 2 | |
| 4 | 253.392 | 41.246 7 | |
| 14 | 1 | 662.410 | 117.947 8 |
| 2 | 715.859 | 114.034 0 | |
| 3 | 739.696 | 105.529 7 | |
| 4 | 522.989 | 77.077 9 |
2.2 辐射连接点提取
受相机安装误差以及卫星运动状态的影响,同轨相邻WFV相机影像重叠区域存在明显的几何错位现象,这在一定程度上影响了辐射连接点信息提取精度及效率。另外,因为WFV传感器相邻相机间属于弱交会成像情况,即影像交会角小于10°,所以本文采用基于DEM辅助的有理函数模型(rational function model,RFM)区域网平差方法,消除同轨相邻相机影像间几何错位问题[25]。
然后,选取多组与辐射控制点数据时相接近的、具有丰富地表覆盖类型的同轨四相机影像,经几何错位消除后,设置一定大小的移动分析窗口,在重叠区域搜索光谱均匀地物位置,进而获取其在相邻两个影像中的DN值信息,将其作为辐射连接点数据。其中,光谱均匀区域应满足差异系数CV(coefficient of variation)即DN值标准差与均值的比值应小于预先设定的阈值。该过程既能够降低传感器辐射性能变化对定标精度的影响,同时能够充分考虑不同响应区间内相机间辐射相关性。利用该方法分别在WFV1和WFV2、WFV2和WFV3、WFV3和WFV4影像重叠区域中获取辐射连接点数据99对、228对和237对。
3 试验结果与分析 3.1 绝对定标精度检验文献[8]采用仿真模拟的方式,建立相邻相机影像重叠区域表观辐亮度相关函数后,可以看出重叠区域表观辐亮度呈现高度线性相关性,其中线性拟合函数的斜率约为1,截距小于0.5 W·m-2·sr-1·μm-1,因此本研究中假定式(2)中的R(wfv, wfv相邻)i和W(wfv, wfv相邻)i的初始值分别为1和0。在此基础上,利用改进型辐射区域网平差技术获取各相机在轨绝对辐射定标系数,如表 3所示。
| 传感器 | 波段 | 本文定标结果/(W·m-2·sr-1·μm-1) | 文献[8]的RE/(%) | 本文的RE/(%) | |
| 增益 | 偏移量 | ||||
| WFV1 | 1 | 0.157 2 | 10.732 4 | 7.42 | 3.37 |
| 2 | 0.127 6 | 9.221 1 | 9.65 | 5.36 | |
| 3 | 0.111 8 | 6.466 7 | 7.03 | 3.22 | |
| 4 | 0.113 1 | 10.117 7 | 15.61 | 8.37 | |
| WFV2 | 1 | 0.155 9 | 12.717 3 | 7.68 | 8.82 |
| 2 | 0.127 3 | 9.648 8 | 7.44 | 9.34 | |
| 3 | 0.112 3 | 6.206 6 | 6.46 | 7.53 | |
| 4 | 0.112 8 | 9.946 2 | 13.49 | 8.71 | |
| WFV3 | 1 | 0.158 7 | 12.344 9 | 4.03 | 4.29 |
| 2 | 0.142 9 | 10.291 4 | 5.92 | 6.05 | |
| 3 | 0.124 9 | 6.762 8 | 2.47 | 3.19 | |
| 4 | 0.116 3 | 10.227 4 | 8.19 | 7.55 | |
| WFV4 | 1 | 0.160 2 | 9.791 6 | 5.75 | 4.68 |
| 2 | 0.144 6 | 7.739 8 | 3.79 | 4.46 | |
| 3 | 0.125 6 | 7.478 2 | 4.19 | 7.24 | |
| 4 | 0.113 6 | 10.116 0 | 4.21 | 7.91 | |
同样采用文献[8]中获取的绝对定标精度检查点,通过利用官方定标系数和本文获得的定标结果计算WFV影像表观辐亮度信息,然后与相应区域的MODIS影像表观辐亮度信息进行比对,利用式(8)获取相对误差
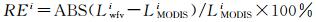 (8)
(8)
式中,REi代表第i波段的相对误差;Lwfvi代表利用官方定标系数或本文获得的定标结果计算得到的第i波段的WFV影像表观辐亮度;LMODISi为第i波段的MODIS表观辐亮度;ABS()为绝对值函数。
从表 3中可以看出,采用本文所构建的定标模型获取的定标结果具有较高的定标精度,各波段相对误差均优于9.34%,且与文献[8]采用分步式处理方式所得定标结果相比,本文定标结果并未出现相对误差明显较大的波段,这是因为本文采用整体平差处理的方式,在一定程度上降低了辐射传递过程中的误差累积。另外,从表 3中也可以看出,虽然WFV3相机缺少辐射控制信息,但是其定标精度并不低,因此今后将进一步分析多种因素(辐射控制点/连接点的选择及分布)对定标结果的影响,优化定标控制方案,进而提高传感器整体定标精度。
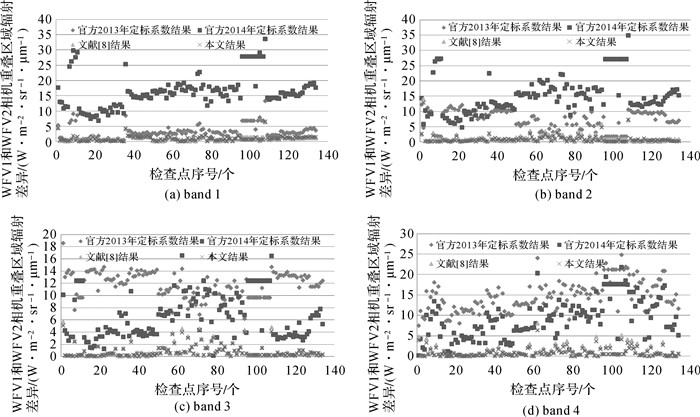
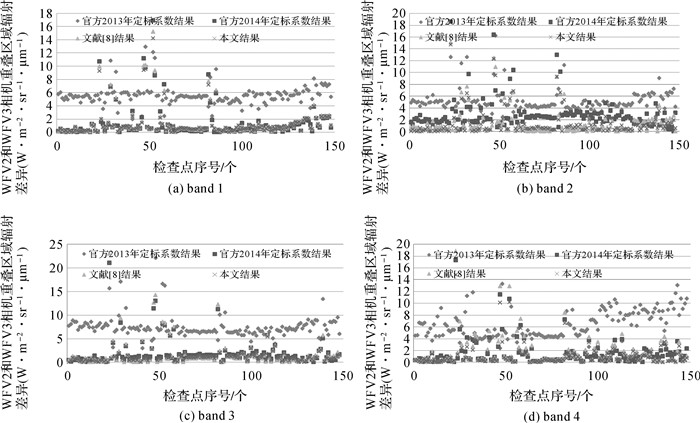
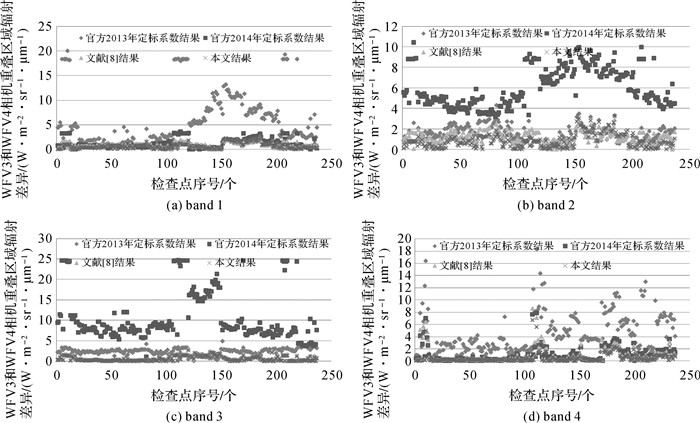
3.2 相机间相对辐射校正精度检验为检验本文定标系数对相机间相对辐射校正处理的效果,分别从WFV1和WFV2、WFV2和WFV3、WFV3和WFV4同轨影像重叠区域内选取了134对、148对和237对光谱均匀地物作为检查点,分别利用2013、2014年官方定标系数、文献[8]及本文定标系数计算每对检查点表观辐亮度,然后统计其差异的绝对值,如图 1-图 3所示,其差异绝对值的平均值列于表 4之中。
|
| 图 1 WFV1和WFV2影像检查点处表观辐亮度差异 Fig. 1 TOA radiance differences of check points in WFV1 and WFV2 |
|
| 图 2 WFV2和WFV3影像检查点处表观辐亮度差异 Fig. 2 TOA radiance differences of check points in WFV2 and WFV3 |
|
| 图 3 WFV3和WFV4影像检查点处表观辐亮度差异 Fig. 3 TOA radiance differences of check points in WFV3 and WFV4 |
| W·m-2·sr-1·μm-1 | |||||
| 重叠区域 | 波段 | 2013官方结果 | 2014官方结果 | 文献[8]结果 | 本文结果 |
| WFV1和WFV2 | 1 | 3.08 | 16.45 | 0.93 | 0.98 |
| 2 | 7.10 | 15.02 | 1.07 | 0.87 | |
| 3 | 11.79 | 6.53 | 1.03 | 0.79 | |
| 4 | 14.75 | 9.09 | 1.16 | 0.86 | |
| WFV2和WFV3 | 1 | 5.56 | 1.30 | 1.26 | 1.32 |
| 2 | 5.00 | 2.82 | 1.49 | 1.27 | |
| 3 | 7.32 | 1.80 | 1.61 | 1.63 | |
| 4 | 6.35 | 1.44 | 1.68 | 1.26 | |
| WFV3和WFV4 | 1 | 6.05 | 1.17 | 0.89 | 0.73 |
| 2 | 1.47 | 6.08 | 1.14 | 0.83 | |
| 3 | 2.36 | 10.61 | 0.65 | 0.59 | |
| 4 | 4.46 | 0.93 | 0.76 | 0.61 | |
从图 1-图 3和表 4中可以看出,利用本文定标结果可以大大降低相机间辐射不一致性。对于4个波段而言,与2013年官方定标系数相比,其辐射不一致性最高分别降低了87.93%、87.75%、93.3%和94.17%;与2014年官方定标系数相比,其辐射不一致性最高分别降低了94.04%、94.21%、94.44%和90.54%;与文献[8]的定标系数相比,其辐射不一致性处理效果大致相同。
3.3 实例验证选取2014年11月18日的一组WFV影像进行实例验证,分别从影像重叠区域中挑选出某一局部区域进行展示。从图 4-图 6和表 5中可以看出,原始图像和利用2013、2014年官方定标系数的处理结果均存在明显辐射差异,其中2013年官方结果各波段辐射平均差异分别约2.57、5.14、7.90和7.33 W·m-2·sr-1·μm-1,2014年官方结果各波段辐射平均差异分别约8.43、6.92、4.19和5.80 W·m-2·sr-1·μm-1,而本文处理结果与文献[8]处理后的目视解译效果近乎相同,均无明显辐射差异,各波段辐射平均差异均优于1 W·m-2·sr-1·μm-1,但本文处理的整体校正精度要比文献[8]略高,相对精度平均提高约10.19%。这也证明了本文定标结果可以有效地实现星载多相机拼接成像传感器相机间相对辐射校正。同时,利用本文方法可以规范不同用户进行相对辐射校正处理的流程,提高其定量产品综合对比的可信度。

|
| 图 4 WFV1和WFV2影像拼接后局部放大图 Fig. 4 Partial enlarged images of WFV1 and WFV2 stitching results |

|
| 图 5 WFV2和WFV3影像拼接后局部放大图 Fig. 5 Partial enlarged images of WFV2 and WFV3 stitching results |

|
| 图 6 WFV3和WFV4影像拼接后局部放大图 Fig. 6 Partial enlarged images of WFV3 and WFV4 stitching results |
| W·m-2·sr-1·μm-1 | |||||
| 重叠区域 | 波段 | 2013官方结果 | 2014官方结果 | 文献[8]结果 | 本文结果 |
| WFV1和WFV2 | 1 | 1.20 | 13.04 | 0.27 | 0.34 |
| 2 | 8.78 | 10.93 | 0.45 | 0.41 | |
| 3 | 12.78 | 4.52 | 0.86 | 0.75 | |
| 4 | 10.80 | 3.89 | 0.74 | 0.62 | |
| WFV2和WFV3 | 1 | 5.22 | 0.63 | 0.29 | 0.12 |
| 2 | 4.99 | 1.97 | 0.45 | 0.35 | |
| 3 | 8.15 | 0.76 | 1.05 | 0.94 | |
| 4 | 7.38 | 1.10 | 0.34 | 0.41 | |
| WFV3和WFV4 | 1 | 1.30 | 11.61 | 0.85 | 0.74 |
| 2 | 1.66 | 7.87 | 0.81 | 0.61 | |
| 3 | 2.76 | 7.30 | 0.62 | 0.59 | |
| 4 | 3.81 | 12.42 | 0.35 | 0.36 | |
4 总结
本文针对星载多相机拼接成像传感器特点,提出了一种基于改进型辐射区域网平差的在轨辐射定标方法。该方法可以实现相机间相对辐射校正和在轨辐射定标的一体化处理。文中指出了现有在轨辐射定标方法存在的不足,介绍了辐射区域网平差基本思想,详细推导了基于改进型辐射区域网平差的在轨辐射定标方法和流程,对比分析了采用本文结果与官方系数进行相机间相对辐射校正的效果,并利用一组WFV影像验证了本文采用的定标方法的有效性。在下一步的研究中将重点分析多种因素(辐射控制点/连接点的选择及分布)对定标结果的影响,优化定标控制方案,进而提高传感器整体定标精度。
致谢: 特别感谢中国资源卫星应用中心为本文研究提供GF-1影像数据,感谢中国科学院遥感与数字地球研究所顾行发研究员、余涛研究员的指导。
| [1] |
白照广.
高分一号卫星的技术特点[J]. 中国航天, 2013(8): 5–9.
BAI Zhaoguang. The Technical Characteristics of GF-1 Satellite[J]. Aerospace China, 2013(8): 5–9. |
| [2] |
韩启金, 傅俏燕, 张学文, 等.
高分一号卫星宽视场成像仪的高频次辐射定标[J]. 光学与精密工程, 2014, 22(7): 1707–1714.
HAN Qijin, FU Qiaoyan, ZHANG Xuewen, et al. High-frequency Radiometric Calibration for Wide Field-of-view Sensor of GF-1 Satellite[J]. Optics and Precision Engineering, 2014, 22(7): 1707–1714. |
| [3] |
傅俏燕, 闵祥军, 李杏朝, 等.
敦煌场地CBERS-02 CCD传感器在轨绝对辐射定标研究[J]. 遥感学报, 2006, 10(4): 433–439.
FU Qiaoyan, MIN Xiangjun, LI Xingchao, et al. In-flight Absolute Calibration of the CBERS-02 CCD Sensor at the Dunhuang Test Site[J]. Journal of Remote Sensing, 2006, 10(4): 433–439. DOI:10.11834/jrs.20060465 |
| [4] |
陈洪耀, 张黎明, 施家定, 等.
高精度星上定标漫射板双向反射分布函数绝对测量系统研究[J]. 大气与环境光学学报, 2014, 9(1): 72–80.
CHEN Hongyao, ZHANG Liming, SHI Jiading, et al. High Accuracy Gonioreflectometer for Solar Diffuser Spectral BRDF Measurement[J]. Journal of Atmospheric and Environmental Optics, 2014, 9(1): 72–80. |
| [5] | XIONG Xiaoxiong, SUN Junqiang, BARNES W, et al. Multiyear On-orbit Calibration and Performance of Terra MODIS Reflective Solar Bands[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(4): 879–889. DOI:10.1109/TGRS.2006.890567 |
| [6] | YANG Aixia, ZHONG Bo, LV Wenbo, et al. Cross-calibration of GF-1/WFV over a Desert Site Using Landsat-8/OLI Imagery and ZY-3/TLC Data[J]. Remote Sensing, 2015, 7(8): 10763–10787. DOI:10.3390/rs70810763 |
| [7] | CHANDER G, MISHRA N, HELDER D L, et al. Applications of Spectral Band Adjustment Factors (SBAF) for Cross-Calibration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(3): 1267–1281. DOI:10.1109/TGRS.2012.2228007 |
| [8] |
韩杰, 谢勇.
GF-1卫星WFV影像间匀色方法[J]. 测绘学报, 2016, 45(12): 1423–1433.
HAN Jie, XIE Yong. Image Dodging Algorithm for GF-1 Satellite WFV Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1423–1433. DOI:10.11947/j.AGCS.2016.20160248 |
| [9] |
王中挺, 辛金元, 贾松林, 等.
利用暗目标法从高分一号卫星16 m相机数据反演气溶胶光学厚度[J]. 遥感学报, 2015, 19(3): 530–538.
WANG Zhongting, XIN Jinyuan, JIA Songlin, et al. Retrieval of AOD from GF-116 m Camera Via DDV Algorithm[J]. Journal of Remote Sensing, 2015, 19(3): 530–538. |
| [10] |
刘国栋, 邬明权, 牛铮, 等.
基于GF-1卫星数据的农作物种植面积遥感抽样调查方法[J]. 农业工程学报, 2015, 31(5): 160–166.
LIU Guodong, WU Mingquan, NIU Zheng, et al. Investigation Method for Crop Area Using Remote Sensing Sampling Based on GF-1 Satellite Data[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(5): 160–166. |
| [11] | CHOI W H, CHO S I, INOUE D, et al. Lineament Analysis Using ASTER Satellite Images in the Southern Part of the Korean Peninsula[J]. Journal of Geological Resource and Engineering, 2015(1): 8–16. |
| [12] |
王密, 潘俊.
面向无缝影像数据库应用的一种新的光学遥感影像色彩平衡方法[J]. 国土资源遥感, 2006, 18(4): 10–13, 79.
WANG Mi, PAN Jun. A New Color Balance Method for Large-scale Seamless Image Database[J]. Remote Sensing for Land & Resources, 2006, 18(4): 10–13, 79. DOI:10.6046/gtzyyg.2006.04.03 |
| [13] |
李德仁, 王密, 潘俊.
光学遥感影像的自动匀光处理及应用[J]. 武汉大学学报(信息科学版), 2006, 31(9): 753–756.
LI Deren, WANG Mi, PAN Jun. Auto-dodging Processing and Its Application for Optical RS Images[J]. Geomatics and Information Science of Wuhan University, 2006, 31(9): 753–756. |
| [14] | YAN W Y, SHAKER A. Radiometric Correction and Normalization of Airborne LiDAR Intensity Data for Improving Land-cover Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(12): 7658–7673. DOI:10.1109/TGRS.2014.2316195 |
| [15] | GEHRKE S, BESHAH B T.Radiometric Normalization of Large Airborne Image Data Sets Acquired by Different Sensor Types[C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences.Prague, Czech Republic:ISPRS, 2016:317-326. |
| [16] | FALALA L, GACHET R, CUNIN L.Radiometric Block-Adjustment of Satellite Images Reference3D Production Line Improvement[C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences.Beijing, China:ISPRS, 2008:319-324. |
| [17] | CHANDELIER L, MARTINOTY G. The Radiometric Aerial Triangulation for the Equalization of Digital Aerial Images and Orthoimages[J]. Photogrammetric Engineering & Remote Sensing, 2009, 75(2): 193–200. |
| [18] | HONKAVAARA E, SAARI H, KAIVOSOJA J, et al. Processing and Assessment of Spectrometric, Stereoscopic Imagery Collected Using a Lightweight UAV Spectral Camera for Precision Agriculture[J]. Remote Sensing, 2013, 5(10): 5006–5039. DOI:10.3390/rs5105006 |
| [19] | GEHRKE S, BESHAH B T.Radiometric Normalization of Large Airborne Image Data Sets Acquired by Different Sensor Types[C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences.Prague, Czech Republic:ISPRS, 2016:317-326. |
| [20] | OLSEN D, DOU Changyong, ZHANG Xiaodong, et al. Radiometric Calibration for AgCam[J]. Remote Sensing, 2010, 2(2): 464–477. DOI:10.3390/rs2020464 |
| [21] | LÓPEZ D H, GARCÍA B F, PIQUERAS J G, et al. An Approach to the Radiometric Aerotriangulation of Photogrammetric Images[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(6): 883–893. DOI:10.1016/j.isprsjprs.2011.09.011 |
| [22] | HONKAVAARA E, HAKALA T, MARKELIN L, et al. A Process for Radiometric Correction of UAV Image Blocks[J]. Photogrammetrie, Fernerkundung, Geoinformation, 2012, 2012(2): 115–127. DOI:10.1127/1432-8364/2012/0106 |
| [23] | PROS A, COLOMINA I, NAVARRO J A, et al.Radiometric Block Adjustment and Digital Radiometric Model Generation[C]//International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences.Hannover, Germany:ISPRS, 2013:293-298. |
| [24] | TEO T A, Wu H M. Radiometric Block Adjustment for Multi-strip Airborne Waveform LIDAR Data[J]. Remote Sensing, 2015, 7(12): 16831–16848. DOI:10.3390/rs71215856 |
| [25] |
汪韬阳, 张过, 李德仁, 等.
资源三号测绘卫星影像平面和立体区域网平差比较[J]. 测绘学报, 2014, 43(4): 389–395.
WANG Taoyang, ZHANG Guo, LI Deren, et al. Comparison between Plane and Stereo Block Adjustment for ZY-3 Satellite Images[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 389–395. DOI:10.13485/j.cnki.11-2089.2014.0058 |



