2. 北京成像技术高精尖创新中心, 北京 100048;
3. 中国科学院遥感与数字地球研究所, 北京 100094
2. Beijing Advanced Innovation Center for Imaging Technology, Beijing 100048, China;
3. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100094, China
车载球面全景影像能够采集来自每个方向的光线信息,并且以二维图像的方式保存起来,获得360°×180°全视场的视觉信息。配合高精度的GPS(Global Positioning System)和IMU(inertial measurement unit),能够获取带有精确位置和姿态信息的高分辨率全景影像,目前已经广泛应用于地理信息采集、街景地图制作、安防监控、交通等领域。比如著名的Google街景在不同地点采集球面全景影像,并放置在地图对应的位置,用户可以很方便地从一个全景场景过渡到另外一个全景场景进行室外浏览。根据采集相机和处理方式的不同,球面全景影像的获取方法也不同。一种方法是利用鱼眼镜头来获取大视场图像,然后利用商业拼接软件(如PTGui)来得到球面全景影像,这种方式将采集与处理分开,处理效率较低。在要求连续、高精度和快速拼接全景的场合,往往采用集成化的商业全景视觉系统,如加拿大PointGrey公司生产的Ladybug。该系统包含6个相机(5个相机水平放置,1个垂直向上拍摄),可以获得水平方向360°,竖直方向接近180°视场的影像信息。Ladybug能够实时完成影像采集、处理、拼接和校正等工作。针对全景影像的研究目前大部分集中于全景构象方程[1-2]、全景相机标定[3]与拼接以及全景匹配[4-6]等。在目前的应用中,全景图像大部分都是用于360°场景的浏览,一般不具备量测的功能。随着全景图像采集设备以及拼接算法的普及,越来越多的研究尝试用全景影像来恢复场景的三维结构[7-10],并应用于文物保护与重建[11-12]、建筑测量[13]、SLAM(simultaneous localization and mapping)技术[14],以及增强现实领域[15]。相比传统的基于面阵影像的三维重建,全景影像独特的投影方式与小孔平面成像模型不同,因此需要对现有的模型进行改造才能运用到全景影像[16]。
相对定向是利用影像进行重建和量测的关键技术,也是进行全自动序列影像三维重建的前提。相对定向利用同名点来恢复立体像对之间的位置和姿态,能够实现初始点云数据的重建,为序列影像的光束法空三[17]提供初始的位置、姿态和三维点坐标信息。与传统摄影测量[18]的相对定向采用迭代求解的方法不同,计算机视觉领域对本质矩阵[19]进行分解来直接获得旋转矩阵与平移量,8点法[19-21]和5点法[22]常用来计算本质矩阵。8点法的优点在于可以直接解算线性方程组来获得唯一解,但是需要的点数较多。5点法的计算相对复杂,但是在内方位元素已知且焦距误差小于10%的情况下精度最高[22]。在本质矩阵的计算中,结合RANSAC(random sample consensus)算法[23]可以提高算法的抗差性,共面误差则用来对RANSAC的每次采样计算进行评价。基于归一化三维坐标的切面距离[7]常用作球面全景共面条件的误差计算方法,该方法直接利用角度信息而且计算简单,但不能反映不同分辨率的全景图像的共面误差变化程度。相对定向结合全景PnP(perspective-n-point)位姿算法[24]的结果可以用于全景影像序列的空三解算[5, 17],实现球面全景的全自动三维点云重建[7]。
本文以三维重建中的核心相对定向为研究对象,对目前广泛使用的5点法相对定向算法[22]进行改进使其适用于球面全景影像,并提出了球面全景的相对定向误差计算方法。模拟数据和实际试验结果表明,本文的相对定向解算的姿态和平移参数能够达到较高的精度,利用相对定向结果生成的全景核线影像的偏移误差达到1个像素以内。
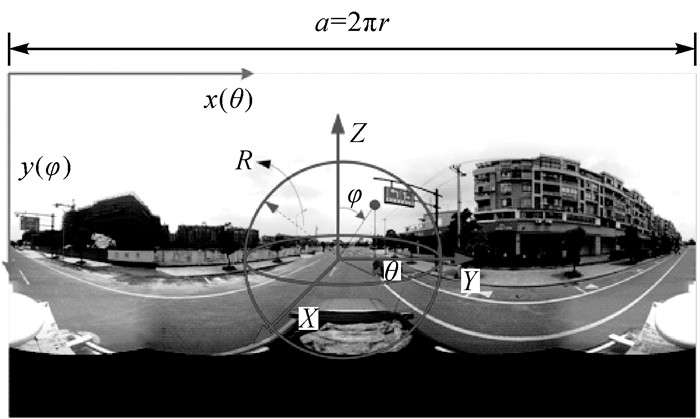
1 球面全景影像成像方程球面全景影像的处理过程涉及3个坐标:影像坐标系、经纬度球面坐标系和三维空间坐标系。3个坐标系的关系如图 1。
|
| 图 1 球面全景坐标系 Fig. 1 Spherical panoramic coordinate system |
图 1中,(x, y)为球面全景影像的像素坐标,(θ, φ)为经纬度,(X, Y, Z)为局部三维坐标系。为了方便计算,经度起始方向是Y轴正方向,纬度起始方向为Z轴正方向,因此经度的取值范围为[0, 360°],纬度的取值范围为[0, 180°]。球面全景影像的宽高比为2:1。设球体的半径为r,那么影像的宽度为2πr。全景图像的像素坐标和经纬度之间的关系为
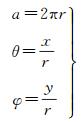 (1)
(1)
式中,a为球面全景影像的宽度。三维坐标系以Y轴的正方向作为经度的起始位置,经纬度与三维坐标的转换关系为
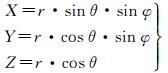 (2)
(2)
根据不同位置拍摄的图像来恢复相机位置和三维场景是一个研究了近两个世纪的问题,最早是在摄影测量领域[18],现在主要是在计算机视觉领域[19, 25]。当相机的内方位元素(即相机的焦距、主点位置、畸变参数)已知时,5对匹配点就可以解算出相机的位置与姿态[19],其中位置只能恢复为相对位置,与真实的位置存在一个比例关系。文献[22]提出了一种有效的数值计算方法。相对定向的理论基础是共面条件,其数学模型为本质矩阵(essential matrix)。当内方位元素已知时,图像坐标与本质矩阵的联系可以用式(3)来描述[19]
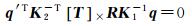 (3)
(3)
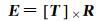 (4)
(4)
式中,E就是本质矩阵,代表了著名的核线约束;[T]×为反对称矩阵(skew symmetric matrix);R为旋转矩阵。式(3)中,q、q ′为第1张和第2张相片的影像齐次坐标,第1张相片的投影中心为坐标系的原点。K1、K2为内方位元素矩阵。
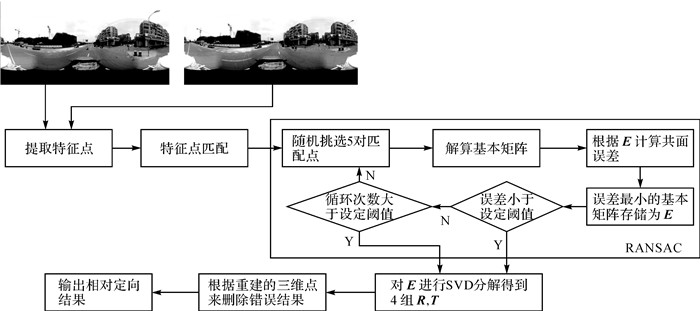
图 2为5点法相对定向算法的流程,算法假设内方位元素已知。基于匹配结果,并结合RANSAC方法可以得到误差最小的本质矩阵。然后对本质矩阵进行奇异值分解来得到相对定向的结果,即R与T的值。最后利用重建的三维点坐标,根据实际成像时目标位于相机前方的事实来排除错误的相对定向结果。
|
| 图 2 平面透视投影5点法相对定向流程 Fig. 2 The flowchart of the 5-point relative pose estimation method for perspective projection |
3 球面全景相对定向
球面全景的成像方式虽然与传统的透视投影成像不同,但是共面条件依然成立,还是可以用本质矩阵来表达。与传统的平面透视投影相比,由于全景成像已经利用相机标定的内方位元素实现了平面投影到球面坐标之间的投影,因此球面全景的球面坐标可以直接用来进行相对定向。球面全景的相对定向流程与平面透视投影5点法是一致的,区别在于共面条件误差的计算和错误组合的剔除与平面透视投影不同。
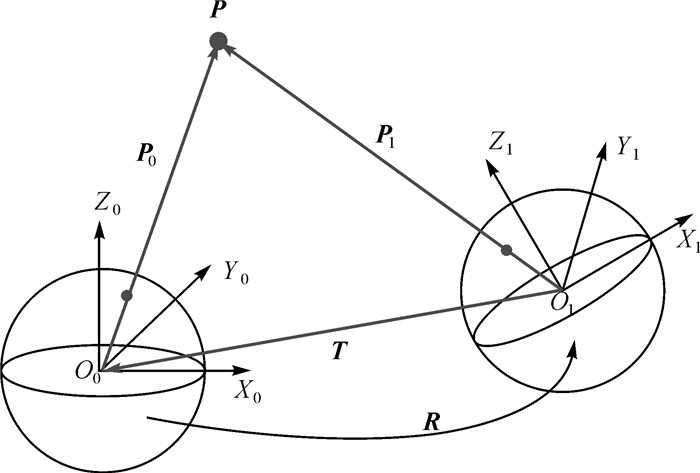
如图 3所示,在球面投影下,矢量P0、P1和T是共面的。O0-X0Y0Z0为第1张相片的局部三维坐标系,也是相对定向中的基准坐标系。O1-X1Y1Z1是第2张相片的局部三维坐标系,R为O0-X0Y0Z0到O1-X1Y1Z1的旋转矩阵,T为旋转后两个坐标系之间的平移量。共面条件可以写为
|
| 图 3 球面投影下的共面条件 Fig. 3 Coplanar condition under spherical projection |
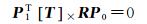 (5)
(5)
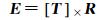 (6)
(6)
式(5)中,P0、P1可以根据公式(2)来计算;式(6)中的本质矩阵E的形式与传统面阵成像投影是一致的,只是输入的坐标是直接根据球面全景计算得到的三维坐标。
3.1 共面条件的误差计算5点法相对定向中结合RANSAC来选择最优本质矩阵时,需要计算共面条件的误差并用来判断本质矩阵是否正确。根据小孔成像的核线原理,同名点位于同名核线上,在平面透视投影中,核线为直线,因此可以采用点到直线的距离作为共面条件的误差项。但是在球面投影中,核线为经过球心的圆,在投影到平面后核线变成不规则的曲线。针对这个问题,本文直接利用球面距离作为共面条件的误差。
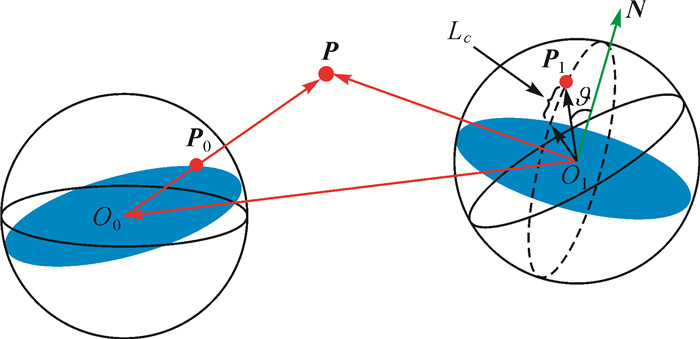
如图 4所示,P0, P1为球面上的两个点的齐次坐标,对应了图像平面的一对同名点。设P为P0对应的物方空间三维坐标,O0PO1为核面,核面与球体相交得到通过球心的两个蓝色圆面。如果P0对应的图像点是正确的同名点,那么这两个点都应该位于蓝色的圆面上。本文用球面点到蓝色圆面的弧面距离Lc作为共面条件的误差。设N为核面O0PO1的法线向量,p1O1和N之间的夹角为ϑ,那么有
|
| 图 4 球面投影下的共面条件误差 Fig. 4 Coplanar condition error under spherical projection |
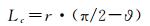 (7)
(7)
根据本质矩阵E的性质,可以利用P0来计算N
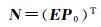 (8)
(8)
半径r根据图像的宽度来计算,因此距离Lc能自动适应不同大小的球面全景影像。
3.2 错误组合的剔除得到本质矩阵E,采用矩阵奇异值分解(singular value decomposition,SVD)方法[22]对E进行分解得到4组候选的R和T值。在传统的5点法相对定向中[22],从4组候选中找到正确的结果的依据是重建的三维点位于相机的前方。但对于球面投影来说,相机可以从360°进行拍摄,因此不能使用这个约束条件。因此对传统的方法进行改进:首先根据正确的图像同名点对来重建物方空间三维点P,然后计算重建后的三维点与投影中心连线矢量和基准图像中的球面三维点矢量P0之间的夹角。如果相对定向的结果正确,那么两个矢量几乎位于同一个方向上,因此两个矢量之间的夹角很小。对每对同名点进行上述操作,将夹角小于一定阈值(本文为1°)的点对记录下来,4个候选中符合上述条件最多的就是正确的相对定向结果。
4 试验结果与分析 4.1 基于模拟数据的球面全景相对定向精度分析模拟全景图像的特征点数据,设定全景图像的宽高为:1024×512。参考的基准大地坐标系的中心设定在左片的投影中心,并假设左片的图像空间坐标系的3个轴与大地坐标系平行,因此左片的3个旋转角度为0°,模拟试验中只需要随机构造右片的外方位元素即可。试验随机模拟100组姿态和位置参数,姿态角的变化范围为:[-10°, 10°],平移量的变化范围为:[-1, 1]。模拟数据假设有15个空间坐标已知的三维点,然后根据模拟数据将三维点投影到二维的球面全景图像。为了模拟实际中的图像特征点定位效果,对投影后的图像坐标加入随机噪音,范围为:[-0.5, 0.5]像素。基于模拟数据,利用本文的相对定向解算出位置和姿态数据,并统计每个姿态角的最小、最大值以及中误差,结果见表 1。
| (°) | |||
| 俯仰角 | 横滚角 | 航向角 | |
| 最小值 | 0.000 6 | 0.000 3 | 0.001 1 |
| 最大值 | 0.249 5 | 0.316 6 | 0.295 4 |
| 中误差 | 0.106 8 | 0.109 5 | 0.104 9 |
由于相对定向无法解算出绝对的平移量,而只能获得一个比例上的相对解,为了评价相对定向算法解算的平移量的精度,通过计算模拟数据的平移量与解算得到的平移量之间的夹角作为误差项进行验证。设模拟的平移量为TS,设解算后的平移量为Tr,那么平移量的夹角为
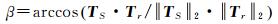 (9)
(9)
夹角越小意味着解算的精度越高。对每组模拟数据进行相对定向得到的夹角值进行统计,结果显示在表 2中。
| (°) | |||
| 最小值 | 最大值 | 中误差 | |
| β | 0.056 8 | 9.551 7 | 1.520 0 |
表 2的结果表明,相对定向算法解算得到的平移量与模拟值之间的夹角小于2°,基本上位于同一个方向上。
4.2 基于实测数据的球面全景相对定向精度分析试验数据为装载在汽车上的Ladybug3相机在杭州市采集得到的41张全景图像。在进行全景数据采集的同时利用POS系统(GPS和IMU)记录了位置信息和姿态信息。试验采用的POS系统为OxTS公司的Inertial+,在双GPS工作状态下的精度如表 3所示。
| 参数 | DGPS |
| 横滚角/俯仰角 | 0.05° |
| 航向角 | 0.1° |
| 位置/m | 0.4 |
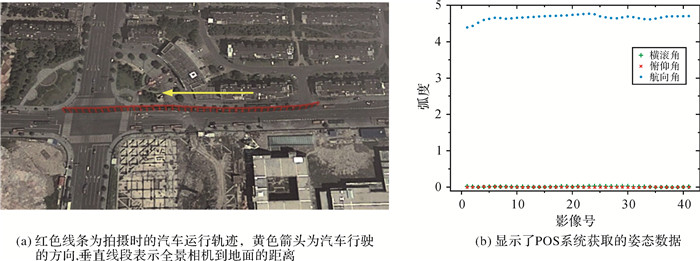
全景相机与POS系统进行集成后安装在汽车上,从东往西行驶。轨迹和姿态数据显示在图 5中。
|
| 图 5 POS获取的位置与姿态数据 Fig. 5 The location and pose data of POS |
POS系统能够获取拍摄时刻的位置和姿态信息。位置数据用经度、纬度和高程来表示,在地图上显示如图 5(a),每条垂直的线段代表了一次拍摄的位置,线段的高度为GPS装置到地面的距离。姿态数据包括俯仰角、横滚角和航向角。由图 5(b)可以看出,横滚角和俯仰角都接近于0,说明拍摄时汽车在马路上水平行驶,POS系统受到的抖动较小。航向角的均值为4.7弧度(即269.3°),说明汽车几乎是朝着正西方向运动。由于GPS和IMU都是以地面坐标系为基准,如果要和相对定向的结果进行对比,需要进行坐标转换。设相邻全景影像的POS旋转矩阵为R1和R2,相对定向的姿态角可以利用矩阵R2R1-1来计算。试验中,利用SIFT(scale-invariant feature transform)[26]算法从相邻的两张全景图像中自动提取特征点,然后进行匹配,最后根据匹配的结果来进行全景相对定向。41张全景图像可以计算出40组相对定向的外方位元素,统计3个姿态角与转换后的POS姿态角之间的差值,并计算最大、最小值和中误差。其统计数据见表 4。
| (°) | |||
| 俯仰角 | 横滚角 | 航向角 | |
| 最小值 | 0.007 3 | 0.006 9 | 0.005 0 |
| 最大值 | 0.456 6 | 0.344 8 | 0.872 4 |
| 中误差 | 0.173 0 | 0.146 0 | 0.361 3 |
与模拟数据类似,根据相对计算获得的平移量和POS数据的位置信息来计算夹角β,其结果见表 5。
| (°) | |||
| 最小值 | 最大值 | 中误差 | |
| β | 0.087 0 | 5.720 2 | 1.950 4 |
表 5为本文相对定向与POS系统提供的姿态角之间的误差的统计结果。可以看出俯仰角和横滚角的精度要高于航向角,这与POS系统的量测精度也是吻合的。真实数据的解算精度要低于模拟数据,原因在于Ladybug的全景影像是由6个相机拍摄的数据拼接生成,因此存在拼接误差,同时特征点的提取误差以及POS系统本身的测量误差,都会导致采用全景数据进行相对定向获得参数的精度降低。
4.3 基于核线的球面全景相对定向精度分析如果相对定向的结果准确,其核线影像的特征点就落在同一条直线上,可以利用这个规律来验证相对定向的精度。41张连续拍摄的全景影像的相邻影像可以组合为40个像对,生成40对核线影像。
图 6为图像序列中一个相邻像可进行相对定向后生成核线影像(图 6(b)),并在核线影像上进行同名点匹配的效果(图 6(c))。在核线影像之间进行特征点提取和匹配,统计每对核线影像上的同名点在核线方向(本文中为x轴)上的像素差值并计算平均值(用eP来表示),可以得到40个eP值

|
| 图 6 核线影像的生成以及特征点匹配效果 Fig. 6 The generation of the epipolar image and the effect of feature point matching |
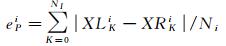 (10)
(10)
式中,ePi第i个核线影像对的坐标误差;Ni为第i个核线影像对提取的同名点的个数;XLKi、XRKi代表第i个核线影像对的第k个同名点的左片和右片的x坐标。
将40个eP进行统计,计算其最大值、最小值和中误差,结果见表 6。可以看出采用相对定向的结果来生成核线影像,同名核线在x方向上的差值的中误差能达到1个像素以内,证明了本文算法的准确与有效性。
| 像素 | |||
| 最小值 | 最大值 | 中误差 | |
| eP | 0.867 9 | 1.186 4 | 0.993 6 |
5 结论
本文对传统的5点法相对定向算法进行改进,使之可以处理球面全景影像之间的位置与姿态估算。本文的贡献和创新在于:①根据球面全景的成像模型推导了球面全景的共面条件公式;②采用球面点到核面的球面距离作为全景相对定向的共面条件误差,相比采用角度以及归一化坐标的误差计算方式,球面距离更接近球面全景影像成像方式下的点到核线绝对距离,并且能够适用于不同分辨率的球面全景影像;③采用模拟数据和实地采集的全景影像和POS数据对本文算法的精度进行验证。本文的球面全景影像的相对定向算法能够为全景影像序列的整体空三优化提供初始的位置与姿态信息,实现全景影像的全自动化摄影测量。后续的研究中要针对不同精度的POS系统来进行影像采集和相对定向试验,进一步验证本文算法的有效性以及在不同传感器和场景下的精度变化问题。同时研究如何在空三中结合POS数据实现全景影像的真实三维重建,并应用于测绘领域。试验中也发现,由于球面全景接收的光线来自360°全范围场景,因此存在一些同名点位于基线方向附近。这些同名点对应的三维点与相机投影中心的连线夹角较小,其三维重建精度较低,因此会对相对定向的结果产生影响,如何来自动消除这些同名点对相对定向的影响也是后续要重点研究的问题。
| [1] |
曾凡洋, 钟若飞, 宋杨, 等.
车载全景影像核线匹配和空间前方交会[J]. 遥感学报, 2014, 18(6): 1230–1236.
ZENG Fanyang, ZHONG Ruofei, SONG Yang, et al. Vehicle Panoramic Image Matching Based on Epipolar Geometry and Space Forward Intersection[J]. Journal of Remote Sensing, 2014, 18(6): 1230–1236. |
| [2] |
季顺平, 史云.
多镜头组合型全景相机两种成像模型的定位精度比较[J]. 测绘学报, 2014, 43(12): 1252–1258.
JI Shunping, SHI Yun. Comparison of Two Sensor Models for Multi-camera Rig System in Measurements[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1252–1258. DOI:10.13485/j.cnki.11-2089.2014.0169 |
| [3] |
石丽梅, 赵红蕊, 李明海, 等.
车载移动测图系统外方位元素标定方法[J]. 测绘学报, 2015, 44(1): 52–58.
SHI Limei, ZHAO Hongrui, LI Minghai, et al. Extrinsic Calibration for Vehicle-based Mobile Mapping System[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 52–58. DOI:10.11947/j.AGCS.2015.20130203 |
| [4] |
张正鹏, 江万寿, 张靖.
自适应运动结构特征的车载全景序列影像匹配方法[J]. 测绘学报, 2015, 44(10): 1132–1141.
ZHANG Zhengpeng, JIANG Wanshou, ZHANG Jing. An Matching Method for Vehicle-borne Panoramic Image Sequence Based on Adaptive Structure from Motion Feature[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1132–1141. DOI:10.11947/j.AGCS.2015.20140622 |
| [5] |
季顺平, 史云.
车载全景相机的影像匹配和光束法平差[J]. 测绘学报, 2013, 42(1): 94–100, 107.
JI Shunping, SHI Yun. Image Matching and Bundle Adjustment Using Vehicle-based Panoramic Camera[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 94–100, 107. |
| [6] |
张正鹏, 江万寿, 张靖.
光流特征聚类的车载全景序列影像匹配方法[J]. 测绘学报, 2014, 43(12): 1266–1273.
ZHANG Zhengpeng, JIANG Wanshou, ZHANG Jing. An Image Match Method Based on Optical Flow Feature Clustering for Vehicle-borne Panoramic Image Sequence[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1266–1273. DOI:10.13485/j.cnki.11-2089.2014.0172 |
| [7] | PAGANI A, GAVA C, CUI Yan, et al. Dense 3D Point Cloud Generation from Multiple High-resolution Spherical Images.[C]//Proceedings of the 12th International Conference on Virtual Reality, Archaeology and Cultural Heritage. Prato, Italy:Eurographics Association, 2011:17-24. |
| [8] | PAGANI A, STRICKER D. Structure from Motion Using Full Spherical Panoramic Cameras[C]//Proceedings of 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops). Barcelona, Spain:IEEE, 2012:375-382. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6130266 |
| [9] | TONG Guofeng, LIU Ran, TAN Jiandong. 3D Information Retrieval in Mobile Robot Vision Based on Spherical Compound Eye[C]//Proceedings of 2011 IEEE International Conference on Robotics and Biomimetics. Karon Beach, Phuket, Thailand:IEEE, 2011:1895-1900. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?reload=true&arnumber=6181567&contentType=Conference+Publications |
| [10] | LUHMANN T, TECKLENBURG W. 3-D Object Reconstruction from Multiple-Station Panorama Imagery[C]//MAAS H G, SCHNEIDER D. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Vol. XXXIV, Part 5/W16. Dresden, Germany:ISPRS, 2004. |
| [11] | FANGI G. Further Developments of the Spherical Photogrammetry for Cultural Heritage[C]//Proceedings of the 22nd CIPA Symposium. Kyoto, Japan:CIPA, 2009. |
| [12] | WAHBEH W, NEBIKER S, FANGI G. Combining Public Domain and Professional Panoramic Imagery for the Accurate and Dense 3D Reconstruction of the Destroyed Bel Temple in Palmyra[C]//ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016, Volume Ⅲ-5. Prague, Czech Republic:ISPRS, 2016:81-88. http://adsabs.harvard.edu/abs/2016ISPAnIII5...81W |
| [13] | FANGI G. The Multi-image Spherical Panoramas as A Tool for Architectural Survey[C]//XXI International CIPA Symposium. Athens, Greece:ISPRS, 2012, 36:256-1840. |
| [14] | TONG Guofeng, WU Zizhang, WENG Ninglong, et al. An Omni-directional vSLAM Based on Spherical Camera Model and 3D Modeling[C]//Proceedings of the 10th World Congress on Intelligent Control and Automation. Beijing, China:IEEE, 2012:4551-4556. |
| [15] | PAGANI A, HENRIQUES J, STRICKER D. Sensors for Location-based Augmented Reality the Example of Galileo and Egnos[J]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XLI-B1. Prague, Czech Republic:ISPRS, 2016: 1173–1177. |
| [16] | FANGI G, NARDINOCCHI C. Photogrammetric Processing of Spherical Panoramas[J]. The Photogrammetric Record, 2013, 28(143): 293–311. DOI:10.1111/phor.12031 |
| [17] | TRIGGS B, MCLAUCHLAN P F, HARTLEY R I, et al. Bundle Adjustment:A Modern Synthesis[C]//TRIGGS B, ZISSERMAN A, SZELISKI R. Vision Algorithms:Theory and Practice. Berlin:Springer, 1999:298-372. |
| [18] |
王佩军, 徐亚明.
摄影测量学[M]. 2版. 武汉: 武汉大学出版社, 2010.
WANG Peijun, XU Yaming. Photogrammetry[M]. 2nd ed. Wuhan: Wuhan University Press, 2010. |
| [19] | HARTLEY R, ZISSERMAN A. Multiple View Geometry in Computer Vision[M]. 2nd ed. Cambridge: Cambridge University Press, 2000. |
| [20] | HARTLEY R I. In Defense of the Eight-point Algorithm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(6): 580–593. DOI:10.1109/34.601246 |
| [21] | LONGUET-HIGGINS H C. A Computer Algorithm for Reconstructing a Scene from Two Projections[J]. Nature, 1981, 293(5828): 133–135. DOI:10.1038/293133a0 |
| [22] | NISTER D. An Efficient Solution to the Five-point Relative Pose Problem[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(6): 756–770. DOI:10.1109/TPAMI.2004.17 |
| [23] | FISCHLER M A, BOLLES R C. Random Sample Consensus:A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM, 1981, 24(6): 381–395. DOI:10.1145/358669.358692 |
| [24] |
邓非, 吴幼丝, 胡玉雷, 等.
球形全景影像位姿估计的改进EPnP算法[J]. 测绘学报, 2016, 45(6): 677–684.
DENG Fei, WU Yousi, HU Yulei, et al. Position and Pose Estimation of Spherical Panoramic Image with Improved EPnP Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 677–684. DOI:10.11947/j.AGCS.2016.20150411 |
| [25] | SZELISKI R. Computer Vision:Algorithms and Applications[M]. New York: Springer-Verlag, 2010. |
| [26] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |



