2. 西安测绘研究所, 陕西 西安 710054
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
随着我国北斗区域卫星导航系统的稳定运行并逐步向全球扩展,其对导航卫星精密定轨与轨道预报的精度需求进一步提升。而卫星轨道确定及预报精度在很大程度上取决于卫星动力学模型的精确程度。中高轨导航卫星的太阳光压摄动力是除地球引力、日月引力外最大的非保守摄动力[1]。由于光压摄动力与卫星姿态控制策略、星体表面材料属性等有关,受太阳活动、卫星姿态控制误差以及卫星表面材料老化等影响,使光压摄动力成为最难以精确建模的作用力。因此,在导航卫星精密轨道确定中,光压建模一直是动力学定轨中一个重要研究内容。
GPS经过多年的积累,已经建立了相对较为完善的光压模型,并不断精化[2-8]。但GPS全部采用MEO卫星,动态偏航姿态控制模式,而北斗卫星导航系统采用GEO、IGSO、MEO 3类卫星,并且与QZSS导航系统类似[9],采用了动态偏航与零偏航两种姿态控制模式。由此出现了北斗卫星在动/零偏切换期间及零偏弧段定轨精度下降的问题[10, 12, 21]。目前相关文献的处理策略是采用增加经验力参数,或在姿态控制模式切换点重新估计光压力[10-13]。两种方法均可提高卫星轨道精度,但仍然达不到动偏的水平,且不利于轨道的预报。鉴于经验型光压模型在应用上更具有通用性,本文以应用较为广泛的ECOM光压模型为基础,在两种姿控模式下,利用实测数据分析获得北斗卫星光压参数变化规律,对ECOM光压模型参数选择策略进行调整,为进一步提高两种姿控模式下的定轨及预报精度探索可能途径,对北斗卫星光压模型构建有重要参考价值。
1 ECOM光压模型参数BERNESE ECOM光压模型采用常数分量加周期分量的形式,在与卫星太阳帆板指向相关的3个相互正交方向上分别使用3组参数来吸收光压摄动力影响,使定轨精度达到厘米级[6]。其模型表达式如下
 (1)
(1)
式中,α0为先验光压摄动力,通常采用分析光压模型;eD为卫星-太阳方向的单位向量,正向指向太阳;eY为飞行器太阳能帆板轴方向的单位向量;eX由eX= eD× eY确定。u为卫星的升交角距。D(u)、Y(u)、X(u)分别为模型三分量系数,依照对导航卫星轨道运动特性分析,上述系数变化特性可用多项式结合周期函数模型描述
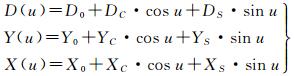 (2)
(2)
式中,D0、DC、DS、Y0、YC、YS、X0、XC和XS为ECOM的9个待估参数。在实际定轨解算中,由于参数间的相关性,并非需要解算全部9参数[3, 14],并且过度参数化,将影响轨道的预报精度。文献[7]中通过详细比对分析,指出解算ECOM模型中的D0、Y0、X0、XC和XS共5参数,可获得较高轨道精度。目前CODE等多个IGS分析中心均采用ECOM 5参数进行GPS卫星轨道确定[3]。在北斗卫星精密定轨中,ECOM模型也是应用较为广泛的光压模型。文献[15-17]采用ECOM 5参数模型,文献[18-19]采用ECOM 9参数。目前尚没有文献针对北斗3类卫星制定ECOM模型的参数选择策略。ECOM 5参数模型是针对GPS卫星分析获得的,其对北斗3类卫星的适用性需要进一步验证。因此如何合理选择模型参数是本文重点讨论的问题。由于北斗卫星目前没有可靠的分析型先验模型,因此,对北斗光压参数的分析采用无先验模型方式。根据文献[20]中的研究成果,在没有先验模型的前提下,采用ECOM模型可取得同等的轨道确定精度,同时还可避免先验光压对ECOM光压参数解算数值的影响,达到准确反映ECOM光压参数变化规律的作用。
2 北斗卫星ECOM参数选择策略分析本文以3天弧段的北斗卫星精密星历作为伪观测量,利用BERNESE ECOM模型进行动力学轨道拟合,分析北斗3类卫星在选用不同ECOM光压参数组合情况下的变化特征及对轨道拟合精度的影响,确定北斗3类卫星的ECOM参数选择策略。根据文献[3],采用精密星历作为伪观测量进行轨道拟合,是开展光压模型构建分析的通用做法。在采用L波段观测数据定轨时,受测量误差及其他模型化误差的影响需要同时解算大气、经验力等参数,可以采用适当增加解算参数个数的方式获得高精度的轨道。而进行光压模型分析时,以高精度事后轨道作为伪观测量,可将注意力主要集中在光压参数的主项上,尽量减少其他解算参数对光压模型参数自身的影响,通过轨道拟合分析光压摄动模型的特征,计算效率也更高。
文中采用的数据为通过IGS网站下载的MGEX工作组武汉大学分析中心计算的北斗卫星精密星历,采样间隔为15 min。时间跨度为2013-01-01-2016-03-12,共计3年3个月。根据各文献报道,武汉大学后处理精密星历采用3个步骤处理完成:①进行GPS/GLONASS联合定轨;②利用定轨结果进行GPS静态PPP解算;③进行北斗与伽利略卫星的联合定轨。定轨解算时将前一步PPP解算的测站坐标、钟差以及两小时一组的天顶对流层延迟作为已知量参与解算。光压模型采用CODE 5参数模型,同时解算延迹方向的常数经验加速度,并加入1.0×10-10 m/s2的先验约束[21]。轨道重叠段精度水平为:3类卫星法向精度优于15 cm,径向优于8 cm,IGSO、MEO卫星切向精度在10~15 cm之间,GEO卫星切向存在1~4 m量级的偏差[15-16, 18, 22]。GEO卫星激光检核视向误差为54.5 cm,IGSO、MEO为10 cm[22]。北斗卫星采用零偏航姿态控制模式期间的重叠轨道精度与采用动态偏航期间基本相当,但是切向和径向精度仍旧较动偏值稍大[10]。
在卫星轨道拟合中采用的动力学模型包括,JGM3地球引力场模型,考虑日月引力,日月位置采用DE405;考虑太阳光压力,相对论和固体潮、海潮引力位影响。地球自转参数采用IERS B公报值。轨道拟合解算参数包括每颗卫星6个轨道初始状态参数以及光压参数。
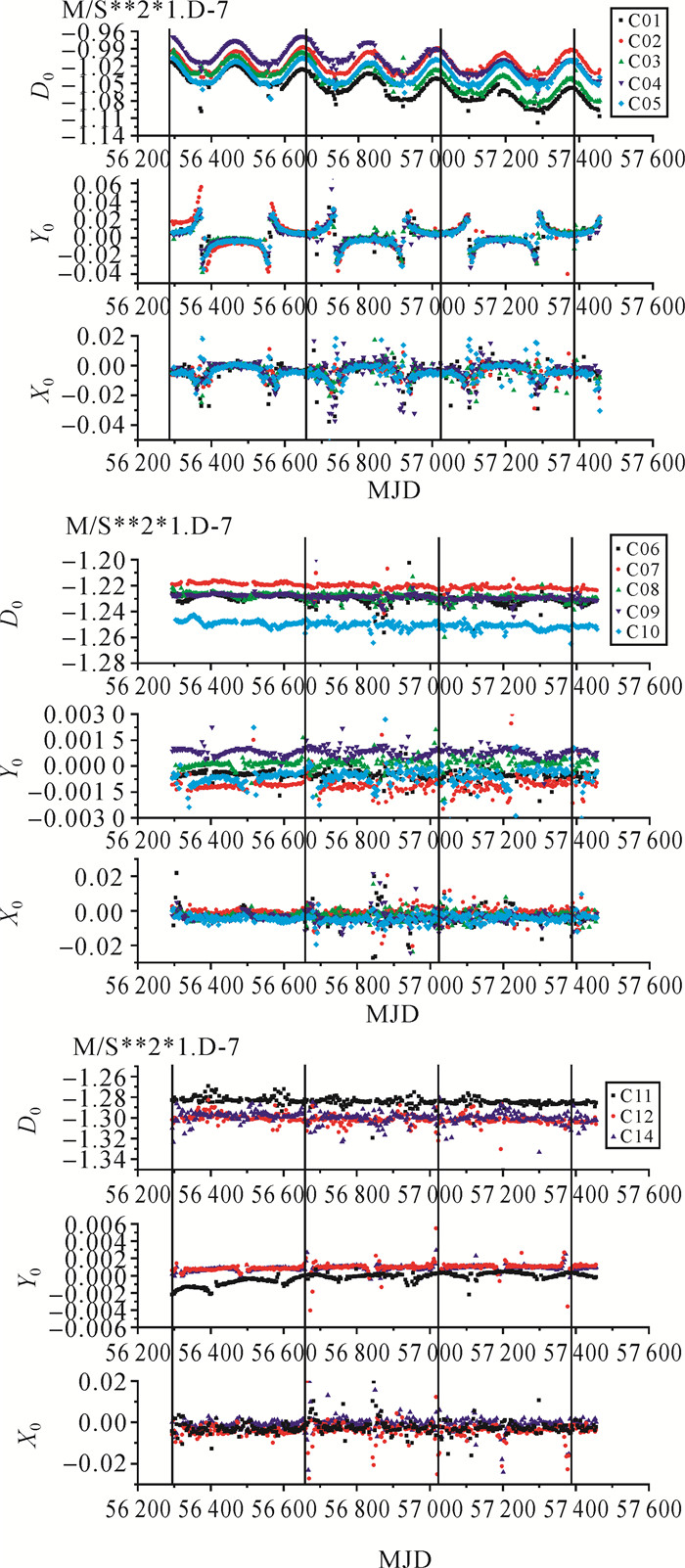
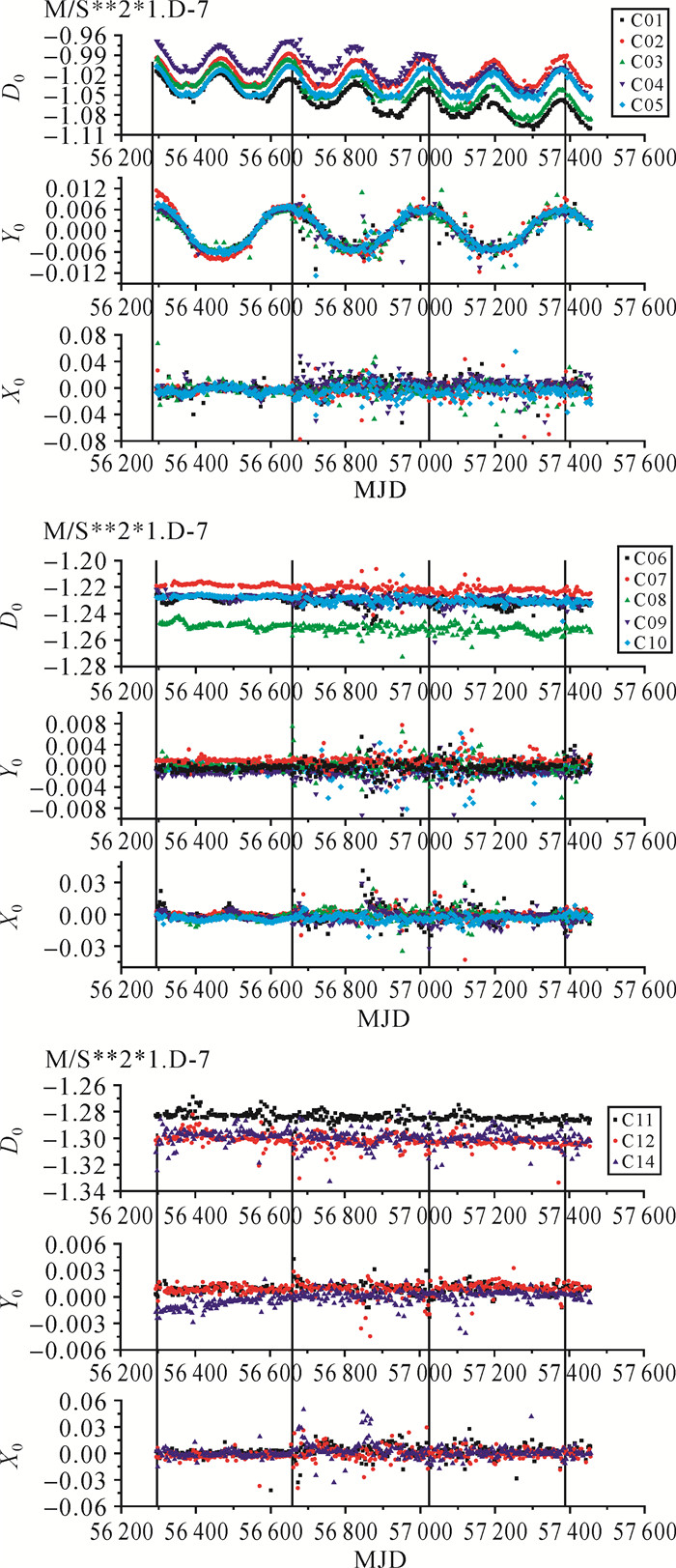
本文首先对比计算了选用ECOM 5参数(D0、Y0、X0、XC、XS)以及ECOM 9参数的计算结果,发现北斗3类卫星在选用ECOM 5参数时均存在以Y0参数为代表的每半年一次的光压参数变化异常,在时间上刚好与GEO卫星的地影周期以及IGSO、MEO卫星的零偏周期相同[10-13]。具体而言,对GEO卫星由于其特殊的轨道特性,各卫星的地影期十分接近(春分、秋分前后)[13],由此在图 1中,各GEO卫星的光压参数异常期也基本相同。对IGSO、MEO卫星,由于其轨位各不相同,各自的零偏时段也不一致,但均涵盖了各自的光压参数异常期。3类卫星光压参数的变化异常以GEO卫星表现最为明显。此现象也与参考文献中的报道的定轨精度下降情况相一致。文献[23]指出GEO卫星在春秋分前后,即GEO卫星的地影期,呈现出定轨精度下降的现象,UERE由正常段的1.5 m下降至7 m[23]。IGSO和MEO卫星在姿态转换期间和零偏期间轨道精度也大幅度降低[10, 12]。分析其产生原因,北斗IGSO、MEO卫星在太阳矢量与轨道面夹角(β角)小于一定的控制角度时,存在动态偏航与零偏航的姿态控制策略切换(与卫星地影期接近),而GEO卫星则全弧段采用零偏航控制模式[10]。零偏航姿态控制模式可以避免卫星正午及午夜机动,但不能确保太阳帆板对太阳的正照。因此这种定轨及轨道拟合精度下降应该与地影期零偏状态下,卫星受照情况变化所造成的光压摄动力变化相关。而采用ECOM 9参数则可有效改善这一现象。北斗卫星采用ECOM 5参数、9参数拟合结果的常数参数(D0、Y0、X0)时间序列如图 1和图 2所示。图中竖线表示划分年。由于IGSO、MEO卫星的零偏弧段与地影期十分接近,因此下文在对3类卫星综合描述时,通称为地影期,不再单独强调零偏。
|
| 图 1 北斗3类卫星ECOM 5参数常数项时间序列图 Fig. 1 Time sequence diagram of the constant items using the ECOM 5 parameters model for the three types of BeiDou satellites |
|
| 图 2 北斗3类卫星ECOM 9参数常数项时间序列图 Fig. 2 Time sequence diagram of the constant items using the ECOM 9 parameters model for the three types of BeiDou satellites |
图 3为采用ECOM 9参数进行轨道拟合获得的ECOM周期参数(XC、XS、DC、DS、YC、YS)时间序列图。由图中可得,ECOM 9参数模型拟合结果中,北斗3类卫星的YC、YS参数较为恒定,未出现周期性,且解算结果接近0,推断YC、YS参数对轨道拟合结果贡献不大。由此本文重点分析采用ECOM 7参数(D0、Y0、X0、XC、XS、DC、DS)的轨道拟合结果。由图 4中结果,ECOM 7参数仍然可以较好地解决ECOM 5参数中地影期轨道拟合异常的问题。

|
| 图 3 北斗卫星ECOM 9参数周期参数时间序列图 Fig. 3 Time sequence diagram of the period items using the ECOM 9 parameters model for the BeiDou satellite |

|
| 图 4 北斗卫星ECOM 7参数时间序列图 Fig. 4 Time sequence diagram of the ECOM 7 parameters for the BeiDou satellites |
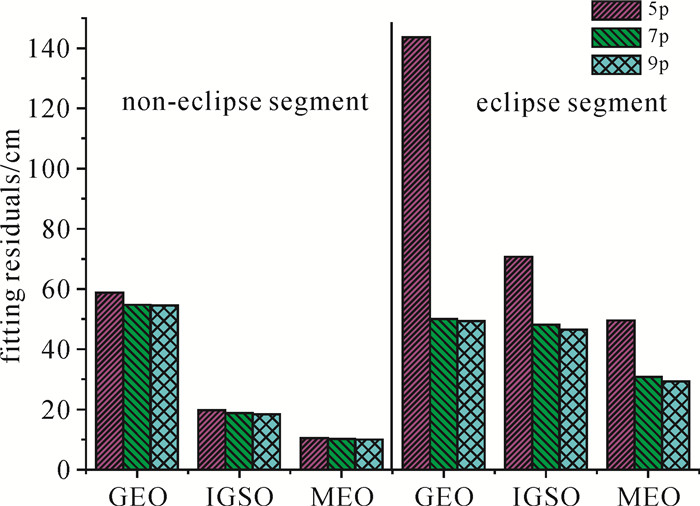
图 5为2013年至2016年所有非地影、地影期3天弧段轨道拟合数据点拟合残差的综合统计结果。图中“5p”“7p”“9p”分别表示ECOM 5参数、7参数、9参数(下文同)。
|
| 图 5 轨道三维位置拟合残差统计(RMS) Fig. 5 Fitting residual statistics of satellite position(RMS) |
在非地影弧段内GEO卫星的拟合残差明显高于IGSO、MEO,这是由于GEO卫星相对特殊的空间位置,导致地面站对GEO卫星的观测几何结构不佳造成的。GEO卫星采用ECOM 7参数的三维提升量最大,这与GEO全弧段采用零偏姿态有关,但其提升量也仅在厘米量级。IGSO、MEO的提升量均在毫米量级。建议采用ECOM 5参数模型。而地影段,与ECOM 5参数相比,3类卫星采用ECOM 7参数进行轨道拟合的残差提升量均可达到分米量级。ECOM 9参数拟合残差的提升量较ECOM 7参数已较小,在厘米量级,因此建议北斗3类卫星在地影期采用ECOM 7参数进行轨道确定。
为验证前文提出的北斗3类卫星ECOM光压参数选取策略的正确性,本文依据卫星在不同情况下的姿态控制策略,以卫星受照情况为研究对象,梳理光压参数选取策略的理论机制。
相对于卫星本体,太阳帆板的面积最大,反射系数最低。卫星姿态控制模式变化对太阳帆板受照的影响,是太阳光压摄动力变化的重要影响因素。在动偏期间,卫星通过太阳敏感器感知太阳位置,自动计算偏航角大小,使太阳帆板始终垂直于卫星-太阳(D)方向。而零偏期间,卫星不再跟踪太阳位置,始终控制偏航角为零。此时,如图 6所示,帆板法向与D方向夹角随时间变化。该入射角随太阳与轨道面夹角β变化而变化,并非严格的线性趋势,不同卫星入射角的变化速率不同,但总体趋势一致,对3类卫星也没有本质区别。

|
| 图 6 零偏帆板法向与D向夹角 Fig. 6 The angle between the D direction and the normal direction of the sailboard |
对卫星帆板而言,在动偏期间,卫星太阳帆板正照,大部分光线被太阳能板吸收转化为能量。其所产生的光压摄动力也完全在卫星-太阳连线方向,即ECOM模型的D方向,不存在与轨道周期相关的力。因此在动偏期间仅解算ECOM模型的5参数即可。在零偏期间,帆板太阳光线的入射角度随卫星位置而变化,对帆板照射所产生的光压力即存在了与轨道周期相关的周期分量。该周期变化同时体现在卫星-太阳连线方向(D方向)和太阳帆板方向(Y方向)。由于YC和XS,YS和XC存在强相关性,相关度达到0.995和0.951[24]。因此在零偏期间仅在ECOM 5参数的基础上,增加D向周期项即可。验证了建议北斗3类卫星在地影期采用ECOM 7参数进行轨道确定的正确性。
3 参数选择策略试验验证为进一步验证北斗卫星光压参数选择策略在轨道确定中的应用效果,本文采用了2016年MGEX网站上提供的全球61个北斗双频L波段地面监测站数据进行了单北斗系统的精密定轨试验。对北斗GEO卫星(C01-C05),采用了2006-03-01-2016-04-08共39天的春分前后地影段数据。此外还对2016-05-19-2016-06-29共42天的非地影段数据进行了对比计算分析。考虑到2016年6月9日至20日C11、C12(MEO)卫星处于零偏弧段,2016年6月19日至6月29日C08(IGSO)卫星处于零偏弧段,同样为了对比分析,本文将C11、C12、C08卫星的计算弧段统一扩大到2016-05-19-2016-06-29。
定轨解算时采用SPODS软件[25],利用3 d弧段5 min采样双频无电离层组合观测量。考虑卫星天线相位中心修正、卫星天线相位缠绕(Wind_up)、相对论效应等。对流层采用Saastamoinen天顶延迟改正及GMF映射函数。采用EGM2008 12阶地球引力场,IERS2003固体潮,三体引力考虑日、月及大行星,采用JPL DE405行星星历。光压模型对比采用无先验ECOM 5参数、7参数模型。解算参数包括6个卫星初始轨道信息,12/d对流层天顶延迟,1/d对流层水平梯度,以及5~7个光压模型参数,固定模糊度。
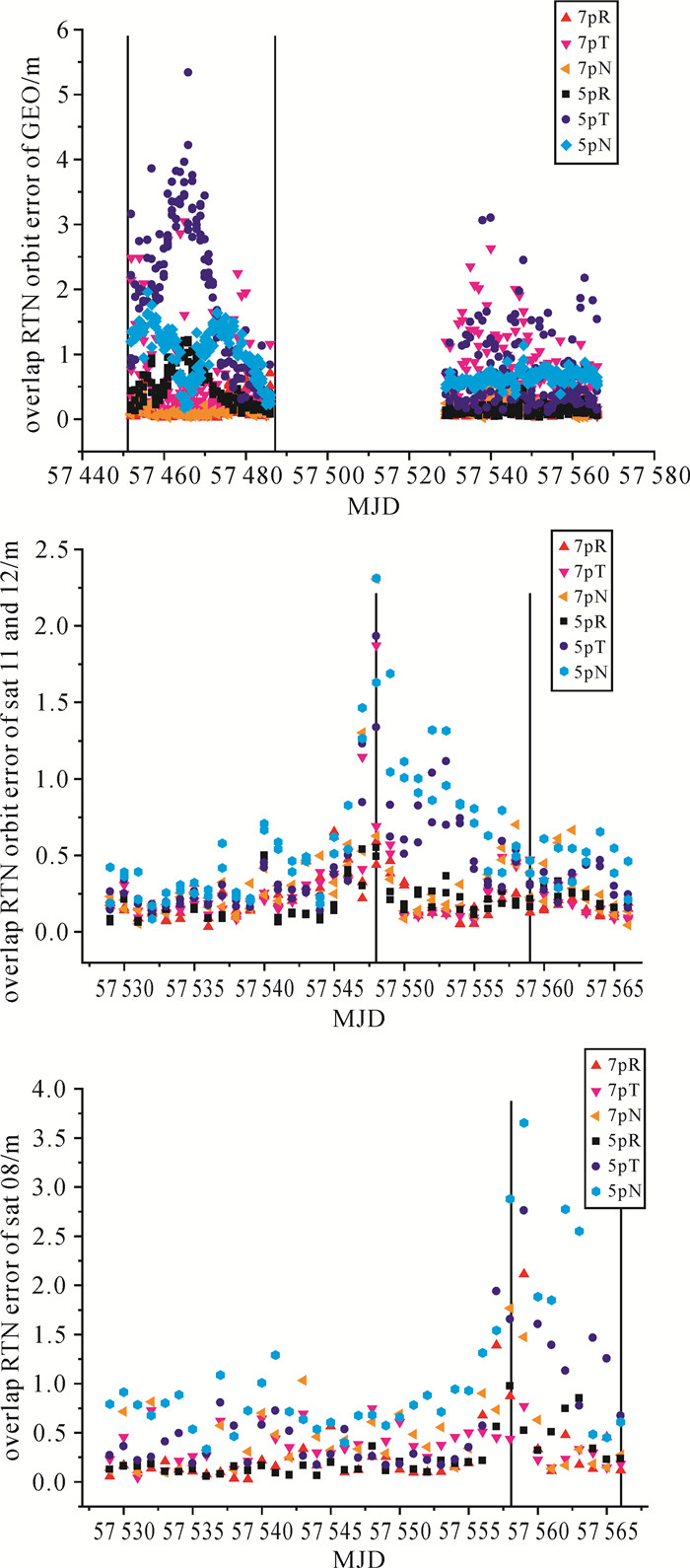
3类卫星3天重叠1天的定轨重叠段时间序列及ECOM 5参数、7参数对比统计结果如图 7、图 8所示。图中R、T、N分别代表径向、切向、法向3方向。两条竖线之间为卫星的地影(GEO)或零偏(IGSO、MEO)弧段。由图中结果可以明显看出在非地影段,ECOM 5参数、7参数定轨结果精度相当,但在地影或零偏弧段内,ECOM 7参数表现明显优于5参数。
|
| 图 7 北斗3类卫星实测定轨重叠段时间序列 Fig. 7 Time sequence diagram of the BeiDou overlap orbit precision calculated using observed data |

|
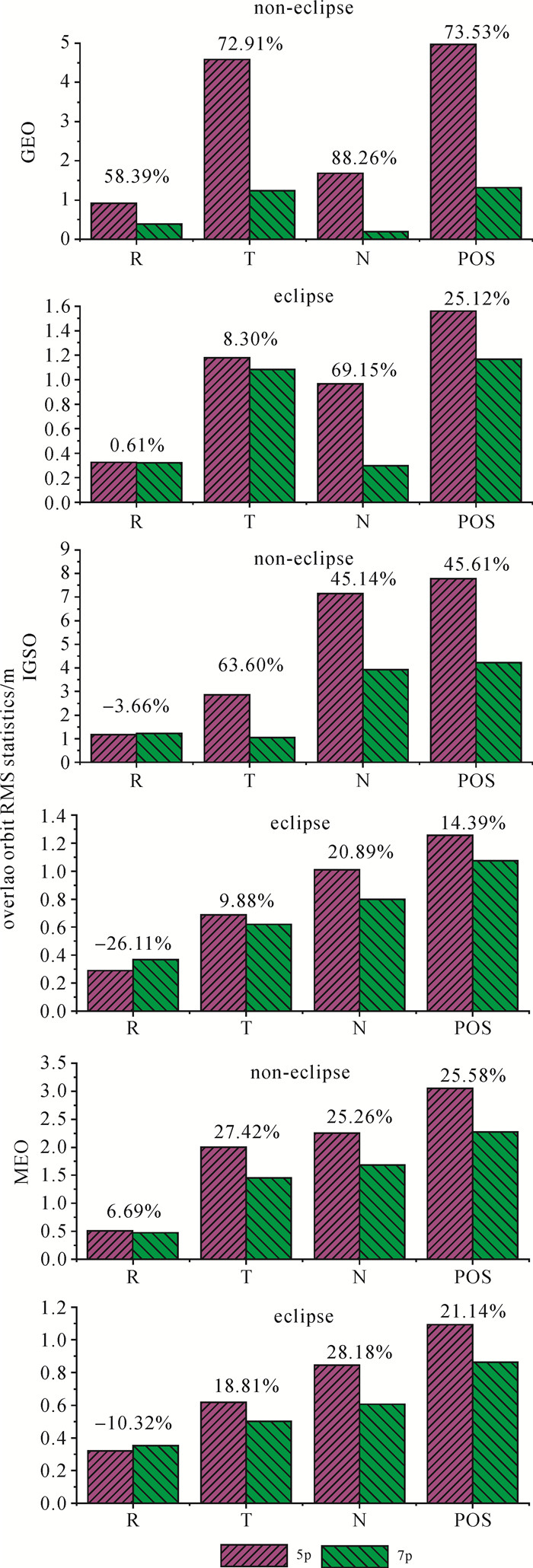
| 图 8 北斗卫星实测定轨重叠段RMS统计结果 Fig. 8 RMS of the BeiDou satellite overlap orbit precision calculated using observed data |
图 8中的百分比数字为相比ECOM 5参数,采用ECOM 7参数定轨重叠段精度的提升百分比。由图中结果统计可得:对地影或零偏弧段而言,采用ECOM 7参数可使定轨重叠段位置精度提高50%~80%,且重点表现在T、N方向,提升量最高可达86.9%。对于正常弧段,采用ECOM 7参数虽然可以实现位置精度的13%~23%的提升,但随之也造成了R方向38%~49%的精度下降,这应该与过度参数化有关。由此再次验证了地影段采用ECOM 7参数、正常段采用ECOM 5参数的结论。
定轨模型参数选择的优劣也同样表现在于预报精度上。本文中定轨结果预报1天与后处理精密轨道相比的误差时间序列及RMS统计结果见图 9和图 10。由图中结果,可以得出与定轨段相同的结论。

|
| 图 9 北斗3类卫星预报1天轨道误差时间序列 Fig. 9 Time sequence of the predicted orbit precision |
|
| 图 10 北斗卫星实测定轨预报段RMS统计结果 Fig. 10 RMS of the predicted orbit precision for BeiDou satellites |
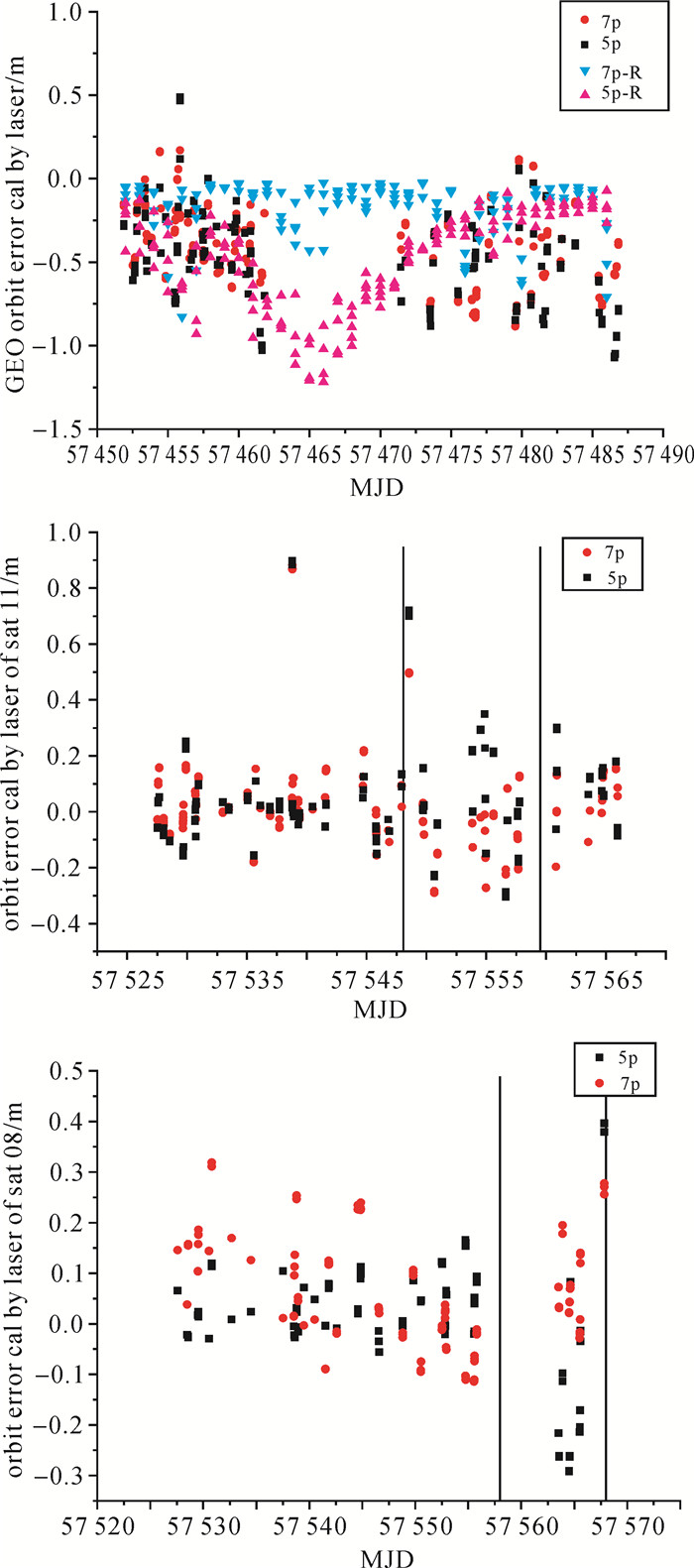
前文采用了重叠弧段的方式来评价定轨精度的优劣,为了更加全面准确的评价定轨结果,本文采用了同期的激光数据,对C01、C11、C08卫星进行精度评估。评估结果时间序列及统计信息见图 11、表 1。对C01卫星,由于激光数据的缺失,未能完成对比最明显的地影中心弧段的精度评估,由此本文将ECOM 5参、7参激光检核结果(5p、7p)与同期ECOM 5参、7参定轨R方向重叠段结果(5p-R、7p-R)绘制在一张图上,以显示激光数据的对应时段。由于在有激光数据的弧段内5参、7参定轨差异还不显著,因此表 1中C01卫星统计结果差异也不十分显著,但也可达到7 cm。对C11、C08卫星均可表现出零偏弧段ECOM 7参数激光检核精度的提升,最大差异为10 cm。但对于C08卫星的正常段,ECOM 7参数的评估结果精度是下降的,这与前文重叠弧段分析结果一致。
|
| 图 11 北斗3类卫星定轨激光检核结果时间序列 Fig. 11 SLR residuals for three types of BeiDou satellites |
| m | |||||
| C01 | C11正常 | C11零偏 | C08正常 | C08零偏 | |
| 5参 | 0.57 | 0.16 | 0.23 | 0.06 | 0.22 |
| 7参 | 0.49 | 0.15 | 0.18 | 0.12 | 0.12 |
另外本文的激光检核结果也与前文献[22]中武大精密星历检核结果精度一致。进一步说明采用ECOM 7参数进行地影零偏弧段的定轨可以达到与武汉大学综合定轨精度相近的水平,避免了ECOM 5参数精度下降的情况。另外本文的验证分析均是基于全球网数据进行计算的。考虑到区域网监测站对北斗卫星的监测弧段短、观测几何相对不足,进而定轨精度较低,这将会淹没光压参数对定轨精度的影响,不利于验证分析。但其在理论上具有一致性,因此本文不再单独针对区域网进行验证分析。
4 结论本文以分析BERNESE ECOM经验型光压模型对北斗卫星的适用性为目标,通过以精密星历为基础的轨道拟合,开展了北斗3类卫星光压参数变化特性分析,制定了北斗卫星光压参数选择策略;进行了北斗卫星动偏、零偏姿态下卫星星体受照情况分析,给出了光压参数选取策略的理论依据。利用北斗MGEX全球网数据进行了定轨试验,验证了该策略的正确性。主要结论如下:
(1) 北斗GEO卫星地影期,IGSO/MEO卫星零偏弧段建议采用ECOM 7参数进行定轨解算。其他弧段建议采用ECOM 5参数。
(2) 本文提出的光压参数选择策略的产生机制为,在地影期零偏姿态下,太阳对卫星帆板不完全正照,存在与卫星轨道相关的周期项,且主要反映在D、Y方向上。考虑参数间的相关性,应当在5参数基础上引入D向周期参数进行吸收。
(3) 通过长达81 d的定轨试验得出:在地影期零偏姿态下,与ECOM 5参数相比,采用ECOM 7参数可有效提高定轨位置精度,提升量达到50%~80%,且重点表现在T、N方向。验证了ECOM光压参数选择策略的有效性。
| [1] | KAPLAN E D, HEGARTY C J. Understanding GPS:Principles and Applications[M]. 2nd ed. Norwood, MA: Artech House Inc, 2005. |
| [2] | FLIGEEL H F, GALLINI T E, SWIFT E R. Global Positioning System Radiation Force Model for Geodetic Applications[J]. Journal of Geophysical Research, 1992, 97(B1): 559–568. DOI:10.1029/91JB02564 |
| [3] | SPRINGER T A. Modeling and Validating Orbits and Clocks Using the Global Positioning System[D]. Berne, Switzerland:Astronomical Institute, University of Berne, 1999. |
| [4] | COLOMBO O L. The Dynamics of Global Positioning System Orbits and the Determination of Precise Ephemerides[J]. Journal of Geophysical Research, 1989, 94(B7): 9167–9182. DOI:10.1029/JB094iB07p09167 |
| [5] | BAR-SEVER Y E. New and Improved Solar Radiation Models for GPS Satellites Based on Flight Data[R]. Pasadena, CA:Jet Propulsion Laboratory, California Institute of Technology, 1997. |
| [6] | BEUTLER G, BROCKMANN E, GURTNER W, et al. Extended Orbit Modeling Techniques at the CODE Processing Center of the International GPS Service for Geodynamics (IGS):Theory and Initial Results[J]. Manuscripta Geodaetica, 1994, 19(6): 367–386. |
| [7] | SPRINGER T A, BEUTLER G, ROTHACHER M. Improving the Orbit Estimates of GPS Satellites[J]. Journal of Geodesy, 1999, 73(3): 147–157. DOI:10.1007/s001900050230 |
| [8] | RODRIGUEZ-SOLANO C J, HUGENTOBLER U, STEIGENBERGER P. Adjustable Box-wing Model for Solar Radiation Pressure Impacting GPS Satellites[J]. Advances in Space Research, 2012, 49(7): 1113–1128. DOI:10.1016/j.asr.2012.01.016 |
| [9] |
周佩元, 杜兰, 方善传, 等.
姿态模式切换期间QZSS卫星轨道及其钟差产品特性分析[J]. 测绘学报, 2016, 45(3): 274–281.
ZHOU Peiyuan, DU Lan, FANG Shanchuan, et al. Analysis of Characteristics of QZSS Satellite Orbit and Clock Products during Yaw Attitude Model Switching[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 274–281. DOI:10.11947/j.AGCS.2016.20150386 |
| [10] |
郭靖. 姿态、光压和函数模型对导航卫星精密定轨影响的研究[D]. 武汉: 武汉大学, 2014. GUO Jing. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites[D]. Wuhan:Wuhan University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10486-1015528772.htm |
| [11] |
毛悦, 宋小勇, 王维, 等.
北斗IGSO/MEO卫星姿态控制及光压差异分析[J]. 测绘科学, 2015, 40(8): 129–134.
MAO Yue, SONG Xiaoyong, WANG Wei, et al. BeiDou IGSO and MEO Navigation Satellites' Yaw-Steering and Orbit-normal Attitude Control Modes and Solar Radiation Pressure Difference Analysis[J]. Science of Surveying and Mapping, 2015, 40(8): 129–134. |
| [12] |
毛悦, 宋小勇, 王维, 等.
IGSO姿态控制模式切换期间定轨策略研究[J]. 武汉大学学报(信息科学版), 2014, 39(11): 1352–1356.
MAO Yue, SONG Xiaoyong, WANG Wei, et al. IGSO Satellite Orbit Determining Strategy Analysis with the Yaw-Steering and Orbit-normal Attitude Control Mode Switching[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11): 1352–1356. |
| [13] |
毛悦, 宋小勇, 贾小林, 等.
北斗导航卫星地影状态分析[J]. 测绘学报, 2014, 43(4): 353–359.
MAO Yue, SONG Xiaoyong, JIA Xiaolin. Earth Eclipse Status Analysis of BeiDou Navigation Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 353–359. DOI:10.13485/j.cnki.11-2089.2014.0053 |
| [14] |
宋小勇, 毛悦, 贾小林.
BERNESE光压模型参数的统计分析[J]. 测绘科学, 2009, 34(3): 25–27.
SONG Xiaoyong, MAO Yue, JIA Xiaolin. Analysis of the Parameter of BERNESE Radiation Force Model by Statistic Method[J]. Science of Surveying and Mapping, 2009, 34(3): 25–27. |
| [15] |
李敏. 多模GNSS融合精密定轨理论及其应用研究[D]. 武汉: 武汉大学, 2011. LI Min. Research on Multi-GNSS Precise Orbit Determination Theory and Application[D]. Wuhan:Wuhan University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10486-1011404080.htm |
| [16] | ZHAO Qile, GUO Jing, LI Min, et al. Initial Results of Precise Orbit and Clock Determination for COMPASS Navigation Satellite System[J]. Journal of Geodesy, 2013, 87(5): 475–586. DOI:10.1007/s00190-013-0622-7 |
| [17] |
刘伟平, 郝金明, 李建文, 等.
多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1132–1138.
LIU Weiping, HAO Jinming, LI Jianwen, et al. Multi-GNSS Joint Precise Orbit Determination of BeiDou Navigation Satellites System[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1132–1138. DOI:10.13485/j.cnki.11-2089.2014.0186 |
| [18] | GE Maorong, ZHANG Hongping, JIA Xiaolin, et al. What is Achievable with Current COMPASS Constellation[DB/OL].[2012-11-01]. http://www.gpsworld.com/what-is.-achievable-with-the-current-compass-constellation. |
| [19] |
刘伟平, 郝金明, 魏伟, 等.
两种北斗卫星精密定轨方法的对比[J]. 大地测量与地球动力学, 2016, 36(3): 211–215.
LIU Weiping, HAO Jinming, WEI Wei, et al. Comparison of Two Methods of Precise Orbit Determination of BeiDou Satellites[J]. Journal of Geodesy and Geodynamics, 2016, 36(3): 211–215. |
| [20] | MONTENBRUCK O, STEIGENBERGER P, HUGEN TOBLER U. Enhanced Solar Radiation Pressure Modeling for Galileo Satellites[J]. Journal of Geodesy, 2015, 89(2): 283–297. |
| [21] | GUO Jing, XU Xiaolong, ZHAO Qile, et al. Precise Orbit Determination for Quad-constellation Satellites at Wuhan University:Strategy, Result Validation, and Comparison[J]. Journal of Geodesy, 2016, 90(2): 143–159. DOI:10.1007/s00190-015-0862-9 |
| [22] |
耿涛, 苏醒, 许小龙, 等.
北斗卫星导航系统精密定轨和广播星历轨道精度分析[J]. 中国科技论文, 2015, 10(9): 1023–1026, 1032.
GENG Tao, SU Xing, XU Xiaolong, et al. Research on Precise and Broadcast Ephemeris Orbit of BeiDou Navigation Satellite System[J]. China Science Paper, 2015, 10(9): 1023–1026, 1032. |
| [23] | LI X J, ZHOU J H, HU X G, et al. Orbit Determination and Prediction for BeiDou GEO Satellites at the Time of the Spring/Autumn Equinox[J]. Science China Physics, Mechanics & Astronomy, 2015, 58(8): 089501. DOI:10.1007/s11433-015-5675-6 |
| [24] |
刘永, 张传定, 李珊珊, 等.
基于IGS精密星历的BERNESE光压模型参数分析[J]. 测绘工程, 2016, 25(1): 29–33, 38.
LIU Yong, ZHANG Chuanding, LI Shanshan, et al. Analysis of BERN SRP Parameters Based on IGS Ephemeris[J]. Engineering of Surveying and Mapping, 2016, 25(1): 29–33, 38. |
| [25] |
魏子卿, 阮仁桂, 贾小林, 等.
卫星定位定轨系统SPODS:理论与测试[J]. 测绘学报, 2014, 43(1): 1–4.
WEI Ziqing, RUAN Rengui, JIA Xiaolin, et al. Satellite Positioning and Orbit Determination System SPODS:Theory and Test[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 1–4. DOI:10.13485/j.cnki.11-2089.2014.0001 |


