随着CHAMP、GRACE和GOCE等3颗重力卫星的发射升空,利用卫星重力观测值恢复地球重力场的研究,已经成为当前地球物理学研究的热点问题之一。文献[1-2]的研究表明,重力梯度张量反映了重力位水准面的曲率和力线弯曲,对重力场中的短波信号变化敏感,所以重力梯度张量更能够反映重力场的精细结构,包含有大量的局部重力场的有效信息。
国内外众多学者就利用卫星重力观测值恢复地球重力场的方法做了大量的研究工作。文献[3]提出了广义轮胎调和分析方法,利用卫星重力梯度张量分量组合以较高的精度还原地球重力场。文献[4]提出了使用最小二乘法恢复地球重力场的方法,通过数值模拟,证明重力异常的梯度对轨道高度的变化不敏感。在文献[5]中研究了全张量重力梯度数据的全局和局部分量的广义球谐谱表示和轨道根数表示,给出了广义球谐函数与球谐函数之间的关系,从理论上得到了全张量重力梯度数据的描述方法和由全张量重力梯度网格数据恢复全球重力位谱系数的基本公式。然而这些研究工作在理论方面都是利用传统的球谐分析法。在表达全球重力场时,球谐分析法有明显的优势,但是对于局部区域重力场的精细结构和重力场高频信息的表述上,球谐分析法存在着不足和缺陷。例如球谐函数不能满足局部重力场的边界条件,在表述高分辨率重力场时,需要求解巨量的球谐系数等[6]。因此需要针对卫星重力梯度恢复局部重力场的理论方法进行系统的研究。
文献[7]在前人的研究基础上总结提出了球冠谐分析理论,对地球北极区域的磁异常做了数值分析。文献[8]利用航磁异常观测值,解算了中国大陆航磁异常的不同阶次球冠谐模型,结合大地构造理论对相关图件进行了分析解释。文献[9]研究了球冠谐函数在重力场中的表达式,并利用球冠谐理论建立了我国的局部重力场模型。文献[10]提出了一种基于点质量模型的多层球冠谐系数迭代构造算法,并对求解矩阵A的病态性和球冠半角与点质量埋藏深度和密度进行了详细的分析研究,通过数值模拟表明当迭代算法收敛时,球冠谐模型能够以高精度拟合重力观测值。文献[11]提出了使用球冠谐模型的重力异常径向导数和曲面导数建立曲面位场的方法。这些研究工作都取得了令人满意的结果。然而利用扰动重力梯度恢复局部球冠谐重力场的研究,到目前为止还不多见。由此,本文从球冠谐理论出发,推导了无δ奇异性球冠谐梯度计算公式,使用GOCE卫星数据产品中地球固定参考框架(terrestrial reference frame,TRF)下的重力梯度数据恢复了4个球冠谐重力场模型,最后在计算点上,与文献[12]中使用GOCE卫星梯度数据建立的GO_CONS_GCF_2_DIR_R5地球重力场模型的扰动重力数值进行了比对分析,检验该方法的正确性。
1 球冠谐和分析扰动位重力梯度模型球冠谐和分析是一种在球冠坐标下的满足位理论边值条件的谱函数法,最早由加拿大人Haines在研究与地壳相关的局部区域磁异常时提出。通过利用非整阶勒让德函数代替整阶勒让德函数,余纬θ的定义域由[0, π]变换到[0,α](α是球冠半角),同时将地球Z轴由北极点沿子午线旋转到球冠中心,以保证球冠上点的经度依然满足周期性的边界条件。采用分离变量法可以得到重力场扰动位在球冠坐标下的解[13]
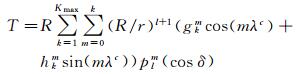 (1)
(1)
式中,R是地球平均半径;r是计算点的地心半径;δ与λc是球冠坐标系下的余纬和经度;l和m是非整阶勒让德函数的非整数阶数和整数级数;k是阶数的序号;Kmax是最大截断阶数序号;gkm与hkm为高斯系数;plm(cos δ)是非整阶勒让德函数[14],简写为plm。引入规格化因子,将其规格化为
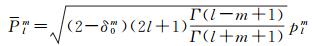 (2)
(2)
式中,δ0m是狄拉克函数。根据非整阶勒让德函数Plm计算公式[14-15],将其代入式(2)整理可得
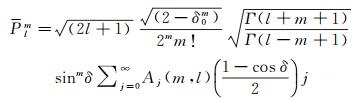 (3)
(3)
系数Aj(m, l)的递推关系如下
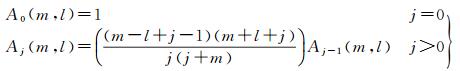 (4)
(4)
定义
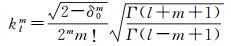 (5)
(5)
则由文献[7]推导的近似式可得
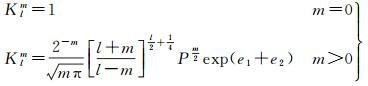 (6)
(6)
式中,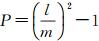
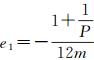
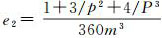
由上述推导过程可知
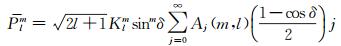 (7)
(7)
如果令

为球冠谐系数,则式(1)可以改写为
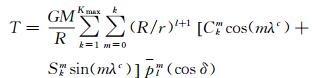 (8)
(8)
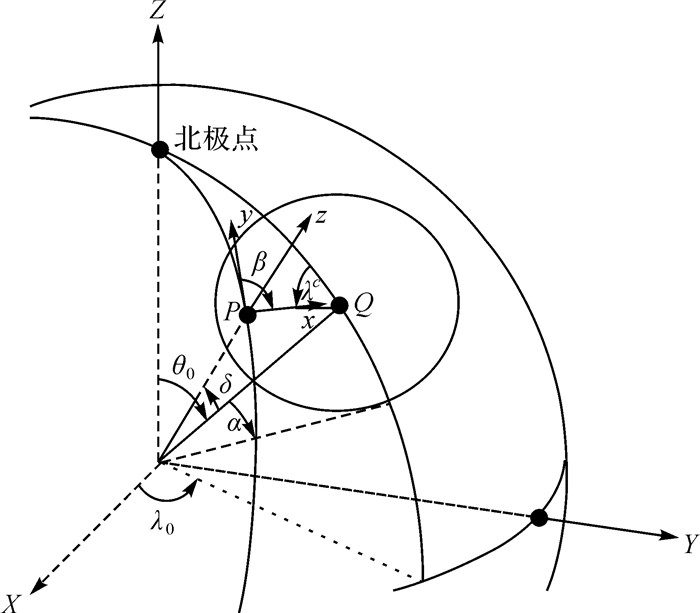
式中,G是万有引力常数;M是地球质量。因为δ与λc是球冠坐标下的余纬和经度(参见图 2),所以将球冠中心Q看作是新的北极点,定义球冠坐标系下的球冠局部指北坐标系(spherical cap local north-oriented reference frame,SCLNOF)的x轴指向球冠极点,z轴平行地心向径,方向向外,y轴与x和z轴构成右手坐标系,则与球谐函数的局部指北坐标系(local north-oriented reference frame,LNOF)下重力梯度张量计算一样,将式(8)代入局部指北坐标系梯度计算公式[16],可以得到球冠局部指北坐标下的扰动重力和扰动重力梯度张量模型公式
|
| 图 2 球冠坐标系 Fig. 2 Spherical cap coordinate system |
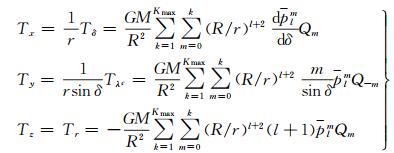 (9)
(9)
 (10)
(10)
式中
 (11)
(11)
从式(9)、(10)中可以看出,在球冠极点附近,当sin δ趋于零时,存在δ奇异性,因此根据非整阶勒让德函数的计算公式,本文推导了如下的去δ奇异性球冠谐重力梯度张量计算公式。记
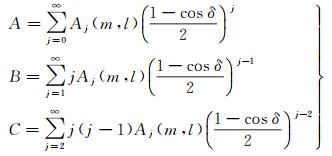 (12)
(12)
对式(7)求一阶和二阶导数,将其代入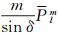
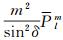
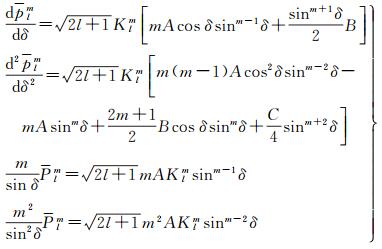 (13)
(13)
从式(13)中看到当m=0时,上述公式中有sinm-1δ和sinm-2δ项的部分都有m,这部分项计算结果为零,所以不存在δ奇异性。当m=1时,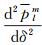
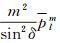

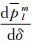
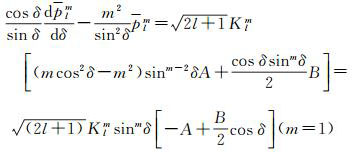 (14)
(14)
从式(14)中可以看到包含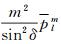
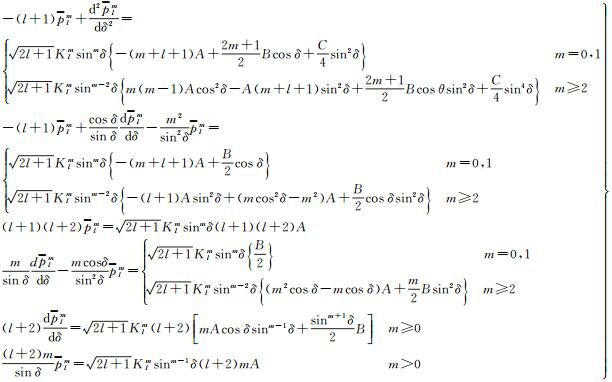 (15)
(15)
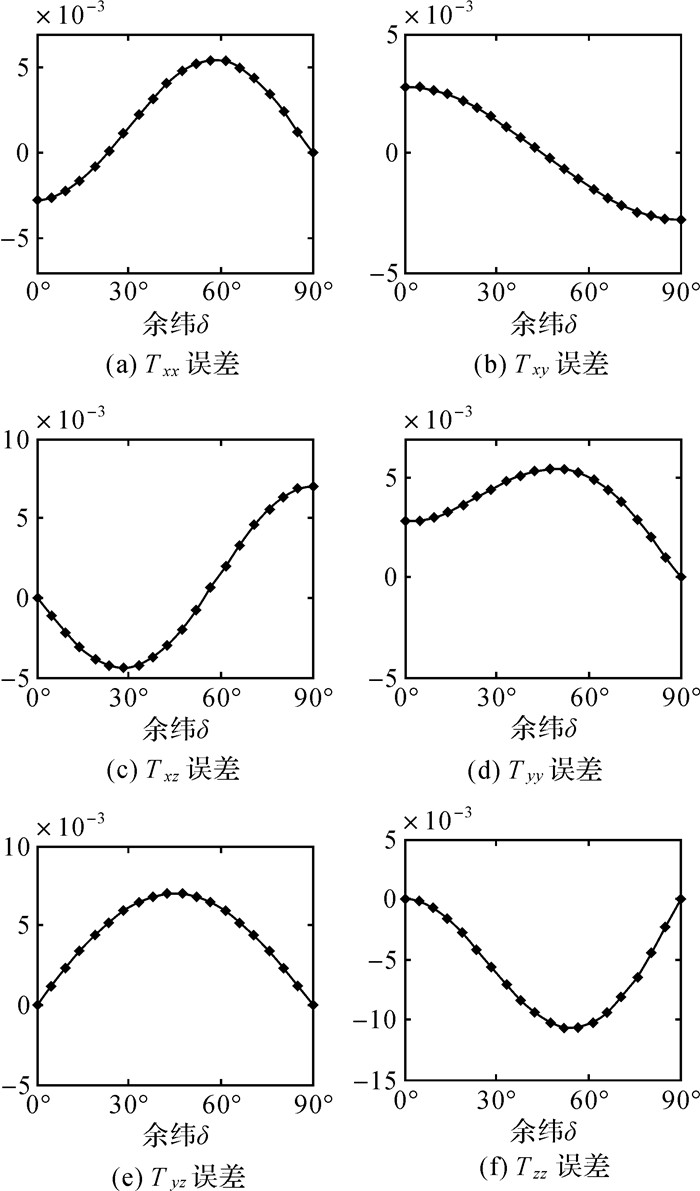
将式(15)代入式(10),就可以得到非奇异的球冠局部指北坐标下扰动重力梯度张量的计算公式。根据球冠谐分析理论,整阶勒让德函数是非整阶勒让德函数的特例[17-18],因此当球冠半角α=π/2时,式(15)中扰动位梯度张量的各个阶数l为整数,这时非整阶勒让德函数的计算结果与整阶勒让德函数的计算结果应当一致。下面取α=π/2,δ∈[0, π/2],通过式(15)计算各个梯度中l=2, 3, m=0, 1, 2, 3对应的非整阶勒让德函数项,并与文献[19]中的扰动重力梯度张量公式中n=2, 3, m=0, 1, 2, 3整阶勒让德函数项计算结果进行比较,统计结果如表 1所示,二者差值的均方根小于10-3数量级。从表 1可见,当m≠0且m≠n时,二者误差较大,这是由于非整阶勒让德函数值使用近似式(6)计算,而当m=0或m=n时,式(6)不可用,必须用式(5)计算,因此误差范围不一致。图 1是l=n=3, m=2时非整阶勒让德函数和整阶勒让德函数扰动重力梯度张量误差。
| n=2、m=0 | n=2、m=1 | n=2、m=2 | n=3、m=0 | n=3、m=1 | n=3、m=2 | n=3、m=3 | |
| Txx | 3.4×10-15 | 0.7×10-3 | 7.2×10-15 | 8.3×10-15 | 9.6×10-3 | 3.4×10-3 | 1.3×10-15 |
| Tyy | 3.2×10-15 | 0.5×10-3 | 5.2×10-15 | 6.8×10-15 | 5.6×10-3 | 4.1×10-3 | 3.1×10-15 |
| Tzz | 6.5×10-15 | 1.2×10-3 | 1.2×10-15 | 1.8×10-15 | 1.5×10-3 | 0.7×10-3 | 3.5×10-15 |
| Txy | 0 | 2.1×10-3 | 2.1×10-15 | 0 | 2.9×10-3 | 0.2×10-3 | 0.6×10-15 |
| Txz | 1.8×10-15 | 8.3×10-3 | 5.4×10-15 | 6.6×10-15 | 1.1×10-3 | 3.9×10-3 | 1.6×10-15 |
| Tyz | 0 | 8.3×10-3 | 2.8×10-15 | 0 | 9.7×10-3 | 4.9×10-3 | 2.3×10-15 |
|
| 图 1 扰动重力梯度误差(l=n=3、m=2) Fig. 1 Error of disturbing gravity gradients(l=n=3、m=2) |
2 不同坐标系下重力梯度张量之间的转换
如图 2所示,GOCE卫星任务Level 2产品的EGG_TRF_2中重力梯度数据的轨道位置使用地心地固坐标系(θ, λ, r)表示,其中θ表示地心余纬,λ表示地心经度,r是卫星轨道距地心距离;重力梯度张量使用的是局部指北坐标系(LNOF),因此使用GOCE卫星重力梯度恢复球冠谐重力场模型时,需要进行坐标变换。首先是将轨道位置坐标(θ, λ)转换到球冠坐标系[20]。定义计算点P在球坐标下的位置用(θ, λ)表示,球冠坐标系下的余纬和经度用δ和λc表示,设球冠中心点Q在球坐标系中为(θ0, λ0),则根据球面三角公式可知,计算点P在球冠坐标系中的余纬δ和λc经度计算公式为
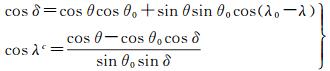 (16)
(16)
然后将重力梯度张量从局部指北坐标系(LNOF)转换到球冠指北坐标系(SCLNOF)中。定义LNOF坐标系到SCLNOF坐标系的转换矩阵。设β为球冠上点P到球冠中心点Q的方位角, 如图 2。显然SCLNOF坐标系就是将点P处的LNOF坐标系绕Z轴旋转一个β角度得到,所以LNOF坐标系到SCLNOF坐标系的梯度张量转换矩阵为
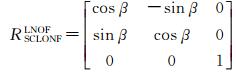 (17)
(17)
式中,方位角β的cos β与sin β的计算公式为
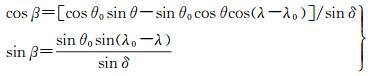 (18)
(18)
式中,δ为点P在球冠坐标下的余纬。
3 球冠谐梯度公式恢复局部重力场的数值模拟计算和分析联合卫星重力梯度张量的不同分量,利用球冠谐模型恢复地球局部重力场的问题,本质上是一个超定边值问题,可以利用超定边值问题的准解理论进行求解[21]。由于球冠区上的非整阶勒让德函数包含dplm(cos δ)/dδ|α=0和plm(cos δ)|α= 0两组基函数,这两组基函数在组内正交,而组间是不正交的[11, 13]。如果只使用其中一组基表示重力场,虽然可以使用直接积分法求解球冠谐系数,但是由于基函数是非完备的,不能同时满足局部区域边界上重力梯度数值的要求。从式(10)中能够知道,如只使用第1组基函数,则要求在球冠边界α处重力梯度Txz为零,而只使用第2组基函数则要求在边界α处重力梯度Tyz和Tzz分量为零,这显然是不成立的。由此使用重力梯度观测值恢复局部球冠谐重力场模型必须同时使用两组基函数,而这时由于组间基函数的非正交性,只能使用最小二乘法(LS)计算模型的系数。使用LS估计球冠谐系数时,由于求解系数矩阵包含大量的复共线性关系,所以LS估计中的法方程矩阵一般是病态的,使得LS估计的均方误差很大,将会导致参数估计的准确性和稳定性下降[22]。本文采用Tikhonov正则化方法解决LS估计中的法方程病态问题,根据Gauss-Markov线性模型,Tikhonov正则化解为[6, 23]
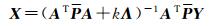 (19)
(19)
式中,k是正则化岭参数;P是等价权矩阵;Λ是正则化矩阵;Y是扰动重力梯度张量中的单个分量或联合分量;X是球冠谐系数的估计值;A是式(10)中的系数求解矩阵。其中等价权矩阵P和正则化矩阵Λ都使用单位阵。最优正则化岭参数k的确定方法有很多,常用的有岭迹法、L曲线法、GCV法和GM估计法等[6]。其中L曲线法是一种较成熟的方法,以对数u(k)=log ||AX-Y||为横坐标,对数v(k)=log||X||为纵坐标,绘制成二维曲线图,得到类似于“L”形状的拟合曲线图形,其中u(k)和v(k)都是以正则化参数为参变量的函数。直观上,曲线上曲率最大点处对应的k值是最优的,该点处满足拟合误差最小情况下,模型的范数最小。L曲线上曲率最大点对应的参数k是L曲线法最优值。以下直接给出最优正则化参数的计算公式,推导计算过程请参考文献[24]
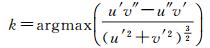 (20)
(20)
式中,u′、v′和u″、v″分别表示u、v的一阶和二阶导数。球冠中心点一般设置在网格中心,但是当δ=0时,经度λc不定,sin λc与cos λc不能计算,所以球冠中心点位置最好避开网格计算点。根据式(16)计算可知将球冠半角α设置为6.7°就可以覆盖10°×10°区域。根据球冠非整阶数l与球冠半角α和截断阶数Kmax之间的关系式[9-10],当球冠函数的截断阶数Kmax=22时,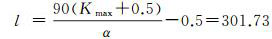
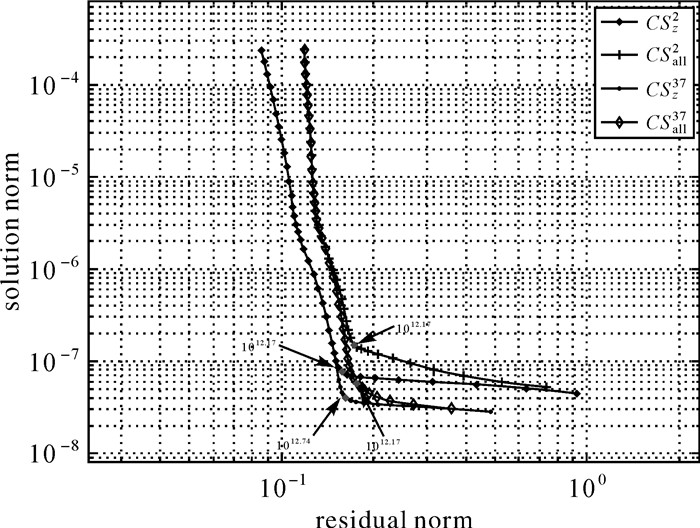
在具体数值试验中,设置观测区域大小为10°×10°,首先从GOCE卫星任务产品EGG_TRF_2一个月的数据文件中截取北纬30°到40°,东经115°到125°位置的沿卫星轨道LNOF坐标系下重力梯度观测值,其次利用EGM2008模型生成GOCE卫星轨道上0~36阶重力梯度模拟值[19]。从GOCE卫星重力梯度观测值中扣除0~36阶重力梯度模拟值得到GOCE卫星扰动重力梯度观测值,然后使用Taylor级数法将GOCE卫星扰动重力梯度观测值延拓到250 km平均轨道高度处,最后使用Shepard插值法归算为12′×12′格网点值[16],作为第1类数据。再次利用EGM2008模型生成平均轨道高度处的网格点上的2~36阶扰动重力梯度,将其加到第1类数据上形成第2类数据。最后将两类LNOF坐标系下扰动重力梯度数据转换到球冠SCLNOF坐标系下,作为数值计算中的扰动重力梯度观测值。其中第1类是不包含2~36阶重力场信息的扰动重力梯度,记为Txx37、Tyy37、Tzz37和Txz37,第2类包含2~36阶重力场信息的扰动重力梯度,记为Txx2、Tyy2、Tzz2和Txz2。在试验计算中,使用扰动重力梯度观测值恢复了4个球冠谐重力场模型,其中式(19)中的Y采用单个径向梯度分量Tzz37和Tzz2,分别计算得到的球冠谐模型记为CSzz37和CSzz2,式(19)中的Y使用扰动重力梯度张量的对角线三分量(Txx37, Tyy37, Tzz37)和(Txx2, Tyy2, Tzz2)分别组成解算方程组的形式,计算得到的球冠谐模型记为CSall37和CSall2。扰动重力梯度观测值中的Txz2和Txz37用于球冠谐模型的拟合精度的检验,拟合精度使用模型与观测值的误差均方根衡量。最后利用GO_CONS_GCF_2_DIR_R5(最高300阶)地球重力场模型在计算点处生成两类扰动重力径向分量Tz2和Tz37,用于球冠谐重力场模型精度检核。模型精度检核方法使用球冠谐模型径向扰动重力与Tz2和Tz37误差均方根衡量。表 2和表 3分别是卫星平均轨道面上扰动重力梯度Txz分量和GO_CONS_GCF_2_DIR_R5模型模拟的扰动重力Tz分量的统计结果。图 3是4个球冠谐重力场模型的L曲线图和最优岭参数值。表 4是球冠谐模型与扰动重力梯度观测值Tzz分量和Txz分量的误差统计结果。表 5是球冠谐模型与GO_CONS_GCF_2_DIR_R5模型在计算点径向扰动重力的误差统计结果。表 6是使用球冠谐模型计算的12′×12′格网点位置扰动重力梯度张量对角线分量Laplace方程统计结果。
| E | ||||
| GOCE卫星重力梯度 | 最大值 | 最小值 | 均值 | 标准差 |
| Txz2 | 0.28 | -0.41 | -0.02 | ±0.19 |
| Txz37 | 0.18 | -0.17 | -0.04 | ±0.06 |
| 10-5 m/s2 | ||||
| GO_CONS_GCF_2_DIR_R5模型扰动重力 | 最大值 | 最小值 | 均值 | 标准差 |
| Tz2 | 11.71 | -16.01 | -3.36 | ±7.37 |
| Tz37 | 2.36 | -2.22 | 0.14 | ±1.13 |
|
| 图 3 球冠谐模型对应的L曲线 Fig. 3 L-curve according to spherical cap harmonic models |
| E | |||||
| GOCE梯度观测值 | 球冠谐模型 | 误差最大值 | 误差最小值 | 误差均值 | 误差均方根 |
| Tzz2 | CSzz2 | 0.037 | -0.022 | 3.2×10-5 | ±0.0061 |
| CSall2 | 0.035 | -0.019 | 5.5×10-5 | ±0.0058 | |
| Tzz37 | CSzz37 | 0.039 | -0.023 | -5.9×10-5 | ±0.0063 |
| CSall37 | 0.038 | -0.021 | 4.9×10-5 | ±0.0064 | |
| Txz2 | CSzz2 | 0.32 | -0.37 | 0.007 | ±0.1745 |
| CSall2 | 0.10 | -0.22 | -0.018 | ±0.0611 | |
| Txz37 | CSzz37 | 0.07 | -0.11 | 0.000 7 | ±0.018 3 |
| CSall37 | 0.05 | -0.11 | 0.001 1 | ±0.016 1 | |
| 10-5 m/s2 | |||||
| GO_CONS_GCF_2_DIR_R5模型 | 球冠谐模型 | 误差最大值 | 误差最小值 | 误差均值 | 误差均方根 |
| Tz2 | CSzz2 | 7.75 | -13.44 | -2.67 | ±5.97 |
| CSall2 | 2.08 | -4.08 | -1.16 | ±1.77 | |
| Tz37 | CSzz37 | 1.26 | -1.55 | -0.048 | ±0.36 |
| CSall37 | 0.62 | -0.99 | -0.045 | ±0.20 | |
| E | ||||
| 球冠谐模型 | 最大值 | 最小值 | 均值 | 标准差 |
| CSzz2 | 2.9×10-7 | -2.6×10-7 | -4.9×10-10 | ±1.9×10-8 |
| CSall2 | 5.5×10-7 | -1.4×10-7 | -9.6×10-10 | ±4.9×10-8 |
| CSzz37 | 3.0 ×10-8 | -1.0 ×10-7 | -2.5×10-10 | ±5.1×10-9 |
| CSall37 | 6.7×10-8 | -6.2×10-8 | -1.6×10-11 | ±4.5×10-9 |
从表 6可以看出,4个球冠谐模型的Laplace方程的精度都在±10-8E,由于GOCE卫星任务的重力梯度张量对角线分量的误差PSD在测量带宽范围内不大于±3.2×10-3 E/Hz1/2(见文献[16]),因此文中计算的球冠谐模型完全满足卫星重力梯度测量的精度要求,可以用于恢复地球局部重力场模型。
从表 4中球冠谐模型的扰动重力梯度Tzz分量的误差来看,4个球冠谐重力场模型的数据拟合精度都很高,与GOCE卫星的扰动重力梯度Tzz的均方根误差都小于±10-3E,但是与GOCE卫星的扰动重力梯度Txz分量的误差均方根来看,球冠谐模型CSzz2的拟合精度很低,其Txz梯度分量的误差均方根只有±0.174 5 E,与表 2中梯度观测值Txz2的标准差±0.19 E的数量级相同。CSzz2模型拟合精度为±5.97×10-5 m/s2,与表 3中的Tz2的标准差±7.37×10-5 m/s2相比也属于同一个数量级,其误差见图 4(a)。从图 4(a)中可以看到Tz2与CSzz2的扰动重力场的差值在图左半部分呈现正的误差值,而右半部分是负的误差值,误差值从左到右由正值到负值均匀变化,说明CSzz2的扰动重力与Tz2的起伏基本一致,但是两者在东西向上差一个倾角。这个倾角反映的是地球重力场的长波长信息。可能是重力场的长波长信息在扰动重力梯度的Tzz分量中包含的很少,所以使用单个梯度分量Tzz2恢复的CSzz2模型中几乎不包含重力场中的长波长信息,球冠谐模型CSzz2的扰动重力与Tz2的误差很大。
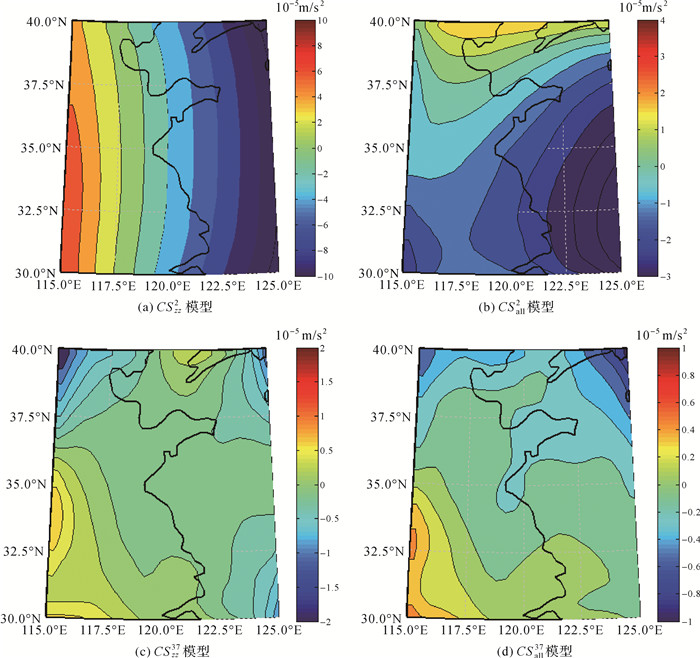
|
| 图 4 球冠谐模型径向扰动重力误差 Fig. 4 Error of the spherical cap harmonic models |
球冠谐模型CSall2的扰动重力梯度Txz分量误差均方根约为±0.06 E,其拟合精度要高于CSzz2。其模型精度为±1.77×10-5 m/s2,高于使用单个梯度值Tz2恢复的CSzz2。但从图 4(b)中可以看到,在使用梯度张量对角线分量联合反演得到的球冠谐CSall2模型中,其扰动重力与Tz2相比,也存在一定的东西向倾角,但相比CSzz2要小的多,说明多个梯度数据联合恢复的CSall2模型中包含一定的重力场低频信息。
球冠谐重力场模型CSzz37和CSall37是使用扣除了2~36阶重力场模型的剩余重力梯度观测值恢复的模型,其模型精度比CSzz2和CSall2模型高出约一个数量级,拟合精度可以达到±10-2 E,模型精度也都达到±0.3×10-5 m/s2(表 4、表 5),球冠谐重力场模型CSzz37和CSall37的精度在一个数量级上,相差不大。并且从图 4(c)、(d)中看到,CSzz37和CSall37模型的扰动重力误差图中没有倾角问题,说明球冠谐模型能够从扰动重力梯度数据中较好的恢复重力场的中短波信号。
4 结论本文从球冠谐分析理论出发,详细推导了球冠坐标系下的扰动位重力梯度计算公式,将GOCE卫星任务重力梯度观测值延拓到平均轨道面上。网格化后,使用Tikhonov正则化算法反演恢复了4个球冠谐重力场模型,最后与使用GO_CONS_GCF_2_DIR_R5重力场模型计算的卫星平均轨道面扰动重力进行比较分析。计算结果表明,由于扰动重力梯度中各个分量对重力场频谱的敏感性是不一样的,因此单一径向扰动重力梯度分量不能恢复全部扰动重力场的信号,所以联合不同的重力梯度分量,利用其频谱的互补性恢复的局部重力场模型,能够包含更多的重力场信号。如果从扰动重力梯度数据中移除重力场的长波信号,这时无论是使用单一径向梯度分量,还是使用多个梯度分量联合的方式恢复的球冠谐模型,都能够很好地拟合扰动重力场中剩余的重力信号,与GO_CONS_GCF_2_DIR_R5模型的差异不大于±0.3x10-5 m/s2。
| [1] |
吴晓平.
利用卫星重力梯度与地面数据确定地球重力场的分析[J]. 测绘学院学报, 1991(1): 19–32.
WU Xiaoping. Some Analyses of the Determination of the Earth's Gravity Field from the Satellite Gravity Gradient and Terrestrial Data[J]. Journal of the Institute of Surveying and Mapping, 1991(1): 19–32. |
| [2] |
孟嘉春, 蔡喜楣.
卫星重力梯度测量及其应用前景探讨[J]. 地球物理学报, 1991, 34(3): 369–376.
MENG Jiachun, CAI Ximei. Approach on Satellite Gravity Gradiometry and Its Vistas of Applications[J]. Acta Geophysica Sinica, 1991, 34(3): 369–376. |
| [3] |
吴星, 张传定, 赵东明.
卫星重力梯度分量的广义轮胎调和分析[J]. 测绘学报, 2009, 38(2): 101–107.
WU Xing, ZHANG Chuanding, ZHAO Dongming. Generalized Torus Harmonic Analysis of Satellite Gravity Gradients Component[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(2): 101–107. |
| [4] | REED G B.Application of Kinematical Geodesy for Determining the Short Wave Length Components of the Gravity Field by Satellite Gradiometry[R].Columbus:Ohio State University, 1973. |
| [5] |
张传定, 吴晓平, 陆仲连.
全张量重力梯度数据的谱表示方法[J]. 测绘学报, 2000, 29(4): 297–304.
ZHANG Chuanding, WU Xiaoping, LU Zhonglian. Spectral Representation of the Full Gravity Tensor[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(4): 297–304. |
| [6] |
王燚, 姜效典, 李德勇.
多源重力数据球冠谐模型抗差融合法[J]. 测绘学报, 2015, 44(9): 952–957.
WANG Yi, JIANG Xiaodian, LI Deyong. The Robust Fusion of Multi-source Gravity Data Based on the Spherical Cap Harmonic Model[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(9): 952–957. DOI:10.11947/j.AGCS.2015.20140345 |
| [7] | HAINES G V. Spherical Cap Harmonic Analysis[J]. Journal of Geophysical Research:Solid Earth, 1985, 90(B3): 2583–2591. DOI:10.1029/JB090iB03p02583 |
| [8] |
申宁华, 王光杰, 王喜臣.
球冠谐和分析算法及其在中国大陆航磁异常分析中的应用[J]. 物探化探计算技术, 1998, 20(1): 9–18.
SHEN Ninghua, WANG Guangjie, WANG Xichen. Spherical Cap Harmonic Analysis and Its Application to the Analysis of the Aeromagnetic Anomalies in China[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1998, 20(1): 9–18. |
| [9] | LI Jiancheng, CHAO Dingbo, NING Jinsheng. Spherical Cap Harmonic Expansion for Local Gravity Field Representation[J]. Manuscripta Geodaetica, 1995, 20(2): 265–277. |
| [10] |
王燚, 姜效典.
地球重力场球冠谐模型的分层构造和分析[J]. 大地测量与地球动力学, 2014, 34(5): 30–34, 39.
WANG Yi, JIANG Xiaodian. Structure and Analysis of Multilayered Spherical Cap Harmonic Model[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 30–34, 39. |
| [11] |
吴招才, 刘天佑, 高金耀.
局部重力场球冠谐分析中的导数计算及应用[J]. 海洋与湖沼, 2006, 37(6): 488–492.
WU Zhaocai, LIU Tianyou, GAO Jinyao. Derivative Calculation and Application in Spherical Cap Harmonic Analysis of Local Gravity Field[J]. Oceanologia et Limnologia Sinica, 2006, 37(6): 488–492. |
| [12] | BRUINSMA S L, FÖRSTE C, ABRIKOSOV O, et al. The New ESA Satellite-only Gravity Field Model via the Direct Approach[J]. Geophysical Research Letters, 2013, 40(14): 3607–3612. DOI:10.1002/grl.50716 |
| [13] |
曹月玲, 王解先.
利用球冠谐分析拟合GPS水准高程[J]. 武汉大学学报(信息科学版), 2008, 33(7): 740–743.
CAO Yueling, WANG Jiexian. Application of Spherical Cap Harmonic Analysis to Fit GPS Level Height[J]. Geomatics and Information Science of Wuhan University, 2008, 33(7): 740–743. |
| [14] |
彭富清, 于锦海.
球冠谐分析中非整阶Legendre函数的性质及其计算[J]. 测绘学报, 2000, 29(3): 204–208.
PENG Fuqing, YU Jinhai. The Characters and Computation of Legendre Function with Non-integral Degree in SCHA[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(3): 204–208. |
| [15] | HWANG C, CHEN S K. Fully Normalized Spherical Cap Harmonics:Application to the Analysis of Sea-level Data from TOPEX/Poseidon and ERS-1[J]. Geophysical Journal International, 1997, 129(2): 450–460. DOI:10.1111/gji.1997.129.issue-2 |
| [16] |
刘晓刚. GOCE卫星测量恢复地球重力场模型的理论与方法[D]. 郑州: 信息工程大学, 2011. LIU Xiaogang.Theory and Methods of the Earth's Gravity Field Model Recovery from GOCE Data[D].Zhengzhou:Information Engineering University, 2011. http://cdmd.cnki.com.cn/article/cdmd-90008-1012325190.htm |
| [17] | HOBSON E W. The Theory of Spherical and Ellipsoidal Harmonics[M]. Cambridge: Cambridge University Press, 1931. |
| [18] |
王竹溪, 郭敦仁.
特殊函数概论[M]. 北京: 北京大学出版社, 1989.
WANG Zhuxi, GUO Dunren. Introduction to Special Function[M]. Beijing: Peking University Press, 1989. |
| [19] |
刘晓刚, 吴晓平, 赵东明, 等.
扰动重力梯度的非奇异表示[J]. 测绘学报, 2010, 39(5): 450–457.
LIU Xiaogang, WU Xiaoping, ZHAO Dongming, et al. Non-singular Expression of the Disturbing Gravity Gradients[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 450–457. |
| [20] |
赵建虎, 王胜平, 刘辉, 等.
海洋局域地磁场球冠谐分析建模方法研究[J]. 测绘科学, 2010, 35(1): 50–52, 9.
ZHAO Jianhu, WANG Shengping, LIU Hui, et al. Study on Establishing Local Geomagnetic Model Using Spherical Cap Harmonic Analysis[J]. Science of Surveying and Mapping, 2010, 35(1): 50–52, 9. |
| [21] |
罗志才, 钟波, 宁津生, 等.
卫星重力梯度测量确定地球重力场的理论与方法[M]. 武汉: 武汉大学出版社, 2015.
LUO Zhicai, ZHONG Bo, NING Jinsheng, et al. Theory and Method for Determining the Earth's Gravity Field from Satellite Gravity Gradiometry[M]. Wuhan: Wuhan University Press, 2015. |
| [22] |
韦博成, 鲁国斌, 史建清.
统计诊断引论[M]. 南京: 东南大学出版社, 1991.
WEI Bocheng, LU Guobin, SHI Jianqing. Introduction to Statistical Diagnostics[M]. Nanjing: Publishing House of Dongnan University, 1991. |
| [23] |
黄谟涛, 欧阳永忠, 刘敏, 等.
融合海域多源重力数据的正则化点质量方法[J]. 武汉大学学报(信息科学版), 2015, 40(2): 170–175.
HUANG Motao, OUYANG Yongzhong, LIU Min, et al. Regularization of Point-mass Model for Multi-source Gravity Data Fusion Processing[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 170–175. |
| [24] | HANSEN P C. Analysis of Discrete Ill-posed Problems by Means of the L-curve[J]. SIAM Review, 1992, 34(4): 561–580. DOI:10.1137/1034115 |


