2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079;
3. 地球空间信息技术协同创新中心, 湖北 武汉 430079;
4. 武汉大学中国南极测绘研究中心, 湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China;
3. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China;
4. Chinese Antarctic Center of Surveying and Mapping, Wuhan 430079, China
平差的实际问题中常存在设计矩阵由含有误差的观测值构成,传统最小二乘方法在求解此类模型的过程中,因忽略设计矩阵中实际存在的误差而具有理论的不完备性。考虑设计矩阵误差,将所有观测值改正数平方和最小作为平差准则的求解方法最初由Adcock于1877年提出[1]。1980年,Golub和Van Loan提出了奇异值分解(SVD)算法,并将这类设计矩阵带有误差的问题命名为整体最小二乘方法(total least square, TLS)[2]。使用SVD解法虽能获得稳定数值解,但计算复杂度高[3],如果设计矩阵中含有误差的元素重复出现,使用SVD解法,同一观测值在不同位置改正数将不一样。另外,使用SVD解法估计参数,难以给出以观测值表达的未知参数平差值表达式,从而无法利用协方差传播率进行精度评定[4]。近些年,文献[4]提出一种顾及设计矩阵随机误差的最小二乘组合新解法,其将设计矩阵中所有含误差的元素作为虚拟观测值引入虚拟观测方程求解模型,解决了TLS方法的精度评定问题。加权整体最小二乘亦有较大进展[5-10]。此外,文献[11]研究了三维坐标转换的通用整体最小二乘解法;文献[12]对部分变量误差模型提出了整体抗差最小二乘估计方法;文献[13]对Partial EIV模型提出了一种新解法;文献[14]提出了一种基于中位数法的抗差整体最小二乘估计方法。
AR模型是一类基本的时间序列模型,在工程实践与导航定位等方面有着广泛应用[15-22]。对于t阶AR模型,任意时刻观测值zm为自身最近t阶滞后项的线性组合[23],如下
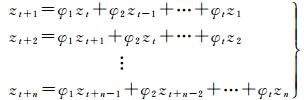 (1)
(1)
式(1)用矩阵形式表达可写为
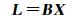 (2)
(2)
式中,观测向量L = [zt+1 zt+2 … zt+n]T,令任意时刻观测值zi的改正数为vi;设计矩阵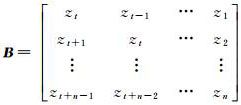
由此可见,含误差的观测值规律地出现在设计矩阵不同位置,且观测向量中元素亦重复出现在设计矩阵中。使用传统最小二乘方法估计AR模型参数,因忽略设计矩阵中存在含误差的元素而理论缺乏严密性。AR模型中,观测向量误差与设计矩阵误差同源,若使用SVD方法估计AR模型参数,则多次出现的同一观测值的改正数不再唯一。文献[24]提出一种非线性的AR模型整体最小二乘迭代算法,但难以应用协方差传播定律给出精度评定公式。
前述方法对求解AR模型存在一定缺陷,本文提出一种顾及设计矩阵误差,适用于AR模型的整体最小二乘新解法,该方法通过引入未在观测向量中出现且含误差的观测值作为虚拟观测值,将设计矩阵对应的改正数与未知参数初值乘积改写为由新设参数改正数及实际观测值改正数表达的线性组合,使得观测向量与设计矩阵中带误差的元素个数相同。由此将整体最小二乘问题转化为经典最小二乘问题,最终使用间接平差方法进行参数求解。本文方法有效地克服了AR模型中同一参数在不同位置改正数不一致的情况,并能依据协方差传播定律进行精度评定。
1 顾及设计矩阵误差的AR模型新解法 1.1 算法推导同时考虑设计矩阵B与观测向量L误差,式(2)可写为
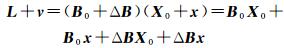 (3)
(3)
忽略二阶小项Δ Bx,式(3)可改写为
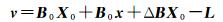 (4)
(4)
式中,v = [vt+1 vt+2 … vt+n]T为观测向量L改正数;X0= φ10 φ20 … φt0]T,由待求参数初值组成,x为未知参数改正数;B0由设计矩阵B中各元素初值构成;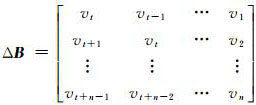
矩阵Δ B中改正数规律地重复出现,为将不同的改正数单独取出,同时考虑未在设计矩阵中出现的改正数vt+n,将Δ BX0作如式(5)所示等价变换
 (5)
(5)
在AR模型中,观测向量L中元素在设计矩阵B中重复出现,两者相同元素改正数应一致。考虑到B中的[z1 z2 … zt]T未在L中出现,为使观测向量L与设计矩阵B中带误差的元素个数相同,引入仅在设计矩阵B中出现且带误差的元素作为虚拟观测值LB,即LB=[z1 z2 … zt]T。令xB=[v1 v2 … vt]T,由此Δ BX0可由xB与观测值改正数v组成的列向量线性表示,即式(6)
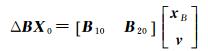 (6)
(6)
式中,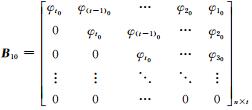

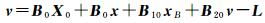 (7)
(7)
将式(7)中右边B20v项移至等式左边,提取公因式v得(E-B20)v。由于矩阵B20中非零元素集中出现在主对角线下方,主对角线及其上方元素全为0,故行列式|E-B20|恒为1,即矩阵E-B20可逆,从而可得式(8)
 (8)
(8)
虚拟观测值误差方程为
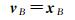 (9)
(9)
如果令
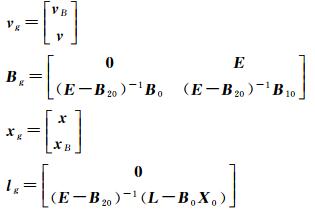
则有
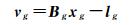 (10)
(10)
式中,vg为z1、z2、…、zt、zt+1、…、zt+n改正数构成的列向量;Bg为等效设计矩阵;xg为所有实际待估参数的和虚拟参数的改正数。算法的估计准则为vgTPvg=min,由此整体最小二乘问题转化为经典最小二乘问题,从而可按经典平差中的间接平差方式求解。
1.2 解算流程本文方法解算流程为:
(1) 确定观测值及虚拟观测值初值,选用普通最小二乘所得的AR系数作为未知参数初值,即X0=(B0TB0)-1B0TL。
(2) 按照式(10)所定义的各矩阵,将AR系数初值或更新值代入,构建等效设计矩阵Bg,矩阵lg,按间接平差原理计算xg= BgTPBg-1BgTPlg,同时更新未知参数X。
(3) 根据式(10)计算vg,更新实际观测值L估值及虚拟观测值LB估值。
(4) 重复步骤(2)、(3)直到未知参数改正数x小于一定阈值停止迭代,得到最终的未知参数结果。
1.3 精度评定在经典最小二乘中,权由观测值精度确定,而观测值出现的次数,则会在平差过程中,通过对系数矩阵的作用,进一步影响法方程进而影响平差结果。但是在整体最小二乘中,系数矩阵中的观测值具有双重身份,除了影响系数矩阵本身外,还作为观测值参与平差,本文认为观测值这部分影响与观测值在系数矩阵中出现的次数也有关系。本文所定义的权阵P由两部分构成,即由观测值精度信息构建的权阵P ′,以及一个与次数有关的因子阵K,其中P=P′K。为简化问题,本文先行假定AR模型各期观测值等精度,即P ′为单位阵,P=K,若观测值不等精度,则在按照精度信息得到的权阵P ′的基础上再乘以一个次数有关的因子阵K。
由于在AR模型中,设计矩阵中元素在不同位置中规律地重复出现,观测值亦重复出现于设计矩阵中,在使用整体最小二乘方法进行求解未知参数时,实际上将同一观测值当作多次相同观测建模,为此,在各期观测值等精度的条件下,模型各观测值权可由观测值出现的次数确定,考虑引入虚拟观测值,该算法权阵P定义如下
 (11)
(11)
使用上述方法经过若干次迭代可以获得未知参数X平差值,单位权中误差σ计算如式(12)所示
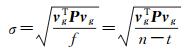 (12)
(12)
式中,模型自由度f=(n+u)-(t+u)=n-t。
在本文算法中,参数X0=[φ10 φ20 … φt0]T的初值为最小二乘所得到的AR系数。需要注意的是,若初值精度不够,则会导致迭代次数多,收敛速度慢,初值精度过差会导致迭代不能收敛。
2 算例分析 2.1 模拟数据为验证算法的可行性与精度,依据式(13)模拟一个平稳的AR(3)模型,其AR系数分别取为φ1= 0.8、φ2=-0.5、φ3=-0.3, 模拟数据如表 1所示。
| 序号 | 模拟值 | 序号 | 模拟值 | 序号 | 模拟值 |
| 1 | 15.918 9 | 11 | 1.177 5 | 21 | -2.857 4 |
| 2 | 14.797 4 | 12 | -10.707 8 | 22 | 4.889 9 |
| 3 | 23.246 2 | 13 | -13.858 2 | 23 | 7.621 5 |
| 4 | 7.357 2 | 14 | -6.001 0 | 24 | 5.039 0 |
| 5 | -10.805 2 | 15 | 5.460 1 | 25 | 0.607 8 |
| 6 | -18.069 2 | 16 | 9.641 9 | 26 | -6.357 2 |
| 7 | -10.567 7 | 17 | 9.125 8 | 27 | -5.792 5 |
| 8 | 2.792 3 | 18 | -1.934 3 | 28 | -1.301 2 |
| 9 | 14.679 2 | 19 | -6.551 9 | 29 | 2.108 4 |
| 10 | 13.126 8 | 20 | -9.401 7 | 30 | 5.830 8 |
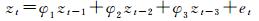 (13)
(13)
式中,et为高斯白噪声,表 1模拟数据所附加噪声et~N(0, 1)。
对于表 1模拟数据,分别采用本文方法(迭代阈值为0.000 000 1)、SVD方法以及直接最小二乘3种方法求解参数及单位权中误差,列于表 2。
| 参数 | SVD | LS | 本文方法 | 真值 |
| φ1 | 0.836 3 | 0.770 9 | 0.804 3 | 0.8 |
| φ2 | -0.546 1 | -0.466 7 | -0.508 4 | -0.5 |
| φ3 | -0.272 5 | -0.324 6 | -0.306 8 | -0.3 |
| σ0 | 1.445 5 | 1.416 0 | 0.904 2 |
从表 2可知,本文方法所得到的参数估值较SVD方法和传统最小二乘方法更接近于真值,由于考虑了设计矩阵误差及同一观测值出现在不同位置改正数应一致等事实,本文方法的单位权中误差明显小于最小二乘方法和SVD方法,并且更加接近虚拟观测噪声的中误差。当对模拟数据不附加高斯白噪声时,本文方法所得参数估值将与真值一致。
2.2 实测沉降数据表 2所示结果验证了算法的可行性与精度。为更好地验证本文算法可行性,采用文献[25]中例3-7实测沉降观测数据,该组实测沉降数据可用AR(3)模型拟合,故对实测沉降数据建立AR(3)模型,φ1、φ2、φ3为待求AR系数。在实测沉降数据中,本文算法所选用的参数初值X0= [φ10 φ20 φ30]T为最小二乘方法所获得的AR系数,在获取参数初值之后,结合实测沉降观测值代入式(10),按照各矩阵定义构造模型,迭代求解以获得最终结果。
本文算法、普通最小二乘(LS)以及SVD 3种方法所得参数估值如表 3所示。实测观测数据及3种方法所得平差值如表 4所示。图 1所示为本文算法、普通最小二乘(LS)以及SVD 3种方法平差结果与原始观测值残差绝对值对比。
| 参数 | SVD | LS | 本文方法 |
| φ1 | -0.374 8 | 0.041 1 | -0.486 3 |
| φ2 | 0.289 8 | 0.327 8 | 0.426 4 |
| φ3 | 1.090 1 | 0.635 1 | 1.067 0 |
| σ0 | 0.895 4 | 0.767 3 | 0.732 0 |
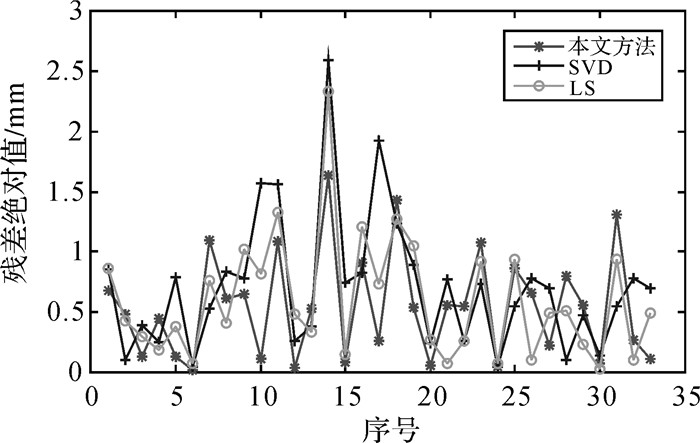
|
| 图 1 3种方法平差结果与原始观测值比较 Fig. 1 Comparative results between original data and adjustment of observation of three value |
| mm | ||||
| 序号 | 原始数据 | 本文方法 | SVD | LS |
| 1 | 26.33 | — | — | — |
| 2 | 26.27 | — | — | — |
| 3 | 26.43 | — | — | — |
| 4 | 25.56 | 26.235 2 | 26.412 1 | 26.418 6 |
| 5 | 26.82 | 26.339 8 | 26.719 1 | 26.397 2 |
| 6 | 26.56 | 26.435 0 | 26.169 1 | 26.265 4 |
| 7 | 25.93 | 26.368 6 | 25.683 3 | 26.115 2 |
| 8 | 26.43 | 26.553 1 | 27.217 7 | 26.804 3 |
| 9 | 26.52 | 26.536 7 | 26.564 2 | 26.453 2 |
| 10 | 25.46 | 26.552 5 | 25.988 6 | 26.220 7 |
| 11 | 26.12 | 26.734 7 | 26.957 1 | 26.524 2 |
| 12 | 27.28 | 26.635 3 | 26.500 6 | 26.261 0 |
| 13 | 26.67 | 26.778 2 | 25.101 6 | 25.851 8 |
| 14 | 27.95 | 26.860 6 | 26.385 9 | 26.626 2 |
| 15 | 26.74 | 26.775 4 | 26.994 0 | 27.215 5 |
| 16 | 27.53 | 27.004 5 | 27.153 4 | 27.198 0 |
| 17 | 25.31 | 26.944 8 | 27.902 1 | 27.646 6 |
| 18 | 26.90 | 26.980 6 | 27.644 0 | 27.046 0 |
| 19 | 28.09 | 27.182 1 | 27.265 8 | 26.885 3 |
| 20 | 26.78 | 27.035 7 | 24.860 6 | 26.045 5 |
| 21 | 28.66 | 27.231 0 | 27.429 8 | 27.391 6 |
| 22 | 26.75 | 27.288 6 | 27.642 8 | 27.795 1 |
| 23 | 27.24 | 27.187 6 | 27.475 4 | 27.501 0 |
| 24 | 28.02 | 27.469 7 | 28.787 6 | 28.088 9 |
| 25 | 26.81 | 27.350 9 | 26.555 2 | 27.068 6 |
| 26 | 28.50 | 27.421 2 | 27.768 9 | 27.585 8 |
| 27 | 27.68 | 27.637 4 | 27.635 1 | 27.753 9 |
| 28 | 26.57 | 27.435 5 | 27.113 2 | 27.505 8 |
| 29 | 28.36 | 27.700 8 | 29.133 9 | 28.264 6 |
| 30 | 27.94 | 27.716 4 | 27.247 4 | 27.453 6 |
| 31 | 26.81 | 27.606 6 | 26.713 5 | 27.318 2 |
| 32 | 28.50 | 27.949 7 | 28.966 7 | 28.270 8 |
| 33 | 27.68 | 27.752 6 | 27.547 9 | 27.703 1 |
| 34 | 26.57 | 27.877 6 | 27.113 2 | 27.505 8 |
| 35 | 28.36 | 28.098 9 | 29.133 9 | 28.264 6 |
| 36 | 27.94 | 27.834 2 | 27.247 4 | 27.453 6 |
表 3中本文方法所求结果与SVD法较为接近,但本文方法所得单位权中误差小于SVD法,直接最小二乘结果与本文结果相差较远,查阅文献[23]知,本文所引用实测沉降数据并非平稳的自回归时间序列,这可能是和直接最小二乘结果估值结果相差较大的原因。由表 4及图 1可知,本文方法所得观测值的平差值更契合原始观测序列变化趋势。新方法看起来误差相对平稳,波动小一些。第14期的结果,其他方法较差,新方法较好,说明新方法由于理论严密,所以对于抑制较大误差效果更好。
2.3 预报精度分析AR模型能利用前若干期观测值预报后若干期观测值,为检验本文算法的外符合精度,以表 4所列前30期实测沉降观测值为基础,分别利用本文算法、普通最小二乘(LS)以及SVD 3种方法求解模型系数并预报第31期至36期沉降数据。依据前30期实测沉降数据所求参数结果及相应方法预报值如表 5所示。图 2所示为本文算法、普通最小二乘(LS)以及SVD 3种方法预报结果与实测沉降观测值残差绝对值对比。
| 项目 | 原始数据 | 本文方法 | SVD | LS |
| φ1 | - | -0.528 0 | -0.580 8 | 0.065 6 |
| φ2 | - | 0.487 7 | 0.423 5 | 0.410 5 |
| φ3 | - | 1.048 8 | 1.164 3 | 0.528 7 |
| σ0 | - | 0.700 1 | 1.036 2 | 0.809 1 |
| 第31期 | 26.81 | 27.986 5 | 28.476 0 | 28.001 6 |
| 第32期 | 28.50 | 28.237 0 | 29.218 1 | 27.980 1 |
| 第33期 | 27.68 | 27.717 6 | 26.538 5 | 27.817 0 |
| 第34期 | 26.57 | 28.489 7 | 30.116 2 | 28.114 7 |
| 第35期 | 28.36 | 28.091 4 | 27.767 3 | 28.056 0 |
| 第36期 | 27.94 | 28.133 5 | 27.526 9 | 28.088 1 |
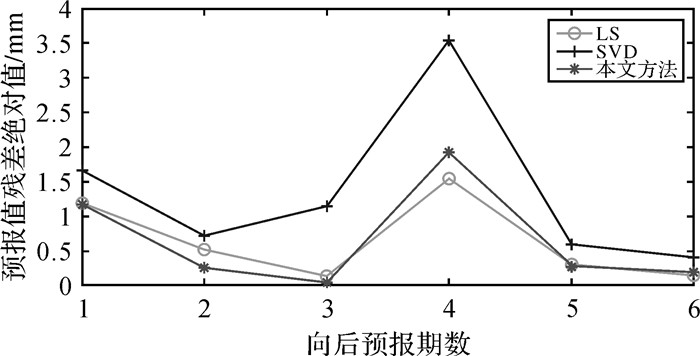
|
| 图 2 3种方法预测结果与实测沉降观测值比较 Fig. 2 Comparative results between original data and forecast result of observation of three value |
由表 5及图 2可知,在第31期至36期数据中,由SVD方法所求参数的预测效果最差,本文算法整体上预测效果最优,在第34期预报中3种方法预测效果均差,可能是观测噪声较大所致。向后预报期数越小,本文算法所求系数的预报结果与普通最小二乘方法相比,更接近与实际观测值,而在较远期预报中,二者效果相当。总体而言,在本文算法、普通最小二乘(LS)以及SVD 3种方法中,本文算法的外符合精度最优。
3 结语在AR模型中,观测向量与设计矩阵的误差同源,观测值规律地重复出现在设计矩阵中,且设计矩阵中自身元素亦重复出现。传统最小二乘方法难以解决系数矩阵及观测值向量皆带误差的数据处理问题。本文提出了一种考虑设计矩阵误差的AR模型整体最小二乘新解法,引入仅在设计矩阵中出现且含误差的元素作为虚拟观测值,使观测向量与设计矩阵中带误差的元素个数相同。然后巧妙地对观测方程进行等价变换,实现了最小二乘框架下求解整体最小二乘问题,有效地克服了传统SVD方法的理论缺陷且能应用协方差传播定律给出未知参数的精度评定公式。最后通过对模拟数据及实测数据的验证,发现本文方法具有比SVD方法及经典最小二乘方法更高的精度及更优的外符合精度。
| [1] | ADCOCK R J. Note on the Method of Least Squares[J]. Analyst, 1877, 4(6): 183–184. DOI:10.2307/2635777 |
| [2] | GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883–893. DOI:10.1137/0717073 |
| [3] | VAN HUFFEL S, ZHA Hongyuan. An Efficient Total Least Squares Algorithm Based on a Rank-revealing Two-sided Orthogonal Decomposition[J]. Numerical Algorithms, 1993, 4(1): 101–133. DOI:10.1007/BF02142742 |
| [4] |
姚宜斌, 孔建.
顾及设计矩阵随机误差的最小二乘组合新解法[J]. 武汉大学学报(信息科学版), 2014, 39(9): 1028–1032.
YAO Yibin, KONG Jian. A New Combined LS Method Considering Random Errors of Design Matrix[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1028–1032. |
| [5] |
曾文宪, 方兴, 刘经南, 等.
附有不等式约束的加权整体最小二乘算法[J]. 测绘学报, 2014, 43(10): 1013–1018.
ZENG Wenxian, FANG Xing, LIU Jingnan, et al. Weighted Total Least Squares Algorithm with Inequality Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1013–1018. DOI:10.13485/j.cnki.11-2089.2014.0173 |
| [6] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415–421. DOI:10.1007/s00190-007-0190-9 |
| [7] | SCHUERMANS M, MARKOVSKY I, VAN HUFFEL S. An Adapted Version of the Element-wise Weighted Total Least Squares Method for Applications in Chemometrics[J]. Chemometrics and Intelligent Laboratory Systems, 2007, 85(1): 40–46. DOI:10.1016/j.chemolab.2006.04.003 |
| [8] | VAN HUFFEL S, VANDEWALLE J. Analysis and Properties of the Generalized Total Least Squares Problem AX≈B When Some or All Columns in A are Subject to Error[J]. SIAM Journal on Matrix Analysis and Applications, 1989, 10(3): 294–315. DOI:10.1137/0610023 |
| [9] | XU Peiliang, LIU Jingnan, SHI Chuang. Total Least Squares Adjustment in Partial Errors-in-variables Models:Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661–675. DOI:10.1007/s00190-012-0552-9 |
| [10] | FANG X.Weighted Total Least Squares Solutions for Applications in Geodesy[D].Hannover, Germany:Leibniz University, 2011. |
| [11] |
方兴, 曾文宪, 刘经南, 等.
三维坐标转换的通用整体最小二乘算法[J]. 测绘学报, 2014, 43(11): 1139–1143.
FANG Xing, ZENG Wenxian, LIU Jingnan, et al. A General Total Least Squares Algorithm for Three-dimensional Coordinate Transformations[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1139–1143. DOI:10.13485/j.cnki.11-2089.2014.0193 |
| [12] |
赵俊, 归庆明.
部分变量误差模型的整体抗差最小二乘估计[J]. 测绘学报, 2016, 45(5): 552–559.
ZHAO Jun, GUI Qingming. Total Robustified Least Squares Estimation in Partial Errors-in-variables Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 552–559. DOI:10.11947/j.AGCS.2016.20150374 |
| [13] |
王乐洋, 余航, 陈晓勇.
Partial EIV模型的解法[J]. 测绘学报, 2016, 45(1): 22–29.
WANG Leyang, YU Hang, CHEN Xiaoyong. An Algorithm for Partial EIV Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 22–29. DOI:10.11947/j.AGCS.2016.20140560 |
| [14] |
陶叶青, 高井祥, 姚一飞.
基于中位数法的抗差总体最小二乘估计[J]. 测绘学报, 2016, 45(3): 297–301.
TAO Yeqing, GAO Jingxiang, YAO Yifei. Solution for Robust Total Least Squares Estimation Based on Median Method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 297–301. DOI:10.11947/j.AGCS.2016.20150234 |
| [15] |
吴富梅, 杨元喜.
基于高阶AR模型的陀螺随机漂移模型[J]. 测绘学报, 2007, 36(4): 389–394.
WU Fumei, YANG Yuanxi. Gyroscope Random Drift Model Based on the Higher-order AR Model[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 389–394. |
| [16] |
潘国荣, 刘大杰.
顾及邻近点变形因素项的动态模型辨识及预测[J]. 测绘学报, 2001, 30(1): 32–35.
PAN Guorong, LIU Dajie. Dynamic Modeling Identification and Predication in Consideration of the Adjacent Point Deformation[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 32–35. |
| [17] |
杨元喜, 崔先强.
动态定位有色噪声影响函数——以一阶AR模型为例[J]. 测绘学报, 2003, 32(1): 6–10.
YANG Yuanxi, CUI Xianqiang. Influence Functions of Colored Noises on Kinematic Positioning:Taking the AR Model of First Class as an Example[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(1): 6–10. |
| [18] |
叶志伟, 尹晖, 张守建.
AR模型谱在超导重力数据信号检测中的分析研究[J]. 武汉大学学报(信息科学版), 2007, 32(6): 536–539.
YE Zhiwei, YIN Hui, ZHANG Shoujian. Using AR Model Spectrum Algorithms to Detect Superconducting Gravimetric Signals[J]. Geomatics and Information Science of Wuhan University, 2007, 32(6): 536–539. |
| [19] |
张昊, 王琪洁, 朱建军, 等.
对钱德勒参数进行时变修正的CLS+AR模型在极移预测中的应用[J]. 武汉大学学报(信息科学版), 2012, 37(3): 286–289.
ZHANG Hao, WANG Qijie, ZHU Jianjun, et al. Application of CLS+AR Model Polar Motion to Prediction Based on Time-varying Parameters Correction of Chandler Wobble[J]. Geomatics and Information Science of Wuhan University, 2012, 37(3): 286–289. |
| [20] |
王乐洋, 许才军, 鲁铁定.
边长变化反演应变参数的总体最小二乘方法[J]. 武汉大学学报(信息科学版), 2010, 35(2): 181–184.
WANG Leyang, XU Caijun, LU Tieding. Inversion of Strain Parameter Using Distance Changes Based on Total Least Squares[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 181–184. |
| [21] |
魏二虎, 殷志祥, 李广文, 等.
虚拟观测值法在三维坐标转换中的应用研究[J]. 武汉大学学报(信息科学版), 2014, 39(2): 152–156.
WEI Erhu, YIN Zhixiang, LI Guangwen, et al. On 3D Coordinate Transformations with Virtual Observation Method[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2): 152–156. |
| [22] |
姚宜斌, 黄书华, 孔建, 等.
空间直线拟合的整体最小二乘算法[J]. 武汉大学学报(信息科学版), 2014, 39(5): 571–574.
YAO Yibin, HUANG Shuhua, KONG Jian, et al. Total Least Squares Algorithm for Fitting Spatial Straight Lines[J]. Geomatics and Information Science of Wuhan University, 2014, 39(5): 571–574. |
| [23] |
CRYER J D, CHAN K S. 时间序列分析及应用[M]. 潘红宇, 译. 北京: 机械工业出版社, 2011. CRYER J D, CHAN K S.Time Series Analysis with Applications in R[M].PAN Hongyu, tran.Beijing:China Machine Press, 2011. |
| [24] |
姚宜斌, 黄书华, 陈家君.
求解自回归模型参数的整体最小二乘新方法[J]. 武汉大学学报(信息科学版), 2014, 39(12): 1463–1466.
YAO Yibin, HUANG Shuhua, CHEN Jiajun. A New Method of TLS to Solving the Autoregressive Model Parameter[J]. Geomatics and Information Science of Wuhan University, 2014, 39(12): 1463–1466. |
| [25] |
王新洲, 陶本藻, 邱卫宁, 等.
高等测量平差[M]. 北京: 测绘出版社, 2013.
WANG Xinzhou, TAO Benzao, QIU Weining, et al. Advanced Surveying Adjustment[M]. Beijing: Mapping Publishing Company, 2013. |



