2. 国家海洋局第一海洋研究所, 山东 青岛 266061;
3. 大连舰艇学院海洋测绘系, 辽宁 大连 116018
2. First Institute of Oceanography, State Oceanic Administration, Qingdao 266061, China;
3. Department of Hydrography and Cartography, Dalian Naval Academy, Dalian 116018, China
海洋垂直基准是陆地和海洋上高程测量的依据,具有陆海高程一致的性质。当前,我国海岸带地形测量采用1985国家高程基准,水深测量采用理论最低潮面,两者分别采用不同的垂直基准面,使得陆海交接处地形图与海图难以无缝拼接,而且海图图幅海域内分别采用离散验潮站确定的深度基准值作为该海域统一的基准值,使得相邻图幅存在基准系统差。陆海高程/深度基准、不同海区深度基准面之间没有建立严密的转换关系,严重影响海岸带海岛礁测绘工作的全面实施及相关测绘成果的推广应用。
验潮站观测数据是构建海洋垂直基准的基础数据之一,能够提供稳定、可靠的调和常数[1]和高精度的平均海平面信息,为精密潮汐模型的外部精度检核、深度基准面模型的构建等提供数据基础。通过与水准点的GNSS联测,获得验潮站站点的多年平均海面高,是构建平均海面高模型和判断全球或区域平均海平面变化的重要数据来源之一。对验潮站数据的处理分析,文献[2-4]分别利用同步潮位序列相关性、潮汐调和分析模型进行缺测值和系统差的探测与修复,文献[5-6]对余水位的性质及应用进行研究,在这类分析中,均以各分潮频率已知但分潮振幅未知作为假设条件,均为基于物理机制的潮汐分析;文献[7-8]利用小波变换、附加风场信息的神经网络模型对潮位数据进行预报,文献[9]利用傅里叶变换对潮汐资料进行频谱分析,这类研究中分潮频率和振幅均设为未知,主要是基于潮位数据进行的理论与方法的研究。在利用验潮站进行海平面变化的研究中,受地壳运动的影响,验潮站观测数据包含海面升降和当地地壳垂直形变两种信息,使得由此确定的高程基准则仅有相对意义。国内外学者对沿海验潮站地壳垂直形变进行了大量的研究[10-15],目前利用GNSS连续观测资料进行验潮站的地壳垂直形变研究[16],对于得到验潮站平均海平面绝对变化具有重要意义。夏威夷大学海平面数据中心(http://www.psmsl.org/)提供的全球596个长期验潮站分布见图 1。

|
| 图 1 全球长期验潮站位置分布 Fig. 1 The distribution of the long-term tidal stations in the world |
高度计数据是构建海洋垂直基准的另一重要数据来源。利用卫星测高数据提取的潮汐信息,在开阔海域能够达到2~3 cm的精度[17],基于此,国际上不断推出并优化全球潮汐模型,如DTU系列[18]、FES系列[19-21]和TPXO系列[22-23]等,国际上常用的潮汐模型见表 1。由于多数全球潮汐模型较少同化中国沿海验潮站数据,使得全球潮汐模型在中国沿海精度较差。受水深、岸线等地理因素[24-25]和对流层、逆气压等物理参数[26-27]的影响,由高度计反演的潮汐信息在浅水海域精度较差,且具有地域差异性[28]。如何提高高度计数据在浅水海域的精度,并量化浅水海域精度与岸线距离的关系是研究的热点问题。
| 潮汐模型 | 空间分辨率 | 主要分潮 | 类型 | |||
| 日分潮 | 半日分潮 | 浅水分潮 | 长周期分潮 | |||
| DTU10 | 1/8°×1/8° | K1, O1, P1, Q1, S1 | M2, S2, N2, K2 | M4 | - | E |
| EOT11a | 1/8°×1/8° | K1, O1, P1, Q1, S1 | M2, S2, N2, K2, 2N2 | M4 | Mm, Mf | E |
| FES2012 | 1/16°×1/16° | K1, O1, P1, Q1, S1 | M2, S2, N2, K2, 2N2 | M4, MS4, M6 | Ssa, Mm, Mf | H |
| GOT4.8 | 1/2°×1/2° | K1, O1, P1, Q1, S1 | M2, S2, N2, K2 | M4 | - | E |
| HAMTIDE12 | 1/8°×1/8° | K1, O1, P1, Q1 | M2, S2, N2, K2 | - | - | H |
| OSU12 | 1/4°×1/4° | K1, O1, P1, Q1, S1 | M2, S2, N2, K2 | M4 | - | E |
| TPXO.8 | 1/30°×1/30° | K1, O1, P1, Q1, S1 | M2, S2, N2, K2 | M4 | - | H |
| NAO.99b | 1/2°×1/2° | K1, O1, P1, Q1 | M2, S2, N2, K2 | - | Sa, Ssa | H |
| NAO.99Jb | 1/12°×1/12° | K1, O1, P1, Q1 | M2, S2, N2, K2 | - | Sa, Ssa | H |
| 注:E为经验模型,H为同化模型;因篇幅限制,仅列出主要分潮 | ||||||
垂直基准是陆海资源环境信息表示、多源多代信息综合与有效使用的数学物理基础,是海岸线及滩涂界定、岛礁识别分类的科学依据,更是一切海洋及海岛资源环境信息、海洋安全及海战场环境信息的基本载体和重要组成部分以及海洋及海岛信息化、智慧化的必要条件。基于潮汐模型和海洋基准面模型建立海洋垂直基准转换关系,构建深度基准面与系列参考椭球面之间的偏差模型,是陆海高程/深度基准统一与转换的基本途径[29]。精密潮汐模型的构建依附于潮波动力学数值模拟,并同化多源高度计反演的潮汐信息与验潮站调和常数[30]。随着中短期验潮站资料、多代高度计数据和具备验潮功能的浮标数据等多源数据的加入,为构建高精度、高分辨率及高覆盖率的海洋垂直基准提供了可能。
1 国际海洋垂直基准的研究进展20世纪80年代国际上很多沿海国家进行了海洋垂直基准的研究和建设。FIG成立垂直基准专题小组,对海洋垂直基准的构建进行专门研究[31]。加拿大利用其布设的874个验潮站构建了不同垂直参考面与WGS-84椭球面的转换关系[32];澳大利亚利用131个验潮站构建大地水准面与WGS-84椭球面的关系,将其扩展到海道测量,进而确定基于WGS-84椭球面的最低天文潮面基准AUSHYDROID[33],但并未考虑高度计数据且假设大地水准面与平均海平面重合[34];英国利用880个验潮站(覆盖约18 000 km岸线)研究建立了基于GRS80椭球面的偏差模型VORF(vertical offshore reference frame)[35],其精度在沿岸海域为±15 cm,近海海域为±10 cm[36];美国利用1987个验潮站(覆盖约8200 km岸线)研制了垂直高程基准转换软件包VDatum,能够实现由最初28种到目前36种潮汐基准、高程基准和椭球垂直基准之间的转换[37],但由于未考虑高度计数据[38],仅能通过验潮站数据插值计算25海里内的垂直基准值,目前仍未实现整个国家沿海海域覆盖。
同时对垂直基准构建过程中存在的问题进行研究。针对高度计数据在近海精度较差的问题,文献[39]采用ERS-2和Poseidon高度计数据对澳大利亚海域进行研究,结果表明距离岸线4 km的海域高度计数据污染严重,4~22 km之间仍存在较大误差。事实上,受岸线和水深等因素的影响,高度计数据在不同海域的精度表现不同,随着物理改正模型精度和数据处理手段的不断提高,能够逐渐提高高度计数据在浅水海域的精度。对于海洋垂直基准转换的途径,文献[40]提出通过分别构建大地水准面与高程基准和深度基准之间的差值模型,其精度可达±3 cm;文献[41]针对沿岸浅水海域提出采用区域水动力模型构建基于似大地水准面的潮位数据,直接确定深度基准与高程基准的偏差。考虑到平均海面高模型在浅水海域精度较差,以平均海面高模型作为中间变量进行陆海基准统一的传统做法也不可避免地存在该问题,(似)大地水准面模型及参考椭球面模型正逐步参与到陆海垂直基准的统一。
目前,海洋垂直基准的转换与统一工作仍在全国沿海或局部海域范围内进行,没有任何一个国家完成对全球海域的海洋垂直基准构建。
2 我国海洋垂直基准的研究进展国内近20年对海洋垂直基准构建与转换方法进行了较深入的研究。《海道测量规范》明确规定我国海洋深度基准采用理论最低潮面,基于中短期潮位资料得到调和常数的不稳定性[42-43],文献[44-47]在深入研究了该基准的计算方法和算法改进,论证了对调和常数附加历元的必要性。文献[48-51]探讨了选取平均海平面、理论最低潮面和CGCS2000椭球面等具有不同意义的基准面作为我国海洋垂直基准的利弊,提出了通过偏差模型构建海洋垂直基准的理论与方法,研究了海洋垂直基准统一与转换的表达精度。
近10年来,我国正逐步实现垂直基准转换的工程化。我国目前拥有100多个长期验潮站,大量具备验潮功能的浮标及我国自主海洋卫星,对构建精密潮汐模型、平均海面高模型和深度基准面模型,并向1985国家高程基准转换发挥了重大作用。山东、浙江等沿海城市及长江口局部海域进行的垂直基准转换模型构建标志着我国在海洋垂直基准统一与转换理论的成熟及具备达到国际先进水平的能力。当然,我国海洋无缝垂直基准的体系构建、动态实现、维持方法和模型精度仍需进一步研究和提高。
目前,我国海洋垂直基准面模型分辨率和精度不断提高。针对全球潮汐模型在南海海域的精度问题,本文采用TOPEX/Poseidon、Jason-1/2高度计数据进行调和分析得到的分潮结果对DTU10模型进行精度评估,结果见表 2。DTU10在南海水深小于200 m的海域8个分潮RSS值为4.45 cm,在水深大于200 m的海域为3.06 cm。由于DTU10是基于FES2004建立的经验改正模型,且加入了包括4年TOPEX/Poseidon、Jason-1交叉任务的多源高度计数据,使得该模型具有较好的精度表现。表 3是采用南海海域37个长期验潮站对多个全球潮汐模型进行的精度评估,各模型中分辨率最高的是TPXO8为2′×2′。结果表明,潮汐模型精度相当,RSS值最大为15.05 cm,其中M2分潮RMS值最大为11.80 cm。
| cm | ||||||||||
| 水深 | 点位个数 | RMS | RSS | |||||||
| Q1 | O1 | P1 | K1 | N2 | M2 | S2 | K2 | |||
| 南海海域 | 8376 | 0.83 | 1.48 | 1.36 | 1.87 | 1.04 | 1.61 | 1.23 | 0.98 | 3.79 |
| <200 m | 4027 | 0.91 | 1.75 | 1.56 | 2.16 | 1.23 | 1.94 | 1.48 | 1.16 | 4.45 |
| >200 m | 4349 | 0.75 | 1.18 | 1.14 | 1.55 | 0.83 | 1.24 | 0.95 | 0.77 | 3.06 |
| cm | ||||||||||
| 潮汐模型 | RMS | RSS | ||||||||
| Q1 | O1 | P1 | K1 | N2 | M2 | S2 | K2 | |||
| DTU10 | 1.13 | 5.21 | 1.99 | 4.65 | 1.93 | 8.41 | 4.76 | 1.87 | 12.43 | |
| EOT11a | 0.92 | 3.46 | 1.47 | 4.21 | 2.78 | 10.08 | 6.07 | 1.99 | 13.52 | |
| FES2004 | 1.36 | 5.05 | 1.82 | 5.04 | 3.23 | 10.67 | 6.38 | 2.31 | 15.05 | |
| GOT4.8 | 1.17 | 5.29 | 1.91 | 5.48 | 2.51 | 10.35 | 4.45 | 2.00 | 14.15 | |
| HAMTIDE12 | 1.11 | 5.50 | 1.50 | 4.68 | 3.13 | 10.13 | 5.45 | 2.51 | 14.28 | |
| OSU12 | 1.36 | 4.41 | 1.47 | 4.04 | 4.26 | 11.80 | 4.95 | 2.08 | 15.03 | |
| TPXO8 | 1.09 | 4.90 | 1.81 | 4.97 | 2.47 | 10.35 | 5.27 | 2.09 | 14.09 | |
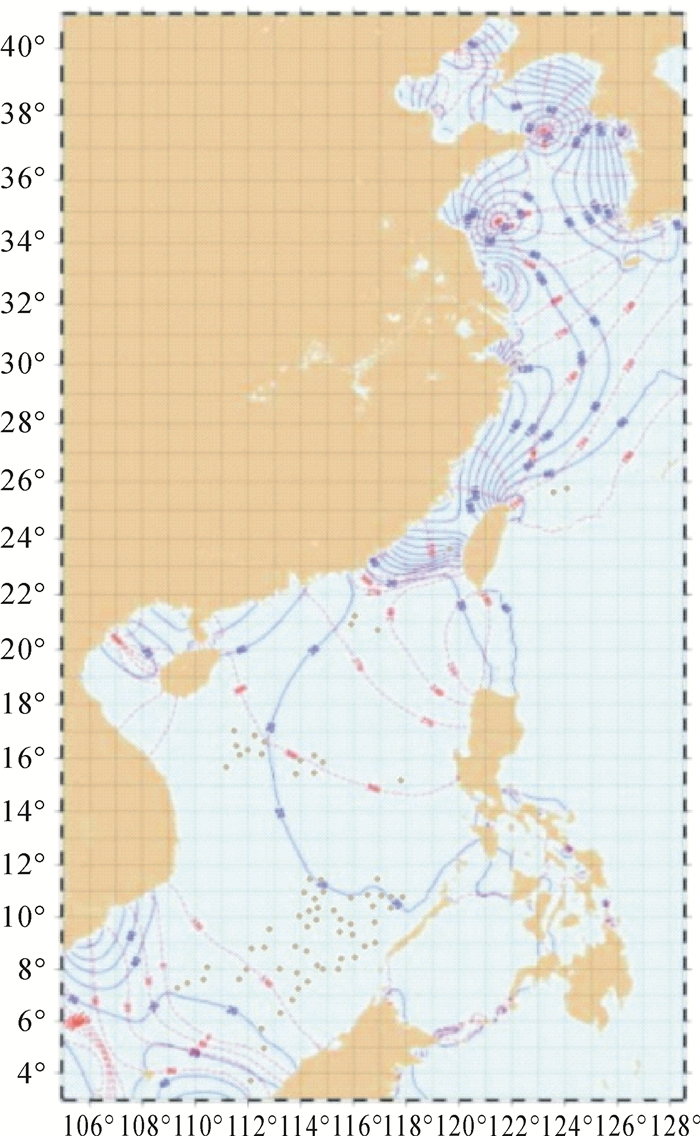
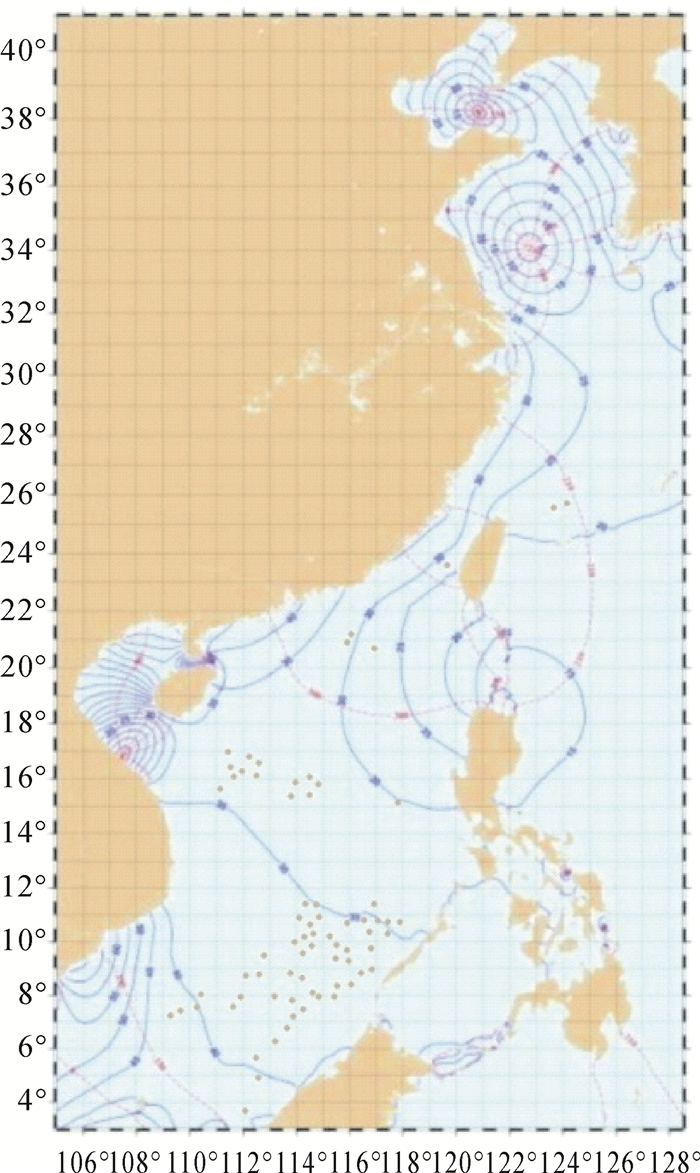
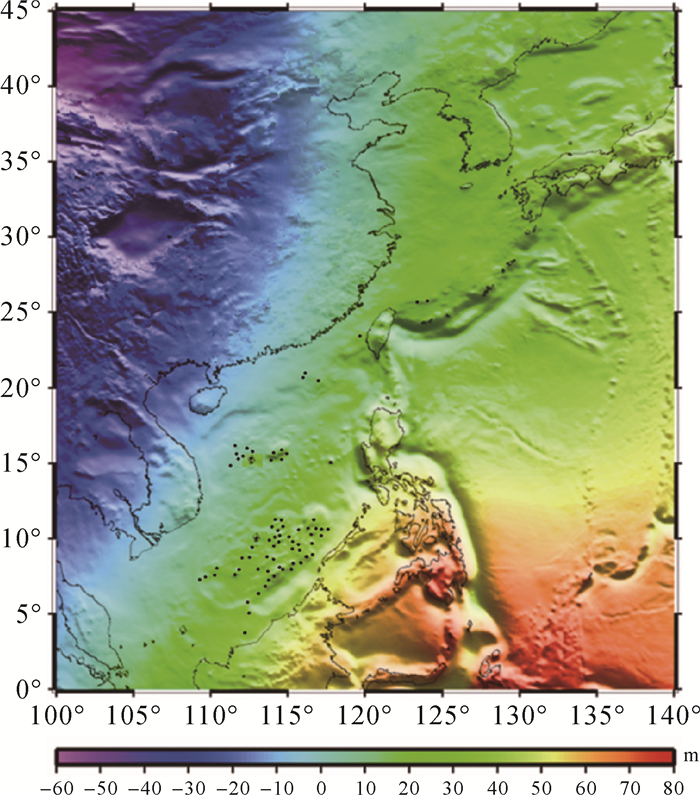
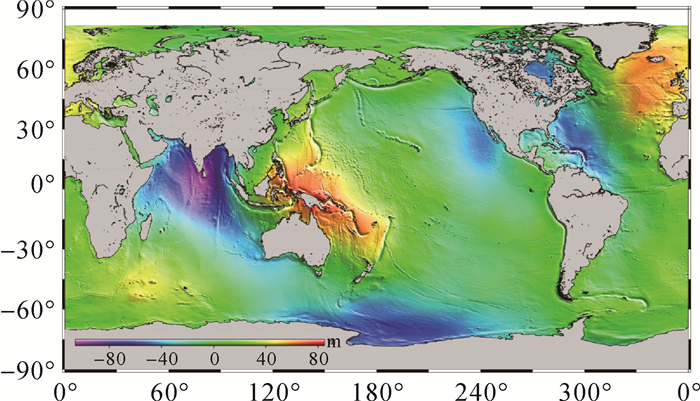
相比以上全球潮汐模型,覆盖中国邻近海域的区域潮汐模型分辨率达到1.2′×1.2′,图 2、图 3分别表示主要分潮M2、K1分潮潮波图,图中实线表示振幅,虚线表示迟角,采用中国沿岸25个长期验潮站进行精度评估表明9个主要分潮的RSS值为12.50 cm[29]。深度基准面模型的精度主要取决于潮汐模型的精度,由上述潮汐模型构建的深度基准面模型中误差优于±13 cm[52]。利用重力异常数据,采用移去恢复法,以EIGEN-5C为参考场,积分得到2′×2′的大地水准面模型,见图 4。采用沿岸85个GPS水准拟合进行精度评估,大地水准面模型在中国海域标准差为±8.50 cm。在全球海域,采用多年TOPEX/Poseidon系列、Geosat/ERM等多源高度计数据,利用最小二乘配置法、移去恢复法等多种关键技术构建的平均海面高模型分辨率达到2′×2′[53],见图 5。该模型与CNES_CLS10、DNSC08和CLS01等国际平均海面高模型在中国近海的标准差分别为±8.20 cm、±15.60 cm和±12.00 cm,可基本实现高分辨率数字化网格形式的、近连续表达的海洋无缝垂直基准。
|
| 图 2 中国邻近海域M2分潮潮波图 Fig. 2 Co-tidal chart of M2 constituent in China seas |
|
| 图 3 中国邻近海域K1分潮潮波图 Fig. 3 Co-tidal chart of K1 constituent in China seas |
|
| 图 4 中国邻近海域大地水准面模型 Fig. 4 The geoid model in the adjacent waters of China |
|
| 图 5 全球海域平均海面高模型 Fig. 5 The global mean sea surface height model |
3 海洋无缝垂直基准构建关键技术
(1) 无缝垂直基准面的选择与相互转换。海洋无缝垂直基准面应按多个种类和多种层级选择,既包括参考椭球面和大地水准面等大地类型的高程基准,又应选择深度基准面和平均海平面等深度基准。研究工作的重点是确定不同垂直基准面的相互关系。海洋深度基准面可以通过平均海面高模型在大地高系统中或通过海面地形模型在国家高程基准中表示,因此,实现海洋深度基准面与陆地高程基准面的相互转换,即实现基于地球椭球的基础数据库数据和海图目标数据的变换以及海图数据与地形数据的转换。
(2) 基准面的高分辨率网格形式表示。由传统离散的基准表现形式发展为现代的模型连续形式,国际和国内多采用利用验潮站基准数据的拟合技术,但从根本上,由潮汐因素决定的垂直基准面应顾及海域潮波变化的物理机制,即以潮汐模型为基础,构建高分辨率网格形式的基准面模型。
(3) 基准面精度指标与确定原则。无缝垂直基准面的关键是实施基准的转换,其精度指标的确定应以不损失不同基准下地理信息数据的转换精度指标为原则。在浅海区域,水深的精度一般限定在20~30 cm,故深度基准面的确定应明显高于该精度指标。构建连续无缝的海域潮汐类型垂直基准面,必须充分考虑不同海域的潮汐特点和可用数据分布情况。对于沿岸、内海和其他的半封闭海域等海洋测绘工程的重点区域,必须根据这类区域的特点,设计科学合理的无缝垂直基准面构建方案。
(4) 海洋垂直基准的维持与维护。海域垂直基准维护技术实际是指长期验潮站的多种数据观测与处理,通过对验潮站长期连续验潮资料、定期以高等级水准点联测或GNSS并置连续观测,进而精确确定基准面间的关系以及监测其他动态变化。海底地形测量或水深测量的海洋测量成果,通常是根据长期验潮站垂直基准关系,进行基于深度基准面或基于1985国家高程基准的成果基准转换。目前,国内长期验潮站的作用主要体现于水位与水文数据的采集,在垂直基准维护方面的作用相对弱化,对各个海洋垂直基准面转换关系在建站确定后通常都未及时进行更新,并且没有并置连续运行GNSS,不能精确确定平均海面的绝对变化。
4 结论与展望垂直基准是表征陆地高度、海洋深度的参考系或尺度标度。海洋垂直基准不仅直接关联海洋几何特征的精细刻画,也支持海洋动态变化过程的认知。海洋垂直基准的表达具有多样性、多层级的特点。利用多源信息构建的海洋垂直基准,可以在明确的坐标系中描述海洋的空间形态和动态过程的机理,实现陆海数据的互联互通,对推动数字海洋建设具有基础支撑作用。
潮汐模型是构建海洋垂直基准的基础,而构建精密潮汐模型主要依赖于验潮站、卫星高度计和浮标等提取的潮汐数据。随着具有长期潮位观测的海洋站进行GNSS连续观测系统的业务化推进,不仅极大地提高了我国海平面变化观测的科学性,更提升了海洋站“一站多能”的能力,使得我国为逐步构建海洋垂直基准体系并进行动态维护创造了条件。
开展更多数据资源、相容技术方法和技术要求在海洋垂直基准体系建设中的研究,实现垂直基准体系科学构建、区域扩展、逐步更新及应用服务的规范化、标准化与工程化,实现垂直基准体系由陆地到海域到海岛、由近海到大洋、由多个海区拼接成片、由区域到全球范围的无缝拓展。对加快建立我国陆海统一的全球垂直基准体系,提高海洋调查资料的高效综合与应用服务能力,全面建成信息化、智慧化海洋海岛,提升海洋海岛信息服务于我国海洋安全、海洋经济发展的能力和水平具有重要的作用和意义。
| [1] | 方国洪, 郑文振, 陈宗镛, 等. 潮汐和潮流的分析和预报[M]. 北京: 海洋出版社, 1986. FANG Guohong, ZHENG Wenzhen, CHEN Zongyong, et al. Analysis and Prediction of Tides and Tidal Currents[M]. Beijing: Maritime Press, 1986. |
| [2] | 赵建虎, 柯灏, 张红梅. 长期验潮站潮位观测误差的综合探测及修复方法研究[J]. 武汉大学学报(信息科学版), 2011, 36(12): 1490–1494. ZHAO Jianhu, KE Hao, ZHANG Hongmei. Comprehensive Detection and Repair Method for Long-period Tidal Gauge Observation Errors[J]. Geomatics and Information Science of Wuhan University, 2011, 36(12): 1490–1494. |
| [3] | 黄辰虎, 刘敏, 陈英凯, 等. 验潮站零点漂移检测及修订方法的改进[J]. 海洋测绘, 2015, 35(2): 4–8. HUANG Chenhu, LIU Min, CHEN Yingkai, et al. Improvement in Zero Drift Detecting and Amending for Tide Gauges[J]. Hydrographic Surveying and Charting, 2015, 35(2): 4–8. |
| [4] | 柯灏, 赵建虎, 张红梅. 短潮位序列系统误差的探测及修复方法研究[J]. 武汉大学学报(信息科学版), 2012, 37(7): 843–846. KE Hao, ZHAO Jianhu, ZHANG Hongmei. Study on the Detection and Repair Method of the Short-period Tidal Gauge Observation System Error[J]. Geomatics and Information Science of Wuhan University, 2012, 37(7): 843–846. |
| [5] | 刘雷, 李宝森, 李冬, 等. 基于余水位订正的海洋潮位推算关键技术研究[J]. 海洋测绘, 2012, 32(2): 11–14. LIU Lei, LI Baosen, LI Dong, et al. Sea Level Forecasting Based on Corrected Residual Sea Level[J]. Hydrographic Surveying and Charting, 2012, 32(2): 11–14. |
| [6] | 周绍炜, 许坚, 张立华, 等. 基于余水位精化潮高模型的水位生成研究[J]. 海洋测绘, 2009, 29(6): 30–33. ZHOU Shaowei, XU Jian, ZHANG Lihua, et al. Determining of Tidal Heights Based on Tidal Model Improved by Residual Water Levels[J]. Hydrographic Surveying and Charting, 2009, 29(6): 30–33. |
| [7] | EL-DIASTY M, AL-HARBI S. Development of Wavelet Network Model for Accurate Water Levels Prediction with Meteorological Effects[J]. Applied Ocean Research, 2015, 53: 228–235. DOI:10.1016/j.apor.2015.09.008 |
| [8] | NITSURE S P, LONDHE S N, KHARE K C. Prediction of Sea Water Levels Using Wind Information and Soft Computing Techniques[J]. Applied Ocean Research, 2014, 47: 344–351. DOI:10.1016/j.apor.2014.07.003 |
| [9] | 吴富梅, 魏子卿, 李迎春. 大港验潮站潮汐分析与国家高程基准面变化[J]. 测绘学报, 2015, 44(7): 709–716. WU Fumei, WEI Ziqing, LI Yingchun. Analysis of Tidal Data for Dagang Tidal Gauge and Study of the Changes for the National Height Datum[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 709–716. DOI:10.11947/j.AGCS.2015.20140110 |
| [10] | BUBLE G, BENNETT R A, HREINSDÓTTIR S. Tide Gauge and GPS Measurements of Crustal Motion and Sea Level Rise along the Eastern Margin of Adria[J]. Journal of Geophysical Research, 2010, 115(B2): 102–109. DOI:10.1029/2008JB006155 |
| [11] | FENOGLIO-MARC L, SCHÖNE T, ILLIGNER J, et al. Sea Level Change and Vertical Motion from Satellite Altimetry, Tide Gauges and GPS in the Indonesian Region[J]. Marine Geodesy, 2012, 35(S1): 137–150. |
| [12] | WÖPPELMANN G, MARCOS M. Coastal Sea Level Rise in Southern Europe and the Nonclimate Contribution of Vertical Land Motion[J]. Journal of Geophysical Research, 2012, 117(C1): C01007. DOI:10.1029/2011JC007469 |
| [13] | 焦文海, 魏子卿, 郭海荣, 等. 联合GPS基准站和验潮站数据确定海平面绝对变化[J]. 武汉大学学报(信息科学版), 2004, 29(10): 901–904. JIAO Wenhai, WEI Ziqing, GUO Hairong, et al. Determination of the Absolute Rate of Sea Level by Using GPS Reference Station and Tide Gauge Data[J]. Geomatics and Information Science of Wuhan University, 2004, 29(10): 901–904. |
| [14] | 刘根友, 朱耀仲, 许厚泽, 等. GPS监测中国沿海验潮站垂直运动观测研究[J]. 武汉大学学报(信息科学版), 2005, 30(12): 1044–1047, 1055. LIU Genyou, ZHU Yaozhong, XU Houze, et al. Study on Height Changes of Chinese Tide Gauges by GPS[J]. Geomatics and Information Science of Wuhan University, 2005, 30(12): 1044–1047, 1055. |
| [15] | 崔树红, 谢志仁, 钟鹤翔, 等. 利用T/P海面高度数据校验验潮站地面升降的初步研究[J]. 地球科学进展, 2005, 20(6): 643–648. CUI Shuhong, XIE Zhiren, ZHONG Hexiang, et al. The Primary Researches that T/P Sea Height Data Is Used for Revised Ground Rise or Fall at the Tide Gauge Station[J]. Advances in Earth Science, 2005, 20(6): 643–648. |
| [16] | 周东旭, 周兴华, 张化疑, 等. 利用GPS连续观测进行中国沿海验潮站地壳垂直形变分析[J]. 武汉大学学报(信息科学版), 2016, 41(4): 516–522. ZHOU Dongxu, ZHOU Xinghua, ZHANG Huayi, et al. Analysis of the Vertical Deformation of China Coastal Tide Stations Using GPS Continuous Observations[J]. Geomatics and Information Science of Wuhan University, 2016, 41(4): 516–522. |
| [17] | FOK H S, SHUM C K, YI Y C, et al. Evidences of Seasonal Variation in Altimetry Derived Ocean Tides in the Subarctic Ocean[J]. Terrestrial, Atmospheric and Oceanic Science, 2013, 24(4): 605–613. |
| [18] | CHENG Yongcun, ANDERSEN O B. Multimission Empirical Ocean Tide Modeling for Shallow Waters and Polar Seas[J]. Journal of Geophysical Research, 2011, 116(C11): 110–119. DOI:10.1029/2011JC007172 |
| [19] | LE PROVOST C, GENCO M L, LYARD F, et al. Spectroscopy of the World Ocean Tides from a Finite Element Hydrodynamic Model[J]. Journal of Geophysical Research, 1994, 99(C12): 24777–24797. DOI:10.1029/94JC01381 |
| [20] | LEFÈVRE F, LYARD F H, LE PROVOST C, et al. FES99:A Global Tide Finite Element Solution Assimilating Tide Gauge and Altimetric Information[J]. Journal of Atmospheric and Oceanic Technology, 2002, 19(9): 1345–1356. DOI:10.1175/1520-0426(2002)019<1345:FAGTFE>2.0.CO;2 |
| [21] | LYARD F, LEFEVRE F, LETELLIER T, et al. Modelling the Global Ocean Tides:Modern Insights from FES2004[J]. Ocean Dynamics, 2006, 56(5-6): 394–415. DOI:10.1007/s10236-006-0086-x |
| [22] | EGBERT G D, EROFEEVA S Y. Efficient Inverse Modeling of Barotropic Ocean Tides[J]. Journal of Atmospheric and Oceanic Technology, 2002, 19(2): 183–204. DOI:10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2 |
| [23] | EGBERT G D, RAY R D. Significant Dissipation of Tidal Energy in the Deep Ocean Inferred from Satellite Altimeter Data[J]. Nature, 2000, 405(6788): 775–778. DOI:10.1038/35015531 |
| [24] | ANZENHOFER M, SHUM C K, RENTSH M. Coastal Altimetry and Applications[R]. Report No.464. Columbus:Ohio State University, 1999. https://www.researchgate.net/publication/245679892_Coastal_Altimetry_and_Applications |
| [25] | CHERNIAWSKY J Y, FOREMAN M G G, CRAWFORD W R, et al. Ocean Tides from TOPEX/Poseidon Sea Level Data[J]. Journal of Atmospheric and Oceanic Technology, 2001, 18(4): 649–664. DOI:10.1175/1520-0426(2001)018<0649:OTFTPS>2.0.CO;2 |
| [26] | LYARD F, LEFEVRE F, LETELLIER T, et al. Modelling the Global Ocean Tides:Modern Insights from FES2004[J]. Ocean Dynamics, 2006, 56(5-6): 394–415. DOI:10.1007/s10236-006-0086-x |
| [27] | DESPORTES C, OBLIGIS E, EYMARD L. On the Wet Tropospheric Correction for Altimetry in Coastal Regions[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(7): 2139–2142. DOI:10.1109/TGRS.2006.888967 |
| [28] | FOK H S, BAKI IZ H, SHUM C K, et al. Evaluation of Ocean Tide Models used for Jason-2 Altimetry Corrections[J]. Marine Geodesy, 2010, 33(S1): 285–303. |
| [29] | 暴景阳, 许军. 卫星测高数据的潮汐提取与建模应用[M]. 北京: 测绘出版社, 2013. BAO Jingyang, XU Jun. Tide Analysis from Altimeter Data and the Establishment and Application of Tide Model[M]. Beijing: Surveying and Mapping Press, 2013. |
| [30] | 岳云飞, 王永刚, 何善方, 等. 基于FVCOM的温州近海潮汐潮流数值模拟[J]. 海洋科学进展, 2015, 33(2): 142–154. YUE Yunfei, WANG Yonggang, HE Shanfang, et al. Numerical Simulation of Tide and Tidal Currents in the Wenzhou Offshore Based on FVCOM[J]. Advances in Marine Science, 2015, 33(2): 142–154. |
| [31] | International Federation of Surveyors. FIG Guide on the Development of a Vertical Reference Surface for Hydrography[R]. FIG Special Publication No. 37. Copenhagen, Denmark:FIG, 2006. https://journals.lib.unb.ca/index.php/ihr/article/view/20784 |
| [32] | WELLS D, KLEUSBERG A, VANICEK P. A Seamless Vertical-reference Surface for Acquisition, Management and Display (ECDIS) of Hydrographic Data[R]. New Brunswick:University of New Brunswick, 1996. https://www.researchgate.net/publication/50244924_A_Seamless_Vertical-Reference_Surface_for_Acquisition_Management_and_ECDIS_Display_of_Hydrographic_Data |
| [33] | MARTIN R J, BROADBENT G J. Chart Datum for Hydrography[J]. The Hydrographic Journal, 2004, 112: 9–14. |
| [34] | ELLMER W, GOFFINET P. Tidal Correction Using GPS-determination of the Chart Datum[C]//ⅩⅩⅢ FIG Congress. Munich, Germany, 2006. |
| [35] | ADAMS R. Seamless Digital Data and Vertical Datums[C]//FIG Working Week 2003. Paris:[s.n.], 2003. https://www.researchgate.net/publication/237217713_Seamless_Digital_Data_and_Vertical_Datums |
| [36] | ILIFFE J C, ZIEBART M K, TURNER J F, et al. Accuracy of Vertical Datum Surfaces in Coastal and Offshore Zones[J]. Survey Review, 2013, 45(331): 254–262. DOI:10.1179/1752270613Y.0000000040 |
| [37] | PARKER B, MILBERT D, HESS K, et al. National VDatum:The Implementation of a National Vertical Datum Transformation Database[J]. Sea Technology, 2003, 44(9): 10–15. |
| [38] | YANG Zizang, MYERS E P, WHITE S A. V Datum for Eastern Louisiana and Mississippi Coastal Waters:Tidal Datums, Marine Grids, and Sea Surface Topography[R]. Silver Spring, Maryland:NOAA, 2010. |
| [39] | DENG X, FEATHERSTONE W E, HWANG C, et al. Estimation of Contamination of ERS-2 and POSEIDON Satellite Radar Altimetry Close to the Coasts of Australia[J]. Marine Geodesy, 2002, 25(4): 249–271. DOI:10.1080/01490410214990 |
| [40] | LEE D H, YUN H S, JUNG H I, et al. Transformation of Vertical Datum Surface in the Coastal Area Using Hybrid Geoid Models[J]. Journal of Coastal Research, 2013, 2(65): 1427–1432. |
| [41] | SLOBBE D C, KLEES R, GUNTER B C. Realization of a Consistent set of Vertical Reference Surfaces in Coastal Areas[J]. Journal of Geodesy, 2014, 88(6): 601–615. DOI:10.1007/s00190-014-0709-9 |
| [42] | 付延光, 周兴华, 杨磊, 等. 中国南海北部潮汐主要分潮的变化趋势分析[J]. 海洋测绘, 2015, 35(1): 14–17. FU Yanguang, ZHOU Xinghua, YANG Lei, et al. Variation Trends of Major Tidal Constituents along the Northern Coast of the South China Sea[J]. Hydrographic Surveying and Charting, 2015, 35(1): 14–17. |
| [43] | 暴景阳, 许军. 中国沿岸验潮站潮汐调和常数的精度评估[J]. 海洋测绘, 2013, 33(1): 1–4. BAO Jingyang, XU Jun. The Accuracy Evaluation of Harmonic Constants for Long Term Tidal Stations Along the Coast of China[J]. Hydrographic Surveying and Charting, 2013, 33(1): 1–4. |
| [44] | 暴景阳, 刘雁春, 晁定波, 等. 中国沿岸主要验潮站海图深度基准面的计算与分析[J]. 武汉大学学报(信息科学版), 2006, 31(3): 224–228. BAO Jingyang, LIU Yanchun, CHAO Dingbo, et al. Computations and Analyses of Chart Datum to Coastal Tide Gauges of China[J]. Geomatics and Information Science of Wuhan University, 2006, 31(3): 224–228. |
| [45] | 王冀, 刘克修. 关于海图深度基准面计算方法的若干问题[J]. 海洋测绘, 2002, 22(4): 10–13. WANG Ji, LIU Kexiu. Some Problems in Calculating the Chart Datum in Accordance with the National Specifications and Standards[J]. Hydrographic Surveying and Charting, 2002, 22(4): 10–13. |
| [46] | 暴景阳, 黄辰虎, 刘雁春, 等. 海图深度基准面的算法研究[J]. 海洋测绘, 2003, 23(1): 8–12. BAO Jingyang, HUANG Chenhu, LIU Yanchun, et al. Research on the Algorithm for Chart Datum[J]. Hydrographic Surveying and Charting, 2003, 23(1): 8–12. |
| [47] | 暴景阳, 许军, 崔杨. 调和常数及深度基准面的变化与历元订正[J]. 海洋测绘, 2013, 33(3): 1–5. BAO Jingyang, XU Jun, CUI Yang. The Variation and Epoch Correction of Harmonic Constants and Chart Datum[J]. Hydrographic Surveying and Charting, 2013, 33(3): 1–5. |
| [48] | 暴景阳, 章传银. 关于海洋垂直基准的讨论[J]. 测绘通报, 2001(6): 10–11. BAO Jingyang, ZHANG Chuanyin. On the Sea and Ocean Vertical Datum[J]. Bulletin of Surveying and Mapping, 2001(6): 10–11. |
| [49] | 柯灏. 海洋无缝垂直基准构建理论和方法研究[D]. 武汉: 武汉大学, 2012. KE Hao. Research on the Theory and Implementation Method of Marine Seamless Vertical Reference Surface[D]. Wuhan:Wuhan University, 2012. http://cdmd.cnki.com.cn/article/cdmd-10486-1012397375.htm |
| [50] | 孙翠羽. 海洋无缝垂直基准面建立方法研究——以渤海海域为例[D]. 青岛: 山东科技大学, 2011. SUN Cuiyu. Study on the Method of Developing a Seamless Vertical Reference:Taking Bohai Sea as a Case Study[D]. Qingdao:Shandong University of Science and Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10424-1012277431.htm |
| [51] | 孙翠羽, 周兴华, 马飞虎, 等. 无缝垂直基准面偏差模型建立方法研究[J]. 测绘通报, 2010: 52–56. SUN Cuiyu, ZHOU Xinghua, MA Feihu, et al. Study on the Establishment Method of Seamless Vertical Datum Deviation Model[J]. Bulletin of Surveying and Mapping, 2010: 52–56. |
| [52] | 暴景阳, 翟国君, 许军. 海洋垂直基准及转换的技术途径分析[J]. 武汉大学学报(信息科学版), 2016, 41(1): 52–57. BAO Jingyang, ZHAI Guojun, XU Jun. Vertical Datums and Their Transformation Approaches for Hydrography[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 52–57. |
| [53] | 金涛勇, 李建成, 姜卫平, 等. 基于多源卫星测高数据的新一代全球平均海面高模型[J]. 测绘学报, 2011, 40(6): 723–729. JIN Taoyong, LI Jiancheng, JIANG Weiping, et al. The New Generation of Global Mean Sea Surface Height Model Based on Multi-Altimetric Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 723–729. |


