2. 山东科技大学测绘科学与工程学院, 山东 青岛 266590
2. College of Geomatics, Shandong University of Science and Technology, Qingdao 266590, China
地图作为一种文化工具,集艺术、科学与技术于一体,在人类的知识宝库中具有十分重要的位置[1];地图学用图形表达区域自然和社会现象的空间分布特征、空间关系及其动态演变规律,其中蕴含着丰富的地理知识;而使用地图探索、分析并描述这些知识过程就是地图综合的过程。自地图学产生之时,地图综合就相伴而生,长期以来,地图综合一直是地图制图学领域研究的热点和难点问题之一。早在20世纪20年代,文献[2]就对制图综合进行了归纳与定义:制图综合是对制图对象进行取舍和概括的一种思维活动;文献[3]认为:制图综合是地图制图者根据地图成图后的用途和制图区域的特点,通过选取、化简等方法抽象、概括的反映制图对象带有规律性的类型特征和典型特点,而将那些对于该图来说是次要的、非本质的地物舍去,从而将地图由大比例尺缩编成小比例尺的过程;文献[4-5]认为,地图综合是在地理认知的基础上进行抽象和概括的过程,并形成对应于特定制图目的、适合于在一定比例尺下显示的地理要素的分类、分级和空间图形格局;文献[6-8]对地图综合的概念进行了梳理,提出制图综合本质上是一项复杂的人脑思维加工(简化或抽象)过程,具有很高的创造性。
随着几十年来相关学科发展和技术手段进步,地图综合也已经由传统手工作业方式逐步向自动化方式过渡转变[9]。Eckert时期,地图制图业界和学界普遍认为制图综合是无规律可循的、强依赖主观制图经验及知识的过程;20世纪40年代,前苏联制图学者Salichtchev在《制图原理》等著作中比较系统地提出了制图综合的基础原理,对地图综合原则、综合方法和综合约束等方面进行了归纳总结,强调地图综合可以作为一种客观的科学方法进行研究。这一思想启发了后续地图自动综合的研究人员,因为这意味着可以使用计算机模拟制图综合中的思维,对制图过程中涉及的规律性、系统性制图规则、专家知识进行自动化实现。
在此之后,Muller等[10]提出地图综合包含两个方面的内容:一是地图综合可以视为观察某些地理现象的视角由大尺度向小尺度演绎的过程;二是地图综合可以视为为了提高数据的易读性而进行的一系列带有空间信息的图形表达变换。与此对应,其过程同样可以概括为两个阶段:模型综合(数据变换)和图形综合(图形表达)。文献[11]认为制图综合是主观过程与客观过程的结合体,并据此将数字综合进一步划分为可以引入主观因素的数字到图形变换过程以及客观的数据到数据的变换过程。这些卓有成效的研究与探索,逐步推动地图综合走向计算机辅助下的人机交互、新阶段。但是,制图综合这一过程的极大主观性以及富有创造意义的本质决定了其自动化的过程注定是复杂的和困难的,直到目前为止尚未形成自动制图综合整体上解决的理论、模型和方法,致使自动制图综合结果的质量和过程的自动化水平一直未有显著提高。为此,本文建立了一种图数统一表达基元模型以及空间关系表达模型,提出了模型实体化时的拓扑自动补偿方法和模型地图化时的制图自动补偿方法,并据此开发了地图工作站,显著提升了制图综合结果的质量和过程的自动化水平。
1 图数统一表达地理模型根据文献[10-11]研究表明,制图综合分为模型综合和制图综合。从大尺度模型到小尺度模型,由于现有空间数据库中大尺度模型更加注重局部区域的地形地物自身形状表达,缺少道路、水系、居民地等要素的拓扑连通性和彼此之间的关联性,若不完成这些拓扑补偿,难以保证模型综合结果质量。当完成模型综合进行地图表达时,同样需要补偿的拓扑信息实现河流水系渐变、移位、境界跳绘等地图正确表达和跨平台保真。系统考虑模型综合易于实现拓扑补偿、易于实现地图表达与保真的要求,结合地图学理论和符号几何特征设计规范,本文建立了图数统一表达的地理模型。从该模型不仅便捷实现拓扑补偿,转变为实体化数据,利于空间分析;也利于实现制图表达和跨平台保真传播。
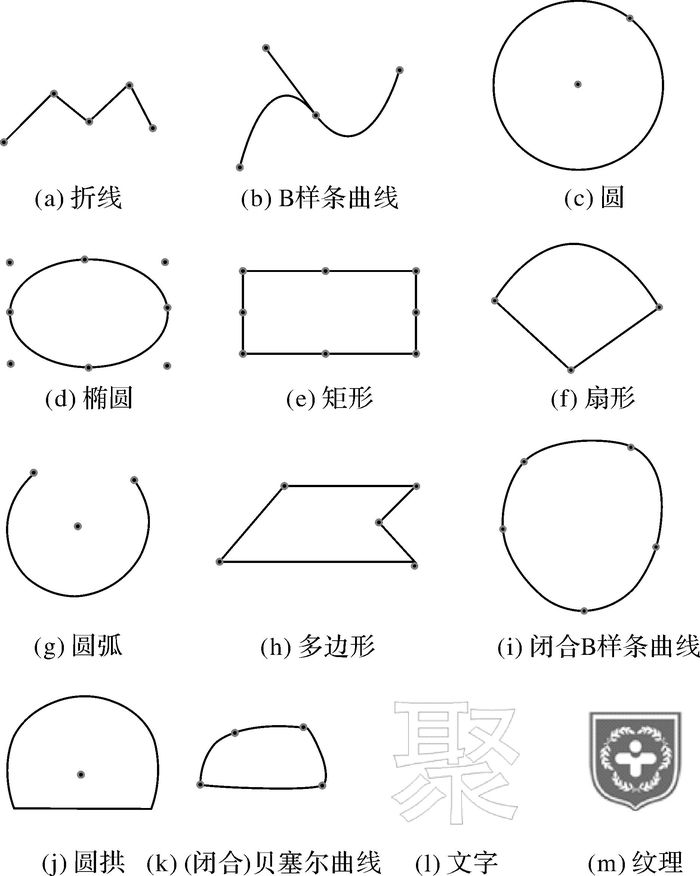
1.1 模型基元图数统一表达的地理模型以14种模型基元为基础,包括折线、B样条曲线、圆、椭圆、矩形、扇形、圆弧、多边形、闭合B样条曲线、圆拱、文字(TrueType文字)、纹理(图片)、贝塞尔曲线和闭合贝塞尔曲线,如图 1所示。
|
| 图 1 14种模型基元示意图 Fig. 1 14 Model units |
1.2 统一表达
依托模型基元,图数统一表达地理模型细分为三部分:地理编码(ID)、地理实体(Entity)和地图表达(Symbol)(见式(1))
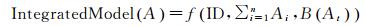 (1)
(1)
式中,地理编码(ID)是依据标准规范形成的唯一标识码,地理实体(∑i=1nAi)是一组模型基元的集合,可用于属性挂接,地图表达B(At)则是矢量参数曲线-贝塞尔曲线的函数,用于地图绘制。
地理实体每一基元的数据结构如表 1所示。
| 序号 | 基元类型 | 实体表达 |
| 1 | 折线 | 由多个点一次连接形成的线 |
| 2 | B样条曲线 | 由一组给定的控制点组成的线 |
| 3 | 圆 | 由两个点组成,其中,第1个点为圆心,第2个点为圆上的任意一点 |
| 4 | 椭圆 | 由两个点组成,两个点分别为椭圆外接矩形的左下点和右上点 |
| 5 | 矩形 | 由两个点组成,两个点分别为矩形的左下点和右上点 |
| 6 | 扇形 | 由3个点组成,其中,第1个点为圆心,第2个点为圆上的任意一点,第3个点为定位扇形的张角,相对于第2个点而言,第3个点不一定在圆周上 |
| 7 | 圆弧 | 由3个点组成,与扇形相似,第1个点为圆心,第2个点为圆上的任意一点,第3个点为定位扇形的张角,相对于第2个点而言,第3个点不一定在圆周上 |
| 8 | 多边形 | 多个点一次连接形成的封闭线 |
| 9 | 闭合B样条曲线 | 将B样条曲线封闭后得到的线 |
| 10 | 圆拱 | 由3个点组成的,与扇形相似,第1个点为圆心,第2个点为圆上的任意一点,第3个点为定位扇形的张角,相对于第2个点而言,第3个点不一定在圆周上 |
| 11 | 文字,即TrueType文字 | 主要由样条曲线和直线构成 |
| 12 | 纹理,即图片,也称为纹理贴图 | 通常为位图 |
| 13 | 贝塞尔曲线 | 三次贝塞尔曲线 |
| 14 | 闭合贝塞尔曲线 | 将贝塞尔曲线封闭后得到 |
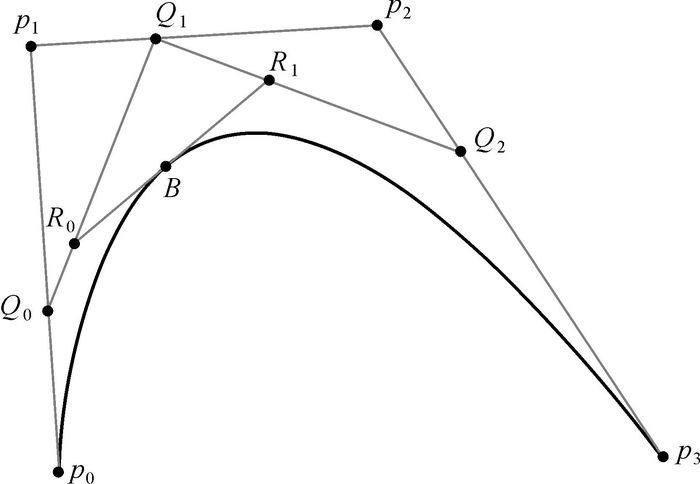
贝塞尔曲线是计算机图形学中常见的矢量参数曲线,支持各种图形渲染引擎[12]。它由起始点、终止点以及两个相互分离的中间点共4个点来创造、编辑图形,三次贝塞尔曲线如图 2所示。P0、P1、P2、P3是定义三次贝塞尔曲线的4个控制点,曲线由P0走向P3,一般不会经过中间控制点;P0和P1之间的间距决定曲线的长度,P1、P2决定曲线的方向。
|
| 图 2 三次贝塞尔曲线 Fig. 2 Cubic Bessel curve |
三次贝塞尔曲线可由低阶贝塞尔曲线的中介点Q0、Q1、Q2、R0、R1所建构。三次贝塞尔曲线的具体参数式如下式所示
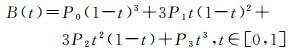 (2)
(2)
式中,B(t)为三次贝塞尔曲线, t为给定参数。闭合贝塞尔曲线为贝塞尔曲线始末点重合的特殊情况,即P0=P3。
1.3 地图绘制通过构造14种基元模型与贝塞尔曲线、闭合贝塞尔曲线之间的严格数学关系,即可实现模型基元的绘制。
(1) 折线,其为三次贝塞尔曲线的特例,即三次贝塞尔曲线的4个控制点中的P0=P1,P2=P3,由此可推导出折线与贝塞尔曲线之间的数学关系式
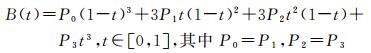 (3)
(3)
(2) 多边形,在折线的基础上,封闭起始点与终止点即可,即多边形与贝赛尔曲线之间的数学关系式
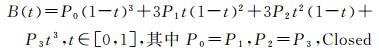 (4)
(4)
(3) 矩形,内角为90°的多边形,即矩形与贝赛尔曲线之间的数学关系式
 (5)
(5)
(4) B样条曲线,采用以下函数式完成从B样条曲线到贝赛尔曲线的转换,即B样条曲线与贝塞尔曲线之间的数学关系式
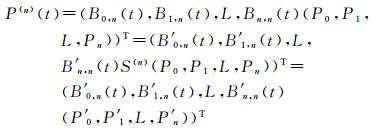 (6)
(6)
式中,Bn, n(t)为n次伯恩斯坦基函数, t为给定参数且t∈[0, 1];(B0, n′(t), B1, n′(t), L, Bn, n′(t))=(B0, n(t), B1, n(t), L, Bn, n(t))(S(n))-1,S(n)是使B样条曲线某一段多项式转换为贝塞尔曲线段的转换矩阵;(P0′, P1′, L, Pn′)T=S(n)(P0, P1, L, Pn)T为贝塞尔曲线的n个控制点。
(5) 闭合B样条曲线。在B样条曲线的基础上,封闭起始点与终止点即可得到闭合B样条曲线。由此可推导出闭合B样条曲线与贝塞尔曲线之间的数学关系式
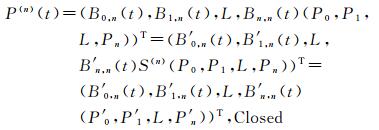 (7)
(7)
(6) 圆弧。给定3个点,P0、P1、P2,其中P0为圆心,P1为起始点,P2终止点;沿逆时针方向,圆弧上每个点与贝塞尔曲线上的点之间的误差不大于δ,半径r=|P1-P0|,求出矢量P1-P0和P2-P0的角度ω0、ω1,若ω1≤ω0,则ω1=ω1+π/2,圆弧总的弧度为Vω=ω1-ω0。
用θ表示在圆弧半径为r的情况下,满足上述误差条件的圆弧弧度的最大值;设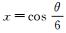
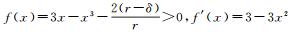
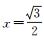
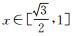
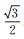
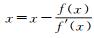
按照θ将圆弧分成n段, n为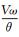
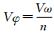
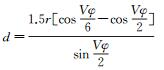
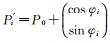
接着,依次建立每段圆弧与贝塞尔曲线之间的数学关系:令Q0=Pi′,Q3=Pi+1′,α=φi,β=φi+1,则Q1=Q0+d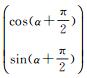
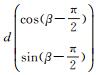
最终,圆弧与贝赛尔曲线之间的数学关系为
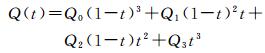 (8)
(8)
(7) 圆拱。在圆弧的基础上,封闭起始点与终止点即可。由此可推导出圆拱与贝塞尔曲线之间的数学关系式
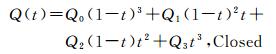 (9)
(9)
(8) 扇形。在圆弧的基础上,绘制P0、P1、P2 3点构成的折线即可得到。
(9) 圆。其为圆弧的特例,即在给定的3个点P0、P1、P2中,P1=P2。
(10) 椭圆。在圆的基础上,通过纵向或横向缩放即可得到。
(11-14) 纹理,即纹理贴图,通常为位图,因此不适用矢量图元与贝塞尔曲线之间的数学关系推导;字可视为一种复杂符号,由样条曲线和直线构成;贝塞尔曲线与封闭贝塞尔曲线绘制方法同上。
2 空间关系模型由模型基元和贝塞尔曲线构成的地理模型,无论拓扑补偿进行空间分析,抑或地图表达均需要地理实体之间的空间关系辅助。然而,依托基元模型建立起来的地理模型,在物理数据结构中并未存储或蕴含空间关系。为了便于后续计算机进行存储与处理,地理要素被离散成简单的点、线和面地理实体,因此,如何地理模型实体化和地图表达,提出建立空间关系模型至关重要,以便准确表达、动态计算和辅助推理。
众所周知,基于点集拓扑的四元组、九元组描述框架,是描述拓扑空间关系较好方法,被GIS界普遍接受,并且在商业化GIS软件中也得到广泛应用。四元组框架通过点集的边界与边界的交集、边界与内部的交集、内部与边界的交集、内部与内部的交集4种元素比较完备的描述了两个简单空间实体(简单点、简单线、简单面)之间的16种拓扑关系[13],但受其描述拓扑关系种类较少所限,某些情况下四元组内部的元素取值相同、对应的空间关系却不同。
为了能够将简单实体的每一种空间关系描述形式对应唯一的物理解释,空间实体的“补”作为空间实体的外部被引入空间关系描述框架,它同空间实体的边界、内部构成了简单空间实体的基本组件[14]。假设空间实体A的边界为∂A,内部为A°,“补”为A-,空间实体B的边界为∂B、内部为B°,“补”为B-,它们两两之间的交集就构成了空间关系描述的九元组模型,如式(10) 所示
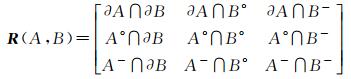 (10)
(10)
式中,内部每一元素的取值都有空、非空两种可能,所以九元组模型理论上可以描述512种空间关系,当然,绝大部分空间关系可能没有意义。作为四元组空间关系描述框架的扩展,九元组框架描述空间关系时,考虑了空间实体所在的空间,因而,四元组不能区分的线与线、线与面之间混淆的情形,在九元组中可以得到澄清。
然而,空间实体的边界、内部、“补”的并集等于二维空间,这说明九元组是一个秩亏矩阵,从理论上讲,这也必然不能区分一些空间物体的拓扑关系,同时,在九元组框架下,根据空间实体的外部定义,两个物体之间的外部有大量重叠,从而导致分离关系概念定义太笼统,容易引起混淆。另外,九元组描述框架仅适用于部分简单目标,难以描述诸如带有空洞的面或环的复杂空间实体,且缺少有效的方法对实体之间的空间邻近关系进行描述。
通过以上分析可以发现,引入空间实体的“补”作为空间实体的外部扩展四元组对空间关系进行描述,虽然增加了对拓扑关系描述的准确性,但其仍然存在对复杂实体通用型不强,不能形式化描述和定义空间邻近、顺序关系等问题。因此,考虑用空间实体的影响范围AV代替空间实体的“补”,重新构造九元组[15-17]。
空间实体的影响范围(AV)是指空间实体的Voronoi多边形的凸域,即AV=Ω(Voronoi(A))。空间实体A、B的各自的边界、内部、影响范围之间的9个交集构成了描述空间关系的新九元组--NIV
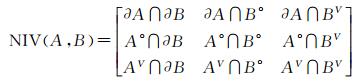 (11)
(11)
式中,∂A、∂B为空间实体A、B的边界;A°、B°为空间实体A、B的内部;AV、BV为空间实体A、B的影响范围。
可以发现,NIV空间关系描述模型处理的对象不再是简单空间实体,也可以是复杂空间实体,在保持了原九元组优点的基础上,对空间实体外部描述的重叠范围缩小,容易操作,同时,NIV模型可以很好地描述占空间关系中绝大部分的分离关系。
拓扑空间关系反映了空间实体之间不随实体的连续变形而改变的与量度和方向无关的一种特性,对于表达空间目标的分布特征、组合关联及邻近关系具有重要意义,为地理模型实体化拓扑补偿和地图表达奠定了理论基础。
3 自补偿拆合方法由模型基元和贝塞尔曲线构成的统一表达地理模型,辅之其空间关系表达和动态计算,当模型数据化,需要拓扑补偿,形成可分析实体模型;当模型地图化,需要制图补偿,形成可视化地图模型。针对以上两个过程,本文提出了自动化补偿拆合方法。“拆”即模型实体化,进行拓扑补偿;“合”即模型地图化,进行制图补偿。
3.1 拓扑补偿模型数据实体化主要包括实体抽象和拓扑修复两部分,如表 2所示。实体抽象是指带有形状、大小的地物转变为拓扑体,如面转点、面转线、实体碎化、实体抽取、宽度分割、网眼毗邻化选取等;拓扑修复是指缺失拓扑信息的修复,如实体修复、实体纠正、道路与水系网络的联通。
| 规则描述 | 图示示例说明 | |
| 实 体 抽 象 | 面转点 | 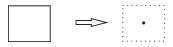 |
| 面转线 |  | |
| 线转面 | 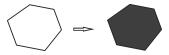 | |
| 线转点 | 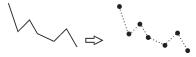 | |
| 点转面 |  | |
| 实体碎化 | 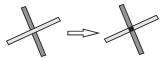 | |
| 实体抽取 | 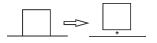 | |
| 宽度分割 |  | |
| 网眼毗邻化 选取 | 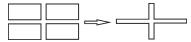 | |
| 拓 扑 修 复 | 实体修复 |  |
| 实体纠正 | 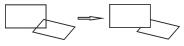 | |
| 网络联通 | 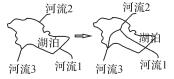 | |
| 分裂溶解 | 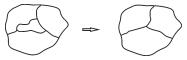 | |
| 挂接 | 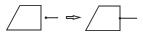 | |
| 结点拟合 | 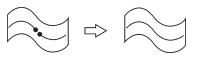 | |
| 形状化简 | 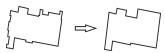 | |
3.1.1 实体抽象
实体抽象是模型实体化的重要内容,规则如下:① 面转点,通过提取规则物体几何中心、面状要素中心线[18-20]上均匀提取等方法实现;② 面转线,通过计算面要素边线(双线)提取中心线、骨架线[19-20]等方式实现;③ 线转面,快速将闭合线要素转化为面要素;④ 线转点,提取线要素首末结点、曲率较大处节点、极值点等特征点,以点要素概括表达线要素;⑤ 点转面,根据点要素属性及方向信息,提升要素表达维度,扩展表达地理实体形状、方向等信息;⑥ 实体碎化,使用实体碎化规则对地理数据进行处理,提取出压盖的公共区域作为一个单位的实体进行管理,同时建立与其连接的地物之间的关联关系;⑦ 实体抽取,对地物特征进行过智能识别,将组合存在的空间地理要素抽取、分离为独立组织、存储的点、线、面实体;⑧ 宽度分割,对地理要素的宽度信息进行分割管理,区分同一地物中具有不同宽度阈值的不同部分,以便于后续地物选取与合并;⑨ 网眼毗邻化,可以通过毗邻化自动选取识别网眼间狭长面,同时将狭长面收缩成线可以使被其分割的离散面要素变为毗邻的面要素。
3.1.2 拓扑修复拓扑修复是模型实体化的另一项重要内容,具体包括:① 实体修复。在空间数据的采集和编辑过程中,经常会出现线断裂、面未闭合等实体缺失错误,需要根据制图规范及属性信息等对实体进行修复,使其变为完整的要素实体。此外,空间数据中,当某一线状要素被分割为多个弧段进行存储时,根据“图形自然过渡”规范,需要对其进行图形衔接修复,将相接的弧段连接为一个整体。② 实体纠正。拓扑错误是空间数据库中常见的一种错误,如悬线、重复线、缺失标识、弧段自相交等,这些错误往往导致空间实体数据与实际地物拓扑不一致,从而降低了数据的质量和可用性,并影响后续的地图制图生产。实体纠正是拓扑预处理的过程,包括检查和修复两个阶段,具体包括冗余点识别及去除、重复线识别及去除、短悬线识别及去除、交点识别及分段等[21-22]。③ 网络联通。在大尺度地图数据中,由于注重于局部地形地物,道路、水系等网络联通性不完整,被湖泊、广场、居民地等大型面状地物阻断,需要根据网络特征进行主观修复。④ 分裂溶解。根据邻近面要素(如地块)的情况,按一定的规则将中心、细小的面要素分裂为与周围要素对应的碎片,并将碎片融合到相应的邻近面要素中。⑤ 挂接。设置一定的距离容限,将长悬线延伸至最近的面状、线状要素上。⑥ 节点拟合。拟合同一类属性约束的邻近结点,保证数据的连通性及完整性。⑦ 形状化简。简化多边形形状,修复V型凹槽、U型凹槽、V型凸槽、U型凸槽、尖角等细碎形状,使整体形状更简单。
3.2 制图补偿模型地图化应“先补偿,后表达”,完成制图补偿,才能较好实现地图可视化表达。其过程包括图形要素图形冲突处理、符号化两个阶段,如表 3所示。
| 规则描述 | 图示说明 | |
| 移 位 处 理 | 点/点移位处理 |  |
| 点/线移位处理 |  | |
| 线/线移位处理 | 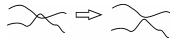 | |
| 线/面移位处理 |  | |
| 面/面移位处理 |  | |
| 注记/要素移位处理 |  | |
| 渐变处理 | 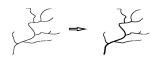 | |
| 压盖处理 | 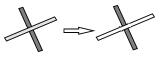 | |
| 跳绘处理 | 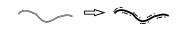 | |
| 自 动 注 记 | 点状要素注记 |  |
| 线状要素注记 | 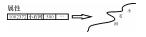 | |
| 面状要素注记 | 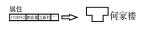 | |
| 组合注记 | 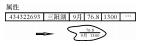 | |
| 符号化 |  | |
| 方 向 调 整 | 点符号方向调整 | 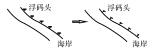 |
| 单线符号方向调整 | 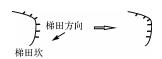 | |
| 双线符号方向调整 | 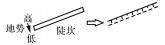 | |
3.2.1 地图要素图形冲突
地图要素冲突处理主要包括以下5种情况:① 移位。当由大比例尺变化至小比例尺时,会出现地物之间相互重叠或相离很近而不能彼此区分等冲突现象需要根据地物周围环境将某一要素沿给定方向及距离进行移位,或者对两要素同时进行相对移位,在保证不影响其他地物分布位置的情况下,为各个图形要素留出可分辨的图形范围空间[23-24]。具体包括:点/点移位、点/线移位、线/线移位、线/面移位、面/面移位、注记/要素移位等。② 渐变处理。渐变处理通常见于水系要素,为了形象的表现水流方向,单线河流一般采用由上游至下游逐渐变粗的线性图式进行表达,可采用角平分线、台阶式平行线对河流进行拟合[25-26]。③ 压盖处理。按顺叠加是计算机制图中地物分层分类组织后形成地图的一般思路,某些符号反映的即是在地图上地物之间相互压盖的自然特征,需要对压盖的情况进行合理设置以在二维地图中反映地理要素的立体关系[27-28]。④ 跳绘。当具有主、次区分的两种地物具有相同的绘制区域(重叠)时,即需要对次要地理要素进行跳绘处理。跳绘通常发生在自然地理要素(道路、水系)与境界要素重叠的区域,为保证真实描述自然地理要素,一般选择对境界符号进行中心跳绘、连续跳绘与间隔跳绘[29]。⑤ 自动注记。计算机自动注记要求注记位置、注记尺寸、注记形态等具有全局或局部最优性,基本原则包括:注记应与其关联的物体紧密结合,明显反应彼此之间的关联关系,同时,要注意不要压盖周围范围的重要地物,不能影响地图区域的可读性[30-34]。注记方式有多种,如内部注记(常用于面要素)、外部注记(常用于点要素)、骨架线注记(常用于面要素)、边界线注记(常用于线、面要素)、组合注记(用于特殊要素,如高程控制点、水库汛期信息等)。
3.2.2 符号化地图符号化是将空间实体数据使用对应符号进行绘制、整饰、输出的过程,是数字地图化的重要环节,其核心是建立符号与空间实体数据的空间位置映射关系,实质是符号局部空间坐标系与地理空间坐标系之间的坐标转换。基本过程如下:① 获取制图范围内地物的地理坐标及相关属性;② 根据地物属性参数在符号库中寻找与其对应的符号图式;③ 设置符号显示大小、颜色、纹理等描述信息;④ 根据地物地理坐标信息和符号局部坐标之间的转换关系,对地物进行符号化。
地图空间中,符号方向关系反映了地理要素的顺序、位置及指向关系,因此,正确的地图符号方向对于维持良好的制图效果具有重要的意义[35-36]。点符号的方向调整依赖于周围邻近要素的空间分布形态,形成对于周围要素的依附关系,如海岸码头方向、停车场进出方向等;单线符号的方向调整通过周围环境的定量计算及自身语义的定性描述;双线符号的方向调整相对复杂,包括线/面要素转换、方向识别、曲线虚实化等步骤。顾及地图要素之间的内在联系进行符号化是地图制图的基本要求之一,制图过程中需尽量运用空间关系推理、语义关系约束等对制图表达进行规范。
4 结束语地图自动综合是一项复杂的思维模拟、信息加工的过程,经过多年的实践、探索与发展,研究人员开展了大量卓有成效的工作,建立了丰富的模型与方法,展现了良好的发展前景。本文在创新的模型基元及其空间关系模型基础上,提出了图数统一表达地理模型,并建立了模型实体化的拓扑补偿和模型地图化的制图补偿自动化实现方法,探索一条解决地图自动综合这一世界性难题的方法与思路。
地图自动综合将是数字时代核心,也是空间数据一致性表达、多尺度数据融合、时空数据挖掘与分析中的关键。未来地图自动综合的突破至少有以下3个方面:① 从侧重综合过程发展到同时注重综合过程及综合结果质量量化评价与评价结果反馈调节方法;② 从分要素、分步骤的综合处理方法发展到全要素自动制图综合链,以提高综合的智能化、自动化程度;③ 从桌面地图综合服务方式发展到在线式综合,提供基于Web的地图综合服务。
| [1] | 陈述彭. 地图学面临的挑战与机遇[J]. 地理学报, 1994, 49(1): 1–8. CHEN Shupeng. Challenges and Opportunities Cartography Faces[J]. Acta Geographica Sinica, 1994, 49(1): 1–8. |
| [2] | ECKERT M. Die Kartenwissenschaft:Forschungen und Grundlagen zu einer Kartographie als Wissenschaft[M]. Berlin: W. de Gruyter, 1921. |
| [3] | 祝国瑞, 徐肇忠. 普通地图制图中的数学方法[M]. 北京: 测绘出版社, 1990. ZHU Guorui, XU Zhaozhong. Mathematical Methods in General Cartography[M]. Beijing: Surveying and Mapping Press, 1990. |
| [4] | 齐清文. GIS环境下智能化地图概括的方法研究[J]. 地球信息科学学报, 1998(1): 64–70, 38. QI Qingwen. Research on the Method of Intelligent Map Generalization in GIS Environment[J]. Geo-Informatics, 1998(1): 64–70, 38. |
| [5] | 齐清文, 刘岳. 非连续分布面状地理现象的图形自动概括方法[J]. 地理研究, 1996, 15(1): 1–10. QI Qingwen, LIU Yue. An Automated Solution to the Graphic Generalization of Discontinuous Area Phenomena[J]. Geographical Research, 1996, 15(1): 1–10. |
| [6] | 王家耀, 李志林, 武芳. 数字地图综合进展[M]. 北京: 科学出版社, 2011. WANG Jiayao, LI Zhilin, WU Fang. Advances in Digital Map Generalization[M]. Beijing: Science Press, 2011. |
| [7] | 王家耀. 地图制图学与地理信息工程学科发展趋势[J]. 测绘学报, 2010, 39(2): 115–119. WANG Jiayao. Development Trends of Cartography and Geographic Information Engineering[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 115–119. |
| [8] | 钱海忠, 武芳, 王家耀. 自动制图综合链理论与技术模型[J]. 测绘学报, 2006, 35(4): 400–407. QIAN Haizhong, WU Fang, WANG Jiayao. Theory and Technique Model of Automated Cartographic Generalization Chain[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 400–407. |
| [9] | 毋河海. 地图综合基础理论与技术方法研究[M]. 北京: 测绘出版社, 2004. WU Hehai. Basic Theory and Technical Method for Map Generalization[M]. Beijing: Surveying and Mapping Press, 2004. |
| [10] | MÜLLER J C, LAGRANGE J P, WEIBEL R. GIS and Generalization Methodology and Practice[M]. CRC Press, 1995. |
| [11] | LI Zhilin, SU Bo. From Phenomena to Essence:Envisioning the Nature of Digital Map Generalisation[J]. The Cartographic Journal, 1995, 32(1): 45–47. DOI:10.1179/caj.1995.32.1.45 |
| [12] | DUNCAN M. Applied Geometry for Computer Graphics and CAD[M]. London: Springer, 2005. |
| [13] | KAINZ W, EGENHOFER M J, GREASLEY I. Modelling Spatial Relations and Operations with Partially Ordered Sets[J]. International Journal of Geographical Information Systems, 1993, 7(3): 215–229. DOI:10.1080/02693799308901953 |
| [14] | EGENHOFER M J, FRANZOSA R D. Point-set Topological Spatial Relations[J]. International Journal of Geographical Information Systems, 1991, 5(2): 161–174. DOI:10.1080/02693799108927841 |
| [15] | CHEN Jun, LI Chengming, LI Zhilin, et al. A Voronoi-Based 9-Intersection Model for Spatial Relations[J]. International Journal of Geographical Information Science, 2001, 15(3): 201–220. DOI:10.1080/13658810151072831 |
| [16] | CHEN J. A Raster-based Method for Computing Voronoi Diagrams of Spatial Objects Using Dynamic Distance Transformation[J]. International Journal of Geographical Information Science, 1999, 13(3): 209–225. DOI:10.1080/136588199241328 |
| [17] | 李成名. 空间关系描述的Voronoi原理与方法[M]. 西安: 西安地图出版社, 2000. LI Chengming. Voronoi Principle and Method of Spatial Relation Description[M]. Xi'an: Xi'an Cartographic Publishing House, 2000. |
| [18] | 何海威, 钱海忠, 刘海龙, 等. 道路网层次骨架控制的道路选取方法[J]. 测绘学报, 2015, 44(4): 453–461, 470. HE Haiwei, QIAN Haizhong, LIU Hailong, et al. Road Network Selection Based on Road Hierarchical Structure Control[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 453–461, 470. DOI:10.11947/j.AGCS.2015.20130787 |
| [19] | 刘远刚, 郭庆胜, 孙雅庚, 等. 地图目标群间骨架线提取的算法研究[J]. 武汉大学学报(信息科学版), 2015, 40(2): 264–268. LIU Yuangang, GUO Qingsheng, SUN Yageng, et al. An Algorithm for Skeleton Extraction between Map Objects[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 264–268. |
| [20] | 乔庆华, 吴凡. 河流中轴线提取方法研究[J]. 测绘通报, 2004(5): 14–17. QIAO Qinghua, WU Fan. Research on Methods for Medial Axis Extraction[J]. Bulletin of Surveying and Mapping, 2004(5): 14–17. DOI:10.3969/j.issn.0494-0911.2004.05.006 |
| [21] | BERTIN J. Graphics and Graphic Information Processing[M]. Berlin: Walter de Gruyter, 1981. |
| [22] | GALANDA M. Automated Polygon Generalization in A Multi-Agent System[D]. Zurich:Zurich University, 2003. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.436.1859&rep=rep1&type=pdf |
| [23] | 武芳, 侯璇, 钱海忠, 等. 自动制图综合中的线目标位移模型[J]. 测绘学报, 2005, 34(3): 262–268. WU Fang, HOU Xuan, QIAN Haizhong, et al. A Model for Road Network Displacement in Automated Map Generalization[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(3): 262–268. |
| [24] | RUAS A. A Method for Building Displacement in Automated Map Generalisation[J]. International Journal of Geographical Information Science, 1998, 12(8): 789–803. DOI:10.1080/136588198241509 |
| [25] | 李霖, 于忠海, 朱海红, 等. 地图要素图形冲突处理方法——以线状要素(道路、水系和境界)为例[J]. 测绘学报, 2015, 44(5): 563–569. LI Lin, YU Zhonghai, ZHU Haihong, et al. Handling Graphic Conflicts between Cartographic Features:Exemplifying Geo-Linear Features (Road, River and Boundary)[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(5): 563–569. DOI:10.11947/j.AGCS.2015.20140129 |
| [26] | 刘纪平. 地图数据库图形输出中要素关系处理[J]. 测绘学报, 1994, 23(3): 222–228. LIU Jiping. Handling of Features' Relationships in the Process of the Graphic Output of Cartographic Data Base[J]. Acta Geodaetica et Cartographica Sinica, 1994, 23(3): 222–228. |
| [27] | 吴小芳, 杜清运, 胡月明, 等. 基于改进Snake模型的道路网空间冲突处理[J]. 测绘学报, 2008, 37(2): 223–229. WU Xiaofang, DU Qingyun, HU Yueming, et al. Disposal of Spatial Conflict Between the Roads Networks Based on Improved Snake Model[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 223–229. |
| [28] | 曹原. 地图制图中符号冲突的自动识别与处理技术[D]. 武汉: 武汉大学, 2010. CAO Yuan. Technology on Automatic Recognition and Resolution of Spatial Conflict in Cartography[D]. Wuhan:Wuhan University, 2010. http://www.oalib.com/paper/4158456 |
| [29] | 杨勇, 李霖, 王红, 等. 地图制图软件中境界跳绘技术研究[J]. 测绘科学, 2007, 32(2): 49–50, 56. YANG Yong, LI Lin, WANG Hong, et al. Research on Boundary Jump-Drawing in Mapping Software[J]. Science of Surveying and Mapping, 2007, 32(2): 49–50, 56. DOI:10.3771/j.issn.1009-2307.2007.02.017 |
| [30] | CHIRIÉ F. Automated Name Placement with High Cartographic Quality:City Street Maps[J]. Cartography and Geographic Information Science, 2000, 27(2): 101–110. DOI:10.1559/152304000783547902 |
| [31] | 李霖, 周玉杰, 于忠海. 面状居民地名称注记自动配置研究[J]. 武汉大学学报(信息科学版), 2016, 41(2): 214–220. LI Lin, ZHOU Yujie, YU Zhonghai. Automated Name Placement for Area Resident Annotations[J]. Geomatics and Information Science of Wuhan University, 2016, 41(2): 214–220. |
| [32] | CHRISTENSEN J, MARKS J, SHIEBER S. An Empirical Study of Algorithms for Point-feature Label Placement[J]. ACM Transactions on Graphics, 1995, 14(3): 203–232. DOI:10.1145/212332.212334 |
| [33] | 樊红, 杜道生, 张祖勋. 地图注记自动配置规则及其实现策略[J]. 武汉测绘科技大学学报, 1999, 24(2): 154–157. FAN Hong, DU Daosheng, ZHANG Zuxun. The Study on the Principles of Automated Placement of Map Name and Its Implementation Approach[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1999, 24(2): 154–157. |
| [34] | KLAU G W, MUTZEL P. Optimal Labeling of Point Features in Rectangular Labeling Models[J]. Mathematical Programming, 2003, 94(2-3): 435–458. DOI:10.1007/s10107-002-0327-9 |
| [35] | 张晓楠, 江南, 张亚军, 等. 一种利用空间布局构建统计制图符号的方法[J]. 武汉大学学报(信息科学版), 2015, 40(12): 1653–1660, 1689. ZHANG Xiaonan, JIANG Nan, ZHANG Yajun, et al. A Building Method of Statistical Cartographic Symbols by Using the Space Layout[J]. Geomatics and Information Science of Wuhan University, 2015, 40(12): 1653–1660, 1689. |
| [36] | 何建华, 刘耀林. GIS中拓扑和方向关系推理模型[J]. 测绘学报, 2004, 33(2): 156–162. HE Jianhua, LIU Yaolin. An Integrated Model for Topology & Direction Relation Reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 156–162. |


