高分辨率卫星遥感是对地观测技术国际竞争的关键领域之一,具有巨大的军事价值和经济效益,其发展和应用在美国、俄罗斯、法国和日本等发达国家得到了高度重视。我国也将高分辨率对地观测系统列为《国家中长期科学和技术发展规划纲要(2006—2020年)》的重大专项之一。卫星姿态作为传感器严格成像模型中的外方位参数,在高分辨率卫星的几何模型构建、数字产品生成和应用等方面起着决定性的作用[1]。另外,由于卫星平台数百千米的飞行高度,姿态角度误差对几何定位精度的影响相比定轨误差更为明显[2]。因此,卫星平台的姿态精确确定和稳定性,是决定高分辨率卫星成像质量和几何定位精度的重要因素之一。
卫星平台颤振是指卫星在轨运行期间,受到外部和内部因素的影响而产生姿态的不稳定和周期性微小振动现象[3-6]。平台颤振直接影响卫星的姿态稳定性,导致与时间相关的相对姿态误差,如果不进行有效的颤振处理和分析,会引起平面上的变形、高程上的失真以及辐射上的模糊,影响影像拼接、几何定位和DSM生成等过程,从而减弱高分辨率卫星的可用性[7-10]。卫星在轨运行时,造成平台颤振的成因很复杂,包括了外部空间环境和内部机械运作两部分,例如引力和温度等空间外部环境扰动、卫星姿态控制机构、太阳帆板和天线等卫星载荷工作产生的振动等因素[11]。颤振是高分辨率卫星在轨运行过程中普遍存在的复杂现象,QuickBird、ALOS、Pleiades以及天绘一号、资源三号等不少国内外卫星都受到了颤振的影响,表 1列出了文献提及的受颤振影响的国内外部分卫星。随着成像传感器分辨率的提高以及卫星平台复杂性和敏捷性的增加,平台颤振对高分卫星影像成像质量、几何处理等方面的影响愈发显著。
| 卫星/传感器 | 国家 | 发射年份 | 主要文献 |
| MOC-NA | 美国 | 1996 | Kirk et al, 2003[12] |
| ASTER | 日本 | 1999 | Teshima and Iwasaki, 2008[4] |
| QuickBird-2 | 美国 | 2001 | Robertson, 2003[13] |
| SPOT-5 (early stage) | 法国 | 2002 | Bouillon et al, 2006[14] |
| ALSat-1 | 阿尔及利亚 | 2002 | Mumtaz and Palmer, 2013[15] |
| Nigeria Sat | 尼日利亚 | 2003 | Mumtaz and Palmer, 2013[15] |
| UK-DMC | 英国 | 2003 | Mumtaz and Palmer, 2013[15] |
| MEX-HRSC | 德国 | 2003 | Gwinner et al, 2010[16] |
| HiRISE | 美国 | 2005 | Mattson et al, 2009[17] |
| Beijing-1 | 中国 | 2005 | Ran et al, 2008[18] |
| ALOS/PRISM | 日本 | 2006 | Takaku and Tadono, 2010[19] |
| LROC | 美国 | 2009 | Mattson et al, 2010[5] |
| Mapping satellite-1 | 中国 | 2010 | Sun et al, 2015[9] |
| Pleiades-HR | 法国 | 2011 | Amberg et al, 2013[20] |
| ZY-3 | 中国 | 2012 | Tong et al, 2014[6] |
| Yaogan-26 | 中国 | 2014 | Wang et al, 2017[21] |
平台颤振是国内外遥感卫星处理共同面临的挑战,很多学者研究在轨卫星颤振探测方法。目前,卫星平台颤振处理主要有3类方法。第1类方法基于高性能姿态传感器,通过直接分析姿态观测数据来探测平台颤振的影响。文献[19]针对ALOS PRISM影像在生成的DEM中探测到周期性的地形起伏误差;而利用更高频率的精确卫星姿态测量数据,对ALOS PRISM影像进行了颤振几何改正后,DEM中不再包含周期性的误差。文献[21]用高采样频域的角位移传感器融合星敏传感器的姿态观测数据对Yaogan-26卫星的颤振进行了探测和补偿。但高性能姿态传感器要求同时具有高测量精度和高采样频率,将增加卫星的生产成本,而且对于已在轨运行的卫星,安装高性能姿态测量传感器在技术上难以实现。第2类方法利用密集地面控制,采用光束法平差等方法补偿卫星姿态的周期性颤振误差。基于火星轨道器激光高度计MOLA数据生成的DEM作为地面控制数据,文献[16]提出了连续摄影测量平差方法采用HRSC影像来探测和改正火星快车的平台颤振,颤振改正后生成的DEM中不再包含周期性的条纹误差。但该方法的使用依赖于外部地面控制数据的精度,实际应用中成本高效率低,不具推广性。第3类方法使用卫星影像或产品数据进行颤振探测,文献[4, 5, 9, 15, 17, 20, 22]分别采用ASTER短波红外传感器的不同波段、LRO的窄角相机NACs的重叠区域、天绘一号卫星的高分辨率全色传感器相邻CCD间的重叠区域、UK-DMC相机线阵间的重叠影像、HiRISE传感器相邻阵列的重叠区域、PLEIADES-HR和资源三号卫星不同波段的多光谱影像对卫星颤振进行了探测。基于卫星成像传感器数据的方法,会受制于成像传感器的成像质量和拍摄性能的制约,并且会受到地面纹理和地形信息以及相应影像处理技术的影响,需要对相关的误差进行去除,对获得的颤振信息进行转换。
综上所述,现有研究主要基于某种单一传感器观测数据处理和分析卫星平台颤振,各类方法有着自身的限制因素,而且单一的颤振探测方法存在可靠性和稳健性等问题,探测结果的准确性难以得到有效的验证。因此,在前期研究的基础上[6, 22-27],本文提出综合多传感器数据处理的卫星颤振探测与补偿技术方法,并以中国资源三号卫星为例,对卫星平台颤振进行了处理与分析。
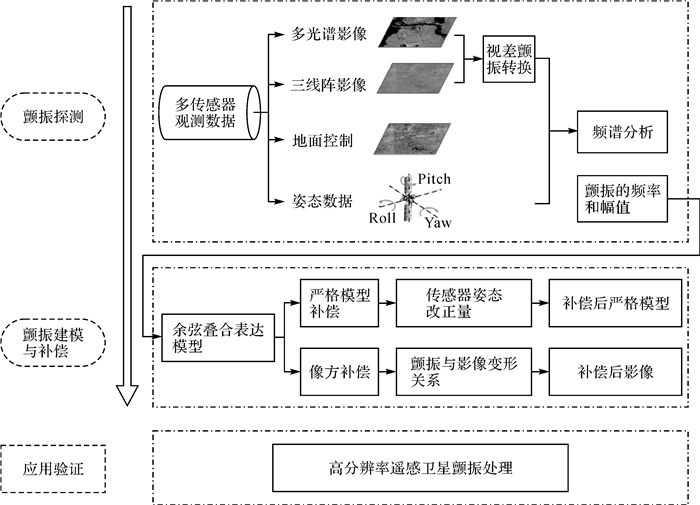
1 综合多传感器数据处理的卫星颤振探测与补偿技术方法 1.1 总体框架综合多传感器观测数据处理的卫星平台颤振探测与补偿方法利用多光谱影像、三线阵全色影像、星上姿态观测数据和密集地面控制来实现颤振的精密探测估计,根据获取的颤振频率和幅值等特性,通过姿态补偿和像方补偿两种方式修正平台颤振的影响。具体的技术路线如图 1所示。
|
| 图 1 卫星平台颤振探测与补偿技术路线 Fig. 1 Workflow of jitter detection and compensation |
1.2 颤振探测
根据采用不同的数据类型,平台颤振探测部分包括4个方面:
1.2.1 基于多光谱影像的颤振探测对于不同波段的多光谱影像,采用影像视差法颤振探测技术,根据成像时间相隔较短的平行线阵CCD间的视差估计随时间变化的颤振引起的像移[22]。在没有颤振影响的情况下,线阵影像间的视差几乎为常量,而当存在平台颤振时,颤振会在影像上产生像方偏移,由于对同一地物在不同时刻成像,所以会导致线阵影像间存在周期性的颤振视差,而颤振视差表示的是两个成像时刻的颤振像移的差值
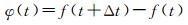 (1)
(1)
式中, f表示卫星颤振像移;
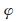
实现高精度的密集匹配是视差法颤振探测的基础。在对待匹配的多光谱影像进行辐射校正、影像增强和初始配准等预处理的基础上,本文采用随机抽样一致性改进的奇异值分解亚像素相位相关匹配算法来精确获取影像间的颤振视差[23]。根据傅里叶变换的平移特性,匹配算法在频域进行相关,利用稳健估计减弱噪声和粗差的影响,波段间匹配精度达到0.05个像元。在获取影像间的视差图后,平均每一行的有效颤振视差得到各成像时刻的颤振视差,通过单频率分量的空域转换方式或多频率分量的频域转换方式实现视差到颤振的转换,频域转换公式[11]为
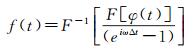 (2)
(2)
式中,i为虚数单位;ω=2πk/N(k为频域下对应t的变量,N为参与傅里叶变换的数据量);F和F-1分别为傅里叶变换和逆傅里叶变换。最终采用基于快速傅里叶变换的频谱分析计算出颤振的频率和幅值等特性。
1.2.2 基于三线阵影像的颤振探测由于三线阵传感器CCD线阵之间的间距时间较大,无法直接采用上述视差法颤振探测技术,本文通过三线阵立体影像间的后向投影偏差来探测估计颤振[24]。为了在受颤振影响下获取三线阵立体影像间的准确密集同名点,采用综合的多视影像匹配方法,集成SIFT特征匹配方法[28]、相对定向方法,几何约束互相关算法[29],相关系数匹配算法和最小二乘匹配算法[30]。根据建立的成像模型,结合相对定向参数,利用三线阵影像上匹配的同名点,通过前方交会计算地面点坐标,确定平均高程面,将前、后视影像上的同名点分别投影至高程面上,计算相应的物方投影点坐标,并将物方投影点后向投影至下视影像的像方空间上,分别计算下视与前后视影像间的后向投影偏差。后向投影偏差由姿态轨道测量误差和内方外元素确定误差等引起的系统性偏差和由姿态颤振引起的周期性偏差两部分组成,采用基于仿射模型的相对定向方法消除系统性误差后用来估计颤振量。
根据傅里叶变换原理,利用余弦叠合表达式对与时间相关的周期性颤振像移f(t)进行建模[31]
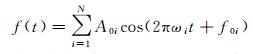 (3)
(3)
式中,N表示颤振分量;ωi、A0i和f0i分别为各分量的频率、幅值及初始相位。相对定向后的后向投影偏差g(t1, t2)可以表示为
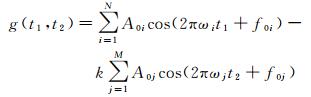 (4)
(4)
式中,t1、t2为两幅影像同名点的成像时间;k为两幅影像的分辨率比。根据获取后向投影偏差,采用遗传算法最优化求解颤振的频率、幅值及初始相位参数。沿轨方向上地形起伏同样会产生视差,立体像对间的后向投影偏差中混叠了地形视差和颤振视差,导致无法解算出平台颤振量,本文采用三视影像提供的冗余信息来计算后向投影偏差,抵消地形视差区分颤振视差[25]。
1.2.3 基于密集地面控制的颤振探测密集地面控制点的获取依赖于外部的参考数据,本文采用影像匹配技术,将卫星影像与地面高精度参考数据(DEM、DOM产品)进行同名点匹配,生成高精度密集地面控制点,据此计算像方残差来估计颤振[26]。
将高斯滤波后的DOM降采样到与卫星影像相同分辨率,采用Förstner特征提取算子[32]提取特征点,并投影到像方空间作为初始值,利用最小二乘匹配获取下视影像上的同名点作为地面控制点,DOM提供平面坐标,DEM提供高程坐标,并采用上述综合的多视影像匹配方法得到地面控制点在三线阵影像上的坐标。根据地面控制点的影像坐标与地面坐标反投影的像点坐标差计算姿态颤振引起的像方偏差,采用频谱分析估计颤振的频率和幅值等特性。
1.2.4 基于姿态数据的颤振探测对于卫星平台颤振的频率低于姿态数据采样频率的一半且颤振幅值高于姿态传感器精度的情况,姿态数据也可以反映出平台颤振现象。采用星上星敏感器和陀螺等姿态传感器的测量数据通过基于卡尔曼滤波的联合定姿方式计算出精确的姿态数据,根据卫星的轨道测量数据将姿态数据转换到轨道坐标系。利用多项式拟合消除轨道系下姿态数据中的线性误差,采用频谱分析估计颤振的频率和幅值等特性。
1.3 颤振补偿根据各种颤振探测方法获取的颤振特性,将周期性颤振表示为式(3) 所示的余弦叠合表达式。对平台颤振影响的补偿,通过像方补偿和姿态补偿两个方面进行。
像方补偿方面,根据建模得到的颤振像移模型,对影像进行重采样,消除影像内颤振引起的影像偏移。为了保持重采样后影像的细节,采用二维三次卷积插值算法来重采样受颤振影响的影像。三次卷积插值采用周围16个点来计算重采样结果,实质上是利用一个三次多项式来近似理论上最佳插值sinc函数。其三次多项式表示为
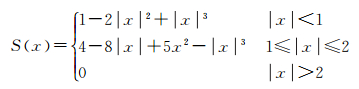 (5)
(5)
姿态补偿即成像模型补偿方面,结合传统的多项式姿态拟合模型和颤振模型对姿态数据建模
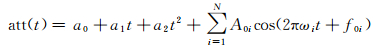 (6)
(6)
式中,(a0, a1, a2)为二次多项式姿态拟合参数;(ωi, A0i, f0i)为估计的卫星颤振参数。将式(6) 的姿态模型带入卫星严格成像模型[33]进行立体定位,提高颤振情况下成像模型的定位精度。
2 试验与分析本文采用资源三号卫星的数据来验证综合多传感器数据处理的卫星颤振探测与补偿技术,并全面分析资源三号卫星平台颤振的规律。试验部分包括4个方面:① 资源三号卫星平台颤振多时序规律分析;② 长序列多光谱影像颤振探测处理;③ 颤振探测方法对比;④ 平台颤振影响严重影像的颤振补偿效果分析。
2.1 资源三号卫星2012年1月9日发射的资源三号卫星是我国第一颗民用三线阵立体测图卫星,其搭载了搭载了3台下视分辨率为2.1 m,前后视为3.5 m的三线阵TDI CCD相机和一台分辨率为5.8 m的4波段多光谱相机。姿态测量系统采用多组陀螺和3台高精度星敏感器,采用星敏感器和陀螺组合测量的方式精确测定卫星平台在J2000惯性坐标系下的姿态,采样频率为4 Hz,事后姿态处理精度优于1″(1σ)[33]。
本文的试验数据包括资源三号卫星的多光谱影像、三线阵影像和姿态数据,以及河南嵩山检校场地区的地面参考数据(DEM和DOM产品)。
2.2 多时序颤振规律分析为了更好地反映资源三号卫星的颤振变化规律,从发射初期的2012年2月开始到2013年10月期间的19个月,共选取了60轨324景多光谱影像数据(每个月至少2轨5景数据)来探测卫星平台颤振,从而分析颤振特性的长时间变化规律。
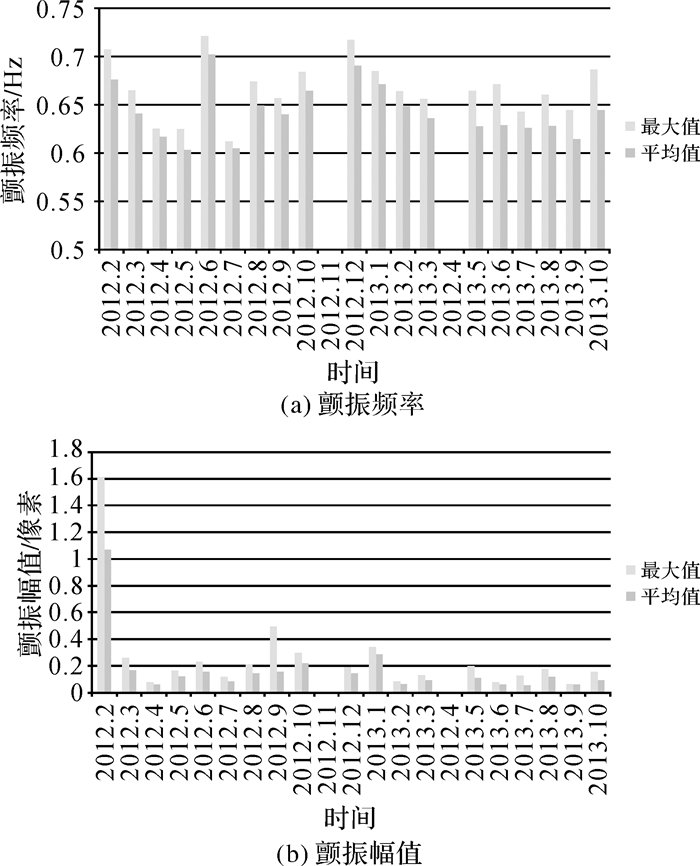
资源三号卫星颤振的频率与幅值特性从在轨早期开始近两年内随时间的变化如图 2所示。从结果可以看出,资源三号卫星存在颤振现象,颤振频率保持在0.6~0.7 Hz的范围,而颤振幅值从发射初期的平均1个像素以上下降到后期的0.4个像素以下,卫星趋于稳定。
|
| 图 2 颤振频率与幅值随时间变化规律 Fig. 2 Variation laws of frequency and amplitude of jitter with respect to data |
2.3 长序列多光谱影像颤振探测
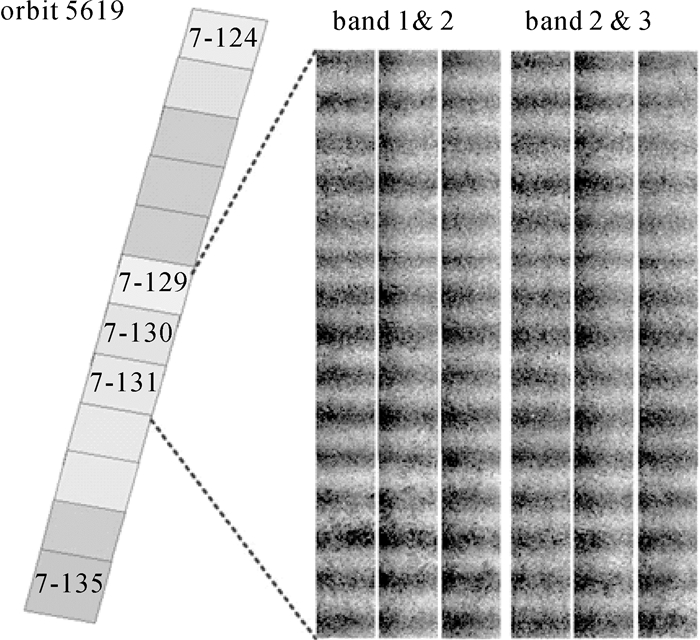
选取一组成像于2013年1月12日,包含12幅标准景的长序列多光谱影像,采用影像视差法进行颤振探测。分别采用了第1、2波段以及第2、3波段的组合分成3片CCD进行计算,其中3幅影像的视差图结果如图 3所示。可以看出不同波段的视差图中出现了由颤振引起的周期性明暗相间的条纹,而且不同波段组合与不同CCD计算的结果相似。
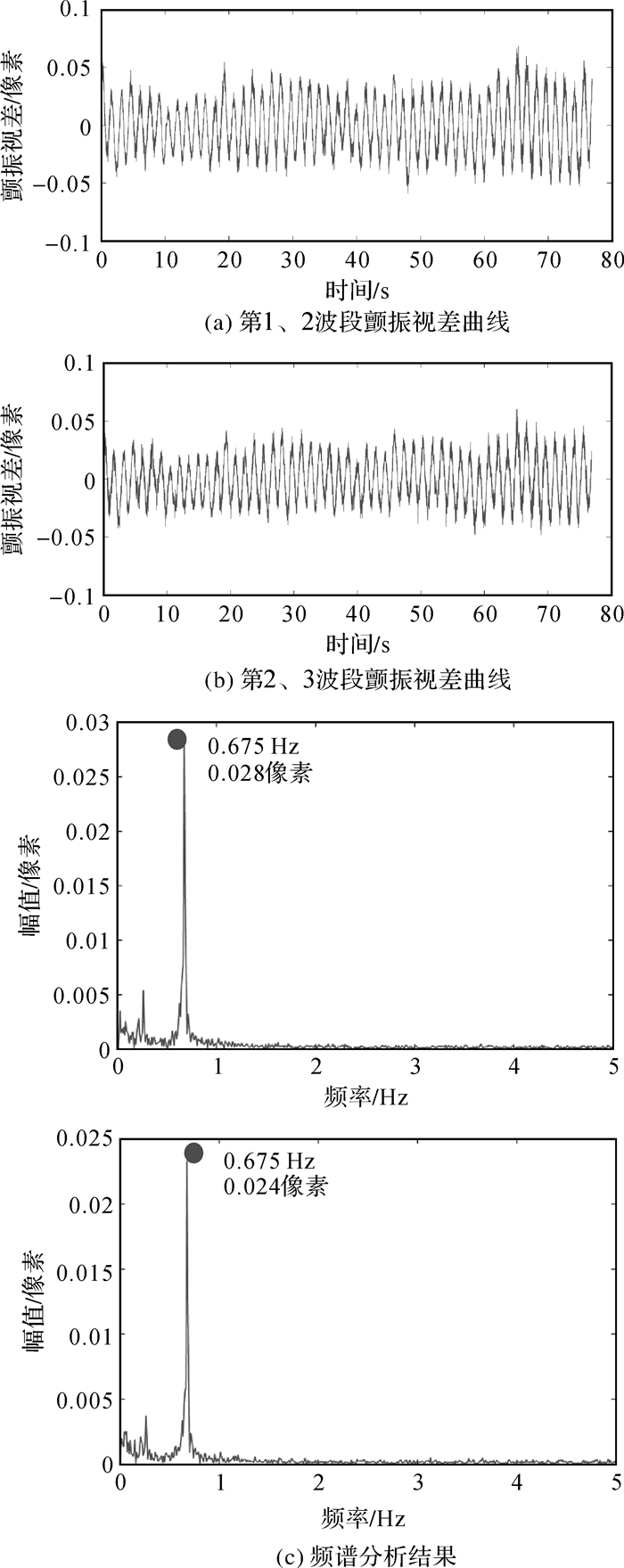
视差图行平均后的结果曲线如图 4(a)和图 4(b)所示。对颤振视差结果进行频谱分析,频谱图如图 4(c)所示,频谱图中出现了明显的峰值,计算颤振的频率为0.675 Hz,根据视差颤振转换,颤振的幅值约为0.055像素,利用第1、2波段以及第2、3波段两种组合计算的结果一致。
|
| 图 4 颤振视差曲线与频谱分析结果 Fig. 4 Jitter disparities and spectral analysis |
2.4 颤振探测方法对比
为了更好地验证综合多传感器观测数据处理的卫星平台颤振探测方法的有效性,采用卫星发射初期2012年2月成像的一组数据以及地面参考数据来对比不同输入数据的4种颤振探测方法的结果。为方便颤振幅值的对比,根据传感器的焦距以及像元大小,将探测的颤振像移转换为姿态角变化量,4种方法计算出的颤振频率与幅值如表 2所示。从结果可以看出,对于颤振现象严重的数据,4种方法都能有效地探测出颤振,而且反演的颤振频率与幅值基本一致,相互验证保证了综合多传感器观测数据的卫星平台颤振探测方法的可靠性,从而为后续的颤振补偿提供了依据。
| 方法 | 分辨率 | 频率/Hz | 幅值/角秒 |
| 基于多光谱影像 | 5.8 m | 0.660 | 2.272 |
| 基于三线阵影像 | 2.1 m | 0.649 | 2.242 |
| 基于密集控制 | 2.1 m | 0.647 | 2.257 |
| 基于姿态数据 | 4 Hz | 0.653 | 2.223 |
2.5 颤振补偿结果分析
对于资源三号卫星,发射初期的平台颤振幅值高达2~3角秒,严重影响了卫星影像的测图精度与应用能力,本文基于构建的颤振模型采用像方补偿与姿态补偿两种形式来减弱平台颤振对卫星成像和几何定位精度的影响。试验数据为上述发射初期覆盖地面参考数据的资源三号影像。
图 5展现了像方补偿的效果,图 5(b)和5(c)分别为颤振补偿前和补偿后的影像视差图。补偿前平台颤振引起的周期性条纹明显,补偿后周期性条纹基本消除,说明了颤振探测的正确以及颤振像方补偿的有效性。

|
| 图 5 颤振像方补偿效果 Fig. 5 Result of jitter compensation on image |
为了检验姿态补偿后几何定位精度提高的效果,根据地面参考数据,在两景影像上均匀选取了40多个地面控制点作为检核点。构建考虑卫星颤振的严格成像模型进行直接立体定位,与补偿前传统基于多项式姿态模型的严格成像模型进行对比。表 3所示为两景影像颤振补偿前后的立体定位精度统计。可以看出补偿后的立体定位精度在平面和高程方向上均有30%的提高。
| m | ||||||
| 影像 | 定位精度 | 补偿前 | 补偿后 | |||
| 最大值 | 均方差 | 最大值 | 均方差 | |||
| 影像1 | 平面 | 6.946 | 4.038 | 5.304 | 2.381 | |
| 高程 | 8.009 | 4.033 | 7.853 | 2.627 | ||
| 影像2 | 平面 | 11.848 | 6.323 | 10.386 | 4.204 | |
| 高程 | 8.528 | 3.997 | 5.021 | 1.990 | ||
3 结论
卫星平台颤振是提升高分卫星高精度对地观测和测图能力的关键问题之一。本文提出了综合多传感器数据处理的卫星颤振探测补偿技术方法,可实现高分卫星的颤振处理与分析。针对中国资源三号卫星,采用影像数据、姿态数据和地面控制数据等多种数据进行了颤振探测补偿,并进行了检核。进一步分析了资源三号卫星多时序的颤振变化规律,发现颤振频率一直保持在0.6~0.7 Hz左右的范围内,而颤振幅值从在轨早期的1个像素下降到趋于平稳。卫星颤振的探测补偿处理分析方法,为测绘卫星数据用于1:5万高精度测图(颤振幅值应小于0.4像元)提供了可信度评价,并通过颤振补偿保障了测图精度。同时,卫星颤振的探测补偿处理分析方法将为在轨卫星姿态控制以及后续卫星平台稳定性设计提供依据。
致谢: 感谢国家测绘地理信息局卫星测绘应用中心、中国天绘卫星中心的项目合作和数据支持。参加本项目的还有谢欢、陈鹏、金雁敏、徐聿升、李凌云、洪中华、王凤香、李天鹏等团队成员10多人,在此一并感谢。
| [1] | TOUTIN T. State-of-the-Art of Geometric Correction of Remote Sensing Data:A Data Fusion Perspective[J]. International Journal of Image and Data Fusion, 2011, 2(1): 3–35. DOI:10.1080/19479832.2010.539188 |
| [2] | 刘斌. 高分辨光学卫星空地一体化定姿及姿态抖动下影像几何处理方法研究[D]. 武汉: 武汉大学, 2011. LIU Bin. Space-ground Intergated Attitude Determination of High-resolution Satellite and Geometric Image Processing Under Jitter Conditions[D]. Wuhan:Wuhan University, 2011. http://www.oalib.com/references/15823143 |
| [3] | KIRK R L, HOWINGTON-KRAUS E, ROSIEK M R, et al. Ultrahigh Resolution Topographic Mapping of Mars with MRO HiRISE Stereo Images:Meter-scale Slopes of Candidate Phoenix Landing Sites[J]. Journal of Geophysical Research:Planets, 2008, 113(E12): E00A24. |
| [4] | TESHIMA Y, IWASAKI A. Correction of Attitude Fluctuation of Terra Spacecraft Using ASTER/SWIR Imagery with Parallax Observation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 222–227. DOI:10.1109/TGRS.2007.907424 |
| [5] | MATTSON S, ROBINSON M, MCEWEN A, et al. Early Assessment of Spacecraft Jitter in LROC-NAC[C]//Proceedings of the 41st Lunar and Planetary Institute Science Conference. The Woodlands, TX:Lunar and Planetary Institute, 2010:1871. |
| [6] | TONG Xiaohua, YE Zhen, XU Yusheng, et al. Framework of Jitter Detection and Compensation for High Resolution Satellites[J]. Remote Sensing, 2014, 6(5): 3944–3964. DOI:10.3390/rs6053944 |
| [7] | MATTSON S, BARTELS A, BOYD A, et al. Continuing Analysis of Spacecraft Jitter in LROC-NAC[C]//Proceedings of the 42nd Lunar and Planetary Institute Science Conference. The Woodlands, TX:Lunar and Planetary Institute, 2011:2756. |
| [8] | 孙阳. 卫星平台在轨颤振对高分辨率遥感器成像质量影响的研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2013. SUN Yang. On-orbit Platform Jitter Effect on Image Quality of High-resolution Remote Sensor[D]. Changchun:Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2013. http://www.irgrid.ac.cn/handle/1471x/681437?mode=full&submit_simple=Show+full+item+record |
| [9] | SUN Tao, LONG Hui, LIU Baocheng, et al. Application of Attitude Jitter Detection Based on Short-time Asynchronous Images and Compensation Methods for Chinese Mapping Satellite-1[J]. Optics Express, 2015, 23(2): 1395–1410. DOI:10.1364/OE.23.001395 |
| [10] | WANG Mi, ZHU Ying, JIN Shuying, et al. Correction of ZY-3 Image Distortion Caused by Satellite Jitter via Virtual Steady Reimaging Using Attitude Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 119: 108–123. DOI:10.1016/j.isprsjprs.2016.05.012 |
| [11] | IWASAKI A. Detection and Estimation of Satellite Attitude Jitter Using Remote Sensing Imagery[M]. //HALL J. Advances in Spacecraft Technologies. Rijeka, Croatia: InTech, 2011: 257-272. |
| [12] | KIRK R L, HOWINGTON-KRAUS E, REDDING B, et al. High-Resolution Topomapping of Candidate MER Landing Sites With Mars Orbiter Camera Narrow-angle Images[J]. Journal of Geophysical Research:Planets, 2003, 108(E12): 8088. |
| [13] | ROBERTSON B C. Rigorous Geometric Modeling and Correction of QuickBird Imagery[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium. Toulouse:IEEE, 2003(2):797-802. https://es.scribd.com/doc/88199361/Words |
| [14] | BOUILLON A, BERNARD M, GIGORD P, et al. SPOT 5 HRS Geometric Performances:Using Block Adjustment as a Key Issue to Improve Quality of DEM Generation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(3): 134–146. DOI:10.1016/j.isprsjprs.2006.03.002 |
| [15] | MUMTAZ R, PALMER P. Attitude Determination by Exploiting Geometric Distortions in Stereo Images of DMC Camera[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(3): 1601–1625. DOI:10.1109/TAES.2013.6558007 |
| [16] | GWINNER K, SCHOLTEN F, PREUSKER F, et al. Topography of Mars from Global Mapping by HRSC High-resolution Digital Terrain Models and Orthoimages:Characteristics and Performance[J]. Earth and Planetary Science Letters, 2010, 294(3-4): 506–519. DOI:10.1016/j.epsl.2009.11.007 |
| [17] | MATTSON S, BOYD A, KIRK R L, et al. HiJACK:Correcting Spacecraft Jitter in HiRISE Images of Mars[C]//Proceedings of European Planetary Science Congress. Potsdam:[s.n.], 2009(4):1-2. http://www.mdpi.com/1424-8220/17/1/83/xml |
| [18] | RAN Qiong, CHI Yaobin, WANG Zhiyong. Property and Removal of Jitter in Beijing-1 Small Satellite Panchromatic Images[C]//International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume ⅩⅩⅩⅦ. Beijing:ISPRS, 2008:929-933. |
| [19] | TAKAKU J, TADONO T. High Resolution DSM Generation from Alos Prism-processing Status and Influence of Attitude Fluctuation[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium. Honolulu:IEEE, 2010:4228-4231. |
| [20] | AMBERG V, DECHOZ C, BERNARD L, et al. In-flight Attitude Perturbances Estimation:Application to PLEIADES-HR Satellites[C]//Proceedings of Volume 8866, Earth Observing Systems ⅩⅧ, San Diego, California, United States:SPIE, 2013(8866):886612. |
| [21] | WANG Mi, FAN Chengcheng, PAN Jun, et al. Image Jitter Detection and Compensation Using a High-frequency Angular Displacement Method for Yaogan-26 Remote Sensing Satellite[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017(130): 32–43. |
| [22] | TONG Xiaohua, XU Yusheng, YE Zhen, et al. Attitude Oscillation Detection of the ZY-3 Satellite by Using Multispectral Parallax Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(6): 3522–3534. DOI:10.1109/TGRS.2014.2379435 |
| [23] | TONG Xiaohua, YE Zhen, XU Yusheng, et al. A Novel Subpixel Phase Correlation Method Using Singular Value Decomposition and Unified Random Sample Consensus[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(8): 4143–4156. DOI:10.1109/TGRS.2015.2391999 |
| [24] | TONG Xiaohua, LI Lingyun, LIU Shijie, et al. Detection and Estimation of ZY-3 Three-line Array Image Distortions Caused by Attitude Oscillation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 101: 291–309. DOI:10.1016/j.isprsjprs.2015.01.003 |
| [25] | TONG Xiaohua, YE Zhen, LI Lingyun, et al. Detection and Estimation of Along-track Attitude Jitter from ZY-3 Three-line-array Images Based on Back-projection Residuals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(8): 4272–4284. DOI:10.1109/TGRS.2017.2690382 |
| [26] | LIU Shijie, TONG Xiaohua, WANG Fengxiang, et al. Attitude Jitter Detection Based on Remotely Sensed Images and Dense Ground Controls:A Case Study for Chinese ZY-3 Satellite[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(12): 5760–5766. DOI:10.1109/JSTARS.2016.2550482 |
| [27] | YE Z, XU Y, WANG F, et al. Estimation of the Attitude Perturbance Using Parallax Imagery-Application to ZY-3 Satellite[C]//ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume Ⅱ-3/W4. Munich:ISPRS, 2015:279-283. |
| [28] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [29] | ZHANG Li, GRUEN A. Multi-Image Matching for DSM Generation from IKONOS Imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(3): 195–211. DOI:10.1016/j.isprsjprs.2006.01.001 |
| [30] | GRUEN A. Adaptive Least Squares Correlation:A Powerful Image Matching Technique[J]. South African Journal of Photogrammetry, Remote Sensing and Cartography, 1985, 14(3): 175–187. |
| [31] | 陈杰, 周荫清, 李春升, 等. 卫星姿态指向抖动与SAR成像质量关系研究[J]. 北京航空航天大学学报, 2001, 27(5): 518–521. CHEN Jie, ZHOU Yinqing, LI Chunsheng, et al. Relationship between Satellite Attitude Jitter and SAR Imaging Quality[J]. Journal of Beijing University of Aeronautics and Astronautics, 2001, 27(5): 518–521. |
| [32] | FÖRSTNER W, GVLCH E. A Fast Operator for Detection and Precise Location of Distinct Points, Corners and Centres of Circular Feature[C]//Proceeding of ISPRS Intercommission Conference on Fast Processing on Photogrammetric Data. Interlaken:ISPRS, 1987:281-305. |
| [33] | 李德仁. 我国第一颗民用三线阵立体测图卫星—资源三号测绘卫星[J]. 测绘学报, 2012, 41(3): 317–322. LI Deren. China's First Civilian Three-Line-Array Stereo Mapping Satellite:ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 317–322. |