2. 香港中文大学太空与地球信息科学研究所, 香港;
3. 香港中文大学深圳研究院, 深圳 518057
2. Institute of Space and Earth Information Science, The Chinese University of Hong Kong, Hong Kong, China;
3. Shenzhen Research Institute, The Chinese University of Hong Kong, Shenzhen 518057, China
目前,随着大量对地观测卫星的发射,能获取到的遥感数据越来越多,而且新发射的卫星传感器均朝着具有高空间、高时间、高光谱分辨率数据获取能力的方向发展,例如中国的高分辨率对地观测系统[1]。然而,在现有卫星传感器的硬件技术条件和卫星发射成本的限制下,卫星传感器空间分辨率的提高只能以牺牲卫星传感器在其他方面的优势来实现,例如时间分辨率、光谱分辨率、扫描幅宽等[2],使得遥感卫星无法获得具有多属性高分辨率的遥感影像,从而制约了遥感影像的应用。
一方面,作为研究地表特征时空特性的关键,卫星传感器的空间分辨率和时间分辨率起着至关重要的作用。然而,由于卫星传感器时间分辨率和空间分辨率之间的矛盾,具有高空间分辨率(简称为高分辨率)遥感影像获取能力的卫星的时间分辨率往往较低,反之,具有高频率重访周期的卫星的通常只具备低空间分辨率(简称为低分辨率)的数据获取能力。因此,这二者之间的矛盾依然存在并且会长期存在[3-5]。另一方面,自从对地观测的遥感卫星发射以来[6-7],已经积累了大量的长时间序列历史观测数据,这些数据由于早期卫星传感器硬件技术以及卫星建造和发射成本的限制,其空间分辨率和时间分辨率之间亦有折中,目前一些典型的光学遥感卫星的时-空分辨率对比以及数据获取方式见表 1。因此,无论是海量历史卫星遥感影像时空信息的进一步挖掘,还是未来新获取影像的充分利用,遥感影像时间-空间分辨率之间的矛盾依然是一个不可忽视、不可避免的现实问题。
| 卫星/传感器 | 波谱类型 | 卫星轨道类型 | 空间分辨率/m | 时间分辨率 | 数据获取方式 |
| QuickBird | 全色/多光谱 | 极轨卫星 | 0.61/2.44 | >30天(不侧摆) | 商业订购 |
| IKONOS | 全色/多光谱 | 极轨卫星 | 1/4 | >30天(不侧摆) | 商业订购 |
| GeoEye-1 | 全色/多光谱 | 极轨卫星 | 0.41/1.65 | >30天(不侧摆) | 商业订购 |
| WorldView-3 | 全色/多光谱 | 极轨卫星 | 0.31/1.24 | >30天(不侧摆) | 商业订购 |
| GF-1 | 全色/多光谱 | 极轨卫星 | 2/8 | 41天(双相机组合,不侧摆) | 商业订购 |
| GF-2 | 全色/多光谱 | 极轨卫星 | 1/4 | 69天(双相机组合,不侧摆) | 商业订购 |
| ZY3-02 | 全色/多光谱 | 极轨卫星 | 2.1/5.8 | 59天(多相机组合,不侧摆) | 商业订购 |
| Landsat 7, 8 | 全色/多光谱 | 极轨卫星 | 15/30 | 16天 | 免费获取 |
| HJ-1/CCD | 多光谱 | 极轨卫星 | 30 | 4天(双相机组合) | 免费获取 |
| Sentinel-2 | 多光谱 | 极轨卫星 | 10/20/60 | 10天 | 免费获取 |
| SPOT 7 | 全色/多光谱 | 极轨卫星 | 1.5/6 | 26天 | 商业订购 |
| MODIS | 多光谱 | 极轨卫星 | 250/500/1000 | 1天 | 免费获取 |
| FY-3/MERSI | 多光谱 | 极轨卫星 | 250/1000 | 1天 | 免费获取 |
| AVHRR | 多光谱 | 极轨卫星 | 1100 | 0.5天 | 免费获取 |
| FY-3/VIRR | 多光谱 | 极轨卫星 | 1100 | 1天 | 免费获取 |
| MTSAT-2 | 多光谱 | 静止卫星 | 1000/4000 | 30分钟 | 免费获取 |
| GOES-15 | 多光谱 | 静止卫星 | 1000/4000 | 30分钟 | 免费获取 |
| FY-2 | 多光谱 | 静止卫星 | 1250/5000 | 30分钟 | 免费获取 |
此外,现阶段的卫星遥感数据面临着“又多又少”的问题[8],即可用的遥感数据越来越多,然而真正能被使用的有用数据却相对很少。例如,由于云层的覆盖,即使Landsat卫星能够在16天内实现对某一地区的重复访问,一年内无云或少云的数据依然较少,一年之内获取到云覆盖率低于10%的遥感影像的概率也只有10%左右[9],这在很大程度上影响了对地表动态变化的监测和研究。
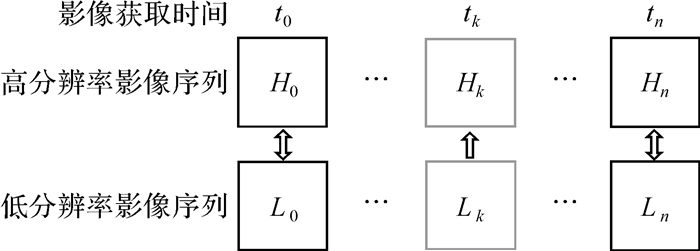
针对时空分辨率矛盾以及其他客观因素的限制,如果从“硬件”的角度出发,需要发射更多、硬件技术要求更高的对地观测卫星来解决这一问题,但是考虑到成本和硬件水平的限制,这一方案往往不切实际。遥感影像时空融合[3, 10-11]作为一种相对较新的影像融合手段,是从“软件”的角度来解决卫星传感器的时-空分辨率矛盾的。遥感影像时空融合是利用已知的“时相密集”的低空间分辨率影像序列和与之部分时间点对应的“时相稀疏”的高空间分辨率影像序列来融合生成与低空间分辨率影像序列时相对应的“时相密集”的高空间分辨率影像序列。时空融合旨在将多源卫星遥感影像的高空间分辨率和高时间分辨率结合起来,通过时空融合算法的处理,生成目标研究区域内具有高频次访问的高空间分辨率遥感影像序列,其算法思想如图 1所示。相对于“硬件”的解决方案,时空融合在无需发射新的对地观测卫星的情况下,是一种低成本、高效率、可行性强的解决技术手段。对于进一步拓展现有遥感影像的应用和研究价值,时空融合依然是一种不可或缺的技术手段[11]。
|
| 图 1 多源遥感影像时空融合示意图 Fig. 1 Spatial-temporal fusion of multi-source satellite imagery |
到目前为止,国内外的学者做了大量关于时空融合算法的研究工作,出现了基于不同算法原理、不同数据类型以及不同应用目的多种时空融合算法。例如,能够预测同质地表季节变化的时空自适应反射率融合模型[10];能够对异质地表的季节性变化得到较好预测结果的自适应时空融合模型[12-13];针对地表反射率突发扰动事件制图的时空自适应算法[14];能够对地表季节和类别变化进行一体化融合的时空融合算法[3-5];能够生成高时空分辨率地表温度数据的时空融合模型[15-17]。这些时空融合算法往往都是基于数据来源、不同的原理或者不同的应用目的而提出的,其发展呈现出一种无序性。面对如此多样化的时空融合算法,本文对其进行了概括总结,分析了现在主要时空融合算法的基础理论假设和算法原理并加以归类,指出了时空融合算法所面临的问题和挑战,并展望了未来时空融合算法的进一步发展所需解决的问题,为相关的数据融合算法以及遥感应用研究提供理论参考和技术支撑。
1 遥感影像时空融合概述及分类总体来说,时空融合都是基于两种理论基础来进行的:① 时相变化模型的空间尺度不变性;② 空间降尺度模型的时间一致性[2]。时相变化模型的空间尺度不变性是指不同空间分辨率的遥感影像序列之间的时相变化模型是相互通用的;空间降尺度模型的时间一致性是指不同时相的高-低分空间分辨率遥感影像之间的空间降尺度模型是相互通用的。
基于这两种理论假设,时空融合算法可以分为:① 基于地物类别组分的时空融合;② 基于地表空间信息的时空融合;③ 基于地物时相变化的时空融合;④ 组合性的时空融合。
1.1 基于地物组分的时空融合基于地物组分的时空融合,其理论基础是不同地物类别的光谱信息在不同空间尺度下的关联模型具有时间一致性。这种类型的时空融合是在对已知时相的高分辨率影像进行分类或者分割的基础上,利用光谱混合理论建立已知时相的高分辨率影像和对应低分辨率影像之间的光谱混合模型;进而将这种光谱混合模型应用到待预测的未知时相的低-高分辨率影像对上,再利用不同地物组分在低分辨率影像上的时相变化信息和对应的光谱混合模型求解出高分辨率的时相变化量,从而预测出未知时相的高分辨率影像。此外基于地物组分的时空融合还需满足两项假设:① 低空间分辨率影像像元内部不同组分所占的比例在观测时段内没有变化;② 同一组分内部的光谱差异可以忽略不计。基于地物组分的时空融合可以表达为
 (1)
(1)
式中,L(xi, yi, tk)是待预测时间点tk的低分辨率像素(xi, yi);N是地物的组分数量;fn是每一种地物组分在低分辨率像素中所占的比例;ρ(n, tk)是组分n的光谱值;ε是线性光谱混合模型的误差项。
由于基于地物组分的时空融合需满足假设①,故而也就限制了其不能应用于地物类别发生变化情况下的时空融合。因为地表的类别变化必然会导致不同组分所占的比例发生变化。同时,由于基于地物组分的时空融合是建立在线性光谱混合模型的基础之上的,因此该类融合亦不适用于地物光谱属于非线性混合的情况。
此外,多数基于地表组分的时空融合都是基于线性的光谱混合模型进行的,该模型中提取出各种地物的端元光谱值是很关键的,即得到纯净像元的像素值。但在实际应用中由于非线性光谱混合现象的大量存在,以及遥感影像空间分辨率和光谱分辨率的限制,各类地物的端元光谱值很难准确地获得,从而会对基于地表组分的时空融合产生不利的影响,增加其预测误差。
1.2 基于地表空间信息的时空融合基于地表空间信息的时空融合,其理论基础是地物的空间细节信息在不同空间尺度下的关联模型具有时间一致性。这种类型的时空融合首先建立已知时相的低-高分辨率影像对之间的空间信息对应关系,并通过线性或者非线性的方式从已知的高分辨率影像中提取出高分辨率空间信息集合;然后将已知时相低-高分辨率影像对之间的空间信息对应关系应用到待预测的未知时相的低-高空间分辨率影像对上,将未知时相的低分辨率影像用对应的高分辨率空间信息集合进行表达,从而预测出未知时相的高分辨率影像。理论上存在一个空间信息降尺度函数,使得
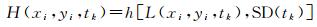 (2)
(2)
式中,h是一个空间尺度映射函数;SD(tk)是待预测时间点的高分辨率空间细节信息集合,它是从已知时间点的高分辨率影像中通过线性[12]或者非线性方式[3]获取并最终被融入到L(xi, yi, tk)之中的。
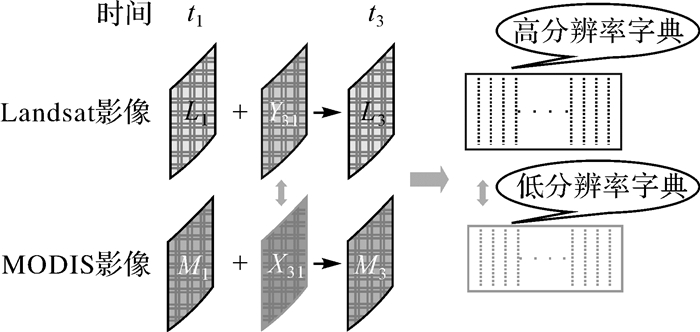
因为线性的空间信息提取和融合方式的前提假设是高分辨率影像像元和低分辨率影像像元的空间尺度转换参数是线性的且具有时间一致性,所以线性的基于地表空间信息的时空融合只适用于土地覆盖未发生类别变化的情况,即为地表的空间细节信息在观测时段内保持不变的情况。而非线性的基于地表空间信息的时空融合则能适用于地表发生类别变化的情况,因为它能从已知时间点影像的所有像元中搜索与L(xi, yi, tk)中像元对应的空间细节信息,而无需空间尺度转换参数具有时间一致性这一假设。例如,文献[3]提出的SPSTFM算法(sparse representation-based spatio-temporal reflectance fusion model)就将稀疏表达的理论引入了时空融合算法,用非线性的方式提取出高-低分辨率的空间细节字典对,并用该字典对去重建待预测的高分辨率遥感影像,其空间细节字典对的训练过程如图 2所示。非线性的基于地表空间信息的融合方式虽然能够更好地重建出地表细节信息,但也会带来算法计算复杂度增加的问题[3-4]。
|
| 图 2 SPSTFM算法字典训练示意图 Fig. 2 The dictionary training process of SPSTFM |
1.3 基于地物时相变化的时空融合
基于地物时相变化的时空融合,其理论基础是地物的时相变化模型具有空间尺度的不变性。这种类型的时空融合首先建立已知时相和未知时相的低分辨率影像之间的时相变化模型,然后将所得到的时相变化模型应用于已知时相的高分辨率影像上,从而得到未知时相的高分辨率影像。这种时空融合可以用下述模型表达
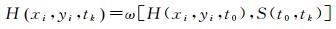 (3)
(3)
式中,ω是一个时间变换映射函数;S(t0, tk)是从已知和待预测时间点的低分辨率影像中获得的地物时相变化模型参数。因为地物的时相变化模型具有空间尺度不变性,所以通过低分辨率影像得到的时相变化模型可以应用到对应高分辨率影像之间的时相变换。
在一个局部窗口内,根据时相变化模型具有尺度不变性这一理论假设,时相变化模型一般可划分为3类:① 差值变化,即为H(xi, yi, tk)=H(xi, yi, t0)+[L(xi, yi, tk)-L(xi, yi, t0)];② 比值变化,即为H(xi, yi, tk)=H(xi, yi, t0)·[L(xi, yi, tk)/L(xi, yi, t0)];③ 比率变化,即为H(xi, yi, tk)=a·H(xi, yi, t0)+b,其中参数a、b由L(xi, yi, tk)=a·L(xi, yi, t0)+b求得。比较有代表性的时空自适应反射率融合模型STARFM[10](spatial and temporal adaptive reflectance fusion model),就是基于局部移动窗口内的差值变化模型实现的。
基于地物时相变化的时空融合应用比较广泛,例如在地表反射率[18]、地表温度[15, 19]、地表蒸散[20]、植被指数[21]和叶面积指数[22]等时序数据的生成;植被季节变化监测[23]、作物长势监测[24]等方面的应用。然而,地物的时相变化模型在不同空间尺度的不变性要求高分辨率影像的像元要位于对应的低分辨率影像像元的内部,或者位于对应低分辨像元临近像元集合的内部,如此这些高-低分辨率像素才能具有相同的变化率。这一要求就限制了这类时空融合在异质地表覆盖情况下的应用,因为异质的土地覆盖对应的低分辨率像元,可能包含了不同种类的高分辨率像元,故而不能保证空间上对应的高-低分辨率像元具有相同的变化率。
1.4 组合性的时空融合对于组合性的时空融合,主要是指利用以上3种类型中的某两种类型的时空融合进行组合而成的一种组合性时空融合模型。
1.4.1 基于地物组分内空间信息的时空融合这种类型的时空融合的理论假设是不同地物组分内部的空间信息在不同的空间尺度下的关联模型具有时间一致性。它是在对已知时间点的高分辨率图像进行分割或者分类之后,在不同的组分内部进行基于地物空间细节信息的时空融合算法处理,
进而预测未知时相的高分辨率影像。文献[5]提出了一个“变化趋势率”的概念,如图 3所示,假设Landsat和MODIS的地表反射率数据在两个观测时间段内的时间变化趋势率是相同的。在此基础上,假设每一种组分内部的空间细节在不同空间分辨率影像之间的关系具有时间一致性并解算出待预测的高分辨率影像。
1.4.2 基于地物组分内时相变化的时空融合
这种组合性的时空融合是基于不同的地物组分而不是低分辨率像素来建立地物的时相变化模型,在对已知时相的高分辨率图像进行分割或者分类从而得到不同的地物组分之后,假设不同组分的时相变化模型具有空间尺度不变性,再预测未知时相的高分辨率影像。文献[25]首先对高分辨率的图像进行分类从而获取高分辨率的地物组分,假设不同组分的时相变化具有空间一致性,然后针对不同的组分进行基于地物时相变化的时空融合。文献[26]首先对低分辨率影像进非监督分类获取低分辨率的地表组分图,通过对应组分内部无云的纯净像元建立回归关系来获得不同时相之间像素的时相变化关系。
2 时空融合面临的问题和挑战多源遥感影像的时空融合需要融合来自不同卫星、不同传感器、不同时相、不同类型的遥感影像,融合结果的精度也理所当然地受这些多源遥感数据的辐射和几何不一致性的影响[25]。因此,也有一部分研究将高分辨率的影像进行降采样之后的模拟低分辨率影像作为低分辨率数据源进行时空融合研究[13, 25, 27]。因此,就能排除数据在辐射和几何方面的不一致性所带来的负面影响,从而聚焦于时空融合算法本身的研究,因为在这种情况下,误差的来源只会是时空融合算法自身[13]。但是,这种实验策略在实际应用情况中是不现实的,因为在处理真实的多源遥感数据时,其几何和空间不一致性不可避免地会给融合精度带来不可忽视的误差[2]。
2.1 多源遥感影像的辐射差异由于地表和大气环境的变化、不同卫星获取数据时的双向反射分布函数(bidirectional reflectance distribution function,BRDF)的差异、多源传感器光谱分辨率的差异、不同卫星辐射定标精度的差异,以及不同空间分辨率的像元混合效应的差别等因素的影响[2, 25, 28-29],导致多源传感器、多时相以及多分辨率的遥感影像相互之间具有辐射亮度的差异。
如果地表覆盖异质性较高,或者时相变化较为复杂,则多源遥感数据的辐射度差异会导致更严重的时空融合误差。此外,如果在融合过程中不对多源数据的辐射度差异进行处理,则会导致基于地表组分的时空融合与其他类型的时空融合结果具有不同的辐射度特征。即为基于地表组分的时空融合结果具有类似于低分辨率影像的辐射度特征,其他类型时空融合方法的结果具有类似于高分辨率影像的辐射度特征[2]。
2.2 多源遥感影像的几何配准差异由于上述的时空融合算法基本都是像素级或者特征级[30]的图像融合算法,故而这些算法都要求待融合的多源遥感影像具有很高的几何配准精度[5, 13, 25]。然而,由于不同卫星的数据获取方式的不同、不同时刻卫星姿态的不同及扰动等因素的影响,导致多源传感器、多时相的遥感影像相互之间往往都不是精确配准的。此外,由于数据预处理步骤的不同或者高级数据产品生产过程中重采样、重投影等处理也会影响遥感影像的几何精度[2]。例如,采用全球正弦投影的MODIS数据标准产品在中纬度和两极地区的图像几何畸变尤为明显[31]。
2.3 混合像元模型的复杂性卫星遥感影像的单个像元记录的是卫星传感器在瞬时视场角内所覆盖的地面范围内总的地物辐射能量。由于卫星传感器空间分辨率的限制、自然界地物的复杂多样性、地表辐射多次散射等因素的影响[8],混合像元普遍存在,且低分辨率影像像元的混合程度更加明显。
一般的,低分辨率的混合像元可以被认为是对应高分辨率影像中纯净像元的加权之和。现有的绝大部分时空融合算法,例如基于地表组分的时空融合模型,所采用的混合像元模型都是线性的[5, 13, 25],即假设到达卫星传感器的地表辐射是由唯一的光谱端元组分直接反射而来[8]。线性的混合像元模型适用于较大面积的同质地物覆盖的情况,当地物复杂度较高、异质性较强的时候,不同地物之间的相互多次散射也会增加,从而使得入瞳辐射产生非线性混合。线性的混合像元模型仅仅是非线性混合像元模型的特例。因此,在时空融合模型中恰当地引入非线性的混合像元模型并提高时空融合的精度,是一个有待进一步研究的问题。
2.4 地物时相变化模型的复杂性针对已知时间点和待预测时间点之间的地物时相变化,多数时空融合算法都是采用线性的地物变化模型[12, 32]。然而在实际情况中,人为因素引起的土地利用变化模型往往是非线性的,例如文献[33]就用WRF/UCM(weather research forecast/urban canopy model)系统来模拟和预测未来城市扩张对城市热岛效应的影响;自然因素引起的地物时相变化也不一定都遵循线性的变化趋势,文献[3]用稀疏表达理论以非线性的方式重建了待预测高分辨率影像中的空间细节信息。因此,将非线性的地物时相变化模型恰当地引入时空融合模型用以模拟复杂多样的地物时相变化,并提高时空融合的精度是必要的。
3 时空融合的前瞻 3.1 算法的通用性虽然现在已经涌现了多种多样的时空融合算法,但这些算法都被局限于特定的数据源、算法原理或者应用目的。一方面,由于不同的数据源具有不同的几何、辐射、量纲属性[2, 13],使得即使是同一种融合算法在应用于不同的数据源时,其融合结果的精度差异都比较大,例如STARFM在应用于同质地表反射率数据时能获得较好的预测效果,但在用于地表温度的时空融合时就难以获得较好的预测效果[15]。另一方面,时空融合算法研究时段内地物的时相变化以及地表覆盖情况是非常复杂的,包括季节变化[10]、类别变化[3-4]以及突发扰动事件[14];同质的地表[10]和异质的地表覆盖[12-13]等。在应对复杂的时相变化和地表覆盖时,采用不同的时空融合算法得到的融合结果差异性较大,例如STARFM在捕捉较为同质的地表覆盖的季相变化时效果较好,但在预测异质地表的时相变化时效果就较差[12]。虽然文献[12]针对异质地表覆盖地貌的时空融合做了改进,但依然无法捕捉到地物的类别变化[3-5]。SPSTFM采用了稀疏表达的理论去重建未知时间点的高分辨率影像,能够实现季节变化和类别变化的一体化融合,但是在应用于大批量、大范围内的遥感影像的时空融合时,其较高的算法复杂度需要采用并行计算或者进一步的算法优化来提高其运行效率。
总的来说,目前尚未有一种能够适用于不同数据源和应用目的的时空融合算法出现,不仅能够考虑数据的多样性,而且能针对不同卫星传感器或者不同类型的数据都获得较好的融合效果,从而达到具有广泛实用性的价值。
3.2 算法的鲁棒性现有的时空融合算法都有特定的一些算法参数,这些算法参数都会在一定程度上影响最终融合结果的精度。例如在STARFM中,预估的地物类别数和移动窗口的尺寸是非常重要的两个参数。预估的地物类别数越高,预测结果的精度越高;移动窗口的尺寸越大,预测结果的精度越高[25];基于一对已知影像进行字典学习的时空融合方法[4]需要设置训练字典的尺寸大小,尺寸过大或者过小都不太适宜。但是当用户在实际应用中面对大批量、多样化的遥感影像时,用户很难去逐个对每一次的时空融合算法处理去设定合适的或者普适的算法参数。因此,降低时空融合算法对模型参数的敏感度、减少时空融合算法对参数的依赖性,以提升算法本身的鲁棒性,对于时空融合算法的推广使用是有很重要的实际意义的。
4 结语遥感影像的时空融合是一种针对地观测系统中卫星传感器的时间-空间分辨率折中而提出的一种成本低、灵活性强、可行性高的解决方案。时空融合既很好地解决了现阶段卫星遥感数据“又多又少”的问题,又为多种遥感应用了高时空分辨率的遥感影像,例如地表反射率、地表温度、植被指数等重要环境因子的时间序列分析研究。时空融合极大地提高了遥感数据的利用率,其数据融合思想也为其他研究领域的数据融合或者数据集成利用奠定了理论参考和科学支撑,并提供了可行的技术手段。
现有时空融合算法的基础理论假设主要包括时相变化模型的空间尺度不变性和空间降尺度模型的时间一致性。基于这两种假设机制,时空融合算法可以分为基于地物类别组分的时空融合、基于地表空间信息的时空融合、基于地物时相变化的时空融合以及组合性的时空融合。现阶段基于不同原理、不同假设、不同应用、不同数据源的时空融合方法研究层出不穷,并且已经成功应用于多种遥感应用之中。
然而,无论是基于何种原理或者何种应用的时空融合算法,它们都有各自的优点和局限性,时空融合算法的发展还未达到成熟的程度。多源遥感影像的几何和辐射特性差异的校正、异质地表混合像元模型的非线性散射特征的处理、地物时相变化模型的精确建模,以及算法的通用性和鲁棒性提升等方面仍有待进一步的深入研究。
| [1] | TONG Xudong, ZHAO Wenbo, XING Jin, et al. Status and Development of China High-resolution Earth Observation System and Application[C]//Proceedings of 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Beijing:IEEE, 2016:3738-3741. |
| [2] | ZHANG H K, HUANG Bo, ZHANG Ming, et al. A Generalization of Spatial and Temporal Fusion Methods for Remotely Sensed Surface Parameters[J]. International Journal of Remote Sensing, 2015, 36(17): 4411–4445. DOI:10.1080/01431161.2015.1083633 |
| [3] | HUANG Bo, SONG Huihui. Spatiotemporal Reflectance Fusion via Sparse Representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 3707–3716. DOI:10.1109/TGRS.2012.2186638 |
| [4] | SONG Huihui, HUANG Bo. Spatiotemporal Satellite Image Fusion Through One-pair Image Learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(4): 1883–1896. DOI:10.1109/TGRS.2012.2213095 |
| [5] | HUANG Bo, ZHANG Hankui. Spatio-temporal Reflectance Fusion via Unmixing:Accounting for Both Phenological and Land-cover Changes[J]. International Journal of Remote Sensing, 2014, 35(16): 6213–6233. DOI:10.1080/01431161.2014.951097 |
| [6] | IRONS J R, DWYER J L, BARSI J A. The Next Landsat Satellite:The Landsat Data Continuity Mission[J]. Remote Sensing of Environment, 2012, 122: 11–21. DOI:10.1016/j.rse.2011.08.026 |
| [7] | CHANDER G, MARKHAM B L, HELDER D L. Summary of Current Radiometric Calibration Coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI Sensors[J]. Remote Sensing of Environment, 2009, 113(5): 893–903. DOI:10.1016/j.rse.2009.01.007 |
| [8] | 赵英时. 遥感应用分析原理与方法[M]. 2版. 北京: 科学出版社, 2013: 108-136. ZHAO Yingshi. The Teory and Methods of Remote Sensing Application Analysis[M]. 2nd ed. Beijing: Science Press, 2013: 108-136. |
| [9] | LECKIE D G. Advances in Remote Sensing Technologies for Forest Surveys and Management[J]. Canadian Journal of Forest Research, 1990, 20(4): 464–483. DOI:10.1139/x90-063 |
| [10] | GAO Feng, MASEK J, SCHWALLER M, et al. On the Blending of the Landsat and MODIS Surface Reflectance:Predicting Daily Landsat Surface Reflectance[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(8): 2207–2218. DOI:10.1109/TGRS.2006.872081 |
| [11] | GAO Feng, HILKER T, ZHU Xiaolin, et al. Fusing Landsat and MODIS Data for Vegetation Monitoring[J]. IEEE Geoscience and Remote Sensing Magazine, 2015, 3(3): 47–60. DOI:10.1109/MGRS.2015.2434351 |
| [12] | ZHU Xiaolin, CHEN Jin, GAO Feng, et al. An Enhanced Spatial and Temporal Adaptive Reflectance Fusion Model for Complex Heterogeneous Regions[J]. Remote Sensing of Environment, 2010, 114(11): 2610–2623. DOI:10.1016/j.rse.2010.05.032 |
| [13] | ZHU Xiaolin, HELMER E H, GAO Feng, et al. A Flexible Spatiotemporal Method for Fusing Satellite Images with Different Resolutions[J]. Remote Sensing of Environment, 2016, 172: 165–177. DOI:10.1016/j.rse.2015.11.016 |
| [14] | HILKER T, WULDER M A, COOPS N C, et al. A New Data Fusion Model for High Spatial-and Temporal-Resolution Mapping of Forest Disturbance Based on Landsat and MODIS[J]. Remote Sensing of Environment, 2009, 113(8): 1613–1627. DOI:10.1016/j.rse.2009.03.007 |
| [15] | HUANG Bo, WANG Juan, SONG Huihui, et al. Generating High Spatiotemporal Resolution Land Surface Temperature for Urban Heat Island Monitoring[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 1011–1015. DOI:10.1109/LGRS.2012.2227930 |
| [16] | WU Penghai, SHEN Huanfeng, AI Tinghua, et al. Land-surface Temperature Retrieval at High Spatial and Temporal Resolutions Based on Multi-sensor Fusion[J]. International Journal of Digital Earth, 2013, 6(S1): 113–133. |
| [17] | WU Penghai, SHEN Huanfeng, ZHANG Liangpei, et al. Integrated Fusion of Multi-scale Polar-orbiting and Geostationary Satellite Observations for the Mapping of High Spatial and Temporal Resolution Land Surface Temperature[J]. Remote Sensing of Environment, 2015, 156: 169–181. DOI:10.1016/j.rse.2014.09.013 |
| [18] | EMELYANOVA I V, MCVICAR T R, VAN NIEL T G, et al. Assessing the Accuracy of Blending Landsat-MODIS Surface Reflectances in Two Landscapes with Contrasting Spatial and Temporal Dynamics:A Framework for Algorithm Selection[J]. Remote Sensing of Environment, 2013, 133: 193–209. DOI:10.1016/j.rse.2013.02.007 |
| [19] | KIM J, HOGUE T S. Evaluation and Sensitivity Testing of A Coupled Landsat-MODIS Downscaling Method for Land Surface Temperature and Vegetation Indices in Semi-arid Regions[J]. Journal of Applied Remote Sensing, 2012, 6(1): 063569. |
| [20] | HASSAN Q K, BOURQUE C P A, MENG Fanrui. Application of Landsat-7 ETM+ and MODIS Products in Mapping Seasonal Accumulation of Growing Degree Days at an Enhanced Resolution[J]. Journal of Applied Remote Sensing, 2007, 1(1): 013539. DOI:10.1117/1.2800284 |
| [21] | OUYANG Wei, HAO Fanghua, SKIDMORE A K, et al. Integration of Multi-sensor Data to Assess Grassland Dynamics in a Yellow River Sub-watershed[J]. Ecological Indicators, 2012, 18: 163–170. DOI:10.1016/j.ecolind.2011.11.013 |
| [22] | ZHANG Hankui, CHEN J M, HUANG Bo, et al. Reconstructing Seasonal Variation of Landsat Vegetation Index Related to Leaf Area Index by Fusing with MODIS Data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(3): 950–960. DOI:10.1109/JSTARS.2013.2284528 |
| [23] | BHANDARI S, PHINN S, GILL T. Preparing Landsat Image Time Series (LITS) for Monitoring Changes in Vegetation Phenology in Queensland, Australia[J]. Remote Sensing, 2012, 4(6): 1856–1886. |
| [24] | SINGH D. Generation and Evaluation of Gross Primary Productivity Using Landsat Data Through Blending with MODIS Data[J]. International Journal of Applied Earth Observation and Geoinformation, 2011, 13(1): 59–69. DOI:10.1016/j.jag.2010.06.007 |
| [25] | GEVAERT C M, GARCíA-HARO F J. A Comparison of STARFM and an Unmixing-based Algorithm for Landsat and MODIS Data Fusion[J]. Remote Sensing of Environment, 2015, 156: 34–44. DOI:10.1016/j.rse.2014.09.012 |
| [26] | GAO Feng, MASEK J G, WOLFE R E, et al. Building a Consistent Medium Resolution Satellite Data Set Using Moderate Resolution Imaging Spectroradiometer Products as Reference[J]. Journal of Applied Remote Sensing, 2010, 4(1): 043526. DOI:10.1117/1.3430002 |
| [27] | WU Mingquan, NIU Zheng, WANG Changyao, et al. Use of MODIS and Landsat Time Series Data to Generate High-resolution Temporal Synthetic Landsat Data Using a Spatial and Temporal Reflectance Fusion Model[J]. Journal of Applied Remote Sensing, 2012, 6(1): 063507. DOI:10.1117/1.JRS.6.063507 |
| [28] | TEILLET P M, FEDOSEJEVS G, THOME K J, et al. Impacts of Spectral Band Difference Effects on Radiometric Cross-calibration Between Satellite Sensors in the Solar-reflective Spectral Domain[J]. Remote Sensing of Environment, 2007, 110(3): 393–409. DOI:10.1016/j.rse.2007.03.003 |
| [29] | ZHANG Hankui, HUANG Bo. Support Vector Regression-based Downscaling for Intercalibration of Multiresolution Satellite Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(3): 1114–1123. DOI:10.1109/TGRS.2013.2243736 |
| [30] | POLH C, VAN GENDEREN J L. Multisensor Image Fusion in Remote Sensing:Concepts, Methods and Applications[J]. International Journal of Remote Sensing, 1998, 19(5): 823–854. DOI:10.1080/014311698215748 |
| [31] | LUO Yi, TRISHCHENKO A P, KHLOPENKOV K V. Developing Clear-sky, Cloud and Cloud Shadow Mask for Producing Clear-sky Composites at 250-Meter Spatial Resolution for the Seven MODIS Land Bands over Canada and North America[J]. Remote Sensing of Environment, 2008, 112(12): 4167–4185. DOI:10.1016/j.rse.2008.06.010 |
| [32] | HAZAYMEH K, HASSAN Q K. Spatiotemporal Image-fusion Model for Enhancing the Temporal Resolution of Landsat-8 Surface Reflectance Images Using MODIS Images[J]. Journal of Applied Remote Sensing, 2015, 9(1): 096095. DOI:10.1117/1.JRS.9.096095 |
| [33] | WANG Juan, HUANG Bo, FU Dongjie, et al. Response of Urban Heat Island to Future Urban Expansion over the Beijing-Tianjin-Hebei Metropolitan Area[J]. Applied Geography, 2016, 70: 26–36. DOI:10.1016/j.apgeog.2016.02.010 |



