2. 上海大学通信与信息工程学院, 上海 200444;
3. 中国科学院大学, 北京 100049
2. School of Communication and Information Engineering, Shanghai University, Shanghai 200444, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
全球导航卫星系统(GNSS),包括美国全球定位系统(GPS)、中国北斗导航卫星系统(BDS)、俄罗斯格洛纳斯系统(GLONASS)和欧洲伽利略导航卫星系统(Galileo),以及区域增强系统,如日本准天顶卫星系统(QZSS)和印度区域导航卫星(IRNSS)等,具有全天候、近实时、高精度的特点,可持续发射L波段信号,广泛应用于定位、导航和授时(PNT)。随着各导航卫星系统的逐渐完善,星座的增多,观测站的增加,其应用领域越来越广泛。GNSS系统不仅仅应用于定位、授时和导航,还可以利用其表面反射信号进行遥感研究。GNSS卫星持续向地球播发无线电信号,其中部分信号会被地球表面反射。从粗糙表面反射回来的GNSS延迟信号可以提供直射和反射信号路径的不同信息。这些信息包括反射信号的波形、幅值、相位和频率等的变化,极化特征的变化直接与反射面相关,结合接收机天线位置和介质信息,利用延迟测量观测和反射表面属性可以确定表面粗糙度和表面特性,即GNSS+R反射测量(global navigation satellite system+refectometry)。
GPS反射测量是由欧空局(ESA)Martin Neira[1]于1993年首次提出来,即GPS地表反射信号和直射信号一起被接收机接收,它们之间延迟可以用于干涉测量,即PARIS(passive reflectometry and interferometry system)。1994年,法国科学家通过进行飞行试验发现接收机可以接收到海面反射信号,但由于其对定位精度的影响,通常将其作为多路径信号剔除[2]。1996年,NASA兰利研究中心的科学家利用双频GPS信号进行海面前向散射以获取并剔除电离层延迟,弥补传统卫星高度计的不足,但地基试验表明传统接收机难以进行长时间的跟踪和有效锁相,需研制新型的接收机[3]。同年,欧空局(ESA)在荷兰进行GNSS+R海面测高试验-PARIS高度计Zeeland桥I试验[4]。2000年10月,美国国家海洋和大气管理局(NOAA)的飓风猎人号飞机搭载了GNSS+R设备从南卡来罗纳州海岸飞入“迈克尔”飓风内,通过分析从热带气旋海面上反射回来的GPS信号得到了风速结果[5]。2003年英国UK-DMC卫星利用搭载的GNSS+R设备成功获得了海面粗糙度等地球表面物理系数[6];静海区域的GPS反射信号同样可以得到高精度的测高结果[7]。同时,2014年第1颗GNSS+R卫星(TDS-1) 发射,提供DDM数据产品,开启了星载反射测量的应用。此外,许多其他科研机构也开展了一系列GNSS反射信号的理论研究和试验、新型GNSS+R接收机的研制,以及基于地基、海岸、桥梁、飞机等不同平台试验,测试信号接收、原理验证,以及检验利用GNSS+R估计海面(如海面高和风速)和陆面等研究,获得了一些初步结果和进展。
本文详细描述了GNSS+R原理和方法及其最新应用进展,包括遥感海洋、陆地、水文、植被和冰雪特征等,特别是最新BDS-R和TDS-1 GNSS+R研究进展。最后给出了将来GNSS+R的应用前景和展望,包括多GNSS系统、GNSS+R接收机、GNSS+R卫星计划和新兴应用,如中小尺度地表特征和目标探测等。
1 GNSS+R原理与方法GNSS+R反射测量技术属于双基雷达,可获得地表粗糙特征和地球物理参数,即利用GNSS测量直射信号与地表镜面反射的信号之间延迟(时间延迟或相位延迟),再根据GNSS卫星、接收机和镜面反射点之间的几何位置关系,可反演地表特征。按照处理数据的方式,GNSS+R测高可以分为传统型GNSS+R测高(cGNSS+R测高)和干涉GNSS+R测高(iGNSS+R)。前者是配置左右圆极化天线并利用接收机记录的直射信号与反射信号的载波相位数据,通过固定模糊度和解算接收机钟差等方式,确定两者之间的传播路径延迟,进而计算天线至地球表面的高度。后者是利用直射信号与反射信号功率波形相关的原理,测得信号时延,进而计算天线到地球表面的垂直距离,但其涉及复杂的多普勒时延算法,数据处理方法复杂。
1.1 传统型GNSS+R这种测高一般是采用传统的大地测量型接收机,利用载波相位观测值作为原始观测量,得到直射信号与反射信号的传播路程差,再根据几何关系得到反射面的高度。如在湖边、海岸或海岛上架设GNSS接收机,进行GNSS+R测高试验,这就是岸基测高。其所架设的接收机高度都较低,其天线的照射面积决定有效的水面散射面积,可有效代替传统的验潮站测量模式。GNSS接收机对所接收到的直射信号与表面反射信号进行相关,并通过测量相关函数的最大值的位置得到时间延迟T,进而可求得接收机到反射面的高度H。在飞机或气球上假设GNSS接收机进行的GNSS+R测高试验就是机载测高。与岸基测高相比,机载测高架设的高度较高,观测的水面面积较大。在LEO卫星上搭载GPS接收机,进行GNSS+R测高试验,这就是星载测高。在500~800 km的高空可以采用LEO卫星搭载GPS接收机来进行海面高度测量,这种测量方式与传统卫星测高相比不需要发射机,也可以直接采用多个LEO卫星组成星座,具有较高的时空分辨率。
1.2 干涉型GNSS+R这种测高是利用特制的可以同时接收直射信号和反射信号的接收机,并将接收到的信号在接收机中进行相关处理,利用时延一维相关函数、多普勒一维相关函数或者时延-多普勒二维相关函数得到两个信号之间时间延迟,再根据几何关系得到反射面高度。
1.2.1 SNR技术多路径效应是GNSS高精度定位的主要误差,它与反射面的结构和电介质参数密切相关。当卫星高度角低于10°时,GNSS接收到的反射信号是右旋极化。这时具有相同频率的反射信号与直射信号会发生相干作用。这一相干现象反映在信噪比SNR的变化上,信噪比SNR观测值是衡量GPS接收机天线接收到的信号的大小的一个量值,反映多路径与多路径误差的大小受卫星信号的发射功率、天线增益、卫星与接收机间的距离及多路径效应等因素的影响。在高度角较高的情况下,天线增益较大使得SNR得到有效提高;而在高度角较低的情况下,一方面天线增益减小,另一方面多路径效应影响使得SNR下降较为严重。因此,对信噪比SNR进行分析可以评估多路径效应,进而估计地表环境参数。
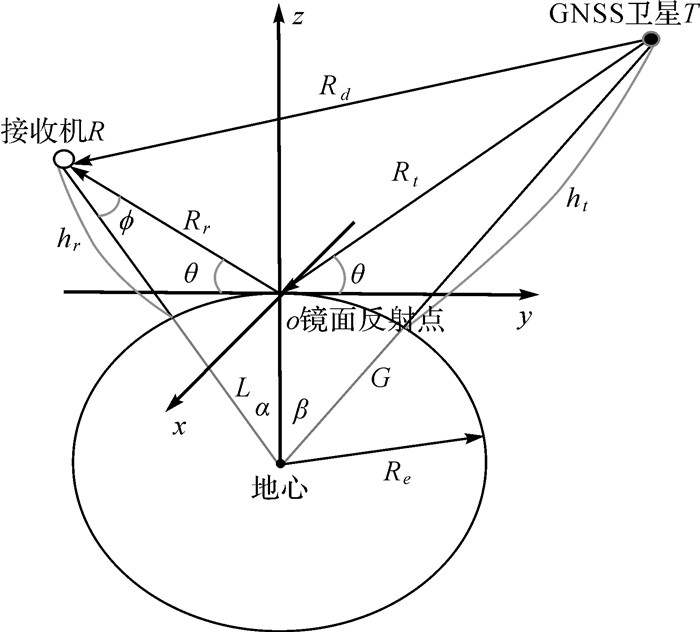
1.2.2 DDM技术GNSS+R海洋遥感主要利用反射信号时延多普勒二维相关功率。其原理是通过计算本地载波信号与散射区域内不同时间延迟和多普勒频率的接收信号的相关功率值。DDM多用于机载和星载GNSS+R,考虑到其距离地面高度较高,首先介绍GNSS+R的镜面反射测量几何关系。GNSS+R几何关系要用到镜面反射点,即从反射区域反射的反射信号中路径延迟最短的理论反射点。根据GNSS卫星、接收机和镜面反射点的几何关系建立如图的本地坐标系。该坐标系的原点为镜面反射点,z轴为地球切面的法线方向,GNSS卫星T,镜面点和接收机R位于yz平面内,x轴按右手定则确定。图 1中,ht为卫星到地球参考椭球面的高度;hr为接收机到地球参考椭球面的高度;Re为地球半径;G为卫星到地心的距离;L为接收机到地心的距离;Rt和Rr分别是卫星和接收机到镜面反射点的距离;β是地心、镜面反射点和GNSS卫星间的夹角;α是地心、镜面反射点和接收机间的夹角;θ为镜面点处卫星的仰角。
|
| 图 1 GNSS镜面反射测量几何关系 Fig. 1 Geometric relation of GNSS specular reflectiometry |
利用镜面反射点与接收机和GNSS卫星之间的关系,以及GNSS反射信号时延多普勒二维相关功率关系可获得地表反射面参数。如对于海洋表面,文献[8]在2000年提出了完整的GNSS信号散射理论模型,其模型是关于时延和多普勒的二维函数,通过此模型可以得到散射区域不同散射点的反射功率,Z-V模型具体表达如下
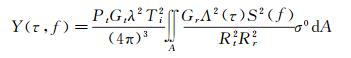 (1)
(1)
式中,Y(τ, f)是接收机处理后的信号相关功率,是关于延迟和多普勒的函数;Pt是卫星发射的信号功率;Gt和Gr是卫星天线和接收机天线增益;Ti是信号处理中相干积分时间;Rt和Rr是卫星和接收机到地面反射点的距离;σ0是与反射面参数有关的项,包括反射系数和粗糙度等;S(f)是多普勒频移函数;Λ(τ)是GNSS码相关函数;A是有效的散射区域,大概是闪耀区大小。
2 GNSS+R最新应用进展 2.1 海洋测高目前岸基传统型大地测量GNSS接收机获得较好测高结果。如文献[4]利用反射信号码相位信息,测高精度达到数米。文献[9]在Crater湖面上利用iGNSS+R设备,解算了采样率为1 Hz的水面高,精度大约在2 cm。文献[10—11]利用反射信号载波相位信息,将精度提高到厘米级。文献[12]利用GNSS+R SNR数据反演出的测高结果与验潮站的观测结果做了对比,结果显示两者之差小于3 cm。另外,文献[13]在飞机上搭载iGNSS+R设备的试验表明,利用GPS反射信号测高的精度能达到5 cm,其空间分辨率能达到5 km。文献[14]将cGNSS+R设备搭载在飞行高度为1 km的飞机上,利用L1载波相位信号解算得到的平均海面高度(SSH)与Jason-1的测量对比,精度在10 cm左右。
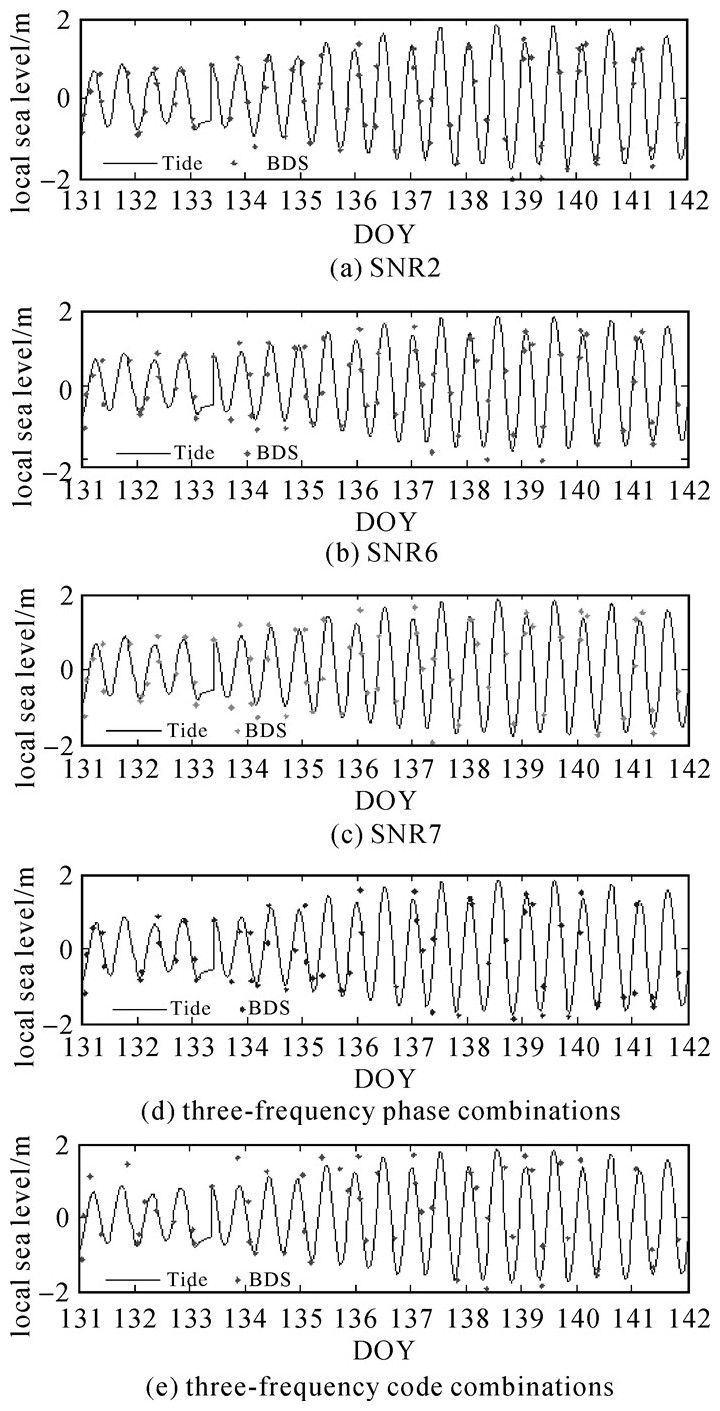
目前国内外利用岸基和机载GNSS+R等获得了一系列的新结果。例如文献[15]首次利用岸基BDS观测获得了海平面变化,与验潮站观测结果有较好的一致(见图 2)。在星载GNSS+R方面,文献[16]首次利用TDS-1数据反演得到海表面高度(sea surface height, SSH), 其结果与全球DTU10的海表面高度数据进行了对比,存在一定的一致性但依然也有较大的差异。
2.2 海面测风
海面在风的作用下会引起波浪,从而引起海面粗糙度的变化。根据海面风场反演原理,反射信号的功率峰值随着风速的增大而减小,波形也相应越扁平。这说明海面散射能量随风速的变化而分布到更大的范围,即闪烁区范围变大。故可以通过和模拟波形相对比反演海面风速。此外,风速和风向还会影响海平面坡度。风向的变化会对闪烁区的非对称性产生影响。沿顺风方向,海面散射功率曲线函数的包络较宽,沿测风方向则相对较窄,表现为曲线波形上的非对称性。
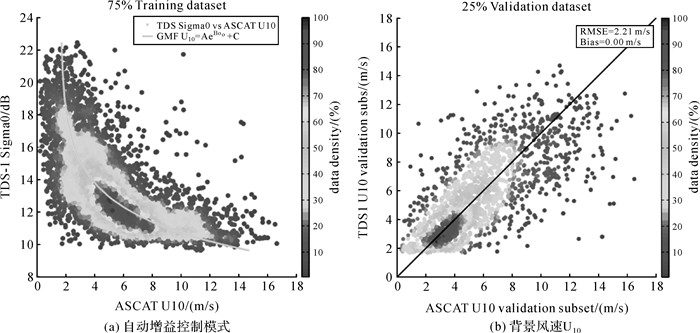
自1997年,NASA兰利研究中心与科罗拉多大学联合开展了关于GNSS+R海面风场反演算法的研究,并进行多次机载飞行试验[3]。试验发现,GPS反射信号的相关功率波形与风速有直接关系,且海面风速越大,波形的后延变化越趋于平缓,反之越陡峭。2000年,文献[8]提出双尺度表面模型(Z-V模型)在早期的GNSS+R海面风场反演模型中较为系统和成熟,但是该模型并没考虑闪烁区之外由海水表面小尺度坡度造成的布拉格散射所产生的反射。后来,文献[17]等对Z-V模型进行了改进。除此之外,NASA/科罗拉多大学、ESA和Starlab研究所等进行了大量机载试验,并根据反演理论对试验数据进行了海面风场反演,风速反演精度达±2 m/s,风向精度为±20°。2014年,文献[18]使用GNSS+R方法获得的时延多普勒图像(DDM)的5个观测量,并使用根据NDBC浮标数据建立的经验地球物理模型函数(GMF),建立了基于回归分析的最小方差风速估算模型,结果表明使用最小方差风速估算模型的均方根误差比仅仅使用单个观测值进行反演的均方根误差要小得多。2016年,文献[19]又针对热带气旋全球导航卫星系统(CYGNSS)的第二等级产品为数据源,并从样本、功率的选择,使用二维地球物理模型函数等方面,改进之前他所提出的海洋测风算法,设置理想的CYGNSS在轨参数仿真得到的时延多普勒图像(DDM)对算法进行测试。同时,文献[20]第一次利用TDS-1数据反演得到了海洋风速结果,该结果与实测数据达到了很好的一致性,如图 3是利用TDS-1卫星数据反演得到的海洋风速结果。
2.3 海冰探测
近年来,全球气候发生显著变化,冰川和冻土加剧融化,从而导致海平面产生明显变化。早期的海冰监测常通过设立观测站和雷达站,并利用海上工具进行实地监测,结合使用声呐技术以及光学测量技术获取海冰厚度,但分辨率低和成本高。随着遥感技术的发展,利用光学遥感和雷达遥感测冰的技术得以发展,但前者会受云层和光照等因素的影响,而微波遥感则具有良好的穿透性且可全天候全天时工作等优势。近些年,全球导航卫星系统的发展与完善,使得GNSS+R反射测量技术在海冰监测方面的研究也取得了显著的成果。
1998年4月,文献[21]通过机载GPS反射实验推导了美国阿拉斯加巴罗附近北极海冰和淡水冰的形成条件以及冻土的冻结/解冻状态条件,向前散射的GPS反射与RADARSAT的向后散射测量的相关性是一致的,根据发射信号特征的差异可以判断冰的不同状态及特征。次年同月,又在北冰洋西北部阿拉斯加州的最北端巴罗地区进行机载试验监测海冰,并将实验结果与模拟结果进行对比,论证了GPS信号可以提供海冰信息,且分析了GPS反射信号功率峰值与雷达卫星的后向散射信号之间存在着相关性。文献[22]指出GNSS+R垂直极化与水平极化之间的相位差与海冰厚度之间有较好的相关性。2003年,文献[23]以雷达高度计的相邻波段为基础建立了海冰GPS反射信号模型,并进行星载与机载的模拟分析,开发了用于模拟GPS反射信号的软件。研究发现GNSS反射信号对雪表粗糙度和一些粒学参数敏感,但是该研究弥补了一直以来在L波段非垂直前向散射方面的欠缺。文献[24]在阿拉斯加州kuskowwim湾用UK-DMC卫星进行海冰监测,测得海冰厚度在30~70 cm之间,与美国国家冰雪中心和微博辐射计(AMSR-E)的观测数据进行对比,验证了利用星载GPS反射信号获取海冰信息的可行性。文献[25]利用TDS-1 DDM数据进行了北极和南极区域的海冰探测,并得到了很好的探测结果。
相较于国外,国内对海冰监测的进展还处于起步阶段。2013年,文献[26]利用欧空局格陵兰岛的数据进行模拟分析,得到GNSS反射信号的极化比与海冰密集度的关系,验证了GNSS+R监测海冰的可行性。文献[27]在中国渤海进行岸基试验,对渤海海冰进行监测,通过模拟GNSS+R信号在海水和海冰表面的反射,建立3层辐射传输模型得到GNSS信号的反射率和海冰厚度及入射角度间的关系,并将结果与2013年天津海冰消融过程的试验数据进行对比分析,进一步验证了GNSS+R信号对海冰监测的敏感。
2.4 土壤湿度土壤湿度是地表土壤的一个重要参数。土壤水分在全球水循环中有着重要作用,是地表能量平衡的重要决定因素,影响着地表农作物的生长和洪水泥石流灾害的发生,也影响着全球天气变化。地面GPS反射信号包含有土壤湿度、介质常数、地面粗糙度以及植被覆盖等方面的信息。2000年,文献[28]延伸了Z-V模型,使其适用于土壤湿度测量,发现反射信号的波形峰值虽然与土壤湿度相关,但是地面粗糙度对波形尾部有影响,这给利用波形反演土壤湿度带来困难,于是产生利用特制双天线接收机来接收信号从而利用反射信号来反演土壤湿度的构想。2002年以后,美国宇航局(NASA)连续执行了一系列GPS反射信号土壤水分遥感试验,分析土壤介电常数与反射信号功率的定性关系。西班牙Starlab研究所设计了SMIGOL(soil moisture interference-pattern GNSS observations at L-band reflectometer)探测装置,用于探测直射信号和反射信号干涉之后的信号,通过分析干涉信号波形特征与土壤水分的关系,反演地表参数,即干涉模式技术(IPT)。文献[29]利用IPT技术,从最简单的裸土模型开始研究土壤水分反演算法,到有植被覆盖的复杂模型,证实土壤水分与干涉信号的振幅有关。以及文献[30]又提出利用传统的GPS接收机也可以进行土壤湿度反演,并对此进行了长期研究,与其他科研学者一起建立了基于物理的多路径正演模型[31-32],很好地分析了多路径信噪比的相位振幅随土壤湿度的变化而变化,促进了GNSS+R技术在土壤湿度监测应用。文献[33]在河南郑州开展的GNSS+R航空飞行试验, 给出土壤湿度的估算方法和结果分析, 为中国GNSS+R观测试验开展、自主载荷研制、陆面观测数据处理等提供参考。但由于地面上植物、树叶及玻璃杂物等因素的存在,GPS多路径信号包含的信息是非常复杂的,从地基GPS多路径信号中提取土壤水分参数的信息,首先必须剔除其他因素的影响。
2.5 植被探测植被探测,包括植物含水量,可以确保农作物的正常生长,及时发现存在的问题并解决。植物覆盖在土壤上,其含水量会影响土壤湿度的监测,而估计植物含水量可以提高土壤湿度的反演精度。随着GNSS系统的完善,GNSS台站已经遍布全球各地,同一时刻可观测的卫星个数、可接收到的卫星信号越来越多,有助于植物监测网的建立。而且GNSS信号属于微波波段,而微波对地表粗糙度、含水量等敏感。一方面有利于对植物含水量的监测,但另一方面在监测植物含水量的同时,受地表粗糙度和土壤湿度的影响,因此在估计植物含水量时,需要采用一定的方法消除这些因素的影响。
文献[30]首次提出了利用传统GPS接收机多路径观测可监测土壤湿度,为GPS反射信号监测植物含水量奠定了基础。文献[34]首次利用GPS的噪声统计量MP1 RMS定性地估计了植物生长,指出信噪比会随着植被的生长而减小。文献[35]用Larson等提出的用于土壤湿度反演的正演模型对植物含水量与信噪比和实际反射面高度进行了定量分析,研究发现在植被含水量不超过1 kg/m2时,植物含水量与信噪比振幅呈线性关系。文献[36]提出了一种较为复杂的基于信噪比干涉图的振幅与频率分析的方法,以消除植被含水量在土壤湿度中的影响,并获得较好的结果。
2.6 积雪厚度积雪是重要的淡水资源,对全球大气和海洋的热状况和区域性气候有着重要影响。积雪的融化一方面补给了地球水资源,但是另一方面却会造成海平面上升,淹没沿海城市,影响人类正常生活。积雪探测十分重要,但是由于积雪的时间、空间变化特性,使得积雪探测十分困难。传统的地基观测方法虽然可以观测到积雪厚度和密度,观测精度也高,但是依然存在时间分辨率较低或缺乏空间动态变化等缺陷,而新型的空基遥感探测,如光学星载传感器虽然可以提供积雪覆盖信息,但是积雪的厚度和密度等信息却无法获得。而近年来,逐步发展起来的GNSS技术,利用其优势在积雪探测方面取得了一定的成果。
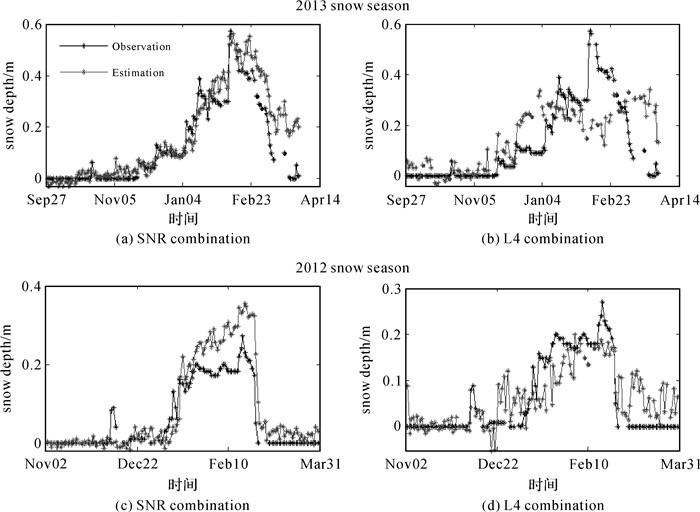
文献[37]利用GNSS+R技术对科罗拉多发生的两次暴风雪的测量在积雪厚度方面的研究取得了初步结果,将GPS信噪比估计得到的积雪厚度与实际的积雪厚度进行对比,证明传统的GPS接收机可以用来测量积雪厚度。文献[32]建立的基于物理的多路径正演模型,充分考虑了GPS发射信号的左旋和右旋极化以及天线/地面的响应特性。他们还利用Matlab建立了该模型的模拟器,使用该模拟器可以用来分析反射测量的特征。并利用多路径正演模型建立了GPS多路径测量积雪厚度的反演模型,估计结果与实测值达到了0.97以上的相关性[38]。文献[39]利用GPS-L4观测值和非参数的自举模型来估计积雪厚度的变化,与实测结果符合度良好,进一步推动了积雪探测的发展;文献[39]利用GPS的L2P观测值的信噪比数据分析积雪厚度的变化,在高度角为5°—30°时计算得到的相关系数高达0.98,表明当GPS卫星高度角在30°以下时更有利于雪深测量。同时,文献[41]又利用GLONASS信噪比观测值与L4相位组合观测值分析了积雪厚度结果,并与GPS结果进行了对比,同时融合两者观测值提高了估计结果精度(见图 4)。
3 前景与展望
目前,新一代的全球导航卫星系统(GNSS),包括美国现代化GPS、俄罗斯现代化GLONASS系统、欧盟Galileo系统和中国北斗系统(BDS),正在不断发展与完善,GNSS正向多频、多模的方向发展。结合空基增强系统(QZSS和IRNSS等),地基GNSS测网可以接收更多频率的多系统GNSS反射信号,这将大大提高时空分辨率,更好地估计地表反射面地球物理参数。另外,随着全球IGS测站以及区域性GPS测站的不断增多,可获得更多的地基GNSS测站周边环境信息,为全球水文研究及气候变化提供了一个新的工具。
3.1 GNSS+R接收机美国喷气推进实验室(JPL)研发的“BlackJack”GPS接收机目前广泛应用于精密定轨及无线电掩星等。为满足未来新任务以及准实时数据处理能力的需求,新型GNSS接收机不仅能够接收和跟踪GPS信号,还将能够接收Galileo、GLONASS及中国北斗等系统信号。目前JPL正在研发新一代的GNSS多频接收机TriG(Tri-GNSS, GPS+Galileo+GLONASS)用于精密定轨及无线电掩星和反射测量。通过跟踪GPS的L1 C/A、L2、L2C和L5以及Galileo、GLONASS等新型系统的信号,TriG可以进行多频GNSS信号折射和反射测量。
为利用GPS反射信号推演海面高度、海况及土壤湿度等相关地球物理参数,加泰罗尼亚理工大学(UPC)研发了“高级GNSS无源反射仪(griPAU)”,griPAU设备利用GPS L1波段的C/A码,可以实时、高精度的得到延迟-多普勒相关值(DDM),并可根据不同的分辨率配置及选择相关或非相关的积分时间来计算24(32复杂点的DDM。griPAU的高灵敏度提高了地球物理参数的恢复质量。现代化的多频GPS、未来的Galileo系统等带来了更多的卫星星座、新的信号和频段,西班牙的ICE也正在进行GNSS+R设备研发、GNSS信号散射和反射应用等方面的研究。
3.2 GNSS+R低轨卫星星载GPS反射试验,如美国国家海洋和大气管理局(NOAA)和国家太空中心(NSPO)计划在2017年发射下一代的FORMOSAT-7/COSMIC-2卫星。新一代的卫星系统将拥有12颗装载GNSS+R接收机的卫星,可接收GPS、GLONAS以及Galileo反射信号。因此它可以收集大量的反射测量数据以用于陆地和海洋等方面的应用。同时,NASA设计的CYGNSS反射测量卫星2016年发射。CYGNSS含有8个绕着运载工具运行的小卫星,在该轨道上,小卫星将接收到来自GPS卫星的直射信号和由反射信号[42]。NASA团队致力于研究海洋表面特性、潮湿大气热力学、判断热带飓风的形成和是否会继续加强以及加强幅度多少的对流辐射动力学之间的关系,而CYGNSS将会改善预报和记录方法。由于快速变化的风暴中心在飓风形成初期和飓风的加剧中扮演着十分重要的角色,CYGNSS将首次帮助科学家探测发生在风暴中心的大气与海洋之间的交互过程。
3.3 新兴应用确定洋面粗糙度和冰冻圈有很多种方法,然而缺少足够的星载数据来验证这些方法以及监视更多的细节,而传统方法实时性不足且空间分辨率较低。在未来几年里,将有更多搭载下一代GNSS遥感接收机的试验卫星发射。在环境遥感的各个领域,高时空分辨率、准实时的GNSS+R将得到更多的应用,如监测海冰、海况、海洋涡流、海面浮油、地质灾害及航天飞机测控等。这些准实时的GNSS反射数据将向公共领域开放,而对这些数据的分析将在预报强风、危险海况、洪涝灾害、海洋涡流以及风暴潮等方面发挥重要作用。此外,高采样率的海面粗糙度数据也将从未来大量的GNSS反射信号中估计出来,这将加深人们对洋面海气通量、浮冰脊、霜花、破冰以及冰雪交界处的粗糙度的认识,尤其是在那些无法接近且环境恶劣的海冰区域。
合成孔径雷达(SAR)可生成关于陆地表面的高分辨率影像,其发射机和接收机可以在同一平台即单基SAR,也可分别安装在不同平台即双基或多基SAR。对于GNSS-SAR,由星载发射机和邻近地表的接收机等组成,其中GNSS卫星作为发射源,这些发射源可以是GPS\GLONASS\Galileo\BDS,接收机可以固定在地表、装置在航空器上或在陆面车辆上。与其他卫星系统相比,作为发射源的GNSS既有优点也有缺点。首先GNSS拥有众多的卫星星座群,对于地球表面的同一点,同时有4~8个卫星可见,来自于多颗卫星的信号有助于建立3D射线表面图,其次GNSS的导航信号具有最佳的遥感同步的特性。但是GNSS的预算功率低而且距离分辨率受发射信号的带宽限制。
4 小结GNSS+R反射测量遥感技术是利用全球导航卫星系统(GNSS)的反射信号对海洋、陆地或冰川雪地进行遥感探测的新兴手段。GNSS卫星作为可提供免费且长期稳定的L波段信号源,可充分发挥GNSS系统自身优势-全天候、全天时、覆盖范围广、时空分辨率高等,在海洋遥感上,可以进行海洋测高、反演海面风场、估计海水盐度以及海面溢油;在陆地遥感上,利用微波波段对水分的敏感的特性,可以估计土壤湿度和植物生长量;在冰川雪地遥感上,充分利用GNSS在时空分辨率上的优势,可以测量海冰厚度、积雪厚度、密度、粗糙度等。目前,GNSS+R在海洋、土壤湿度和冰雪等遥感监测等取得较好的进展。随着GNSS+R反射测量技术的发展,将来或可能监测火山、地震形变和滑坡等自然灾害。随着越来越多的多频GNSS导航卫星星座及空基增强系统,以及空基GNSS反射测量任务的实施(如接下来的FORMOSAT-7/COSMIC-2和CYGNSS任务),人们将获取更多的高时空分辨率的地表特征信息。另外,相关人员正在研发更加先进的GNSS接收机,为了能够满足不同的应用需求而改进了算法,为满足未来空基高性能任务的需求而具有准实时数据处理能力(例如具备多模GNSS反射和折射技术的下一代Tri-GNSS接收机)。未来几年里,公众使用一些大学等机构研发的低成本卫星将成为可能,GNSS信号在遥感领域的应用也将扩展到全球范围内。
| [1] | MARTIN-NEIRA M. A Passive Reflectometry and Interferometry System (PARIS) Application to Ocean Altimetry[J]. ESA Journal, 1993, 17(4): 331–355. |
| [2] | AUBER J C, BIBAUT A, RIGAL J M. Characterization of Multipath on Land and Sea at GPS Frequencies[C]//Proceedings of the 7th International Technical Meeting of the Satellite Division of the Institute of Navigation. Salt Lake City, UT:Institute of Navigation, 1994:1155-1171. https://eprints.soton.ac.uk/377882/ |
| [3] | KATZBERG S J, GARRISON JR J L. Utilizing GPS to Determine Ionospheric Delay over the Ocean[R]. NASA Technical Memorandum 4750, 1996:1-13. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19970005019.pdf |
| [4] | MARTIN-NEIRA M, CAPARRINI M, FONT-ROSSELLO J, et al. The PARIS Concept:An Experimental Demonstration of Sea Surface Altimetry Using GPS Reflected Signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 142–150. DOI:10.1109/36.898676 |
| [5] | KATZBERG S J, WALKER R A, ROLES J H, et al. First GPS Signals Reflected from the Interior of a Tropical Storm:Preliminary Results from Hurricane Michael[J]. Geophysical Research Letters, 2001, 28(10): 1981–1984. DOI:10.1029/2000GL012823 |
| [6] | GLEASON S, HODGART S, SUN Yiping, et al. Detection and Processing of Bistatically Reflected GPS Signals from Low Earth Orbit for the Purpose of Ocean Remote Sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(6): 1229–1241. DOI:10.1109/TGRS.2005.845643 |
| [7] | GLEASON S, GOMMENGINGER C, CROMWELL D. Fading Statistics and Sensing Accuracy of Ocean Scattered GNSS and Altimetry Signals[J]. Advances in Space Research, 2010, 46(2): 208–220. DOI:10.1016/j.asr.2010.03.023 |
| [8] | ZAVOROTNY V U, VORONOVICH A G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(2): 951–964. DOI:10.1109/36.841977 |
| [9] | TREUHAFT R N, LOWE S T, ZUFFADA C, et al. 2-cm GPS Altimetry over Crater Lake[J]. Geophysical Research Letters, 2001, 28(23): 4343–4346. DOI:10.1029/2001GL013815 |
| [10] | LÖFGREN J S, HAAS R, JOHANSSON J M. Monitoring Coastal Sea Level Using Reflected GNSS Signals[J]. Advances in Space Research, 2011, 47(2): 213–220. DOI:10.1016/j.asr.2010.08.015 |
| [11] | LÖFGREN J S, HAAS R. Sea Level Measurements Using Multi-frequency GPS and GLONASS Observations[J]. EURASIP Journal on Advances in Signal Processing, 2014, 10: 50–58. |
| [12] | SANTAMARíA-GÓMEZ A, WATSON C, GRAVELLE M, et al. Levelling Co-located GNSS and Tide Gauge Stations Using GNSS Reflectometry[J]. Journal of Geodesy, 2015, 89(3): 241–258. DOI:10.1007/s00190-014-0784-y |
| [13] | LOWE S T, KROGER P, FRANKLIN G, et al. A Delay/Doppler-mapping Receiver System for GPS-reflection Remote Sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(5): 1150–1163. DOI:10.1109/TGRS.2002.1010901 |
| [14] | RUFFINI G, SOULAT F, CAPARRINI M, et al. The Eddy Experiment:Accurate GNSS-R Ocean Altimetry from Low Altitude Aircraft[J]. Geophysical Research Letters, 2004, 31(12): L12306. |
| [15] | JIN Shuanggen, QIAN Xiaodong, WU X. Sea Level Change from BeiDou Navigation Satellite System-reflectometry (BDS-R):First Results and Evaluation[J]. Global and Planetary Change, 2017(149): 20–25. |
| [16] | CLARIZIA M P, RUF C, CIPOLLINI P, et al. First Spaceborne Observation of Sea Surface Height Using GPS-reflectometry[J]. Geophysical Research Letters, 2016, 43(2): 767–774. DOI:10.1002/2015GL066624 |
| [17] | ELFOUHAILY T, THOMPSON D R, LINSTROM L. Delay-Doppler Analysis of Bistatically Reflected Signals from the Ocean Surface:Theory and Application[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(3): 560–573. DOI:10.1109/TGRS.2002.1000316 |
| [18] | CLARIZIA M P, RUF C S, JALES P, et al. Spaceborne GNSS-R Minimum Variance Wind Speed Estimator[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(11): 6829–6843. DOI:10.1109/TGRS.2014.2303831 |
| [19] | CLARIZIA M P, RUF C S. Wind Speed Retrieval Algorithm for the Cyclone Global Navigation Satellite System (CYGNSS) Mission[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(8): 4419–4432. DOI:10.1109/TGRS.2016.2541343 |
| [20] | FOTI G, GOMMENGINGER C, JALES P, et al. Spaceborne GNSS Reflectometry for Ocean Winds:First Results from the UK TechDemoSat-1 Mission[J]. Geophysical Research Letters, 2015, 42(13): 5435–5441. DOI:10.1002/2015GL064204 |
| [21] | KOMJATHY A, MASLANIK J, ZAVOROTNY V U, et al. Sea Ice Remote Sensing Using Surface Reflected GPS Signals[C]//Proceedings of IEEE 2000 International Geoscience and Remote Sensing Symposium. Honolulu, HI:IEEE, 2000(7):2855-2857. |
| [22] | ZAVOROTNY V, ZUFFADA C. A Novel Technique For Characterizing The Thickness of First-Year Sea Ice With The GPS Reflected Signal[C]//American Geophysical Union, Fall Meeting.[S.l.]:AGU, 2002. http://adsabs.harvard.edu/abs/2002AGUFM.C11A0980Z |
| [23] | WIEHL M, LEGRÉSY B, DIETRICH R. Potential of Reflected GNSS Signals for ice Sheet Remote Sensing-Abstract[J]. Progress in Electromagnetics Research, 2003, 40(7): 177–205. |
| [24] | GLEASON S.Towards Sea Ice Remote Sensing with Space Detected GPS Signals:Demonstration of Technical Feasibility and Initial Consistency Check Using Low Resolution Sea Ice Information[C]//American Geophysical Union, Fall Meeting. Montreal, QC, Canada:AGU, 2010:2017-2039. |
| [25] | ALONSOARROYO A, ZAVOROTNY V U, CAMPS A. Sea Ice Detection Using GNSS-R Data from UK TDS-1[C]//Proceedings of 2016 IEEE International Geoscience and Remote Sensing Symposium. Beijing, China:IEEE, 2016:2001-2004. |
| [26] | 张云, 郭建京, 袁国良, 等. 基于GNSS反射信号的海冰检测的研究[J]. 全球定位系统, 2013, 38(2): 1–6. ZHANG Yun, GUO Jianjing, YUAN Guoliang, et al. Sea Ice Study Bases on GNSS-R Signal[J]. GNSS World of China, 2013, 38(2): 1–6. |
| [27] | 尹聪, 曹云昌, 朱彬, 等. GNSS-R海冰遥感的模拟和试验验证[J]. 华中师范大学学报(自然科学版), 2016, 50(4): 612–618. YIN Cong, CAO Yunchang, ZHU Bin, et al. Simulation and Experimental Verification of Sea Ice Remote Sensing Using GNSS-R[J]. Journal of Central China Normal University (Natural Sciences), 2016, 50(4): 612–618. |
| [28] | ZAVOROTNY V U, VORONOVICH A G. Bistatic GPS Signal Reflections at Various Polarizations from Rough Land Surface with Moisture Content[C]//Proceedings of IEEE 2000 International Geoscience and Remote Sensing Symposium. Honolulu, HI:IEEE, 2000:2852-2854. |
| [29] | RODRIGUEZ-ALVAREZ N, CAMPS A, VALL-LLOSSERA M, et al. Land Geophysical Parameters Retrieval Using the Interference Pattern GNSS-R Technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 71–84. DOI:10.1109/TGRS.2010.2049023 |
| [30] | LARSON K M, SMALL E E, GUTMANN E, et al. Using GPS Multipath to Measure Soil Moisture Fluctuations:Initial Results[J]. GPS Solutions, 2008, 12(3): 173–177. DOI:10.1007/s10291-007-0076-6 |
| [31] | ZAVOROTNY V U, LARSON K M, BRAUN J J, et al. A Physical Model for GPS Multipath Caused by Land Reflections:Toward Bare Soil Moisture Retrievals[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2010, 3(1): 100–110. DOI:10.1109/JSTARS.2009.2033608 |
| [32] | NIEVINSKI F G, LARSON K M. Forward Modeling of GPS Multipath for Near-surface Reflectometry and Positioning Applications[J]. GPS Solutions, 2014, 18(2): 309–322. DOI:10.1007/s10291-013-0331-y |
| [33] | WAN Wei, BAI Weihua, ZHAO Limin, et al. Initial Results of China's GNSS-R Airborne Campaign:Soil Moisture Retrievals[J]. Science Bulletin, 2015, 60(10): 964–971. DOI:10.1007/s11434-015-0789-9 |
| [34] | SMALL E E, LARSON K M, BRAUN J J. Sensing Vegetation Growth with Reflected GPS Signals[J]. Geophysical Research Letters, 2010, 37(12): L12401. |
| [35] | CHEW C C, SMALL E E, LARSON K M, et al. Effects of Near-surface Soil Moisture on GPS SNR Data:Development of a Retrieval Algorithm for Soil Moisture[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 537–543. DOI:10.1109/TGRS.2013.2242332 |
| [36] | CHEN Qiang, WON D, AKOS D M, et al. Vegetation Sensing Using GPS Interferometric Reflectometry:Experimental Results with a Horizontally Polarized Antenna[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(10): 4771–4780. DOI:10.1109/JSTARS.2016.2565687 |
| [37] | LARSON K M, GUTMANN E D, ZAVOROTNY V U, et al. Can We Measure Snow Depth with GPS Receivers?[J]. Geophysical Research Letters, 2009, 36(17): L17502. DOI:10.1029/2009GL039430 |
| [38] | NIEVINSKI F G, LARSON K M. Inverse Modeling of GPS Multipath for Snow Depth Estimation:Part Ⅱ:Application and Validation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(10): 6564–6573. DOI:10.1109/TGRS.2013.2297688 |
| [39] | JIN Shuanggen, NAJIBI N. Sensing Snow Height and Surface Temperature Variations in Greenland from GPS Reflected Signals[J]. Advances in Space Research, 2014, 53(11): 1623–1633. DOI:10.1016/j.asr.2014.03.005 |
| [40] | JIN Shuanggen, QIAN Xiaodong, KUTOGLU H. Snow Depth Variations Estimated from GPS-reflectometry:A Case Study in Alaska from L2P SNR Data[J]. Remote Sensing, 2016, 8(1): 63. DOI:10.3390/rs8010063 |
| [41] | QIAN Xiaodong, JIN Shuanggen. Estimation of Snow Depth from GLONASS SNR and Phase-based Multipath Reflectometry[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensin, 2016, 9(10): 4817–4823. DOI:10.1109/JSTARS.2016.2560763 |
| [42] | RUF C S, GLEASON S, JELENAK Z, et al. The CYGNSS Nanosatellite Constellation Hurricane Mission[C]//Proceedings of 2012 IEEE International Geoscience and Remote Sensing Symposium. Munich, Germany:IEEE, 2012:214-216. |