2. 北京航空航天大学电子信息工程学院, 北京 100083
2. School of Electronic and Information Engineering, Beihang University, Beijing 100083, China
2012年12月27日,北斗区域卫星导航系统宣布正式投入运行。目前北斗卫星导航系统的定位、导航和授时(PNT)服务性能已基本达到或超过设计性能指标[1-5]。北斗高精度定位的研究一直备受关注[6-8]。为满足国民经济各行业和人们日常生活对北斗高精度位置服务的需求,2014年,北斗地基增强系统(NBASS)作为我国北斗卫星导航系统的一个重要组成部分,正式启动研制建设,一期工程建设已于2016年完成,建成全国范围广域分布的150个北斗/GNSS实时连续测站,可提供米级、分米、厘米级的高精度实时定位服务。
本文采用IGS[9]、MGEX[10]与NBASS观测网络的实时观测数据,实现北斗高精度广域服务系统,实时处理北斗高精度轨道、钟差、区域电离层产品。在对各类产品的精度进行评估分析的基础上,通过北斗双频、单频实时精密单点定位等多种定位模式对实时服务性能进行评估与分析。
1 北斗实时高精度产品处理策略北斗实时高精度产品包括实时卫星轨道、卫星钟差、电离层改正产品。数据处理系统由轨道、钟差、电离层3个处理器组成,实时处理系统产品处理综合考虑产品更新时间、产品精度以及观测数据质量等因素,处理流程如图 1所示。北斗实时轨道与钟差处理采用北斗/GPS融合处理的方法[11-12],基于武汉大学研制的高精度卫星导航数据处理与分析软件PANDA(position and navigation data analysist)[13-14]。实时轨道处理采用每小时准实时观测数据文件进行弧段拼接,通过长弧段(72 h)批处理解算轨道参数与动力学参数,并预报24 h弧段作为实时轨道产品,处理更新间隔为3 h。考虑到批处理解算弧段长达72 h,为了更好地描述卫星受力情况,定轨解算中每隔12 h估计一组速度脉冲来提高力模型估计精度。实时卫星钟差处理采用每秒更新的实时观测数据流,固定卫星预报轨道以及测站坐标,通过滤波方式逐历元处理,接收机端的信号系统间偏差(ISB)按天常数进行估计。观测模型采用非差伪距与相位历元间差分组合模型[11, 15],卫星钟差初始钟偏收敛时间设定为20 min。
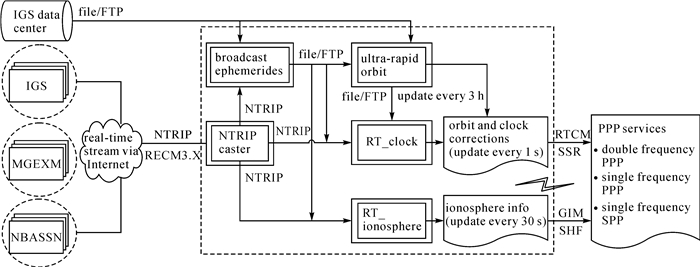
|
| 图 1 北斗实时精密产品处理流程 Fig. 1 Flow chart of BDS real-time precise products processing |
北斗实时轨道处理采用无电离层组合的非差伪距(PC)和相位(LC)观测值,根据卫星高度角进行加权。GPS的卫星天线相位中心采用igs08.atx改正,北斗卫星采用ESA估计的参数改正。接收机端的天线相位中心改正:GPS卫星采用igs08.atx改正,北斗卫星由于改正产品尚未发布,暂不考虑。对于卫星姿态模型,GPS采用Kouba姿态模型[16],北斗GEO采用零偏模型,北斗IGSO/MEO采用动偏、零偏切换的姿态模型[11],详细的处理策略见表 1和表 2。北斗实时轨道与钟差解算使用的测站及其分布可参见文献[17]。
| 参数 | 轨道处理 | 钟差处理 |
| 估计器 | LSQ | SRIF |
| 数据处理间隔 | 300 s | 1 s |
| 模糊度 | GPS和IGSO/MEO卫星分别固定 | 历元差分消除 |
| 地球自转参数 | 强约束估计 | 固定 |
| 测站坐标 | 强约束估计 | 固定 |
| 观测量 | 非差伪距和相位无电离层组合观测值 | |
| 观测值加权 | 根据高度角加权,p=1, e > 30°; p=sin2e, e≤30° (p为观测值权值;e为卫星高度角) | |
| 截止高度角 | 7° | |
| 卫星天线相位中心改正 | GPS采用igs08.atx改正[19];北斗卫星采用ESA估计的参数改正[20] | |
| 卫星姿态模型 | GPS采用Kouba姿态模型[16];北斗GEO采用零偏模型;北斗IGSO/MEO采用动偏、零偏切换的姿态模型[11] | |
| 相位缠绕 | 模型改正[20] | |
| 伪距偏差 | 模型改正北斗伪距偏差[22] | |
| 对流层延迟 | Saastamoinen模型[23]+GPT2模型[24]+随机游走估计 | |
| 卫星钟差 | 白噪声估计 | |
| 接收机钟差 | 白噪声估计 | |
| 系统间偏差 | 采用零均值基准,常参数估计 | |
由于目前北斗定位服务范围主要在中国区域,因此,本文仅采用NBASS网的北斗/GPS实时观测数据处理生成区域电离层改正数。区域电离层改正处理采用电离层延迟相关的相位平滑伪距(P4L4) 获得精确的斜路径总电子含量,选择5阶球谐函数建立垂直总电子含量VTEC改正模型。建立区域电离层模型时,由于卫星观测值不连续或者观测值很少,导致测站接收机和卫星硬件延迟偏差(DCB)的分离会产生一定的偏差,考虑到卫星硬件延迟偏差比较稳定的特点,本文固定IGS提供的卫星硬件延迟偏差,实时待估参数包括36个球谐参数和接收机DCB参数,电离层处理更新时间30 s。电离层处理采用国内NBASS网150个测站实时观测数据流,测站分布如图 2所示。
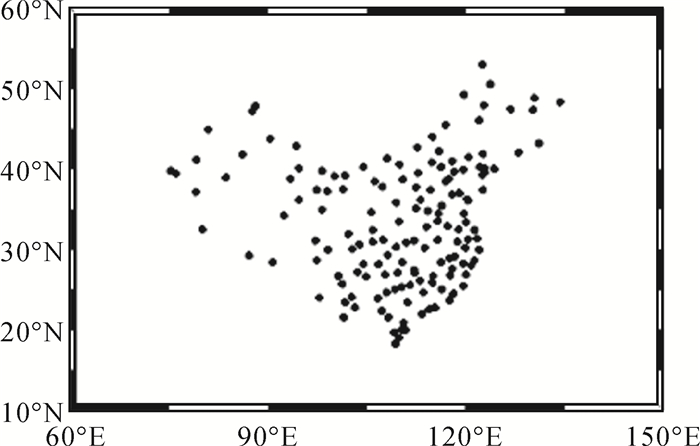
|
| 图 2 NBASS网实时测站分布 Fig. 2 Distribution of NBASS real-time network stations (本图为专题内容示意图,不涉及国家版图信息) |
2 实时产品精度评估
实时产品精度评估分为轨道精度、URE、电离层精度评估分析。北斗卫星实时轨道评估将每3 h预报的轨道拼接成一天24 h的轨道,与武汉大学(WHU)北斗事后精密轨道进行比较,分别统计径向(R)、法向(C)、切向(A)3个方向的精度;卫星钟差评估考虑轨道与钟差的自洽特性[24],通过计算实时产品URE进行评估,其计算公式如式(1),URE评估选取WHU北斗事后精密钟差产品作为参考值,评估采用的历元时间间隔为30 s。
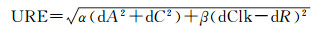 (1)
(1)
式中,dR、dA、dC分别为卫星径向、切向和法向的轨道误差;dClk为卫星钟差误差(转换为等效距离单位);α和β为系数常数
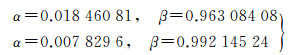 (2)
(2)
本文对2017年DOY 021—028连续8 d的实时精密轨道产品进行评估分析,统计结果如图 3所示。从图中可以看出:IGSO与MEO卫星径向精度均优于10 cm,三维精度约30 cm,相比较IGSO与MEO卫星,GEO卫星的定轨精度较差,尤其在切向存在系统性偏差,GEO卫星定轨精度不佳主要是由于其静地特性造成的。需要说明的是IGSO卫星C07卫星由于在2017年DOY 008—2017年DOY 020处于零偏状态,而轨道处理策略采用3天解,有3 d的轨道弧度处于动零姿态转换期间,影响精密定轨与预报精度。另外,通过3 h弧段更新实现实时轨道确定中,轨道更换期间相邻弧段轨道存在不连续情况,轨道差值在径向达到5 cm左右,而在切向差异达到分米量级。
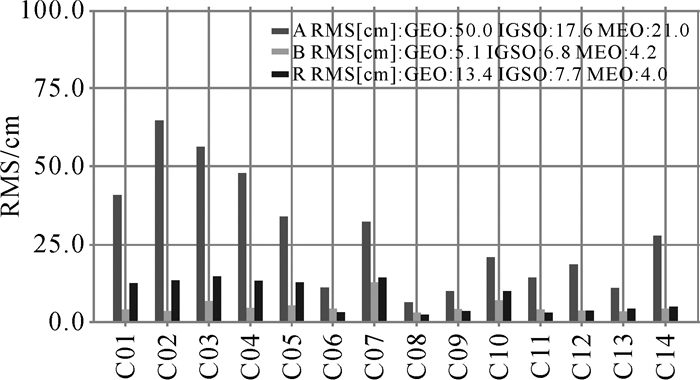
|
| 图 3 北斗实时轨道精度统计 Fig. 3 BDS real-time orbit accuracy statistics |
2.2 实时钟差产品
以下对2017年DOY 021—028连续8 d的北斗实时轨道与钟差产品的URE进行偏差(BIAS)和STD统计分析(如图 4所示),其中C01为参考卫星,由于BIAS可以被相位模糊度吸收,因此BIAS的大小仅影响伪距单点定位精度及PPP收敛时间,STD大小影响PPP收敛后的定位精度。从图中可以看出:北斗URE的BIAS为0.5~1.5 m,STD为1 cm左右,满足米级伪距定位与厘米级双频PPP定位要求。总体上,GEO、IGSO卫星URE的BIAS和STD优于MEO卫星。分析原因,主要是因为境外MGEX提供北斗观测站数量少且分布不均匀,影响MEO卫星的实时钟差估计精度。另外,上节分析北斗轨道更换期间相邻弧段间的差值达到分米级,虽然北斗钟差可以吸收部分差值影响,但对URE时间序列还存在一定程度的影响。图 5给出了弧段更换的URE跳跃绝对值的统计信息,可以看出平均跳跃值为2 cm,略大于URE的STD,最大值达到10 cm左右,将影响北斗双频相位的精度。因此,提高轨道弧段更新期间的轨道平滑性,降低预报轨道弧段间差值对URE的影响将进一步研究。
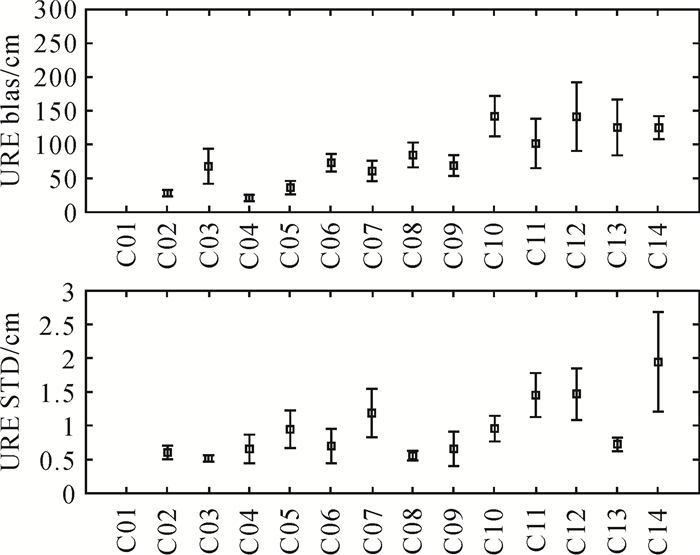
|
| 图 4 BDS卫星URE所有天BIAS和STD统计图 Fig. 4 Bias and STD of BDS URE in all days 方格表示均值,误差棒为标准方差 |
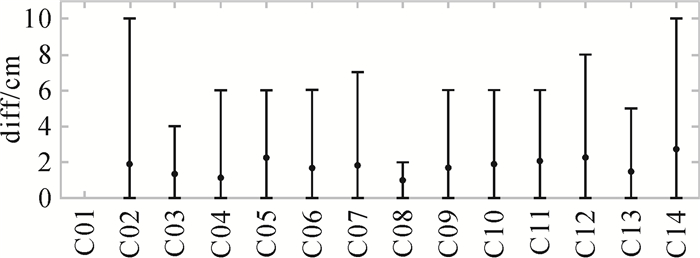
|
| 图 5 弧段更换的URE跳跃绝对值的统计 Fig. 5 Statistics of absolute value of URE jumps during orbits switch 圆点表示均值,误差棒的上端和下端表示最大值和最小值 |
2.3 实时电离层产品精度
为了更为客观地评估实时电离层精度,采用实测数据计算电离层残差进行RMS统计分析。本文采用不参与区域电离层建模的全国分布的陆态网测站2017 DOY 021—028连续8 d的GPS观测数据对实时区域电离层产品进行评估,图 6给出评估结果。从图 6(a)中不同测站的平均电离层残差可以看出,由于区域电离层模型仅采用中国区域的测站观测值,边缘区域的电离层精度在6 TECU左右,中纬度区域精度达到2.0 TECU左右,低纬度区域精度为4.0 TECU左右,统计中国区域陆态网测站,电离层精度平均为3.4 TECU。
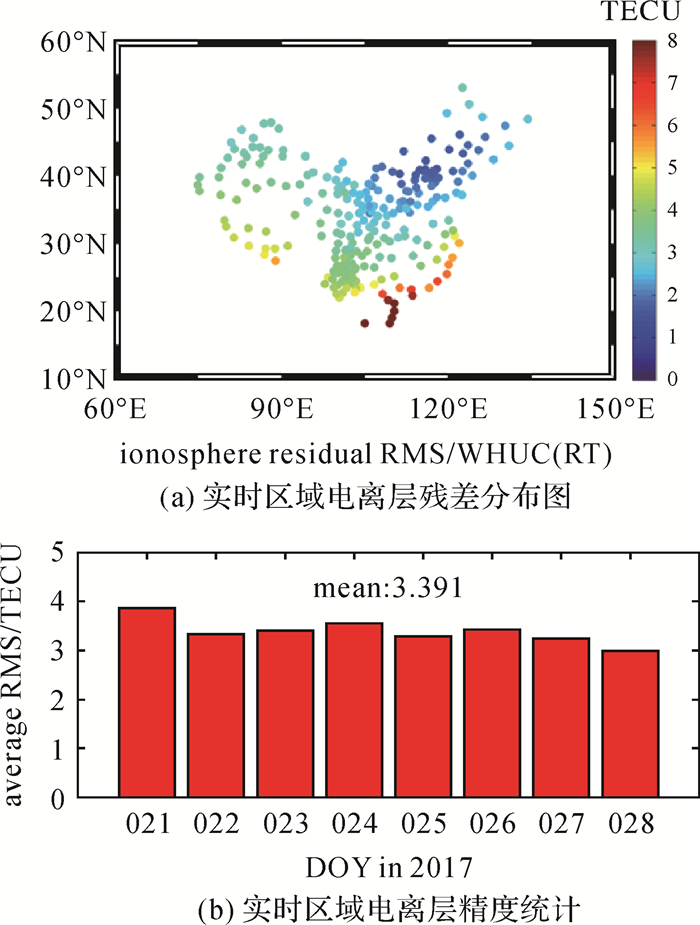
|
| 图 6 电离层残差分布与实时精度统计 Fig. 6 Residual distribution and accuracy of real-time regional ionospheric delay (本图为专题内容示意图,不涉及国家版图信息) |
3 北斗实时精密单点定位性能分析
为了评估服务系统北斗实时定位性能,本文选取全国均匀分布的26个测站(未参与定轨以及钟差估计)分别进行单北斗、单GPS以及北斗/GPS 3种模式的双频PPP(DF-PPP)、单频PPP(SF-PPP)以及单频伪距单点动态定位(SF-SPP)分析,统计分析2017 DOY 021—028连续8 d不同定位模式的平面和高程定位精度及收敛时间(均按95%置信度统计)[26-27]。
3.1 定位精度分析图 7分别给出了测站单北斗、单GPS以及北斗/GPS双频PPP平均精度。从图中可以得出:北斗双频PPP精度存在明显的区域特征,高程方向尤为显著,这主要与目前北斗系统的卫星星座构成与分布相关。高纬度地区以及西部边缘地区的定位精度较差,如DZAL、DZWI、DZKR测站,平面约0.2 m,高程约0.3 m;中部地区定位精度相对较高,平面优于0.1 m,高程优于0.2 m。单GPS双频PPP定位精度分布均匀,平面和高程方向均优于0.1 m。图 7(c)给出北斗/GPS组合PPP不同测站定位精度,与单北斗和单GPS相比,双系统PPP均有一定提升,如DZYS测站,平面和高程方向,相对单北斗分别提升41.9%和26.9%,相对单GPS提升7.0%和15.8%,表明多系统可以提供更高精度的定位服务。
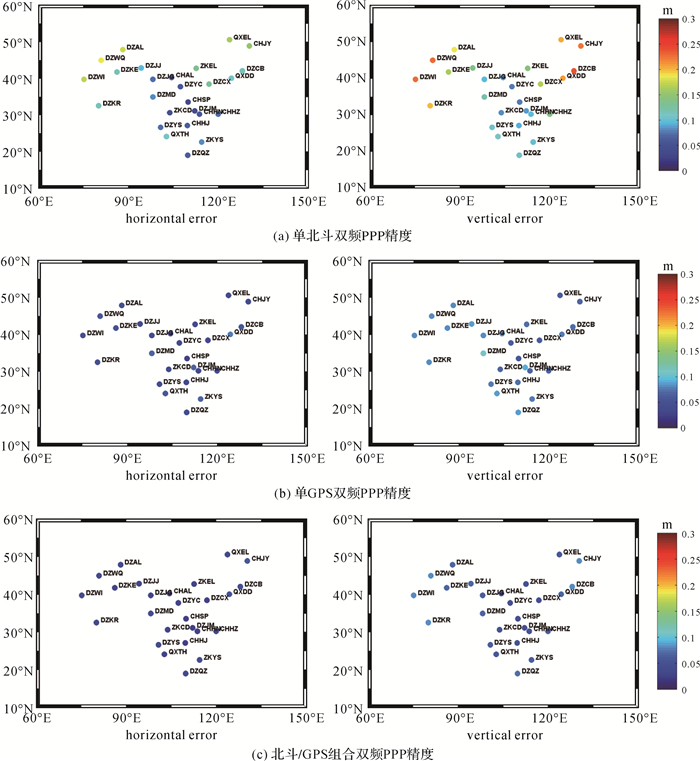
|
| 图 7 北斗、GPS及其组合的双频PPP精度(95%) Fig. 7 BDS, GPS and BDS/GPS real-time dual-frequency PPP accuracy at 95% confidence level (本图为专题内容示意图,不涉及国家版图信息) |
图 8给出26个测站连续8 d北斗、GPS以及北斗/GPS单频PPP平面和高程方向的平均精度。与双频PPP不同,单频PPP除了卫星轨道、钟差影响外,电离层改正对单频PPP定位性能影响较大。因此,北斗、GPS以及北斗/GPS单频PPP均表现出一定的区域性:对于单北斗单频PPP,中部地区定位精度最好,可达到平面0.5 m,高程优于1.0 m,这与北斗系统区域星座观测条件和电离层改正精度综合影响相关;对于北斗/GPS组合单频PPP模式,高纬度地区可实现平面0.3 m,高程0.5 m。受电离层改正精度的影响,北斗、GPS以及北斗/GPS单频PPP在低纬度地区精度相对较低,如海南的DZQZ的北斗/GPS定位精度平面约0.6 m、高程约0.8 m,精度明显比其他区域测站差。
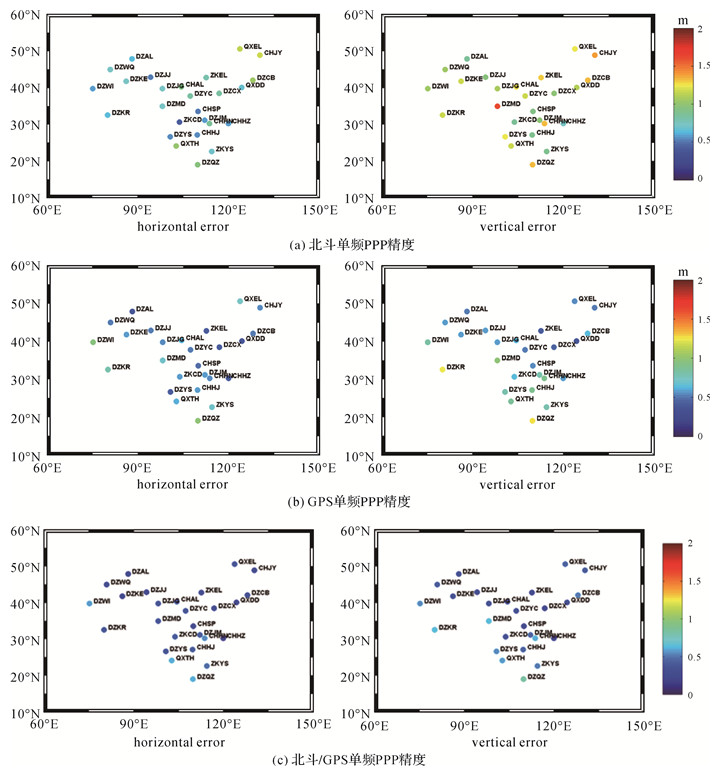
|
| 图 8 北斗、GPS及其组合的单频PPP精度(95%) Fig. 8 BDS, GPS and BDS/GPS real-time single-frequency PPP accuracy at 95% confidence level (本图为专题内容示意图,不涉及国家版图信息) |
对于高精度导航用户应用,一般采用单频伪距定位实现。以下验证分析实时系统可提供伪距高精度定位性能。图 9给出26个测站北斗、GPS以及北斗/GPS连续8 d的SF-SPP平均精度。SF-SPP主要受到电离层改正精度的影响,因此SF-SPP的精度在一定程度上可以验证实时电离层改正模型的精度。与SF-PPP类似,3种定位模式下(北斗、GPS以及北斗/GPS)均表现出一定的区域性。比较发现,西部、东北部和南部地区的测站在不同定位模式下的精度均相对降低,如DZWI、CHJY、DZQZ等测站。分析原因,一方面电离层在低纬度地区较为活跃,改正模型精度不高,另一方面采用低阶球谐模型建立区域改正模型边缘性,在边缘地区精度较低。除边缘地区外,北斗单频SPP可达到平面2 m,高程3 m的定位精度需求,GPS和北斗/GPS单频SPP精度相对较高,可实现平面优于1.5 m,高程优于2 m的定位精度。
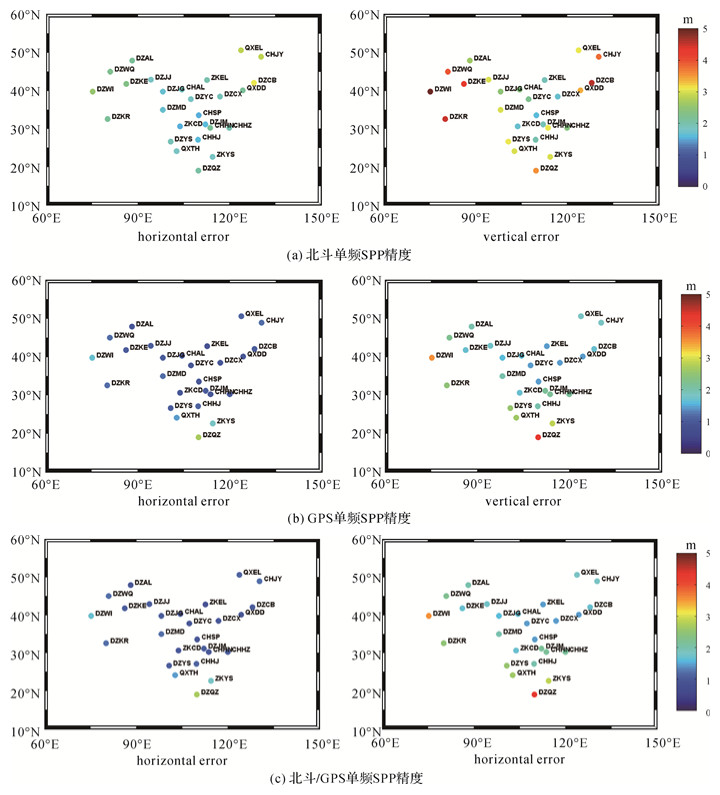
|
| 图 9 北斗、GPS及其组合的单频SPP精度(95%) Fig. 9 BDS, GPS and BDS/GPS real-time single-frequency SPP accuracy at 95% confidence level (本图为专题内容示意图,不涉及国家版图信息) |
3.2 收敛时间分析
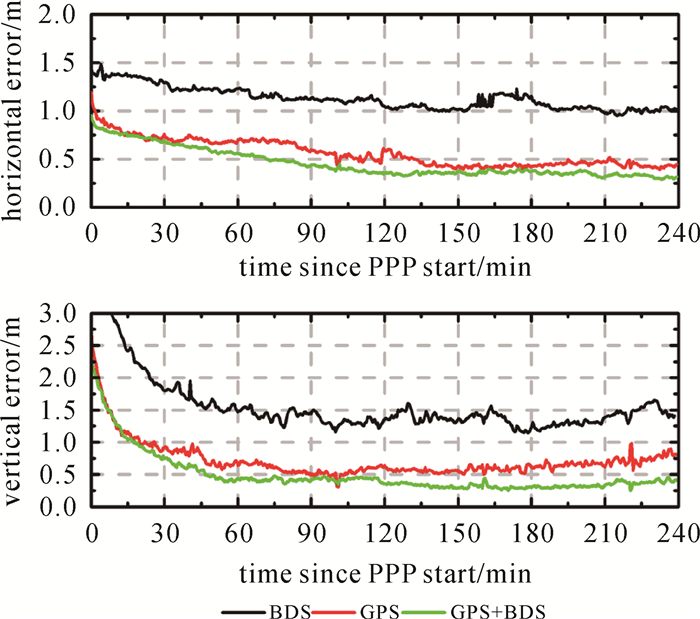
实时动态PPP处理中,收敛时间是用户非常关注的性能指标。本文分别统计了2017年DOY021—028连续8 d 26个测站北斗、GPS以及北斗/GPS单双频PPP的收敛时间。以全部定位样本(826) 平面方向和高程方向定位精度(95%置信度)的时间序列分析不同定位模式的收敛时间。图 10和图 11分别给出北斗、GPS以及北斗/GPS双频PPP和单频PPP的收敛时间序列。可以看出,北斗单频、双频PPP的收敛性能均差于GPS,其中,北斗双频PPP平面和高程方向收敛至0.2 m(95%)需要90~120 min,且收敛后北斗双频PPP平面和高程方向精度约0.2 m(95%)。与单北斗双频PPP相比,GPS双频PPP收敛时间较短,平面和高程达到0.2 m的时间仅需要50 min,且收敛后可实现厘米级定位,但是需要约2 h。通过北斗和GPS组合后,双频PPP性能明显改善,20 min即可实现平面和高程0.2 m的定位精度,且实现厘米级定位的时间也大大缩短,仅需45 min左右。
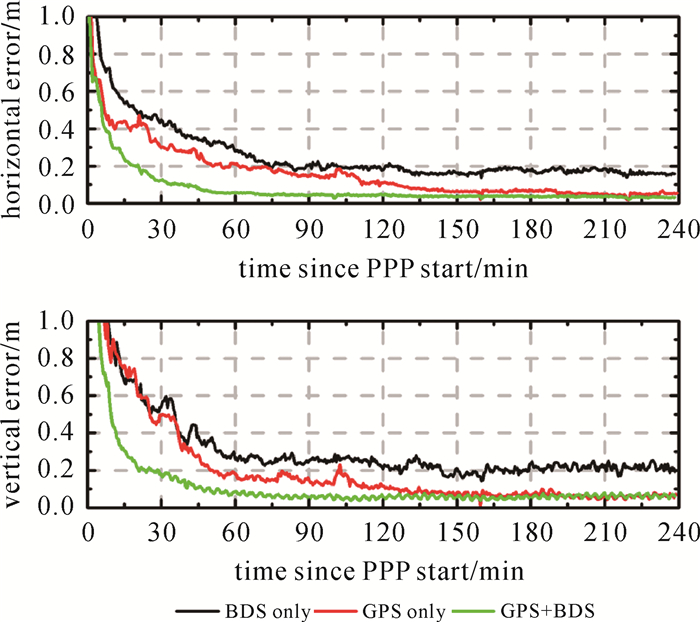
|
| 图 10 双频PPP收敛时间序列 Fig. 10 The convergence time of real-time dual-frequency PPP |
|
| 图 11 单频PPP收敛时间序列 Fig. 11 The convergence time of real-time single-frequency PPP |
与双频PPP相比,单频PPP有类似的结论,北斗单频PPP收敛以及定位性能最差。北斗单频PPP收敛后可实现平面1.0 m,高程优于1.5 m的定位精度,但是收敛时间较长。单GPS单频PPP仅需要1~2 min即可实现平面优于1 m的定位精度,高程方向收敛相对较慢,需要16 min左右才能实现优于1.0 m的定位精度。使用北斗和GPS组合单频PPP后,收敛至1.0 m需要的时间并未有明显改善,但是大大提升了收敛后的定位精度,平面和高程精度均优于0.5 m。
4 结论本文采用IGS、MGEX、北斗地基增强网的实时观测数据,基于实时精密单点定位模式,给出了北斗实时卫星轨道、实时卫星钟差、区域电离层产品的处理方法与策略,实现中国区域的北斗双频PPP、北斗单频PPP、北斗单频伪距单点定位服务。通过对实时产品性能的评估结果表明:北斗卫星实时轨道与钟差产品URE精度约为2.0 cm,实时电离层精度优于4 TECU。
对全国分布的26个实时测站动态定位精度(95%置信度)评估分析表明:北斗双频PPP精度存在明显的区域特征,高纬度以及西部边缘地区的定位精度平面约0.2 m,高程约0.3 m;中部地区定位精度平面优于0.1 m,高程优于0.2 m,接近GPS实时PPP精度水平;北斗与GPS融合可以提高单北斗、单GPS的定位性能,尤其显著加快了PPP收敛时间,收敛时间缩短到20 min以内。另外,除边缘地区外,北斗单频PPP可实现平面0.5 m,高程1.0 m;北斗单频伪距单点定位可实现平面2.0 m,高程3.0 m。
整体性能分析表明,北斗广域实时精密定位与GPS相比目前仍存在一定的差距,尤其是收敛时间偏长,是GPS的两倍左右。主要原因是由北斗卫星的卫星星座构成特点造成的,且北斗卫星(尤其是北斗GEO卫星)实时轨道、钟差精度与GPS相比仍存在一定差距,并存在动零姿态转换期间轨道钟差精度进下降、实时预报轨道模式与方法不完善等有待进一步研究的问题。另外,相关结果表明通过北斗/GPS组合定位可以显著改善单北斗、单GPS的定位性能,体现了北斗系统对实时定位的贡献。
致谢: 特别感谢武汉大学卫星导航定位技术研究中心辜声峰、张卫星、戴小蕾、李显杰、郭海林为本文的数据处理、分析做出的相应工作。
| [1] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [2] | YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Science Bulletin, 2011, 56(26): 2813–2819. DOI:10.1007/s11434-011-4627-4 |
| [3] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Initial Assessment of the Compass/BeiDou-2 Regional Navigation Satellite System[J]. GPS Solutions, 2013, 17(2): 211–222. DOI:10.1007/s10291-012-0272-x |
| [4] | SHI Chuang, ZAHO Qile, HU Zhigang, et al. Precise Relative Positioning Using Real Tracking Data from Compass GEO and IGSO Satellites[J]. GPS Solutions, 2013, 17(1): 103–119. DOI:10.1007/s10291-012-0264-x |
| [5] | 杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 57(1): 144–152. YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J]. Science China:Earth Sciences, 2014, 57(1): 144–152. |
| [6] | HE Haibo, LI Jinlong, YANG Yuanxi, et al. Performance Assessment of Single-and Dual-frequency BeiDou/GPS Single-epoch Kinematic Positioning[J]. GPS Solutions, 2014, 18(3): 393–403. DOI:10.1007/s10291-013-0339-3 |
| [7] | GU Shengfeng, LOU Yidong, SHI Chuang, et al. BeiDou Phase Bias Estimation and Its Application in Precise Point Positioning with Triple-frequency Observable[J]. Journal of Geodesy, 2015, 89(10): 979–992. DOI:10.1007/s00190-015-0827-z |
| [8] | 朱永兴, 冯来平, 贾小林, 等. 北斗区域导航系统的PPP精度分析[J]. 测绘学报, 2015, 44(4): 377–383. ZHU Yongxing, FENG Laiping, JIA Xiaolin, et al. The PPP Precision Analysis Based on BDS Regional Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 377–383. DOI:10.11947/j.AGCS.2015.20140082 |
| [9] | DOW J M, NEILAN R E, RIZOS C. The International GNSS Service in a Changing Landscape of Global Navigation Satellite Systems[J]. Journal of Geodesy, 2009, 83(3-4): 191–198. DOI:10.1007/s00190-008-0300-3 |
| [10] | MONTENBRUCK O, STEIGENBERGER P, KHACHIKYAN R, et al. IGS-MGEX:Preparing the Ground for Multi-constellation GNSS Science[J]. Inside GNSS, 2014, 9(1): 42–49. |
| [11] | DAI Xiaolei, GE Maorong, LOU Yidong, et al. Estimating the Yaw-attitude of BDS IGSO and MEO Satellites[J]. Journal of Geodesy, 2015, 89(10): 1005–1018. DOI:10.1007/s00190-015-0829-x |
| [12] | ZHANG Weixing, LOU Yidong, GU Shengfeng, et al. Joint Estimation of GPS/BDS Real-time Clocks and Initial Results[J]. GPS Solutions, 2016, 20(4): 665–676. DOI:10.1007/s10291-015-0476-y |
| [13] | LIU Jingnan, GE Maorong. PANDA Software and Its Preliminary Result of Positioning and Orbit Determination[J]. Wuhan University Journal of Natural Sciences, 2003, 8(2B): 603–609. |
| [14] | SHI Chuang, ZHAO Qile, GENG Jianghui, et al. Recent Development of PANDA Software in GNSS Data Processing[C]//Proceedings of the International Conference on Earth Observation Data Processing and Analysis. Wuhan, China:SPIE, 2008. |
| [15] | GE Maorong, CHEN Junping, DOUŠA J, et al. A Computationally Efficient Approach for Estimating High-rate Satellite Clock Corrections in Realtime[J]. GPS Solutions, 2012, 16(1): 9–17. DOI:10.1007/s10291-011-0206-z |
| [16] | KOUBA J. A Simplified Yaw-attitude Model for Eclipsing GPS Satellites[J]. GPS Solutions, 2009, 13(1): 1–12. DOI:10.1007/s10291-008-0092-1 |
| [17] | SHI Chuang, ZHENG Fu, LOU Yidong, et al. National BDS Augmentation Service System (NBASS) of China:Progress and Assessment[J]. Remote Sensing, 2017, 9(8): 837. DOI:10.3390/rs9080837 |
| [18] | RODRIGUEZ-SOLANO C, HUGENTOBLER U, STEIGENBERGER P. Solar Radiation Pressure and Attitude Modeling of GNSS Satellites[C]//Proceedings of the American Geophysical Union Fall Meeting 2011. San Francisco:AGU, 2011. |
| [19] | SCHMID R, STEIGENBERGER P, GENDT G, et al. Generation of a Consistent Absolute Phase-center Correction Model for GPS Receiver and Satellite Antennas[J]. Journal of Geodesy, 2007, 81(12): 781–798. DOI:10.1007/s00190-007-0148-y |
| [20] | DILSSNER F, SPRINGER T, SCHÖNEMANN E, et al. Estimation of Satellite Antenna Phase Center Corrections for BeiDou[C]//Proceedings of the IGS Workshop 2014. Pasadena:IGS, 2014:23-27. |
| [21] | WU J T, WU S C, HAJJ G A, et al. Effects of Antenna Orientation on GPS Carrier Phase[C]//Astrodynamics 1991:Proceedings of the AAS/AIAA Astrodynamics Conference. San Diego, CA:Univelt Inc., 1992:1647-1660. |
| [22] | LOU Yidong, GONG Xiaopeng, GU Shengfeng, et al. Assessment of Code Bias Variations of BDS Triple-frequency Signals and Their Impacts on Ambiguity Resolution for Long Baselines[J]. GPS Solutions, 2017, 21(1): 177–186. DOI:10.1007/s10291-016-0514-4 |
| [23] | SAASTAMOINEN J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites[M]//HENRIKSEN S W, MANCINI A, CHOVITZ B H. The Use of Artificial Satellites for Geodesy. Washington DC:American Geophysical Union, 1972:247-251. |
| [24] | LAGLER K, SCHINDELEGGER M, BÖHM J, et al. GPT2:Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1069–1073. DOI:10.1002/grl.50288 |
| [25] | LOU Yidong, ZHANG Weixing, WANG C, et al. The Impact of Orbital Errors on the Estimation of Satellite Clock Errors and PPP[J]. Advances in Space Research, 2014, 54(8): 1571–1580. DOI:10.1016/j.asr.2014.06.012 |
| [26] | SHI Chuang, GU Shengfeng, LOU Yidong, et al. An Improved Approach to Model Ionospheric Delays for Single-frequency Precise Point Positioning[J]. Advances in Space Research, 2012, 49(12): 1698–1708. DOI:10.1016/j.asr.2012.03.016 |
| [27] | LOU Yidong, ZHENG Fu, GU Shengfeng, et al. Multi-GNSS Precise Point Positioning with Raw Single-frequency and Dual-frequency Measurement Models[J]. GPS Solutions, 2016, 20(4): 849–862. DOI:10.1007/s10291-015-0495-8 |


