地球参考系统是表达地球空间信息及描述地球形状的基础。大地测量系统规定了大地测量的起算基准、尺度标准及实现的理论与方法,具体体现为坐标原点的位置、长度单位、坐标轴指向,同时定义一个与之相对应的椭球。在此基础上采用大地测量手段实现大地测量参考框架,框架实现的精度与我们对地球的认识及采取的技术手段有关。我国经济建设初期及经济发展到一定阶段,分别基于克拉索夫斯基椭球及国际IUGG推荐的1975椭球,采用经典大地测量手段建立和实现了1954北京坐标系、1980西安坐标系两个参心坐标系[1]。在此坐标系下测制了不同比例尺地形图,为国民经济发展与建设提供了基础数据。随着空间大地测量技术的发展,特别是卫星导航系统的发展,基于国际地球参考系ITRS定义实现了系列国际地球参考框架(international terrestrial reference frame,ITRF),并成为国际标准为各国所接受。各国基于ITRF框架建立和实现了本国地心坐标框架,在我国即为2000国家大地坐标系(CGCS2000)。
1 我国地心坐标框架实现和维持技术现状从技术实现上说,CGCS2000是基于ITRF97框架建立起来的区域地心参考框架。原点为包括海洋和大气的整个地球的质量中心;Z轴由原点指向历元2000.0的地球参考极的方向。基于这个框架我国完成了已有测绘成果向CGCS2000的转换[2-5],至此我国已实现了基于GPS技术的地心坐标框架。但从后续ITRF框架的发展来看,ITRF97框架在基准的确定上和后续框架有很大的区别,ITRF2000从基准实现上来说是一个转折点。ITRF97框架基准定义是由VLBI、SLR、GPS一起参与的,由于GPS高程序列周期性特性直接影响了基准尺度的精度(引起尺度上差异为1~2×10-9),因此自ITRF2000以后,框架基准的确定不再使用GPS技术。而从框架维持上分析,地球框架的理想实现应该是由固连在地球表面的一系列基准站组成,具体表现为这些基准站在某一历元下的坐标和速度场。CGCS2000是基于ITRF97框架实现在2000历元下的坐标,却没有与之相适应的速度场。即便基于此基准确定了速度场,与后续框架相比速度场的精度差异较大,下面以ITRF97和ITRF2014框架为例,给出国际IGS站分别以ITRF97框架下的速度场和ITRF2014下的速度场进行归算,得到在2000历元下的归算坐标,并与各测站在2000历元平差坐标进行比较后的差异(见图 1),统计分析见表 1。
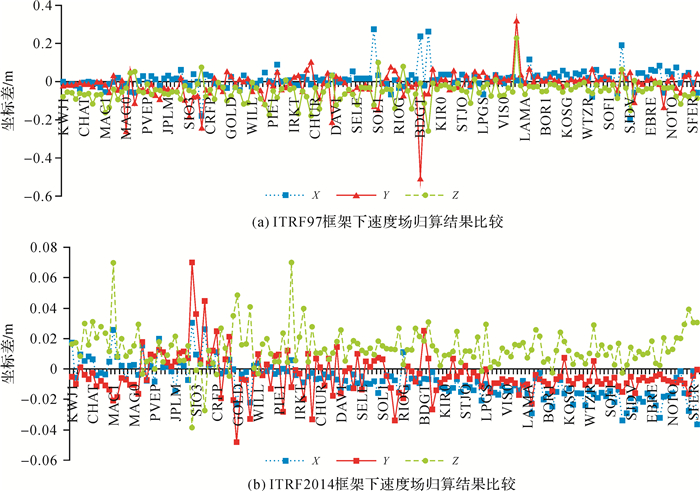
|
| 图 1 不同框架下速度场归算结果比较 Fig. 1 The difference of coordinates transformed derived from velocity field under different frames |
| ITRF97 | ITRF2014 | ||||||
| X | Y | Z | X | Y | Z | ||
| 平均值 | 0.012 | -0.011 | -0.049 | -0.007 | -0.004 | 0.013 | |
| 方差 | 0.051 | 0.061 | 0.053 | 0.011 | 0.013 | 0.012 | |
从上述分析可以看出,ITRF2014框架速度场相比ITRF97速度场的精度有显著提高。因此,框架站点坐标的历元归算建议采用后续精度高的速度场完成相应的现历元坐标到CGCS2000的归算。目前CGCS2000速度场是基于ITRF2005框架确定的速度场,严格来说与CGCS2000框架不匹配,但考虑到框架速度场本身的精度及目前大多数应用,即是将现框架现历元下的坐标向CGCS2000所在历元的归算,而不是从时间尺度上向前推算,因此归算后可以满足厘米级精度的需求。
2 全球基准的实现与维持技术发展目前国际上通用的ITRF是由一组固定在固体地球表面的参考点(基准站)组成, 这些参考点的历元坐标和速度场, 就具体定义了一个ITRF。受地球构造与非构造因素的影响,运动表现为非线性。最新发布的ITRF2014框架实现时已顾及了部分非线性因素的影响,但由于影响站坐标非线性因素的复杂性, 致使基准站的站坐标仍未达到毫米级,而维持的精度只能到厘米级,这样的地球参考框架显然已不能满足当今毫米级地球动态变化监测的需要。而从应用上,地壳运动的监测已从厘米级向毫米级发展, 毫米级地壳非线性运动特征的监测和研究, 需要在一个毫米级的地球参考框架中来描述。
随着空间技术的发展和完善,同时全球导航卫星已从单一的GPS卫星发展到GPS、Galileo、GLONASS、BDS 4系统共存,尤其是北斗卫星将发展第三代卫星,实现信号的全球覆盖,因此发展以北斗卫星为主的毫米级全球基准将是我国基准发展的未来目标。毫米级地球参考框架的构建是当今国际地球科学的前沿研究课题,也是国际地球参考框架发展的趋势。建立毫米级全球框架需要:
(1) 完善数据融合的理论和方法;
(2) 构建精细的误差改正模型;
(3) 实现站点位置的精确表达;
通常,基准站在任意时刻(某一个历元)的坐标可以用式(1) 准确地描述
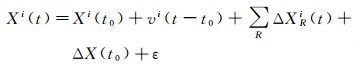 (1)
(1)
式中,Xi(t)表示基准站在任意时刻的位置;Xi(t0)和vi分别表示基准站在参考历元t0的位置和线性速度;ε为残差;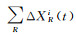
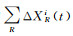
协议地球参考框架(CTRF)的原点定义为地球(包括大气和海洋)的质量中心(center of mass of earth system,CM)。而作为协议地球参考系的参考点的观测台站则位于固体地球的表面, 由这些观测台站构建的ITRF的原点, 从概念上讲应是固体地球表面的形状中心(CF)。目前全球ITRF框架反映的是坐标框架点长期运动的平均值,原点为CM,但在短时间尺度上,由于大气环流与海洋潮汐等因素的影响,CM有相对于地壳的运动,ITRF在短时间尺度上应视为CF参考框架。CF相对于CM的运动即为地球质心的运动(也称地心运动)。为建立我国自主的动态基准框架并进行毫米级框架维护,需解决全球长期框架与高精度短期框架基准实现不一致的问题。
获取地心位置的方法大致分为两类:即直接法和间接法。直接法包括“网络平移法(network shift approach)”[6-8]、动力学法和运动学法。直接法监测地心运动的理论很简单,就是利用位于地球表面的测站跟踪围绕CM运动的卫星轨道。实现ITRF的空间技术——SLR、VLBI、DORIS、GPS中,SLR和GPS是基于卫星观测根据卫星动力学轨道理论实现地球参考系,由于卫星轨道对地球引力场变化十分敏感,因此SLR和GPS实现的地球参考系原点为地球质心,可采用SLR来约束其原点,但由于其测站数量较少,且南北半球分布不均匀,导致SLR所约束的CM也并不十分理想[9-10]。DORIS的观测结果中虽然可能包含有地心信号,但由于其自身的系统误差,基于DORIS的地心运动结果并不理想[11]。GNSS系统测站分布最为广泛且最为密集,但目前的卫星定轨的精度还不足以满足地心运动精密监测的需要[11-13]。网络平移法也归入直接方法,是因为它是直接估计不同框架之间的平移量来估计地心变化,受站分布密度及站分布均匀性限制结果差异较大。因此采用直接法监测地心运动误差较大且不太稳定。
间接方法大致有一阶形变法[14]和地表质量负载反演地心运动[15]。间接方法都是通过监测地球内部的质量迁移或地表负载变化反演地心运动。
基于地球系统内部的质量迁移是引起地心运动的主因,地球内部质量迁移可以通过GRACE监测,GRACE第一次提供了全球范围内的质量迁移监测,然而其并不能提供地球重力场一阶项的变化[15]。实际上,其给出的二阶项结果也不够可靠,需要利用SLR的结果来代替。季节性的地心运动主要由地球表面的大气、海洋和陆地水的质量迁移而引起,可以基于全球范围的水文模型来建模,但由于这些水文模型的建模还不够理想,尤其是对于高纬度地区数据资料的缺乏,以及缺少作为一个整体质量守恒的约束,水文模型建模得到的地心运动不够可靠,相较于SLR的结果普遍偏小[11, 16-18]。文献[19]第一次基于全球分布的GPS测站的位移反演地表负载变化的一阶项,进而基于地表负载变化的一阶项反演得到了地心运动时间序列。利用GPS反演地心运动的相关研究主要有[20-24]。
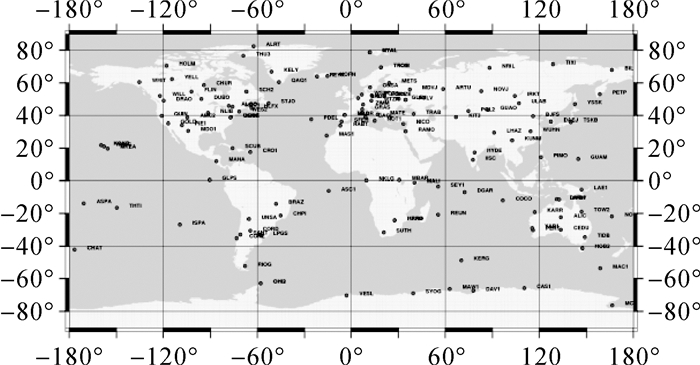
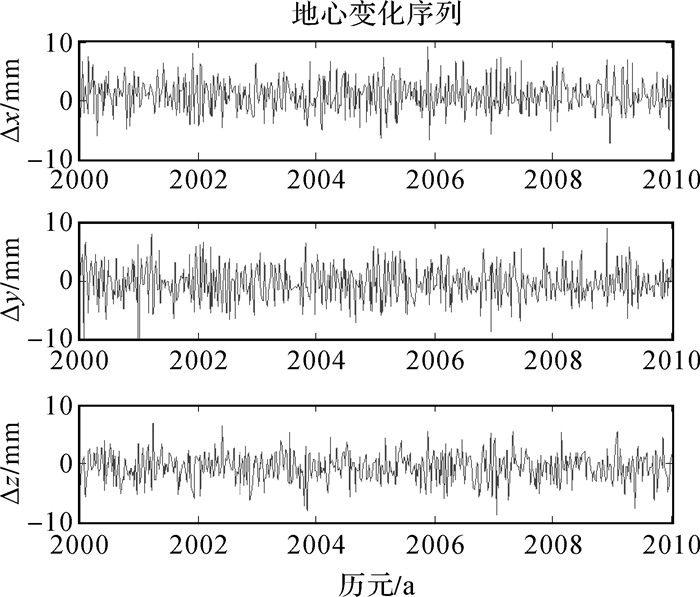
2.1 一阶形变法反演文献[25]选用全球分布的IGS05框架点,同时考虑到分布不同会对反演结果产生影响,共设计分布、站数都不相同的3个方案,采用一阶形变法反演得到了近10年地心运动的时间序列。其中132个框架点分布(如图 2所示)及结果(见图 3)为地心运动X、Z分量变化量在2~3 mm,而Y分量的变化在5 mm量。同时设计的66个站分布(南北半球测站均衡)和48个站分布(均衡东西分布)反演的结果见表 2。表 2中同时列出了国内外采用不同技术反演的地心运动结果。
|
| 图 2 IGS05框架的132个框架点 Fig. 2 The distribution of 132 sites in IGS05 frame |
|
| 图 3 GPS跟踪站位移反演的地心变化 Fig. 3 Geocenter motion series derived from GPS data for 2000-2009 |
| 反演方法 | X | Y | Z | time span | ||||||
| 振幅/mm | 相位/(°) | 振幅/mm | 相位/(°) | 振幅/mm | 相位/(°) | |||||
| GPS[25] | 132 | 5.01±0.2 | 307±6 | 1.01±0.3 | 66±16 | 6.20±0.3 | 330±8 | |||
| 66 | 2.33±0.3 | 327±6 | 5.45±0.2 | 342±9 | 8.13±0.3 | 318±6 | 2000.0-2010.0 | |||
| 48 | 5.09±0.2 | 308±4 | 2.29±0.2 | 313±9 | 7.20±0.3 | 324±5 | ||||
| GPS[27] | 1.8±0.4 | 229±15 | 2.5±0.3 | 164±5 | 3.9±0.4 | 211±5 | 2002.3-2004.2 | |||
| GPS&GRACE[26] | 3.9 | 22 | 2.7 | 25 | 7.6 | 57 | 1999.5-2004.5 | |||
| GRACE&OBP[15] | 1.5 | 49 | 2.6 | 331 | 1.5 | 58 | 2003.0-2007.0 | |||
| GPS GRACE&OBP[32] | 1.8±0.1 | 49±4 | 2.7±0.1 | 329±2 | 4.2±0.2 | 31±3 | 2002.3-2009.0 | |||
| GPS GRACE&OBP[33] | 2.1 | 242 | 3.4 | 144 | 2.6 | 207 | 2003.0-2009.0 | |||
| 大气、海洋、地表水负载[34] | 4.2 | 224 | 3.2 | 339 | 3.5 | 235 | 1992.0-1995.0 | |||
| 大气负载[6] | 2.4 | 244 | 2.0 | 270 | 4.1 | 228 | 1992.7-1997.0 | |||
| 大气负载[9] | 2.1 | 28 | 2.1 | 342 | 2.7 | 49 | 1993.0-2006.0 | |||
| ECCO OBP[25] | 3.41 | 297 | 4.88 | 294 | 3.67 | 331 | 1999.0-2011.0 | |||
由于GPS的跟踪站集中在陆地上,占地球面积70%的海洋并没有相应的观测资料,受目前IGS站全球分布不够密集,监测高阶地表形变的能力有限,文献[26-27]提出利用海底压强模型OBP(ocean bottom pressure)计算地心运动。
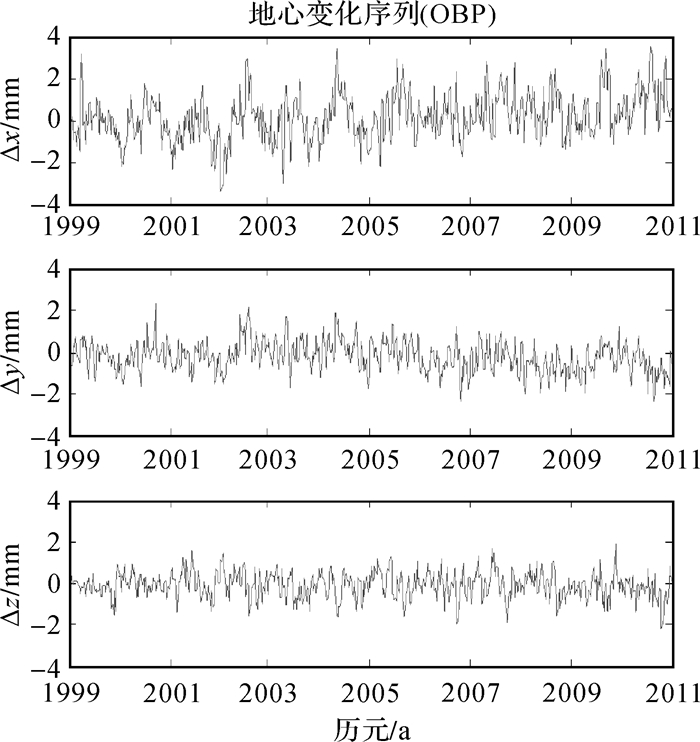
2.2 海底压强模型反演的地心运动采用由美国喷气动力实验室(JPL)开发的海洋循环和气候估计系统(ECCO)提供的采样率为12 h的格网海底气压资料对非潮汐海洋质量负载进行计算,时间跨度为1999.0-2011.0,反演得到地心3个分量的变化情况见图 4,振幅和相位结果见表 2。
|
| 图 4 由海底压强模型计算得到的近10年地心变化 Fig. 4 Geocenter motion series derived from OBP data for 1999-2011 |
从表 2中可以看出不同技术、不同数据、同类数据分布不同结果差异很大。采用GPS或GPS联合GRACE、OBP反演的地心结果,X、Y、Z分量的振幅相差1~2 mm。用海底压强模型OBP反演的地心运动3个分量的变化,相比GPS 3个布站方案反演结果,与66个站反演结果比较接近,但X方向振幅变大,Z方向振幅变小,整个序列来看噪声明显要小于GPS反演的地心运动。
而采用单一GPS观测序列反演,就分布而言,选取66个测站(南北半球测站均衡)与48个测站(均衡东西分布)反演地心运动X、Y、Z无论振幅和相位差异都很大。48个站布站较66个站分布反演的结果X方向振幅变大,但Y方向振幅变小。Z方向的振幅和相位在3种方案的选择中,反演结果相对其他两个方向的结果均较为稳定。即南北半球测站分布情况主要影响Y方向的反演结果,东西半球分布情况主要影响X方向的反演结果(详细结果见文献[25])。即GPS网络的中心CN来代替地球的形心CF,两者之间的差异是GPS反演地心的误差源之一,此外由GPS测站的位置变化来获得的一阶项里面挤进了很多高阶项,这是由于GPS测站分布北多南少,且广阔的海洋上测站稀疏所引起的。因此,探索最为合适的GPS网形分布来反演地心运动,可以同时克服以上两个问题。文献[22]提出以各坐标轴为中心线,分别计算轴两边站的个数占总数的百分比,接近50%的则比较合理。本文则提出采用网的重心坐标,当将重心坐标转换为大地坐标时,经线应接近起始子午面,纬线应接近赤道,大地高应接近地心,依此来判定网分布的均衡性。
3 站点位置的精确表达尽管目前ITRF中基准站的历元坐标和速度场已达到了毫米级,但GPS坐标时间序列上却呈现显著的非线性变化,尤其是垂直方向周期变化更明显(较大的年振幅可达1 cm),因此按线性速度维持ITRF框架的精度只能达到厘米量级的精度。要精确表达站点坐标,常采用两种方式描述非线性运动。
(1) 不考虑引起站点位置非线性变化的物理机理,只根据时间序列本身的运动趋势建模;
(2) 从产生形变的物理机理着手,分析各因素影响从而对位置进行改正。
3.1 地球物理效应分析通常认为地球物理效应及与GPS技术相关的系统误差是造成测站非线性变化的主要因素。可通过分析引起地壳非线性运动各种地球物理因素并建模得到计算站点, 尤其是高程方向的周年及半周年变化信息,文献[28]对并置了多项空间大地测量技术的国际IGS站点的GPS时序,采用地球物理因素分析方法得到了大气、积雪、土壤贮水量等各类质量负载引起的地球弹性形变年和半年的振幅和相位信息。并与这些站点SLR、VLBI技术监测结果进行比对,进而分析技术、模型与实际运动序列的匹配程度。由分析结果得出各技术结果符合得比较好。随之又对中国区域的IGS站进行分析,分别采用美国的NCEP和欧盟的ECMWF模型计算大气负载引起的站垂向周年振幅和相位,相位符合得较好,但振幅相差比较大,最大可超过1 mm。文献[29]也对中国区域的IGS站采用地球物理模型(模型见表 3)进行计算分析,得到不同地表质量负载造成的测站位移,利用此结果对ITRF2005框架下中国区域11个IGS基准站1995-2010年的位置时间序列进行修正,但改正后的结果并不理想,文中推断并猜想各物理因素并不是造成测站U分量半周年运动及水平方向周年运动的主要原因,而S1、S2大气潮汐可能是造成中国区域IGS基准站周年运动,尤其是中南部测站垂向周年运动的主要因素之一。
| 负载 | 模型 | 分辨率 | 测站位移/mm | ||
| N | E | U | |||
| 非潮汐大气压负载 | NCEP全球地表气压 | 2.5°×2.5° | -2~2 | -2~2 | 10 |
| 非潮汐海洋负载 | ECCO全球海底压力格网数据 | 1°×(0.3~1.0°) | 0.5 | 1 | 2 |
| 土壤湿度积雪负载 | NCEP再分析数据 | 1.875°×1.875° | 2 0.2 |
5 0.5 |
10 1 |
从以上结果分析上述地球物理模型在国外站点的符合性好,而在中国区域符合性较差,有可能是由于计算质量负载所采用地球物理模型均来自全球模型, 建模时没有采用中国地区地表气象资料水文资料和海洋资料,因此计算的地壳垂向周年运动误差较大,若要得到比较好的结果,需补充我国特有的高精度高密度中国地区地表气象资料、地质水文资料和海洋资料, 建立能更好反映我国自然环境的有关地球物理模型。鉴于目前建模型的条件有限,因此本文的关注点更倾向于由站点本身的运动信息进行建模。
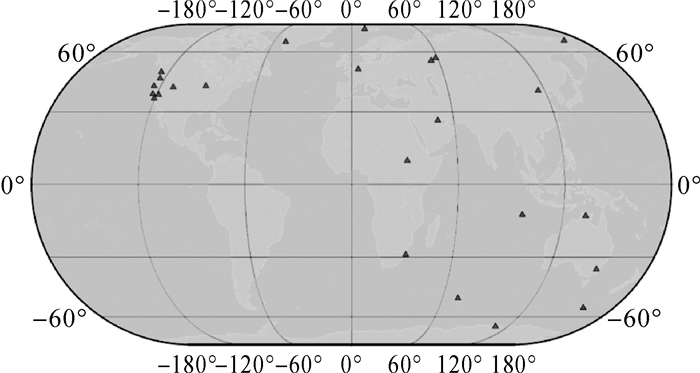
3.2 基于奇异谱分析的非线性运动建模奇异谱分析SSA(singular spectrum analysis)是一种统计分析方法,此方法的优越性在于无需任何先验信息和假设条件,通过数据内在结构分析确定最佳的滤波器,能高效、高精度地完成框架点运动特性建模,较传统方法具有更高的精度、自适应性和可靠性。文献[30]采用SSA对全球24个IGS站(分布见图 5)1999-2008共10 a站点坐标时序进行分析,建立了非线性运动模型。同时在建模过程中解决了缺失数据插补、粗差剔除、地震跳变等问题。
|
| 图 5 24个IGS的分布图 Fig. 5 The distribution of 24 IGS sites |
3.2.1 缺失值插补
在序列数据中构造了5个具有不同特性的数据缺失段(4个数据段是连续缺失,1个数据段是随机缺失),见表 4。其中最大连续缺失长度为200 d,总的数据缺失率约为20%。采用SSAM(singular spectrum analysis for missing)进行插补,具体过程参见文献[31]。插值精度统计信息见表 5。试验结果表明该方法的插值精度在水平方向优于5 mm,高程方向稍大于5 mm(同含噪声的原始坐标序列对比)。
| 数据段 | 连续缺失 | 起止时间 | 缺失天 |
| 1 | yes | 2002 47-2002 147 | 100 |
| 2 | no | 2002 192-2003 232 | 84 |
| 3 | yes | 2004 167-2005 1 | 200 |
| 4 | yes | 2005 301-2005 331 | 30 |
| 5 | yes | 2006 306-2006 336 | 30 |
| mm | |||||||||||||||
| 测站 | RMS | 测站 | RMS | 测站 | RMS | 测站 | RMS | ||||||||
| N | E | U | N | E | U | N | E | U | N | E | U | ||||
| SVIN | 1.3 | 2.0 | 3.2 | BRUS | 3.8 | 3.7 | 3.4 | EOUT | 1.6 | 1.6 | 5.5 | KERG | 3.5 | 3.1 | 6.3 |
| STR1 | 1.6 | 2.4 | 4.8 | CAS1 | 2.5 | 2.2 | 3.7 | BJFS | 1.7 | 1.6 | 4.1 | MAC1 | 2.4 | 2.8 | 3.9 |
| SCH2 | 3.7 | 2.1 | 4.0 | COCO | 2.6 | 3.5 | 5 | BAMF | 1.3 | 1.8 | 4.5 | NKLG | 3.9 | 5.2 | 5.8 |
| RNCH | 2.6 | 3.5 | 2.8 | WATC | 1.0 | 1.2 | 2.7 | ARTU | 1.7 | 1.4 | 5.3 | NLIB | 2.0 | 2.2 | 4.7 |
| PTSG | 1.2 | 1.3 | 3.2 | JAB1 | 2 | 3.1 | 4.6 | BAHR | 2.0 | 2.6 | 3.6 | NYAL | 3.8 | 3.1 | 3.8 |
| P411 | 1.3 | 1.5 | 3.4 | KELY | 3.8 | 1.8 | 4.3 | BILI | 3.8 | 3.1 | 4.5 | RBAY | 1.7 | 1.9 | 2.8 |
构造了粗差和缺失数据的时间序列T1,同时采用SSAM和SSA-IQR对序列进行插补及粗差探测后,残差与模拟噪声对比见图 6。
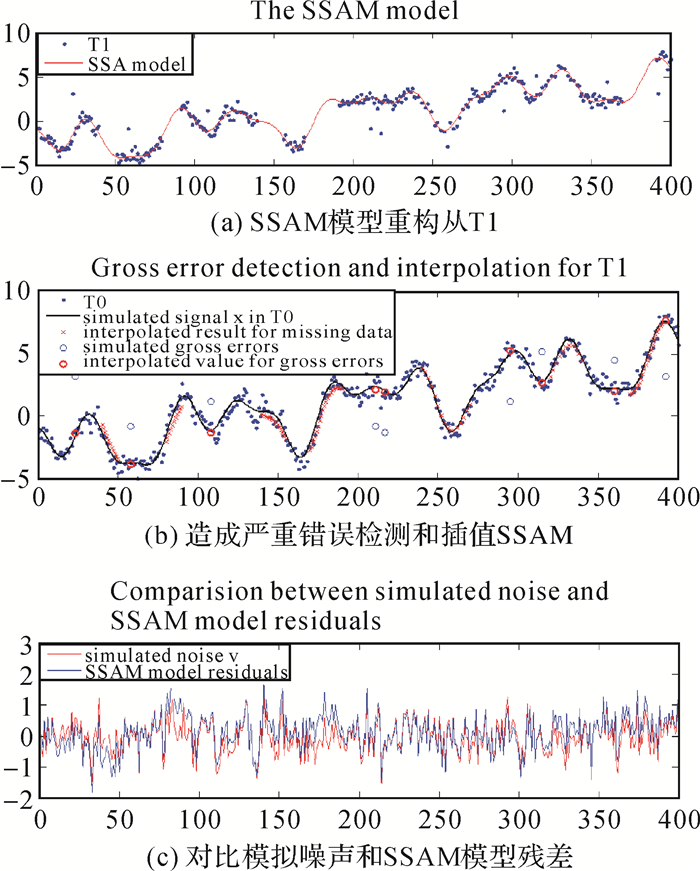
|
| 图 6 采用SSAM和SSA-IQR对序列进行插补及粗差探测后残差与模拟噪声对比 Fig. 6 The residuals compared with simulated noise after using SSAM and SSA-IQR |
可以看出采用SSA技术进行非线性运动建模有很好的自适应性,且建模精度较高。
3.2.2 信号重构及SSA-P非线性预报文献[31]采用SSA技术对站点非线性运动进行预报,考虑了复杂站运动情形(尤其是震后站点的运动)的预报建模。如包含有阶跃(受地震或者仪器更换等影响),震后余滑引起的站点非线性运动及其年/半年周期项的振幅可能会存在随时间变化的特性。图 7为SSA对含有非线性趋势项,振幅随时间变化的周期项和阶跃项的时间序列模拟数据的拟合结果。结果表明拟合结果的中误差(同模拟的信号部分相比)为1.7 mm。
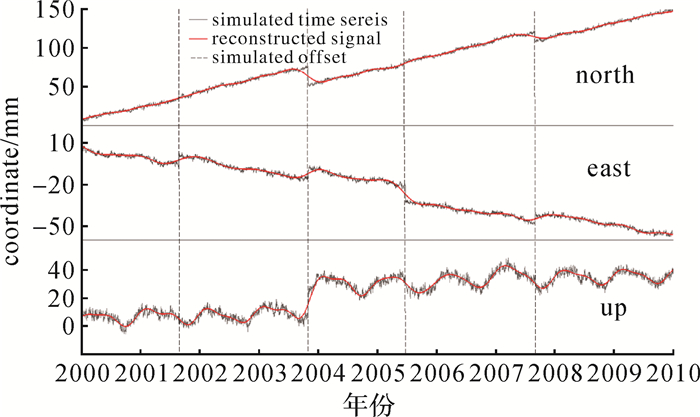
|
| 图 7 SSA对模拟的含阶跃的三维CORS站点坐标时间序列拟合结果(灰色虚线为阶跃的位置) Fig. 7 Reconstructed signal component using SSA-PD from time series containing offsets |
图 9为SSA-P对3种不同的模拟数据的拟合和预报结果。3类模拟数据分别为:① 线性趋势项+年/半年周期+有色噪声(闪烁噪声+白噪声);② 线性趋势项+年/半年周期+有色噪声+阶跃;③ 非线性趋势项+年/半年周期+有色噪声+阶跃。结果表明3类数据的模拟结果均优于2 mm,① 和② 类数据的预报结果为3 mm。但对于具有复杂结构的③ 类数据,其预报结果在前1.5 a约为3 mm,在后1.5 a精度降低到10 mm。这也说明对具有复杂运动特性的框架站点,应该利用最新的观测资料进行框架坐标的及时更新,以实现坐标框架的高精度维护。
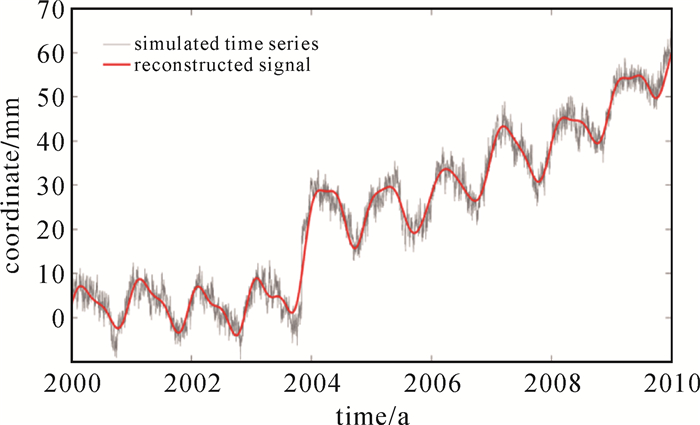
|
| 图 8 SSA对具有非线性趋势项,振幅随时间变化的周期项和阶跃的坐标时间序列的拟合结果 Fig. 8 Reconstructed signal component f SSA-PD from time series containing offsets and a nonsecular trend |
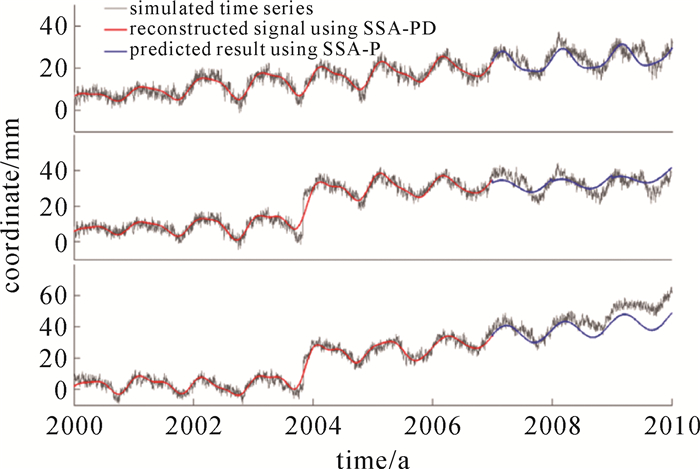
|
| 图 9 SSA-PD和SSA-P对3种构造数据的拟合和预报结果 Fig. 9 Prediction result from SSA-P for the three types of data |
4 结语
我国建立并实现地心坐标框架CGCS2000后,随着BDS卫星的全球覆盖,建立基于多星多技术实现基准定义、并建立毫米级框架是我国基准建立和发展的趋势。国内目前在地球质心反演、毫米级框架点表达上都进行了相关研究和分析试验。研究全球框架非线性坐标框架建模方法,基于SSA的SSA-P非线性建模和非线性预测方法完成了对全球框架及CGCS2000框架动态特性及非线性建模的研究及分析,可以提高全球进而提高我国坐标框架精度,为北斗导航定轨和定位提供高精度的基准支持。
| [1] | 程鹏飞, 成英燕, 秘金钟, 等. 2000国家大地坐标系建立的理论与方法[M]. 北京: 测绘出版社, 2014. CHENG Pengfei, CHENG Yingyan, BEI Jinzhong, et al. Theory and Method for Establishment of the China Geodetic Coordinate System 2000[M]. Beijing: Surveying and Mapping Press, 2014. |
| [2] | 程鹏飞, 文汉江, 孙罗庆, 等. 中国大陆GPS速度场的球面小波模型及多尺度特征分析[J]. 测绘学报, 2015, 44(10): 1063–1070. CHENG Pengfei, WEN Hanjiang, SUN Luoqing, et al. The Spherical Wavelet Model and Multiscale Analysis of Characteristics of GPS Velocity Fields in Mainland China[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1063–1070. DOI:10.11947/j.AGCS.20152.0140141 |
| [3] | 程鹏飞, 成英燕, 秘金钟, 等. CGCS2000板块模型构建[J]. 测绘学报, 2013, 42(2): 159–167. CHENG Pengfei, CHENG Yingyan, BEI Jinzhong, et al. CGCS2000 Plate Motion Model[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 159–167. |
| [4] | 程鹏飞, 文汉江, 成英燕, 等. 2000国家大地坐标系椭球参数与GRS 80和WGS 84的比较[J]. 测绘学报, 2009, 38(3): 189–194. CHENG Pengfei, WEN Hanjiang, CHENG Yingyan, et al. Parameters of the CGCS 2000 Ellipsoid and Comparisons with GRS 80 and WGS 84[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 189–194. DOI:10.3321/j.issn:1001-1595.2009.03.001 |
| [5] | 程鹏飞, 成英燕, 秘金钟, 等. 国家大地坐标系建立的理论与实践[M]. 北京: 测绘出版社, 2017. CHENG Pengfei, CHENG Yingyan, BEI Jinzhong, et al. Theory and Practice for Establishment of National Geodetic Coordinate System[M]. Beijing: Surveying and Mapping Press, 2017. |
| [6] | CHEN J L, WILSON C R, EANES R J, et al. Geophysical Interpretation of Observed Geocenter Variations[J]. Journal of Geophysical Research:Solid Earth, 1999, 104(B2): 2683–2690. DOI:10.1029/1998JB900019 |
| [7] | BLEWITT G, HEFLIN M B, WEBB F H, et al. Global Coordinates with Centimeter Accuracy in the International Terrestrial Reference Frame Using GPS[J]. Geophysical Research Letters, 1992, 19(9): 853–856. DOI:10.1029/92GL00775 |
| [8] | DONG D, YUNCK T, HEFLIN M. Origin of the International Terrestrial Reference Frame[J]. Journal of Geophysical Research:Solid Earth, 2003, 108(B4): 2200. DOI:10.1029/2002JB002035 |
| [9] | COLLILIEUX X, ALTAMIMI Z, RAY J, et al. Effect of the Satellite Laser Ranging Network Distribution on Geocenter Motion Estimation[J]. Journal of Geophysical Research:Solid Earth, 2009, 114(B4): B04402. |
| [10] | ALTAMIMI Z, COLLILIEUX X, MÉTIVIER L. ITRF2008:An Improved Solution of the International Terrestrial Reference Frame[J]. Journal of Geodesy, 2011, 85(8): 457–473. DOI:10.1007/s00190-011-0444-4 |
| [11] | CRÉTAUX J F, SOUDARIN L, DAVIDSON F J M, et al. Seasonal and Interannual Geocenter Motion from SLR and DORIS Measurements:Comparison with Surface Loading Data[J]. Journal of Geophysical Research:Solid Earth, 2002, 107(B12): :ETG 16-1–ETG 16-9. DOI:10.1029/2002JB001820 |
| [12] | KANG Z G, TAPLEY B, CHEN J L, et al. Geocenter Variations Derived from GPS Tracking of the GRACE Satellites[J]. Journal of Geodesy, 2009, 83(10): 895–901. DOI:10.1007/s00190-009-0307-4 |
| [13] | REBISCHUNG P, GARAYT B. Recent Results from the IGS Terrestrial Frame Combinations[C]//ALTAMIMI Z, COLLILIEUX X. Reference Frames for Applications in Geosciences. International Association of Geodesy Symposia, Vol 138. Berlin, Heidelberg:Springer, 2013. |
| [14] | TREGONING P, VAN DAM T. Effects of Atmospheric Pressure Loading and Seven-parameter Transformations on Estimates of Geocenter Motion and Station Heights from Space Geodetic Observations[J]. Journal of Geophysical Research:Solid Earth, 2005, 110(B3): B03408. DOI:10.1029/2004JB003334 |
| [15] | SWENSON S, CHAMBERS D, WAHR J. Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output[J]. Journal of Geophysical Research:Solid Earth, 2008, 113(B8): B08410. DOI:10.1029/2007JB005338 |
| [16] | SCHERNECK H G, JOHANSSON J M, WEBB F H. Ocean Loading Tides in GPS and Rapid Variations of the Frame Origin[C]//Geodesy Beyond 2000-the Challenges in the First Decade, Vol. 121. Berlin:Schwarz, Springer, 2000. |
| [17] | KLEMANN V, MARTINEC Z. Contribution of Glacial-isostatic Adjustment to the Geocenter Motion[J]. Tectonophysics, 2009, 511(3-4): 99–108. DOI:10.1016/j.tecto.2009.08.031 |
| [18] | DONG Danan, QU Weijing, FANG Peng, et al. Non-linearity of Geocentre Motion and Its Impact on the Origin of the Terrestrial Reference Frame[J]. Geophysical Journal International, 2014, 198(2): 1071–1080. DOI:10.1093/gji/ggu187 |
| [19] | BLEWITT G, LAVALLÉE D, CLARKE P, et al. A New Global Mode of Earth Deformation:Seasonal Cycle Detected[J]. Science, 2001, 294(5550): 2342–2345. DOI:10.1126/science.1065328 |
| [20] | WU Xiaoping, ARGUS D F, HEFLIN M B, et al. Site Distribution and Aliasing Effects in the Inversion for Load Coefficients and Geocenter Motion from GPS Data[J]. Geophysical Research Letters, 2002, 29(24): 63–1. DOI:10.1029/2002GL016324 |
| [21] | WU Xiaoping, HEFLIN M B, IVINS E R, et al. Large-scale Global Surface Mass Variations Inferred from GPS Measurements of Load-Induced Deformation[J]. Geophysical Research Letters, 2003, 30(14): 1742. DOI:10.1029/2003GL017546 |
| [22] | LAVALLÉE D A, VAN DAM T, BLEWITT G, et al. Geocenter Motions from GPS:A Unified Observation Model[J]. Journal of Geophysical Research:Solid Earth, 2006, 111(B5): B05405. DOI:10.1029/2005JB003784 |
| [23] | CLARKE P J, LAVALLÉE D A, BLEWITT G, et al. Basis Functions for the Consistent and Accurate Representation of Surface Mass Loading[J]. Geophysical Journal International, 2007, 171(1): 1–10. DOI:10.1111/j.1365-246X.2007.03493.x |
| [24] | WU Xiaoping, RAY J, VAN DAM T. Geocenter Motion and Its Geodetic and Geophysical Implications[J]. Journal of Geodynamics, 2012(58): 44–61. |
| [25] | YU Nan, CHENG Pengfei, CHENG Yingyan, et al. The Geocentre Inversion Based on the Global Climate Models and GPS Site Displacements[J]. Survey Review, 2017: 1–9. DOI:10.1080/00396265.2017.1329077 |
| [26] | KUSCHE J, SCHRAMA E J O. Surface Mass Redistribution Inversion from Global GPS Deformation and Gravity Recovery and Climate Experiment (GRACE) Gravity Data[J]. Journal of Geophysical Research:Solid Earth, 2005, 110(B9): B09409. DOI:10.1029/2004JB003556 |
| [27] | WU Xiaoping, HEFLIN M B, IVINS E R, et al. Seasonal and Interannual Global Surface Mass Variations from Multisatellite Geodetic Data[J]. Journal of Geophysical Research, 2006, 111(B9): B09401. |
| [28] | 宋淑丽, 朱文耀, 熊福文, 等. 毫米级地球参考框架的构建[J]. 地球物理学报, 2009, 52(11): 2704–2711. SONG Shuli, ZHU Wenyao, XIONG Fuwen, et al. Construction of mm-Level Terrestrial Reference Frame[J]. Chinese Journal of Geophysics, 2009, 52(11): 2704–2711. |
| [29] | 姜卫平, 李昭, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列非线性变化的成因分析[J]. 地球物理学报, 2013, 56(7): 2228–2237. JIANG Weiping, LI Zhao, LIU Hongfei, et al. Cause Analysis of the Non-Linear Variation of the IGS Reference Station Coordinate Time Series Inside China[J]. Chinese Journal of Geophysics, 2013, 56(7): 2228–2237. DOI:10.6038/cjg20130710 |
| [30] | WANG Xiaoming, CHENG Yingyan, WU Suqin, et al. An Enhanced Singular Spectrum Analysis Method for Constructing Nonsecular Model of GPS Site Movement[J]. Journal of Geophysical Research:Solid Earth, 2016, 121(3): 2193–2211. DOI:10.1002/2015JB012573 |
| [31] | WANG Xiaoming, CHENG Yingyan, WU Suqin, et al. An Effective Toolkit for the Interpolation and Gross Error Detection of GPS Time Series[J]. Survey Review, 2016, 48(348): 202–211. DOI:10.1179/1752270615Y.0000000023 |


