GRACE(gravity recovery and climate experiment)卫星观测数据在大地测量学等多个地球科学取得了广泛应用[1-4],利用GRACE数据反演高精度、高分辨率的地球重力场模型是这些应用的基础。目前,国际全球重力场模型中心ICGEM(International Centre for Global Earth Models)已经发布的数十套GRACE时变重力场模型主要由动力学法解算[5-11],部分采用短弧边值法[12-14]和加速度法[15-16]解算,我国学者利用这些方法也解算了多种静态与时变重力场模型[17-21]。这3种解算方法都以牛顿运动定律和万有引力定律为基础,在理论上是等价的。本质上都是根据卫星位置、星间距离和速度观测量(或其加速度和星间相对加速度导出量)相对于卫星参考轨道(或其星间距离、速度和加速度导出量)的线性摄动量建立线性观测方程进行求解。动力学法以轨道起始点的状态向量(3个坐标和3个速度分量)为初值,利用先验力模型积分计算出整个弧段的参考轨道;积分外推导致线性化误差随轨道弧段的增长而迅速增大,且观测方程系数矩阵的性质也快速变差;需要通过迭代来减小线性化误差的影响。短弧边值法以轨道弧段两个端点的位置向量为初值,利用先验力模型内插解算出整个弧段参考轨道相对于几何轨道的改正量。这样求得参考轨道与几何轨道非常接近,因此解算重力场模型时忽略计算保守力时参考轨道改正量的影响。然而,由于改正量的数目随弧段增长而迅速增加,且改正量解算方程的稳定性也迅速变差,因此短弧边值法的弧段不能太长,通常只有2~3 h。加速度法将相邻3个历元的卫星位置和星间距离观测值进行二阶差分求得卫星加速度和星间相对加速度,并表示成3个历元对应弧段参考轨道加权平均加速度的线性摄动量,因此加速度法线性摄动量的观测方程形式相对简单,然而差分计算必然放大观测误差,通常需要进行滤波处理[22]。根据文献[23]以几何轨道为初值进行线性化的思路,文献[24]对保守力模型中的几何轨道直接引入误差改正数,并以几何轨道为初值进行线性化,在解算重力场模型的同时估计轨道改正数。因此在解算地球重力场时不需要再计算参考轨道,且理论上更加严密和自洽,并用该线性化方法改进了短弧边值法和加速度法,解算了重力场模型[13-14, 17]。
为了满足相关学科的科学研究和全球气候变化分析与灾害评估的需求,时变地球重力场需要达到100 km空间分辨率、1天至数天的时间分辨率且精度提高1个数量级,因此,国际上正在研究新一代重力卫星观测计划[25-27],我国不仅在研制低低跟踪模式的重力卫星[28],且也在研究下一代重力卫星计划[29]。下一代重力卫星计划采用两对低低跟踪重力卫星进行观测,并采用激光干涉以纳米级精度测定重力卫星的星间距离,这需要改进重力反演解算方法,必须将计算误差控制在纳米级精度。卫星重力反演方法的发展主要在以下3个方面:① 采用长弧重力反演。因长弧段积分不仅可平滑随机误差的影响,而且使微小的作用力产生可观的位置变化,理论上可以解算更高精度的重力场模型,但需要构建新的轨道计算方法,使轨道计算误差能够满足纳米级观测精度的要求,并控制轨道积分误差随弧段长度的积累;② 改进参数化方式。其中,地球重力场采用点质量模型表示,非保守力的偏差参数采用2次多项式或样条模型表示,并将非保守力变换到惯性系时对姿态引入参数进行改正;③ 构建约束解模型,主要利用海洋区域和陆地水流域等不同区域质量变化的频谱特性构建约束模型。此外,大气和海洋混叠改正模型将是影响下一代重力卫星解算精度重要因素,需要利用各种类型数据构建更精确的改正模型。由于动力学法是目前卫星重力反演的主要方法,因此研究动力学法的特点并合理改进,不仅对提高GRACE数据的重力反演精度有参考价值,而且对下一代重力卫星的数据处理也有重要意义。本文主要基于理论模型,分析讨论动力学法反演地球重力场的特点,在此基础上提出一些改进设想。
1 理论基础地球引力位V在地固坐标系中可表示成如下球函数展开式
 (1)
(1)
式中,r、θ、λ分别为球坐标的向径、余纬和经度;GM为万有引力常数与地球质量之积;R为地球平均半径;Pnm为缔合勒让德函数;u={… Cnm, Snm …}称为重力场模型系数。由于地球引力是低轨卫星的主要作用力,如果对日月引力、大气和海洋潮汐等保守力精确建模,对大气阻力、太阳光压等非保守力精确测定,就可根据低轨卫星轨道观测值解算地球重力场模型系数。
利用GRACE卫星高精度的轨道、星间距离或速度,以及非保守力观测量解算地球重力场的理论基础是如式(2) 所示的牛顿运动方程
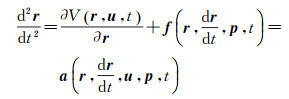 (2)
(2)
式中,r为惯性坐标系中的卫星位置向量,是时间t的函数;∂V(r, u, t)/∂r和f(r, dr/dt, p, t)分别为卫星单位质量所受的引力和其他摄动力;a(r, u, p, t)为两者之和;u为待估的地球重力场模型系数;p为其他待估参数。在式(2) 的力模型中,所有保守力都与卫星位置有关;但当大气阻力等非保守力用加速度计实测时,式(2) 右边的力模型与卫星速度无关。动力学法和短弧边值法都是以式(2) 积分得到的卫星速度和位置为基础建立GRACE卫星的位置和星间速度观测方程;二者的区别主要是对6个积分常数和参考轨道的处理。
2 基于轨道积分公式线性化的重力解算模型动力学法以轨道起始点的位置r0(t0)和速度
 (3)
(3)
式中,t0和t为轨道的起始时刻和观测时刻;上标“·”表示对时间的一阶导数,参数x=(uT, pT)T。若将(3) 式中的起始点初值、力模型参数用其近似值和改正数表示,则式(3) 可线性化为
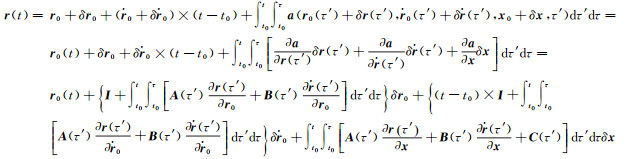 (4)
(4)
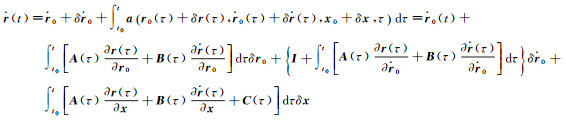 (5)
(5)
式中,I为3×3阶单位阵;r0、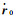

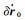
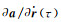

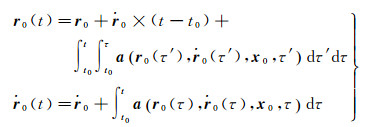 (6)
(6)
引入辅助量
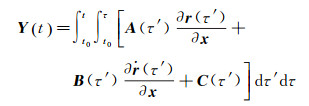 (7)
(7)
则其对时间t的一阶导数可表示为
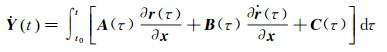 (8)
(8)
在初始时刻t=t0时,式(7) 和式(8) 积分的上下限相同,显然有
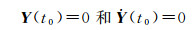 (9)
(9)
将式(7) 和式(8) 分别代入式(4) 和式(5) 得
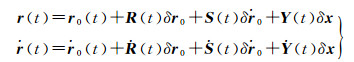 (10)
(10)
式中
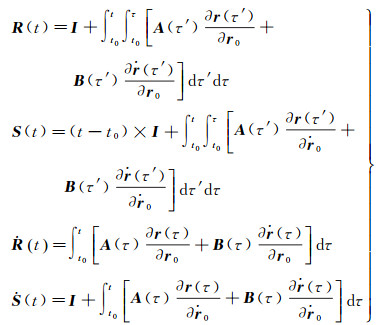 (11)
(11)
根据泰勒级数展开理论,式(10) 中的展开系数可以表示为Y(t)=∂r(t)/∂x、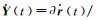
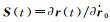
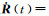
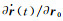
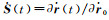
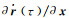

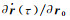
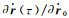

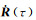
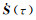
由于在初始时刻式(9) 为0,这表明摄动量δx对式(10) 中初始位置和速度的摄动影响均为0。将式(10) 的第一式的r(t)用轨道观测值rg(t)和改正数vr(t)表示,则其观测方程为
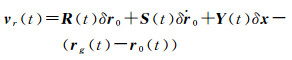 (12)
(12)
由式(11) 可得,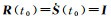
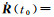

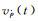
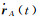
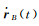
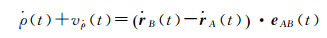 (13)
(13)
式中,eAB(t)为A、B卫星视线方向的单位向量。将式(10) 的第2式代入式(13) 就可求得星间速度的观测方程。
不难验证,式(7) 和式(8) 就是动力学法关于参数x的变分方程
 (14)
(14)
满足初值条件式(9) 时的解。而且,式(11) 也是动力学法关于初始位置和速度的变分方程
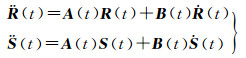 (15)
(15)
满足初值为单位阵时的解。由此可见,动力学法本质上是以参考轨道为初值的线性摄动解,摄动参数δx对起始点位置和速度的摄动量影响为0必然导致变分方程式(14) 的初值为0。文献[30]所讨论问题的本质上并非是卫星相对于参考轨道线性摄动问题,因此认为变分方程初值不应该为0。
3 算法特点与改进设想由动力学法观测方程式(12) 和式(13) 可以看出,GRACE数据解算地球重力场的核心是卫星位置和速度的线性摄动公式(10),以及参考轨道积分公式(6) 和系数计算公式(7)、式(8) 和式(11)。下面从线性化误差、参数化方式和长弧段轨道积分三个方面讨论算法的特点和改进设想。
3.1 线性化误差由于轨道初值、力模型参数都存在误差,因此式(6) 积分计算的参考轨道r0(t)和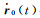
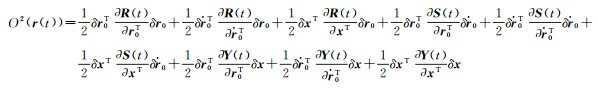 (16)
(16)
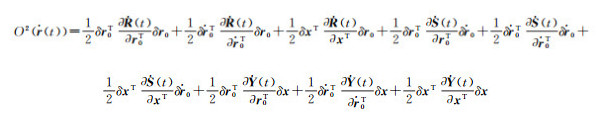 (17)
(17)
式中,O2(·)表示二次项的影响,记号∂(·)/∂xT=[∂(·)/∂x]T。R(t)、S(t)、

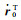

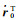
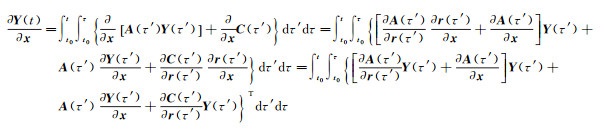 (18)
(18)
式(8) 应用了矩阵对向量的导数规则以及立体矩阵的运算规则,并顾及了矩阵C(τ′)仅是位置r(τ′)的函数。偏导数∂A(τ′)/∂r(τ′)和∂C(τ′)/∂r(τ′)约为A(τ′)和C(τ′)的1/r(τ′),说明二次舍弃项约为线性项的1/r(τ′)。然而,式(7) 中Y(t)经过时间t的二次积分得到,且积分号中也包含Y(τ′)项,因此Y(t)接近按t的4次方速度递增。式(18) 包含了Y(τ′)乘积项的时间二次积分,这意味着偏导数∂Y(t)/∂x接近按时间10次方的速度递增。同理可发现
根据式(16) 和式(17),欲减小线性化误差,可从两个方面着手,即控制参数改正量δr0、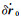
动力学法采用轨道起始点的位置和速度向量参数,重力位参数和非保守力加速度的尺度与偏差参数进行参数化。这种参数化方式导致式(10) 中参考轨道与观测轨道之差随时间快速增加,式(7)、式(8) 和式(11) 中的系数矩阵R(t)、S(t)、Y(t)按时间4次方的速度递增,
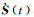
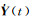
改进参数化方式,有望改善观测方程的性质。改善位置和速度系数阵性质的最简单办法是改变其速度单位,若以1天为弧段长度,只要取km/s为速度单位即可。动力学法迭代收敛后,位置、速度和力模型参数改正量都趋向于0,观测方程式(12) 的常数项主要反映了观测误差的影响。由于迭代收敛后,参考轨道的平差改正量完全可以忽略,即式(4) 和式(5) 中的δr(τ′)和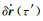
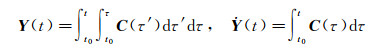 (19)
(19)
显然,式(19) 中的Y(t)和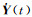
由于短弧边值法可直观理解为轨道内插问题,动力学法解算初值参数属于轨道外推问题,因此短弧边值法观测方程性质应该优于动力学法。考虑到迭代收敛后弧段中各点的轨道已经固定,边值公式已经不受弧段长度的限制,因此用短弧边值公式作最后一次解算,也有望进一步提高解算结果的精度。
3.3 轨道积分方式由于卫星的力模型复杂,给出完整的轨道解析解非常困难,因此轨道数值积分对于动力学法是不可避免的。尽管采用目前常用数值积分器积分1天的轨道精度能满足目前GRACE重力反演的精度要求。然而下一代重力卫星的激光干涉观测精度将达到纳米量级,比目前的K波段微波测距精度提高约1000倍,因此需要更高的轨道积分精度。长弧重力反演计算可提高观测方程的信噪比,有利于提高重力场参数的解算精度,但轨道积分精度必须要满足长弧段解算的要求。因此,卫星轨道的数值积分精度是下一代重力卫星数据处理和长弧段重力反演的一个重要瓶颈问题。
式(3) 的第1式是二重积分,利用分步积分可转化成如下一重积分
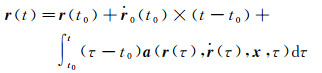 (20)
(20)
利用式(20) 进行数值积分,其计算误差将明显小于式(3)。当采用多步法积分时,式(20) 积分所需的力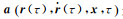


外推系数:19 494 601/11 404 800, -99 642 413/22 809 600, 40 413 623/2 851 200, -4 955 916 683/159 667 200, 278 428 507/5 702 400, -4 496 090 419/79 833 600, 955 625 177/19 958 400, -2 374 517 119/79 833 600, 1 050 348 479/79 833 600, -627 827 071/159 667 200, 84 671/118 800, -4671/78 848
内插系数:-4139/79 833 600, 19 567/22 809 600, -107 539/13 305 600, 17 274 001/159 667 200, 6 386 783/7 983 360, 326 441/3 193 344, -53/399 168, -58 213/11 404 800, 226 637/79 833 600, -4121/4 561 920, 317/1 900 800, -317/22 809 600
其中,外推系数的数值和正负变化量要明显大于内插系数,因此,内插系数的数值积分精度将明显优于外推系数。低轨重力卫星的主要作用力是地球引力,相对于地球中心引力,C20项引力约为10-3量级,其他各项引力最大只有10-6量级,日月引力等保守力摄动和非保守力摄动也只有10-6量级。若将式(20) 的力模型分离成中心引力与C20项引力项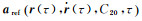

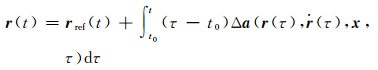 (21)
(21)
式中
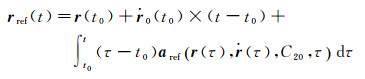 (22)
(22)
如果只考虑地球中心引力和C20项引力作用,可导出卫星运行的解析公式[32],因此理论上式(22) 可用解析公式表示,只需要对式(21) 进行数值积分计算。顾及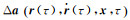
本文直接利用动力学轨道的积分公式进行线性化,导出了线性化观测方程系数矩阵的积分计算公式,阐明了传统动力学方法本质上是相对于参考轨道的线性摄动问题,因此对力模型参数的偏导数初值必定为0。利用导出的积分公式分析了线性化误差随轨道弧长快速增大,线性观测方程性质也随轨道弧长增长也变差等特点。建议通过迭代计算和进一步改进以几何轨道为初值的线性化模型,减少长弧段重力反演的线性化误差;通过改变初始速度单位改善初始状态参数系数矩阵的性质,采用迭代收敛后轨道直接计算设计矩阵,改善线性观测方程的性质。考虑到下一代重力卫星计划采用高精度星间距离观测数据和长弧段重力反演计算都需要高精度数值积分计算卫星轨道,建议保守力模型采用内插法计算,并将地球中心引力和C20项引力采用解析公式计算,其他保守力和非保守力采用数值积分公式计算,以提高卫星轨道的计算精度。
本文并未涉及卫星重力反演的星座和载荷指标的优化、非保守力改正模型的精化、大气和海洋改正混叠影响等,这些问题都是下一代卫星重力计划需要研究的重要内容。
| [1] | TAPLEY B D, BETTADPUR S, WATKINS M, et al. The Gravity Recovery and Climate Experiment:Mission Overview and Early Results[J]. Geophysical Research Letters, 2004, 31(9): L09607. |
| [2] | 许厚泽, 陆洋, 钟敏, 等. 卫星重力测量及其在地球物理环境变化监测中的应用[J]. 中国科学(地球科学), 2012, 42(6): 843–853. XU Houze, LU Yang, ZHONG Min, et al. Satellite Gravity and Its Application to Monitoring Geophysical Environmental Change[J]. Scientia Sinica (Terrae), 2012, 42(6): 843–853. |
| [3] | CHEN J L, WILSON C R, TAPLEY B D. Satellite Gravity Measurements Confirm Accelerated Melting of Greenland Ice Sheet[J]. Science, 2006, 313(5795): 1958–1960. DOI:10.1126/science.1129007 |
| [4] | FENG Wei, ZHONG Min, LEMOINE J M, et al. Evaluation of Groundwater Depletion in North China Using the Gravity Recovery and Climate Experiment (GRACE) Data and Ground-based Measurements[J]. Water Resources Research, 2013, 49(4): 2110–2118. DOI:10.1002/wrcr.20192 |
| [5] | DAHLE C, FLECHTNER F, GRUBER C, et al. GFZ GRACE Level-2 Processing Standards Document for Level-2 Product Release 0005[R]. Scientific Technical Report STR 12/02. Potsdam:Deutsches GeoForschungsZentrum GFZ, 2012. DOI:10.2312/GFZ.b103-1202-25,GFZ. |
| [6] | BETTADPUR S. Gravity Recovery and Climate Experiment UTCSR Level-2 Processing Standards Document for Level-2 Product Release 0005[M]. Austin: Center for Space Research, University of Texas, 2012. |
| [7] | WATKINS M, YUAN D N. GRACE JPL Level-2 Processing Standards Document for Level-2 Product Release 05[M]. GRACE 327-744(v 5.0). Pasadena, USA: Jet Propulsion Laboratory, 2012. |
| [8] | MAYER-GVRR T, BEHZADPOUR S, ELLMER M, et al. ITSG-Grace2016-Monthly and Daily Gravity Field Solutions from GRACE[M/OL]. GFZ Data Services, 2016, http://doi.org/10.5880/icgem.2016.007. |
| [9] | SAVE H, BETTADPUR S, TAPLEY B D. High-resolution CSR GRACE RL05 Mascons[J]. Journal of Geophysical Research:Solid Earth, 2016, 121(10): 7547–7569. DOI:10.1002/2016JB013007 |
| [10] | FÖRSTE C, BRUINSMA S, ABRIKOSOV O, et al. EIGEN-6S4 a Time-variable Satellite-only Gravity Field Model to D/O 300 Based on LAGEOS, GRACE and GOCE Data from the Collaboration of GFZ Potsdam and GRGS Toulouse[R].[S.l.]:GFZ, 2016, http://adsabs.harvard.edu/abs/2015EGUGA..17.3608F |
| [11] | ZHOU Hao, LUO Zhicai, ZHOU Zebing, et al. HUST-GRACE2016s:A New GRACE Static Gravity Field Model Derived from a Modified Dynamic Approach over a 13-year Observation Period[J]. Advances in Space Research, 2017, 60(3): 597–611. DOI:10.1016/j.asr.2017.04.026 |
| [12] | MAYER-GVRR T, EICKER A, ILK K H. ITG-Grace02s:A GRACE Gravity Field Derived from Short Arcs of the Satellites Orbit[C]//Proceedings of the 1st International Symposium of the International Gravity Field Service "Gravity Field of the Earth". Istanbul:Harita Dergisi, 2007. 193-198. |
| [13] | CHEN Qiujie, SHEN Yunzhong, ZHANG Xingfu, et al. Monthly Gravity Field Models Derived from GRACE Level 1B Data Using a Modified Short-arc Approach[J]. Journal of Geophysical Research, 2015, 120(3): 1804–1819. |
| [14] | CHEN Qiujie, SHEN Yunzhong, CHEN Wu, et al. An Improved GRACE Monthly Gravity Field Solution By Modeling the Non-conservative Acceleration and Attitude Observation Errors[J]. Journal of Geodesy, 2016, 90(6): 503–523. DOI:10.1007/s00190-016-0889-6 |
| [15] | DITMAR P, KUZNETSOV V, VAN ECK VAN DER SLUIJS A A, et al. 'DEOS_CHAMP-01C_70':A Model of the Earth's Gravity Field Computed from Accelerations of the CHAMP Satellite[J]. Journal of Geodesy, 2006, 79(10-11): 586–601. DOI:10.1007/s00190-005-0008-6 |
| [16] | LIU X, DITMAR P, SIEMES C, et al. DEOS Mass Transport Model (DMT-1) Based on GRACE Satellite Data:Methodology and Validation[J]. Geophysical Journal International, 2010, 181(2): 769–788. |
| [17] | CHEN Qiujie, SHEN Yunzhong, CHEN Wu, et al. A Modified Acceleration-based Monthly Gravity Field Solution from GRACE Data[J]. Geophysical Journal International, 2015, 202(2): 1190–1206. DOI:10.1093/gji/ggv220 |
| [18] | 徐天河, 杨元喜. 利用CHAMP卫星几何法轨道恢复地球重力场模型[J]. 地球物理学报, 2005, 48(2): 288–293. XU Tianhe, YANG Yuanxi. CHAMP Gravity Field Recovery Using Kinematic Orbits[J]. Chinese Journal of Geophysics, 2005, 48(2): 288–293. |
| [19] | 王长青, 许厚泽, 钟敏, 等. 利用动力学方法解算GRACE时变重力场研究[J]. 地球物理学报, 2015, 58(3): 756–766. WANG Changqing, XU Houze, ZHONG Min, et al. An Investigation on GRACE Temporal Gravity Field Recovery Using the Dynamic Approach[J]. Chinese Journal of Geophysics, 2015, 58(3): 756–766. DOI:10.6038/cjg20150306 |
| [20] | 王正涛, 李建成, 姜卫平, 等. 基于GRACE卫星重力数据确定地球重力场模型WHU-GM-05[J]. 地球物理学报, 2008, 51(5): 1364–1371. WANG Zhengtao, LI Jiancheng, JIANG Weiping, et al. Determination of Earth Gravity Field Model WHU-GM-05 Using GRACE Gravity Data[J]. Chinese Journal of Geophysics, 2008, 51(5): 1364–1371. |
| [21] | 肖云, 夏哲仁, 王兴涛. 用GRACE星间速度恢复地球重力场[J]. 测绘学报, 2007, 36(1): 19–25. XIAO Yun, XIA Zheren, WANG Xingtao. Recovering the Earth Gravity Field from Inter-satellite Range-rate of GRACE[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 19–25. DOI:10.3321/j.issn:1001-1595.2007.01.004 |
| [22] | 宁津生, 钟波, 罗志才, 等. 基于卫星加速度恢复地球重力场的去相关滤波法[J]. 测绘学报, 2010, 39(4): 331–337, 343. NING Jinsheng, ZHONG Bo, LUO Zhicai, et al. Decorrelation Filtering Methods for Gravity Field Recovery Based on Satellite Acceleration Data[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 331–337, 343. |
| [23] | XU Peiliang. Position and Velocity Perturbations for the Determination of Geopotential from Space Geodetic Measurements[J]. Celestial Mechanics and Dynamical Astronomy, 2008, 100(3): 231–249. DOI:10.1007/s10569-008-9117-x |
| [24] | SHEN Y, CHEN Q, HSU H, et al. A Modified Short Arc Approach for Recovering Gravity Field Model[C]//Oral Presentation at the GRACE Science Team Meeting. Austin:Center of Space Research, University of Texas, 2013. |
| [25] | FLECHTNER F, WATKINS M, MORTON P, et al. Status of the GRACE Follow-on Mission[C]//Joint GSTM/SPP Final Colloquium. Potsdam, Germany:[s.n.], 2012. |
| [26] | GRUBER T, MURBÖCK M, PAIL R, et al. Earth System Mass Transport Mission 2 e. Motion2-proposal for an Earth Explorer 9 Mission[C]//Asia Oceania Geoscience Society 13th Annual Meeting, Session SE01. Beijing:AOGS, 2016. |
| [27] | LOOMIS B D, NEREM R S, LUTHCKE S B. Simulation Study of A Follow-on Gravity Mission to GRACE[J]. Journal of Geodesy, 2012, 86(5): 319–335. DOI:10.1007/s00190-011-0521-8 |
| [28] | 刘晓刚, 肖云, 李婧, 等. 低低卫——卫跟踪模式中卫星轨道高度和星间距离的指标设计论证[J]. 地球物理学进展, 2013, 28(5): 2247–2255. LIU Xiaogang, XIAO Yun, LI Jing, et al. Demonstration on the Indexes Design of Satellite Orbit Height and Inter-satellite Range in the Low-low Satellite-to-satellite Tracking Mode[J]. Progress in Geophysics, 2013, 28(5): 2247–2255. DOI:10.6038/pg20130506 |
| [29] | 冉将军, 许厚泽, 沈云中, 等. 新一代GRACE重力卫星反演地球重力场的预期精度[J]. 地球物理学报, 2012, 55(9): 2898–2908. RAN Jiangjun, XU Houze, SHEN Yunzhong, et al. Expected Accuracy of the Global Gravity Field for Next GRACE Satellite Gravity Mission[J]. Chinese Journal of Geophysics, 2012, 55(9): 2898–2908. DOI:10.6038/j.issn.0001-5733.2012.09.009 |
| [30] | XU Peiliang. Zero Initial Partial Derivatives of Satellite Orbits with Respect to Force Parameters Violate the Physics of Motion of Celestial Bodies[J]. Science in China Series D:Earth Sciences, 2009, 52(4): 562–566. DOI:10.1007/s11430-009-0049-4 |
| [31] | 陈秋杰, 沈云中, 张兴福, 等. 基于GRACE卫星数据的高精度全球静态重力场模型[J]. 测绘学报, 2016, 45(4): 396–403. CHEN Qiujie, SHEN Yunzhong, ZHANG Xingfu, et al. GRACE Data-based High Accuracy Global Static Earth's Gravity Field Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 396–403. DOI:10.11947/j.AGCS.2016.20150422 |
| [32] | XU Guochang. Orbits[M]. Berlin: Springer, 2008. |
| [33] | ELLMER M, MAYER-GVRR T. High Precision Dynamic Orbit Integration for Spaceborne Gravimetry in View of GRACE Follow-on[J]. Advances in Space Research, 2017, 60(1): 1–13. DOI:10.1016/j.asr.2017.04.015 |


