2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan 430079, China
高程基准是国家或地区表示地形高程的起算依据,一般由一个水准基面和一个永久性水准原点组成。水准基面是高程为零的起算面,一般是过高程零点的大地水准面或似大地水准面。但水准原点一般不是高程零点,而是实际水准测量高程的起算点。水准原点的高程通常是将验潮站的平均海面作为“零”基准起算通过精密水准测量获得,而精密水准测量是通过几何水准高差和沿水准路线的重力位差进行高程传递。由于水受到地球引力作用往低处流,因而将海面作为高程零起算面符合人们对自然现象的直观认识,传统上就是以海平面为依据定义高程基准。具体实施时要利用沿海单个或多个验潮站多年的潮位观测资料,通过一定原理和方法求取平均海面作为高程基准的零点。例如,我国1985高程基准是以青岛单验潮站的平均海面为高程零点[1],北美垂直基准是以加拿大魁北克里穆斯基的局部平均海面作为北美高程零点,欧洲统一高程基准是以荷兰阿姆斯特丹的单个验潮站的平均海面为高程零点,韩国是以韩国半岛东北边仁川湾验潮站观测的平均海面作为韩国高程零点[2]。而澳大利亚1971年高程基准是以澳大利亚沿岸30个验潮站的平均海面作为澳大利亚的高程零点,也就是30个验潮站的高程都为零[3]。
显然,由于全球各地平均海面的大地高不同,因此不同国家或地区间的高程基准面也不相同,这影响和制约了全球空间信息的共享与交换,例如,长距离水调工程、油气输送管网工程、跨境跨国高速公路、铁路等线路工程建设中,需要统一的高程信息,否则无法确保工程项目的联合施工作业与对接。欧洲多年来一直在建设欧洲统一水准网和欧洲垂直参考网,目的就是试图统一欧洲高程基准[4],南美洲也在全球统一高程系统框架内开展南美洲垂直参考系统SIRGAS(Sistema de Referencia Geocéntrico para las Américas)的定义与实现[5]。统一全球高程参考系统已经成为全球大地测量观测系统一体化(IGGOS:Integrated Global Geodetic Observation System)的基础任务之一。
针对高程基准的统一问题,文献[6]指出,只要基于不同高程基准的两个水准点的高程值已知,且可用水准联测,那么这两个高程基准完全可以连接统一。如果两个高程基准之间无法用水准联测,则可以基于位理论原理,借助全球重力场模型,进行高程基准统一。国外很多学者早就开展了卓有成效的研究,在理论方法和数值结果方面取得许多有重要参考价值的成果。文献[7]计算了英国、德国、美国和澳大利亚几个国家高程基准与全球大地水准面的差异;文献[8-9]计算了波罗的海周边国家的高程基准重力位;文献[10]计算了瑞典与芬兰两国高程基准间的垂直差异;文献[11]计算了澳大利亚高程基准、北美垂直基准与全球高程基准间的位差及垂直差异;文献[2]计算了韩国高程基准与全球基准间的基准差异。事实上,一个国家陆地与远距离岛屿之间的跨海高程传递,其本质上也是一种高程基准统一问题。例如,文献[12]在将黄海高程由陆地传递到距离上海芦潮港30 km的洋山岛时,将小洋山的潮位资料计算的平均海面与GPS水准引测高程计算的平均海面比较,实现了岛屿高程与陆地高程基准的统一。
考虑到国家或地区间尤其是洲际间水准测量联测难以甚至无法实施,目前高程基准统一连接一般是联合全球重力场模型和GPS水准数据,计算不同基准间的重力位差或者直接计算基准几何差异。位差法是利用重力场模型和GPS水准点的位置信息,计算局部区域水准点的重力位,再根据水准观测的海拔高程,反算水准点相对于高程零点的位差或大地位数,进而得到高程零点重力位。最后结合选取的全球基准重力位,得到局部基准与全球基准的位差,进而转换成基准差异[13-15]。事实上,对于两个区域高程基准,分别利用各基准下的GPS水准数据,计算两个区域高程基准零点重力位,就可以根据位差法实现两个区域高程基准的统一连接。几何差异法一般称为高程异常差法或者大地水准面高差法,是利用重力场模型和GPS观测信息,计算得到“重力”高程异常(或大地水准面)。同时,将GPS大地高减去水准海拔高,得到“几何”高程异常(或大地水准面),两个高程异常(或大地水准面)之差反映了高程基准间的差异[7, 13, 15-16]。由全球重力场模型计算高程异常(或大地水准面)时,已经默认了正常重力位U0所表示的大地水准面作为全球高程基准面,因此,几何差异法一般用于区域基准与全球基准的统一连接。
从1985国家高程基准建立开始,国内学者一直都在研究和讨论我国高程基准与全球高程基准的差异问题。早在1989年,文献[17]就利用全国一等水准资料,联合近海验潮站的水准联测高程,推算了中国近海平均海面相对于1985国家高程基准的高程,得出了中国近海平均海面呈现“南高北低”的结论。采用海洋学的方法,利用海水密度、温盐资料也可以得出我国沿海平均海面这种特点[18]。这些结果说明采用青岛单个验潮站资料建立的1985高程基准面与我国沿海地区平均海面存在偏差,与全球平均海面同样也存在偏差。前面论述的位差法、高程异常差法和海洋学方法,都在确定我国高程基准与全球基准方面得到了实际应用,由于选取的全球高程基准并不完全一致,因此推算的我国高程基准与全球基准的差异在22~46 cm之间[13-16, 19]。
目前,大地测量领域常用异常位法、正常高反算法、高程异常差法确定高程基准差异[13-16],3种方法虽然实现上有区别,但其实质都是利用物理大地测量学中位理论和高程系统定义推导得到,其在模型上并未完全统一。本文从高程基准差异的定义出发,推导现有3种方法的统一数学模型,探讨各种方法的关联性和区别;分析大地测量参考系和椭球参数对确定高程基准差异的影响;最后基于我国实测GPS和水准资料,确定我国85高程基准与全球高程基准的差异,并针对区域高程基准与全球高程间基准差异的确定给出几个结论和建议。
1 高程基准差异确定的理论与方法从理论上讲,在忽略水准和重力测量误差及重力或正常重力平均值计算误差的情况下,不同高程基准之间的偏差均可描述为从某个高程基准点上推算另一个基准点得到的高程不为零,该高程值代表了两个基准之间的差异。因此若有A和B两个基准点,根据A和B两点之间的水准联测和重力测量可以算出两点之间的位差ΔW(或位基数),将ΔW除以重力或正常重力的平均值即为A和B两个基准点的垂直差异。但该方法仅在不同区域高程系统之间可联测的情况下可行,在不可联测的情况下,可采用全球重力场模型计算高程基准的位值来建立其关联性,同样可以推算不同基准点之间的垂直差异,这也是目前进行区域和全球高程基准统一中常用的方法。根据高程系统的定义,考虑到位差(位基数)的大小不依赖于高程系统,因此将其作为推算高程基准差异的依据是非常合理的选择。
若全球和区域高程基准面对应的“真实”重力位分别为W0和W0r,则区域高程基准与全球高程基准的垂直差距定义如下
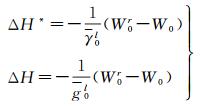 (1)
(1)
式中,ΔH*和ΔH分别对应正常高系统和正高系统下的高程基准差异;γ0l和g0l是区域高程基准点上正常重力和重力的平均值。这里可以理解为将全球高程基准作为计算区域高程基准点的基准,得到区域高程基准点相对于全球高程基准的高程。
下面基于该定义推导目前常用方法的实用公式。对于任意观测点P(r, θ, λ),可分别采用区域和全球基准来表达该点的位。在区域高程系统中,P点的重力位可用水准高、重力及区域基准位W0r表示为
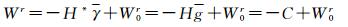 (2)
(2)
式中,Wr为P点的重力位;H*为P点的正常高;H为P点的正高;γ和g是沿着力线从P点到高程基准面间的正常重力平均值和重力平均值;C表示位基数。由式(2) 得到区域基准重力位后,代入式(1),则区域高程基准与全球高程基准之间的差异表示为
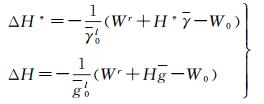 (3)
(3)
式(3) 的内涵是利用重力场模型由GPS水准点位置计算P点的重力位,再利用水准观测的海拔高计算位差或位基数,进而得到区域高程基准点的重力位W0r,最后计算位差,并将其除以正常重力平均值或重力平均值,得到高程基准的差异,这就是常说的位差法。
P点重力位Wr既可利用重力场模型直接按照引力位的球谐级数展开加上离心力位计算,其也可通过重力场模型计算的高程异常或大地水准面高,然后再推算P点的重力位,表示为
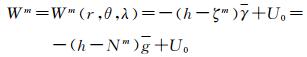 (4)
(4)
式中,h为P点的大地高;ζm和Nm分别为模型计算的高程异常和大地水准面高;U0表示由位模型计算高程异常或大地水准面高时选择参考椭球的正常重力位,也即相应大地水准面上的位常数。这里Wm是由重力场模型通过高程异常(或大地水准面)计算的P点重力位,亦即P点以全球高程基准位U0起算的重力位。
将式(3) 中的Wr用式(4) 的Wm代替,得到
 (5)
(5)
若假设γ0l=γ,g0l=g,则式(5) 可以简化为
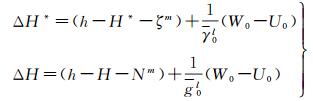 (6)
(6)
式中,右边第1项对应(似)大地水准面观测值和模型计算值的偏差;第2项代表选择的全球基准重力位与模型大地水准面重力位之差,其对应着零阶项改正,若选择全球高程基准重力位数值为U0,则后面一项为零。式(5) 或式(6) 的实质是先利用GPS水准点上的大地高h减去海拔高(H*或H),得到相应的“几何”高程异常(或大地水准面高),同时利用重力场模型,计算GPS水准点处的“重力”高程异常ζm(或大地水准面Nm),再顾及正常重力位U0与高程基准重力位W0不相等后,两类高程异常(或大地水准面)之间的差值,就是两个高程的基准差异。这种计算方法不直接计算重力位,而是由相应扰动位的位模型直接计算高程异常(或大地水准面),可以称之为高程异常差法(大地水准面高差法)。
将式(5) 进行变形得到
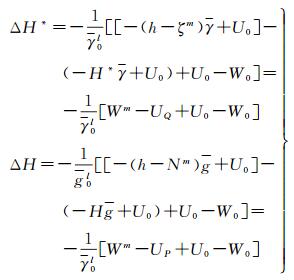 (7)
(7)
式中,UQ=-H*γ+U0=-Hg+U0,表示P点投影到似地形表面上点对应的正常重力位;WP表示由U0和GPS水准观测资料计算得到的P点重力位。
式(7) 中的第1个表达式是Molodensky理论用于正常高的直接反映,即P点的重力位应该与P点对应似地形表面上Q点的正常重力位相等,其不同表达了区域高程基准与参考椭球正常重力位U0对应基准面之间的偏差,基于该表达式计算的方法即为文献[13-15]采用的异常位法;第2个表达式中,模型计算P点重力位和实测数据计算P点位的差异同样表达了区域高程基准与参考椭球对应大地水准面之间的偏差。
从前面的公式推导和理论分析可知,式(3)、式(5)、式(6) 和式(7) 所表示的高程基准差异本质上是相同的,但位差法的公式最严密,高程异常差法(大地水准面高差法)和异常位法的公式表达的含义完全一致,仅是形式上略有差异,本文后续计算的结果说明了3种方法在区域高程基准与全球高程基准统一中,计算结果基本相同。
采用GPS水准观测数据确定区域高程基准与全球高程基准间的基准差异时,需要借助全球重力场模型来计算重力位及大地水准面高或高程异常。地球外部空间任意点P(r, θ, λ)的重力位W(r, θ, λ)是该点的引力位V(r, θ, λ)和离心力位Φ(r, θ, λ)之和
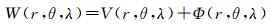 (8)
(8)
式中,引力位V(r, θ, λ)和离心力位Φ(r, θ, λ)的表达如下
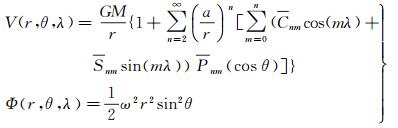 (9)
(9)
式中,GM为引力位模型给定的地心引力常数;a为正常椭球的长半轴;Cnm和Snm为完全规格化引力位模型系数,n、m表示模型的阶和次;Pnm(cos θ)为n阶m次完全规格化缔合勒让德函数。
通常来讲,地球自转角速度ω是精确已知,且其在不同大地测量参考系或采用的参考椭球之间没有差异,因此基于模型计算重力位的主要问题在于引力位的计算。
在利用模型计算某点的大地水准面或高程异常时,通常是先计算扰动位,然后利用布隆斯公式ζ=T/γ计算高程异常,再顾及地形影响将其转换为大地水准面高,扰动位T的表达式如下
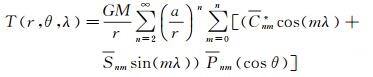 (10)
(10)
式中,Cnm*表示模型位系数与正常位系数之间的差值。
2 高程基准统一中的若干问题高程基准的定义问题是解决全球高程基准统一的前提,无论是局部高程基准还是全球高程基准,如果仅从表达空间点的高度来说都可以任意定义或选取。但是为了遵从自然现象并符合人类对自然现象的认识,又赋予了高程基准严密的科学意义和实用性。考虑到在经典高程系统的严格定义与实现中均是将某点的重力位与高程基准点的重力位之差(位基数)作为计算高程的基础,而且等位面具有全球相等重力位的特性,因此自然可以选择某个全球的等位面作为全球高程基准。一旦选择了某个重力位常数,即是选择了对应的等位面为高程基准。
2.1 以正常椭球重力位U0作为全球高程基准重力位U0是参考椭球的正常重力位,是地球总质量、旋转角速度及椭球形状的综合反映,由其定义的大地水准面,基本反映了地球的真实情形。如果选取某个参考椭球对应的U0作为全球高程基准重力位,此时大地水准面重力位W0=U0,这是物理大地测量学的经典定义,也是许多公式应用的前提,大大简化了公式推导和计算。因此,选择U0作为全球基准在理论上具有重要的意义。虽然不同的参考系统(GRS80,WGS-84,CGCS2000等)对应的椭球参数并不相同,其相应正常重力位U0也不同,但U0可以直接由椭球4个基本参数计算。
2.2 以全球海面高平均重力位作为全球高程基准重力位虽然选取U0作为全球高程基准理论意义直接,但U0所定义的大地水准面与全球平均海面不符合,偏离大家对以海面为零高程起算的客观实际。因此,选择Gauss-Listing定义的经典大地水准面作为全球高程基准更有实际意义,其是与全球平均海面最接近的重力位等位面,它不仅综合考虑了全球平均海面,而且还是严格的等位面。此时,以该大地水准面作为全球高程基准,那么全球海洋上海面地形均值理应为零,符合常规高程基准定义。
利用卫星测高观测资料,国内外学者使用不同时期、不同区域的测高数据,计算获得了全球平均海面平均重力位多个数值结果[11, 20-25]。其基本思想是利用全球平均海面高模型,内插形成1°×1°的海面高,联合重力场模型计算格网海面高重力位,并依据一定的准则计算海面平均重力位,将其作为全球高程基准的基准重力位,这种方法得到全球基准,满足海面地形均值为零[20, 26]。事实上,国内学者早在1985年就提出了以高程基准统一为目的来确定大地水准面的思想[27]。
表 1是利用DTU15MSS-2min全球平均海面高模型,基于EGM2008、EIGEN-6C4及SGG-UGM-1几个模型采用不同参考椭球确定的全球平均海面重力位WMSS,计算重力位前已经将海面高从TP椭球分别转换到GRS80、WGS-84、CGCS2000椭球,采用不同椭球计算时选择椭球对应的正常位U0作为基准重力位。计算中为了减弱近海区域潮汐的影响,将海面高数据只保留海深大于2000 m的数值,共计33 951个点。从表中结果可知,在相同重力场模型下,WGS-84与CGCS2000下的全球平均海面平均重力位结果相同。使用不同重力场模型和相同参考椭球计算时,虽然最大值及最小值之间的差异最大可达1.13 m2s-2,但重力位平均值的差异小于0.04 m2s-2,由此可见,虽然模型之间精度上有差异,但在全球平均的意义上差异不大。
| 重力场模型 | 参考系 | 点数 | 最大值/(m2s-2) | 最小值/(m2s-2) | 平均值/(m2s-2) | 标准差/(m2s-2) |
| EGM2008 | GRS80 | 33 951 | 62 636 889.683 9 | 62 636 850.966 4 | 62 636 865.176 2 | 8.104 3 |
| WGS-84 | 33 951 | 62 636 880.532 1 | 62 636 841.833 2 | 62 636 856.038 9 | 8.095 9 | |
| CGCS2000 | 33 951 | 62 636 880.532 1 | 62 636 841.833 2 | 62 636 856.038 9 | 8.095 9 | |
| EIGEN-6C4 | GRS80 | 33 951 | 62 636 889.270 5 | 62 636 850.451 2 | 62 636 865.176 8 | 8.111 7 |
| WGS-84 | 33 951 | 62 636 880.118 8 | 62 636 841.318 0 | 62 636 856.039 6 | 8.103 4 | |
| CGCS2000 | 33 951 | 62 636 880.118 8 | 62 636 841.318 0 | 62 636 856.039 6 | 8.103 4 | |
| SGG-UGM-1 | GRS80 | 33 951 | 62 636 888.557 6 | 62 636 848.911 4 | 62 636 865.139 3 | 8.087 7 |
| WGS-84 | 33 951 | 62 636 879.405 8 | 62 636 839.786 6 | 62 636 856.002 1 | 8.079 5 | |
| CGCS2000 | 33 951 | 62 636 879.405 7 | 62 636 839.786 6 | 62 636 856.002 1 | 8.079 5 |
2.3 参考椭球与重力场模型
在利用GPS水准点数据计算区域和全球高程基准差异时,需要计算GPS水准点的大地水准面高或者高程异常,大地水准面高或者高程异常一般是相对于参考椭球面的大地高,因此涉及参考椭球的选取。参考椭球是一个旋转水准椭球,由4个基本参数定义,包括椭球长半轴a、扁率f(或者动力形状因子J2),用以确定椭球尺度和形状,及地心引力常数GM和地球自转角速度ω。其中,GM、ω和J2具有物理意义。由这4个基本参数,可以导出椭球其他几何及物理参数,后者包括正常重力位、正常重力等正常重力场的相关参数。表 2给出了GRS80、WGS-84和CGCS2000 3个常用大地测量参考系的基本参数[28-31]。此外,GPS水准点重力位、大地水准面高或者高程异常的计算中使用的地球重力场模型及其参数如表 3所示。
| 参考系 | a/m | 1/f | GM/(m3s-2) | ω/(rad/s) | U0/(m2s-2) | J2/(×10-3) |
| GRS80 | 6 378 137 | 298.257 222 101 | 3.986 005 000×1014 | 7.292 115×10-5 | 62 636 860.850 0 | 0.484 166 854 896 119 |
| WGS-84 | 6 378 137 | 298.257 223 563 | 3.986 004 418×1014 | 7.292 115×10-5 | 62 636 851.714 6 | 0.484 166 774 983 522 |
| CGCS2000 | 6 378 137 | 298.257 222 101 | 3.986 004 418×1014 | 7.292 115×10-5 | 62 636 851.714 9 | 0.484 166 779 879 169 |
| 模型名称 | a/m | C2, 0 | GM/(m3s-2) | 潮汐系统 |
| EGM2008[33] | 6 378 136.3 | -0.484 165 143 790 815×10-3 | 3.986 004 415×1014 | 无潮汐 |
| -0.484 169 317 366 974×10-3 | 零潮汐 | |||
| -0.484 183 229 287 503×10-3 | 平均潮汐 | |||
| EIGEN-6C4 | 6 378 136.46 | -0.484 165 217 061 000×10-3 | 3.986 004 415×1014 | 无潮汐 |
| SGG-UGM-1 | 6 378 136.3 | -0.484 165 398 595 000×10-3 | 3.986 004 415×1014 | 无潮汐 |
从表 3可以看出,不同重力场模型的基本参数不同、潮汐系统不同、位模型系数不同,特别是重力场模型使用的长半轴和地心引力常数,与大地测量参考系的椭球参数不同。因此,当要利用表 3的重力场模型,计算表 2参考系下的重力场参量时,需要将重力场模型参数转换到相应的参考系下。重力场模型参数的转换主要是利用重力场模型的长半轴和地心引力常数(表 3)与参考系椭球的长半轴和地心引力常数(表 2),按照式(11) 转换[32]
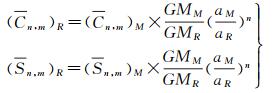 (11)
(11)
式中,参数下标M表示重力场模型参数值; 下标R表示参考椭球参数值。进行转换后,球谐系数与选择的参考椭球相匹配,随后计算就使用参考椭球的长半轴和地心引力常数,不再使用重力场模型的长半轴和地心引力常数。
2.4 全球高程基准重力位W0和零阶项的影响计算不同高程基准间的位差或垂直偏差时,可以直接利用重力场模型计算GPS水准点的重力位(式(8) 和式(9)),再基于位差方法按式(1) 或式(3) 计算区域高程基准相对于全球高程基准间的基准差异。同时,按照式(11) 将模型位系数转换到同一参考系,再用转换后所有阶次位系数计算站点的重力位或引力位。但采用高程异常差法(式(5) 或式(6))时,若选择的全球高程基准重力位W0与参考椭球面正常重力位U0不相等时,还需要进一步考虑零阶项的影响。由广义Bruns公式可得[34]
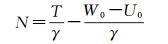 (12)
(12)
因此,常规计算扰动位采用式(10),该式的前提条件是球谐模型涉及的椭球参数与参考椭球参数一致。当两者不一致时,可采用式(11) 进行转换,转换后扰动位按照式(10) 计算。由此计算的球谐系数是转换后与参考椭球匹配的系数,GM和a是定义参考椭球的两个基本参数,不再是球谐模型的原始参数。如果不考虑参考椭球参数与模型参数不一致的影响,仅因为零阶项的影响就可能达到几十厘米,例如:对于当前常用的重力场模型(EGM2008) 和大地参考系椭球(GRS80) 来说,GM之间的差异对扰动位零阶项的影响约为9.18 m2s-2,相当于高程误差0.94 m。同时,如果选择的全球高程基准对应大地水准面的重力位W0与参考椭球正常重力位U0或者与位模型计算大地水准面上位的不相等时,还需要考虑式(12) 右边第2项即零阶项的影响。
2.5 潮汐系统的影响此外,高程系统与潮汐系统还有密切的联系。在高程基准定义与统一中,有以下几个方面涉及潮汐系统问题:① 局部高程基准零点由潮位观测资料推算的平均海面确定,潮位资料的处理与潮汐系统紧密有关,因此,不同的潮汐系统下平均海面不一致;② 如果利用卫星测高观测资料确定的平均海面计算全球基准重力位,虽然研究指出大地水准面重力位与潮汐系统无关[35],但测高平均海面高的处理中已经包含了潮汐的影响与改正,例如前面用到的DTU15MSS模型已进行了潮汐改正;③ 地球引力场模型(EGM2008等)与潮汐系统有关,不同的潮汐系统下位系数C20不同,本文后面的计算模型均采用无潮汐系统;④ GPS/水准点的空间位置信息与潮汐系统相关,GPS解算地面点位置,解算过程中顾及了潮汐影响改正,水准观测的海拔高也进行了潮汐改正[36]。从以上4点来看,高程基准统一中的每一项数值都与潮汐系统有关,因此潮汐系统必须统一。
3 我国1985高程基准与全球高程基准的差异在计算我国1985高程基准与全球高程基准的差异时,本文仅选取了青岛市周边二等GPS水准观测数据,总共152个点,其空间分布如图 1所示。选择该区域数据的主要原因有两点:一方面,水准测量的观测误差有随距离累积的特点,因此不宜选择与青岛原点距离较远的点;另一方面,当前现有超高阶重力场模型在不同区域的模型误差和截断误差的差异较大,尤其是平原和山区的截断误差相差较大,将其与GPS水准观测比较时结果会产生较大离散度,因此可能降低基准差异估计的可靠性。下面分别基于本文推导的式(3)(即位差法)和式(6)(即高程异常差法)计算我国1985高程基准与全球高程基准的差异。

|
| 图 1 青岛周边GPS水准点示意图 Fig. 1 The distribution of GPS/leveling measurements around Qingdao |
3.1 重力位差法
首先,利用青岛周边152个GPS水准点,以GRS80、WGS-84、CGCS2000为参考系,计算得到青岛85高程零点在各自参考系下的重力位,统计结果如表 4所示(前6列),其中由于WGS-84与CGCS2000椭球参数几乎一致,得到的高程零点重力位一致。采用不同重力场模型,在相同参考系下所得的平均重力位略有不同,最大差异是EGM2008与SGG-UGM-1模型的差异,约为0.27 m2s-2,由此计算的基准差异的互差小于3 cm。
| 重力场模型 | 参考系 | 最大值 /m2s-2 |
最小值 /m2s-2 |
平均值 /m2s-2 |
标准差 /m2s-2 |
重力位差 /m2s-2 |
基准差异 /m |
| EGM2008 | GRS80 | 62 636 865.712 6 | 62 636 859.898 8 | 62 636 862.950 3 | 0.987 7 | 2.100 3 | -0.214 4 |
| WGS-84 | 62 636 856.576 3 | 62 636 850.763 1 | 62 636 853.814 3 | 0.987 7 | 2.099 7 | -0.214 3 | |
| CGCS2000 | 62 636 856.576 7 | 62 636 850.763 4 | 62 636 853.814 7 | 0.987 7 | 2.099 8 | -0.214 3 | |
| EIGEN-6C4 | GRS80 | 62 636 865.413 6 | 62 636 861.234 0 | 62 636 863.115 0 | 0.875 2 | 2.265 0 | -0.231 2 |
| WGS-84 | 62 636 856.277 7 | 62 636 852.098 2 | 62 636 853.979 0 | 0.875 2 | 2.264 4 | -0.231 1 | |
| CGCS2000 | 62 636 856.278 0 | 62 636 852.098 6 | 62 636 853.979 3 | 0.875 2 | 2.264 7 | -0.231 1 | |
| SGG-UGM-1 | GRS80 | 62 636 865.603 7 | 62 636 861.320 4 | 62 636 863.220 1 | 1.001 6 | 2.370 1 | -0.241 9 |
| WGS-84 | 62 636 856.467 8 | 62 636 852.184 7 | 62 636 854.084 1 | 1.001 7 | 2.369 5 | -0.241 8 | |
| CGCS2000 | 62 636 856.468 1 | 62 636 852.185 0 | 62 636 854.084 5 | 1.001 7 | 2.369 6 | -0.241 8 |
如果取全球基准大地水准面的重力位W0等于大地测量参考系椭球面正常重力位U0(表 2),则按照式(3),将青岛高程零点重力位减去全球基准重力位,利用EGM2008、EIGEN-6C4和SGG-UGM-1模型计算得到的重力位差分别约为2.10 m2s-2、2.26 m2s-2和2.37 m2s-2(表 4中第7列)。在3个参考系下,位差接近且均为正值,说明了我国青岛高程零点低于U0所表示的全球基准。利用青岛零点的概略正常重力为9.798 247 m/s2,根据式(3) 分别用EGM2008、EIGEN-6C4和SGG-UGM-1模型计算得到青岛高程零点低于U0定义的全球基准分别约21.4 cm、23.1 cm和24.2 cm。
如果取全球高程基准重力位W0等于全球平均海面的平均重力位WMSS,利用表 1的全球基准重力位(第6列)与表 4中青岛高程零点重力位(第5列),可以计算出表 5的重力位差及基准差异。由表可以看出,当以全球平均海面的平均重力位定义全球高程基准时,利用EGM2008、EIGEN-6C4和SGG-UGM-1模型计算得到青岛高程零点高于全球基准分别约22.7 cm、21.0 cm和19.6 cm。
| 重力场模型 | 参考系 | 重力位差/m2s-2 | 基准差异/m |
| EGM2008 | GRS80 | -2.225 9 | 0.227 2 |
| WGS-84 | -2.224 6 | 0.227 0 | |
| CGCS2000 | -2.224 2 | 0.227 0 | |
| EIGEN-6C4 | GRS80 | -2.061 8 | 0.210 4 |
| WGS-84 | -2.060 6 | 0.210 3 | |
| CGCS2000 | -2.060 3 | 0.210 3 | |
| SGG-UGM-1 | GRS80 | -1.919 2 | 0.195 9 |
| WGS-84 | -1.918 0 | 0.195 7 | |
| CGCS2000 | -1.917 6 | 0.195 7 |
从表 4和表 5中还可以看出,不同的参考系下高程基准差异的计算结果互差非常小,其中WGS-84与CGCS2000之间因为参数差异较小,计算结果几乎相同,影响不大。
3.2 高程异常差法利用全球重力场模型EGM2008、EIGEN-6C4、SGG-UGM-1,分别在GRS80、WGS-84、CGCS2000参考系下,模型计算全球大地水准面的重力位取值为W0=U0,此时式(6) 后面一项为零。首先利用3个模型计算式(6) 中高程异常ζm,再利用GPS/水准资料计算“几何”高程异常ζ=h-H*, 最后可以直接得到表 6所示基准差异。
| m | |||||
| 模型 | 参考系 | 最大值 | 最小值 | 平均值 | 标准差 |
| EGM2008 | GRS80 | 0.097 1 | -0.496 3 | -0.214 4 | 0.100 8 |
| WGS-84 | 0.097 1 | -0.496 2 | -0.214 3 | 0.100 8 | |
| CGCS2000 | 0.097 1 | -0.496 2 | -0.214 3 | 0.100 8 | |
| EIGEN-6C4 | GRS80 | -0.039 2 | -0.465 8 | -0.231 2 | 0.089 3 |
| WGS-84 | -0.039 2 | -0.465 7 | -0.231 1 | 0.089 3 | |
| CGCS2000 | -0.039 2 | -0.465 7 | -0.231 1 | 0.089 3 | |
| SGG-UGM-1 | GRS80 | -0.048 0 | -0.485 2 | -0.241 9 | 0.102 2 |
| WGS-84 | -0.048 0 | -0.485 1 | -0.241 8 | 0.102 2 | |
| CGCS2000 | -0.048 0 | -0.485 1 | -0.241 8 | 0.102 2 | |
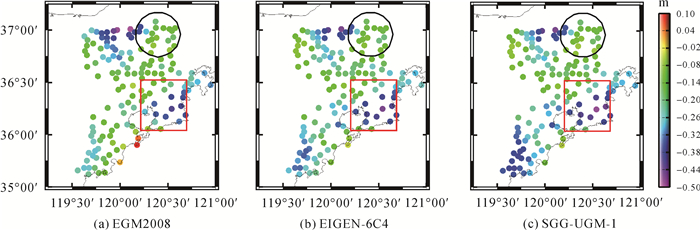
图 2给出了不同模型与GPS水准比较的差值空间分布。与重力位差结果(表 4)相比,两者结果一致。数值结果说明了我国青岛85高程基准高程零点低于GRS80、WGS-84、CGCS2000相应正常重力位U0表示的全球高程基准,依次为21.4 cm、23.1 cm和24.2 cm。从表 6还可看出,不同模型计算的高程异常与GPS水准观测值之差的数据离散程度(标准差)不同,EIGEN-6C4的离散程度最小,可以认为该模型的精度最高,其计算的系统偏差可靠性更高。但从差值的最大最小值来看,如果GPS水准精度非常可靠,那么模型自身的精度(包括模型误差和截断误差)则表现为差值变化区间的大小,3个模型变化区间分别为0.59、0.42和0.44,表明EGM2008模型精度较差。同时,从图 2可以看出模型与GPS水准数据的差值存在明显的系统性,若仅选择青岛原点周边23个水准点(图中红色方框内)来计算,则对于3个模型EGM2008、EIGEN-6C4、SGG-UGM-1计算的基准差异分别为-0.263 m、-0.304 m、-0.319 m,其与全部区域范围计算的基准差异达到了7 cm。这说明模型精度在不同区域差异较大,进而导致计算的基准差异也有较大的偏差,若选择图中东北角区域(黑色圆圈内)的数据,则会导致计算的基准差异比整个区域数据计算的基准差异偏大约10 cm。以上分析说明,基于当前全球重力场模型确定我国85国家高程基准与全球基准之间的差值在精度和可靠性方面还需要进一步提高,模型的精度与用于计算的区域相关,这对基准差异的估计有较大影响,因此需要进一步提高全球重力场模型在局部区域的精度。
|
| 图 2 不同模型计算152个高程点上似大地水准面的差异的空间分布 Fig. 2 Spatial distribution of the quasi-geoid height differences of 152 GPS/leveling points calculated from different global geopotential field models |
如果取平均海面重力位WMSS(表 1)作为全球基准重力位,由于现在U0≠WMSS,需要顾及零阶项的影响。又因为表 1所列WMSS是在各自对应参考系下计算的,针对不同的参考系,计算零阶项只需考虑式(6) 或式(12) 中等号右边第二项即可。利用表 1中的平均重力位WMSS与表 2中的正常重力位U0,以及青岛高程基准零点正常重力位概略值9.798 247 m/s2,可以得到表 7(第5列)所示的基准差异的零阶项部分。因此,WMSS定义的基准面低于U0定义的基准面约0.44 m。联合表 6(第5列)给出的青岛高程零点与U0定义基准面的差异,就可以得到表 7(第6列)中青岛高程零点与WMSS所表示全球基准之间的差值。利用EGM2008、EIGEN-6C4、SGG-UGM-1模型计算时,青岛高程零点比平均海面定义的全球基准分别高约22.7 cm、21.0 cm和19.6 cm。与表 5(第4列)相比,基准差异结果一致。
| 重力场模型 | 参考系 | WMSS平均值/m2s-2 | U0理论值/m2s-2 | 零阶项/m | 基准差异/m |
| EGM2008 | GRS80 | 62 636 865.176 2 | 62 636 860.850 0 | -0.441 5 | 0.227 1 |
| WGS-84 | 62 636 856.038 9 | 62 636 851.714 6 | -0.441 3 | 0.227 0 | |
| CGCS2000 | 62 636 856.038 9 | 62 636 851.714 9 | -0.441 3 | 0.227 0 | |
| EIGEN-6C4 | GRS80 | 62 636 865.176 8 | 62 636 860.850 0 | -0.441 6 | 0.210 4 |
| WGS-84 | 62 636 856.039 6 | 62 636 851.714 6 | -0.441 4 | 0.210 3 | |
| CGCS2000 | 62 636 856.039 6 | 62 636 851.714 9 | -0.441 4 | 0.210 3 | |
| SGG-UGM-1 | GRS80 | 62 636 865.139 3 | 62 636 860.850 0 | -0.437 8 | 0.195 9 |
| WGS-84 | 62 636 856.002 1 | 62 636 851.714 6 | -0.437 6 | 0.195 8 | |
| CGCS2000 | 62 636 856.002 1 | 62 636 851.714 9 | -0.437 5 | 0.195 7 |
4 结论与建议
本文从经典高程系统确定的理论和定义出发,给出了不同区域和全球高程基准差异的定义,并推导可将现有3种方法统一的数学模型。基于此,探讨了计算区域与全球高程基准差异需要考虑的几个问题,包括全球高程基准的选择、大地参考系和椭球参数对确定高程基准差异的影响等问题。最后,由我国青岛周边实测GPS水准资料及全球超高阶重力场模型,确定了我国85高程基准与全球高程基准的差值。主要有以下几个结论和建议:
(1) 本文将当前用于高程基准统一的3种方法进行了统一,不同高程基准间的基准差异均可定义为基准之间的位差与平均重力或平均正常重力比值的形式,确定位差时不依赖于采用的高程系统,确保了差值的唯一性。实际数值结果(表 4与表 6,表 5与表 7)进一步证明了3种方法的计算结果之间的差异可以忽略。
(2) 在高程基准比较时,必须要考虑不同参考系参考椭球参数的影响。特别是在涉及重力位时,不同重力位值的比较必须在相同参考系下进行,否则没有意义。利用地球引力位模型计算重力位或其他相关的重力场参量,需要按照式(11) 进行位系数的转换,其本质等同于选定参考系,数值结果都是针对于选定参考系的。
(3) 在根据大地水准面或高程异常计算基准差异时,除了按照式(11) 转换位系数之外,还要考虑全球大地水准面重力位与参考椭球正常重力位的差异,这就是零阶项的问题。例如早期用EGM96模型在WGS-84下计算大地水准面时,需要加上-53 cm的零阶项改正[37],以及用最新的EGM2008模型在WGS-84下计算大地水准面时,需要加上-41 cm改正[32]。本文利用全球平均海面作为全球高程基准,此时的全球高程基准重力位与选择参考椭球的正常重力位U0不等,产生的零阶项影响约为-44 cm(表 7),与当前EGM2008模型给出的41 cm数值接近。
(4) 综合本文的理论推导和数值结果与分析,可以得出我国1985国家高程基准的总体情况:当选取GRS80、WGS-84、CGCS2000参考系正常重力位U0所定义大地水准面作为全球高程基准时,基于青岛原点152个水准点和EIGEN-6C4模型,得到我国1985高程基准低于全球高程基准约23.1 cm;当选取全球平均海面的平均重力位定义全球高程基准时,我国1985高程基准高于全球基准约21.0 cm。因此我国高程基准与全球基准之差,主要取决于全球基准位的选择和所使用的GPS水准观测数据。国内关于我国高程基准差异数值结果的不同[13-16, 19],其主要差别就在于全球基准面选择和所采用的GPS水准观测数据不同。
(5) 计算区域与全球高程基准差异时,应该选择距离区域高程基准零点较近的GPS水准数据。一方面水准传递误差小,另一方面,重力场模型在小范围区域内的精度差异较小,因此,选择青岛周边GPS水准资料。从青岛152个GPS水准数据与全球重力场模型计算高程异常的差异看出,当前重力场模型在青岛周边不同点的精度差别依然较大,导致选择不同区域数据对确定我国1985国家高程基准与全球基准差异的影响较大。例如,本文的结果与早期使用青岛周边65个GPS水准数据联合EGM2008计算的基准差异有7.1 cm的不同[15],也说明了同样的问题。因此,如要实现厘米级精度的区域与全球高程基准统一,目前全球重力场模型的精度还不能满足要求。但是,随着时频测量技术发展及精度的不断提高,利用时频观测重力位及位差的方法有望用于高程基准的统一[38-39]。
致谢: 感谢晁定波教授和邹贤才教授对本文提出富有建设性的修改意见。
| [1] | 陈宗镛, 周天华, 于宜法, 等. 1985国家高程基准的研究[J]. 青岛海洋大学学报, 1988, 18(1): 9–14. CHEN Zongyong, ZHOU Tianhua, YU Yifa, et al. A Study on the 1985 National Datum Level of Altitude[J]. Journal of Ocean University of Qingdao, 1988, 18(1): 9–14. |
| [2] | JEKELI C, HYO J Y, JAY H K. The Offset of the South Korean Vertical Datum from a Global Geoid[J]. Journal of Civil Engineering, 2012, 5(16): 816–821. |
| [3] | ROELSE A, GRANGER H W, GRAHAM J W, et al.The Adjustment of the Australian Levelling Survey 1970-1971[R].2nd ed.Canberra, Australia:Department of Minerals and Energy/Division of National Mapping, 1975. |
| [4] | ADAM J, AUGATH W, BROUWER F, et al.Status and Development of the European Height Systems:Geodesy beyond 2000[C]//Proceedings of the International Association of Geodesy Symposia, 2000.Berlin:Springer, 2000. |
| [5] | SÁNCHEZ L.Definition and Realization of the SIRGAS Vertical Reference System within a Globally Unified Height System[C]//Proceedings of the IAG Symposia 2007.Berlin:Springer Verlag, 2007. http://www.springerlink.com/content/g0nr270737q81048 |
| [6] | RUMMEL R, TEUNISSEN P. Height Datum Definition, Height Datum Connection and the Role of the Geodetic Boundary Value Problem[J]. Bulletin Géodésique, 1988, 62(4): 477–498. DOI:10.1007/BF02520239 |
| [7] | RAPP R H. Separation between Reference Surfaces of Selected Vertical Datum[J]. Bulletin Geodesique, 1994, 69: 26–31. DOI:10.1007/BF00807989 |
| [8] | ARDALAN A, GRAFAREND E, KAKKURI J. National Height Datum, the Gauss-Listing Geoid Level Value W0 and its Time Variation, Baltic Sea Level Project, Epochs 1990.8, 1993.8, 1997.4[J]. Journal of Geodesy, 2002, 76: 1–28. DOI:10.1007/s001900100211 |
| [9] | GRAFAREND E W, ARDALAN A A. W0:An Estimate in the Finnish Height Datum N60, Epoch 1993.4, from Twenty-five GPS Points of the Baltic Sea Level Project[[J]. Journal of Geodesy, 1997, 71: 673–679. DOI:10.1007/s001900050134 |
| [10] | PAN M, SJÖBERG L E. Unification of Vertical Datums by GPS and Gravimetric Geoid Models with Application to Fennoscandia[J]. Journal of Geodesy, 1998, 72: 64–70. DOI:10.1007/s001900050149 |
| [11] | BURŠA M, KOUBA J, MÜLLER A, et al. Determination of Geopotential Differences between Local Vertical Datums and Realization of a World Height System[J]. Studia Geophysica et Geodaetica, 2001, 45: 127–132. DOI:10.1023/A:1021860126850 |
| [12] | 李建成, 姜卫平. 长距离跨海高程基准传递方法的研究[J]. 武汉大学学报(信息科学版), 2001, 26(6): 514–517, 532. LI Jiancheng, JIANG Weiping. Height Datum Transference within Long Distance across Sea[J]. Geomatics and Information Science of Wuhan University, 2001, 26(6): 514–517, 532. |
| [13] | 郭海荣, 焦文海, 杨元喜, 等.1985国家高程基准的系统差[J].武汉大学学报(信息科学版), 2004, 29(8):715-719. GUO Hairong, JIAO Wenhai, YANG Yuanxi, LIU Guangming.Systematic Error of the 1985 National Height Datum[J].Geomatics and Information Science of Wuhan University, 2004, 29(8):715-719. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=whch200408013&dbname=CJFD&dbcode=CJFQ |
| [14] | 焦文海, 魏子卿, 马欣, 等. 1985国家高程基准相对于大地水准面的垂直偏差[J]. 测绘学报, 2002, 31(3): 196–200. JIAO Wenhai, WEI Ziqing, MA Xin, et al. The Origin Vertical Shift of National Height Datum 1985 with Respect to the Geoidal Surface[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 196–200. |
| [15] | 赫林, 李建成, 褚永海. 1985国家高程基准与全球高程基准之间的垂直偏差[J]. 测绘学报, 2016, 45(7): 768–774. HE Lin, LI Jiancheng, CHU Yonghai. The Vertical Shift between 1985 National Height Datum and Global Vertical Datum[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 768–774. DOI:10.11947/j.AGCS.2016.20160029 |
| [16] | 郭海荣, 焦文海, 杨元喜. 1985国家高程基准与全球似大地水准面之间的系统差及其分布规律[J]. 测绘学报, 2004, 33(2): 100–104. GUO Hairong, JIAO Wenhai, YANG Yuanxi. The Systematic Difference and Its Distribution between the 1985 National Height Datum and the Global Quasigeoid[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 100–104. |
| [17] | 余兆康, 高家墉, 巫锡良. 中国平均海面与国家高程基准之间的偏差[J]. 台湾海峡, 1989, 8(2): 97–104. YU Zhaokang, GAO Jiayong, WU Xiliang. Difference between Mean Seal level and National Geoid (1985) along the Coast of China[J]. Journal of Oceanography in Taiwan Strait, 1989, 8(2): 97–104. |
| [18] | 赵明才, 韩晓宏. 中国近海海面地形及青岛站高程基准的差距[J]. 海洋通报, 1990, 9(2): 15–22. ZHAO Mingcai, HAN Xiaohong. China Offshore Sea-surface Topography and Qindao Station Elevation Datums's Difference[J]. Marine Science Bulletin, 1990, 9(2): 15–22. |
| [19] | 方国洪, 魏泽勋, 方越, 等. 依据海洋环流模式和大地水准测量获取的中国近海平均海面高度分布[J]. 科学通报, 2001, 46(18): 1572–1575. FANG Guohong, WEI Zexun, FANG Yue, et al. Distribution of Mean Sea Surface Height of China Sea with Ocean Circulation Model and Geodetic Leveling J][J]. Chinese Science Bulletin, 2001, 46(18): 1572–1575. DOI:10.3321/j.issn:0023-074X.2001.18.018 |
| [20] | 褚永海, 李建成. 联合全球重力场模型和海面高模型确定平均海面位常数[J]. 大地测量与地球动力学, 2012, 32(5): 58–62. CHU Yonghai, LI Jiancheng. Determination of Mean Sea Level Geopotential from Global Gravity Field Model and Global Sea Surface Height Model[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 58–62. |
| [21] | BURŠA M, KOUBA J, RADĚJ K, et al. Mean Earth's Equipotential Surface from TOPEX/Poseidon Altimetry[J]. Studia Geophysica et Geodaetica, 1998(42): 459–466. |
| [22] | BURŠA M, KOUBA J, KUMAR M, et al. Geoidal Geopotential and World Height System[J]. Studia Geophysica et Geodaetica, 1999(43): 327–337. |
| [23] | BURŠA M, KENYON S, KOUBA J, et al. Long-term Stability of Geoidal Geopotential from TOPEX/Poseidon Satellite Altimetry 1993-1999[J]. Earth, Moon, and Planets, 2001(84): 163–176. |
| [24] | BURŠA M, KENYON S, KOUBA J, et al. A Global Vertical Reference Frame Based on Four Regional Vertical Datum[J]. Studia Geophysica et Geodaetica, 2004(48): 493–502. |
| [25] | DAYOUB N, EDWARDS S J, MOORE P. The Gauss-Listing Geopotential Value W0 and Its Rate from Altimetric Mean Sea Level and GRACE[J]. Journal of Geodesy, 2012(86): 681–694. |
| [26] | 晁定波, 申文斌, 王正涛. 确定全球厘米级精度大地水准面的可能性和方法探讨[J]. 测绘学报, 2007, 36(4): 370–376. CHAO Dingbo, SHEN Wenbin, WANG Zhengtao. Investigations of the Possibility and Method of Determining Global Centimeter-level Geoid[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 370–376. |
| [27] | 梁振英. 大地水准面的严密定义和我国高程基准的选择[J]. 测绘通报, 1985(2): 1–7. LIANG Zhenying. The Rigorous Definition of the Geoid and the Choice of National Height Datum[J]. Bulletin of Surveying and Mapping, 1985(2): 1–7. |
| [28] | MORITZ H. Geodetic Reference System 1980[J]. Journal of Geodesy, 2000, 74(1): 128–133. DOI:10.1007/s001900050278 |
| [29] | GROTEN E. Parameters of Common Relevance of Astronomy, Geodesy and Geodynamics[J]. Journal of Geodesy, 2000, 74(1): 134–140. DOI:10.1007/s00190-000-0134-0 |
| [30] | 程鹏飞, 文汉江, 成英燕, 等. 2000国家大地坐标系椭球参数与GRS 80和WGS 84的比较[J]. 测绘学报, 2009, 38(3): 189–194. CHENG Pengfei, WEN Hanjiang, CHENG Yingyan, et al. Parameters of the CGCS 2000 Ellipsoid and Comparisons with GRS80 and WGS84[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 189–194. |
| [31] | DEFENSE-MAPPING-AGENCY.Department of Defense World Geodetic System 1984:Its Definition and Relationships with Local Geodetic Systems[R].Washington D, C:The Defense Mapping Agency, 1987. http://www.mendeley.com/research/world-geodetic-system-1984-definition-relationships-local-geodetic-systems/ |
| [32] | BARTHELMES F.Definition of Functionals of the Geopotential and Their Calculation from Spherical Harmonic Models, STR09/02[R].Berlin:Deutsches Geo Forschungs Zentrum, 2013. |
| [33] | PAVLIS N K, HOLMES S A, KENYON S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008(EGM2008)[J]. Journal of Geophysical Research, 2012, 117: 440–448. |
| [34] | HOFMANN-WELLENHOF B, MORITZ H. Physical Geodesy[M]. Wien: Springer-Verlag, 2006: 403. |
| [35] | BURŠA M. Geoidal Potential Free of Zero-frequency Tidal Distortion[J]. Earth Moon & Planets, 1995, 71(1-2): 59–64. |
| [36] | 张红英, 郭佳, 张新兵, 等. 日月潮汐改正对精密水准测量的影响[J]. 海洋测绘, 2011, 31(3): 12–15. Zhang Hongying, Guo Jia, Zhang Xinbing, et al. The Effect on the Precise Leveling about the Correct to Luni Solar Tides[J]. Hydrographic Surveying and Charting, 2011, 31(3): 12–15. |
| [37] | LEMOINE F G, KENYON S C, FACTOR J K, et al.The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96[R].Washington DC:NASA/NIMA, 1998. http://www.sciencedirect.com/science/article/pii/S0273117716305555 |
| [38] | SHEN Z, SHEN W, ZHANG S. Formulation of Geopotential Difference Determination Using Optical-atomic Clocks Onboard Satellites and on Ground Based on Doppler Cancellation System[J]. Geophysical Journal International, 2016(206): 1162–1168. |
| [39] | SHEN Z, SHEN W, ZHANG S. Determination of Gravitational Potential at Ground Using Optical-atomic Clocks on Board Satellites and on Ground Stations and Relevant Simulation Experiments[J]. Survey Geophysics, 2017, 38(4): 757–780. DOI:10.1007/s10712-017-9414-6 |


