2. 北京跟踪与通信技术研究所, 北京 100094
2. Beijing Institute of Tracking and Telecommunication Technology, Beijing 100094, China
相机检校是摄影测量及计算机视觉至关重要的一个问题,相机检校是否精确,会影响到后续测图及三维重建的精度。影响相机检校结果的因素很多,包括相机自身因素和外部因素等,如相机制造工艺、相机焦距、调节光圈、更换镜头、相机晃动、更换电池、光照条件、检校靶标数量、靶标点提取精度、安装角、测量误差、相机模型选择等[1-4],因此在进行摄影测量时,在获得相机的初始参数后,还需进行相机检校,减少相机参数对测量精度的影响[5-6]。摄影测量领域的传统方法通常是在专用检校场(鉴定场)进行相机检校[7-8],但检校场建造维护代价很高,且要综合考虑气候条件、地形地貌等的影响。为了满足相机鉴定的迫切需求,使相机鉴定更加方便灵活,文献[9-12]使用靶标进行相机鉴定。基于靶标的相机鉴定结果精度很高,稳健性强,但需要制作特定靶标,而且需要精密仪器测量世界坐标。
最好、最适宜的相机检校方法取决于实际应用类型[13],立体相机根据两个相机之间固定相对关系建立约束进行标定[14],存在“空间平行线”等建筑物场景时,则可利用灭点进行相机检校[15]。为了真实精确反映航空摄影测量时所获取图像的相机参数和畸变系数,提高解算精度,进行精确三维建模。本文提出基于航空影像的相机自检校方法,联合所有航空影像同名点基于共面约束进行相机检校。对于高分辨率大尺寸航空影像,中心及边缘的畸变差异较大,为了提高畸变参数解算精度,提出分区域网格划分检校法。
1 相机检校航空影像是现代信息化战场的重要信息来源,为了提高数据处理精度,保证数据的可信性,关键一步就是对相机进行严格的检校,求出相机的内方位元素及各项畸变系数。在数据处理中消除影像的畸变差,提高同名像点的空间解算精度,实现高精度三维重建。本文提出基于航空影像的相机自检校方法,具体步骤如下:首先进行航空影像同名点匹配,构建立体像对;然后基于共面约束使用直接解法和迭代优化进行相对定向,解算相机位置与姿态;最后对航空影像进行区域划分,使用最小二乘优化方法解算相机内方位元素和畸变系数。由于该方法联合所有影像同名点进行解算,为了避免大量同名点对存储和计算速度的影响,优化了矩阵解算策略,使方程解算与同名点数量无关。该方法操作简单,对图像无特殊要求,不需要制作精良靶标,也不需要使用特定检校场。使用大比例尺航空影像进行解算能真实精确反映摄影测量时所获取图像的相机参数和畸变系数,避免检校环境与使用环境不同解算得到的相机畸变参数不能真实反映所获取影像的畸变问题;使用所有同名点解算,避免由于选择不同特征点或控制点对检校精度的影响[16],同时,焦距、像主点和相机畸变系数可以独立解算,降低了参数之间的耦合度[12]。
在进行相机检校前首先必须根据实际应用选择合理的相机畸变模型,模型的选择要比参数估计更重要,同时还需要选择合适的评价指标衡量选择的模型[17]。本文研究了小孔模型、经典的畸变模型及在x、y方向使用不同的径向畸变系数的畸变模型,同时提出区域网格划分法进行畸变解算,并对检校结果进行了比较。同名点误差及共面约束误差对三维重建精度影响很大,因此本文选择同名点误差及共面误差衡量各模型的性能。
1.1 相机模型被广泛使用的相机模型为小孔成像模型,如式所示
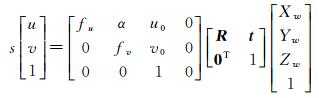 (1)
(1)
式中,s为空间点深度或尺度因子;(u, v)为以像素为单位的图像坐标;(Xw, Yw, Zw)为世界坐标系中的坐标;(u0, v0)为像主点坐标;α是u轴和v轴不垂直因子;(fu, fv)分别是相机以像素为单位的横坐标轴和纵坐标轴上的焦距;R为旋转矩阵;t为平移向量。
本文设u轴和v轴具有相同的尺度因子,即fu=fv,并假设成像平面的横、纵轴垂直,则最终的相机投影变换模型为
 (2)
(2)
式中,f为等效焦距;K为内方位元素矩阵或投影变换矩阵;M为外参数矩阵,包含旋转矩阵R和平移向量t。
由于制造工艺等多种因素,相机通常都会存在畸变,如式(3)所示
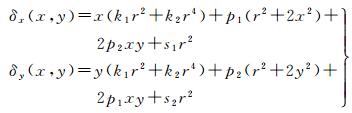 (3)
(3)
式中,(x, y)为中心化的像点坐标,x=x0-cx, y=y0-cy;(x0, y0)为实际像点坐标;cx、cy为光心坐标;r为像点到光心的距离,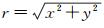
对于高分辨率大尺寸航空影像,x、y方向的径向畸变系数可能并不相同,因此在进行解算时,设x、y方向具有不同的径向畸变系数kx1、kx2及ky1、ky2,如式(4)所示
 (4)
(4)
由于径向畸变的影响远大于其他畸变[18-19],因此本文只考虑径向畸变。
1.2 相机检校 1.2.1 同名点匹配同名点匹配是进行相机检校的基础。输入图像为无序的遥感影像集,因此必须首先提取特征点,进行同名点匹配,进而确定各影像间的邻接关系,建立立体模型。从无序影像集构建立体模型的策略如下:首先提取所有影像的特征点;对于任意两幅影像,进行特征匹配,因为从不同视点拍摄的两幅影像存在缩放、旋转等仿射变换,基于RANSAC算法求解它们之间的仿射变换关系,以判断匹配的有效性:若两幅图像无重叠或误点太多,则无法得到一个有效的仿射变换,该像对被剔除;对于有重叠并匹配成功的两幅影像,通过RANSAC算法可以剔除少量误匹配点,最终获得一定数量的可靠同名像点,对应的两幅影像即构成了一个立体像对[20]。在立体像对模型内进行稠密同名点匹配,获取大量的观测值,可以为后续的最小二乘优化提供大量的观测方程。
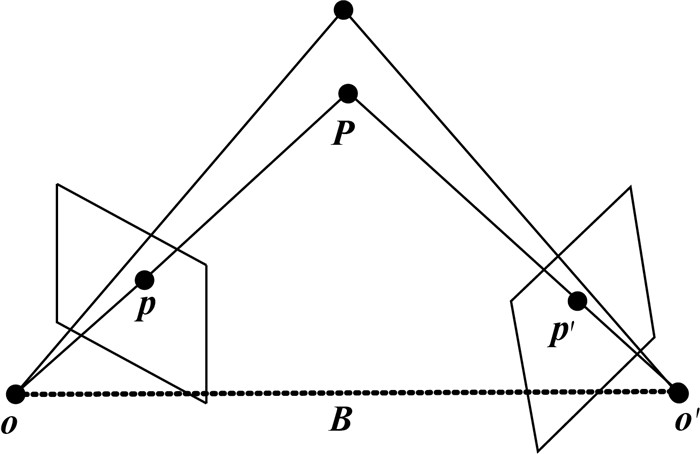
1.2.2 相对定向根据解析法相对定向,同名射线在空间对对相交,射线op、o′p′及摄影基线B共面,如图 1所示,根据三矢量共面,它们的混合积为0,可得约束公式
|
| 图 1 共面约束示意图 Fig. 1 Coplanarity constraint |
 (5)
(5)
式中,op、o′p′为同名射线矢量;B为基线矢量。
首先采用直接解法相对定向获取各相机位置与姿态初值,然后使用最小二乘进行迭代优化,依据共面约束,建立优化函数如式(6)所示
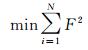 (6)
(6)
式中,F=B·op×o′p′。
具体过程如下:①选择系列图像中中间位置的图像作为主图,相邻的一幅图作为辅图,邻接图为相互有重叠的图,从其他未定位图中找一幅邻接点最多的邻接图作为候选图。通过提取主图与邻接图间的同名点,由相对定向过程,即可确定邻接图对应相机的相对位置和姿态;重复上述过程,即可确定全部相机的相对位置和姿态。②以位置与姿态参数为优化目标,基于共面约束建立优化函数,解算各相机位置与姿态参数。对于多幅航空影像,为了快速解算位置与姿态,迭代解算能够收敛,避免参数过多相互干扰,采用如下策略:对主、辅图定位后,主、辅图只绕Z轴旋转κ1、κ2,不进行平移变换,其他图像进行平移调整(txi, tyi, tzi),同时绕Z轴旋转κi,经过迭代调整后使同名像点重合。此次位置与姿态解算不加入相机内方位元素。主、辅图各对应1个位置与姿态参数,其他图像对应4个位置与姿态参数,对于M幅图像N对同名点,则可生成包含(4M-6)个未知数N个方程的线性约束方程组,如式(7)所示
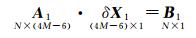 (7)
(7)
式中
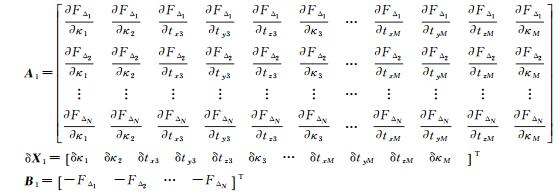
经过直接解算与迭代优化后可以解算出相机相对位置与姿态。
1.2.3 相机内方位元素解算在相对定向解算的位置与姿态基础上加入相机内方位元素(焦距、像主点、畸变系数)进行联合解算,进一步优化位置与姿态参数,解算相机内方位元素。约束方程和优化目标不变,以相机相对于公共坐标系的旋转角参数、平移向量及相机内方位元素为未知量,作为最小二乘参数迭代优化,如式(8)所示
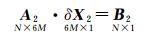 (8)
(8)
式中
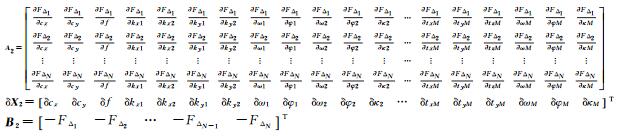
在调整过程中,主图绕X、Y轴旋转ω1、φ1,辅图绕3个轴旋转ω2、φ2、κ2,其他图像进行平移调整(txi, tyi, tzi),同时绕3个轴旋转ωi、φi、κi。主、辅图对应5个位置与姿态参数,其他图像对应6个位置与姿态参数,共有7个相机参数(f, cx, cy, kx1, kx2, ky1, ky2),对于M幅图像N对同名点,则可生成包含6M个未知数、N个方程的线性约束方程组。
经过最小二乘迭代优化,可以解算出相机的内方位元素和畸变系数及更精确的位置与姿态参数。
1.2.4 分区域畸变校正对于高分辨率大尺寸航空影像,图像中心及边缘的畸变差异较大,为了准确地解算相机畸变系数,进行畸变校正,对图像进行了区域网格划分,分区域进行畸变校正。将航空影像划分为m×n矩形网格,m、n分别为x、y方向的网格数。联合所有影像同名点使用双线性插值和最小二乘迭代优化算法解算网格交点畸变量,然后根据网格交点处畸变量校正该网格区域内像点。通过联合计算所有航空影像并通过合理划分矩形网格,能够最真实地反映摄影时相机的内方位元素及畸变系数,对像点进行畸变校正。
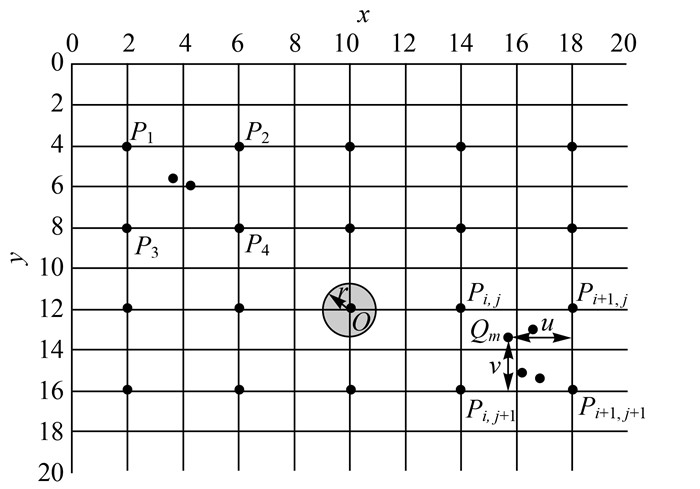
在图 2中,设网格(i, j)交点pij的畸变量为δxpi, j、δypi, j,则根据双线性插值,同名像点Qk处的畸变量为
|
| 图 2 区域网格划分 Fig. 2 Mesh partition |
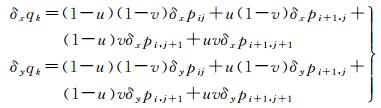 (9)
(9)
式中,u、v分别为Qk到直线Pi+1, jPi+1, j+1和Pi, j+1Pi+1, j+1的归一化距离。然后进行最小二乘优化迭代,在位置与姿态参数、相机内方位元素的基础上加入所有网格交点处畸变量进行迭代优化。x、y方向的网格数分别为m、n,则网格交点畸变量参数个数为2×m×n,对于N对同名点,构成的线性约束方程组如式(10)所示
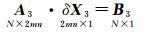 (10)
(10)
式中
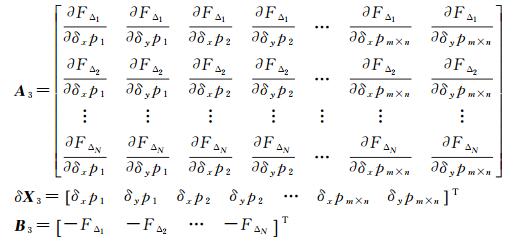
联合所有航空影像大规模同名点进行解算,对存储和计算要求较高。本文采用最小二乘方法进行迭代优化,方程AX=B与ATAX=ATB同解,为了节省存储空间,不保存系数矩阵A而直接构造ATA,方程右边直接构造ATB,对于式(8)最终所需的存储单元仅为6M×(6M+1)。常规方法需要的存储单元为2N×(6M+1),这样的处理使此方法的方程解算规模与引入的同名点数量无关,从而极大地减少了存储量,提高了计算速度。多次迭代直至||δX2||<ε(ε为某一小值),进而得到未知量的最优解。
2 试验 2.1 试验数据试验数据1采用威海天福山试验场拍摄的航空影像[21],试验场面积为2 km2,场区内均匀布设了183个精确量测的地面控制点,每个控制点都制作了明显的地面标志,控制点坐标精度优于0.01 m。用有人驾驶飞机对场区进行航拍,得到了5条航线、共115幅航空影像,原始影像数据量约为20 GB;图像分辨率为8956×6708像素。图像的航向重叠率约为60%,旁向重叠率大于20%,影像空间拍摄相机为哈苏H4D-60,镜头焦距为50 mm,像元大小为6 μm。无POS记录。图 3(a)为试验用的部分影像。

|
| 图 3 航空影像数据 Fig. 3 Aerial images |
试验数据2采用使用佳能5DⅡ相机对青岛王家村进行航空摄影拍摄的航空影像,全航区共拍摄了78(13×6航线)幅影像,镜头焦距为35 mm,像元大小为6.4 μm,图像大小为5616×3744像素。部分试验数据如图 3(b)所示。
2.2 试验结果从数据1威海天福山试验场的22幅航空影像64个同名点文件中匹配14幅图像32个同名点文件进行了相机内方位元素及畸变联合解算,同名点对数量约为640 000对。参数初始值(区域网格划分时网格交点畸变量初值为0)及试验结果如表 1所示。畸变量(δx,δy)为位于图片角上的像点在x、y方向的径向畸变,用于评估畸变大小。共面误差(MSE)为左像同名点和基线构成平面与右像同名点的距离的均方误差。方法1和方法2为文献[18]基于室外检校场联立全部影像和4幅影像的检校结果;方法*-1(*=1, 2, 3)为本文方法单独解算焦距(f)和像主点(cx, cy);方法*-2(*=1, 2, 3)为使用传统畸变模型解算相机内方位元素和畸变系数;方法*-3为x、y方向使用不同的径向畸变参数解算相机内方位元素和畸变系数;方法*-4、*-5和*-6为采用区域网格划分进行畸变解算,网格数分别为16×12,32×24,64×48。
| 方法 | 焦距/像素 | 像主点/像素 | 畸变系数 | 畸变量/像素 | 共面误差 /像素 |
|||||
| f | cx | cy | kx1(k1) | kx2(k2) | ky1 | ky2 | δx | δy | MSE | |
| 方法1 | 8 303.0 | 4 433.3 | 3 415.5 | 3.21e-11 | -1.94e-18 | - | - | 4.01 | 3.00 | - |
| 方法2 | 8 313.2 | 4 431.9 | 3 417.2 | 3.96e-11 | -1.43e-18 | - | - | 0.72 | 0.54 | - |
| 初始值1 | 8 308.3 | 4 477.5 | 3 353.5 | 0 | 0 | 0 | 0 | - | - | - |
| 方法1-1 | 8 332.2 | 4 433.8 | 3 413.3 | - | - | - | - | - | - | 0.441 |
| 方法1-2 | 8 336.9 | 4 433.7 | 3 413.6 | 3.03e-11 | 6.40e-19 | - | - | 7.05 | 5.28 | 0.435 |
| 方法1-3 | 8 343.9 | 4 433.0 | 3 413.7 | 3.83e-11 | 5.30e-19 | 2.80e-11 | 9.72e-19 | 7.69 | 6.13 | 0.435 |
| 方法1-4 | - | - | - | - | - | - | - | 8.15 | 6.26 | 0.343 |
| 方法1-5 | - | - | - | - | - | - | - | 7.89 | 6.17 | 0.341 |
| 方法1-6 | - | - | - | - | - | - | - | 7.76 | 6.15 | 0.338 |
| 初始值2 | 8 303.0 | 4 433.3 | 3 415.5 | 0 | 0 | 0 | 0 | - | - | - |
| 方法2-1 | 8 331.8 | 4 433.4 | 3 413.5 | - | - | - | - | - | - | 0.438 |
| 方法2-2 | 8 337.4 | 4 433.7 | 3 413.5 | 3.05e-11 | 6.43e-19 | - | - | 7.09 | 5.31 | 0.435 |
| 方法2-3 | 8 344.6 | 4 433.1 | 3 413.7 | 3.87e-11 | 5.32e-19 | 2.82e-11 | 9.76e-19 | 7.76 | 6.16 | 0.435 |
| 方法2-4 | - | - | - | - | - | - | - | 8.07 | 6.28 | 0.341 |
| 方法2-5 | - | - | - | - | - | - | - | 7.79 | 6.19 | 0.338 |
| 方法2-6 | - | - | - | - | - | - | - | 7.70 | 6.13 | 0.336 |
| 初始值3 | 8 333.3 | 4478 | 3 354.0 | 0 | 0 | 0 | 0 | - | - | - |
| 方法3-1 | 8 332.2 | 4 433.7 | 3 413.2 | - | - | - | - | - | - | 0.441 |
| 方法3-2 | 8 336.8 | 4 433.7 | 3 413.5 | 3.02e-11 | 6.40e-19 | - | - | 7.04 | 5.27 | 0.435 |
| 方法3-3 | 8 343.9 | 4 433.0 | 3 413.7 | 3.83e-11 | 5.31e-19 | 2.79e-11 | 9.73e-19 | 7.69 | 6.12 | 0.434 |
| 方法3-4 | - | - | - | - | - | - | - | 8.18 | 6.30 | 0.368 |
| 方法3-5 | - | - | - | - | - | - | - | 7.88 | 6.15 | 0.342 |
| 方法3-6 | - | - | - | - | - | - | - | 7.85 | 6.17 | 0.337 |
从表 1试验结果可以看出,本文方法可以有效求出相机内方位元素,且精度较高。像主点解算结果非常稳定,与基于室外检校场的解算精度相当。基于区域网格划分的畸变校正方法共面误差明显小于其他畸变校正方法。相机焦距的检校结果与初始值及文献[18]相差较大,经分析主要原因如下:一是由于相机镜头加工、装配过程中引入的误差,使实际值与标称值存在误差;二是在不同的环境下拍摄,摄影测量时外部条件变化等引入的误差[1, 22-27];如不同的摄影距离下主距和像主点也会发生变化,不同的检校场、图像集检校结果也会有差异[27-28]。
表 2为本文方法焦距和结果分析,可以看出该方法对优化算法初值不敏感,解算的结果非常稳定。表 3和图 4为各图定向后同名点误差,使用区域网格划分的畸变解算算法精度明显高于其他方法,同名点误差显著减少,解算结果对初值不敏感,所有最小二乘迭代优化均小于7次收敛。
| 像素 | |||||
| 参数 | 均值 | 标准差 | 最小值 | 中值 | 最大值 |
| cx | 4 433.4 | 0.34 | 4 433.0 | 4 433.7 | 4 433.8 |
| cy | 3 413.7 | 0.68 | 3 413.2 | 3 413.6 | 3 415.5 |
| f | 8 337.7 | 5.26 | 8 331.8 | 8 336.9 | 8 344.6 |
| 像素 | ||||||||||||||
| 方法 | 图像编号 | |||||||||||||
| 9062 | 9063 | 9064 | 9065 | 9088 | 9089 | 9090 | 9091 | 9092 | 9112 | 9113 | 9114 | 9115 | 9116 | |
| 方法1-1 | 0.384 | 0.388 | 0.413 | 0.465 | 0.560 | 0.389 | 0.389 | 0.401 | 0.365 | 0.568 | 0.405 | 0.361 | 0.407 | 0.570 |
| 方法1-2 | 0.403 | 0.398 | 0.419 | 0.488 | 0.576 | 0.407 | 0.416 | 0.420 | 0.377 | 0.578 | 0.417 | 0.369 | 0.409 | 0.571 |
| 方法1-3 | 0.400 | 0.396 | 0.418 | 0.487 | 0.578 | 0.407 | 0.416 | 0.419 | 0.377 | 0.578 | 0.418 | 0.372 | 0.410 | 0.573 |
| 方法1-4 | 0.322 | 0.325 | 0.354 | 0.413 | 0.498 | 0.312 | 0.308 | 0.329 | 0.316 | 0.548 | 0.362 | 0.271 | 0.249 | 0.444 |
| 方法1-5 | 0.319 | 0.324 | 0.353 | 0.411 | 0.496 | 0.310 | 0.306 | 0.327 | 0.313 | 0.543 | 0.357 | 0.267 | 0.244 | 0.441 |
| 方法1-6 | 0.316 | 0.321 | 0.350 | 0.409 | 0.494 | 0.308 | 0.304 | 0.324 | 0.310 | 0.540 | 0.354 | 0.265 | 0.243 | 0.439 |
| 方法2-1 | 0.406 | 0.399 | 0.417 | 0.481 | 0.581 | 0.414 | 0.422 | 0.423 | 0.391 | 0.585 | 0.422 | 0.383 | 0.424 | 0.578 |
| 方法2-2 | 0.403 | 0.398 | 0.419 | 0.488 | 0.576 | 0.407 | 0.416 | 0.420 | 0.377 | 0.578 | 0.417 | 0.369 | 0.409 | 0.571 |
| 方法2-3 | 0.400 | 0.396 | 0.418 | 0.487 | 0.578 | 0.407 | 0.416 | 0.419 | 0.377 | 0.578 | 0.418 | 0.372 | 0.410 | 0.573 |
| 方法2-4 | 0.319 | 0.323 | 0.353 | 0.411 | 0.495 | 0.310 | 0.306 | 0.326 | 0.314 | 0.546 | 0.356 | 0.266 | 0.244 | 0.439 |
| 方法2-5 | 0.316 | 0.322 | 0.352 | 0.410 | 0.494 | 0.309 | 0.304 | 0.323 | 0.310 | 0.541 | 0.353 | 0.263 | 0.241 | 0.437 |
| 方法2-6 | 0.313 | 0.320 | 0.350 | 0.408 | 0.492 | 0.307 | 0.302 | 0.320 | 0.307 | 0.538 | 0.350 | 0.261 | 0.239 | 0.435 |
| 方法3-1 | 0.406 | 0.399 | 0.417 | 0.481 | 0.581 | 0.414 | 0.422 | 0.423 | 0.391 | 0.585 | 0.422 | 0.383 | 0.424 | 0.578 |
| 方法3-2 | 0.403 | 0.398 | 0.419 | 0.488 | 0.576 | 0.407 | 0.416 | 0.420 | 0.377 | 0.578 | 0.417 | 0.369 | 0.409 | 0.571 |
| 方法3-3 | 0.400 | 0.396 | 0.418 | 0.487 | 0.578 | 0.407 | 0.416 | 0.419 | 0.377 | 0.578 | 0.418 | 0.372 | 0.410 | 0.573 |
| 方法3-4 | 0.344 | 0.347 | 0.372 | 0.428 | 0.509 | 0.334 | 0.332 | 0.355 | 0.332 | 0.552 | 0.393 | 0.308 | 0.291 | 0.478 |
| 方法3-5 | 0.321 | 0.325 | 0.354 | 0.413 | 0.496 | 0.312 | 0.308 | 0.329 | 0.315 | 0.544 | 0.358 | 0.267 | 0.245 | 0.442 |
| 方法3-6 | 0.314 | 0.320 | 0.350 | 0.408 | 0.492 | 0.307 | 0.302 | 0.321 | 0.308 | 0.539 | 0.351 | 0.262 | 0.240 | 0.436 |
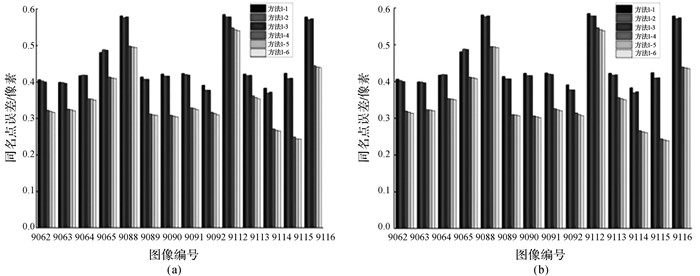
|
| 图 4 同名点误差柱状图 Fig. 4 The error of corresponding points after calibration |
表 4-表 6和图 5为畸变校正前后共面误差,采用本文方法进行畸变校正后共面误差显著减小,使用分区域畸变校正后,共面误差在0.4像素以内。
| 像素 | ||||||
| 方法 | 方法1-1 | 方法1-2 | 方法1-3 | 方法1-4 | 方法1-5 | 方法1-6 |
| 畸变校正前 | 8.256 | 8.256 | 8.256 | 8.256 | 8.256 | 8.256 |
| 畸变校正后 | 0.441 | 0.435 | 0.435 | 0.343 | 0.341 | 0.338 |
| 像素 | ||||||
| 方法 | 方法2-1 | 方法2-2 | 方法2-3 | 方法2-4 | 方法2-5 | 方法2-6 |
| 畸变校正前 | 8.235 | 8.235 | 8.235 | 8.235 | 8.235 | 8.235 |
| 畸变校正后 | 0.438 | 0.435 | 0.435 | 0.341 | 0.338 | 0.336 |
| 像素 | ||||||
| 方法 | 方法3-1 | 方法3-2 | 方法3-3 | 方法3-4 | 方法3-5 | 方法3-6 |
| 畸变校正前 | 8.247 | 8.247 | 8.247 | 8.247 | 8.247 | 8.247 |
| 畸变校正后 | 0.441 | 0.435 | 0.434 | 0.368 | 0.342 | 0.337 |
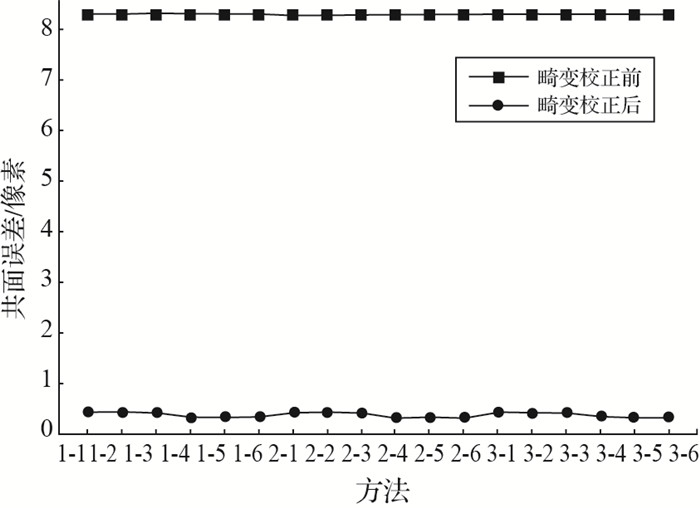
|
| 图 5 共面误差比较 Fig. 5 Error of coplanarity constraint |
为了进一步验证本文方法对普通数码相机的标定精度,使用数据2中10幅图像进行了试验,试验结果如表 7所示。从试验结果可以看出,该方法对普通数码相机标定精度也很高。
| 方法 | 焦距/像素 | 像主点/像素 | 畸变系数 | 畸变量/像素 | 共面误差 /像素 |
|||||||||
| f | cx | cy | kx1(k1) | kx2(k2) | ky1 | ky2 | δx | δy | MSE | |||||
| 初始值1 | 5 468.0 | 2 807.5 | 1 871.5 | |||||||||||
| 方法1-1 | 5 457.2 | 2 768.3 | 1 860.7 | |||||||||||
| 方法1-2 | 5 460.6 | 2 768.4 | 1 860.5 | 2.48E-09 | -1.66E-16 | - | - | 18.1 | 12.0 | 1.012 | ||||
| 方法1-3 | 5 462.8 | 2 768.6 | 1 860.8 | 2.52E-09 | -1.75E-16 | 2.21E-09 | -1.41E-16 | 15.9 | 12.4 | 0.891 | ||||
| 方法1-4 | 16.3 | 12.8 | 0.612 | |||||||||||
| 方法1-5 | 16.8 | 12.7 | 0.548 | |||||||||||
3 结论
本文提出了基于大比例尺航空影像利用共面约束的相机自检校方法。与传统方法相比,该方法操作简单,精度较高,能真实反映航空摄影测量时相机参数。通过对高分辨率大尺寸航空影像进行区域划分解算相机畸变量,进一步提高了解算精度。通过实际图像运算结果可以看出,畸变校正后同名点匹配精度有了显著提高,共面误差在0.4像素以内,该方法已应用于大规模航空影像拼接,进行三维重建。
| [1] | 支健辉, 董新民, 孔星炜, 等. 相机标定的外界影响因素分析[J]. 应用光学, 2014, 35(2): 286–291. ZHI Jianhui, DONG Xinmin, KONG Xingwei, et al. Analysis of External Influence Factors in Camera Calibration[J]. Journal of Applied Optics, 2014, 35(2): 286–291. |
| [2] | SUN Wei, COOPERSTOCK J R. An Empirical Evaluation of Factors Influencing Camera Calibration Accuracy Using Three Publicly Available Techniques[J]. Machine Vision and Applications, 2006, 17(1): 51–67. DOI:10.1007/s00138-006-0014-6 |
| [3] | LIN J Y, CHIO S H. The Accuracy Influence of Different Camera Calibration Conditions to Bundle Adjsutment of Closerange Images[C]//Proceedings of the 33rd Asian Conference on Remote Sensing 2012. Pattaya, Thailand:Asian Association on Remote Sensing, 2012:1672-1681. |
| [4] | WANG J H, WU Y P, YANG Z. Investigation of Factors Influencing Calibration Accuracy of Camera[J]. Advanced Materials Research, 2013, 712-715: 2331–2335. DOI:10.4028/www.scientific.net/AMR.712-715 |
| [5] | HUO Ju, YANG Ning, YANG Ming, et al. An On-line Calibration Method for Camera with Large FOV Based on Prior Information[J]. Optik-International Journal for Light and Electron Optics, 2015, 126(15-16): 1394–1399. DOI:10.1016/j.ijleo.2015.04.024 |
| [6] | 袁枫, 张继贤, 齐维君, 等. 非量测数字相机实验室几何标定[J]. 测绘学报, 2016, 45(5): 601–607. YUAN Feng, ZHANG Jixian, QI Weijun, et al. Laboratory Geometric Calibration of Non-metric Digital Camera[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 601–607. DOI:10.11947/j.AGCS.2016.20140539 |
| [7] | SZELISKI R. Computer Vision:Algorithms and Applications[M]. London: Springer, 2011. |
| [8] | 曹良中, 杨辽, 阚培涛, 等. 地面检校场的非量测型数码相机检校[J]. 测绘科学, 2015, 40(2): 132–137. CAO Liangzhong, YANG Liao, KAN Peitao, et al. Calibration of Non-metric Digital Camera Based on Calibration Field[J]. Science of Surveying and Mapping, 2015, 40(2): 132–137. |
| [9] | ZHANG Zhengyou.Flexible Camera Calibration by Viewing a Plane from Unknown Orientations[C]//Proceedings of the Seventh IEEE International Conference on Computer Vision. Kerkyra:IEEE, 1999, 1:666-673. |
| [10] | SUN Xiangyang, DUAN Jie. Design of Multi-parameter Target Used in Calibration of High Precision CCD Camera[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(2): 548–552. DOI:10.1016/j.ijleo.2015.10.109 |
| [11] | 徐潺, 黄东兆, 杨天龙, 等. 基于平面靶标的相机内部参数标定精度分析[J]. 湖南科技大学学报(自然科学版), 2015, 30(1): 41–46. XU Chan, HUANG Dongzhao, YANG Tianlong, et al. Camera Internal-parameters Calibration of Accuracy of Analysis Based on Planar Target[J]. Journal of Hunan University of Science & Technology (Natural Science Edition), 2015, 30(1): 41–46. |
| [12] | JIA Zhenyuan, YANG Jinghao, LIU Wei, et al. Improved Camera Calibration Method Based on Perpendicularity Compensation for Binocular Stereo Vision Measurement System[J]. Optics Express, 2015, 23(12): 15205–15223. DOI:10.1364/OE.23.015205 |
| [13] | HAMID N A, AHMAD A.Calibration of High Resolution Digital Camera Based on Different Photogrammetric Methods[C]//Proceedings of the 8th International Symposium of the Digital Earth. Kuching, Sarawak, Malaysia:IOP Publishing, 2014:012030. |
| [14] | 郑顺义, 黄荣永, 郭宝云, 等. 附约束条件的立体相机标定方法[J]. 测绘学报, 2012, 41(6): 877–885. ZHENG Shunyi, HUANG Rongyong, GUO Baoyun, et al. Stereo-camera Calibration with Restrictive Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 877–885. |
| [15] | 李畅. 利用灭点进行相机检校与定姿的充要条件及其不确定性分析[J]. 测绘学报, 2012, 41(6): 851–856. LI Chang. The Necessary and Sufficient Condition of Camera Calibration and Attitude Determination Based on Vanishing Points with Their Uncertainty Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 851–856. |
| [16] | 李晓明, 郑珂银. 图像对应点选择对摄像机自标定精度的影响[J]. 山西大学学报(自然科学版), 2014, 37(3): 365–370. LI Xiaoming, ZHENG Keyin. Influences on Self-calibration Precision with Different Corresponding Points[J]. Journal of Shanxi University (Natural Science Edition), 2014, 37(3): 365–370. |
| [17] | 李晓明, 姚剑, 张继福. 摄像机畸变模型的比较与选择[J]. 计算机辅助设计与图形学学报, 2015, 27(5): 824–831. LI Xiaoming, YAO Jian, ZHANG Jifu. Comparison and Selection of Camera Models with Lens Distortion[J]. Journal of Computer-aided Design & Computer Graphics, 2015, 27(5): 824–831. |
| [18] | WEI Guoqing, MA Songde. Implicit and Explicit Camera Calibration:Theory and Experiments[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(5): 469–480. DOI:10.1109/34.291450 |
| [19] | HANNING T. A Least Squares Solution for Camera Distortion Parameters[J]. Journal of Mathematical Imaging and Vision, 2013, 45(2): 138–147. DOI:10.1007/s10851-012-0350-2 |
| [20] | 杨晟, 李学军, 朱诗兵. 遥感影像匹配中的反定位误匹配剔除算法[J]. 武汉大学学报(信息科学版), 2013, 38(9): 1083–1087. YANG Sheng, LI Xuejun, ZHU Shibing. The Reverse Positioning Refining Algorithm for Auto-matching of the Remote Sensing Images[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9): 1083–1087. |
| [21] | 杨阿华, 李学军, 魏勇, 等. 基于室外检校场的航空数码相机检校方法[J]. 装备学院学报, 2014, 25(3): 77–82. YANG Ahua, LI Xuejun, WEI Yong, et al. Aerial Digital Camera Calibration Approach Based on Outdoor Calibration Yard[J]. Journal of Equipment Academy, 2014, 25(3): 77–82. |
| [22] | 韩龙, 汪增福. 基于几何约束的高精度特征点检测和相机标定[J]. 中国科学技术大学学报, 2008, 38(10): 1211–1217. HAN Long, WANG Zengfu. High Precision Feature Detection and Camera Calibration Based on Geometrical Constraint[J]. Journal of University of Science and Technology of China, 2008, 38(10): 1211–1217. |
| [23] | 尹洪涛, 刘成, 李一兵, 等. 相机标定误差因素分析[J]. 信息通信, 2012(1): 28–30. YIN Hongtao, LIU Cheng, LI Yibing, et al. Analysis of Factors on the Error of the Camera Calibration[J]. Informotion & Communications, 2012(1): 28–30. |
| [24] | 詹总谦, 张祖勋, 张剑清. 基于LCD的相机标定精度及其误差分析[J]. 武汉大学学报(信息科学版), 2008, 33(11): 1142–1145. ZHAN Zongqian, ZHANG Zuxun, ZHANG Jianqing. Precision and Error Analysis of LCD-based Camera Calibration Method[J]. Geomatics and Information Science of Wuhan University, 2008, 33(11): 1142–1145. |
| [25] | 黄青青, 赵鸿志, 杨健. 环境星宽覆盖特征CCD影像几何定位及误差分析[J]. 武汉大学学报(信息科学版), 2014, 39(12): 1425–1429. HUANG Qingqing, ZHAO Hongzhi, YANG Jian. Geometric Rectification and Error Analysis for HJ-1 CCD Image with Wide Coverage Feature[J]. Geomatics and Information Science of Wuhan University, 2014, 39(12): 1425–1429. |
| [26] | 袁铭, 苏显渝, 刘晓青. 影响摄像机标定精度的因素分析[J]. 光学与光电技术, 2010, 8(4): 18–21. YUAN Ming, SU Xianyu, LIU Xiaoqing. Analysis of Factors on the Precision of the Camera Calibration[J]. Optics & Optoelectronic Technology, 2010, 8(4): 18–21. |
| [27] | SEMENIUTA O. Analysis of Camera Calibration with Respect to Measurement Accuracy[J]. Procedia CIRP, 2016, 41: 765–770. DOI:10.1016/j.procir.2015.12.108 |
| [28] | 李伟, 任超峰. 室内控制场数码相机检校应用于通用航空摄影测量的可行性研究[J]. 测绘工程, 2012, 21(4): 49–52. LI Wei, REN Chaofeng. Research on the Feasibility of Non-metric Digital Camera Calibration in Indoor Control Field Applies to General Aero Photography[J]. Engineering of Surveying and Mapping, 2012, 21(4): 49–52. |


